Устные упражнения в структуре современного урока математики в начальной школе (на арифметическом материале)

Устные упражнения в структуре современного урока математики в начальной школе (на арифметическом материале)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КАЛУЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. К.Э. ЦИОЛКОВСКОГО»

ИНСТИТУТ ПЕДАГОГИКИ

КАФЕДРА ТЕОРИИ И МЕТОДИКИ ДОШКОЛЬНОГО, НАЧАЛЬНОГО И СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ

Дипломная работа

Тема: «Устные упражнения в структуре современного урока математики в начальной школе (на арифметическом материале)»

Дисциплина: Методика обучения математике в начальной школе

Калуга, 2015

Оглавление

Введение

Глава 1. Устные упражнения в структуре современного урока математики в начальной школе

1.1 Урок математики в начальных классах

1.2 Устных упражнениях их роль и место в современном уроке математики      

1.3 Формы и виды устной работы учащихся

Глава 2. Методические аспекты использования устных упражнений при изучении арифметического материала

2.2 Задания на устный счёт в учебниках

2.3 Комплекс заданий для устной работы      

2.4 Приемы повышения эффективности использования устных упражнений

Заключение

Список литературы

Приложение

Введение

Математики как учебному предмету отводиться особая роль. Математика вооружает обучающихся нужными умениями, навыками и знаниями, которые в дальнейшем применяются при изучении других школьных предметов, таких как физика и химия, информатика и другие. Изучение математики требует от обучающихся немалых умственных и волевых усилий, развитого воображения, высокой концентрации внимания. Кроме того, математика формирует и развивает многие качества обучающегося. Например, развивается пространственное и логическое мышление ученика, в целом расширяется кругозор ребенка.

Важнейшая наука - это математика, каждый человек в своей жизни встречается с математикой. В связи с этим, учитель должен формировать и развивать у детей интерес к своему предмету, то есть замотивировать их. Существенной задачей обучения математики младших школьников считается формирование и развитие вычислительных умений и навыков, основа которых - использование вычислительных приемов. Требование современного мира, стремительно развивающегося - это умения быстро вычислять «на ходу». Умения быстро вычислять пригодятся в дальнейшем и при обучении в школе, и в институте, и в жизни.

Педагог (учитель) должен помочь учащимся овладеть базой математических знаний, которые понадобятся им в дальнейшей жизни, в их профессиональной деятельности. Владение устным счётом является неотъемлемой частью нашей жизни (умение рассчитывать стоимость услуг или товаров, подсчёт процентов и т.п.). Я считаю, что познавательный интерес к математике можно развивать при помощи использования разных видов устного счёта или же привлекая обучающихся к подготовке и проведению данного этапа урока или же урока в целом.

Устный счет - это неотъемлемым этапом каждого урока математики и в 1-ом и 9-м и в 11-м классах. На данном этапе возможно решение основной задачи урока- сформировать у школьников навыки выполнения арифметических действия и решение задач с их помощью.

От того, какие задания подобраны педагогом для устных упражнений и в какой последовательности они присутствуют на уроке, существенно зависит достижение целей урока и уровень активности обучающихся. Для того чтобы заинтересовать учащихся, нужно подбирать всевозможные задания и упражнения, которые будут рассчитаны как на «слабых», так и на «сильных» детей. Например, вычислительные задания (арифметические действия с натуральными числами, дробями, решение элементарных уравнений или неравенств), разгадывание ребусов, задания на внимание, геометрические упражнения. [3] Для достижения правильности и беглости устных вычислений в течение всего периода обучения в начальной школе на каждом уроке нужно выделять примерно по 10 минут для проведения упражнений в устных вычислениях.

Устные упражнения должны быть регулярными и одновременно с этим иметь некую последовательность, определенную программой по математике начальной школы.

Важность устных упражнений активизируют мыслительную деятельность обучающихся, но и имеют воспитательную роль в обучении - дисциплинируют детей, развивают такие качества у детей как терпение, учат их ждать отставших товарищей, приходить им на помощь. Устный счёт является связующим элементом между этапами урока и может переключить ребенка с одного вида деятельности на другую, подготовить их к изучению новой темы, кроме того в устный счет могут включаться задание на повторение или обобщение изученного материала.

Прививая интерес к устным упражнениям, педагог помогать обучающимся активно действовать с учебным материалом, побуждать у них стремление улучшать способы вычислений и решения задач, менее рациональные заменять более экономичными. А это является важнейшим условием сознательного усвоения материала. Направленность мыслительной деятельности на поиск рациональных путей решения задачи подтверждает вариативность мышления.

Цель моего дипломного проекта - определить возможность использования устных упражнений на уроках математики в начальной школе, с целью эффективности вычислительного навыка.

Объектом исследования является урок математики в начальной школе. В качестве предмета исследования выступает особенность организации устного счета на уроках математики в начальной школе.

Исходя из вышепоставленной цели, были поставлены следующие задачи:

Установить особенности проведения урока математики в начальной школе;

Провести отбор и систематизацию учебно-познавательные задачи для устных вычислений;

Обобщение психолого-педагогических и дидактический условий, которые обеспечивают процесс формирования и развития навыков устного вычисления.

Изучение форм и методов проведения уроков, при помощи которых возможно формирование устных навыков вычисления

При работе над дипломным проектом использовались такие методы исследования как:

) теоретический анализ;

) анализ и систематизация материалов психолого-педагогической и методической литературы.

Глава 1. Устные упражнения в структуре современного урока математики в начальной школе

.1 Урок математики в начальных классах

Урок - это важнейшее звено процесса обучения, где реализуются принципы и методы обучения, разрабатываемые методикой. На уроке обучающиеся усваивают новые знания, приобретают навыки практического применения.

Урок математики в начальной школе обладает своими особенностями. Они в первую очередь связаны с особенностями и принципами построения начального курса математики. В начальном курсе математики одновременное изучение на уроках арифметического, алгебраического и геометрического материала, это оказывает своё влияет на построение хода урока и требует оптимального вы бора и совмещения разных методов обучения (17).

Параллельное изучение вопросов практического и теоретического характера требует от педагога рационального сочетания усвоения знаний с процессом формированием умений и навыков. Учитель на уроке должен формировать у обучающихся некоторые способности, которые в силу возрастных и психологических особенностей детей ещё не развиты в достаточной степени у них.

Помимо обучения детей математики, учитель должен процесс учения совмещать с процессом воспитания детей, а именно с воспитанием у них общеучебных навыков и умений (1).

Требования к уроку делятся на группы: организационные, дидактические, воспитательные. Данные требования могут конкретизироваться в зависимости от целей конкретной темы.

К уроку математики, как к технологическому процессу, предъявляют следующие требования: 1) целенаправленность; 2) организационное и материальное обеспечение урока; 3) психологический аспект урока; 4) определенный ритм и темп работы обучающихся; 5) систематическая последовательность и преемственность учебных операций; 6) завершенность каждого этапа и операций; 7) экономия времени; 8) непрерывный самоконтроль и контроль; 9) восстановление делового равновесия в случае его нарушения; 10) совершенствование и закрепление знаний, умений и навыков; 11) непрерывное совершенствование учебного процесса. (12)

Система разных вариантов взаимодействий между элементами урока, которая возникает в процессе обучения и обеспечивает целенаправленную деятельность, представляет собой структуру урока (5).

Каждому уроку соответствуют свои этапы, следует учитывать, что для всех уроков постоянными этапами является этап организации (организационный инструктаж) и объяснение домашнего задания(4).

Очень многие дети, не услышав объяснения домашнего задания, не смогут его выполнить самостоятельно, они либо обратятся к родителям, либо к товарищам. В связи с этим снизится общая результативность изучения конкретной темы.

Другие этапы урока носят вариативный характер, так как они могут меняться в зависимости от цели урока и задач. К таким этапам относятся этапы:

Изучения нового материала;

Проверка и анализ домашней работы;

Закрепление изученного;

Углубление или расширение знаний.

Существует очень много классификаций уроков, но самая приемлемая на мой взгляд классификация предложенная Махмутовым М.И. Он разделил уроки согласно цели организации. Типы уроков:

Урок изучения нового материала;

Урок совершенствования ЗУН;

Урок обобщения и систематизации;

Комбинированный урок;

Урок контроля и коррекции ЗУН;

Нетрадиционный урок;

Перед тем как выяснить какова структура конкретного урока, надо сформулировать цель, далее определить тип урока, затем выбрать структуру и рассчитать время, затраченное на каждый этап урока. В приложении приведены структуры уроков.

Приведенные (в приложении 1) структуры уроков даны в очень общем виде. На практике только единичные уроки представлены именно такими структурами. На практике структура урока видоизменяется, некоторые этапы заменяются другими. Устная работа учеников может включаться на этап проверки домашнего задания. Например, можно подобрать некоторые задания подобные тем, что были заданы домой и попросить решить их устно, либо прокомментировать ход их решения. На этапе актуализации знаний, тоже возможно включение заданий для устного решения(4).

Конспект современного урока оформляется в виде технологической карты. Перед самой технологической картой записывается «шапка» урока. То есть тема урока, УМК, цели урока, планируемые результаты, используемые средства (ЭОР или ЦОР, средства ИКТ). Сама технологическая карта представляет собой таблицу (таблица 1).

Таблица 1 - Технологическая карта урока

Записывая этап урока - устные упражнения с целью актуализации знаний по теме или с целью проверки домашнего задания и т.д. в графе планируемые результаты записывается, чего хочет достигнуть учитель на данном этапе. Например: предметные УУД - умение выполнять вычисления в уме, умение сравнивать числа или выражения и т.д.; личностные и метапредметные - умение выражать свои мысли, умение слушать других, вступать в споры и вести диалог и т.п.

Вывод: Современный урок - это сложный педагогический процесс, это важнейшее звено процесса обучения, в котором реализуются принципы и методы обучения, разрабатываемые методикой.

Урок математики в начальной школе в первую очередь связаны с особенностями и принципами построения начального курса математики. В начальном курсе математики одновременное изучение на уроках арифметического, алгебраического и геометрического материала, это оказывает своё влияет на построение хода урока и требует оптимального вы бора и совмещения разных методов обучения (17).

Помимо обучения детей математики, учитель должен процесс учения совмещать с процессом воспитания детей, а именно с воспитанием у них общеучебных навыков и умений (1).

К уроку математики, как к технологическому процессу, предъявляют такие требования как: целенаправленность; организационное и материальное обеспечение урока; психологический аспект урока и многие другие. (12)

Самая приемлемая, на мой взгляд классификация предложенная Махмутовым М.И.Типы уроков:

Урок изучения нового материала;

Урок совершенствования ЗУН;

Урок обобщения и систематизации;

Комбинированный урок;

Урок контроля и коррекции ЗУН;

Нетрадиционный урок;

В приложении 1представлены структуры уроков в очень общем виде. На практике только единичные уроки представлены именно такими структурами.

1.2 Устных упражнениях их роль и место в современном уроке математики

Упражнения - это система заданий, направленная на общее (математическое) развитие обучающихся и на развитие каких-то навыков. Устные упражнения - это специально подобранный комплекс упражнений, которые учащиеся должны выполнить в уме и представить учителю только ответ, при этом нельзя использовать черновики, калькуляторы и т.п(20).

Устные упражнения - это те упражнения, решение которых возможно производить в уме. Основное их преимущество перед другими видами вычислений состоит в большой экономии времени, затрачиваемого на вычисления. Устные упражнения, обладают особенностью вызывать высокое напряжение мышления, большую сосредоточенность внимания. Эта напряженная мыслительная деятельность может быть использована с большим эффектом для формирования у учащихся прочных и глубоких математических знаний. Для этого разрабатывается система устных вычислительных упражнений - задач, каждая из которых имеет определенное назначение: или подготовить учащегося к восприятию вновь вводимого понятия, или способствовать выявлению свойств понятия и их доказательству, или побудить учащегося к творческому решению возникшей проблемы (14).

Устная работа на уроках математики в начальной школе, а особенно в первом классе, имеет большое значение - это и беседы педагога с классом и с конкретными, дети учатся проводить рассуждения при выполнении определенных заданий и другое.

Раньше устные упражнения сводились к обычным вычислениям, в результате за ними закрепилось название «устный счёт». Устный счёт сохраняется до сих пор, несмотря на то, что изменилось содержание программы, система устных упражнений(12). Введен алгебраический и геометрический материал, уделяется большое внимание свойствам действий над числами и величинами и многим другим вопросам. Кравченко В.С. утверждает, что происходит некоторая путаница при использовании словосочетания «устный счёт», кто-то использует данный термин в его прямом смысле, кот-то нет. Поэтому, целесообразно использовать термин устные упражнения, а не устный счет. (10)

По словам Зайцева О.П. необходимость и важность устных заданий доказывать не надо, об этом он рассказывает в своей статье «Роль устного счета в формировании вычислительных навыков и развития личности ребенка». В формировании и совершенствовании знаний по нумерации, в развитии личностных качеств обучающегося, большое значение имеют устные упражнения. Создав определенную систему устных упражнений, возможно, успешное повторение ранее изученного материала и даёт учащимся шанс усвоить знания и применять их автоматически. Устные задания находятся в методической взаимосвязи с темой урока и обладают проблемным характером. (5)

В течение 4-х лет необходимо на каждом уроке отводить в среднем по 7 минут, для работы с устными заданиями, таким образом можно будет добиться от учащихся правильного и быстрого решения устных заданий.

Устные задания проводят в вопросно-ответной форме, при этом все дети выполняют одновременно одни и те же задания.

При выполнении устной работы у ребенка активизируется мыслительная деятельность, развивается память и внимание, речь, формируются и развиваются способности восприятия сказанного на слух, быстрота реакции (22).

Процесс овладения навыками устных вычислений обладает значительным образовательным, практическим и воспитательным значением.

Наилучшему усвоению приёмов письменных вычислении помогают устные упражнения и вычисления. Практическая значимость устных вычислений заключается ы том, что грамотность, правильность и скорость таких вычислений необходима в повседневной жизни. Устные упражнения содействуют развитию мышления школьников, развитию их сообразительности, наблюдательности и математической зоркости(24).

Основная цель устных вычислений - это формирование и развитие вычислительных навыков или навыков быстрого счёта. Устные упражнения подбираются педагогом либо из специализированных сборников или журналов, либо составляются им самостоятельно. Устные упражнения должны отвечать целям урока и его теме, способствовать усвоению учебного материала на конкретном уроке или усвоению ранее изученного материала(25).

Устные упражнения и устный счёт в том числе не надо проводить на последних этапах урока, так как учащиеся уже утомлены, а устные упражнения требуют от детей большого напряжения, мышления, памяти и внимания. Число заданий должно быть таким, что бы и дети не утомились при их решении и не тратили слишком много времени от всего урока (3).

В зависимости от общей цели урока которой стремится достичь учитель могут быть различные цели и задачи при использовании устных заданий на уроках математики.

Целью этапа урока, на котором решаются устные задания можно сформулировать следующим образом:

) как элемент достижения поставленных целей урока. Например, на уроке поставлена цель научиться складывать числа в пределах ста. Учитель объяснил материал, далее следует решение заданий (коллективное), а в конце урока может быть выделен отдельный этап, цель которого проверить как учащиеся могут выполнять сложение чисел в пределах сотни в уме(7). Таким образом, устная работа выступает как один из элементов достижения цели урока.

) совершенствование вычислительных навыков. Пример, на одном из первых этапов урока предлагается работа с рядом устных упражнений, которые направлены на отработку вычислительных навыков (умножение чисел или деление, сложение или вычитание и т.д.).

) развитие или совершенствование математической речи и культуры. Тут подразумевается использование упражнений, которые требуют рассуждений на чисто математическом языке, оперируя математическими терминами, например, такими как сумма и разность, периметр или площадь и т.п.

) способность систематизировать и обобщать, а также переносить ранее приобретенные знания в новую ситуацию. Это могут быть упражнения на сложение и вычитание двухзначных чисел, среди примеров один пример с трехзначными числами, таким образом дети могут, во-первых, повторить материал сложение двухзначных чисел, а затем его перенести на действия с трехзначными числами. (7)

Задачи этапа урока, на котором работают с устными заданиями могут быть следующими:

Воспроизводство и корректировка конкретных знаний, умений и навыков обучающихся, нужных для их дальнейшей самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя.

Контроль педагога за состоянием знаний обучающихся.

Психологическая подготовка детей к восприятию нового материала.

Повышение познавательного интереса.

Список требований, которые должны выполняться на этапе устных вычислений:

Подбор заданий процесс целенаправленный, а не случайный;

Разнообразие в заданиях. Не должно быть слишком простых заданий и заданий требующих трудных вычислений;

Заранее подготовить текст упражнения, рисунок или чертёж;

В устной работе принимают участие все обучающиеся;

Заранее определены критерии оценивания ответов;

Современный урок математики сложный педагогический процесс со своей структурой. Устные упражнения в том числе и устные вычисления являются одним из этапов всего урока, имеющего свои цели и задачи. Устные упражнения как этап урока своей целью имеют систематизацию и обобщение знаний по какому-либо материалу, это способ активизации деятельности учащихся.

Вывод: Устные упражнения - это те упражнения, решение которых возможно производить в уме. Основное их преимущество перед другими видами вычислений состоит в большой экономии времени, затрачиваемого на вычисления. Устные упражнения, обладают особенностью вызывать высокое напряжение мышления, большую сосредоточенность внимания. (14).

При выполнении устной работы у ребенка активизируется мыслительная деятельность, развивается память и внимание, речь, формируются и развиваются способности восприятия сказанного на слух, быстрота реакции (22). Устные упражнения содействуют развитию мышления школьников, развитию их сообразительности, наблюдательности и математической зоркости(24).

Основная цель устных вычислений - это формирование и развитие вычислительных навыков или навыков быстрого счёта. Устные упражнения подбираются педагогом либо из специализированных сборников или журналов, либо составляются им самостоятельно. Устные упражнения должны отвечать целям урока и его теме, способствовать усвоению учебного материала на конкретном уроке или усвоению ранее изученного материала(25).

Устные упражнения в том числе и устные вычисления являются одним из этапов всего урока, имеющего свои цели и задачи. Устные упражнения как этап урока своей целью имеют систематизацию и обобщение знаний по какому-либо материалу, это способ активизации деятельности учащихся.

1.3 Формы и виды устной работы учащихся

Формы устного счёта:

Упражнения для устного счёта должны быть такими, что бы они с лёгкостью воспринимались детьми либо на слух, либо зрительно или и то и другое.

Самой подходящей, в особенности для детей 7-11 лет является игровая форма устного счёта, при этом необходимо жать возможность отвечать либо по готовности, либо по желанию. В данном случае психологическая нагрузка будет сводиться к минимуму, будет сформирована благоприятная рабочая атмосфера. Недостатком такой работы является то, что в основном работают только 5-10 человек из класса 9 из 20) и это в основном «сильные» учащиеся. А те учащиеся, которым нужен данный вид тренинга, отмалчиваются и с любопытством наблюдают за работой одноклассников и всего лишь. Задача учителя, подобрать задания так чтобы в работу был включен весь класс. Для этого можно применять на уроке при устном счёте задания с вариантами ответов или с готовыми решениями, в этом случае ребенку необходимо будет выбрать только ответ(26). Психологи утверждают, что в подобной ситуации сознание ребенка не ущемлено, это связано с тем, что ученик видя варианты решения, которые предложены педагогом, он ищет ошибки других, а не совершает своих(32).

Устный счёт следует использовать на первых этапах урока, если педагогу удалось правильно организовать этот этап урока, то и весь урок будет организован с математической точки зрения. Усвоение знаний, умений и навыков зависит от содержания заданий и от их числа.

Любой педагог старается сделать, так что бы ученики выполнили как можно больше разнообразных упражнений и заданий в течение всего урока. Творческий педагог может найти для себя и своих учеников оптимальный вариант урока, то ест определить дозировку устной работы, при этом самостоятельно составить варианты упражнений, отталкиваясь от общей подготовки класса.

Дети очень любят устные упражнения и задания, так как при грамотном руководстве со стороны учителя, одни ученики могут проявить инициативу, а другие могут оказать помощь товарищам или получить её от педагога. Не стоит забывать, что устные задания способствуют развитию грамотной математической речи и в целом развивают коммуникативные компетенции учащихся. Навыки устных вычислений формируются и развиваются в результате выполнения всевозможных задании.

Виды устных вычислений:

Нахождение значения математических выражений

Учащимся предлагаются математические выражения в какой-либо форме, нужно найти значение выражения. Подобные задания имеют разные вариации. Можно предлагать числовые математические выражения и буквенные, в этом случае буквам (переменным) даются числовые значения, и находится значение всего выражения. Главная цель подобных заданий - сформировать и развить у детей, твердые навыки вычисления, которые в свою очередь позволят легко усвоить вопросы теории арифметических действий.

Пример:

найти разность чисел 50 и 14; 200 и 8.

Найти значение выражения А-В, если А=200, В=8.

Выражения могут предлагаться детям в различной словесной форме.

Пример:

из двухсот вычесть восемь;

Двести минус восемь;

Уменьшаемое двести, вычитаемое девять, найдите разность;

Найдите разность чисел двести и восемь;

Уменьшите двести на восемь.

Такие формулировки могут использоваться не только учителем, но и учащимися.

Можно использовать выражения, включающие одно или два действия. При этом действия могут быть одной ступени или разных ступеней.

Пример:

-23+14;

:7-5;

- 8:4 и т.д.

Выражения могут содержать скобки.

Пример:

(200-150):10;

-60:15.

Подобные выражения могут быть даны в словесной форме.

Например,

из ста вычесть частное чисел шестидесяти и пятнадцати;

уменьшаемое сто, вычитаемое выражено частным шестидесяти и пятнадцати.

Выражения могут задаваться числами однозначными, двухзначными и трёхзначными и т.д., с натуральными числами или с дробями, с величинами.

Пример:

С однозначными числами (9-5);

С двузначными числами (65-15 или 82-16);

С трехзначными (520- 310 или 270+150) и т.д.;

С натуральными (900 - 15);

С дробями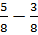

С величинами (3 дм - 2 см). В подобных выражениях вычисления производятся с числами меньшими 100.

Возможно использования таких выражений как 5200 - 3100 и др.. в этом случае вычисления сводятся к 52-31, а значит такое задания уместны на этапах устного счёта. (4)

Выражения могут быть заданы в табличном виде (таблица 2).

Таблица 2 - Упражнение на устный счет в табличном виде

Сравнение математических выражений.

Подобные упражнения также вариативны. Например, заданы два выражения, необходимо выяснить, равны ли их значения, если нет, то какое из них меньше, какое больше. Второй вариант - в задании дан знак отношения между двумя выражениями, одно выражение задано, а другое выражение необходимо дополнить или составить. Основная задача подобных заданий - способствовать процессу усвоения теоретических знаний об арифметических действиях и их свойствах.

Такие задания также, как и прошлые вариативны. Например, могут быть заданы два выражения, при этом надо поставить между ними знак равенств или больше, или меньше.

Пример:

+3*3-5 и 21+ 4*7+4;

*2 и 13*5

-2 и 13-5

Вместо «и» поставить знак <, >, =.

В некоторых выражениях изначально может быть задан знак неравенства и задано одно выражение, второе выражение необходимо дополнить, что бы получить верное равенство или неравенство. Например: 9*(11+7) = 6*…

В подобные задания могут включаться одно-, двух-, трехзначные числа, величины, дроби и т.д. В выражениях могут быть различные действия.

Как было сказано выше, главная цель упражнений - способствовать усвоению теоретических знаний об арифметических действиях и их свойствах, о равенствах, о неравенствах. Кроме того они помогают выработке вычислительных навыков.

Третий вид заданий: решение уравнений.

Уравнения должным быть самыми элементарными и чуть сложнее самых простых (Х+4=25; 11*Х-5=61).

Предлагать уравнения можно в разных формах.

Например:

решить уравнение - 28:Х=7

К какому числу надо прибавить 17 чтобы получить 65;

Определите чему равно неизвестное число: 65 - Х= 65-41;

Я задумала число, умножила его на 3 и получил 51. Какое число я задумала?

Решение задач

При устном счете можно использовать простые задачи или составные. Подобные задания используются с целью выработки умения решать задачи, способствовать усвоению теоретического материала и отработки вычислительных навыков. Учитель должен находить разные виды работы над задачами.

Так как мышление младших школьников в основном опирается на образы, то для них характерно формирование геометрических знаний на уровне представлений. Основная задача при обучении младших школьников - это заложение той базы, которая в дальнейшем понадобиться при изучении геометрии в среднем и старшем звене. Ребята должны познакомиться с такими понятиями как длина, площадь и объем. Научиться оперировать данными понятиями, кроме того дети должны научиться пользоваться линейкой и циркулем. Геометрия способствует развитию логического мышления и пространственного воображения школьников.

Логические задания

Упражнения и задания на логику помогут овладеть такими понятиями как слева, справа, ниже или выше, шире, раньше, дальше и т.п. Важная роль отводиться уровню развития познавательных процессов, таких как внимание и восприятие, воображение и наблюдение, мышление и память.

Кроме того, выделяют следующие виды устных заданий (упражнений):

. Слуховые упражнения. В этом случае учащийся воспринимает числа на слух, при этом ничего не записывает и никакими справочниками и пособиям не пользуется. Задание может читаться учеником или учителем, либо можно включить магнитофонную запись. При восприятии упражнения на слух большая нагрузка приходится на память, из-за этого обучающиеся очень быстро утомляются. Но подобные задания полезны, они развивают слуховую память.

. Зрительные упражнения. Ученики воспринимают числа зрением, в этом случае возможно использование разных наглядных пособий (таблицы, плакаты, записи на доске, счеты, диапозитивы и т.д. В этом случае запись задания облегчает вычисления, так как не надо запоминать числа. В некоторых случаях без записи трудно иногда даже невозможно выполнить упражнение. Например, надо выполнить действие с величинами, выраженными в единицах двух наименований, заполнить таблицу или выполнить действия при сравнении выражений.

. Зрительно - слуховые упражнения или комбинированные. Числа воспринимаются на слух и зрением. (3)

При работе с детьми можно использовать:

обратную связь (показывать ответы с помощью карточек).

задания по вариантам (таким образом обеспечивается самостоятельность)

упражнения в форме игры (например, молчанка, продолжи цепочку, стук-стук или хлопки).

Упражнения для устного счёта по форме разделяются на упражнения воспринимающиеся либо на слух, либо зрительно либо и то и другое.

Устный счёт следует использовать на первых этапах урока, если педагогу удалось правильно организовать этот этап урока, то и весь урок будет организован с математической точки зрения. (36)

К видам устных упражнений относятся - упражнения на нахождение значения математических выражений; упражнения на сравнение математических выражений, а также решение задач и логические задания.

Устные упражнения очень важный этап каждого урока. В зависимости от видов устных упражнений можно достичь различных целей. Устные упражнения представляют собой способ, с помощью которого учитель может контролировать процесс усвоения детьми определенных знаний. Используя устные упражнения, появляется возможность натренировать обучающихся решать некоторые задания. В процессе работы развиваются коммуникативные умения школьников, они учатся слушать друг друга, высказывать свои точки зрения и т.д.

Глава 2. Методические аспекты использования устных упражнений при изучении арифметического материала

.1 Методика обучения арифметическим действиям и формирование вычислительных навыков

Изначально школьников обучают сложению и вычитанию в пределах десяти. С этими основными арифметическими действиями детей уже знакомят после изучения числа 2. При изучении каждого из чисел, входящих в первый десяток, изучается вычитание и сложение в пределах конкретного числа, но это не относится к единице. Арифметические действия сложения и вычитания изучаются параллельно друг другу(4).

Обучающихся знакомят со знаками сложения - плюсом (+) и вычитания- минусом (-), знаком равенства - равно (=).

По окончанию изучения данной темы, дети должны овладеть приемами вычисления, обрести прочные вычислительные навыки, заучить результаты сложения и вычитания в пределах десяти, и состав чисел первого десятка, опознавать и показывать компоненты и результаты 2-х арифметических действий и понимать их названия в речи педагога(19).

В результате овладения обучающимися натуральной последовательностью чисел и свойством данного ряда необходимо знакомить и с приемами сложения и вычитания, которые опираются на это свойство натурального ряда чисел. Ребята учатся этим приемам прибавлять и вычитать единицу из числа, иными словами присчитывать и отсчитывать по 1.

Когда обучающиеся научились прибавлять и вычитать по одному, необходимо учить их прибавлять по два.

Когда учащиеся овладели приемами присчитывания, педагог знакомит детей с приемами отсчитывания.

Если приемами присчитывания ребята 1-го класса овладевают довольно быстро, то приемами отсчитывания - намного медленнее.

Трудность заключается в том, что прием отсчитывания базируется на хорошем знании обратного счета, а обратный счет для многих детей 1-го класса труден. Помимо этого, ученики плохо запоминают - сколько нужно отнять, сколько уже отняли, сколько ещё надо отнять(20).

При изучении каждого числа 1-го десятка учащиеся получают представление и о составе данных чисел.

Изначально нужно давать такие упражнения, в которых одно из слагаемых воспринимаются детьми наглядно, а второе они отыскивают по представлению.

При выполнении действий сложения и вычитания в пределах данного числа вводятся решение примеров с отсутствующим компонентом. Его обозначают точками, рамками, знаками вопросов и т.д., например:

[] + 1= 3, 4 +... = 6, ? - 2 = 4. 6 - ? = 2.

Запишем 1-1=0 (отсутствие предметов обозначают цифры 0) Решаются еще примеры, когда разность равна нулю.

Нуль сравнивается с единицей. Определяется, что ноль меньше единицы, единица больше нуля, поэтому ноль должен стоять перед единицей. Но педагог должен помнить, что ноль не относится к натуральным числам.

Следовательно, ряд натуральных чисел должен начинаться с единицы.

Вводить число ноль в качестве вычитаемого, а затем и слагаемого следует на большом числе упражнений. Смысл действий с нулем будет лучше понять детям, если ноль в качестве вычитаемого и ноль в качестве слагаемого будет вводиться не одновременно. Затем проводятся упражнения на дифференциацию примеров, в которых ноль будет слагаемым и вычитаемым(24).

Полезно показать учащимся и зависимость изменения суммы от применения слагаемых, а также изменения остатка от изменения уменьшаемого.

Учителю 1-го класса надо обращать внимание детей на то, что сумма всегда больше каждого из слагаемых, а остаток всегда меньше уменьшаемых.

Уменьшаемое больше или равно вычитаемому, в противном случае вычитание произвести невозможно.

Уже с 1-го класса дети должны быть приучены к проверке правильности решения примеров.

Далее изучается сложение и вычитание в пределах 20.

Овладение вычислительными приемами сложения и вычитания в пределах 20 основано на хорошем знании сложения и вычитания в пределах 10, знание нумерации и состава чисел в пределах 20.

При изучении действий сложения и вычитания в пределах 20, как и при изучении соответствующих действий в пределах 10, большое значение имеет наглядность и практическая деятельность с пособиями самих учащихся. Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут применение и при изучении арифметических действий(1).

Действия сложения и вычитания целесообразнее изучать параллельно после знакомства с определенным случаем сложения изучать соответствующий случай вычитания сопоставления со сложением.

Во втором классе учащиеся должны знать название компонентов действий сложения и вычитания.

. Приемы сложения и вычитания, основанные на знаниях десятичного состава чисел.

. Сложение и вычитание без перехода через десяток:

а) к двухзначному числу прибавляется однозначное число. Из двухзначного числа вычитается однозначное число;

б) получение суммы 20 и вычитание однозначного числа из 20;

в) вычитание из двухзначного числа двухзначного: 15-12, 20-15.

Решение примеров такого вида можно объяснить разными приемами:

. Разложить уменьшаемое и вычитаемое на десятки и единицы и вычитать десятки из десятков, единицы из единиц.

. Разложить вычитаемое на десяток и единицы. Вычитать из уменьшаемого десятки, а из полученного числа - единицы.

. Сложение и вычитание с переходом через ряд представляет наибольшие трудности для учащихся, с психофизическими нарушениями. вычитание с переходом через десяток тоже требует ряд операций;

уменьшаемое разложить на десяток и единицы

вычитаемое разложить на два числа, одно из которых равно числу уменьшаемого единицы

вычесть единицы

вычесть из десятка оставшееся число единиц

Подготовительная работа должна заключаться в повторении:

а) таблица сложения и вычитания в пределах 10,

б) состава чисел первого десятка (всех возможных вариантов из двух чисел)

в) дополнение чисел до 10

г) разложение двухзначного числа на десятки и единицы

д) вычитание из десяти однозначных чисел

е) рассмотрение случаев вида 17-7, 15-5.

Сложение и вычитание в пределах 100.

При обучении сложению и вычитанию в пределах 100 соблюдаются все требования, которые предъявляются к обучению выполнению действий в пределах 20. Многие трудности, которые испытывают дети при выполнении действий сложения и вычитания в пределах 20, не снимаются и при выполнении этих же действий в пределах 100. Как показывают опыт и специальные исследования, по-прежнему большие затруднения учащиеся испытывают при выполнении действия вычитания. Наибольшее количество ошибок возникает при решении примеров на сложение и вычитание: из единиц вычитаемого единицы уменьшаемого(24).

Последовательность изучения действий сложения и вычитания обусловлено нарастанием ступени трудности при рассмотрении различных случаев. Различают:

. Сложение и вычитание круглых десятков (30 + 20, 50-20, решение основано на знании нумерации круглых десятков)

. Сложение и вычитание без перехода через разряд.

. Сложение двухзначного числа с однозначным числом, когда в сумме получается круглые десятки. Вычитание из круглых десятков однозначного и двухзначного числа.

. Сложение и вычитание с переходом через разряд.

Все действия с примерами 1,2, групп выполняются приемами устных вычислений, то есть вычисления надо начинать с единиц высших разрядов. Запись примеров производится в нумерации, десятичного состава чисел, таблиц сложения и вычитания в пределах 10. Действия сложения и вычитания изучаются параллельно.

Методика изучения табличного умножения и деления.

В практике работы школы в начальных классах получила рассмотрение следующая система изучения действий умножения и деления:

. Введение понятия об умножении как сумм одинаковых слагаемых.

. Составление таблицы умножения числа 2.

. Понятие деления на равные части.

. Составление таблицы деления на 2.

. Составление таблицы умножения в пределах 20.

. Составление таблицы деления в пределах 20.

. Деление по содержанию.

.Сопоставление умножения и деления как взаимообратных действий.

. Изучение умножения в пределах 100. Составление таблиц умножения и деления. Практическое знакомство с переместительным законом умножения.

. Деление с остатками

. Умножение на 1 и единицы. Деление на 1. Ноль как компонент умножения. Ноль как делимое. При обучении умножению и делению перед учителем стоит сложная задача - раскрыть смысл каждого арифметического действия на конкретном материале.

Обучение табличному умножению и делению в пределах 20.

В 2 классе учащиеся получают понятие об умножении и знакомятся с действиями умножения и деления в пределах 20. Лучшему осознанию учащимся смысла действия умножения способствует подготовительная работа: счет равными группами предметов, а также счет по 2, 3, 4, 5, до 20.

После того как учащиеся получают первое представление об умножении, познакомятся со знаком умножения и записью этого действия, можно переходить к изучению таблицы умножения числа 2.

Таблица умножения составляется по постоянному множимому. Этапы знакомства с табличным умножением числа 2:

. Счет предметов от 2 до 20.

. Счет изображений предметов по 2 на рисунках или числовых фигурках и составление примеров на сложение.

. Замена сложения умножением и чтения таблицы умножения.

Обучение табличному умножению в пределах 1000.

В 2 классе повторяется табличное умножение в пределах 20 и заканчивается изучение всего табличного умножения и деления. По-прежнему много внимания уделяется наглядной основе и счета равными группами их числам(20).

После составления таблицы умножения числа 6 учитель должен обратить внимание на то что ответ каждого последующего примера может быть получен из предыдущего путем прибавления 6 (единиц множимого).

Обучение табличному делению в пределах 20.

В начальных классах действие деления рассматривается в зависимости от действия умножения. Только тогда дети хорошо усваивают сущность деления, когда сопоставляется с умножением, устанавливается взаимосвязь между этими двумя действиями. Опыт показывает, что вывод деления из умножения без объявления сущности самого процесса деления оказывается малопонятным.

Деление с остатком вводится после изучения табличного деления. На деление с остатком дети допускают много ошибок. Они либо не записывают, либо прибавляют его к частному, либо получают остаток больше делителя.

Методика изучения арифметических действий в пределах 1000

Все действия в пределах 1000 без перехода через разряд учащиеся выполняют приемами устных вычислений с записью в строчку, а с переходом через разряд - приемами письменных вычислений с записью в столбик.

Важно постепенно нарастание трудности при решении арифметических примеров, каждый последующий уровень в решении примеров должен опираться на знание предыдущих случаев. Непреодолимые трудности для ребенка могут возникнуть при несоблюдении степени трудности решения примеров. Поэтому очень важно соблюдать последовательность в выборе примеров, учитывая их нарастающую степень трудности, и тщательно отрабатывать каждый случай(19).

Сложение и вычитание в пределах 1000.

В изучении действий сложения и вычитания в пределах 1000 можно выделить следующие этапы:

. Сложение и вычитание без перехода через разряд.

сложение и вычитание круглых сотен. Действие производится на основе знаний нумерации, и сводятся по существу к действиям в пределах 10;

сложение и вычитание круглых сотен и единиц, круглых сотен и десятков;

сложение и вычитание круглых десятков, а также круглых сотен десяток;

сложение трехзначных чисел с однозначным числом, двухзначным и трехзначным без перехода через разряд и соответствующие случаи вычитания;

особые случаи сложения и вычитания. К ним относятся случаи, которые вызывают наибольшие трудности и в которых чаще всего допускают ошибки. Учащихся больше всего затрудняют действия с нулем, (ноль находится в середине или в конце)

. Сложение и вычитание с переходом через разряд.

Сложение и вычитание с переходом через разряд - это наиболее трудный материал. Поэтому учащиеся выполняют действия в столбик. Сложение и вычитание в столбик производятся над каждым разрядом в отдельности и сводятся к сложению и вычитанию в пределах 20.

При решении примеров на сложение и вычитании с переходом на разряд соблюдается следующая последовательность:

. Сложение и вычитание с переходом через разряд в одном разряде (единиц или десятков)

. Сложение и вычитание с переходом через разряд в двух разрядах (единиц или десятков)

. Особые случаи сложения и вычитания, когда в сумме или разности получается один или два нуля, когда в уменьшаемом содержится один или два нуля, когда в уменьшаемом содержится единица.

. Вычитание трехзначных, двухзначных и однозначных чисел из 1000.

Умножение и деление в пределах 1000.

Умножение и деление также как сложение и вычитание, могут производиться как устными, так и письменными приемами вычислений, записываться в строчку или в столбик.

. Устное умножение и деление в пределах 1000:

умножение и деление круглых сотен

умножение и деление круглых десятков на однозначное число:

а) рассматриваются случаи умножения и деления круглых десятков, которые сводятся к табличному умножению и делению;

б) рассматриваются случаи, которые сводятся к нетабличному умножению и делению без перехода через разряд.

. Умножение и деление трехзначных чисел на однозначное число без перехода через разряд.

. Умножение десяти и ста, умножение на десять и сто.

. Деление на десять и сто:

письменное умножение и деление в пределах 1000;

умножение и деление на однозначное число с переходом через разряд;

умножение двухзначного числа на однозначное с переходом через разряд в разряде десятков или единиц;

умножение двухзначного числа на однозначное с переходом через разряд в разряде единиц и десятков;

умножение трехзначного числа на однозначное число с переходом через разряд в одном разряде - единиц или десятков;

умножение трехзначного числа на однозначное число с переходом через разряд в двух разрядах - единиц и десятков

особый случай умножения - первый множитель - трехзначное число с нулем на конце или в середине;

умножение двухзначного числа на круглые десятки.

Деление изучается в такой последовательности.

. Число сотен, десятков и единиц делитель без остатка на делитель.

. Число сотен делится на делитель без остатка, а число десятков без остатка на делитель не делится.

. Число сотен не делится без остатка на делитель.

. Число сотен делимого меньше числа единиц делителя, в частном получается двухзначное число.

. Особый случай деления, когда в частном на конце или в середине получается ноль.

. Деление на круглые десятки.

Сложение и вычитание многозначных чисел.

Сложение и вычитание многозначных чисел, кроме случаев, указанных выше, выполняются приемами письменных вычислений. Основой алгоритмов сложения и вычитания чисел любого класса является поразрядное сложение и вычитание.

Умножение и деление многозначных чисел.

Умножение и деление многозначных чисел представляет гораздо больше трудностей, чем сложение и вычитание. Это связано с тем, что ученики не твердо знают таблицу умножения. Даже те учащиеся, которые запоминают таблицу умножения, затруднялись применить её при решении примера с многозначными числами, то есть актуализировать свои знания и использовать их(1).

Трудности возникают и тогда, когда надо единицы высшего разряда перевести в низший разряд, удержать их в памяти. Неумение долгое время сосредоточить внимание на выполнение действия приводит к тому, что учащиеся низшие разряды числа умножают правильно, а при умножении высших разрядов допускают ошибки.

Вывод: Материал курса математики начальной школы изучается постепенно, с течением времени немного усложняясь. Изначально изучают числа, например до 10-ти, и параллельно арифметические операции с пройденными числами (сложение и вычитание). Если с первых уроков математики включить в структуру устные упражнения, то ребятам будет легче усвоить и выучить пройденный материал. Например, устные упражнения на знание таблицы умножения и т.п.

Для начальной школы существует несколько учебников математики, которые могут использоваться образовательными организациями и соответствуют требованиям ФГОС. Это учебники таких авторских коллективов как:

Башмаков М.И. и Нефедова М.Г.;

Демидова Т.Е., Козлова С.А. и Тонких А.П. и др.;

Дорофеев Г.В. и Миракова Т.Н.;

Моро М.И., Волкова С.И. и Степанова С.В.;

Петерсон Л.Г.;

Рудницкая В.Н. и др.;

Муравьева Г.Л. и Урбан М.А.;

Чеботаревская Т.М. и Николаева В.В.

Практически ко всем учебникам есть рабочая тетрадь и электронное приложение (диск). Рабочие тетради и электронные пособия включают ряд заданий, некоторые из которых дублируют задания данные в учебники, а некоторые несколько отличаются от данных в учебнике (35).

Если просмотреть задания в учебниках, то по каждой теме в учебном пособии присутствуют задания, которые можно использовать для устного вычисления. Среди всех заданий можно найти все четыре вида заданий: вычисления, сравнения, уравнения и задачи. В зависимости от способностей конкретного класса можно разделять задания на те, которые выполняются письменно и те которые выполняются устно. Для переключения внимания обучающихся, для смены вида деятельности и для активизации обучающихся целесообразно использовать электронные учебные пособия, то есть диски предлагающиеся к учебникам. В учебниках даны очень интересные для детей задания, которые сопровождаются красочными рисунками. Например: сравнить количество шариков или количество животных и т.п. Задания, в которых необходимо решить уравнения присутствую и обычные уравнения и уравнения, записанные при помощи геометрических фигур или слов.

Примеры заданий, которые могут решаться устно (из тетрадей и учебников Петерсон Л.Г.)

Уравнения (рис.1):

Рис. 1

Задания на сравнения (рис.2):

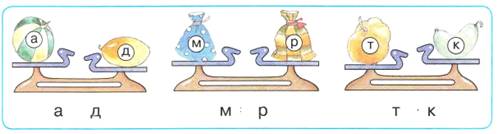
Рис. 2

Устный счёт (рис.3):

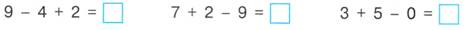
Рис. 3

Задачи (рис.4):

Рис. 4

Следующие четыре задания возможно включить на этап устной работы (рис.5):

Рис. 5

При работе над данными заданиями ученики отрабатывают навыки анализировать информацию, выбирать критерии и основания для классификации или сравнения.

Следующее задание (рис.6):

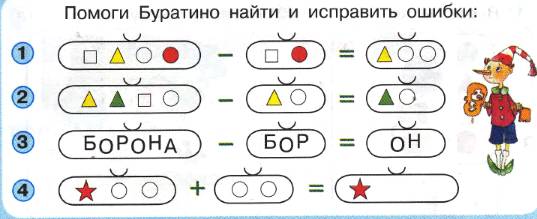
Рис. 6

Данное задание похоже по своему принципу на решение уравнения. При работе над заданием у детей развивается внимательность, логическое мышление.

Рассмотрим более подробно задания для выполнения, устно представленные в учебнике и рабочей тетради для первого класса автора Рудницкая В.Н. и др.

Например, урок 35. Название урока - работаем с числами от 1 до 20.

При работе на этом уроке можно отдельным этапом выделить устную работу класса с целью обобщения и систематизации знаний по теме сложение и вычитание чисел, сравнение чисел. Работа рассчитана на 5-7 минут.

Задания берутся из тетради учебника.

Например, задание на сравнение (из учебника) (рис.7):

Рис. 7

При работе над заданием ученики ещё раз закрепляют умение сравнивать числа в уме. Они учатся строить логические цепочки рассуждений, работая над второй частью задания. Умения работать над такими заданиями очень важны для дальнейшего усвоения детьми тем из теории вероятности и статистики. Анализируя задания дающиеся обучающимся на экзаменах ОГЭ и ЕГЭ, в какой-то степени вторая часть задания схоже с заданием, данным на экзамене. Например, в заданиях 18 ЕГЭ базового уровня задано высказывание, необходимо выяснить, какие из предлагающихся высказываний верны или нет, выполняются или нет. Поэтому я считаю, что устная работа с подобными заданиями начиная с 1-го класса необходима. Постепенно усложняя задания ребята к ним привыкнут и без особого усилия справятся с ними.

Аналогично и второе задание (рис.8):

Рис. 8

Задача на сложение чисел (из рабочей тетради) (рис.9):

Рис. 9

Задание на вычитание и сложение чисел (из рабочей тетради) (рис.10):

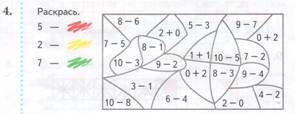
Рис. 10

Эти же примеры заранее выписать на доске или выводятся на слайде презентации, и предлагается детям решить их устно.

А затем дети самостоятельно выполнят задание в тетради и раскрасят фигуры нужным цветом.

На данном уроке также возможно использование мультимедийной презентации. Например, перед каждым учеником ПК, открыта мультимедийная презентация с примерами: 7-1 8-1; 4-2 3+4 и другие. Необходимо расставит знаки <,> или =. Лучше всего разработать два варианта работы. При выполнении работы ученики должны выполнять работу в уме и только расставлять нужные знаки. Учитель, проходя между рядами, проверяет выполненную детьми работу.

Возможно, использовать задания воспринимаемые учениками на слух. Например: Что больше шесть или десять? Пятнадцать или одиннадцать? и т.д. Сколько получиться, если к двум прибавить двенадцать? Если из пятнадцати вычесть девять и т.д.

Рис. 11

Урок 38. Составление и решение задач.

Изначально необходимо провести работу со всем классом. Показать, как составляются задачи, дать детям возможность самим составить задачи. После, можно провести устную работу по составлению задач. Для этого можно использовать 1-3 задачи из рабочей тетради (рис.11).

При работе над 1 и 2 заданиями, каждый ребенок имеет возможность составить свою задачу, задание имеет много решений. У педагога будет возможность спросить достаточно много учеников. Работая над этими заданиями, у учеников формируются способности выражать свои мысли, внимательно слушать друг друга, при необходимости отстаивать свою точку зрения.

На этом же уроке можно показать ребятам часть какого-то мультфильма, это может быть даже мультик «волк и семеро козлят» или любой анимированный мультфильм созданный самим учителем. На определенном моменте показ мультфильма прерывается, и дети должны продолжить рассказ сюжета и составить задачу.

Математика 1 кл. М.И.Башмаков. По теме «равенство и неравенство» подобран ряд рисунков с разными предметами, животными и насекомыми. Суть задания расставить знаки <,>,=. Эти задания можно выполнять устно после знакомства детей с понятиями больше, меньше и равно. Например, каждому ребенку раздаются таблички со знаками больше, меньше и равно. Учитель называет пару картинок, дети смотрят на них и показывают каждый свой вариант ответа. В учебники математики для 1-го класса (Моро, Волкова и др.) по данной теме даны примеры на сравнение с числами, а не с рисунками предметов. Но задания, как мне кажется можно построить аналогичным образом. В учебнике Дорофеева и др. материал темы «сравнения» изложен немного иначе и при работе над упражнениями ребятам надо считать предметы и сравнивать затем полученные значения. Надо уметь выполнять арифметические действия ( сложения и вычитания). В учебнике Петерсона упражнения аналогичны как и в учебнике Башмакова, мне кажется и можно выполнять устно таким же образом как и при работе над учебником Башмакова.

Просмотрев все учебники математики для 1-4-х классов, можно заметить что в учебниках Башмакова и Петерсона по всем темам, и в том числе по темам связанным с арифметическими операциями упражнения в основном даны с картинками, где изображены предметы или животные, сказочные персонажи и т.д. Например, из 4-х яблок вычитают одно и необходимо подсчитать сколько яблок получиться. В учебнике Моро и Дорофеева упражнения в основном с числами, а не с рисунками, там конкретно даны примеры, например: 7-3, 4+2 и т.д.

Вывод: Во всех учебниках математики для начальной школы которые входят в список допущенных учебников, представлено множество различных задач, которые можно использовать в качестве устных упражнений. Мне кажется, что для детей наиболее приемлемы учебники Башмакова и Петерсон, так как в них большое количество наглядного материала, и мне кажется что детям будет легче воспринимать учебный материал. Но с другой стороны, такое изобилие наглядного материала, может вызвать затруднения при дальнейшем изучении математики в 5-м классе.

2.3 Комплекс заданий для устной работы

Далее будут приведены примеры разработанных мною заданий, которые могут быть использованы на уроках математики в начальной школе на этапе устной работы.

Задание 1: Догадайтесь, по какому правилу составлены схемы, вставьте числа в «окошки» (рис.12).

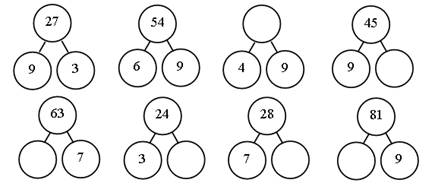
Рис. 12

Это задание может быть дано после изучения детьми всей таблицы умножения. Это может быть урок обобщения и систематизации знаний, либо любой другой урок целью которого будет решение задач и примеров на отработку вычислительных навыков. При подобной работе у каждого ученика на парте лежат картонные таблички с цифрами от 0 до 9. Каждый ребенок поднимает табличку с вариантом ответа. Учитель видит ответы всех детей, кроме того можно попросить кого-то прокомментировать ответ.

Задание 2: Поставьте знаки «+» или «-».

… 40 … 8 = 21   17 … 70 … 2 = 89

… 5 … 30 = 40   31 … 60 … 7 = 98

Задание 3: Сравните значения выражений.

+ 27 400 + 29

+ 163 163 + 829

- 15 100 - 20

Какие знания помогли вам выполнить это задание?

Задание 2 и 3 может быть использовано на уроке обобщения и систематизации знаний по теме «Сравнение чисел».

Как один из вариантов устной работы - дети могут поднимать табличку со знаками (аналогично предыдущему случаю).

Второй вариант - у каждого ребенка пульт, на пульте они нажимают вариант своего ответ, у учителя на компьютере высвечивается список фамилий, номер задания и ответ, который выбрал конкретный ученик. Учитель, моментально оценив ответы детей на мониторе своего компьютера может попросить прокомментировать ответ кого-то из учеников.

Третий вариант - при работе с заданием 3, знак больше - один хлопок, меньше - два хлопка.

Задание 4: За три дня рабочие отремонтировали 24 троллейбуса: в первый день 8 троллейбусов, во второй - 10. Сколько троллейбусов они отремонтировали в третий день?

Задание 5: Вставьте числа в «окошки», чтобы получились верные равенства:

+ 7 +  = 62                 4 + 8 +  = 42

+ 4 +  = 92                 7 + 4 +  = 61

Задание 5 и 4 может выполняться на уроках обобщения и систематизации знаний по теме «Действия с числами». Эти задания направлены на развитие не только вычислительных навыков, но и на развитие математической речи.

Задание 6: Геометрия на спичках.

а) Сколько на чертеже квадратов? Сколько всего многоугольников? Какие они?

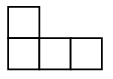
б) Уберите одну палочку так, чтобы осталось 2 квадрата.

в) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите два решения и сравните их.

г) Уберите две палочки так, чтобы остался 1 квадрат. Найдите два решения и сравните их.

Задание 6 может быть использовано на уроках после изучения тем «Геометрические фигуры». Задание направлено на развитие математической речи, на развитие пространственного воображения.

В данном пункте мной были представлены разработки заданий которые можно использовать на уроках математики в начальной школе. Эти задания могут быть использованы при изучении арифметического материала на уроке математики, так как при работе над ними необходимо показать умения выполнять элементарные арифметические действия, сравнивать числа и т.п.

2.4 Приемы повышения эффективности использования устных упражнений

Очень часто на практике можно наблюдать что дети неактивно участвуют в устной работе, для некоторого этого этапа урока проходит не заметно, и они стараются отсидеть молча на уроке, не следя за действиями учителя и одноклассников.

Поэтому целесообразно выбрать пути повышения эффективности применения устных упражнений.

Повысить эффективность использования устных упражнений можно за счёт применения цифровых образовательных ресурсов или средств ИКТ. ЦОР и ИКТ сами по себе представляют для детей интерес, так как современные дети очень любят компьютерные игры и всевозможные приложения. Поэтому некоторым образом компьютерная программа с интересной графикой и определенным звуковым сопровождением может повысить интерес детей к заданиям и как следствие включить большее количество детей в работу.(35)

Применение вспомогательных материалов, например, каких-то карточек или табличек, значков или эмблем, может своеобразным образом отразиться на работе детей. Например, при решении задания требуется выбрать правильный ответ из 4-х предлагающихся. В этом случае возможно каждому ученику раздать по 4 карточки с вариантами ответов (А, Б, В, Г), карточки картонные (не просвечиваются). При такой работе учитель сможет увидеть ответ каждого ребенка и оценить его, ребята сидящее за 2-ой, 3-ей и 4-ой партами не видят ответы одноклассников, сидящих впереди них.

При работе с упражнениями где необходимо выбрать один из двух вариантов ответов, можно использовать такие способы ответа как поднятие правой руки - если верно (или ответ А) и поднятие левой руки - если неверно (ответ Б) и т.п. Возможно даже проведение физкультминуток в таком режиме. Например, если ответ на вопрос под определенной буквой - садимся или подпрыгиваем, наклоняемся в лево или в право и т.п.

Каждый педагог борется за повышение качества образования, применения средств информационных технологий на уроке, в том числе и на уроке математики, в некоторой степени может влиять на повышение качества образования. Одна из новых форм организации образовательного процесса - применение ИКТ. При использовании информационно-коммуникативных технологий подразумеваем реализацию или применение какой-то учебной программы, которая нацелена на самостоятельную работу обучающихся. Компьютер как электронный ассистент, обладает рядом функциональных специфических возможностей, которые способствуют формированию мировоззрения и развитию интеллекта ребенка (1).

Мультимедийные средства и средства ИКТ оказывают психологическое воздействие на учащихся. Например, некоторые учебные программы могут сопровождаться приятным звуковым сопровождением или различными персонажами, которые определенным образом воздействуют на эмоциональный настрой ребенка.(36)

В процессе применения мультимедийных средств реализуются следующие принципы:

Наглядность.

Природосообразности.

Прочности.

Научности

Доступности

Системности

Последовательности

От целей урока и целей конкретного этапа урока зависят формы, в которых используются компьютерные технологии и определяется их место.

Функции могут быть следующие: инструментальные (изготовление наглядных пособий); демонстрирующие (показ готовых демонстрационных программ, слайдов, презентаций и др.); обучающие (тренажеры); контролирующие(35).

Пример: Показ готовых презентаций - это может быть показ сладов презентации на которых показаны задания (устные упражнения).

Тренажеры - это специализировано подготовленные программы, это могут быть и программы для устного счёта, в которых надо на время подсчитать ответ и ввести его в графу ответ.

Контролирующие программы - это могут быть программы, созданные по аналогии с тренажёрами.

В случае, когда ребята работают с тренажерами и контрольными программами, каждый ученик садиться за свой компьютер и работает со своим вариантом задания самостоятельно.

Правильное и рациональное использование возможностей современных информационных технологий в образовательном процессе способствует:

активизации познавательной деятельности, повышению уровня комфортности обучения;

достижению целей обучения при помощи современных электронных учебных материалов, предназначенных для использования на уроках в начальной школе;

снижению дидактических затруднений, развитию навыков самообразования и самоконтроля у младших школьников;

повышению активности и инициативности младших школьников на уроке;

развитию информационного мышления, формирование информационно-коммуникационной компетенции.

Следовательно, внедрение информационных технологий в образовательный процесс начальной школы помогает педагогу дифференцировать процесс обучения, учитывая их индивидуальные особенности, раскрывает возможности творческому учителю расширить способы представления учебной информации, является социально значимым и актуальным(35).

Устные задания весьма ценны в методическом отношении. Они могут использоваться в качестве подготовительной ступени при объяснении нового материала (в соответствии с известным дидактическим принципом «от лёгкого к трудному, от простого к сложному, от известного к неизвестному»), а также при переходе к решению трудных задач. Устные задания вносят разнообразие в преподавание математики, способствуя закреплению знаний и давая возможность быстро проверять эти знания.

Пример физкультминутки цель которого не только отвлечь детей от письменной работы, сменить вид деятельности, но и совместить это с устными упражнениями. Задание: дети встают, на обороте доски записаны примеры на сложение и вычитание в пределах 4-х. Если в результате решения получается 1 - дети один раз подпрыгивают, если 2 - два раза приседают, если три - выполняю три хлопка, если четыре - выполняют четыре наклона вперед, если ноль - садятся на место. Под примерами записано что дети выполняют и в случае какого ответа.

Примеры:

-2 = 3-2= 4-3= 4-1= 2-1= 3-2= 2+1= 1+3= 2+2= 1+1= 3-3=

Следующее задание направлено на оценку уровня усвоения детьми темы сложения и вычитания в пределах 3-х. На парте у каждого ребенка таблички с цифрами 0, 1, 2, 3. Учитель показывает ряд примеров, после прочтения примера учителя ребята должны понять табличку с вариантом ответа. Педагог оценивает каждого учащегося просматривая ответы.

Примеры: 2-1, 3-1, 2-2, 1-1, 1+2, 1+1, 2+1, 3-0, 3-2, 1-1.

Следующее задание аналогично предыдущему, нацелено на проверку усвоения детьми темы прошлого урока, например - вычитание и сложение в пределах 5-ти. У каждого ребенка в руках пульт, который связан с программным обеспечением, установленным на компьютере учителя и интерактивной доске. На доске представлен ряд примеров, дети нажимают на клавишу правильного ответа (число, получающееся в ответе), ответы детей моментально высвечиваются на компьютере у педагога. У учителя есть таблица, в которой представлен список фамилий, номер задания и ответ ребенка.

Учитель выводит на экран по одному примеру, детям на обдумывание ответа дается не более 20 секунд, когда вся работа выполнена, учитель просит прокомментировать отдельные примеры, некоторых учеников.

Примеры: 2+3, 1+4, 4-2, 1-1, 0+2, 4+1, 5-3, 2-0, 3+1 и т.д.

Вывод:

При планировании структуры урока необходимо тщательно продумывать каждый этап урока. Этап устных вычислений - важный этап урока, который требует особой подготовки. При планировании этого этапа необходимо тщательно продумать сами упражнение так чтобы они соответствовали общей цели урока, соответствовали уровню знаний и умений детей. От учителя на данном этапе требуется внимания и умений организовывать работу детей. Стоит продумать, как дети будут отвечать и как ответы будут фиксироваться и т.п.

Использование средств ИКТ при решении устных упражнений способствует привлечению внимания детей к процессу решения заданий. Средства ИКТ позволяют более наглядно и красочно представить материал перед детьми. В связи с этим у детей повышается интерес к выполняемым заданиям, их мыслительная деятельность активизируется. Использование интерактивных упражнений способствует развитию навыков самоконтроля учащихся.

Вывод: мной был рассмотрен вопрос, каким образом возможно использовать средства ИКТ при работе с устными упражнениями. Можно сделать вывод что использование средств ИКТ при решении устных упражнений способствует привлечению внимания детей к процессу решения заданий. Средства ИКТ позволяют более наглядно и красочно представить материал перед детьми. В связи с этим у детей повышается интерес к выполняемым заданиям, их мыслительная деятельность активизируется. Использование интерактивных упражнений способствует развитию навыков самоконтроля учащихся.

В данной главе мной была рассмотрена методика обучения арифметическим действиям и формирование вычислительных навыков, представлены задания, которые можно использовать при устной работе детей на уроке. Также мной били рассмотрены возможности применения средств ИКТ на уроках математики, там же представлены примеры устных упражнений.

Заключение

математика устный упражнение учебник

В моей работе был рассмотрен вопрос «Устные упражнения на уроках математики в начальной школе».

Рассмотрены основные требования к современному уроку и основные типы уроков с их структурой. Определено на каком этапе урока можно использовать устные упражнения.

Устный счет - одна из основных составляющих каждого урока математики. Устные упражнения способствуют формированию и развитию различных УУД. Устные упражнения должны сопровождать каждый урок математики и в начальной школе и в 5-11 классах. Основная цель устных упражнений довести действия детей до автоматизма. Ребенок, закончивший первый класс, должен научиться в уме решать элементарные примеры на сложение и вычитание, на умножение и деление. Помимо предметных УУД при работе с устными упражнениями возможно развитие способностей слышать друг друга, высказывать свои мысли. При решении устных заданий развиваются навыки контроля и самоконтроля. Устные задания можно использовать на многих этапах урока математики, данные задания могут активизировать деятельность детей и способствовать лучшему переключению детей с одного вида деятельности на другой.

Мной была изучена научно-методическая литература по данному вопросу. Также в своей работе я рассмотрела, какие задания из учебника математики, возможно, использовать на уроке в качестве устных заданий. Мной били приведены примеры заданий из учебника по математики для первого класса авторов Петерсон Л.Г. и Рудницкой В.Н..

Сформулируем основные выводы, по рассматриваемому вопросу:

Устные задания можно проводить на уроке в различных формах:

беглый слуховой счет, который можно сопровождать показом карточек-ответов детьми;

зрительный счет, запись в тетради примеров с ответами;

комбинированная форма счета, то есть устные вычисления с последующей записью результатов вычислений;

устное решение задач.

Устные упражнения имеют огромное значение для овладения навыками письменных вычислений.

При выборе приемов устных вычислений нужно опираться на сознательность выбора, а не механическое их применение.

К числу основных приемов устного счета относятся приемы сложения, вычитания, умножения и деления, основанные на представлении числа в виде разрядных единиц и произведении действий, начиная с единиц высшего разряда, а также прием округления компонентов действий.

Контроль за рациональными приемами вычислений, постепенное ознакомление детей с разнообразными упрощениями основных приемов арифметических действий - одно из главных условий правильности обучения устному счету.

Быстрота счета возникает в результате длительных упражнений. Для того чтобы избежать однообразного повторения одних и тех же упражнений, которые порождают скуку на уроках и притупляют интерес к предмету, необходимо прибегать к различным приемам, соответствующим развитию быстроты вычислений, а также проводить надлежащий подбор упражнений.

Мне кажется, мне пригодятся все те знания которые я приобрела в результате написания данного дипломного проекта и я смогу их применить на практике при работе в школе.

Список литературы

1.      Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. М.: Просвещение 2004-335с.

.        Башмаков М.И., Нефедова М.Г. Математика. 1 класс. Учебник в 2 ч. 2011, 128с., 144с.

.        Белошистая А.В. Прием формирования устных вычислительных умений в пределах 100 //Математика №7. - С. 44.

.        Белошистая А.В., Методика обучения математике в начальной школе. 2007.

.        Бурлакова Устный счёт на уроках математики. //Н.ш. 1969 №10

.        Бурлыга А.Я. Интересные приёмы устного счёта. //Н.ш. 1985г. №5

7.      Демидова Т.Е., Козлова С.А., Тонких А.П. и др. Моя математика. Учебник для 1 класса. В 3-х ч. (2005, 224с.) <http://www.alleng.ru/d/math/math697.htm>

.        Дорофеев Г.В., Миракова Т.Н. Математика. 1 класс. В 2 ч. (2011; 128с., 96с.) <http://www.alleng.ru/d/math/math1392.htm>

.        Жикалкина Т.К. Игровые и занимательные задания по математике для 1класса. М.: ”Просвещение” 2000г.

.        Зайцева О.П. Роль устного счёта в формировании вычислительных навыков и в развитии личности ребёнка //Н.ш. 2011г. №1

.        Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. //Н.ш. 1990 №6 с.44-46

.        Иванова Т. Устный счёт. //Н.ш.1999г. с.11-14

.        Истомина Н.Б. Методика обучения математике в начальных классах Изд.Академия, 2011.

.        Истомина Н.Б. Методика обучения математики в начальных классах. Учебное пособие. М.: “Академия”, 2009г. - 288с.

.        Князева С.И. Как провести устный счет //Математика № 5. С. 54

.        Кочурова Е.Э.Математика. 1 класс. Рабочие тетради к учебнику Рудницкой В.Н. и др. - 2011; 48с., 64с.

.        Кравченко В.С. Устные упражнения по математике в 1-3 классе. Пособие для учителя. М.: Просвещение 1979г.

.        Крамских Т.И. Устный счет по литературным произведениям // Математика № 9. С. 77.

.        Курманалина Ш., Методика преподавания математики в начальных классах, 2011

.        Липатникова Н.Г. Роль устных упражнений на уроках математики. //Н.ш. 1998 №2 с.34-38

.        М.В Дубова «Содержание математической компетентности выпускника начальной школы»\НШ плюс до и после,№9,2013,стр34-40.

.        Мезенцева Т.А. Дифференцированный подход в обучении младших школьников на уроках математике // НШ плюс до и после,№3,2013,стр58-61.

.        Моро М.И., Волкова С.И., Степанова С.В.Математика. 1 класс. В 2 ч. (2015; 128с., 112с.) <http://www.alleng.ru/d/math/math669.htm>

.        Моро М.И., Пышкало А.М. методика обучению математики в 1-3 классе. Пособие для учителя. М.: Просвещение 1975г.

.        Муравьева Г.Л., Урбан М.А.Математика. 1 класс. В 2 ч. МИНСК; 2015, 248с.) <http://www.alleng.ru/d/math/math1760.htm>

.        Н.В. Пиликина. Освоение первоклассниками приёмов организации своей деятельности на уроках математики. //НШ плюс до и после №11 С.36

.        Петерсон Л.Г. Математика. 1 класс. Учебник в 3 ч. (2012, 224с.) <http://www.alleng.ru/d/math/math665.htm>

.        Попова Е.В. Устный счет - «изюминка» моих уроков математики // Математика. № 9. С. 76.

.        Рудницкая В.Н. и др. Математика. 1 класс. В 2 ч. 2011; 128с., 144с. <http://www.alleng.ru/d/math/math1342.htm>

.        Т.В Ульяницкая «Развитие логического мышления младших школьников на уроке математики»\НШ плюс до и после,№12,2012,стр43-46.

.        Фаддейчева Т.И. Обучение устным вычислениям // Математика. № 10. С. 66.

.        Фаттахова З.Х. Устный счет с интересом //№7. С. 62.

.        Чеботаревская Т.М., Николаева В.В. Математика. 1 класс. В 2 ч. МИНСК; 2015, 2011)

.        Эрдниев П.М. Обучение математике в начальных классах. М.: Педагогика,2010 г.

.        Wiki.vspu.ru/workroom/ikto/m5/kristina141190/mathematics - икт на уроках математики в начальной школе;

.        Роньшина О.Н.Использование ИКТ на уроках в начальной школе в условиях реализации ФГОС. Сетевое издание «Учитель сегодня», выпуск №6(22), 2015г.

Приложение

Урок изучения нового материала.

Структура:

Организационный момент (или мобилизующее начало урока). Продолжительность 1-2 минуты;

Подготовка к изучению новой темы (5-7 минут);

Формулировка (или сообщение) темы и цели урока, задач урока. Мотивация учебной деятельности. (От 1 до 5 минут);

Знакомство с новым материалом. (20 минут);

Первичное осмысление и применение полученных знаний ( 10 минут);

Подведение итогов урока или рефлексия (3 минуты);

Домашнее задание и инструктаж к выполнению (5 минут).

Урок совершенствования ЗУН

Структура:

Мобилизующее начало урока (1 минута);

Формулировка темы урока и его целей (2 минуты);

Проверка домашнего задания (3 минуты);

Актуализация знаний и умений (5 минут);

Определение границ возможного использования знаний (3 минуты);

Пробное применение знаний (15 минут);

Упражнения по образцу и в аналогичных ситуациях с целью выработки умений безошибочного применения знаний (5 минут);

Упражнения с переносом знаний в новую ситуацию (7 минут);

Итог урока (рефлексия), домашнее задание и его инструктаж (4 минуты).

Урок обобщения и систематизации ЗУН

Структура:

Организационный момент (1 минута);

Формулировка темы урока и целей, задач (1 минута);

Проверка домашнего задания (3 минуты);

Самостоятельное выполнение заданий с целью обобщения и систематизации знаний (15 минут);

Проверка работ и коррекционная работа (10 минут);

Формулировка выводов по теме урока (5 минут);

Рефлексия, подведение итогов (6 минут);

Домашнее задание и его объяснение (3 минуты);

Комбинированный урок.

Структура:

Мобилизующее начало урока (1 минута);

Проверка домашнего задания (2 минуты);

Формулировка целей и задач урока, темы урока (1 минута);

Опрос (фронтальный, индивидуальный и т.д.) с целью актуализации знаний по теме (5 минут);

Подготовка к восприятию нового материала (3 минуты);

Усвоение новых знаний (10 минут);

Решение заданий с целью закрепления знаний (17 минут);

Итоги урока, рефлексия (3 минуты);

Домашнее задание (3 минуты).

Контролирующий урок.

Структура:

Мобилизующее начало урока (1 минута);

Сообщение темы и цели урока (1 минута);

Комментирование заданий контрольной работы или самостоятельной (2 минуты);

Выполнение проверочной работы (40 минут);

Итоги урока (1 минута);

Урок корректировки знаний умений и навыков.

Структура:

Организационный момент (1 минута);

Формулировка темы урока и целей (1 минута);

Анализ выполненных работ. Объяснение заданий вызвавших затруднения. (11 минут);

Работа учащихся над ошибками (30 минут);

Итог урока, домашнее задание (2 минуты).