Определение свойств картографических проекций по их уравнениям

Определение свойств картографических проекций по их уравнениям

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

Кафедра геодезии и фотограмметрии

Лабораторная работа № 1

Определение свойств картографических проекций по их уравнениям

Выполнила: ст.4к.2 гр.

Кононова Е.И.

Проверила: Ларионова Е.В.

Горки 2015

Цель работы: усвоение положений общей теории картографических проекций, которые являются основополагающими при изучении раздела "Математическая картография"

Исходные данные: Картографическая проекция задана уравнениями:

картографическая проекция масштаб длина

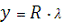
По заданным уравнениям картографической проекции определить:

ортогональность картографической сетки;

частные масштабы длин m, n, a, b, масштаб площадей р, максимальное искажение углов ω;

группу проекций по характеру искажений, к которой относится заданная проекция;

вид картографической сетки.

Математическая зависимость между координатами точек земной поверхности и плоскими прямоугольными координатами этой точки на плоскости может быть выражена следующей формулами:

Y=f₂,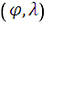

Где х, у - плоские прямоугольные координаты на кате;

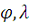
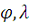 - географические координаты этой точки на шаре или эллипсоиде.

Функции f₁, f₂ - конечные, непрерывные для изображаемой области, свойства проекции зависят от вида этих функций.

Последовательность выполнения задания рассмотрим на конкретном примере. Пример. Картографическая проекция задана уравнениями:

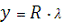
Сначала определим частные производные

;

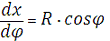
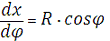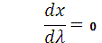
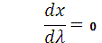
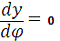
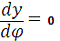
Найдем коэффициенты Гауса:

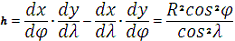
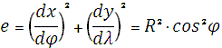
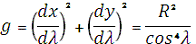
1.      Определение ортогональной плоскости картографической сетки

Сетка проекции является ортогональной, так как коэффициент Гаусса f=0.

2.      Вычисление частных масштабов длин m, n, a, b, масштаба площади р, максимального искажения ω

Частный масштаб длин вдоль меридианов определяется выражением

Поскольку сетка проекции ортогональна, то главные направления совпадают с меридианами и параллелями а экстремальные масштабы длин a и b совпадают с масштабами длин m и n. В данном случае: если m>n, то a=m и b=n

Если m<n, то a=n, т.е. 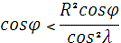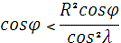, то а=n=, и b=m=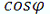

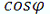
Частный масштаб площадей рассчитывается по формуле:

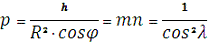
Максимальное искажение углов ω находим по одной из формул:

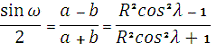
3.      Определение группы проекций по характеру искажений

Все проекции по характеру искажений делятся на три группы равноугольные, равновеликие и произвольные. Т.к. выполняется условие: f=0, m≠n, то картографическая проекция не является равноугольной.

Т.к. p≠cons’t, то картографическая проекция является не является равновеликой.

Из этого следует, что проекция произвольная, где присутствуют искажения в разных видах.

4.      Определение вида картографической сетки.

Из общей теории картографических проекций известно, что

F₁ (x, y, φ) =0 - уравнение параллелей;

F₂ (x, y,λ) =0 - уравнение меридианов, поэтому для получения уравнения параллелей из данных уравнений проекции необходимо исключить долготу λ, а для получения уравнения меридианов - широту φ.

В нашем случае уравнение x=R φsin λ является уравнением параллелей, поскольку х является функцией одного аргумента - широты.

Последнее уравнение является уравнением меридиана и в то же время уравнением синусоиды. Для построения эскиза сетки необходимо определить вид географического полюса в проекции.

Географический полюс Р в проекции может изображаться:

в виде точки

в виде прямой линии

В данном случае полюс в проекции не будет изображаться вовсе.

Вывод: По заданным уравнениям картографической проекции мною было определено следующее: сетка ортогональна (коэффициент Гауса равен 0), масштабы длин m и b совпадают с масштабами длин m и n, картографическая проекция произвольна, где присутствуют искажения в разных видах.