Динамическая метеорология
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО
СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ УЗБЕКИСТАНА
ИМЕНИ МИРЗО УЛУГБЕКА
Фатхуллаева
З.Н.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по дисциплине
ДИНАМИЧЕСКАЯ МЕТЕОРОЛОГИЯ
Ташкент - 2004
УДК 556.537
Одобрено учебно-методическим советом Национального Университета им. М.
Улугбека (протокол №4 от 28.01.2004)
Методические указания. Динамическая метеорология. - Т., изд. НУУз, 2004.
- 45.
Указания предназначены для бакалавров физических и географических
факультетов, магистров, содержат рекомендации по изучению разделов дисциплины,
вопросы для самопроверки, контрольные работы.
Составители: Фатхуллаева З.Н. канд. физ.-мат. наук, доцент
Ó Национальный Университет Узбекистана им. М. Улугбека, 2004.
ОБЩИЕ УКАЗАНИЯ
Динамическая метеорология является фундаментальной дисциплиной,
формирующей у студента глубокое понимание атмосферных процессов.
Задачей динамической (теоретической) метеорологии является изучение
закономерностей атмосферных процессов и строения атмосферы на основе общих
принципов гидротермодинамики.
Студенты, усвоившие материал, должны уметь:
1) объяснять особенности основных атмосферных явлений, исходя из
общих законов гидромеханики и термодинамики;
2) формулировать и решать задачи, связанные с разнообразными
процессами, протекающими в атмосфере.
Знания, полученные по динамической метеорологии, используются в
синоптической метеорологии, гидродинамических прогнозах, климатологии, ФОВАП,
экологии и охране атмосферы.
Цель методических указаний - помочь студентам в освоении материала,
акцентировать внимание на узловые вопросы, дать рекомендации для закрепления
полученных по учебнику знаний, развить творческий подход и навыки в процессе
изучения материала.
Литература
1. Динамическая
метеорология. Под ред. Д.Л. Лайхтмана. - Л.: Гидрометеоиздат, 1976.-607с.
2. Основы
динамической метеорологии. Под ред. Д.Л. Лайхтмана и М.М. Юдина. - Л.:
Гидрометеоиздат, 1955.-647с.
. Матвеев
Л.Т. Курс общей метеорологии. Физика атмосферы. - Л.: Гидрометеоиздат,
1984.-751с.
. Фатхуллаева
З.Н., Холматжанов Б.М. Динамическая метеорология. Конспект лекций.- Т.: изд.
НУУз, 2001.-58с.
. Задачник
по динамической метеорологии.- Л.: Гидрометеоиздат, 1984.-165с.
I. ВВЕДЕНИЕ
Предмет и задачи динамической метеорологии. Связь динамической
(теоретической) метеорологии с другими разделами метеорологии. Основные этапы
развития динамической метеорологии.
Литература [1], [2].
II. ОБЩИЕ
ПРИНЦИПЫ. ОСНОВНЫЕ УРАВНЕНИЯ ГИДРОТЕРМОДИНАМИКИ АТМОСФЕРЫ
Силы, действующие в атмосфере. Силы, действующие в атмосфере делятся на
массовые и поверхностные
Массовые или объемные силы.
К массовым силам относятся те силы, которые действуют на каждый
элементарный объем воздуха, и обычно, рассчитываются на единицу массы. К ним
относятся:
Сила
тяжести 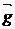 представляет собой векторную сумму двух сил: силы
земного притяжения, направленной к центру Земли, и центробежной силы,
возникающая из-за вращения Земли вокруг своей оси и направленная по радиусу
круга широты, проходящей через рассматриваемую точку.
представляет собой векторную сумму двух сил: силы
земного притяжения, направленной к центру Земли, и центробежной силы,
возникающая из-за вращения Земли вокруг своей оси и направленная по радиусу
круга широты, проходящей через рассматриваемую точку.
Сила
Кориолиса (отклоняющая сила вращения земли)  связана
с вращением Земли вокруг своей оси и действует на движущиеся относительно Земли
частицы воздуха (на воздушные течения атмосферы). Сила Кориолиса возникает в
результате переносного вращательного движения Земли и одновременного движения
частиц воздуха относительно земной поверхности.
связана
с вращением Земли вокруг своей оси и действует на движущиеся относительно Земли
частицы воздуха (на воздушные течения атмосферы). Сила Кориолиса возникает в
результате переносного вращательного движения Земли и одновременного движения
частиц воздуха относительно земной поверхности.
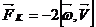 или
или 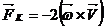 .
.
где
ω
- угловая скорость вращения Земли.
Применяя
формулы векторного анализа получим составляющие силы Кориолиса по осям
координат.
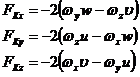
Поверхностные
силы. К поверхностным силам относятся те силы, которые действуют на
соприкасающиеся поверхности слоя воздуха.
Сила
давления (сила барического градиента) 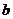 возникает
за счет неравномерного распределения давления. Вектор силы барического
градиента определяется соотношением
возникает
за счет неравномерного распределения давления. Вектор силы барического
градиента определяется соотношением
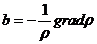 ,
,
а
его составляющие, отнесенные к единице массы, по осям координат, имеют
следующий вид:
 ,
, 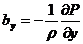 ,
, 
Сила
трения 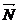 возникает при движении воздуха, когда различные его
объемы имеют разную скорость движения. Если рассматривать движение воздуха, как
движение вязкой жидкости, то при движении двух соседних слоев жидкости с
различными скоростями, между ними развиваются касательные силы внутреннего
трения (касательное напряжение), или силы вязкости. Составляющие этой силы по
осям координат:
возникает при движении воздуха, когда различные его
объемы имеют разную скорость движения. Если рассматривать движение воздуха, как
движение вязкой жидкости, то при движении двух соседних слоев жидкости с
различными скоростями, между ними развиваются касательные силы внутреннего
трения (касательное напряжение), или силы вязкости. Составляющие этой силы по
осям координат:
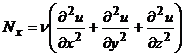 ,
, 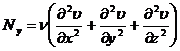 ,
, 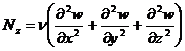 .
.
 -
кинематический коэффициент турбулентной вязкости, а
-
кинематический коэффициент турбулентной вязкости, а 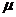 - динамический коэффициент вязкости.
- динамический коэффициент вязкости.
Уравнение
движения. В соответствии с законом изменения количества движения (второй закон
Ньютона), уравнение движения в векторной форме имеет вид:

Обозначая
проекции вектора скорости 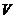 на оси x, y, z, соответственно через u, v, w и
раскрывая полную производную по времени
на оси x, y, z, соответственно через u, v, w и
раскрывая полную производную по времени
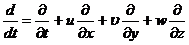 .
.
получим
уравнения движения в проекциях на оси координат.
В
проекции на ось x оно имеет вид:
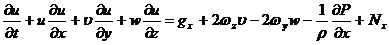 .
.
Получите
уравнения движения в проекциях на оси y, z.
Уравнение
неразрывности является выражением закона сохранения массы. Оно связывает
изменение плотности во времени с распределением скорости движения в
пространстве.
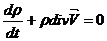 ,
,
где
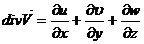 - дивергенция скорости.
- дивергенция скорости.
Дайте
вывод этого уравнения. Получите другую форму уравнения неразрывности, которая
наиболее часто используется в метеорологических исследованиях:
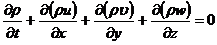 .
.
Уравнение
притока тепла выводится на основании закона сохранения энергии. Применительно к
метеорологическим процессам этот закон физики, известен как первое начало
термодинамики:
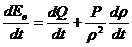 .
.
Его
можно сформулировать так: изменение внутренней энергии фиксированной массы за
единицу времени обусловлено притоком тепла извне в единицу времени и работой
расширения или сжатия.
Часто
при решении метеорологических задач, пользуются притоком тепла  к единичному объему в единицу времени.
к единичному объему в единицу времени.
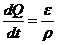
Изменение
внутренней энергии воздуха ненасыщенного водяным паром связано с изменением
температуры воздуха:
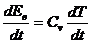 ,
,
где
Cv - удельная теплоемкость воздуха при постоянном
объеме.
С
учетом двух последних соотношений уравнение первого начала термодинамики
принимает вид:
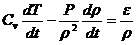
Это
уравнение притока тепла. Оно показывает, что приток тепла к единице массы в
единицу времени расходуется на изменение температуры и на работу расширения или
сжатия воздуха.
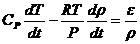
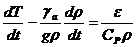 ,
,
где
Cp - удельная теплоемкость при постоянном давлении; 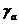 - сухоадиабатический градиент температуры.
- сухоадиабатический градиент температуры.
Следует
обратить внимание на различные виды притоков тепла.
Литература:
[1], [2], [4].
Вопросы для самопроверки
1. Какие силы действуют на воздушную
частицу в атмосфере?
2. Какое влияние на поток оказывает сила
Кориолиса при горизонтальном движении?
3. Показать, что сила Кориолиса не может
совершать работу.
Показать,
что в случае стационарного процесса и при движении вдоль изостерической
поверхности ρ=const,
уравнение неразрывности принимает вид 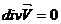 .
.
1. На основании какого закона выводится
уравнение притока тепла?
2. Перечислите виды притоков тепла.
III.
УПРОЩЕНИЕ УРАВНЕНИЙ ДИНАМИКИ АТМОСФЕРЫ
Основы теории подобия. Общая система уравнений динамики атмосферы
является весьма сложной. Поэтому возникает задача упрощения этих уравнений,
применительно к особенностям изучаемых процессов. Для этого необходимо выявить
главные факторы, определяющие свойства изучаемого движения и пренебречь теми,
которые не оказывают существенное влияние. Таким образом, можно значительно
упростить уравнения динамики атмосферы. Один из методов упрощения уравнений
динамики атмосферы основан на теории подобия.
Теория подобия позволяет установить, как изменяются соотношения различных
сил, действующих в атмосфере, при изменении масштабов движений и характерных
скоростей.
Введем характерные значения и масштабы:- характерное значение длины.* -
характерное время.- характерная скорость
П - характерная плотность.
DP - характерная разность давления.
Если все величины выражать в виде отношений их к характерным для них
значениям, то эти величины будут безразмерными. Любая функция от безразмерных
координат и времени, составленная для подобных движений, должна быть совершенно
одинакова.
Найдем критерии подобия движения вязкой сжимаемой жидкости. Рассмотрим
первое уравнение движения.

С
помощью указанных выше характерных масштабов переходим к безразмерным
величинам. Оценкой порядка величины каждого слагаемого в уравнении служит
стоящий при нем постоянный коэффициент, составленный из характерных масштабов и
имеющий размерность ускорения. Разделим все слагаемые уравнения на один из
размерных постоянных коэффициентов, стоящий при каком-либо слагаемом. Получим
безразмерное уравнение движения, все коэффициенты которого будут безразмерными
величинами, составленными из характерных масштабов и один из них будет равен единице.
Эти безразмерные коэффициенты называются критериями подобия.
Введем
для этих коэффициентов следующие обозначения:
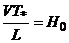 - число
гомохронности.
- число
гомохронности.
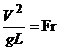 - число
Фруда.
- число
Фруда.
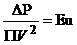 - число
Эйлера.
- число
Эйлера.
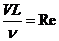 - число
Рейнольдса.
- число
Рейнольдса.
 .
.
Чтобы
два движения были подобны друг другу необходимо, чтобы они имели одинаковые
числа H0, Fr, Eu, Re, De.
Пользуясь
критериями подобия перепишем безразмерное уравнение движения. Аналогичное ему
уравнение можно получить для составляющих ускорения по y, z.
Проанализировать
полученные уравнения движения и показать влияние сил тяжести, Кориолиса и силы
вязкости при изменении масштабов и скорости.
Получить
критерий подобия, характеризующий влияние сжимаемости на свойства атмосферных
движений и объяснить при каких скоростях движения можно пренебречь сжимаемостью
воздуха.
Классификация
атмосферных движений. Атмосферные процессы по своим масштабам могут значительно
отличатся друг от друга. Таким образом, характерные величины в различных
задачах динамической метеорологии изменяются в широких пределах. Так,
характерная длина L изменяется: 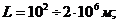
Классификацию
атмосферных движений можно произвести с помощью основных критериев подобия:
числа Fr, De, Re. Для этого необходимо оценить нижний и верхние пределы
возможных значений указанных критериев подобия. Учитывая интервалы изменения

рассчитайте
пределы изменения указанных чисел и объясните каково влияние сил тяжести,
Кориолиса и вязкости на атмосферные движения. Поясните, соотношение каких сил
может служить критерием для классификации атмосферных движений по горизонтали и
на какие три класса их можно разделить.
Порядки
величин основных метеорологических элементов и их производных. Другой метод
упрощения уравнений динамики атмосферы основан на учете порядка величин
метеорологических элементов.
Под
порядком величины какой-либо функции понимают значение этой функции в
диапазоне, включающем не менее 99% всех возможных ее значений.
Фридманом
и Гессельбергом по эмпирическим данным была составлена таблица порядка величин
метеорологических элементов и их производных. С помощью этой таблицы можно производить
упрощение уравнений.
Практически
для упрощения уравнений удобно пользоваться таблицей средних квадратичных
значений метеоэлементов и их производных составленной Юдиным.
Для
прогноза погоды, в первую очередь, представляют интерес крупномасштабные
атмосферные движения. Характерным масштабом времени для таких движений можно
принять 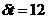 ч. или 24 ч. Характерный масштаб длины
ч. или 24 ч. Характерный масштаб длины  км и
км и 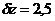 км.
км.
Пользуясь
таблицей средних квадратичных значений метеоэлементов и их производных (см.
[2,5]), оценим порядок величин отдельных членов уравнений динамики атмосферы.
Запишем
уравнения горизонтального движения атмосферы, в которых составляющие силы
турбулентного трения приближенно могут быть представлены выражениями вида: 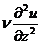 и
и 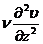 .
Подставив значения порядков величин под соответствующими слагаемыми получим:
.
Подставив значения порядков величин под соответствующими слагаемыми получим:

Ясно,
что слагаемыми с порядком 10-6 вполне можно пренебречь по сравнению с
остальными слагаемыми уравнений. В результате упрощения имеем:
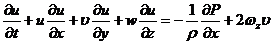 ,
,
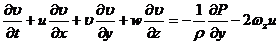 .
.
Произвести
аналогичным образом упрощения третьего уравнения движения, неразрывности и
притока тепла, дать их анализ. Обратите внимание на упрощение третьего
уравнение движения и объясните для каких процессов оно не верно.
Литература
[2], [4], [5].
Вопросы для самопроверки
1. Назовите методы упрощения уравнений
динамики атмосферы.
2. Перечислите основные критерии подобия
и что они характеризуют?
3. Из какого уравнения вытекает критерий
подобия, характеризующий сжимаемость воздуха?
4. Классификация атмосферных движений по
горизонтали.
5. Деление атмосферы на свободную и
пограничный слой. Почему в последнем выделяют приземный слой?
6. Какие силы близки по своему порядку в
свободной атмосфере?
IV. НЕКОТОРЫЕ ВОПРОСЫ ТЕРМОДИНАМИКИ
АТМОСФЕРЫ
Термодинамика атмосферы является частью динамической метеорологии,
изучающей изменения параметров внутреннего состояния движущегося воздуха и,
связанные с этими изменениями, процессы перехода тепловой энергии в
механическую и обратно.
Политропические изменения термодинамического состояния воздуха. Переход
массы воздуха из одного термодинамического состояния в другое может
осуществляться различными путями.
Простейшим процессами являются политропические процессы, при которых
приток тепла пропорционален приращению температуры:
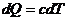 ,
,
где
c - политропическая теплоёмкость, считается постоянной.
Подставляя
это соотношение в уравнение первого начала термодинамики:
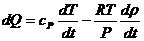
и
выполнив интегрирование получите уравнение политропического процесса:
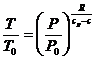 .
.
Используя
уравнение состояния, получите другую форму уравнения политропы:
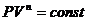 ,
,
где
 - показатель политропы.
- показатель политропы.
Определите
показатель политропы для адиабатического, изотермического процессов. Выведите
следующую формулу для политропически перемещающейся частицы воздуха:
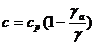 ,
,
где
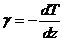 .
.
Запишите
уравнение первого начала термодинамики для адиабатического процесса и получите
уравнение Пуассона. Объясните его физический смысл. Рассмотрите изменение
температуры перемещающейся по вертикали частицы при адиабатическом и
политропическом процессах.
Потенциальная
температура - это температура, которую принимает сухой воздух, если привести
его адиабатически к стандартному давлению равному 1000 гПа.
Объясните
необходимость введения потенциальной температуры, каким свойством она обладает.
Изменение
состояния влажного воздуха.
Уровень
конденсации. Рассмотрим изменение состояния влажного воздуха адиабатически
поднимающегося вверх. Уровень, на котором поднимающийся воздух достигает
состояния насыщения, называется уровнем конденсации. На уровне конденсации 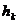 температура поднимающегося воздуха
температура поднимающегося воздуха  оказывается равной температуре точки росы
оказывается равной температуре точки росы 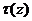
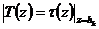 .
.
Получите
формулу для высоты уровня конденсации и объясните от чего она зависит.
Влажноадиабатический
градиент. Рассмотрим изменения состояния поднимающегося воздуха выше уровня
конденсации. В этом случае воздух уже насыщен водяным паром, подъем и
охлаждение сопровождается конденсацией и выделением скрытой теплоты
конденсации. Поэтому уравнение первого начала термодинамики для
влажноадиабатического процесса принимает вид:
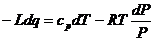 (*)
(*)
Величина,
на которую изменится температура порции влажного насыщенного воздуха при
адиабатическом перемещении по вертикали на единицу расстояния, называется
влажноадиабатическим градиентом температуры.
Используя
уравнение (*) и формулу удельной влажности

получите
выражение для влажноадиабатического градиента и объясните его физический смысл.
Условия
вертикальной устойчивости атмосферы. Одной из главных причин, вызывающих
развитие вертикальных движений в атмосфере является разность между температурой
движущейся порции воздуха и температурой окружающей ее атмосферы. При наличии
этой разности температур возникает Архимедова сила, сообщающая движущей порции
воздуха положительное или отрицательное ускорение.
Состояние
атмосферы, при котором порция воздуха, начавшая движение по вертикали, получает
ускорение в том же направлении, стремящееся удалить частицу от исходного уровня
(положительное ускорение) называется неустойчивым состоянием. Если же порция
воздуха, начавшая смещение, получает ускорение в направлении противоположном ее
движению, стремящееся вернуть частицу на исходный уровень (отрицательное
ускорение) называется устойчивым. Безразличным называется такое состояние
атмосферы, когда вертикальное движение массы воздуха зависит только от
начальной скорости, а вертикальное ускорение равно нулю.
Ускорение
частицы воздуха можно определить из третьего уравнения движения. Обозначим
вертикальную скорость частицы воздуха w.
P, ρ,T - параметры частицы, 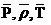 -
окружающего воздуха. Тогда
-
окружающего воздуха. Тогда
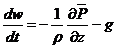 .
.
Считая
процесс квазистатическим и используя уравнение статики, состояния получите
формулу для определения критериев устойчивости атмосферы и поясните ее. Дайте
определение уровня конвекции и от чего зависит его высота.
Энергия
неустойчивости. Энергией неустойчивости называется работа, которую может
совершить Архимедова сила, возникающая при вертикальном подъеме единицы массы
воздуха. Неустойчивой стратификации соответствует положительная энергия
неустойчивости, а устойчивой стратификации - отрицательная энергия
неустойчивости.
Получим
формулу для расчета энергии неустойчивости E. Работа,
совершаемая единицей массы воздуха на высоту dz равна
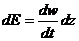 ;
; 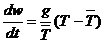
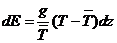
Используя
уравнение статики и интегрируя полученное выражение, напишите формулу для
расчета полной работы, которую совершает подъемная сила в слое от P0 до
P и дать ее анализ. Поясните как можно с помощью
аэрологической диаграммы проанализировать устойчивость слоя воздуха. Выясните
связь энергии неустойчивости с кинетической энергией вертикально перемещающейся
воздушной массы.
Литература:
[1-3], [5].
Вопросы для самопроверки
1. Какой процесс называется политропическим?
2. Получите формулу для изменений с высотой температуры в
поднимающейся массе сухого воздуха при заданном притоке тепла.
. Получите формулу для сухоадиабатического градиента.
. Что такое потенциальная температура и каковы ее свойства?
. Что такое уровень конденсации? От чего зависит его высота?
. Какой процесс называется влажноадиабатическим? От каких
характеристик зависит влажноадиабатический градиент?
. Какие основные типы температурной стратификации атмосферы и
критерии для их определения?
. Что такое уровень конвекции?
. В чем удобство введения такой характеристики стратификации
атмосферы, как энергии неустойчивости?
. Какая стратификация соответствует положительной энергии
неустойчивости?
V. ДИНАМИКА СВОБОДНОЙ АТМОСФЕРЫ
Абсолютный и относительный геопотенциал. Геопотенциалом или потенциалом
силы тяжести, называется работа, которую необходимо совершить, чтобы поднять
единицу массы от исходного уровня до данной точки.
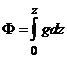 (1)
(1)
Поверхность
равных значений геопотеницала называется поверхностью уровня. Если исходным
уровнем является уровень моря, то геопотенциал рассчитанный относительно этого
уровня называется абсолютным геопотенциалом. Если же геопотенциал
рассчитывается относительно любого другого уровня, то этот геопотенциал
называется относительным геопотенциалом. Карты барической топографии
представляют топографию одной изобарической поверхности по отношению к
поверхности моря или по отношению к другой изобарической поверхности. В первом
случае она называется картой абсолютной топографии, а во втором - картой
относительной топографии.
С
помощью (1), учитывая уравнение статики и состояния, получите формулы
абсолютного и относительного геопотенциала, а также их изменений, дайте их анализ.
Обратите внимание на их отличие.
Геострофический
ветер. Геострофическим ветром называется ветер без ускорения в свободной
атмосфере (при отсутствии трения).
Уравнение
геострофического ветра получим из уравнения движения для свободной атмосферы,
положив в них 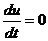 ,
, 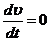 .
.
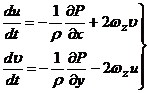 (1)
(1)
Из
(1) следует, что
 (2)
(2)
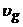
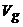
 y
y
x

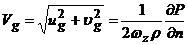
 (3)
(3)
где
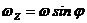 , n - нормаль к изобаре.
, n - нормаль к изобаре.
Дайте
анализ формулы (3). Выясните основные свойства геострофического ветра. Обратите
внимание на его зависимость от географической широты.
Получите
формулу для расчета скорости геострофического ветра, удобную для практического
использования
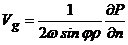 ,
,
если
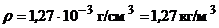 ,
, 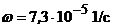 ,
,  ,
, 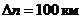 .
.
Изменение
геострофического ветра с высотой. Термический ветер. Будем исходить из
геострофических соотношений (см. в 5.2. (2)) и уравнения статики. Исключая из
них плотность, с помощью уравнения состояния, будем иметь:
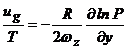 (1)
(1)
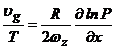 (2)
(2)
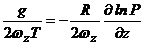 (3)
(3)
Уравнения
(1)-(2) продифференцируем по z, (3) - по x и y, а затем приравняем правые части
и проинтегрируем уравнения от z0 до z:
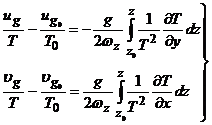 (4)
(4)
Формула
(4) неудобна для анализа, из-за наличия интегралов, они могут быть вычислены
при различных предположениях о вертикальном распределении температуры.
Рассматривая
случай политропной атмосферы 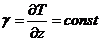 , или
, или 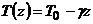 , т.е. случай, когда температура линейно меняется с
высотой, получите формулу изменения геострофического ветра с высотой и
проанализируйте ее. Дайте определение термического ветра и выясните его
основные свойства. Обратите внимание на направление ветра относительно
изотермы.
, т.е. случай, когда температура линейно меняется с
высотой, получите формулу изменения геострофического ветра с высотой и
проанализируйте ее. Дайте определение термического ветра и выясните его
основные свойства. Обратите внимание на направление ветра относительно
изотермы.
Получите
формулу для определения термического ветра на высотах с помощью карт
относительной топографии.
Рассмотрите
четыре случая изменения геострофического ветра с высотой для северного
полушария, если градиенты температуры и давления на начальном уровне: 1)
параллельны, 2) антипараллельны, 3) угол между ними равен  , 4) угол между ними равен -
, 4) угол между ними равен - . Обратите внимание на случай, когда происходит
обращение ветра с высотой.
. Обратите внимание на случай, когда происходит
обращение ветра с высотой.
Локальное изменение температуры при геострофическом ветре. Рассмотрим
изотермическое геострофическое движение воздуха, при котором
атмосфера метеорологический воздух геопотенциал

Оценивая
слагаемые, пренебрегая последним, получим.
Из
формулы следует, что локальное изменение температуры имеет место вследствие
горизонтального движения воздуха. Такие изменения называются адвективными
изменениями температуры или адвекцией температуры.
Адвективные
изменения температуры при геострофическом ветре называются геострофической
адвекцией температуры.
Подставляя
в (1) геострофическое соотношение, получите формулу геострофической адвекции и
объясните ее физический смысл.
Обратите
внимание, когда будет максимальная адвекция и когда адвекции не будет.
Рассмотрите
изменение геострофического ветра с высотой для северного полушария в различных
частях циклона и антициклона, если градиент температуры направлен с юга на
север и какова будет адвекция температуры.
Отклонение
ветра от геострофического. Движение, не подчиняющееся геострофическим
соотношениям, называется агеострофическим движением. При геострофическом ветре ускорение
равно нулю. Если же имеется отклонение ветра от геострофического, то ускорение
существует.
Обозначим
через 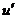 и
и  -
отклонение от геострофического ветра.
-
отклонение от геострофического ветра.
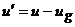 ,
,  (1)
(1)
Введя
в уравнение движения для свободной атмосферы геострофическое соотношение,
получите формулы для отклонения ветра от геострофического. Выясните его
основные свойства, обратите внимание на то, как направлено отклонение ветра от
геострофического, относительно ускорения.
Вертикальные
токи в свободной атмосфере. Согласно наблюдениям, отношение  . Будучи небольшим по величине, отклонение ветра от
геострофического играет существенную роль в эволюции барических образований,
развитии вертикальных движений в свободной атмосфере. Для получения выражения
для вертикальной скорости, запишем уравнение неразрывности
. Будучи небольшим по величине, отклонение ветра от
геострофического играет существенную роль в эволюции барических образований,
развитии вертикальных движений в свободной атмосфере. Для получения выражения
для вертикальной скорости, запишем уравнение неразрывности
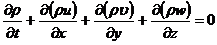 ,
,
в
котором не будем учитывать малые влияния нестационарности плотности  .
.
Интегрируя
уравнение неразрывности от z1 до z2 получим

Подставляя
сюда 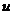 и
и 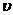 из (1)
(см. 5.4.) и учитывая, что члены
из (1)
(см. 5.4.) и учитывая, что члены  и
и 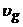 сократятся
сократятся

Эта
формула показывает, что вертикальная скорость связана с отклонениями ветра от
геострофического.
Получите
формулу изменения вертикальной скорости с высотой с помощью поля давления и
оцените слагаемые уравнения.
Литература
[1], [2], [4], [5].
Вопросы для самопроверки
1. Что такое геопотенциал?
2. Определение абсолютного и
относительного геопотенциала. От чего они зависят?
3. Определение геострофического ветра.
От чего зависит его скорость?
4. Как изменяется геострофический ветер
в зависимости от широты?
5. Покажите, что геострофический ветер
перпендикулярен градиенту давления. При каких углах между изобарами и
изотермами геострофический ветер растет с высотой, а при каких убывает?
6. Что такое термический ветер? Чем
определяется его величина и направление?
7. Что такое уровень обращения? При
каком взаимном расположении градиентов давления и температуры он может
наблюдаться?
8. От чего зависит локальное изменение
температуры при геострофическом ветре?
9. Чем вызывается отклонение ветра от
геострофического и как оно направлено?
10.Какое уравнение
служит для определения вертикальной скорости?
VI. НАТУРАЛЬНАЯ СИСТЕМА КООРДИНАТ
Уравнения движения в натуральной системе координат. Натуральной системой
координат называется ортогональная, в общем случае, криволинейная система отсчета,
в которой координатными линиями являются линии тока «s» и нормали «n» к
ним, при этом кратчайший поворот от положительного направления s к положительному направлению n совершается влево, т.е. n отклоняется влево от s.
y
n 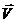 s
s
b
b x
Обозначим
через 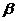 угол между осью x и касательной
к линии тока s, отсчитываемой против часовой стрелки. Этот угол
характеризует направление ветра и меняется от точки к точке и с течением
времени
угол между осью x и касательной
к линии тока s, отсчитываемой против часовой стрелки. Этот угол
характеризует направление ветра и меняется от точки к точке и с течением
времени 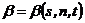 .
.
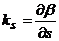 -
кривизна лини тока (1)
-
кривизна лини тока (1)
Кривизна
линии тока, характеризует изменение угла (поворот линии тока) на единицу длины
ее дуги.
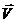 s
s
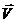 b
b
b x
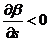 s
s
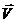
b
b  x
x
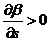
Кривизна линии тока отрицательна, когда кривая поворачивает вправо
(антициклоническая кривизна). При циклонической кривизне поворот происходит
влево и угол увеличивается.
 -
кривизна нормали (2)
-
кривизна нормали (2)
Кривизна
нормали, характеризует изменение угла 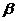 при
перемещении по нормали на единицу расстояния. При положительной (циклонической)
кривизне нормалей линии тока расходятся по течению, а при отрицательной
(антициклонической) кривизне нормалей лини тока сходятся по течению.
при
перемещении по нормали на единицу расстояния. При положительной (циклонической)
кривизне нормалей линии тока расходятся по течению, а при отрицательной
(антициклонической) кривизне нормалей лини тока сходятся по течению.
n
S
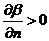 n
s
n
s 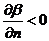
Рассмотрим
кривизну траектории, т.е. поворот пути частицы на единицу пройденного
расстояния.
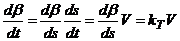
 -
кривизна траектории (3)
-
кривизна траектории (3)
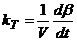 (4)
(4)
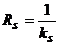 ,
,  ,
, 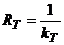 (5)
(5)
Радиусы
кривизны линии тока, нормали к ней и траектории.
Запишем
уравнения движения в виде
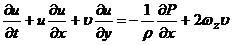 (6)
(6)
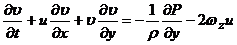 (7)
(7)
Используя
формулы перехода от декартовой системы координат к натуральной системе (см.
[2], [4]), получите уравнения движения в натуральной системе координат.
Градиентный
ветер - это ветер, при котором линии тока (вблизи рассматриваемой точки и в
рассматриваемый момент времени) совпадают с изобарами, т.е. 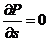 .
.
Используя
уравнения движения в натуральной системе координат:
 (8)
(8)
 (9)
(9)
Выясните
свойства градиентного ветра. Покажите, что геострофический ветер является
частным случаем градиентного ветра.
Градиентный
ветер при круговых изобарах. Запишем основное уравнение градиентного ветра.
 (1)
(1)
Все
величины, входящие в это уравнение, постоянны вдоль круговой изобары.
Проанализируйте знаки различных членов этого уравнения.
Рассмотрите
как направлены силы в циклоне (RT>0), антициклоне (RT<0) в
северном полушарии (ωZ>0).
Используя уравнение (1) получите формулу скорости градиентного ветра при
круговых изобарах и дайте ее анализ.
Вопросы для самопроверки
1. Что является координатными линиями в
натуральной системе координат?
2. Что характеризует кривизна линии
тока, нормали и траектории?
3. Дайте определение градиентного ветра.
4. Чем отличаются градиентный и
геострофический ветер?
5. Как направлены силы в случае
установившихся воздушных течений в свободной атмосфере в области циклонов и
антициклонов?
6. Какова скорость градиентного ветра
при одном и том же барическом градиенте в циклонах и антициклонах по сравнению
с геострофическим?
VII. поверхности раздела
в атмосфере
Общие свойства поверхности раздела. В атмосфере встречаются области, где
происходит резкое изменение метеоэлементов. На поверхности раздела нарушается
непрерывность ряда метеоэлементов. Следовательно, нарушается их
дифференцируемость. Поэтому на поверхности раздела дифференцирование уравнений
динамики атмосферы оказывается неприменимыми и должны быть заменены другими
соотношениями, полученными с учетом разрыва непрерывности метеоэлементов на
поверхности раздела.
Выведите соотношения, которые должны выполняться на поверхности раздела,
используя закон сохранения массы и закон изменения количества движения. В
результате будут получены уравнения, которые являются аналогами уравнения
неразрывности и движения при наличии поверхности раздела. Используя эти
уравнения, рассмотрите свойства поверхности раздела.
Угол наклона стационарной поверхности раздела. Пусть имеется поверхность
раздела. Выберем около этой поверхности две пары точек.
+
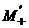
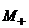

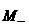 -
-
Так
как давление непрерывно, то 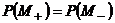 и
и 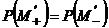 , и вычтем
, и вычтем
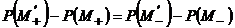 .
.
Если
будем сближать точки, то получим  или в
развернутом виде
или в
развернутом виде

Введя
обозначение для скачков, перепишем это соотношение
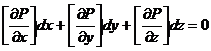 (1)
(1)
 -
скачок.
-
скачок.
Наклон
поверхности раздела к горизонту можно характеризовать двумя углами или 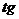 и берем
и берем
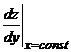 ,
,  .
.
Направим
ось x вдоль фронта, а ось y по нормали к фронту.
+
-
α y
 (2)
(2)
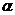 - угол
наклона поверхности раздела.
- угол
наклона поверхности раздела.
Используя
(1) получим  ,
,
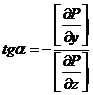 (3)
(3)
Используя
уравнения геострофического ветра и статики, получите формулу угла наклона
стационарной поверхности раздела (ф-ла Маргулеса) и дайте ее анализ.
Рассмотрите поле ветра и давления вблизи стационарной поверхности раздела.
Влияние
кривизны изобар, перемещения и ускорения на угол наклона поверхности раздела.
Нами был рассмотрен простой случай, когда ветер считался геострофическим, фронт
являлся изобарой, а изобары были прямолинейны. Для получения выводов более
общего характера необходимо освободится от этих ограничений.
Влияние
кривизны изобар на угол наклона поверхности раздела. Для учета кривизны изобар
используется уравнение движения градиентного ветра
 (1)
(1)
Получите
формулу угла наклона поверхности раздела, используя уравнение (1) и проанализируйте
ее. Обратите внимание на зависимость угла наклона поверхности раздела от
циклонической и антициклонической кривизны изобар.
Влияние
перемещения фронта на угол наклона поверхности раздела. Формула Маргулеса была
получена для стационарного фронта.
Выведите
формулу угла наклона поверхности раздела с учетом движения фронта, считая ветер
по обе стороны фронта геострофическим. Объясните, почему перемещение фронта не
оказывает влияния на угол наклона поверхности раздела? Рассмотрите поле ветра и
давления вблизи подвижного фронта.
Влияние
ускорения (т.е. отклонение ветра от геострофического) на угол наклона
поверхности раздела. Для этого нужно заменить уравнения геострофического ветра
полными уравнениями движения для свободной атмосферы. Получите формулу угла
наклона поверхности раздела с учетом ускорения и объясните как оно влияет на
угол наклона.
Литература:[2], [4].
Вопросы для самопроверки
1. Что такое поверхность раздела в
атмосфере?
2. Почему на поверхностях раздела
неприменимы дифференциальные уравнения динамики атмосферы?
3. Перечислите свойства поверхности
раздела.
4. От чего зависит угол наклона
стационарной поверхности раздела? Напишите формулу Маргулеса.
5. Как влияет перемещение фронта на угол
наклона фронтальной поверхности?
6. Как влияет на наклон фронтальной
поверхности отклонение ветра от геострофического?
КОНТРОЛЬНАЯ
РАБОТА
Общие указания
Для закрепления теоретических знаний, решение задач совершенно
необходимо. Поэтому контрольная работа содержит задачи.
При выполнении контрольной работы следует дать подробное объяснение
решения задачи. Обязательно соблюдать размерность величин и выражать их в
принятых единицах измерения с использованием стандартных обозначений. Например,
атмосферное давление выражается в гектопаскалях (гПа), температура в градусах
термодинамической температурной шкалы (градусы Кельвина К) или международной
практической температурной шкалы (градусы Цельсия °С). Для этого рекомендуется
воспользоваться [5], где даны физические постоянные, необходимые табличные
материалы.
Здесь приведены четыре контрольные работы. При решении задач контрольной
работы №1 используются такие понятия, как дифференциальные характеристики
метеорологических полей (градиент, дивергенция и вихрь скорости ветра), связь
между полной и частной производной по времени. При использовании значений
составляющих скоростей u, v должен учитываться их знак в
соответствии с направлением осей x и y.
В контрольной работе №2 при решении задач используется уравнение первого
начала термодинамики, уравнение состояния и статики [1-3]. Здесь следует
обратить внимание на размерность величин.
При выполнении контрольной работы №3 используется понятие геопотенциала,
выражение для геострофического ветра и его измерение с высотой, а также
адвективное изменение температуры. [1, 2, 4] Изменение ветра с высотой показать
на рисунке и обратить внимание на направление ветра.
В контрольной работе №4 при решении задач используются формулы
дивергенции и вихря скорости в натуральной системе координат, выражение для
градиентного ветра и агеострофических отклонений [2, 4]. При расчете
градиентного ветра в циклонах и антициклонах используются как точные, так и
приближенные формулы.
Контрольная работа № 1
Вариант 1.
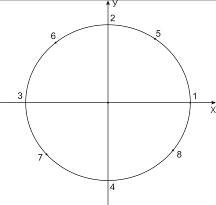
Задача
1. Определить величину и направление горизонтального градиента температуры в
центре круга радиусом 500 км, если в восьми точках, равномерно расположенных на
окружности круга, температура составляет (рис. 1) 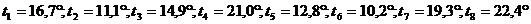
Задача
2. За какое время температура в будке уменьшится на 2°С при скорости восточного ветра 7м/с, если температура убывает с запада
на восток на 4°С/100км, а движение воздушной массы происходит
изотермически?
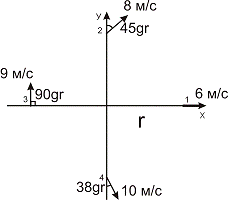
Задача
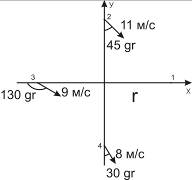
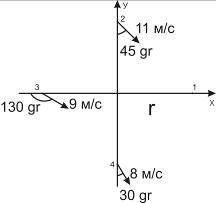
3. Определить дивергенцию и вихрь скорости по данным, приведенным на рис.2, где
r=500км.
Вариант
2
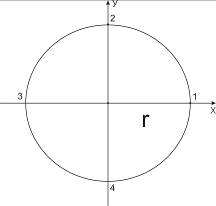
Задача
1. Определить горизонтальный градиент и лапласиан давления в точке, где
давление равно p0=1001 гПа, если в окружающих четырех точках,
удаленных на r=500 км (см. рис. 3), давление равно p1=991гПа,
p2=993гПа, p3=995гПа, p4=994гПа.
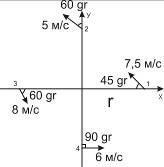
Задача
2. Увеличение температуры в движущейся воздушной массе равно уменьшению
температуры в фиксированной точке. Найти угол между градиентом температуры,
равным 6°С/100км и скоростью ветра, равной 7м/с, если за 3 часа
температура в точке понизилась на 2°С.
Задача
3. Определить дивергенцию и вихрь скорости ветра по данным, приведенным на рис.
4, где r=500км.
Вариант
3.
Задача
1. Граница циклонической области является окружностью радиусом 1500 км. В
центре области давление равно 976 гПа, а в северной, восточной, южной и
западной точках окружности - соответственно 994 гПа, 998 гПа, 995 гПа и 992
гПа. Найти среднее значение лапласиана давления в области.
Задача
2. Воздушная масса поднимается вдоль горного склона, имеющего уклон 4° и через 26 мин достигает вершины. Скорость движения воздушной массы
8м/с. Вертикальный градиент температуры равен 0,5°С/100м
(температура убывает с высотой). Горизонтальный градиент температуры равен
нулю. Как изменится температура воздуха над вершиной горы за это время, если
процесс происходит адиабатически?
Задача
3. Найти скорость и направление ветра в точке 1 по данным приведенным на рис.
5, считая движение безвихревым и бездивергентным.
Контрольная работа № 2
Вариант 1.
Задача
2. Вертикально поднимающаяся масса воздуха получает тепло от окружающей среды
вследствие теплопроводности. На каждые 100 м поднятия приток тепла равен 20,9
Дж/г. Найти вертикальный градиент температуры частицы и показатель политропы,
описывающий изменение состояния массы воздуха.
Задача
3. Опускающаяся масса воздуха получает от окружающей среды (вследствие
теплопроводности) тепло 0,38 Дж/г на 100м опускания. Средний температурный
градиент в атмосфере - 0,65°С/100м. Определить состояние
устойчивости и показатель политропы.
Вариант
2.
Задача
1. Поднимающийся воздух вследствие большого содержания пыли и водяного пара
поглощает 251 Дж/кг солнечной радиации на каждые 100 м поднятия. Как изменится
ее температура при поднятии на 1км?
Задача
2. Вертикально поднимающаяся частица воздуха получает тепло. Температура
частицы понижается на 0,24°С/100м. Определить показатель
политропы и приток тепла к 1г на 100м подъема.
Задача
3. Масса воздуха опускается. Вследствие лучистого теплообмена ее потенциальная
температура возрастает на 1,5°С на 1км. Определить состояние
устойчивости, если градиент температуры в атмосфере - 0,65°С/100м. Принять 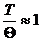 .
.
Вариант
3.
Задача
1. Как должна изменяться с высотой температура вертикально поднимающейся
частицы воздуха, чтобы ее плотность оставалась постоянной? Каков при этом
приток тепла к частице, имеющей массу 1г, на каждые 100м поднятия? При
вычислениях принять 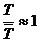 .
.
Задача
2. Доказать, что работа расширения адиабатически и квазистатически
поднимающейся частицы воздуха может быть выражена следующей формулой: 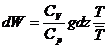 .
.
Задача
3. Состояние поднимающейся частицы воздуха изменяется по политропическому
закону, С=0,2 Дж/г×К. Средний температурный градиент в атмосфере - 1,2°С/100м. Определить состояние устойчивости и показатель политропы.
Контрольная работа № 3
Вариант 1.
Задача
1. Как должно измениться давление на уровне моря, если при повышении средней
температуры на 3°С, изобарическая поверхность 500гПа поднялась на 3
гп.дам? 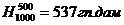 , давление на уровне моря 1000 гПа.
, давление на уровне моря 1000 гПа.
Задача
2. Определить скорость и направление геострофического ветра на высоте 2 км,
если ветер на уровне 1км направлен с юга на север и равен 7,9 м/с, а средний
горизонтальный градиент температуры равен 2°С/100м и направлен с
севера на юг. Широта места 55°.
Задача
3. При каком градиенте температуры геострофическая адвекция на карте АТ500 на
широте 45° составляет 8°С/сут, если изогипсы
на этой карте отстоят друг от друга на 1,3см и перпендикулярны к изотермам.
Масштаб карты 1:1,5×107.
Вариант
2.
Задача
1. Каково изменение температуры  , если
при повышении давления на уровне моря на 5гПа, изобарическая поверхность 500гПа
поднялась на 5 гп.дам. Принять p0=1000гПа,
, если
при повышении давления на уровне моря на 5гПа, изобарическая поверхность 500гПа
поднялась на 5 гп.дам. Принять p0=1000гПа,  .
.
Задача
2. Найти высоту обращения геострофического ветра на станции, широта которой 40°, если на высоте 500 м геострофический ветер равен 6 м/с, а средний горизонтальный
градиент температуры 2°С/100м.
Задача
3. Каким должен быть угол между градиентом абсолютного геопотенциала
1гп.дам/100км и градиентом температуры 0,8°С/100км, чтобы
геострофическая адвекция на широте 55° составляла - 3°С/сут?
Вариант
3.
Задача
1. Относительный геопотенциал  увеличился
на 15гп.дам. при неизменном вертикальном градиенте температуры. Найти изменение
температуры на уровне 1000гПа, при
увеличился
на 15гп.дам. при неизменном вертикальном градиенте температуры. Найти изменение
температуры на уровне 1000гПа, при 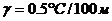 и
и 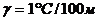 .
.
Задача
2. Оценить величину и направление геострофического ветра на высоте 2 км, на
широте 50°, если известно, что геострофический ветер на высоте
1км - южный и равен 11м/с, а геопотенциал  растет к
югу на 2гп.дам на каждые 3см расстояния на карте масштаба 1:1,5×107.
растет к
югу на 2гп.дам на каждые 3см расстояния на карте масштаба 1:1,5×107.
Задача
3. На уровне 300гПа, над некоторым пунктом, на широте 45° наблюдается струйное течение с градиентом геопотенциала
10гп.дам/200км, термический градиент на этом уровне равен 1,5°С/100км и отклонен на 10° влево от
барического. Определить геострофическую адвекцию.
Контрольная работа № 4
Вариант 1.
Задача 1. Каков радиус кривизны линии тока, если движение безвихревое, а
скорость ветра на линиях тока, отстоящих друг от друга на 400 км, составляет соответственно
7,5м/с и 12,5м/с?
Задача 2. В области с изотермами, направленными по широтным кругам и
отстоящими друг от друга в среднем на 400км.ветер, согласно шаропилотным
данным, западный, направлен под углом 30° к изобарам и имеет скорость 8м/с. Найти величину и
направление вектора отклонение ветра от геострофического. Широта места 60°.
Задача 3. Расстояние между соседними круговыми изогипсами в циклоне на
карте АТ500 масштаба 1:2×107 равно 1,5 см. Определить скорость градиентного ветра в точке на расстоянии
500 км от центра циклона. Широта места 50°. Рассчитать по точной формуле.
Вариант 2.
Задача 1. На сколько процентов и как должна меняться на расстоянии 500 км
скорость ветра в направлении потока, чтобы несмотря на расходимость на 15° линий тока, отстоящих друг от друга
на 450км, движение было бездивергентным?
Задача 2. Чему равен и как направлен на широте 50° вектор ускорения движения воздушного
потока, если геострофический ветер 8,7 м/с отклонен на 30° влево от реального ветра, скорость
которого составляет 10 м/с?
Задача 3. Найти максимально возможную скорость градиентного ветра в
антициклоне в точках, удаленных на 500 км от центра, и минимально возможное
расстояние между изогипсами на карте абсолютной топографии масштаба 1:2×107, отвечающее этому значению.
Широта места 55°.
Вариант 3
Задача 1. На сколько градусов должны сходиться линии тока, отстоящие друг
от друга в среднем на 350 км, чтобы, несмотря на рост скорости ветра 11 м/с на
2 м/с на каждые 500 км вдоль потока, движение было бездивергентным?
Задача 2. На сколько процентов и как изменится скорость воздушного потока
за 3 часа, если отклонение ветра от геострофического направлено на 30° влево от реального ветра и меньше
его в 5 раз? Широта места 60°.
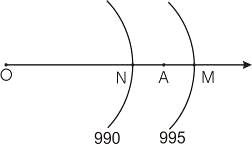
Задача 3. Определить скорость градиентного ветра в циклоне при следующих
данных на синоптической карте (рис. 6) ОА=r=800км, AN=200
км, AM=160км. Широта места 55°.