Астрономические соотношения, используемые при построении навигационных систем
Контрольная работа
АСТРОНОМИЧЕСКИЕ СООТНОШЕНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ
ПОСТРОЕНИИ НАВИГАЦИОННЫХ СИСТЕМ
Содержание
1. Небесная сфера и система координат на ней
. Измерение времени
. Геоцентрические координаты светил. Изменение
координат во времени
. Связь между координатами точки места
наблюдения и координатами светил на сфере
Литература
Приложение
1. Небесная сфера и система
координат на ней
Понятие небесной сферы широко
используется в сферической астрономии, откуда оно и было заимствовано для
решения задач; связанных с определением таких навигационных параметров, как
координаты и курс.
Положение небесных светил в
пространстве можно было бы характеризовать линейными координатами в некоторой
ортогональной системе координатных осей. Однако расстояния от нашей планеты до
светил самые различные и, более того, точные значения этих расстояний для
многих светил просто неизвестны. В силу этого задание положения светил
линейными координатами оказывается невозможным.
При решении целого ряда
астрономических и навигационных задач требуется знать не расстояние до светила,
а только положение в пространстве линии, характеризующей направление на него.
Если связать с этой линией
единичный вектор S, начало которого расположить в точке наблюдения светила, то
положение этого вектора в пространстве может быть определено так называемыми
сферическими координатами. При этом центр сферы, естественно, будет
располагаться в точке, в которой производится наблюдение светила, а радиус
может быть произвольным, в том числе равным модулю единичного вектора (рис. 1).
При использовании сферических
координат для определения положения светил необходимо выбрать так называемую
основную (базовую) плоскость и за одну из координат принять угол, который
вектор S образует с этой плоскостью. В качестве базовой может быть принята
любая плоскость, проходящая через центр сферы. На рис.1 это плоскость Q, линия
OP - перпендикуляр к ней, а плоскость Q1 проходит через линию OP и
вектор S. Линия OM образована пересечением плоскостей Q и Q1. Угол
Ф, отсчитываемый в плоскости Q1 от линии OM, является одной угловой
координатой вектора S.
В качестве второй координаты
обычно берется угол, отсчитываемый в плоскости, принятой за основную. Если в
этой плоскости провести произвольную линию ON (см. рис.1), то угол А между этой
линией и линией OM является вторым углом, определяющим положение единичного
вектора.
Так как наблюдения светил
производятся с нашей планеты, то за основную плоскость целесообразно принимать
ту или иную плоскость, связанную с Землей. В астрономии за основные плоскости
принимаются либо плоскость горизонта места, либо плоскость земного экватора.
Если за базовую плоскость
принять плоскость местного горизонта, то положение вектора S будет
охарактеризовано двумя углами, называемыми горизонтальными координатами
светила.
Аналогично два угла,
характеризующие положение линии направления на светило (положение вектора S) в
случае, если за основную плоскость выбрана плоскость экватора, называют
экваториальными координатами светила.
Рассмотрим, как образуются эти
углы, приняв за основную плоскость местного горизонта. Пусть плоскость Q
(рис.2) соответствует плоскости горизонта. Перпендикуляр к этой плоскости
(линия ZZ1), проходящий через точку местонахождения наблюдателя,
совпадает с направлением отвесной линии в этой точке. Отвесная линия пересекает
единичную сферу (или сферу произвольного радиуса) в двух точках Z и Z1.
Первая точка носит название зенит, а вторая - надир.
Построим плоскость, проходящую
через линию зенит - надир (отвесную линию) и линию направления
на светило (вектор S). Эта плоскость в астрономии получила название плоскости
вертикала светила.
Теперь положение вектора S
относительно плоскости горизонта можно охарактеризовать углом h, который в
астрономии называют высотой светила. Высота светила отсчитывается от плоскости
горизонта к зениту и изменяется от 0 до p/2.
При отсчете от плоскости
горизонта к точке надира изменение высоты происходит от 0 до -
p/2.
Вместо высоты светила иногда
используется понятие зенитного расстояния светила z, определяемое следующим
образом: z = p/2 - h.
Для задания второй координаты,
определяющей положение вектора S, поступим следующим образом. Пересечем
единичную сферу плоскостью, совпадающей с плоскостью меридиана точки 0 -
точки, в которой находится наблюдатель. Напомним, что плоскость меридиана
проходит через ось вращения Земли и отвесную линию точки наблюдения.
Следовательно, для построения
этой плоскости на рис.2 необходимо провести линию, параллельную оси вращения
Земли и воссоздать плоскость, проходящую через эту линию и линию зенит-надир.
Полагая, что линия РСРЮ параллельна оси вращения Земли,
находим, что плоскость Q2 соответствует плоскости меридиана места.
Эту плоскость в астрономии называют плоскостью небесного меридиана.
Линия, параллельная оси
вращения Земли, получившая название оси мира, пересекает сферу в двух точках РС
и РЮ, называемых полюсами мира.
Вращение Земли вокруг своей оси
вызывает кажущееся вращение светил вокруг оси мира. Полюс, относительно
которого кажущееся вращение светил происходит против часовой стрелки (для
наблюдателя, находящегося в центре сферы), назван северным полюсом мира,
противоположный - южным полюсом.
Плоскость меридиана пересечет
плоскость местного горизонта по линии СЮ, называемой полуденной линией. Эта
линия пересекает сферу в двух точках С и Ю. Первая, расположенная наиболее
близко к северному полюсу мира, носит название точки Севера, а противоположная
ей точка называется точкой Юга.
Теперь вторую координату,
определяющую положение вектора S, можно задать углом, который в плоскости
горизонта составляют между собой полуденная линия СЮ и линия пересечения
плоскостей вертикала светила и истинного горизонта OM. Этот угол, называемый
азимутом светила, отсчитывается от Ю до точки M, т. е. определяется дугой ЮМ.
Обозначается этот угол обычно АЮ или просто А и изменяется от О до 2p.
В навигации за азимут светила принимается угол, определяемый дугой СЮМ и
обозначается АС.
Нетрудно видеть, что
С
= p
+ АЮ.
Заметим, что поскольку азимут
светила измеряется в плоскости горизонта, то эту плоскость часто называют
азимутальной плоскостью или плоскостью азимута. Таким образом, положение линии
направления на светило, или положение светила на сфере будет охарактеризовано
двумя углами: высотой светила h и его азимутом А. Углы высоты и азимута обычно
называют горизонтальными координатами светила.
В астрономии вводятся некоторые
понятия, связанные с использованием горизонтальной системы координат. Так,
плоскость, проходящую через отвесную линию ZZ1 и перпендикулярную
плоскости меридиана, называют плоскостью первого вертикала. Линия, образованная
пересечением плоскостей горизонта и первого вертикала, проходит через две точки
на сфере: Востока (В) и Запада (3).
Если пересечь сферу плоскостью,
параллельной плоскости истинного горизонта и проходящей через точку, в которой
линия направления на светило пересекает сферу (плоскость Q3 на
рис.2), то в результате на сфере получим так называемый малый круг (в отличие
от больших кругов, образующихся при пересечении сферы плоскостями, проходящими
через ее центр). Этот малый круг в астрономии называют альмукантаратом.
Перейдем к рассмотрению
экваториальных координат светила. В этом случае за основную плоскость
принимается плоскость, параллельная экватору (плоскость Q на рис.3), а ось мира
будет перпендикулярна к этой плоскости. Построим также плоскость истинного
горизонта (плоскость Q1). Обе эти плоскости перпендикулярны
плоскости PСZPЮ, т. е. плоскости меридиана места
(небесного меридиана).
Очевидно, что линия пересечения
этих плоскостей будет перпендикулярна плоскости меридиана. Следовательно, эти
плоскости пересекаются по линии Восток-Запад.
Определим угол между полуденной
линией и линией пересечения плоскостей экватора и местного меридиана.
На рис.3 линия OZ есть отвесная
линия, проведенная в точке нахождения наблюдателя. Угол, который эта линия
образует с линией пересечения плоскостей экватора и меридиана, есть широта
места j.
Нетрудно видеть, что угол между полуденной линией и линией пересечения
плоскостей экватора и меридиана будет 90°- j.
Проведем через ось мира и линию
направления на светило плоскость и зададим положение вектора S относительно
плоскости экватора углом d (см. рис.3). Этот угол в астрономии
носит название склонения светила, а плоскость, в которой он измеряется -
плоскость склонений. Изменяется склонение от 0 до +p/2
при отсчете к северному полюсу мира. Или от 0 до -p/2 при
отсчете к южному полюсу.
За вторую координату,
определяющую положение вектора, примем угол t, который образуют между собой
линии пересечения плоскости склонения и меридиана с плоскостью экватора. Этот
угол называют часовым углом светила. Отсчет угла t в астрономии ведется от
южной точки экватора к точке Запада (по ходу часовой стрелки). Изменяется этот
угол от 0 до 2p или от 0 до 24 ч. Углы d
и t образуют так называемые экваториальные координаты светила.
Однако использование в качестве
координаты, определяющей положение вектора S, часового угла светила t не
является единственно возможным решением.
В принципе, в качестве второй
угловой координаты можно использовать угол между линией пересечения плоскостей
склонений и экватора и некоторой линией, лежащей в плоскости экватора. В
астрономии за эту линию принимается прямая, по которой пересекаются плоскости
экватора и эклиптики.
В первом приближении за
плоскость эклиптики можно принять плоскость, в которой расположена траектория,
описываемая Солнцем при его видимом годичном движении (т. е. та траектория,
которую видит наблюдатель, находящийся на Земле).
В действительности имеет место
движение системы Земля - Луна вокруг Солнца (точнее, центра
масс солнечной системы).
Движение происходит в
плоскости, проходящей через линию, соединяющую центр масс солнечной системы с
центром масс системы Земля - Луна, и вектор скорости этой
системы.
Указанная плоскость не занимает
неизменного положения в мировом пространстве, а совершает весьма сложное
движение, определяемое движением центра масс системы Земля -
Луна, которое слагается из длиннопериодических, или вековых, изменений и
короткопериодических колебаний.
За плоскость эклиптики в
астрономии принимают плоскость, проходящую через линию, соединяющую центр масс
солнечной системы с центром масс системы Земля - Луна, и
вектор скорости последней и совершающую только вековые колебания в
пространстве.
Эта плоскость получила название
гелиоцентрической плоскости эклиптики. Параллельную ей плоскость, проходящую
через центр Земли, называют геоцентрической плоскостью эклиптики. Последняя
наклонена к плоскости Земного экватора под углом e (рис.4).
Этот угол в силу вековых изменений положения гелиоцентрической плоскости
эклиптики не остается постоянным. Однако его изменения чрезвычайно малы. Так, в
момент начала 1900г. величина угла наклона эклиптики к плоскости экватора
составляла e = 23° 27’09", 26, а к началу 1960 г. e
= 23° 26' 40", 15. Линия пересечения плоскостей эклиптики и экватора
используется в качестве начальной при отсчете одной из экваториальных координат
светила. Эта линия пересекает большой круг экватора в двух точках: точке,
обозначаемой знаком ¡ (знак созвездия Овна),
называемой точкой весеннего равноденствия, и противоположной ей точке осеннего
равноденствия, обозначаемой знаком ?. B точке весеннего
равноденствия Солнце, двигаясь из южного полушария в северное, оказывается
ежегодно 21 марта, а в точке осеннего равноденствия -
23 сентября, когда имеет место движение Солнца из северного полушария в южное.
На рис.3 линия O¡
соответствует линии пересечения плоскостей эклиптики и экватора. Отсчитываемый
от этой линии (против часовой стрелки) угол a называется прямым
восхождением светила, он изменяется от 0 до 2p. Итак, в
качестве экваториальных координат светила используются либо углы d
и t, либо d и a.
В качестве базовой плоскости
можно принять плоскость эклиптики. Линия OP, перпендикулярная этой плоскости
(рис.5), пересекает сферу в точке P, называемой эклиптическим полюсом.
Проведя плоскость, проходящую
через линию OP и вектор S, определим положение вектора 5 двумя углами b к L,
называемыми соответственно эклиптическими широтой и долготой. Последний угол
отсчитывается от линии, проходящей через точки ¡
и ?.
Координаты b и L b астрономии
называют эклиптическими.
. Измерение времени
Для измерения времени
необходимо установить некоторую единицу или систему таких единиц.
В качестве единицы можно
использовать период повторяемости какого-либо природного или искусственного
процесса (например, колебания маятника), лишь бы продолжительность этого
периода была одинаковой.
В астрономии и повседневной
практике измерение времени основано на наблюдении кажущегося вращения Солнца
или звезд, вызванного вращением Земли вокруг своей полярной оси. За счет этого
вращения небесное светило проходит через меридиан наблюдателя. Моменты
прохождения светила через меридиан наблюдателя (небесный меридиан) в астрономии
называют кульминацией. Верхней кульминацией называют момент, когда светило
находится на меридиане наблюдателя в точке, наиболее близко расположенной к
зениту. Нижняя кульминация - это момент прохождения светила
через меридиан наблюдателя в точке, наиболее удаленной от зенита. Интервал
времени между двумя последовательными кульминациями светила называют сутками.
Различают следующие понятия
суток:
Звездные сутки -
интервал времени между двумя последовательными верхними кульминациями выбранной
звезды. Обычно принимается, что продолжительность звездных суток одинакова для
всех «неподвижных» звезд. Поскольку отсчет начала звездных суток можно вести от
кульминации произвольно выбранной звезды, то для устранения возможных при этом
недоразумений отсчет звездных суток в астрономии производят от момента верхней
кульминации точки весеннего равноденствия.
На рис.6 изображен вид на
небесную сферу со стороны северного полюса мира: линия PСM1 соответствует линии пересечения
меридиана наблюдателя с экватором; линия РC ¡
соответствует линии пересечения плоскости склонения точки ¡
с экватором; линия PСS образована пересечением плоскости склонений
звезды с экватором.
Из рис.6 следует
= t¡
= a
+ t .(1)
Таким образом, звездное время S
на меридиане наблюдателя в любой момент численно равно часовому углу точки
весеннего равноденствия.
Если звезда находится в верхней
кульминации, то t = 0 и S = a.
При нахождении звезды в нижней кульминации S = a
+ 12h.
На рис.7 линия РСГ соответствует
линии пересечения гринвичского меридиана и экватора; линия РСМ2
образована пересечением меридиана второго наблюдателя и экватора.
Из рисунка легко получить
следующие соотношения:
t1 = tГ +
l2
; t2 = t1 + l2;(2)1
= t1 + a,; S2 = t2 + a,
(3)
где tГ -
гринвичский часовой угол.
Из которых следует
2
-
t1 = l2
-
l1;
S2- S1 = l2
-
l1
.
(4)
Истинные солнечные сутки -
это интервал времени между двумя последовательными нижними кульминациями центра
Солнца.
Продолжительность истинных
солнечных суток не одинакова. Разница между самыми «длинными» и самыми
«короткими» истинными солнечными сутками составляет примерно 51 с. Это
объясняется тем, что кажущееся движение Солнца по эклиптике происходит
неравномерно, и в силу этого вращение геоцентрического радиуса-вектора
Солнца вокруг оси мира будет совершаться с переменной угловой скоростью.
Средние солнечные сутки -
это интервал времени между двумя последовательными нижними кульминациями
среднего Солнца.
Под средним Солнцем понимается
воображаемая точка, которая равномерно движется (один оборот в год) по большому
кругу экватора, причем ее геоцентрический радиус-вектор
вращается вокруг оси мира так, что его вращение, наблюдаемое со стороны
северного полюса мира, происходит против часовой стрелки (вращается в ту же
сторону, что и геоцентрический радиус-вектор Солнца).
Продолжительность средних солнечных
суток постоянна.
Истинное солнечное время на
данном меридиане
mʘ
= tʘ
+ 12h ,
где ʘ - астрономический
знак истинного Солнца. Среднее солнечное время на меридиане наблюдателя
mÅ
= tÅ
+
12h,
где Å
-
знак среднего Солнца.
Для установления связи между
истинным и средним солнечным временем вводится так называемое уравнение
времени.
= aÅ
+ tÅ;
= aʘ
+ tʘ ,
tÅ
-
tʘ = aÅ -
aʘ
= Е.(5)
Выражение (5) носит название
уравнения времени. Значения E даются в астрономических ежегодниках на каждый
день года. Разность времени, исчисляемого по среднему и истинному Солнцу в
течение года, изменяется в пределах от +14,4 до - 16,4 мин.
В авиационной навигации
необходимость учета уравнения времени возникает, главным образом, тогда, когда
требуется определить гринвичский часовой угол истинного Солнца. Для этой цели
на борту ЛА используются соответствующие таблицы или номограммы.
Из (1) и (5) нетрудно найти,
что
trʘ
=
tr Å -
Е.
(6)
Значение же гринвичского
часового угла среднего Солнца trÅ
может
давать бортовой хронометр.
В астрономии местное среднее
солнечное время гринвичского меридиана называют всемирным или мировым временем
и обозначают T0.
Очевидно, что: T0 = tr
Å .
Местное (на данном меридиане) среднее солнечное время будет равно
т = T0 + lh,
где lh
-
восточная долгота в единицах времени.
Путем многочисленных наблюдений
установлено, что интервал времени между, двумя последовательными прохождениями
Солнца через точку весеннего равноденствия составляет 365,2422 средних
солнечных суток. Принимается, что среднее Солнце последовательно проходит через
точку весеннего равноденствия за этот же промежуток. Следовательно, прямое
восхождение среднего Солнца ежесуточно возрастает на
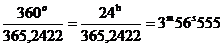
и при этом среднее Солнце смещается
среди неподвижных звезд к Востоку. Вследствие этого средние солнечные сутки
оказываются продолжительнее звездных на 3m56s,555 и точка
весеннего равноденствия за год будет иметь одну «лишнюю» верхнюю кульминацию по
сравнению со средним Солнцем. Таким образом, в году будет 366,2422 звездных
суток.
Если интервал времени в звездных
единицах есть DS, а в
средних солнечных Dm, то
DS = kDm,
где k = 366,2422/365,2422 =
1,002738. Соответственно,
Dm = k1DS,
где k1 =
365,2422/366,2422 = 0,99727.
Для определения местного
звездного времени по известной долготе и местному среднему солнечному времени,
а также для определения гринвичского звездного времени Sr используют
разработанные в астрономии методики [1]. Если, например, в точке старта JlA
определена величина Sr , то ее изменение в процессе полета можно
воспроизвести с помощью звездного бортового хронометра.
Положим, что в процессе полета
определен (вычислен) часовой угол некоторой звезды
= S -
a
= Sr - а. (7)
Поскольку в (7) известны
величины t, Sr и а, то можно определить lВ.
Поясное время введено с целью
избежать неудобств, возникающих в связи с тем, что на каждом меридиане местное
время имеет свое значение.
Вся поверхность земного шара
разделена на 24 часовых пояса (протяженность каждого пояса по долготе 15°) и
время в каждом пункте, лежащем в пределах данного пояса, принято равным времени
основного (среднего) меридиана данного пояса.
Основной меридиан начального,
нулевого пояса есть гринвичский меридиан.
Границы часовых поясов не
проходят строго по дугам больших кругов меридианов, а проведены согласно
государственным границам, большим рекам, водоразделам, железным дорогам и т. п.
Декретное время. Декретом
Совета Народных Комиссаров от 16 июня 1930г. в нашей стране было установлено
время, согласно которому стрелки всех часов были переведены на час вперед по
сравнению с поясным временем. Это было сделано из соображений более полного
использования светлого времени суток. Таким образом, декретное время отличается
от поясного на один час. Декретное время второго часового пояса в СССР называется
московским временем.
В ряде стран стрелки часов
переводятся на 1 ч вперед против поясного времени только летом. Такое время
называют летним временем. Начало и конец летнего времени устанавливаются
распоряжением правительства.
Эфемеридное время. Практически
существует два понятия времени - полученное из наблюдений и определяемое
вращением Земли и равномерное, служащее аргументом при различных вычислениях.
Наблюдаемое время зависит от колебаний угловой скорости Земли и в силу этого
неравномерно. Под эфемеридным или ньютоновским временем понимают равномерное
время, являющееся аргументом при вычислении положения небесных тел и, в
частности, при составлении Астрономических Ежегодников, в которых даются
предвычисленные значения координат светил.
. Геоцентрические координаты
светил. Изменение координат во времени
При введении в рассмотрение
сферических координат светила предполагается, что центр единичной сферы -
О (или центр сферы произвольного радиуса) расположен в точке, в которой
находится наблюдатель.
Наблюдение светила производится
либо с поверхности Земли, при этом наблюдатель участвует в суточном вращении
Земли и движется вместе с нею по ее орбите, либо с подвижного объекта
(самолета). В этом случае помимо указанных движений точка наблюдения (астрономический
прибор) участвует еще и в движении относительно Земли.
Естественно, встает такой
вопрос -
будут ли изменяться сферические координаты светила при изменении положения в
пространстве точки наблюдения? Если координаты изменяются, то для каждого
положения точки наблюдения (центра сферы) значение координат будет свое. Если
наблюдаемые координаты светил не зависят от положения точки наблюдения, то,
следовательно, центр сферы может располагаться в произвольной точке, например в
центре Земли.
Угловые координаты светил могут
менять свою величину из-за влияния следующих факторов:
- изменения положения в
пространстве орта S, которое имеет место при перемещении точки начала вектора и
точки, в которую он направлен;
- изменения пространственного
положения базовых плоскостей и линий, от которых производится отсчет углов.
Перенос начала вектора S (точки
приложения), например, из точки наблюдения в центр Земли теоретически приводит
к изменению угловых координат наблюдаемых светил (явление параллакса). Однако
для удаленных звезд это изменение столь мало, что практически для целей
навигации им можно пренебречь, поскольку величина годичного параллакса звезд не
превышает 1². Можно также не принимать во внимание
собственное движение звезд. Средний суточный параллакс Солнца достигает
примерно 8². Суточный параллакс близких планет составляет
примерно 1², а для Луны - до 2°. Для
искусственных путников параллакс может достигать существенных величин.
Таким образом, применительно к
звездам совмещение центра сферы с центром Земли не приводит к существенным
искажениям угловых координат. При наблюдении же других небесных тел явление
параллакса должно приниматься во внимание. Координаты светил, определяемые на
небесной сфере, центр которой совмещен с центром Земли, называют геоцентрическими.
При отсчете экваториальных
координат светил базовой является плоскость экватора, определяемая как
плоскость, перпендикулярная оси вращения Земли. Ориентация мгновенной оси
вращения Земли относительно звезд, строго говоря, не является постоянной. Из-за
наличия лунно-солнечной прецессии вектор угловой скорости Земли движется по
образующей конуса, ось которого нормальна к плоскости эклиптики. Период
прецессии примерно 26 000 лет. За счет этого движения направление оси вращения
Земли изменяет свою ориентацию примерно на 20" в год, а линия пересечения
плоскостей эклиптики и экватора, проходящая через точки ¡
и ?
поворачивается в плоскости эклиптики на 50" в год. Этот эффект должен
учитываться при использовании значений экваториальных координат светил при точных
навигационных расчетах.
К изменению экваториальных
координат приводят также нутационные колебания Земли (I" за год), вращение
плоскости эклиптики (0,5" в год) и движение Земли относительно центра масс
системы Земля - Луна (0,1" в год). Однако влиянием этих
факторов при построении астронавигационных устройств обычно пренебрегают.
Таким образом, если
экваториальные координаты a и d
определены с учетом их изменения за счет лунно-солнечной прецессии, то на
интервале времени полета атмосферного летательного аппарата (самолета) можно
принять:
- склонения и прямые восхождения
звёзд не меняют своих величин;
- ось вращения Земли неизменно
направлена в пространстве;
- плоскости склонений звезд в
пространстве располагаются неизменно.
Часовой угол звезды не является
постоянной величиной. Выше часовой угол был определен, как двугранный угол
между плоскостью склонений и плоскостью меридиана места (небесного меридиана).
Плоскость склонений звезды не
меняет своего положения в пространстве, как при движении Земли, так и при
полете JlA относительно Земли. Плоскость же меридиана места (небесного
меридиана) вращается вокруг полярной оси Земли (оси мира) со скоростью, равной
угловой скорости Земли и, если наблюдатель находится на поверхности Земли. Если
же кроме того наблюдатель движется относительно Земли в восточном или западном
направлении, то плоскость меридиана места вращается в пространстве с угловой
скоростью, равной сумме и и скорости изменения долготы lВ.
Следовательно, часовой угол
светила изменяется либо со скоростью, равной - и (для
наблюдателя, находящегося на поверхности Земли), либо со скоростью -
= и + lВ
при полете на восток или -
= и -
l3
при полете на запад.
В астрономии и навигации
используется понятие гринвичского часового угла светила. Это двугранный угол
между плоскостями склонения светила и гринвичского меридиана. Обозначается этот
угол обычно tr.
Из рис.8 следует, что
r
= t -
lВ
или tr = t + l В.
Скорость изменения tr
определяется выражением tr = - и. Итак, для звезд
экваториальные координаты: склонение и прямое восхождение можно считать
постоянными, на интервале времени полета JIA, а часовой угол t изменяется из-за
вращения Земли и движения JIA относительно Земли.
Для планет Солнечной системы, а
также и для Солнца, постоянство величин d и a
уже не имеет места в силу их движения по собственным орбитам. Так, например,
склонение Солнца в период летнего солнцестояния "достигает величины
23°27',а в период зимнего солнцестояния - 23°27', т. е. за
год склонение Солнца изменяется примерно на 47°. Нетрудно видеть, что скорость
изменения склонения Солнца весьма мала. Так как скорости изменения склонения и
прямого восхождения Солнца невелики, то при непродолжительных полетах можно
считать углы a и d Солнца практически
постоянными.
Рассмотрим теперь, как изменяются
горизонтальные координаты светила в случае, когда имеет место движение ЛА, на
котором установлен астрономический прибор (находится наблюдатель) относительно
Земли.
Если для экваториальных
координат закономерности их изменения нетрудно было установить из качественного
рассмотрения, то в случае горизонтальных координат из чисто качественного
рассмотрения не удается получить полной картины. Поэтому определим выражения
для угловых скоростей h и АЮ аналитически.
Производную от единичного
вектора S запишем в виде
dS/dt = w
x S , (8)
где w
-
вектор абсолютной угловой скорости орта S.
С другой стороны, эту же
производную можно представить так:
dS/dt = 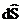 /dt + W x S, (9)
/dt + W x S, (9)
где локальная производная от вектора
- вектор
dS/dt характеризует угловую скорость, с которой вектор S меняет свое положение
относительно системы координатных осей, вращающейся с абсолютной угловой
скоростью W. Подставляя
(9) в (8), находим
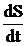 = S x (W - w). (10)
= S x (W - w). (10)
Представим векторы S и W в координатной форме в осях
трехгранника X0Y0Z0:
= i0S1 + j0S2
+ k0S1 = -
io cos h cos АЮ + j0 sin h - k0 cos h sin AЮ,
(11)
где i0, j0, k0
- орты осей
трехгранника X0Y0Z0.
Проецируя вектор u + l на оси трехгранника X0,
Y0, Z0, находим
W1 = (и + l)
cos j;
W2
= (и + l)
sin j.
(12)
Вектор j
направлен по оси Z0 и, следовательно,
W2
= -
j.
(13)
Используя (11), получим
выражение для локальной производной:
/dt = i0 (h sin h
cos АЮ + АЮcos h sin Аю) + j0h cos
h + k0 (h sin h sin АЮ - АЮ
cos h cos AЮ). (14)
Теперь, раскрывая векторное
произведение в правой части (10) и принимая при этом w
= 0, получаем следующую группу скалярных равенств:
sin h cos АЮ + АЮ
cos h sin АЮ = - j sin h + (u
+ l)
sin j
cos h sin АЮ;
hcosh = -j cos h cosAЮ
-
(и + l)
cos j
cos h sin АЮ; (15)
h sin h sin АЮ -
АЮ cos h cos AЮ = - (u + ) sin j
cos h cos AЮ - (u + l) cos j
sin h.
Из второго равенства (15) и из
совокупности первого и третьего получаем:
= -
j
cos АЮ - (и + l) cos j
sin АЮ;
АЮ = (u + l)
sin j
+ [(u + l)
cos j
cos АЮ - j sin АЮ]
tg h. (16)
Выражения (16) образуют замкнутую
систему нелинейных дифференциальных уравнений, решение которой при начальных
условиях h0 и  позволяют
найти функции A(t) и h(t). При этом конечно, должен быть известен характер
движения точки наблюдения относительно Земли, т. е. должны быть известны
функции j (t) и l (t) либо их производные.
позволяют
найти функции A(t) и h(t). При этом конечно, должен быть известен характер
движения точки наблюдения относительно Земли, т. е. должны быть известны
функции j (t) и l (t) либо их производные.
В частном случае, когда точка
наблюдения неподвижна относительно Земли система уравнений (16) принимает вид
h = -
и cos j0
sin AЮ;
АЮ = и sinj
+ и cosj
+ и cos j0
cos АЮ tg h, (17)
где j0
-
широта точки наблюдения.
. Связь между координатами
точки места наблюдения и координатами светил на сфере
Выражение (11) определяет
проекции вектора S на оси базиса i0, j0, k0
через горизонтальные координаты светила - углы h и АЮ.
Воспользовавшись рис.10,
выразим эти же проекции через экваториальные координаты d
и t:
= i0 (cos j
sin d
-
sin j
cos д cos d) + j0 (sin j
sin d+
cos j
cos d
cos t) -
k0 cos d cos t. (18)
Приравнивая члены при
соответствующих ортах в правых частях равенств (11) и (18), получаем следующую
группу равенств:
h cos АЮ = sin j
cos d
cos d
cos t -
cos j
cos d;h
= sin j
sin d
+ cos j
cos d
cos t; (19)
cos h sin AЮ = cos d
cos t,
sin h -
sin j
sin d
+ cos j
cos d
cos t;
 .
.
Учитывая, что
t = S - a
= Sr + lВ
-a,
выражения (19) и (20) можно
представить в виде
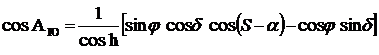
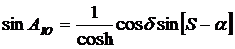 h = sin j sin d + cos j cos d cos (S - a); (21)
h = sin j sin d + cos j cos d cos (S - a); (21)
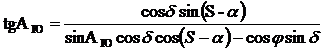 .
.
Полученные равенства устанавливают
связь между координатами светила на небесной сфере и координатами точки места
наблюдателя. Совокупность выражений (21) можно рассматривать как систему
трансцендентных уравнений относительно переменных j и S , если полагать, что
горизонтальные координаты светила h и АЮ измерены, а его
экваториальные координаты a
и d известны.
Координаты точки места j и S могут
быть определены путем решения системы - уравнений, образуемой третьим
выражением из (21) и любым из трех остальных. При этом, если в качестве второго
уравнения используется последнее выражение из (21), то, как нетрудно видеть,
система уравнений будет иметь точки разрыва при АЮ = p/2 и j = p/2.
Определив из (21) угол S, можно
найти долготу точки места наблюдения
lВ = S -
Sr . (22)
Для определения Sr -
достаточно иметь бортовой звездный хронометр.
Изложенный подход к определению
координат точки места наблюдения используется при астрономических определениях,
а в навигации он получил название метод определения координат по одному
светилу.
Если полагать, что осуществлено
измерение высот двух звезд, то, воспользовавшись третьим равенством из (21),
можем записать:
h1 = sin d1
sin j
+ cos d1
cos j
cos (S -
a1);h2
= sin d2
sin j
+ cos d2
cos j
cos (S -
a2),
(23)
где d1,2
и a1,2
-
склонения и прямые восхождения звезд.
Выражения (23) также образуют
систему трансцендентных уравнений относительно переменных j
и S.
Решая систему уравнений (23) в
бортовом вычислителе, можно определить j и S и по (22)
найти долготу точки места.
В навигации такой подход к
определению координат называют методом высот двух светил.
Соотношения вида (21) позволяют решать и
обратную задачу: по известным координатам точки места вычислить координаты
светил. Такого рода задачи могут возникать при наведении телескопов на
определенный участок неба в процессе поиска светил. Кроме того, по сути,
аналогичная задача должна решаться при астрономическом определении курса
летательного аппарата, для чего нужно знать угол азимута светила. Если
положить, что путем решения системы уравнений (23) определены координаты j
и lВ,
или эти координаты получены от других устройств, имеющихся на борту ЛА, то,
используя первую тройку выражений из (21), можно вычислить азимут светила,
причем по сочетанию знаков функций sin AЮ и cos AЮ
определить принадлежность угла азимута к определенной четверти.
Отметим, что выражения вида
(21) могут быть получены и иным путем, который обычно используется в
сферической астрономии.
Рассмотрим треугольник на сфере
с вершинами в точках РC, S и
Z (рис. 11), который в астрономии
называют параллактическим треугольником. Стороны этого треугольника можно определить
так:
C
= 90° -
d;
SZ = 90° - h; ZPC = 90° - j.
Углы при вершинах Z и Рс
соответственно будут:
CZS
= 180° -
AЮ; SPC = 180° - t.
Угол при вершине S обычно
обозначают q и называют параллактическим углом.
Поскольку определены пять
элементов параллактического треугольника, то, воспользовавшись основными
теоремами сферической тригонометрии, можно получить соотношения, связывающие
между собой элементы треугольника, в том числе соотношения вида (21).
Литература
Основная.
. Помыкаев Н.И., Селезнев В.П.,
Дмитриенко Л.А. Навигационные приборы и системы: Учебное пособие для вузов/Под
редакцией Н.И. Помыкаева. -М.:Машиностроение. 2013.
. Квареус Г., Маккэнлесс Ф.
Проектирование систем астронавигации. М.: Мир. 1970.
. Селезнев В.П. Навигационные устройства.
-М.:Машиностроение.
2004.
Дополнительная.
Справочник по космонавтике/Под редакцией
Н.Я.Кондратьева и В.А.Одинцова. -М.:Воениздат. 1966.
Приложение

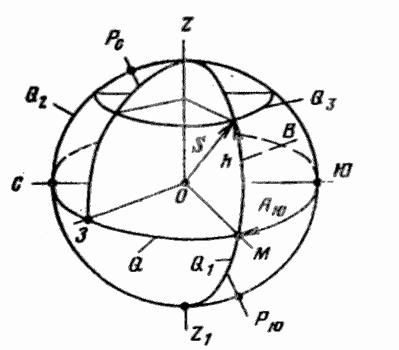
Рис. 2. Горизонтальные
координаты светила

Рис. 3. Экваториальные координаты светила
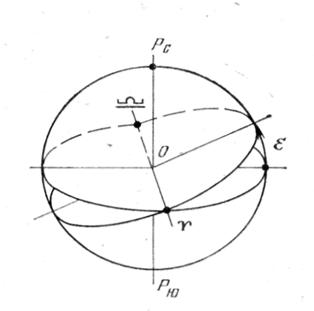
Рис.4. Расположение плоскостей эклиптики и
экватора

Рис.5. Эклиптические координаты светила
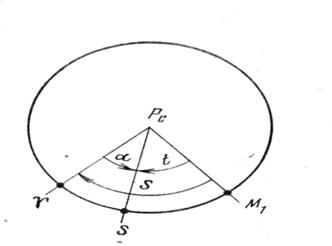
Рис. 6. Связь координат и звездного времени
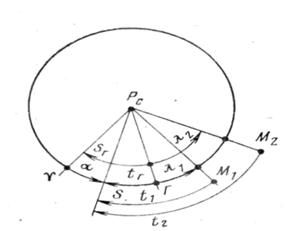
Рис.7. Связь координат и
времени
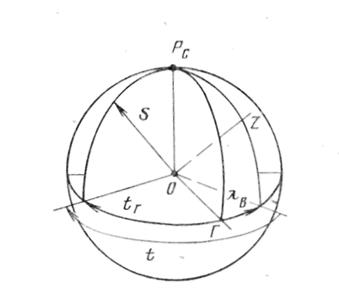
Рис. 8. Связь часового угла и долготы

Рис. 9. Угловые скорости горизонтального базиса