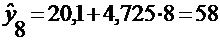Эконометрические задачи
Задача 1
Исследуется зависимость
производительности труда (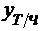 ) от уровня
механизации работ (
) от уровня
механизации работ ( %) по данным
14 промышленных предприятий (
%) по данным
14 промышленных предприятий ( - порядковый номер предприятия).
Статистические данные приведены в таблице.
- порядковый номер предприятия).
Статистические данные приведены в таблице.
Требуется:
) Найти оценки параметров линейной
регрессии 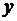 на
на 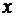 . Построить
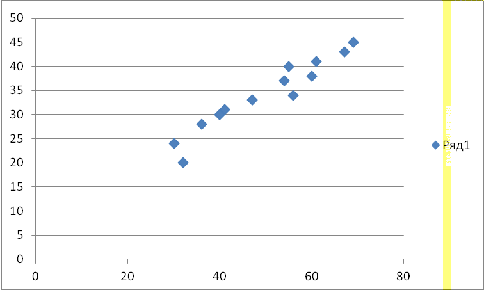
диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
. Построить
диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
) На уровне значимости 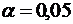 проверить
гипотезу о согласии линейной регрессии с результатами наблюдений.
проверить
гипотезу о согласии линейной регрессии с результатами наблюдений.
) С надежностью  найти
доверительные интервалы для параметров линейной регрессии.
найти
доверительные интервалы для параметров линейной регрессии.
регрессия
производительность статистика эконометрический
|
 1234567891011121314 1234567891011121314
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
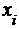 6459657173803634404445516058 6459657173803634404445516058
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
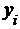 4244454749522428323435373841 4244454749522428323435373841
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
1) Для уравнения прямой регрессии 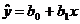 по
статистическим данным найдем оценки
по
статистическим данным найдем оценки 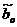 и
и 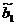 ее параметров методом наименьших
квадратов. Применим формулы:
ее параметров методом наименьших
квадратов. Применим формулы:
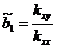 ,
, 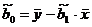 , где
, где 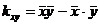 ,
, 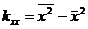 ;
;
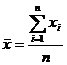 ,
, 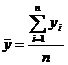 ,
, 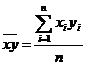 ,
, 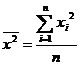 , n =14
, n =14
Вычисления  организуем в
форме следующей расчетной таблицы:
организуем в
форме следующей расчетной таблицы:
|
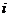  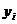 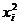 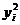 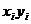
|
|
|
|
|
|
|
1
|
64
|
42
|
4096
|
1764
|
2688
|
|
2
|
59
|
44
|
3481
|
1936
|
2596
|
|
3
|
65
|
45
|
4225
|
2025
|
2925
|
|
4
|
71
|
47
|
5041
|
2209
|
3337
|
|
5
|
73
|
49
|
5329
|
2401
|
3577
|
|
6
|
80
|
52
|
6400
|
2704
|
4160
|
|
7
|
36
|
24
|
1296
|
576
|
864
|
|
8
|
34
|
28
|
1156
|
784
|
952
|
|
9
|
40
|
32
|
1600
|
1024
|
1280
|
|
10
|
44
|
34
|
1936
|
1156
|
1496
|
|
11
|
45
|
35
|
2025
|
1225
|
1575
|
|
12
|
51
|
37
|
2601
|
1369
|
1887
|
|
13
|
60
|
38
|
3600
|
1444
|
2280
|
|
14
|
58
|
41
|
3364
|
1681
|
2378
|
|
 780548461502229831995 780548461502229831995
|
|
|
|
|
|

Далее вычисляем ковариации
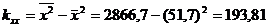 ;
;
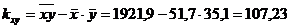 ;
;
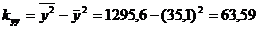 ;
;
и по указанным выше формулам находим
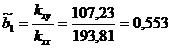 ;
;
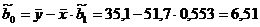 .
.
В результате получаем уравнение
прямой регрессии
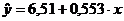 .
.
) Проверим согласованность выбранной
линейной регрессии с результатами наблюдений. Это выполняется как решение
следующей задачи проверки статистической гипотезы.
На заданном уровне значимости 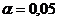 выдвигается
гипотеза
выдвигается
гипотеза 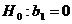 об
отсутствии линейной статистической связи. Для проверки выдвинутой гипотезы
используется коэффициент детерминации
об
отсутствии линейной статистической связи. Для проверки выдвинутой гипотезы
используется коэффициент детерминации 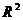 и применяется статистика Фишера F.
и применяется статистика Фишера F.
В случае парной линейной регрессии
коэффициент детерминации 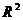 равен
квадрату выборочного коэффициента корреляции Пирсона, т.е.
равен
квадрату выборочного коэффициента корреляции Пирсона, т.е.
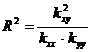 .
.
Статистика F выражается формулой
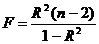 .
.
и при условии справедливости
гипотезы имеет классическое распределение Фишера с 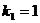 и
и  степенями
свободы.
степенями
свободы.
В соответствии с приведенными
формулами вычисляем коэффициент детерминации и наблюдаемое значение статистики
Фишера:
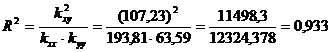 ;
;
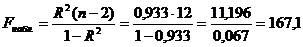 .
.
Критическое значение статистики
Фишера 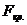 находим по
таблице квантилей распределения Фишера ([4]), исходя из равенства
находим по
таблице квантилей распределения Фишера ([4]), исходя из равенства
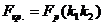 ,
,
где 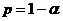 (порядок квантили),
(порядок квантили), 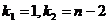 . В данном
случае
. В данном
случае 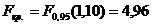 .
.
Сравниваем между собой наблюдаемое и
критическое значения статистики Фишера. Так как 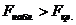 , то выдвинутая гипотеза
, то выдвинутая гипотеза 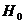 решительно
отвергается, что свидетельствует о согласии линейной регрессионной связи с
результатами наблюдений.
решительно
отвергается, что свидетельствует о согласии линейной регрессионной связи с
результатами наблюдений.
) Так как линейная регрессия 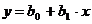 согласуется
со статистическими данными, найдем (с надежностью
согласуется
со статистическими данными, найдем (с надежностью 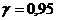 )
доверительные интервалы для параметров
)
доверительные интервалы для параметров 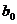 и
и 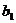 линейной регрессии.
линейной регрессии.
Применим известные формулы для
доверительных интервалов:
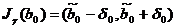 ; где
; где
 ,
,
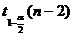 - квантиль распределения Стьюдента
порядка
- квантиль распределения Стьюдента
порядка
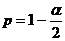 с
с 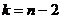 степенями свободы,
степенями свободы,
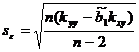 ;
;
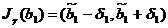 , где
, где
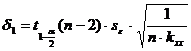 .
.
В данном случае 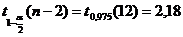 ;
;
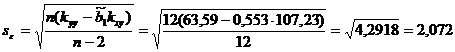 ;
;
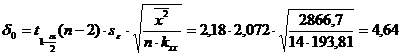 ;
;
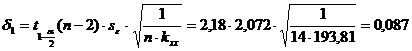 .
.
Применив приведенные выше формулы для
доверительных интервалов, окончательно получим
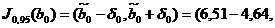
 ;
;
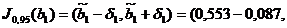
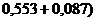 ;
;
следовательно,
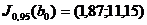 ;
;
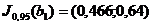 .
.
Задача 2
Исследуется зависимость
производительности труда y (условные единицы) от уровня механизации работ х1
(%) и среднего возраста работников х2 (лет) по данным 14 промышленных
предприятий (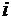 -
порядковый номер предприятия). Статистические данные приведены в таблице.
-
порядковый номер предприятия). Статистические данные приведены в таблице.
Требуется:
) Вычислить ковариации и составить
ковариационную матрицу.
) Найти оценки параметров
множественной линейной регрессии и составить уравнение плоскости регрессии 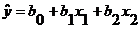 .
.
) На уровне значимости 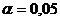 проверить
гипотезу о согласии линейной множественной регрессии с результатом наблюдений.
проверить
гипотезу о согласии линейной множественной регрессии с результатом наблюдений.
) С надежностью 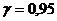 найти
доверительные интервалы для параметров множественной линейной регрессии.
найти
доверительные интервалы для параметров множественной линейной регрессии.
|
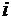 1234567891011121314 1234567891011121314
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
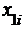 3230364041475654605561676976 3230364041475654605561676976
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
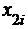 3331413946433438423539444041 3331413946433438423539444041
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
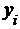 2024283031333437384041434548 2024283031333437384041434548
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
)Для вычисления ковариаций применим формулы
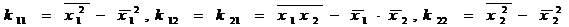
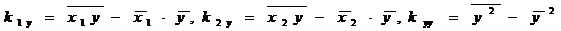 .
.
)Вычисления средних величин,
входящих в эти формулы, организуем в форме следующей расчетной таблицы:
|
i
|
X1
|
X2
|
y
|
X12
|
X22
|
y2
|
X1
* X2
|
X1
* y
|
X2
* y
|
|
1
|
32
|
33
|
20
|
1024
|
1089
|
400
|
1056
|
640
|
660
|
|
2
|
30
|
31
|
24
|
900
|
961
|
576
|
930
|
720
|
744
|
|
3
|
36
|
41
|
28
|
1296
|
1681
|
784
|
1476
|
1008
|
1148
|
|
4
|
40
|
39
|
30
|
1600
|
1521
|
900
|
1560
|
1200
|
1170
|
|
5
|
41
|
46
|
31
|
1681
|
2116
|
961
|
1886
|
1271
|
1426
|
|
6
|
47
|
43
|
33
|
2209
|
1849
|
1089
|
2021
|
1551
|
1419
|
|
7
|
56
|
34
|
34
|
3136
|
1156
|
1156
|
1904
|
1904
|
1156
|
|
8
|
54
|
38
|
37
|
2916
|
1444
|
1369
|
2052
|
1998
|
1406
|
|
9
|
60
|
42
|
38
|
3600
|
1764
|
1444
|
2520
|
2280
|
1596
|
|
10
|
65
|
35
|
40
|
4225
|
1225
|
1600
|
2275
|
2600
|
1400
|
|
11
|
61
|
39
|
41
|
3721
|
1521
|
1681
|
2379
|
2501
|
1599
|
|
12
|
67
|
44
|
43
|
4489
|
1936
|
1849
|
2948
|
2881
|
1892
|
|
13
|
69
|
40
|
45
|
4761
|
1600
|
2025
|
2760
|
3105
|
1800
|
|
14
|
76
|
41
|
48
|
5776
|
1681
|
2304
|
3116
|
3648
|
1968
|
|
Σ
|
734
|
546
|
492
|
41334
|
21544
|
18138
|
28883
|
27307
|
19384
|
|
Σ/n
|
52,43
|
39
|
35,143
|
2952,4
|
1538,9
|
1295,6
|
2063,1
|
1950,5
|
1384,6
|
Затем последовательно вычисляем ковариации:
 ,
, 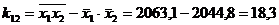 ,
,
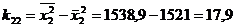 ,
,
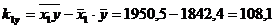 ,
,
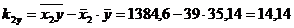 ,
,
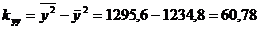 .
.
Далее составим ковариантную матрицу
объясняющих переменных 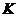 и
вектор-столбец
и
вектор-столбец 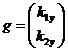 .
.
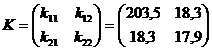 ,
, 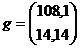 .
.
)Уравнение плоскости регрессии имеет
вид 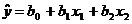 . По
статистическим данным найдем оценки
. По
статистическим данным найдем оценки 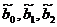 параметров множественной линейной
регрессии методом наименьших квадратов. Применим известную матричную формулу
параметров множественной линейной
регрессии методом наименьших квадратов. Применим известную матричную формулу
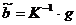 ,
,
где 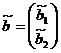 ; при этом
; при этом 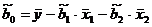 .
.
Развернутые формулы принимают вид
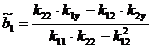 ,
, 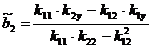 ,
,
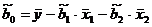 .
.
По этим формулам находим
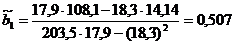 ;
;
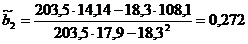 ;
;
Таким образом, уравнение плоскости
регрессии имеет вид
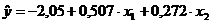 .
.
)На уровне значимости 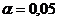 проверим
согласованность линейной трехмерной регрессионной модели со статистическими
данными. Это выполняется как решение следующей задачи проверки статистической
гипотезы. Выдвигается гипотеза
проверим
согласованность линейной трехмерной регрессионной модели со статистическими
данными. Это выполняется как решение следующей задачи проверки статистической
гипотезы. Выдвигается гипотеза 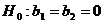 об отсутствии линейной
регрессионной связи. Для проверки выдвинутой гипотезы используется коэффициент
детерминации
об отсутствии линейной
регрессионной связи. Для проверки выдвинутой гипотезы используется коэффициент
детерминации 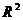 и
применяется статистика Фишера F .
и
применяется статистика Фишера F .
В случае трехмерной линейной
регрессии коэффициент детерминации и статистика Фишера выражается формулами
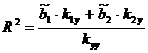 ,
, 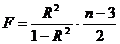 .
.
При условии справедливости гипотезы 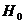 случайная
величина F имеет классическое распределение Фишера с
случайная
величина F имеет классическое распределение Фишера с 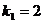 и
и 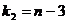 степенями
свободы.
степенями
свободы.
В соответствии с приведенными
формулами вычисляем коэффициент детерминации 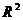 и наблюдаемое значение статистики
Фишера
и наблюдаемое значение статистики
Фишера 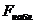 :
:
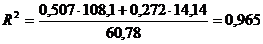 ;
;
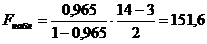 .
.
Критическое значение статистики
Фишера 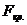 находим по
таблице квантилей распределения Фишера , исходя из равенства
находим по
таблице квантилей распределения Фишера , исходя из равенства
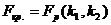 , где
, где 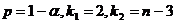 .
.
В рассматриваемом случае 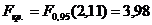 .
.
Так как, 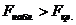 , то
выдвинутая гипотеза
, то
выдвинутая гипотеза 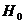 решительно
отвергается, что свидетельствует о согласии линейной трехмерной регрессии с
результатами наблюдений.
решительно
отвергается, что свидетельствует о согласии линейной трехмерной регрессии с
результатами наблюдений.
)Поскольку линейная множественная
регрессия 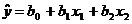 согласуется
со статистическими данными, найдем (с надежностью
согласуется
со статистическими данными, найдем (с надежностью 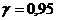 )
доверительные интервалы для параметров
)
доверительные интервалы для параметров 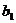 и
и 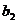 плоскости регрессию
плоскости регрессию
Применим известные формулы для
доверительных интервалов:
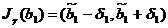 ,
, 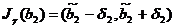 ,
,
где 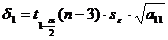 ,
, 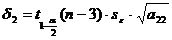 ,
,
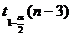 - квантиль распределения Стьюдента
порядка
- квантиль распределения Стьюдента
порядка 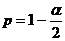 с
с 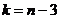 степенями
свободы,
степенями
свободы,
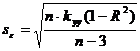 ;
; 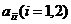 - соответствующий диагональный
элемент матрицы
- соответствующий диагональный
элемент матрицы 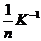 , т.е.
, т.е.
 ;
; 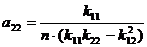 .
.
В данном случае
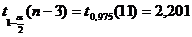 ;
;
 ;
;
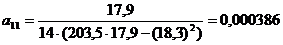 ;
; 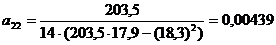 .
.
Следовательно,
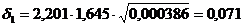 ;
; 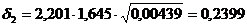 .
.
Таким образом,
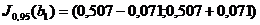 ,
,
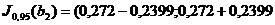 .
.
или окончательно
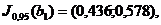
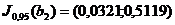
Задача 3
Исследуется зависимость
себестоимости единицы продукции (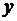 тыс. р.) от объема произведенной
продукции (
тыс. р.) от объема произведенной
продукции (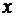 тыс. шт.)
по данным 15 предприятий (
тыс. шт.)
по данным 15 предприятий (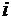 -
порядковый номер предприятия). Статистические данные приведены в таблице.
-
порядковый номер предприятия). Статистические данные приведены в таблице.
Требуется:
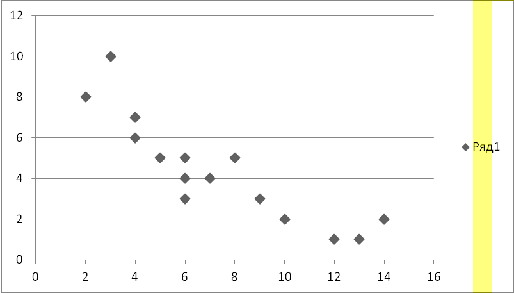
) Построить диаграмму рассеяния.
Убедиться, что между себестоимостью и объемом произведенной продукции
существует нелинейная связь.
) Считая, что регрессия 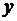 по
по 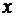 представляется
многочленом второй степени, найти оценки параметров параболической регрессии и
составить уравнение линии регрессии.
представляется
многочленом второй степени, найти оценки параметров параболической регрессии и
составить уравнение линии регрессии.
) Построить кривую регрессии и
нанести ее на диаграмму рассеяния.
|
 123456789101112131415 123456789101112131415
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
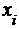 2344566678910121314 2344566678910121314
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 8107655434532112 8107655434532112
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Строим диаграмму рассеяния, нанося
на систему координат экспериментальные точки 
По характеру расположения
экспериментальных точек имеются все основания считать, что между переменными X
и Y существует нелинейная статистическая связь.
)Пусть уравнение линейной регрессии
Y по X имеет вид : 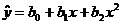
По статистическим данным задачи
найдем MHK - оценки 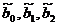 параметров
параболической регрессии. Применение метода наименьших квадратов приводит к
следующей системе нормальных уравнений :
параметров
параболической регрессии. Применение метода наименьших квадратов приводит к
следующей системе нормальных уравнений :
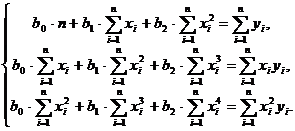
Разделим все уравнения на  и введем
обозначения:
и введем
обозначения:
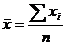 ,
, 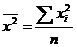 ,
, 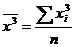 ,
, 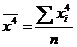 ,
,
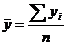 ,
, 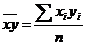 ,
, 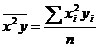 .
.
Тогда система нормальных уравнений
примет вид:
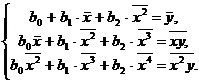
Из первого уравнения системы выразим
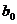
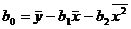
и подставим во 2-е и 3-е уравнения:
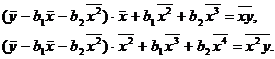
В результате для определения
параметров 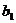 и
и 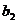 получим
следующую систему 2-х линейных уравнений:
получим
следующую систему 2-х линейных уравнений:

|
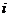  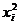 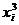 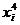 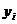 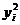 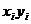 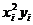
|
|
|
|
|
|
|
|
|
|
1
|
2
|
4
|
8
|
16
|
8
|
64
|
16
|
32
|
|
2
|
3
|
9
|
27
|
81
|
10
|
100
|
30
|
90
|
|
3
|
4
|
16
|
64
|
256
|
7
|
49
|
28
|
112
|
|
4
|
4
|
16
|
64
|
256
|
6
|
36
|
24
|
96
|
|
5
|
5
|
25
|
125
|
625
|
5
|
25
|
25
|
125
|
|
6
|
6
|
36
|
216
|
1296
|
5
|
25
|
30
|
180
|
|
7
|
6
|
36
|
216
|
1296
|
4
|
16
|
24
|
144
|
|
8
|
6
|
36
|
216
|
1296
|
3
|
9
|
18
|
108
|
|
9
|
7
|
49
|
343
|
2401
|
4
|
16
|
28
|
196
|
|
10
|
8
|
64
|
512
|
4096
|
5
|
25
|
40
|
320
|
|
67
|
9
|
81
|
729
|
6561
|
3
|
9
|
27
|
243
|
|
69
|
10
|
100
|
1000
|
10000
|
2
|
4
|
20
|
200
|
|
76
|
12
|
144
|
1728
|
20736
|
1
|
1
|
12
|
144
|
|
14
|
13
|
169
|
2197
|
28561
|
1
|
1
|
13
|
169
|
|
15
|
14
|
196
|
2744
|
38416
|
2
|
4
|
28
|
392
|
|
∑
|
109
|
981
|
10189
|
115893
|
66
|
384
|
363
|
2551
|
|
∑/n
|
7,27
|
65,4
|
679,2667
|
7726,2
|
4,4
|
25,6
|
24,2
|
170,0667
|
|
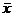 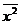 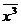  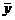 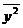 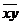 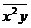
|
|
|
|
|
|
|
|
Для вычисления коэффициентов этой системы
составим расчетную таблицу
Отсюда находим
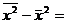 65.4-7.272 =12.55
65.4-7.272 =12.55
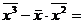 679.27-7.27*65.4=203.812
679.27-7.27*65.4=203.812
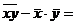 24.2-7.27*4.4= -7.788
24.2-7.27*4.4= -7.788
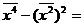 7726.2-65.42=3449
7726.2-65.42=3449
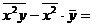 170.0667-65.4*4.4= -117.69
170.0667-65.4*4.4= -117.69
Таким образом, система линейных
уравнений имеет вид:
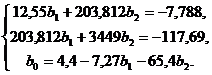
Разделим первое уравнение на 12,55,
второе уравнение на 203,18 и вычтем из второго уравнения первое. Получим:
,68b2=0,433, откуда b2=
0,063=-0,621-16,24*0,063=-1,64,= 4.4-7.27*(-1,64)-6.4*0,063=15,92
Решая полученную систему, нашли
статистические оценки параметров параболической регрессии:
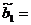 -1,64
-1,64 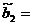 0,063,
0,063, 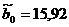 .
.
Следовательно, уравнение линии
регрессии Y по Х принимает вид:
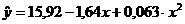 .
.
Задача 4
Поквартальная динамика объема
реализованной продукции (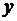 млн. р.)
объединения представлена в таблице.
млн. р.)
объединения представлена в таблице.
Требуется:
) Оценить параметры линейного тренда
методом наименьших квадратов.
) На основании линейной модели
определить прогноз экономического показателя 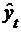 в 4-ом квартале 2013 года.
в 4-ом квартале 2013 года.
|
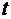 1
кв. 2012 г.2 кв. 2012 г.3 кв. 2012 г.4 кв. 2012 г.1 кв. 2013 г.2 кв. 2013 г.3
кв. 2013 г. 1
кв. 2012 г.2 кв. 2012 г.3 кв. 2012 г.4 кв. 2012 г.1 кв. 2013 г.2 кв. 2013 г.3
кв. 2013 г.
|
|
|
|
|
|
|
|
|
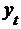 25293440444853 25293440444853
|
|
|
|
|
|
|
|
Решение:
По статистическим данным найдем
статистические оценки 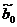 и
и 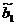 параметров
параметров 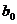 и
и 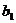 линейного
тренда
линейного
тренда 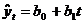 методом
наименьших квадратов. Для этого применим известные формулы:
методом
наименьших квадратов. Для этого применим известные формулы:
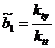 ,
, 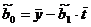 ,
,
где 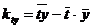 ,
,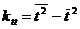 ;
;
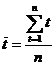 ,
, 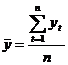 ,
, 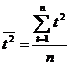 ,
, 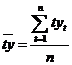 .
.
Вычисления средних значений 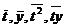 организуем
в форме расчетной таблицы.
организуем
в форме расчетной таблицы.
|
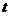
|
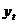
|

|
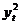
|
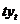
|
|
1
|
25
|
1
|
625
|
25
|
|
2
|
29
|
4
|
841
|
58
|
|
3
|
34
|
9
|
1156
|
102
|
|
4
|
40
|
16
|
1600
|
160
|
|
5
|
44
|
25
|
1936
|
220
|
|
6
|
48
|
36
|
2304
|
288
|
|
7
|
53
|
49
|
2809
|
371
|
|

|
28
|
273
|
140
|
11271
|
1224
|
|
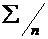
|
4
|
39,0
|
20,0
|
1610,1
|
174,9
|
|
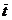
|
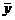
|
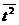
|
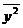
|
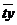
|
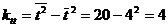 ;
;
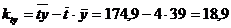
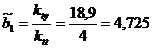
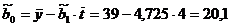
Таким образом, искомые оценки
параметров линейного тренда
равны 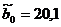 ,
,  .
.
Уравнение линейного тренда имеет вид
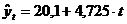
Проверка согласованности линейной
трендовой модели со статистическими данными выполняется как решение задачи
проверки статистической гипотезы 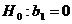 об отсутствии линейной
статистической связи на заданном уровне значимости
об отсутствии линейной
статистической связи на заданном уровне значимости 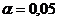 . Для
проверки гипотезы используется коэффициент детерминации
. Для
проверки гипотезы используется коэффициент детерминации 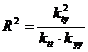 и
применяется статистика Фишера
и
применяется статистика Фишера 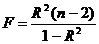 с
с 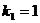 и
и  степени свободы.
степени свободы.
В рассматриваемом случае  1610.1-392=89.1
1610.1-392=89.1
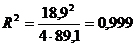
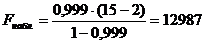
Критическое значение статистики
Фишера равно
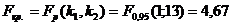 .
.
Так как 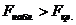 , то
выдвинутая гипотеза
, то
выдвинутая гипотеза 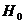 отвергается,
что свидетельствует о согласии линейной трендовой модели с результатами
наблюдений.
отвергается,
что свидетельствует о согласии линейной трендовой модели с результатами
наблюдений.
По полученному уравнению линейного
тренда
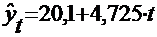
найдем точечный прогноз показателя Y
на один шаг вперед (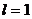 - период
упреждения). Для этого подставим в уравнение тренда значение времени
- период
упреждения). Для этого подставим в уравнение тренда значение времени
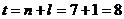 (здесь n - длина данного временного
ряда). Таким образом,
(здесь n - длина данного временного
ряда). Таким образом,