Свойства эконометрических уравнений
Контрольная
работа
Свойства
эконометрических уравнений
. Системы эконометрических уравнений
Отдельно взятое уравнение регрессии не всегда
может точно охарактеризовать влияние факторов на результативный признак, так
как факторы невозможно изменять независимо друг от друга. Кроме того, не всегда
можно определить какая переменная является зависимой, а какая независимой
переменной. В этом случае используют систему эконометрических уравнений.
В эконометрике выделяют следующие виды систем:
. Система независимых уравнений.
. Система рекурсивных уравнений.
. Система взаимозависимых (одновременных,
совместных) уравнений.
Система независимых уравнений
Система независимых переменных - это
система, где каждая зависимая переменная  рассматривается как функция только
от предопределенных независимых переменных
рассматривается как функция только
от предопределенных независимых переменных 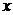 .
.
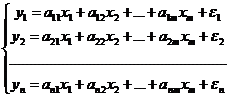
Набор факторов 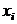 в каждом
уравнении системы может меняться.
в каждом
уравнении системы может меняться.
Каждое уравнение системы может быть
рассмотрено отдельно. Параметры каждого уравнения системы находят с помощью
метода наименьших квадратов (МНК), так как мы не можем утверждать, что величина
зависимой переменной полностью объяснена влиянием только включенных в модель
факторов, в уравнение регрессии вносим свободный член уравнения  . Например,
система уравнений для трех независимых переменных и четырех факторов имеет вид:
. Например,
система уравнений для трех независимых переменных и четырех факторов имеет вид:
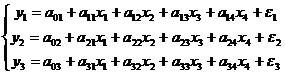
Система рекурсивных уравнений
Система рекурсивных уравнений -
система, в которой в каждом последующем уравнении зависимая переменная представляет
функцию от всех зависимых и преопределенных переменных предшествующих
уравнений.

Каждое уравнение системы может быть
рассмотрено отдельно. Параметры каждого уравнения системы находят с помощью
метода наименьших квадратов (МНК).
Примером системы рекурсивных
уравнений может служить модель предложения и спроса вида:
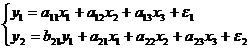
Где 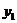 - производительность труда.
- производительность труда.
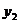 - фондоотдача.
- фондоотдача.
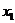 - фондовооруженность труда.
- фондовооруженность труда.
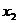 - энерговооруженность труда.
- энерговооруженность труда.
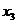 - затраты труда.
- затраты труда.
Система взаимозависимых уравнений
Система взаимозависимых уравнений -
система, в которую одни и те же зависимые переменные в одних уравнениях входят
в левую часть, а в других уравнениях входят в правую часть системы.
Так как в данной системе одни и те
же переменные рассматриваются как зависимые переменные в одних уравнениях и как
не зависимые уравнения в других, систему взаимосвязанных уравнений называют,
также системой одновременных уравнений.
Примером системы одновременных
уравнений может служить модель динамики цены и заработной платы вида:

Где  - темп изменения ежемесячной
заработной платы.
- темп изменения ежемесячной
заработной платы.
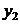 - темп изменения цен.
- темп изменения цен.
 - процент безработных.
- процент безработных.
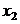 - темп изменения постоянного
капитала.
- темп изменения постоянного
капитала.
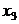 - темп изменения цен на сырье.
- темп изменения цен на сырье.
По форме система одновременных
уравнений может быть структурной или приведенной системой.
. Структурные и приведенные системы
одновременных уравнений
Структурные системы уравнения
описывают такие реальные процессы и явления экономики, которые, в силу своей
сложности, невозможно описать с помощью независимых или рекурсивных уравнений.
квадрат косвенный идентификация эконометрический
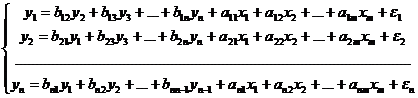
Коэффициенты 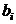 и
и 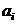 называются
структурными коэффициентами модели.
называются
структурными коэффициентами модели.
В первой части структурная модель
содержит коэффициент 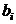 при
эндогенной переменной и коэффициент
при
эндогенной переменной и коэффициент 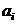 при экзогенной переменной.
при экзогенной переменной.
В приведенной выше структурной
системе уравнений переменные выражены не фактической их величиной, а в
отклонениях от среднего уровня, то есть 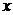 это
это 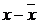 ,
,  это
это 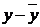 , поэтому свободный член в
уравнениях системы отсутствует.
, поэтому свободный член в
уравнениях системы отсутствует.
где:  - эндогенные переменные, это
зависимые переменные, число которых равно числу уравнений в системе, формируют
свое значение внутри модели.
- эндогенные переменные, это
зависимые переменные, число которых равно числу уравнений в системе, формируют
свое значение внутри модели.
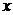 - экзогенные переменные, это
предопределенные переменные, формируют свое значение внутри системы, оказывают
влияние на эндогенные переменные, но не зависят от них.
- экзогенные переменные, это
предопределенные переменные, формируют свое значение внутри системы, оказывают
влияние на эндогенные переменные, но не зависят от них.
В структурной системе одновременных
уравнений каждое уравнение системы не может быть рассмотрено отдельно и расчет
параметров при помощи традиционного МНК невозможен. Поэтому для определения
параметров уравнения структурная форма преобразуется в приведенную форму
модели.
Приведенная форма модели - система
независимых уравнений, в которой все текущие эндогенные переменные выражены
через экзогенные переменные.
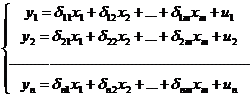
Где  - коэффициенты приведенной формы
модели;
- коэффициенты приведенной формы
модели;
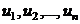 - случайные ошибки приведенной
формы модели.
- случайные ошибки приведенной
формы модели.
Так как приведенная модель состоит
из независимых уравнений, то для расчета параметров используется традиционный
МНК. Рассчитав приведенные параметры  , затем определяют эндогенные
переменные через экзогенные переменные.
, затем определяют эндогенные
переменные через экзогенные переменные.
Например, имеется структурная
модель:
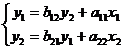
Необходимо данную структурную модель
выразить в приведенной форме.
. выразим эндогенную переменную 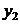 из первого
уравнения
из первого
уравнения  , как:
, как:
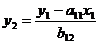
. тогда, систему уравнений можно
записать как:

. имеем равенство:

. отсюда:

. или:
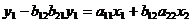
. выразим  :
:

. обозначим:
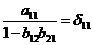
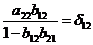
. первое уравнение структурной
модели предстанет в виде приведенной формы модели:

. выразим переменную  из второго
уравнения структурной модели
из второго
уравнения структурной модели  , как:
, как:
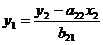
. подставим данное выражение в
первое уравнение структурной модели, получим равенство:

. выразим 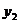 :
:

. обозначим:

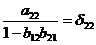
. второе уравнение структурной
модели предстанет в виде приведенной формы модели:
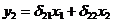
. приведенная форма модели будет
иметь вид:

3. Проблема идентификации. Необходимое и
достаточное условие идентификации
Рассчитав параметры приведенной модели можно
определить параметры структурной модели, но лишь при условии того, что модель
является идентифицируемой.
Все структурные модели могут быть:
1. идентифицируемые модели.
2. неидентифицируемые модели.
. сверхидентифицируемые модели.
Идентифицируемая модель - модель, все уравнения
которой точно идентифицируемы.
Идентифицированное уравнение - уравнение, оценки
структурных коэффициентов которого, можно однозначно (единственным способом)
определить по коэффициентам приведенной модели.
Неидентифицируемая модель - модель, в которую
входит хотя бы одно неидентифицируемое уравнение.
Неидентифицируемое уравнение - уравнение, оценки
структурных коэффициентов которого, невозможно определить по коэффициентам
приведенной модели
Сверхидентифицируемая модель - модель, среди
уравнений которой есть хотя бы одно сверхидентифицируемое уравнение.
Сверхидентифицируемое уравнение - уравнение, для
некоторых структурных параметров которого, можно получить более одного
численного значения.
Необходимое условие идентификации уравнения
модели: уравнение модели может быть идентифицируемо, если число предопределенных
переменных, не входящих в уравнение, было не меньше «числа эндогенных
переменных, входящих в уравнение минус единица»
 т.е.
т.е.
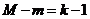 - уравнение точно идентифицируемо,
система имеет статистическое решение.
- уравнение точно идентифицируемо,
система имеет статистическое решение.
 - уравнение неидентифицируемо,
система не имеет статистического решения.
- уравнение неидентифицируемо,
система не имеет статистического решения.
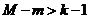 - уравнение сверхидентифицируемо,
система имеет статистическое решение.
- уравнение сверхидентифицируемо,
система имеет статистическое решение.
Где  - число предопределенных переменных
в модели.
- число предопределенных переменных
в модели.
 - число предопределенных переменных
в данном уравнении.
- число предопределенных переменных
в данном уравнении.
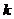 - число эндогенных переменных в
данном уравнении.
- число эндогенных переменных в
данном уравнении.
Данное условие является необходимым,
но оно не является достаточным условием, т.е. если оно не выполняется,
уравнение однозначно признается неидентифицируемым, если же оно выполняется, то
это еще не значит, что уравнение точно идентифицируемо.
Например, рассмотрим три системы
уравнений:
система

Проанализируем первое уравнение:
Число экзогенных переменных в нем  , всего
экзогенных переменных в системе
, всего
экзогенных переменных в системе  , а число эндогенных переменных в
первом уравнении
, а число эндогенных переменных в
первом уравнении  , отсюда,
так как,
, отсюда,
так как, 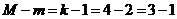 , первое
уравнение системы точно идентифицируемо.
, первое
уравнение системы точно идентифицируемо.
Проанализируем второе уравнение:
Число экзогенных переменных в нем  , всего
экзогенных переменных в системе
, всего
экзогенных переменных в системе 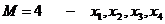 , а число эндогенных переменных в
первом уравнении
, а число эндогенных переменных в
первом уравнении 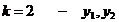 , отсюда,
так как,
, отсюда,
так как, 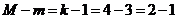 , второе
уравнение системы точно идентифицируемо.
, второе
уравнение системы точно идентифицируемо.
Проанализируем третье уравнение:
Число экзогенных переменных в нем  , всего
экзогенных переменных в системе
, всего
экзогенных переменных в системе 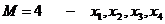 , а число эндогенных переменных в
первом уравнении
, а число эндогенных переменных в
первом уравнении  , отсюда,
так как,
, отсюда,
так как, 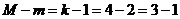 , третье
уравнение системы точно идентифицируемо.
, третье
уравнение системы точно идентифицируемо.
Так как, все включенные в
рассмотренную систему уравнения точно идентифицируемы, система признается
идентифицируемой и имеет статистическое решение.
система
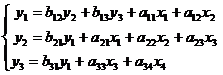
Проанализируем первое уравнение:
Первые два уравнения в нем точно
идентифицированы (см. систему 1).
Проанализируем третье уравнение:
Число экзогенных переменных в нем 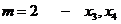 , всего
экзогенных переменных в системе
, всего
экзогенных переменных в системе  , а число эндогенных переменных в
первом уравнении
, а число эндогенных переменных в
первом уравнении 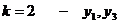 , отсюда,
так как,
, отсюда,
так как,  , третье
уравнение системы сверхидентифицируемо.
, третье
уравнение системы сверхидентифицируемо.
Так как, одно из уравнений системы
сверхидентифицируемо, и система не содержит неидентифицируемых уравнений, все
система признается сверхидентифицируемой и имеет статистическое решение.
3 система
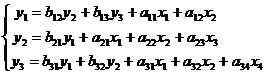
Первые два уравнения в нем точно
идентифицированы (см. систему 1).
Проанализируем третье уравнение:
Число экзогенных переменных в нем  , всего
экзогенных переменных в системе
, всего
экзогенных переменных в системе 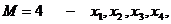 , а число эндогенных переменных в
первом уравнении
, а число эндогенных переменных в
первом уравнении  , отсюда,
так как,
, отсюда,
так как, 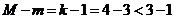 , третье
уравнение системы неидентифицируемо.
, третье
уравнение системы неидентифицируемо.
Так как, одно из уравнений системы
неидентифицируемо, все система признается неидентифицируемой, т.е. система
статистического решения не имеет.
Приведенное выше «счетное» условие  , как уже
говорилось, необходимое, но не достаточное.
, как уже
говорилось, необходимое, но не достаточное.
Достаточное условие идентификации:
уравнение будет идентифицируемо, если ранг матрицы  (состоящей
из коэффициентов при переменных, которые не входят в это уравнение) будет равен
(состоящей
из коэффициентов при переменных, которые не входят в это уравнение) будет равен
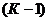
где 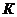 - число эндогенных переменных в
модели.
- число эндогенных переменных в
модели.
Ранг матрицы - наибольший минор
матрицы (наибольшая квадратная подматрица), определитель которого не равен
нулю.
Например, рассмотрим приведенную
систему уравнений:

) Составим матрицу для первого
уравнения системы. Так как, в первом уравнении отсутствует только одна
переменная 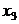 , матрица,
состоящая из коэффициентов при этой переменной, имеет вид:
, матрица,
состоящая из коэффициентов при этой переменной, имеет вид:
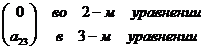
Ранг данной матрицы равен 1, 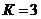 . Ранг
матрицы меньше, чем
. Ранг
матрицы меньше, чем  , то есть
1-е уравнение системы неидентифицируемо.
, то есть
1-е уравнение системы неидентифицируемо.
) Составим матрицу для второго
уравнения системы. В нем отсутствуют переменные - 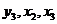 , матица
имеет вид:
, матица
имеет вид:

Ранг данной матрицы равен 2, 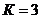 . Ранг
матрицы равен
. Ранг
матрицы равен  , то есть
2-е уравнение системы идентифицировано.
, то есть
2-е уравнение системы идентифицировано.
) Составим матрицу для третьего
уравнения. В нем отсутствуют переменные -  , матица имеет вид:
, матица имеет вид:
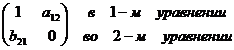
Ранг данной матрицы равен 2, 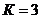 . Ранг
матрицы равен
. Ранг
матрицы равен  , то есть
3-е уравнение системы также идентифицировано.
, то есть
3-е уравнение системы также идентифицировано.
Рассматривая все систему, можно
сказать, что система неидентифицируема, так как неидентифицируемо 1-е уравнение
системы.
. Оценивание параметров структурной
модели
Параметры структурной модели
оценивают следующими способами:
1. косвенный метод наименьших квадратов;
2. двухшаговый метод наименьших квадратов;
. трехшаговый метод наименьших квадратов;
. метод максимального правдоподобия с
полной информацией;
. метод максимального правдоподобия при
ограниченной информации.
Косвенный метод наименьших квадратов (КМНК)
КМНК используют если структурная модель точно
идентифицируемо.
КМНК включает три шага:
1. Преобразование структурной модели в
приведенную форму модели, и выражение коэффициентов приведенной формы через
структурные переменные.
2. Оценивание коэффициентов каждого
уравнения приведенной формы модели обычным МНК.
. Преобразование коэффициентов
приведенной формы модели в коэффициенты структурной модели, используя
соотношения определенные в первом шаге.
Применение КМНК рассмотрим на примерах.
Пример 23. Имеем точно идентифицированную
структурную форму модели спроса и предложения.

Где 1. Определяемыми внутри модели
переменными являются эндогенные взаимозависимые переменные:
· 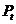 - цена
- цена
· 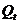 - количество товара.
- количество товара.
2. Предопределенными переменными являются:
· 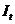 - доход - экзогенная переменная
- доход - экзогенная переменная
· 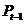 - цена в предыдущий период времени
- лаговая эндогенная переменная
- цена в предыдущий период времени
- лаговая эндогенная переменная
. 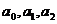 и
и 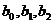 - структурные параметры модели.
- структурные параметры модели.
.  и
и  - случайные переменные.
- случайные переменные.
За ряд лет имеются данные таблица 1.
Таблица 1
|
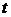 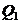 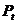  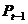
|
|
|
|
|
|
1
|
102
|
8
|
11
|
10
|
|
2
|
128
|
6
|
13
|
13
|
|
3
|
98
|
7
|
12
|
11
|
|
4
|
117
|
9
|
14
|
13
|
|
5
|
122
|
8
|
17
|
13
|
|
6
|
119
|
9
|
18
|
12
|
|
Итого
|
686478572
|
|
|
|
шаг.
Составим приведенную форму модели, не исключая
свободный член уравнения, то есть расчет будем вести не по отклонениям от
средних а по фактическим величинам:
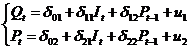
шаг.
Оценим коэффициенты каждого
уравнения приведенной формы модели обычным МНК.
Для первого уравнения приведенной
формы модели

Расчеты проведем в Microsoft Excel.
Первое. В новой книге Microsoft Excel внесем
исходные данные (рис 1).
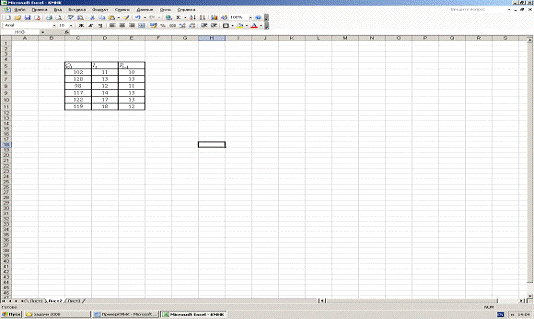
Рисунок 1
Далее нажимаем кнопку Сервис и в открывшийся
панели нажимаем кнопку Анализ данных (рис 2):
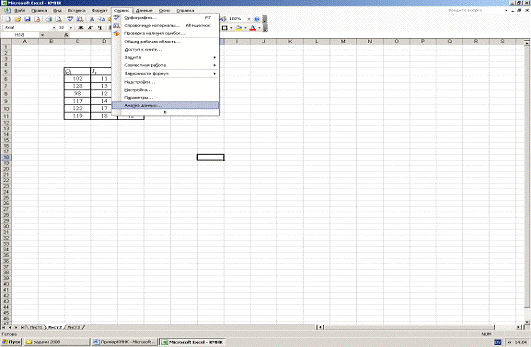
Рисунок 2.
В панели Анализ данных нажимаем Регрессия:
В панели регрессия вводим входной
интервал 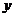 (столбик
(столбик 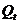 ), выделяя
столбик, содержащий данные результативного признака, и входной интервал
), выделяя
столбик, содержащий данные результативного признака, и входной интервал 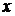 , выделяя
столбики, содержащий данные факторов (столбики
, выделяя
столбики, содержащий данные факторов (столбики 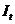 и
и 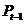 ). Ответ можно поместить на новом
рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая
выходной интервал, для чего указываем графа-клетку начала размещения ответа
(рис 3).
). Ответ можно поместить на новом
рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая
выходной интервал, для чего указываем графа-клетку начала размещения ответа
(рис 3).

Рисунок 3.
Нажимаем ОК. Появится таблица, содержащая
результаты регрессионного анализа (рис 4).
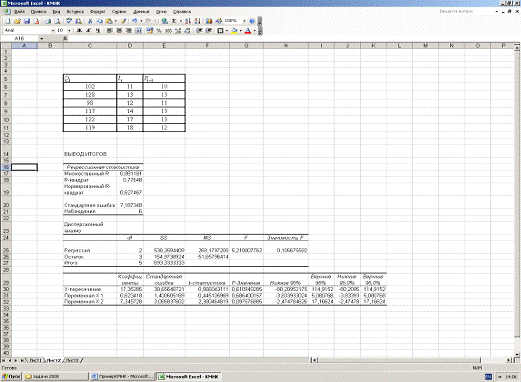
Рисунок 4.
Параметр 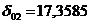 в данной
таблице находится на пересечении столбика «коэффициенты» и строки «Y-пересечение»,
параметр
в данной
таблице находится на пересечении столбика «коэффициенты» и строки «Y-пересечение»,
параметр  - находится
на пересечении столбика «коэффициенты» и строки «переменная Х1»,
- находится
на пересечении столбика «коэффициенты» и строки «переменная Х1», 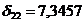 - на
пересечении столбика «коэффициенты» и строки «переменная Х2».
- на
пересечении столбика «коэффициенты» и строки «переменная Х2».
Первое уравнение приведенной формы
примет вид
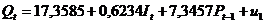
Параметры второго уравнения
приведенной модели
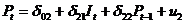
Рассчитаем, также используя пакет Microsoft Excel.
Второе уравнение приведенной модели
примет вид
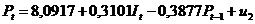
Приведенная форма модели примет вид:
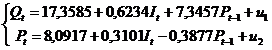
шаг.
Преобразуем параметры приведенной
формы модели.
Для того чтобы получить 1-е
уравнение структурной формы модели (зависимость  от
от  и
и 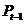 ) из 2-го уравнения приведенной
формы
) из 2-го уравнения приведенной
формы 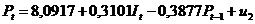 выразим
выразим  (ошибку
(ошибку 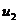 на данном
этапе расчетов проигнорируем).
на данном
этапе расчетов проигнорируем).
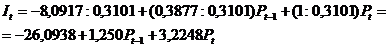
Полученное выражение  подставим в
1-е уравнение приведенной формы
подставим в
1-е уравнение приведенной формы
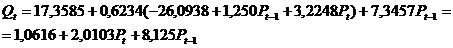
Получили первое уравнение
структурной модели
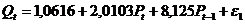
где:  ,
, 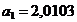 ,
, 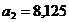
Для того чтобы определить 2-е
уравнение структурной формы модели (зависимость 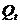 от
от 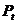 и
и  ) из 2-го уравнения приведенной
формы
) из 2-го уравнения приведенной
формы  выразим
выразим 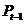 .
.
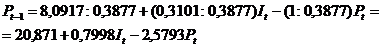
Полученное выражение 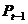 подставим в
1-е уравнение приведенной формы
подставим в
1-е уравнение приведенной формы
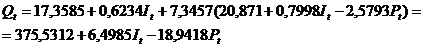
Получили второе уравнение
структурной модели
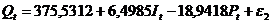
где: 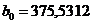 ,
,  ,
, 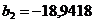
Структурная форма модели будет иметь
вид

Классический МНК даст другие,
смещенные, оценки параметров модели.
Пример 24. Имеем простейшую точно
идентифицируемую структурную модель:
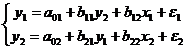
В данной модели имеем две эндогенные
переменные  и две
экзогенные
и две
экзогенные 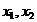 . Имеются
следующие данные таблица 2.
. Имеются
следующие данные таблица 2.
Таблица 2
|
№
|
 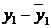 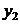   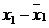 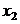 
|
|
|
|
|
|
|
|
|
1
|
21
|
-3,1250
|
24
|
-3,4375
|
0,1
|
-0,2938
|
2,05
|
-0,1406
|
|
2
|
22
|
-2,1250
|
23
|
-4,4375
|
0,2
|
-0,1938
|
2,01
|
-0,1806
|
|
3
|
21
|
-3,1250
|
22
|
-5,4375
|
0,1
|
-0,2938
|
2,06
|
-0,1306
|
|
4
|
23
|
-1,1250
|
24
|
-3,4375
|
0,3
|
-0,0938
|
2,08
|
-0,1106
|
|
5
|
24
|
-0,1250
|
29
|
1,5625
|
0,1
|
-0,2938
|
2,09
|
-0,1006
|
|
6
|
23
|
-1,1250
|
25
|
-2,4375
|
0,2
|
-0,1938
|
2,06
|
-0,1306
|
|
7
|
25
|
0,8750
|
27
|
-0,4375
|
0,4
|
0,0062
|
2,12
|
-0,0706
|
|
8
|
21
|
-3,1250
|
28
|
0,5625
|
0,6
|
0,2062
|
2,11
|
-0,0806
|
|
9
|
23
|
-1,1250
|
26
|
-1,4375
|
0,2
|
-0,1938
|
2,16
|
-0,0306
|
|
10
|
26
|
1,8750
|
28
|
0,5625
|
0,5
|
0,1062
|
2,18
|
-0,0106
|
27
|
2,8750
|
29
|
1,5625
|
0,3
|
-0,0938
|
2,15
|
-0,0406
|
|
12
|
24
|
-0,1250
|
30
|
2,5625
|
0,8
|
0,4062
|
2,19
|
-0,0006
|
|
13
|
25
|
0,8750
|
31
|
3,5625
|
0,6
|
0,2062
|
2,23
|
0,0394
|
|
14
|
26
|
1,8750
|
30
|
2,5625
|
0,2
|
-0,1938
|
2,25
|
0,0594
|
|
15
|
27
|
2,8750
|
31
|
3,5625
|
0,8
|
0,4062
|
2,29
|
0,0994
|
|
16
|
28
|
3,8750
|
32
|
4,5625
|
0,9
|
0,5062
|
3,02
|
0,8294
|
|
Итого
|
386
|
|
439
|
|
6,3000
|
|
35,05
|
0
|
|
В
среднем
|
24,1250
|
|
27,4375
|
|
0,3938
|
|
2,1906
|
|
Все переменные выражены в
отклонениях от среднего уровня, то есть 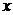 как
как 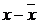 ,
,  как
как  , поэтому свободный член в
уравнениях системы отсутствует, т.е.
, поэтому свободный член в
уравнениях системы отсутствует, т.е.

шаг.
Преобразуем структурную форму модели
в приведенную:

шаг.
Оценим коэффициенты каждого
уравнения приведенной формы модели обычным МНК. Для первого уравнения
приведенной формы модели 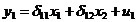 МНК даст
систему:
МНК даст
систему:
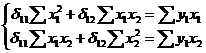
Рассчитаем все возможные значения в
таблице 3 и подставим их в систему.
Таблица 3
|
№
|
 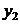  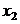 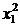 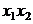  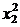 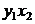
|
|
|
|
|
|
|
|
|
|
1
|
-3,1250
|
-3,4375
|
-0,2938
|
-0,1406
|
0,0863
|
0,0413
|
0,9181
|
0,0198
|
0,4394
|
|
2
|
-2,1250
|
-4,4375
|
-0,1938
|
-0,1806
|
0,0376
|
0,0350
|
0,4118
|
0,0326
|
0,3838
|
|
3
|
-3,1250
|
-5,4375
|
-0,2938
|
-0,1306
|
0,0863
|
0,0384
|
0,9181
|
0,0171
|
0,4081
|
|
4
|
-1,1250
|
-3,4375
|
-0,0938
|
-0,1106
|
0,0088
|
0,0104
|
0,1055
|
0,0122
|
0,1244
|
|
5
|
-0,1250
|
1,5625
|
-0,2938
|
-0,1006
|
0,0863
|
0,0296
|
0,0367
|
0,0101
|
0,0126
|
|
6
|
-1,1250
|
-2,4375
|
-0,1938
|
-0,1306
|
0,0376
|
0,0253
|
0,2180
|
0,0171
|
0,1469
|
|
7
|
0,8750
|
-0,4375
|
0,0063
|
-0,0706
|
0,0000
|
-0,0004
|
0,0055
|
0,0050
|
-0,0618
|
|
8
|
-3,1250
|
0,5625
|
0,2063
|
-0,0806
|
0,0426
|
-0,0166
|
-0,6447
|
0,0065
|
0,2519
|
|
9
|
-1,1250
|
-1,4375
|
-0,1938
|
-0,0306
|
0,0376
|
0,0059
|
0,2180
|
0,0009
|
0,0344
|
|
10
|
1,8750
|
0,5625
|
0,1063
|
-0,0106
|
0,0113
|
-0,0011
|
0,1993
|
0,0001
|
-0,0199
|
|
11
|
2,8750
|
1,5625
|
-0,0938
|
-0,0406
|
0,0088
|
0,0038
|
-0,2697
|
0,0016
|
-0,1167
|
|
12
|
-0,1250
|
2,5625
|
0,4063
|
-0,0006
|
0,1651
|
-0,0002
|
-0,0508
|
0,0000
|
0,0001
|
|
13
|
0,8750
|
3,5625
|
0,2063
|
0,0394
|
0,0426
|
0,0081
|
0,1805
|
0,0016
|
0,0345
|
|
14
|
1,8750
|
2,5625
|
-0,1938
|
0,0594
|
0,0376
|
-0,0115
|
-0,3634
|
0,0035
|
0,1114
|
|
15
|
2,8750
|
3,5625
|
0,4063
|
0,0994
|
0,1651
|
0,0404
|
1,1681
|
0,0099
|
0,2858
|
|
16
|
3,8750
|
4,5625
|
0,5063
|
0,8294
|
0,2563
|
0,4199
|
1,9619
|
0,6879
|
3,2139
|
|
Итого
|
0
|
0
|
0
|
0
|
1,1097
|
0,6281
|
5,0132
|
0,8259
|
5,2488
|

Разделим первое уравнение на 1,1097,
а второе на 0,6281, получим:

из второго уравнения вычтем первое
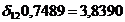
Отсюда 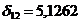
Подставим значение 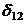 в первое
уравнение системы и найдем значение
в первое
уравнение системы и найдем значение 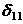
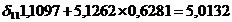
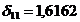
Первое уравнение приведенной формы
модели составит
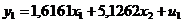
Для второго уравнения
приведенной формы модели
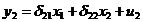
МНК
даст систему:

Рассчитаем все возможные значения в
таблице 4 и подставим в систему.
Таблица 4
|
№
|
 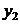  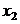 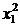 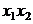 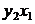 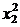 
|
|
|
|
|
|
|
|
|
|
1
|
-3,1250
|
-3,4375
|
-0,2938
|
-0,1406
|
0,0863
|
0,0413
|
1,0099
|
0,0198
|
0,4833
|
|
2
|
-2,1250
|
-4,4375
|
-0,1938
|
-0,1806
|
0,0376
|
0,0350
|
0,8600
|
0,0326
|
0,8014
|
|
3
|
-3,1250
|
-5,4375
|
-0,2938
|
-0,1306
|
0,0863
|
0,0384
|
1,5975
|
0,0171
|
0,7101
|
|
4
|
-1,1250
|
-3,4375
|
-0,0938
|
-0,1106
|
0,0088
|
0,0104
|
0,3224
|
0,0122
|
0,3802
|
|
5
|
-0,1250
|
1,5625
|
-0,2938
|
-0,1006
|
0,0863
|
0,0296
|
-0,4591
|
0,0101
|
-0,1572
|
|
6
|
-1,1250
|
-2,4375
|
-0,1938
|
-0,1306
|
0,0376
|
0,0253
|
0,4724
|
0,0171
|
0,3183
|
|
7
|
0,8750
|
-0,4375
|
0,0063
|
-0,0706
|
0,0000
|
-0,0004
|
-0,0028
|
0,0050
|
0,0309
|
|
8
|
-3,1250
|
0,5625
|
0,2063
|
-0,0806
|
0,0426
|
-0,0166
|
0,1160
|
0,0065
|
-0,0453
|
|
9
|
-1,1250
|
-1,4375
|
-0,1938
|
-0,0306
|
0,0059
|
0,2786
|
0,0009
|
0,0440
|
|
10
|
1,8750
|
0,5625
|
0,1063
|
-0,0106
|
0,0113
|
-0,0011
|
0,0598
|
0,0001
|
-0,0060
|
|
11
|
2,8750
|
1,5625
|
-0,0938
|
-0,0406
|
0,0088
|
0,0038
|
-0,1466
|
0,0016
|
-0,0634
|
|
12
|
-0,1250
|
2,5625
|
0,4063
|
-0,0006
|
0,1651
|
-0,0002
|
1,0411
|
0,0000
|
-0,0015
|
|
13
|
0,8750
|
3,5625
|
0,2063
|
0,0394
|
0,0426
|
0,0081
|
0,7349
|
0,0016
|
0,1404
|
|
14
|
1,8750
|
2,5625
|
-0,1938
|
0,0594
|
0,0376
|
-0,0115
|
-0,4966
|
0,0035
|
0,1522
|
|
15
|
2,8750
|
3,5625
|
0,4063
|
0,0994
|
0,1651
|
0,0404
|
1,4474
|
0,0099
|
0,3541
|
|
16
|
3,8750
|
4,5625
|
0,5063
|
0,8294
|
0,2563
|
0,4199
|
2,3100
|
0,6879
|
3,7841
|
|
Итого
|
0
|
0
|
0
|
0
|
1,1097
|
0,6281
|
9,1452
|
0,8259
|
6,9256
|

Разделим первое уравнение на 1,1097,
а второе на 0,6281
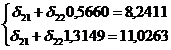
Вычтем из второго уравнение первое

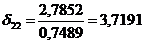
Подставим значение 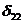 в первое
уравнение системы и найдем значение
в первое
уравнение системы и найдем значение 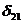
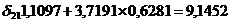
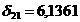
Второе уравнение приведенной формы
модели составит
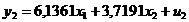
· Приведенная форма модели будет иметь вид

шаг.
Преобразуем параметры приведенной
формы модели в параметры структурной модели

· Исключим 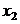 из первого уравнения
из первого уравнения 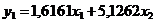 приведенной
модели, для чего выразим его из второго уравнения приведенной модели
приведенной
модели, для чего выразим его из второго уравнения приведенной модели 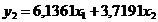 , т.е.
, т.е.

Подставим полученное выражение в
первое уравнение приведенной системы
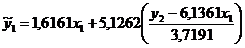
Первое уравнение структурной модели
примет вид
 или
или 
· Исключим из второго уравнения 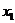 из второго
уравнения
из второго
уравнения  приведенной
модели, для чего выразим его из первого уравнения приведенной модели
приведенной
модели, для чего выразим его из первого уравнения приведенной модели , т.е.
, т.е.
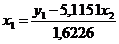
Подставим полученное выражение во второе
уравнение приведенной системы
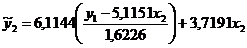
Второе уравнение структурной модели
примет вид
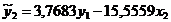 или
или 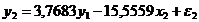
Структурная форма модели будет иметь
вид
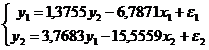
Для расчета свободных членов
уравнения 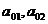 , перейдя
тем самым, от отклонений переменных от средних
, перейдя
тем самым, от отклонений переменных от средних 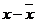 и
и  , к исходным переменным
, к исходным переменным 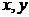 воспользуемся
готовыми формулами
воспользуемся
готовыми формулами
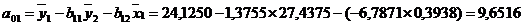

Структурная модель будет иметь вид
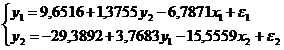
Двухшаговый метод наименьших
квадратов (ДМНК)
Параметры сверхидентифицированного
уравнения нельзя определять ни МНК ни КМНК, что связанно с наличием в данных
уравнениях в качестве фактора эндогенной переменной 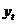 .
.
При оценке сверхидентифицированного
уравнения применяется ДМНК.
Смысл ДМНК заключается в замене в
уравнении регрессии переменной 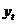 инструментальной переменной
инструментальной переменной  .
.
Инструментальная переменная  это
переменная, которая обладает следующими свойствами:
это
переменная, которая обладает следующими свойствами:
· находится в тесной связи с переменной 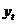
· не взаимосвязана со случайной составляющей.
При замене переменной 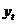 инструментальной
переменной
инструментальной
переменной 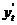 к
преобразованному уравнению можно применять классический МНК.
к
преобразованному уравнению можно применять классический МНК.
ДМНК включает следующие шаги:
1. Составление приведенной формы модели.
2. Получение значений приведенных
параметров, применяя классический МНК к каждому уравнению приведенной системы.
. Расчет эндогенных переменных,
являющимися факторами в структурной форме модели.
. Расчет структурных параметров каждого
уравнения использую классический МНК, подставляя в качестве факторов входящие в
это уравнение предопределенные переменные и расчетные значения эндогенных
переменных, полученных при шаге 1.
Данный метод называется двушаговым, так как МНК
используется два раза:
1. На первом шаге при определении
приведенной формы модели и нахождении на ее основе эндогенной переменной.
2. На втором шаге МНК применяется к
структурному сверхидентифицируемому уравнению для расчета структурных
коэффициентов модели по расчетным значениям эндогенных переменных.
Применение ДМНК рассмотрим на примере.
Пример 25. Имеем следующую модель спроса и
предложения.
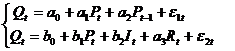
Где 1. Первое уравнение - функция
предложения.
. Второе уравнение - функция спроса.
.Определяемыми внутри модели
переменными являются эндогенные взаимозависимые переменные:
· 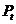 - цена
- цена
·  - количество товара.
- количество товара.
4. Предопределенными переменными являются:
·  - доход - экзогенная переменная
- доход - экзогенная переменная
· 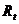 - благосостояние потребителей -
экзогенная переменная
- благосостояние потребителей -
экзогенная переменная
· 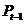 - цена в предыдущий период времени
- лаговая эндогенная переменная
- цена в предыдущий период времени
- лаговая эндогенная переменная
. 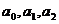 и
и 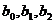 - структурные параметры модели.
- структурные параметры модели.
.  и
и  - случайные переменные.
- случайные переменные.
За ряд лет имеются данные таблица 5.
Таблица 5
|
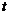    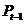 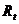 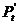
|
|
|
|
|
|
|
|
1
|
102
|
8
|
11
|
10
|
32
|
7,8674
|
|
2
|
128
|
6
|
10
|
13
|
30
|
6,6092
|
|
3
|
98
|
10
|
19
|
9
|
38
|
10,1575
|
|
4
|
117
|
9
|
14
|
13
|
35
|
7,8737
|
|
5
|
122
|
8
|
17
|
13
|
38
|
8,7245
|
|
6
|
119
|
9
|
18
|
12
|
35
|
8,7692
|
В данном случае функция предложения
является сверхидентифицированной, и применение МНК будет являться нарушением
предпосылок применения данного метода (это связанно с наличием, в качестве
фактора, эндогенной переменной  ).
).
Для расчета применим ДМНК.
шаг.
Составим приведенную форму модели:
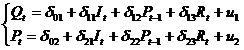
Из второго уравнения найдем значения
инструментальной переменной 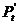
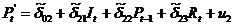
Теперь второе уравнение системы
можно записать как

где: 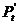 - является линейной комбинацией трех
предопределенных переменных
- является линейной комбинацией трех
предопределенных переменных 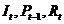 .
.
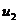 - случайная
составляющая, не коррелирует с
- случайная
составляющая, не коррелирует с 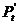
Заменим в первом уравнении
(сверхидентифицированная функция предложения)  , получим:
, получим:
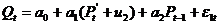
или

где: 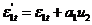
В данном уравнении переменная 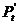 является
инструментальной переменной, так как обладает ее свойствами, а именно:
является
инструментальной переменной, так как обладает ее свойствами, а именно:
· находится в тесной связи с переменной 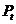
· не взаимосвязана со случайной составляющей  .
.
2 шаг.
Используя классический МНК определим параметры
приведенной модели:
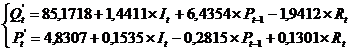
шаг.
Используя второе уравнение
приведенной модели, 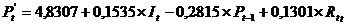 рассчитаем
значения
рассчитаем
значения 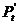 , подставляя
в него значения
, подставляя
в него значения  , результат
занесем в таблицу 33.
, результат
занесем в таблицу 33.
шаг.
Использую МНК рассчитаем структурные
параметры функции предложения

Таким образом, мы получили первое
уравнение системы - сверхидентифицированную функцию предложения:

Второе уравнение системы (функция
спроса) является точно идентифицированной, поэтому для расчета эго параметров
используем КМНК.
Из второго уравнения приведенной
системы
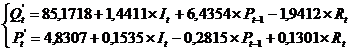
выразим переменную 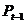 .
.
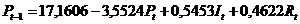
Полученное выражение подставим в первое
уравнение приведенной модели
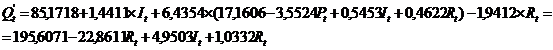
Получили второе уравнение системы
(функция спроса) структурной модели.
Итак, структурная форма модели имеет
вид:
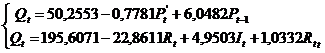
Литература
1.
Артамонов Н.В.: Введение в эконометрику. - М.: МЦНМО, 2011
.
Белолипецкий А.А.: Экономико-математические методы. - М.: Академия, 2010
.
Валентинов В.А.: Эконометрика. - М.: Дашков и К, 2010
.
Валентинов В.А.: Эконометрика: Практикум. - М.: Дашков и К, 2010
.
Колемаев В.А.: Эконометрика. - М: ИНФРА-М, 2010
.
Красс М.С.: Математические методы и модели для магистрантов экономики. - СПб.:
Питер, 2010
.
Красс М.С.: Математические методы и модели для магистров экономики. - СПб.:
Питер, 2010
.
Красс М.С.: Моделирование эколого-экономических систем. - М.: ИНФРА-М, 2010