Применение математических методов в экономике

Содержание

1. Дифференциальные уравнения

Дифференциальное уравнение первого порядка

Линейные дифференциальные уравнения первого порядка

Применение дифференциальных уравнений первого порядка в экономике

2. Интеграл

3. Производная

Геометрический смысл производной

Экономический смысл производной

Достаточные условия экстремума функции нескольких переменных

Использование производной для решения задач по экономической теории

4. Числовые последовательности

Основные понятия и определения числовой последовательности

Применение последовательности в экономике

Заключение

Список литературы

1. Дифференциальные уравнения

Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.

Дифференциальное уравнение первого порядка

Рассмотрим вопросы теории дифференциальных уравнений на примере уравнений первого порядка, разрешенных относительно производной, т.е. таких, которые допускают представление в виде:

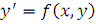 (1.1)

где f - некоторая функция нескольких переменных.

Теорема существования и единственности решения дифференциального уравнения.

Пусть в дифференциальном уравнении (1.1) функция 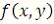 и ее частная производная 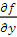 непрерывны на открытом множестве Г координатной плоскости Оху.

Тогда:

Для всякой точки  множества Г найдется решение y=y (x) уравнения (1.1), удовлетворяющее условию 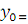y ();

2. Если два решения y=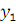 (x) и y= 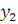(x) уравнения (1.1) совпадают хотя бы для одного значения x=, т.е. если  то эти решения совпадают для всех тех значений переменной х, для которых они определены. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде

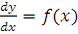 g (y) (1.2)

или в виде

M (x) N (y) dx+P (x) Q (y) dy=0, (1.3)

где , M (x), P (x) - некоторые функции переменной х, g (y), N (y), Q (y) - функции переменной у.

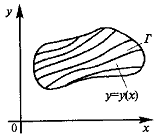
(рис. 1)

Линейные дифференциальные уравнения первого порядка

Уравнение вида:

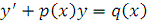, (2.1)

где р (х) и q (x) - непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Неизвестная функция и ее производная входят в указанное уравнение в первой степени - линейно, что и объясняет название уравнения.

Если q (x) 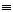 0, то уравнение (2.1) называется линейным однородным уравнением; если же функция q (x) не равна тождественно нулю, то уравнение (3.1) называется линейным неоднородным уравнением.

Для линейного уравнения первого порядка можно выписать общее решение с помощью метода вариации постоянной. Здесь это решение приводится без вывода:

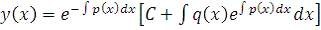. (2.2)

Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции у (х). К таковым относится уравнение Бернулли:

, (2.3)

где р и q - непрерывные функции, a n - некоторое постоянное число. При п = 0 имеем линейное неоднородное уравнение, а при n = 1 - линейное однородное уравнение Пусть п ≠ 0, n ≠ 1. Введем новую функцию:

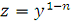_{, (}2.4) тогда .

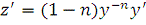Поделим обе части уравнения (2.3) на :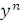

.

Умножая обе части этого уравнения на (1 - n), с учетом выражений для новой функции z и ее производной получаем линейное дифференциальное неоднородное уравнение относительно неизвестной функции z (x):

. (2.5)

В этом уравнении, метод решения которого нам известен, функция z (x) связана с искомой функцией у (x) соотношением (2.4).

Применение дифференциальных уравнений первого порядка в экономике

Задача 1. Об эффективности рекламы.

Пусть торговой фирмой реализуется некоторая продукция, о которой в момент времени t = 0 из рекламы получили информацию x₀ человек из общего числа N потенциальных покупателей. Далее эта информация распространяется посредством общения людей, и в момент времени t > 0 число знающих о продукции людей равно x (t). Сделаем предположение, что скорость роста числа знающих о продукции пропорциональна как числу осведомлённых в данный момент покупателей, так и к числу неосведомленных покупателей. Это приводит к уравнению

.

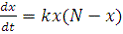Здесь k - положительный коэффициент пропорциональности. Из уравнения получаем равенство дифференциалов двух функций аргумента t:

.

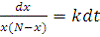Интегрируя левую и правую части, находим общее решение дифференциального уравнения:

.

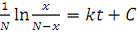В общее решение входит неопределенная константа С. Полагая NC = D, получим равенство:

,

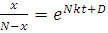из которого определим функцию x (t):

.

Здесь E = 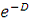. Такого вида функция называется логистической, а её график - логистической кривой.

Если теперь учесть, что х (0) = х₀ и положить х₀ = N/a, где a > 0, то можно найти значение константы Е. Логистичеcкая функция примет вид:

.

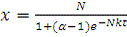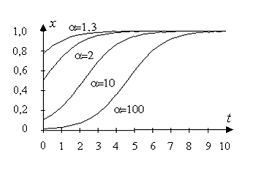
Рисунок 1.1

дифференциальное уравнение производная последовательность экономика

На рисунке 1.1 приведены примеры логистических кривых, полученных при различных значениях α. Здесь величина N условно принималась за 1, а величина k бралась равной 0,5.

2. Интеграл

Интеграл функции - аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции. Процесс нахождения интеграла называется интегрированием

Определённый интеграл - аддитивный <#"880422.files/image030.gif">

λR - длина частичного отрезка;

σR - интегральная сумма от функции f (x) на [a; b] соответствующей разбиению R;

λR - максимальная длина части отрезка.

Традиционно практическое приложение интеграла иллюстрируется вычислением площадей различных фигур, нахождением объемов геометрических тел и некоторыми приложениями в физике и технике. Однако роль интеграла в моделировании экономических процессов не рассматривается. Зачастую об экономических приложениях интеграла не идет речи и в классах экономического направления. Вместе с тем, интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике.

Начнем с широко используемого в рыночной экономике понятия потребительского излишка (разница между ценой, которую потребитель готов заплатить за товар, и той, которую он действительно платит при покупке). Предложение отдельного товара изображается графически в виде кривой с положительным наклоном, отражающей взаимосвязь между ценой единицы этого товара P и количеством товара Q, которое потребители готовы продать при каждой цене.

Отметим, что экономисты сочли удобным изображать аргумент (цену) по оси ординат, а зависимую переменную (количество товара) по оси абсцисс. Поэтому графики функций спроса и предложения выглядят следующим образом (рис.2.1).

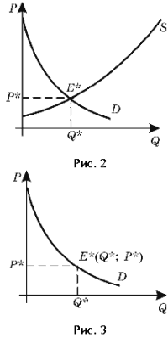
Рисунок 2.1.

Введем понятие, играющее большую роль в моделировании экономических процессов - рыночное равновесие (equilibrium). Состояние равновесия характеризуют такие цена и количество, при которых объем спроса совпадает с величиной предложения, а графически рыночное равновесие изображается точкой пересечения кривых спроса и предложения (рис.2.1), E* (p*; q*) - точка равновесия 2.

Перейдем теперь к рассмотрению приложений интегрального анализа для определения потребительского излишка. Для этого изобразим на графике обратную функцию спроса P = f (Q). Но предположим теперь, что товар в количестве Q* продается продавцами не сразу, а поступает на рынок небольшими партиями Q. Отметим, что данное допущение вполне оправдано, потому что такая схема реализации товара довольно распространена на практике и вытекает из цели продавца поддерживать цену на товар как можно выше.

Тогда получим, что сначала предлагается товар в количестве Q1 = D Q (рис.5), который продается по цене P1 = f (Q1). Так как по предположению величина Q мала, то можно считать, что вся первая партия товара реализуется по цене P1, при этом затраты покупателя на покупку такого количества товара составят P1D Q, что соответствует площади заштрихованного прямоугольника S1 (рис.5).

Далее на рынок поступает вторая партия товара в том же количестве, которая продается по цене P2 = f (Q2), где Q2 = Q1 + D Q - общее количество реализованной продукции, а затраты покупателя на покупку второй партии составят P2D Q, что соответствует площади прямоугольника S2.

Продолжим процесс до тех пор, пока не дойдем до равновесного количества товара Q* = Qn. Тогда становится ясно, какой должна быть величина D Q для того, чтобы процесс продажи товара закончился в точке Q*:

В результате получим, что цена n-й партии товара Pn = f (Qn) = f (Q*) = P*, а затраты потребителей на покупку этой последней партии товара составят PnD Q, или площадь прямоугольника Sn.

Таким образом, мы получим, что суммарные затраты потребителей при покупке товара мелкими партиями D Q равны:

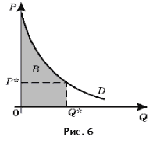
Рисунок 2.2.

Так как величина D Q очень мала, а функция f (Q) непрерывна, то заключаем, что приблизительно равна площади фигуры B (рис.6), которая, как известно, при малых приращениях аргумента D Q равна определенному интегралу от обратной функции спроса при изменении аргумента от 0 до Q*, т.е. в итоге получим, что

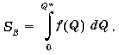
Вспомнив, что каждая точка на кривой спроса Pi = f (Qi) (i = 1, 2,., k) показывает, какую сумму потребитель готов заплатить за покупку дополнительной единицы продукта, получим, что площадь фигуры B соответствует общей денежной сумме, которую потребитель готов потратить на покупку Q* единиц товара. Разность между площадью фигуры B и площадью прямоугольника A есть потребительский излишек при покупке данного товара - превышение общей стоимости, которую потребитель готов уплатить за все единицы товара.

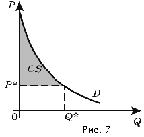
Рисунок 2.3.

Таким образом, потребительский излишек можно посчитать по следующей формуле:

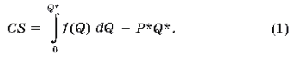
Задача 2.

Известно, что спрос на некоторый товар описывается функцией 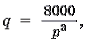а предложение данного товара характеризуется функцией q=500p. Найдите величину излишка потребителя при покупке данного товара.

Решение. Для расчета излишка потребителя сначала определим параметры рыночного равновесия (p*; q*). Для этого решим систему уравнений

Таким образом, p* = 2, q* = 1000.

Запишем формулу для вычисления потребительского излишка (1), где f (q) - функция, обратная функции

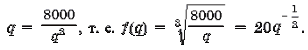
Отсюда

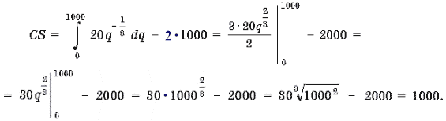
Задача 2.1 Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f (t) = 2t + 5.

Имеем:

=.

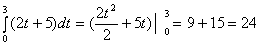3. Производная

Производной функции y = f (x) в фиксированной точке x называется предел 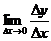 при условии существования этого предела.

Производная обозначается следующим образом f' (x) или y'. Это обозначение, а также термин первая производная ввел Ж. Лагранж

Геометрический смысл производной

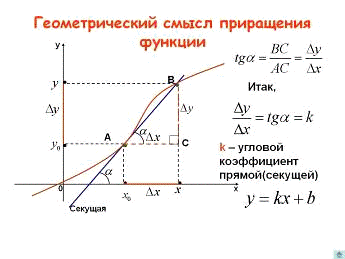
Пусть f (x) определена на некотором промежутке (a, b). Тогда 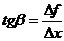 тангенс угла наклона секущей к графику функции

,

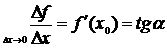где a - угол наклона касательной к графику функции f (x) в точке (x0, f (x0)). Уравнение касательной к кривой: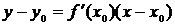

Уравнение нормали к кривой:

.

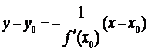Фактически производная функции показывает скорость изменения функции, т.е. как изменяется функция при изменении переменной.

Экономический смысл производной

Пусть функция u (t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t0. За период от t0 до 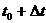количество продукции изменится от u (t0) до  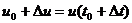Тогда средняя производительность труда за этот период 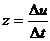, поэтому производительность труда в момент t0

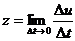
Рассмотрим еще некоторые понятия, иллюстрирующие экономический смысл производной.

Пусть y (x) - функция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение y (x) /x описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением .

Производная  выражает предельные (маргинальные) издержки производства. Величину Mf (x) = y' называют мгновенным приростом или мгновенной скоростью измененияy. Аналогично можно определить предельную выручку, предельный доход, предельную полезность и другие предельные величины.

Частной производной функции нескольких переменных по одной из этих переменных называется производная, взятая по этой переменной при условии, что все остальные переменные остаются постоянными. Например для функции двух переменных z = f (x, y) частной производной по переменной x называется производная этой функции по x при постоянном y. Обозначается частная производная по x следующим образом:

.

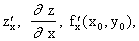
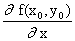Говорят, что функция  имеет в точке 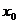 строгий локальный максимум (минимум), если эту точку можно окружить такой окрестностью (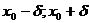), содержащейся на промежутке, где задана функция, что для всех ее точек x выполняется строгое неравенство

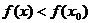 или

Если существует такая окрестность в пределах которой выполняется нестрогое неравенство

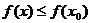 или

то говорят, что функция имеет в точке 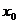 нестрогий локальный максимум (минимум).

Для максимума или минимума существует и объединяющий их термин - экстремум.

Те значения аргумента, при которых достигаются экстремумы функции, называются точками экстремума функции.

Теорема (необходимое условие экстремума).

В точке экстремума дифференцируемой функции производная ее равна нулю.

Теорема (достаточное условие экстремума) (первое правило).

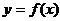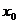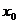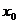Пусть функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала, кроме, может быть, самой точки . Если при переходе аргумента слева направо через точку производна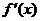я меняет знак с плюса на минус, то функция в этой точке имеет строгий локальный максимум. Если при переходе через точку 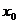производная 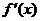меняет

знак с минуса на плюс, то функция имеет в этой точке строгий локальный минимум.

Если при переходе через точку 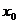производная  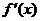сохраняет постоянный знак, то функция не имеет строгого локального экстремума.

Теорема 2 (второе правило).

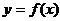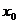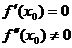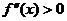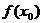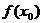Если функция дважды непрерывно дифференцируема в некоторой окрестности точки и  то в этой точке  имеет строгий локальный экстремум; а именно: если , то - строгий локальный минимум функции , и если, то-строгий локальный максимум функции  Вектор с координатами , характеризующий направление максимального роста функции 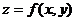в точке , называется градиентом функции 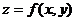 в этой точке и обозначается 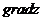или 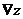. Градиент совпадает с нормалью к линии уровня 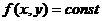) в точке .

функции. В этом состоит механический смысл градиента. С геометрической точки зрения градиент выражает направление наибольшего наклона графика функции, а с экономической - такую линейную комбинацию факторов х и у, при которой

наблюдается наибольший выход продукции на единицу этого состава.

Максимумом (минимумом) функции 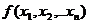 в точке M.

Называется такое значение 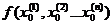, которое больше (меньше) всех других ее значений, принимаемых в точках M, достаточно близких к точке М и отличных от нее.

Необходимое условие экстремума функции нескольких переменных

В точке экстремума дифференцируемой функции нескольких переменных частные производные равны нулю.

Достаточные условия экстремума функции нескольких переменных

Пусть 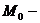стационарная точка, т.е. точка в которой выполняется равенство

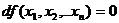
) если 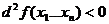 то 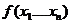 максимум функции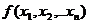

) если  то 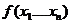 минимум функции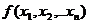

С помощью дифференциального исчисления в экономике вычисляются предельные величины, например предельные издержки. Решают задачи максимизации прибыли, оптимизации налогообложения предприятия, минимизация средних издержек, выясняют эластичность и многие другие.

Использование производной для решения задач по экономической теории

Задача 3.

Цементный завод производит Х т. цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т. цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т. в день.

Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид: К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200

Наша задача сводится к отысканию наибольшего и наименьшего значения функции У= - х2+98х+200. На промежутке [20; 90].

Вывод: x=49, критическая точка функции. Вычисляем значение функции на концах промежутках и в критической точке.

(20) =1760 f (49) =2601 f (90) =320.

Таким образом, при выпуске 49 тонн цемента в день удельные издержки максимальны, это экономически не выгодно, а при выпуске 90 тонн в день минимально, следовательно, можно посоветовать работать заводу на предельной мощности и находить возможности усовершенствовать технологию, так как дальше будет действовать закон убывающей доходности. И без реконструкции нельзя будет увеличить выпуск продукции.

4. Числовые последовательности

Основные понятия и определения числовой последовательности

Числовая последовательность есть функция натурального аргумента. Понятие числовой последовательности возникло и развивалось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей:

1) 1, 2, 3, 4, 5, … - последовательность натуральных чисел.

2) 2, 4, 6, 8, 10, … - последовательность четных чисел.

3) 1, 3, 5, 7, 9, … - последовательность нечетных чисел.

4) 1, 4, 9, 16, 25, … - последовательность квадратов натуральных чисел.

5) 2, 3, 5, 7, 11, … - последовательность простых чисел.

Число членов каждой последовательности бесконечно. Все перечисленные последовательности, кроме последнего примера, являются заданными в виду того, что для каждой из них известен общий член, то есть правило получения члена с любым номером. Для последовательности простых чисел общий член не известен, однако, еще в III в. до н.э. александрийский ученый Эратосфен указал способ получения n-го её члена ("решето Эратосфена").

Определение 1. Если каждому числу n натурального ряда чисел 1, 2,…, n,… ставится в соответствие по определенному закону некоторое вещественное число xn, то множество вещественных чисел , , 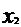, …, , 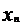(1) расположенных в порядке возрастания номеров n, называется xn числовой последовательностью.

Числа называются элементами или членами последовательности (1).

Например,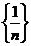 обозначается последовательность 1, 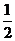, …, , …, 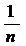а

{1+ (-1) ⁿ} - последовательность 0, 2, 0, 2, ….

Различают следующие виды последовательности:

а) монотонные последовательности;

b) ограниченные и неограниченные последовательности;

c) бесконечно малые последовательности;

d) последовательности Аршона;

e) последовательность, устанавливающаяся приближенным методом (процесс радиоактивного распада).

Применение последовательности в экономике

На финансовом рынке кредитор получает доход от предоставления денег в долг в виде, например, помещения денег на сберегательный счет, покупки акций, выдачи ссуды и т.д. Получаемый доход называется процентами и определяется кредитной ставкой.

Различают два вида процентных ставок: простые и сложные. Начисления при ставке простого процента предполагает применение ставки только к первоначальной сумме на протяжении всего срока долга. Пусть 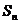 - наращенная сумма долга через 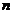 периодов после предоставления ссуды в размере  денежных единиц, а простая ставка процента за период равна i процентов. Тогда в каждом периоде процентные начисления постоянны и равны 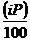. Найдем наращенную сумму долга в каждом из периодов:

, ,

.

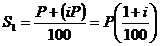Данная формула

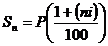, n = 0,1,.,

называется формулой простых процентов,  - множителем наращения.

Рассмотрим теперь, как изменяется сумма долга при начислении сложного процента. В этом случае доход определяется применением процентной ставки к первоначальной сумме вместе с начисленными в предыдущих периодах процентами.

При первоначальной сумме P и сложной ставке за период начисления i% наращенная сумма меняется следующим образом:

, , ,

,

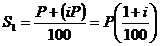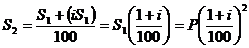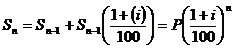Формула:

, n = 0,1, 2,.,

называется формулой сложных процентов. (3.1)

Задача 4.

Компании необходимо производить замену оборудования каждые 8 лет. Для этого выделяются определенные средства. Если компания может выделить 100000 рублей ежегодно и разместить их под 4% годовых, то какая сумма будет в ее распоряжении по окончании восьми лет?

Решение.

Пусть первоначальный депозит (сумма денег, помещённая вкладчиком в банк на определённый или неопределённый срок.

Банк пускает эти деньги в оборот, а в обмен выплачивает вкладчику проценты) 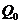помещен в банк под i=100% годовых, тогда через год сумма депозита удвоится. Предположим, что через полгода счет закрыт с результатом

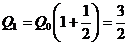
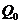
и эта сумма снова помещается на депозит. В конце года депозит будет равен

.

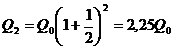Аналогично, при ежеквартальном размещении депозит в конце года будет равен

.

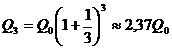Если ежемесячно повторять ту же операцию, то

,

при ежечасной операции

.

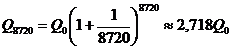Заметим, что последовательность значений увеличения первоначального вклада совпадает с последовательностью 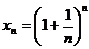, предел которой равен .

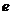В общем случае, если i - процент начисления и год разбит на n частей, то через t лет сумма депозита будет равна:

 или .

Введем новую переменную 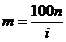, при n®¥ получим m ® ¥.

.

Данная формула называется формулой непрерывных процентов.

Ответ:

Заключение

Математика в настоящее время перестала быть предметом занятий только научной элиты; теперь занятия математикой привлекают к себе всё большее число одарённых людей. Значительно расширились область математических исследований и применения математического аппарата. Приложения математических методов проникают далеко за пределы собственно математики: в физику, новые отрасли техники, биологию, в экономику и другие социальные науки; без строгой математической логики невозможна работа юриста или менеджера. Информационно - компьютерные технологии способствовали появлению новых областей научных исследований, имеющих, несомненно, чрезвычайно огромное значение как для самой математики, так и для всех наук, непосредственно связанных с ней.

Для жизни в современном информационном обществе важным является формирование математического стиля мышления, проявляющегося в умении применять индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию. Для того чтобы уверенно чувствовать себя в современном мире, человек должен уметь проанализировать возникающую проблему, учесть все ее аспекты и сделать правильный выбор. Занятия математикой не столько самоцель, сколько средство к углублённому изучению теории и вместе с тем средство развития мышления, путь к осознанию окружающей действительности, тропинка к пониманию мира.

Список литературы

1.      Галабурдин А.В. Высшая математика. Мини-справочник для вузов. Дифференциал функции. Теорема о дифференцируемых функциях, стр.69, 2014;

2.      Галабурдин А.В. Высшая математика. Мини-справочник для вузов. Определенный интеграл, стр.111, 2014;

.        Галабурдин А.В. Высшая математика. Мини-справочник для вузов. Свойства определенного интеграла, стр.112;

.        Галабурдин А.В. Высшая математика. Мини-справочник для вузов. Частные производные, стр.89.2014;

.        Красс.М.С., Чупрынов. Б.П. Понятие производной, стр.66. Применение в экономике, стр.96, "Дело", 2010;

.        Красс.М.С., Чупрынов. Б.П. Числовые последовательности, стр.28. Применение в экономике, стр.35, "Дело", 2010.