Модифицированный симплексный метод
1. Сущность модифицированного симплексного
метода
При решении задач линейного программирования, в
которых n (количество переменных) существенно больше m (количество
ограничений), модифицированный симплекс-метод требует по сравнению с другими
значительно меньшего количества вычислительных операций и объема памяти ЭВМ.
В вычислительной схеме симплекс-метода
реализуется упорядоченный процесс, при котором, начиная с некоторой исходной
допустимой угловой точки (обычно начало координат), осуществляются последовательные
переходы от одной допустимой экстремальной точки к другой до тех пор, пока не
будет найдена точка, соответствующая оптимальному решению.
Общую идею симплекс-метода можно
проиллюстрировать на примере модели, построенной для нашей задачи. Исходной точкой
алгоритма является начало координат. Решение, соответствующее этой точке,
обычно называют начальным решением. От исходной точки осуществляется переход к
некоторой смежной угловой точке.
Выбор каждой последующей экстремальной точки при
использовании симплекс-метода определяется следующими двумя правилами.
1 Каждая
последующая угловая точка должна быть смежной с предыдущей. Этот переход
осуществляется по границам (ребрам) пространства решений.
2 Обратный
переход к предшествующей экстремальной точке не может производиться.
Таким образом, отыскание оптимального решения
начинается с некоторой допустимой угловой точки, и все переходы осуществляются
только к смежным точкам, причем перед новым переходом каждая из полученных
точек проверяется на оптимальность.
Определим пространство решений и угловые точки
алгебраически. Требуемые соотношения устанавливаются из указанного в таблице
соответствия геометрических и алгебраических определений
Симплекс-алгоритм
состоит из следующих шагов.
Шаг 0.
Используя линейную модель стандартной формы, опреде-ляют начальное допустимое
базисное решение путем приравнива-ния к нулю п - т ( небазисных )
переменных.
Шаг 1.
Из числа текущих небазисных (равных нулю) переменных выбирается включаемая в
новый базис переменная, увеличение которой обеспечивает улучшение значения
целевой функции. Если такой переменной нет, вычисления прекращаются, так как
текущее базисное решение оптимально. В противном случае осуществляется переход
к шагу 2.
Шаг 2.
Из числа переменных текущего базиса выбирается исключаемая переменная, которая
должна принять нулевое значение (стать небазисной) при введении в состав
базисных новой переменной.
Шаг 3.
Находится новое базисное решение, соответствующее новым составам небазисных и
базисных переменных. Осуществляется переход к шагу 1.
Модифицированный симплекс-метод, в особенности в
мультипликативной форме, обладает значительными преимуществами по сравнению со
стандартной формой. Это относится к точности, скорости и требованиям к памяти.
Большая часть этих преимуществ определяется тем фактором, что, как правило,
матрицы больших линейных задач (то есть с n>m>100) являются слабо
заполненными, содержат малый процент ненулевых элементов. Обычной является
плотность 5% или менее. Модифицированная форма симплекс-метода в большей
степени способна использовать преимущества, вытекающие из этого факта. В этой
форме характеристические разности и ведущий вектор вычисляются непосредственно
по исходным данным. Поскольку исходная матрица слабозаполнена, а перемножение
следует производить только тогда, когда оба сомножителя отличны от нуля, то
время вычислений значительно сокращается. В дополнение к этому использование
только исходных данных приводит к тому, что уменьшается возможность накопления
ошибок округления. Наоборот, стандартные симплексные таблицы, даже если они
первоначально являются слабо заполненными, в ходе итеративного процесса быстро
заполняются ненулевыми элементами. Таким образом, время вычислений
увеличивается, и, поскольку каждая таблица вычисляется из предшествующей,
накопление ошибок может начать играть более серьезную роль.
. Анализ задач модифицированным симплексным
методом
Если в результате применения
симплексного метода к расширенной задаче получен оптимальный план, в котором
все искусственные переменные  , то его первые n компоненты
дают оптимальный план исходной задачи.
, то его первые n компоненты
дают оптимальный план исходной задачи.
Если в оптимальном плане М-задачи хотя бы одна
из искусственных переменных отлична от нуля, то исходная задача не имеет
допустимых планов, т. е. ее условия несовместны.
Пусть исходная задача решается на
максимум. Если для некоторого опорного плана все оценки 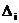
 неотрицательны,
то такой план оптимален. Если исходная задача решается на минимум и для
некоторого опорного плана все оценки
неотрицательны,
то такой план оптимален. Если исходная задача решается на минимум и для
некоторого опорного плана все оценки 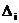
 неположительны, то такой план
оптимален.
неположительны, то такой план
оптимален.
Пусть некоторая производственная
единица (цех, завод, объединение и т. д.), исходя из конъюнктуры рынка,
технических или технологических возможностей и имеющихся ресурсов, может
выпускать n различных
видов продукции (товаров), известных под номерами, обозначаемыми индексом j  . Ее будем
обозначать
. Ее будем
обозначать  .
.
Предприятие при производстве этих
видов продукции должно ограничиваться имеющимися видами ресурсов, технологий,
других производственных факторов (сырья, полуфабрикатов, рабочей силы,
оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов
называют ингредиентами 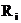 . Пусть их
число равно m; припишем
им индекс i
. Пусть их
число равно m; припишем
им индекс i  . Они
ограничены, и их количества равны соответственно
. Они
ограничены, и их количества равны соответственно  условных единиц. Таким образом,
условных единиц. Таким образом,  - вектор
ресурсов. Известна экономическая выгода (мера полезности) производства
продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его
прибыльности, издержкам производства, степени удовлетворения потребностей и т.
д. Примем в качестве такой меры, например, цену реализации
- вектор
ресурсов. Известна экономическая выгода (мера полезности) производства
продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его
прибыльности, издержкам производства, степени удовлетворения потребностей и т.
д. Примем в качестве такой меры, например, цену реализации

 , т. е.
, т. е.  -вектор цен.
Известны также технологические коэффициенты
-вектор цен.
Известны также технологические коэффициенты  , которые указывают, сколько единиц i-го ресурса
требуется для производства единицы продукции j-го вида.
Матрицу коэффициентов
, которые указывают, сколько единиц i-го ресурса
требуется для производства единицы продукции j-го вида.
Матрицу коэффициентов  называют
технологической и обозначают буквой А. Имеем
называют
технологической и обозначают буквой А. Имеем  . Обозначим
через
. Обозначим
через 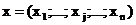 план
производства, показывающий, какие виды товаров
план
производства, показывающий, какие виды товаров  нужно производить и в каких
количествах, чтобы обеспечить предприятию максимум объема реализации при
имеющихся ресурсах.
нужно производить и в каких
количествах, чтобы обеспечить предприятию максимум объема реализации при
имеющихся ресурсах.
Так как  - цена
реализации единицы j'-й продукции, цена реализованных
- цена
реализации единицы j'-й продукции, цена реализованных  единиц
будет равна
единиц
будет равна  , а общий
объем реализации
, а общий
объем реализации
Это выражение - целевая функция,
которую нужно максимизировать.
Так как  - расход i-го ресурса
на производство
- расход i-го ресурса
на производство  единиц j-й
продукции, то, просуммировав расход i-го ресурса
на выпуск всех n видов продукции, получим общий
расход этого ресурса, который не должен превосходить
единиц j-й
продукции, то, просуммировав расход i-го ресурса
на выпуск всех n видов продукции, получим общий
расход этого ресурса, который не должен превосходить 
 единиц:
единиц: 
Чтобы искомый план  был
реализован, наряду с ограничениями на ресурсы нужно наложить условие
неотрицательности на объёмы
был
реализован, наряду с ограничениями на ресурсы нужно наложить условие
неотрицательности на объёмы  выпуска продукции:
выпуска продукции: 
 .
.
Таким образом, модель задачи о
наилучшем использовании ресурсов примет вид:
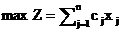 при ограничениях:
при ограничениях:




Так как переменные  входят в
функцию
входят в
функцию  и систему
ограничений только в первой степени, а показатели
и систему
ограничений только в первой степени, а показатели  являются
постоянными в планируемый период, то (1)-(3) - задача линейного
программирования.
являются
постоянными в планируемый период, то (1)-(3) - задача линейного
программирования.
3. Решение задачи линейного программирования с
помощью симплекс-метода
Фирма, производящая некоторую продукцию
осуществляет её рекламу двумя способами: через радиосеть и через телевидение.
Стоимость рекламы на радио обходится фирме в 5 $ , а стоимость телерекламы - в
100$ за минуту. Фирма готова тратить на рекламу по 1000 $ в месяц. Также
известно, что фирма готова рекламировать свою продукцию по радио по крайней
мере в 2 раза чаще, чем по телевидению. Опыт предыдущих лет показал, что
телереклама приносит в 25 раз больший сбыт продукции, нежели радиореклама.
Задача заключается в правильном распределении финансовых средств фирмы.
X1 - время
потраченное на радиорекламу.
X2 - время
потраченное на телерекламу.
Z - искомая целевая
функция, отражающая максимальный сбыт от 2-ух видов рекламы .
X1=>0 , X2=>0 , Z=>0 ;Z =
X1 + 25X2 ;
X1 + 100X2 <=1000 ;1
-2X2 => 0
Использование графического способа удобно только
при решении задач ЛП с двумя переменными. При большем числе переменных
необходимо применение алгебраического аппарата. В данной главе рассматривается
общий метод решения задач ЛП , называемый симплекс-методом .
Информация, которую можно получить с помощью
симплекс-метода, не ограничивается лишь оптимальными значениями переменных.
Симплекс-метод фактически позволяет дать экономическую интерепритацию
полученного решения и провести анализ модели на чувствительность .
Процесс решения задачи линейного
программирования носит итерационный характер: однотипные вычислительные
процедуры в определенной последовательности повторяются до тех пор, пока не
будет получено оптимальное решение. Процедуры, реализуемые в рамках
симплекс-метода, требуют применения вычислительных машин - мощного средства
решения задач линейного программирования.
1. Исходное
ограничение, записанное в виде неравенства типа <= (=>), можно
представить в виде равенства, прибавляя остаточную переменную к левой части
ограничения (вычитая избыточную переменную из левой части).
Например, в левую часть исходного ограничения
X1 + 100X2
<= 1000
вводится остаточная переменная S1
> 0, в результате чего исходное неравенство обращается в равенство
5X1
+ 100X2 + S1
= 1000 , S1 => 0
Если исходное ограничение определяет расход
некоторого ресурса, переменную S1
следует интерпретировать как остаток, или неиспользованную часть, данного
ресурса.
Рассмотрим исходное ограничение другого типа :
X1 - 2X2
=> 0
Так как левая часть этого ограничения не может
быть меньше правой, для обращения исходного неравенства в равенство вычтем из
его левой части избыточную переменную S2
> 0 . В результате получим
X1 - 2X2 - S2 = 0 , S2 => 0
2 Правую
часть равенства всегда можно сделать неотрицательной, умножая оби части на -1 .
Например равенство X1
- 2X2 - S2
= 0 эквивалентно равенству - X1
+ 2X2 + S2
= 0
3 Знак
неравенства изменяется на противоположный при умножении обеих частей на -1 .
Например можно вместо 2 < 4 записать - 2 >
- 4 , неравенство X1 - 2X2
<= 0 заменить на - X1
+ 2X2 => 0
Сначала необходимо представить целевую функцию и
ограничения модели в стандартной форме:
Z - X1
- 25X2 +0S1
-0S2
= 0 ( Целевая функция )
X1 + 100X2
+ S1 = 1000 (
Ограничение )
X1 + 2X2
+ S2 = 0 ( Ограничение
)
Как отмечалось ранее, в качестве начального
пробного решения используется решение системы уравнений, в которой две
переменные принимаются равными нулю. Это обеспечивает единственность и допустимость
получаемого решения. В рассматриваемом случае очевидно, что подстановка X1
= X2 = 0 сразу же
приводит к следующему результату: S1
= 1000, S2 = 0. Величина Z
в этой точке равна нулю, так как и X1
и X2 имеют нулевое
значение. Поэтому, преобразовав уравнение целевой функции так, чтобы его правая
часть стала равной нулю, можно убедиться в том, что правые части уравнений
целевой функции и ограничений полностью характеризуют начальное решение. Это
имеет место во всех случаях, когда начальный базис состоит из остаточных
переменных.
Полученные результаты удобно представить в виде
таблицы:
|
Базисные
переменные
|
Z
|
X1
|
X2
|
S1
|
S2
|
Решение
|
|
|
Z
|
1
|
-
25
|
0
|
0
|
0
|
Z - уравнение
|
|
S1
|
0
|
5
|
100
|
1
|
0
|
1000
|
S1 -уравнение
|
|
S2
|
0
|
-1
|
2
|
0
|
1
|
0
|
S2 - уравнение
|
Эта таблица интерпретируется следующим образом.
Столбец «Базисные переменные» содержит переменные пробного базиса S1,
S2, значения которых
приведены в столбце «Решение». При этом подразумевается, что небазисные
переменные X1 и X2 (не
представленные в первом столбце) равны нулю. Значение целевой функции Z
= 1*0 + 25*0 + 0*1000 + 0*1 равно нулю, что и показано в последнем столбце
таблицы.
Определим, является ли полученное пробное
решение наилучшим (оптимальным). Анализируя Z
- уравнение, нетрудно заметить, что обе небазисные переменные X1
и X2, равные нулю,
имеют отрицательные коэффициенты. Всегда выбирается переменная с большим
абсолютным значением отрицательного коэффициента (в Z
-
уравнении),
так как практический опыт вычислений показывает, что в этом случае оптимум
достигается быстрее.
Это правило составляет основу используемого в
вычислительной схеме симплекс-метода условия оптимальности, которое состоит в
том, что, если в задаче максимизации все небазисные переменные в Z
-
Уравнение имеют неотрицательные коэффициенты,
полученное пробное решение является оптимальным. В противном случае в качестве
новой базисной переменной следует выбрать ту, которая имеет наибольший по
абсолютной величине отрицательный коэффициент.
Применяя условие оптимальности к исходной
таблице, выберем в качестве переменной, включаемой в базис, переменную Х2.
Исключаемая переменная должна быть выбрана из совокупности базисных переменных S1,
S2. Процедура выбора
исключаемой переменной предполагает проверку условия допустимости,
требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных
текущего базиса, которая первой обращается в нуль при увеличении включаемой
переменной X2 вплоть до
значения, соответствующего смежной экстремальной точке.
Интересующее нас отношение (фиксирующее искомую
точку пересечения и идентифицирующее исключаемую переменную) можно определить
из симплекс-таблицы. Для этого в столбце, соответствующем вводимой переменной X2,
вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются
отношения постоянных, фигурирующих в правых частях этих ограничений, к
оставшимся элементам столбца, соответствующего вводимой переменной X2.
Исключаемой переменной будет та переменная текущего базиса, для которой
указанное выше отношение минимально.
С точки зрения практического использования
результатов решения задач ЛП классификация переменных, предусматривающая их
разделение на базисные и небазнсные, не имеет значения и при анализе данных,
характеризующих оптимальное решение, может не учитываться. Переменные,
отсутствующие в столбце «Базисные переменные», обязательно имеют нулевое
значение. Значения остальных переменных приводятся в столбце «Решение».
Отсюда следует, что уменьшение количества денег
выделенных на рекламу вызывает пропорциональное уменьшение целевой функции с
тем же коэффициентом пропорциональности, равным 27/110.
Так как мы оперируем с линейными функциями, полученный вывод можно
обобщить, считая, что и увеличение количества денег выделенных на
рекламу ( эквивалентное введению избыточной переменной S1
<
0 ) приводит к пропорциональному увеличению Z
с тем же коэффициентом пропорциональности, равным 27/110.
В результате проведенного исследования, было
получено подтверждение о выгодности использования математико-экономического
проектирования и методов системного анализа для анализа и планирования
экономических систем.
Список литературы
модифицированный симплексный
моделирование программирование
1. Боборыкин В.А.
Математические методы решения транспортных задач. СПб.: СЗПИ, 2014. - 170с.
2. Горчаков А.А., Орлова А.А.
Компьютерные экономико-математические модели. М.: ЮНИТИ, 2015. - 242с.
. Дадаян В.С.
Макроэкономические модели. М.: МГУ, 2013. - 184с.
4. Дегтярев Ю. И. Исследование
операций. М.: Высшая школа, 2014. - 320с.
. Конюховский П.В. Математические
методы исследования операций в экономике. СПб.: Питер, 2013. - 208с.
. Лэсдон Л.С. Оптимизация больших
систем. /Пер. с англ. - М.: Прогресс, 2011. - 232с.
. Фомин Г.П. Математические методы
и модели в коммерческой деятельности. М.: Финансы и статистика, 2015. - 616c.