Задача оптимального управления инвестициями в макроэкономической модели, описывающая влияние террористических угроз на индустрию туризма
Министерство образования и науки
Российской Федерации
Федеральное агентство по образованию
Государственное образовательное
учреждение
высшего профессионального образования
Выпускная квалификационная работа на
тему:
«ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ИНВЕСТИЦИЯМИ
В МАКРОЭКОНОМИЧЕСКОЙ МОДЕЛИ, ОПИСЫВАЮЩАЯ ВЛИЯНИЕ ТЕРРОРИСТИЧЕСКИХ УГРОЗ НА
ИНДУСТРИЮ ТУРИЗМА»
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. Общая постановка задачи
оптимального управления для непрерывных и дискретных процессов
.1 Постановка задачи для непрерывных
процессов
.2 Постановка задачи для дискретных
процессов
. Принцип максимума Понтрягина
.1 Формулировка принципа максимума в
общей задаче с закрепленными концами
.2 Формулировка принципа максимума в
случае задачи общего вида с нефиксированными начальным и конечным моментами
времени
.3 Достаточность условий принципа
максимума
.4 Задача оптимизации управляемых
процессов на бесконечном промежутке времени (“бесконечный горизонт
планирования”)
. Оптимальный баланс инвестиций в
макроэкономической модели, описывающей влияние террористических угроз на
индустрию международного туризма
.1 Описание модели. Постановка
задачи оптимального управления
.2 Исследование задачи оптимального
управления
.2.1 Уравнения состояния
.2.2 Принцип максимума
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЯ
ВВЕДЕНИЕ
Сегодня международный туризм является весьма распространенным явлением.
Этой областью охвачено порядка 800 миллионов человек. Международный туризм
составляет существенный сегмент экономики ряда современных государств. Так, 35%
ВВП Испании составляют доходы от туристического бизнеса, более 50% - на Кипре и
около 70% - на Гаити. Наибольшее развитие международный туризм получил в
Западной Европе. Сегодня доля этого региона составляет порядка 70% мирового
туристического рынка, 20% составляют страны Америки, 10% примерно поровну
распределено между Африкой, Австралией и Азией. В список стран, наиболее
востребованных в индустрии международного туризма, входят Бельгия, США,
Германия, Дания, Новая Зеландия, Голландия, Австралия, Швеция, Англия, Канада.
Самыми "принимающими" странами по данным социологов являются Турция,
Австрия, Испания, Италия, Португалия, Швейцария, Мексика, Греция, Франция и
Кипр. Практика международного туризма свидетельствует о том, что с увеличением
количества путешествующих (предполагается, что к 2020 г. количество
международных туристских прибытий превысит уровень 2000 г. в 3 раза и составит
1,6 млрд, человек) и расширением географии туристских поездок актуальность
вопросов обеспечения безопасности в международном туризме неуклонно возрастает.
Как утверждает британский журнал "Холидей-Уик" (2004 г.), каждый
двухсотый турист в мире подвергается нападению. И если доля пострадавших
туристов в Италии составляет 2,2 %, в Израиле - 2,6 %, в Марокко - 3 %, то в странах
Центральной и Восточной Европы (ЦВЕ) этот показатель выше: Венгрия - 5,9 %,
Польша - 5,3 %, страны СНГ - 4,3 %.
На безопасность международного туризма влияют экономические,
медико-социальные, политические факторы, а также активизация международного терроризма.
За последние пятнадцать лет в мире произошло несколько десятков
террористических актов, направленных против туристов. Только на счету исламских
экстремистов из группировки "Аль-Гамаа аль-Исламия" их около полутора
десятков. Самый кровавый из них - расстрел туристского автобуса в ноябре 1997
г. в Луксоре, в результате чего погибли 68 туристов. Незадолго до этого боевики
"Исламии" расстреляли в центре Каира 18 немецких туристов. Всего в
период 1992-1997 гг. египетские исламисты убили более ста туристов и нанесли
значительный ущерб экономике Египта. Это потребовало от египетских властей
применения чрезвычайных мер - создания туристской полиции. По данным ВТО, спрос
на услуги туристских компаний в первые месяцы после террористических актов 11
сентября 2001 г. сократился во всем мире на три четверти. В Турции угрозу для
туристов представляют экстремисты из Курдской рабочей партии: в 1999-2001 гг.
они организовали серию взрывов в местах скопления туристов, в том числе в
гостиницах Стамбула. Взрывы в США отразились даже на итальянской индустрии
отдыха, так как эта страна является четвертой по популярности среди
американских путешественников. Суммарные убытки американских авиакомпаний по
итогам 2001 г. превысили 5 млрд дол. США. В апреле 2002 г. на острове Джерба в
Тунисе была взорвана древнейшая в Африке синагога, в результате чего погибли 14
немецких туристов. Ответственность за это взяла на себя "Аль-Каида".
Страдает от действий террористов и туристский бизнес Испании. Каждый год
баскская сепаратистская группировка "ЭТА" грозит развернуть кампанию,
направленную против туристов.
Как правило, террористические акты удается предотвратить, однако в 2002
г. 35 британских и ирландских туристов были ранены, когда в аэропорту Реус
взорвалась бомба, заложенная боевиками "ЭТА". Взрывы 11 марта 2004 г.
в мадридских электричках, устроенные испанскими экстремистами, тут же сказались
на туризме. Многие иностранные турагентства отказались от забронированных
авиабилетов и гостиничных номеров.
Чаще всего террористические акты случаются в местах массового скопления,
как местных жителей, так и туристов. Не стал исключением и захват заложников в
октябре 2003 г. в Театральном центре на Дубровке в Москве. Как известно, мюзикл
"Норд-Ост" был признан "особо значимым культурным проектом"
и продвигался в качестве туристской достопримечательности Москвы. 12 октября
2003 г. на индонезийском острове Бали боевиками "Аль-Каиды" был
организован взрыв на дискотеке. В результате террористического акта погибло
около 200 туристов из Австралии, Японии, Германии и других стран. С целью
борьбы с международным терроризмом и лишения его организационной и финансовой
поддержки Госдепартамент США, анализируя ситуацию в мире, дважды в год
публикует на своем сайте рекомендации гражданам США воздерживаться от поездок в
потенциально небезопасные страны. Международный терроризм превращается в
глобальную военно-политическую проблему, угрожающую существованию человеческой
цивилизации. Именно такое звучание получила эта проблема на прошедшей 60-й
Генеральной Ассамблее ООН (сентябрь 2005 г.). Таким образом, развитие
международного туризма в XXI в. зависит от консолидированных усилий всех стран
мирового сообщества в борьбе с международным терроризмом.
В Турции угрозу для туристов представляют экстремисты
из Курдской рабочей партии: в 1999-2001 гг. они организовали серию взрывов в
местах скопления туристов, в том числе в гостиницах Стамбула.
По данным ВТО, спрос на услуги туристских компаний в
первые месяцы после террористических актов 11 сентября 2001 г. сократился во
всем мире на три четверти. Взрывы в США отразились даже на итальянской
индустрии отдыха, так как эта страна является четвертой по популярности среди
американских путешественников. Суммарные убытки американских авиакомпаний по
итогам 2001 г. превысили 5 млрд дол. США.
В апреле 2002 г. на острове Джерба в Тунисе была
взорвана древнейшая в Африке синагога, в результате чего погибли 14 немецких
туристов. Ответственность за это взяла на себя «Аль-Каида».
Страдает от действий террористов и туристский бизнес
Испании. Каждый год баскская сепаратистская группировка «ЭТА» грозит развернуть
кампанию, направленную против туристов. Как правило, террористические акты
удается предот-вратить, однако в 2002 г. 35 британских и ирландских туристов
были ранены, когда в аэропорту Реус взорвалась бомба, заложенная боевиками
«ЭТА».
Взрывы 11 марта 2004 г. в мадридских электричках,
устроенные испанскими экстремистами, тут же сказались на туризме. Многие
иностранные турагентства отказались от забронированных авиабилетов и гостиничных
номеров.
Чаще всего террористические акты случаются в местах
массового скопления как местных жителей, так и туристов. Не стал исключением и
захват заложников в октябре 2003 г. в Театральном центре на Дубровке в Москве.
Как известно, мюзикл «Норд-Ост» был признан «особо значимым культурным
проектом» и продвигался в качестве туристской достопримечательности Москвы.
октября 2003 г. на индонезийском острове Бали
боевиками «Аль-Каиды» был организован взрыв на дискотеке. В результате
террористического акта погибло около 200 туристов из Австралии, Японии,
Германии и других стран.
С целью борьбы с международным терроризмом и лишения
его организационной и финансовой поддержки Госдепартамент США, анализируя
ситуацию в мире, дважды в год публикует на своей интернет-странице (#"879946.files/image001.gif">Rn, координаты которого xi, i =
1,2,…, n, называются фазовыми координатами объекта. Движение объекта
происходит таким образом, что его координаты в каждый момент времени
определяются m величинами, u1, u2,....,um,
называемыми управлениями. Управление u является m-мерным вектором
u = col{u1, u2,...., um}, в свою очередь
изменяющимся во времени. Однако изменение управляющего параметра u в
определенной степени зависит только от управляющего субъекта.
Пусть
задано некоторое замкнутое множество U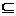 Rm. Обычно в
теории оптимального управления функция u(t) называется допустимым
управлением, если значения u(t) принадлежат множеству U, и
вектор-функция u(t) является кусочно-непрерывной (или, в общем
случае - ограниченной измеримой функцией).
Rm. Обычно в
теории оптимального управления функция u(t) называется допустимым
управлением, если значения u(t) принадлежат множеству U, и
вектор-функция u(t) является кусочно-непрерывной (или, в общем
случае - ограниченной измеримой функцией).
Пусть
задано начальное состояние объекта
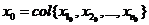
и закон движения в виде системы обыкновенных дифференциальных уравнений
первого порядка:
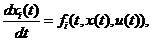 i = , i = 1,2,…,n,
i = , i = 1,2,…,n,
где функции fi предполагаются непрерывными по совокупности
переменных и непрерывно дифференцируемых по xi (i =1,2,…,n)
и по t.
Если теперь задать некоторое допустимое управление u(t), то
система дифференциальных уравнений (при некоторых достаточно естественных
предположениях о правых частях системы уравнений) вместе с начальным условием x(0)
= x0 однозначно определит траекторию x(t). Задача теории
оптимального управления состоит в том, чтобы среди допустимых управлений u(t)
выбрать такое, которое бы определяло траекторию x(t),
минимизирующую (максимизирующую) некоторый заданный критерий.
В достаточно общем виде постановка задач оптимального управления может
быть представлена следующим образом.
Пусть задана управляемая система, описываемая задачей Коши вида
 (1.1)
(1.1)
x(t)
|t=t0 + 0= x0 . (1.2)
Пусть далее управление u(t), t  [t0,t1], является
кусочно - непрерывной функцией с конечным числом точек разрыва, принимающей
значения во множестве U
[t0,t1], является
кусочно - непрерывной функцией с конечным числом точек разрыва, принимающей
значения во множестве U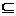 Rm. Под решением задачи Коши (1.1)-(1.2)
понимается непрерывная функция x(t), t
Rm. Под решением задачи Коши (1.1)-(1.2)
понимается непрерывная функция x(t), t [t0,t1],
удовлетворяющая интегральному уравнению
[t0,t1],
удовлетворяющая интегральному уравнению
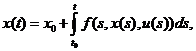 t
t [t0
, t1]. (1.3)
[t0
, t1]. (1.3)
Ясно, что определенное с помощью равенства решение задачи Коши x(t),
t  [t0,t1] обладает
кусочно-непрерывной производной.
[t0,t1] обладает
кусочно-непрерывной производной.
Начальный и конечный моменты времени, а также длительность управляемого
процесса могут зависеть от управления (например, в задачах «быстродействия»), а
потому не всегда задаются заранее. В подобных случаях обычно указывают
ограничения
t0
 Θ0,
t1
Θ0,
t1  Θ1, (1.4)
Θ1, (1.4)
где Θ0 , Θ1 - заданные подмножества вещественной прямой R.
Помимо ограничений вида u(t) U, t
U, t [t0,t1], на фазовые
координаты управляемого объекта могут быть заданы аналогичные ограничения вида
[t0,t1], на фазовые
координаты управляемого объекта могут быть заданы аналогичные ограничения вида
x(t) G(t)
G(t)
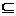 Rn , t
Rn , t  [t0,t1], (1.5)
[t0,t1], (1.5)
называемые фазовыми ограничениями. Специфические и потому выделяемые
и рассматриваемые отдельно фазовые ограничения могут быть наложены и в
начальный и конечный моменты времени. Их обычно записывают в виде
x(t0) S0(t0),
t0
S0(t0),
t0  Θ0, x(t1)
Θ0, x(t1)
 S1(t1),
t1
S1(t1),
t1 Θ1, (1.6)
Θ1, (1.6)
причем считается, что
S0(t0)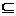 G(t0), S1(t1)
G(t0), S1(t1)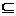 G(t1). (1.7)
G(t1). (1.7)
Наряду с фазовыми ограничениями могут накладываться интегральные
ограничения
вида
[u] ≤ 0, i = 1,2,..., p, Ji[u]
= 0, i = p + 1, p + 2,..., p + q , (1.8)
 , i = 1,2,..., p + q.
, i = 1,2,..., p + q.
Набор параметров {t0 Θ0,
t1
Θ0,
t1 Θ1,
x0
Θ1,
x0 Rn, u(t)
Rn, u(t) U, t
U, t  [t0,t1]}, а также движение управляемого
объекта и управления x0
[t0,t1]}, а также движение управляемого
объекта и управления x0 Rn, u(t)
Rn, u(t) U, t
U, t  [t0,t1] называются допустимыми,
если управление u(t), t
[t0,t1] называются допустимыми,
если управление u(t), t [t0,t1], является
кусочно непрерывной функцией с конечным числом точек разрыва и выполнены
перечисленные выше ограничения.
[t0,t1], является
кусочно непрерывной функцией с конечным числом точек разрыва и выполнены
перечисленные выше ограничения.
В достаточно общей форме оптимизационная задача ставится следующим
образом. Среди допустимых управлений {x0 Rn,
u(t)
Rn,
u(t) U, t
U, t  [t0,t1]}
требуется найти управление u0(t), доставляющее минимум критерию
качества
[t0,t1]}
требуется найти управление u0(t), доставляющее минимум критерию
качества
В тех случаях, когда критерием качества (целевым функционалом) является
длительность управляемого процесса, говорят о задаче быстродействия.
Одной из простейших задач описанного типа является следующая задача с
функциональными ограничениями типа неравенств.
Пусть заданы функционалы Ji , i =1,2,..., p, (J0, J1, J2 ,..., Jp ) R p+1. Как и выше, набор {x(t),
u(t)}, для которого выполняются условия: u(t)
R p+1. Как и выше, набор {x(t),
u(t)}, для которого выполняются условия: u(t) U, t
U, t  [t0,t1];
и является кусочно непрерывной функцией с конечным числом точек разрыва;
[t0,t1];
и является кусочно непрерывной функцией с конечным числом точек разрыва;
 Rn ,
Rn ,
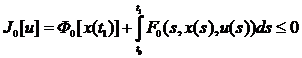 , i =1,2,...,
p ,
, i =1,2,...,
p ,
будем называть допустимым. Среди допустимых управлений требуется найти
управление u0(t), доставляющее минимум критерию качества, то есть
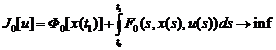
1.2 Постановка задачи для дискретных процессов
Наряду с рассмотренной в предыдущем пункте задачей, значительный интерес
представляет также задача, являющаяся ее дискретным аналогом. Такие задачи
возникают, например, при решении с помощью разностных методов задач с
непрерывным временем. Однако они представляют и самостоятельный интерес,
поскольку, например, описывают «импульсные» системы, в которые сигналы
управления поступают в дискретные моменты времени. Такого рода «импульсные»
системы применяются и для описания экономических систем (технологические
модели, в которых присутствует естественный временной масштаб - длительность
технологического цикла).
Пусть задана управляемая система, описываемая задачей вида
xs+1 = fs(xs ,us), s = 0,1, 2, ...,
N -1, (1.10)
x0 = x G0
G0 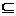 Rn. (1.11)
Rn. (1.11)
Здесь управление u ≡ {un , n = 0, 1, 2, ... , N -1}, где un ≡
|u(n), u(·) : I ≡ {0, 1, 2, ... , N -
1} → Rm принимает значения в множестве U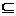 Rm (un
Rm (un U, n
U, n I). Допустимыми управлениями называются такие управления,
для которых решение задачи (1.10), (1.11) удовлетворяет фазовому ограничению xn
I). Допустимыми управлениями называются такие управления,
для которых решение задачи (1.10), (1.11) удовлетворяет фазовому ограничению xn Gn
Gn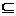 Rn, n
Rn, n I. В дальнейшем, не оговаривая это особо, считаем
непустыми множества допустимых управлений в этой и во встречающихся ниже
задачах.
I. В дальнейшем, не оговаривая это особо, считаем
непустыми множества допустимых управлений в этой и во встречающихся ниже
задачах.
Рассмотрим следующую оптимизационную задачу. Среди допустимых управлений u
= (un U,
n
U,
n I) требуется найти управление u0, доставляющее
минимум критерию качества
I) требуется найти управление u0, доставляющее
минимум критерию качества

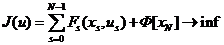 . (1.12)
. (1.12)
Можно рассмотреть и более общие оптимизационные задачи, вполне
аналогичные оптимизационной задаче с непрерывным временем (1.1)-(1.9).
Выводы
Проведение расчётов и моделирование режимов работы объектов является
актуальной и до конца не решённой задачей, так как с одной стороны
моделирование важно для улучшения эффективности работы, но с другой стороны
существует большое количество методов моделирования и все они не идеальны и
имеют недостатки. В ходе данной части исследования были рассмотрены основные
группы методов моделирования производственных процессов и выполнена постановка
задачи, которая позволит в дальнейшем создать работоспособную модель указанного
процесса.
2. ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
2.1 Формулировка принципа максимума в общей
задаче с закрепленными концами и закрепленным временем
Пусть требуется минимизировать функционал
 (1.13)
(1.13)
при условиях
 , (1.14)
, (1.14)
x(t0) S0, x(T)
S0, x(T)  ST , (1.15)
ST , (1.15)
u(t) U, t0 ≤ t ≤ T , (1.16)
U, t0 ≤ t ≤ T , (1.16)
где управление u(t) U, t0
≤ t ≤ T предполагается ограниченной измеримой функцией, так
что u(·)
U, t0
≤ t ≤ T предполагается ограниченной измеримой функцией, так
что u(·)
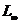 {[t0, T],U}.
{[t0, T],U}.
Предполагаем, что правый конец траектории либо свободен (ST = Rn),
либо принадлежит множеству ST, которое представляется в одном из
следующих вариантов:
ST = {x Rn : gj (x) = 0, j =1,
2, ..., sT };
Rn : gj (x) = 0, j =1,
2, ..., sT };
ST ={x Rn : gj (x) ≤ 0, j
=1, 2 ,..., mT , gj (x) = 0, j = mT + 1
,..., sT }.
Rn : gj (x) ≤ 0, j
=1, 2 ,..., mT , gj (x) = 0, j = mT + 1
,..., sT }.
Аналогичным образом предполагаем, что левый конец траектории либо свободен
( S0 = Rn), либо принадлежит множеству S0, которое
представляется в одном из вариантов:
S0 = {x Rn : hj (x) = 0, j =
1, 2, ..., s0};
Rn : hj (x) = 0, j =
1, 2, ..., s0};
S0 = {x Rn : hj (x)
Rn : hj (x) 0, j =1, 2,..., m0, hj
(x) = 0, j = m0 +1, ..., s0}.
0, j =1, 2,..., m0, hj
(x) = 0, j = m0 +1, ..., s0}.
Относительно функций {fi}, {gi}, {hi} и Ф
предполагается, что они имеют частные производные по переменным {xi} и
непрерывны вместе с указанными производными по совокупности своих аргументов.
Определим функцию Гамильтона-Понтрягина:

ψ = col{ψ1, ψ2 , ... , ψn}, ψ0 = const .
Для управления u(·)
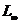 {[t0, T],U} и x(t), t0 ≤ t ≤ T -
решения уравнения (1.14), отвечающего этому управлению - рассматриваем
«сопряженную» систему обыкновенных дифференциальных уравнений, линейных
относительно «сопряженных» переменных
{[t0, T],U} и x(t), t0 ≤ t ≤ T -
решения уравнения (1.14), отвечающего этому управлению - рассматриваем
«сопряженную» систему обыкновенных дифференциальных уравнений, линейных
относительно «сопряженных» переменных
ψ(t) = col{ψ1(t), ψ2(t), ... , ψn(t)}:
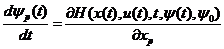 , p = 1,2,…,n, (1.17)
, p = 1,2,…,n, (1.17)
которую, как и выше, можно записать также в векторной форме следующим
образом
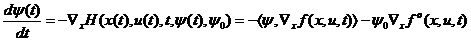 (1.18)
(1.18)
Теорема 1.1 (принцип максимума). Пусть{x(t), u(t)},
t0 ≤ t ≤ T -
решение задачи (1.13)-(1.16). Тогда необходимо существуют непрерывная
вектор-функция ψ (t) , t0 ≤ t ≤ T,
и постоянная ψ0 такие, что:
) ψ0 ≤ 0 , |ψ0| + |ψ(t)| ≠ 0, t0 ≤ t ≤ T.
) ψ(t) является решением сопряженной системы (1.17),
(1.18), соответствующим рассматриваемому решению {x(t), u(t)},
t0 ≤ t ≤ T.
) При почти всех t  [t0,T] функция H(x(t), u,
t, ψ(t), ψ0) переменной u
[t0,T] функция H(x(t), u,
t, ψ(t), ψ0) переменной u U достигает своей верхней грани на множестве U при
u = u(t), t0 ≤ t ≤ T, т.е.
U достигает своей верхней грани на множестве U при
u = u(t), t0 ≤ t ≤ T, т.е.
H(x(t), u(t), t, ψ(t), ψ0) = sup H(x(t), u, t,
ψ(t), ψ0), t0 ≤ t ≤
T.
u U
U
) На левом и правом концах траектории {x(t), t0 ≤ t ≤ T}
выполняются условия трансверсальности, которые означают, что вектор ψ
(T) -
ψ0 Фx {x(T)}
ортогонален к множеству ST в точке x(T) ST, а вектор ψ(t0) ортогонален к множеству S0
в точке x(t0)
ST, а вектор ψ(t0) ортогонален к множеству S0
в точке x(t0) S0.
S0.
Комментарий к теореме 1.1 (расшифровка условий трансверсальности).
Правый конец
1) Правый конец траектории свободен, ST = Rn. Вектор
ψ(T) - ψ0Фx{x(T)} ортогонален к Rn,
что означает, что
ψ(T) - ψ0Фx{x(T)} = 0 .
Данное условие есть граничное условие краевой задачи принципа максимума.
) Правый конец траектории подвижен, причем терминальное множество имеет
следующий вид: ST = {x Rn : gj(x) = 0, j =1,
2, ... , sT }.
Rn : gj(x) = 0, j =1,
2, ... , sT }.
Гиперплоскость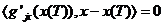 представляет собой касательную плоскость к поверхности Sj
= {x
представляет собой касательную плоскость к поверхности Sj
= {x Rn : gj(x) = 0} в точке x(T) .
Rn : gj(x) = 0} в точке x(T) .
Аффинное множество Г = {x Rn: (
Rn: (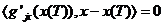 j = 1, 2, ..., sT} есть касательная плоскость к
множеству ST в точке x(T) .
j = 1, 2, ..., sT} есть касательная плоскость к
множеству ST в точке x(T) .
Ортогональность вектора h к множеству ST в точке x(T)
означает, по определению, ортогональность вектора h к аффинному
множеству
Г = {x Rn : (
Rn : (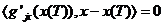 j =
1, 2, ..., sT };
j =
1, 2, ..., sT };
или

 .
.
Значит, условия трансверсальности означают, что вектор ψ(T) - ψ0Фx{x(T)} удовлетворяет условию:
ψ(T) - ψ0Фx{x(T)}, x - x(T ) = 0,
= 0,  ,
,
Г = {x Rn : (
Rn : (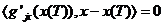 j =
1, 2, ..., sT}.
j =
1, 2, ..., sT}.
В силу теоремы Фаркаша существуют числа a1,...,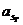 такие, что
такие, что
Сюда необходимо добавить условия принадлежности точки x(T)
к ST, т.е. условие
(x(T)) = 0, j =1, 2, ..., sT.
) Правый конец траектории подвижен, причем терминальное множество имеет
следующий вид: ST = {x Rn: gj (x) ≤ 0, j
=1, 2, ..., mT , gj (x) = 0, j = mT +1,
... , sT}. Пусть, кроме того, g’jx (x(T)) ≠
0, j =1, 2, ..., sT .
Rn: gj (x) ≤ 0, j
=1, 2, ..., mT , gj (x) = 0, j = mT +1,
... , sT}. Пусть, кроме того, g’jx (x(T)) ≠
0, j =1, 2, ..., sT .
В этом случае существуют числа a1,..., 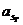 такие, что
такие, что
 ,
,
и, кроме того, имеют место соотношения:
aj gj (x(T)) = 0 , aj ≥0, j
=1,2,...,mT,
gj (x(T))
= 0 , j = mT +1,..., sT ,
Левый конец
1) Левый конец траектории свободен, S0 = Rn. Вектор ψ(t0) ортогонален к Rn,
что означает, что
ψ(t0) = 0.
Данное условие есть граничное условие краевой задачи принципа максимума.
) Левый конец траектории подвижен, причем терминальное множество имеет
следующий вид: S0 ={ x Rn : hj (x) = 0, j =1,
2, ..., s0}. В этом случае существуют числа b1, ...,
Rn : hj (x) = 0, j =1,
2, ..., s0}. В этом случае существуют числа b1, ...,  такие, что
такие, что
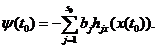
Кроме того, к данным условиям необходимо добавить условия принадлежности
точки
(t0) к S0 , т.е. условие
hj (x(t0
)) = 0, j =1, 2, ..., s0 .
) Левый конец траектории подвижен, причем терминальное множество имеет
следующий вид: S0 = {x Rn : hj(x) ≤ 0, j
= 1, 2, ..., m0, hj(x) = 0, j = m0 +1,
..., s0}. Пусть, кроме того, hjx (x(t0)) ≠ 0
, j =1, 2, ..., s0.
Rn : hj(x) ≤ 0, j
= 1, 2, ..., m0, hj(x) = 0, j = m0 +1,
..., s0}. Пусть, кроме того, hjx (x(t0)) ≠ 0
, j =1, 2, ..., s0.
В этом случае существуют числа b1, ...,  такие, что,
такие, что,
и, кроме того, имеют место соотношения:
bj hj (x(t0)) = 0 , bj ≥ 0, j
=1, 2, ..., m0,
hj (x(t0))
= 0 , j = m0 +1, ..., s0.
2.2 Формулировка принципа максимума в случае
задачи общего вида с нефиксированными начальным и конечным моментами времени
Рассмотрим задачу, когда начальный и конечный моменты времени, вообще
говоря, неизвестны и также подлежат определению.
Пусть требуется минимизировать функционал
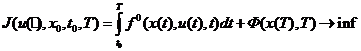 (1.19)
(1.19)
при условиях
 , (1.20)
, (1.20)
x(t0) S0 (t0 ), x(T)
S0 (t0 ), x(T) ST(T) , (1.21)
ST(T) , (1.21)
u(t) U, t0 ≤ t ≤ T, (1.22)
U, t0 ≤ t ≤ T, (1.22)
где, как и выше, управление u(t) U, t0 ≤ t ≤
T предполагается ограниченной измеримой
функцией, так что u(·)
U, t0 ≤ t ≤
T предполагается ограниченной измеримой
функцией, так что u(·)
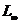 {[t0, T],U}.
{[t0, T],U}.
Предполагаем, что правый конец траектории либо свободен ( ST(T)
= Rn), либо принадлежит множеству ST (T) , которое
представляется в виде:
ST (T) = {x Rn : gj (x,T) ≤ 0, j =1, 2, ..., mT, gj (x,T) = 0, j = mT +1,
..., sT}, T
Rn : gj (x,T) ≤ 0, j =1, 2, ..., mT, gj (x,T) = 0, j = mT +1,
..., sT}, T  R .
R .
Аналогично левый конец траектории либо свободен (S0(t0) = Rn),
либо принадлежит множеству S0(t0) , которое представляется в
виде:
S0(t0) = {x Rn : hj(x, t0) ≤
0, j = 1, 2, ..., m0, hj(x, t0) = 0, j = m0
+1, ..., s0}. t0
Rn : hj(x, t0) ≤
0, j = 1, 2, ..., m0, hj(x, t0) = 0, j = m0
+1, ..., s0}. t0 R .
R .
Относительно функций {f i}, {g i}, {h i} и Ф, как и
выше, предполагается, что они имеют частные производные по переменным {xi}
и непрерывны вместе с указанными производными по совокупности своих аргументов.
Теорема 1.2 (принцип максимума).
Пусть {x(t),u(t)}, t0 ≤ t ≤ T -
решение задачи (1.19)-(1.22). Тогда необходимо существуют непрерывная
вектор-функция ψ(t) , t0 ≤ t ≤
T, и постоянная ψ0
такие, что:
) ψ0 ≤ 0 , | ψ 0 | + |
ψ (t) |≠0
, t0 ≤ t ≤ T.
) ψ (t) является решением сопряженной системы (1.17),
(1.18), соответствующим рассматриваемому решению {x(t),u(t)},
t0 ≤ t ≤ T.
) При почти всех t  [t0,T] функция H(x(t),u,
t, ψ(t), ψ0) переменной u
[t0,T] функция H(x(t),u,
t, ψ(t), ψ0) переменной u V достигает своей верхней грани на множестве U при
u = u(t), t0 ≤ t ≤ T, т.е.
V достигает своей верхней грани на множестве U при
u = u(t), t0 ≤ t ≤ T, т.е.
H(x(t),u(t), t, ψ(t), ψ0) = sup H(x(t), u, t,
ψ(t), ψ0), t0 ≤ t ≤
T
u U
U
) На левом и правом концах траектории {x(t), t0 ≤ t ≤ T}
выполняются условия трансверсальности.
Комментарий к теореме 1.2 (расшифровка условий трансверсальности)
Правый конец
1) Правый конец траектории свободен, ST(T) = Rn .
Тогда
ψ (T) -
ψ0Фx{x(T
),T} = 0 ,
 H(x(T),u(T),T,ψ (T), ψ0) - ψ0Фt{x(T ),T}
= 0 .
H(x(T),u(T),T,ψ (T), ψ0) - ψ0Фt{x(T ),T}
= 0 .
Данные условия суть граничные условия краевой задачи принципа максимума.
) Правый конец траектории подвижен:
ST (T) = {x Rn : gj (x,T) ≤ 0, j =1, 2, ..., mT , gj (x,T) = 0, j = mT +1,
..., sT}.
Rn : gj (x,T) ≤ 0, j =1, 2, ..., mT , gj (x,T) = 0, j = mT +1,
..., sT}.
Пусть, кроме того, g’jx (x(T),Т) ≠
0, g’jt (x(T),Т)
≠ 0 j =1, 2, ..., sT.
В этом случае существуют числа a1,..., 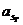 такие, что
такие, что

aj gj (x(T),T) = 0 , aj ≥0,
j =1,2,...,mT,
gj (x(T),T) = 0 , j = mT +1,...,
sT
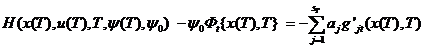 .
.
3) Правый конец траектории закреплен. В этом случае
(T) = xT ,
H(xT,u(T),T,ψ(T),ψ0) - ψ0Фt{x(T ),T}
= 0 .
туризм инвестиции оптимальный управление
Значительный прикладной интерес представляют ситуации, когда необходимые
условия оптимальности (принцип максимума Понтрягина) оказываются достаточными.
Приведем один частный вид задач оптимального управления, для которых
необходимые
условия оптимальности совпадают с достаточными.
Если u0 - решение следующей задачи оптимального управления
 , (1.23)
, (1.23)
x(0)=x0, (1.24)
u(t) U, t0
≤ t ≤ T (1.25)
U, t0
≤ t ≤ T (1.25)
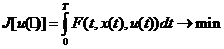 (1.26)
(1.26)
то необходимые условия оптимальности, в силу теоремы 3.1 имеют вид:
H(x0(t), u0(t), t, ψ(t)) = max H(x0(t),
u, t, (t))
для п.в. t [0,T], (1.27)
[0,T], (1.27)
u U
U
где H(x, u, t, ψ) =  ψ, f (t, x, u)
ψ, f (t, x, u) - F(t, x, u)
и ψ - решение задачи
- F(t, x, u)
и ψ - решение задачи
 , (1.28)
, (1.28)
ψ (T) = 0 . (1.29)
Теорема 1.3 (достаточность условий принципа максимума для
линейно-выпуклой по фазовым переменным задачи).
Пусть в уравнении (1.23) функция f (t, x, u)
имеет вид f ≡A(t)x + G(t,
u) , где A(t)-(n n)- матрица, а функция F(t,x,u)
представима в виде F ≡ g0(t, x) + g1(t,u)
, где функция g0 (t, x) выпукла по x для
любого t.
n)- матрица, а функция F(t,x,u)
представима в виде F ≡ g0(t, x) + g1(t,u)
, где функция g0 (t, x) выпукла по x для
любого t.
Тогда если u0 - допустимое управление, удовлетворяющее условиям
(1.27)-(1.29), то u0 - глобальное оптимальное управление задачи
(1.23)-(1.26).
2.4 Задача оптимизации управляемых
процессов на бесконечном промежутке времени (“бесконечный горизонт
планирования”)
К числу наиболее специфических особенностей математических задач
экономической динамики относятся многочисленные оптимизационные задачи с
бесконечным горизонтом планирования.
Формально такие задачи получаются при переходе от оптимизационных задач с
конечным горизонтом планирования (связанным с рассмотрением управляемого
процесса на промежутке t [t0 , t1]) к задачам, в которых осуществлена
замена t1 на ∞.
[t0 , t1]) к задачам, в которых осуществлена
замена t1 на ∞.
В соответствии с этим оптимизационная задача с бесконечным горизонтом
планирования - аналог задачи с конечным горизонтом планирования, может быть
поставлена следующим образом. Ограничимся рассмотрением задач с функционалами
типа Лагранжа.
Пусть управляемая система описывается следующей задачей Коши
 (1.30)
(1.30)
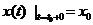 . (1.31)
. (1.31)
Среди допустимых управлений {x0 Rn, u(t)
Rn, u(t) U , t
U , t [t0 ,∞) }, для которых
выполняются неравенства
[t0 ,∞) }, для которых
выполняются неравенства
 , i =1,2,..., p , (1.32)
, i =1,2,..., p , (1.32)
требуется найти управление u0(t), доставляющее минимум
критерию качества
 . (1.33)
. (1.33)
Считаем, как и выше, что управление u(t), t [t0,∞), является кусочно
непрерывной функцией с конечным числом точек разрыва, принимающей значения в
множестве U
[t0,∞), является кусочно
непрерывной функцией с конечным числом точек разрыва, принимающей значения в
множестве U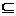 Rm . Допустимыми управлениями в дальнейшем называются такие
управления, для которых решение задачи (1.30), (1.31) удовлетворяет фазовому
ограничению x(t)
Rm . Допустимыми управлениями в дальнейшем называются такие
управления, для которых решение задачи (1.30), (1.31) удовлетворяет фазовому
ограничению x(t) G(t)
G(t)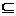 Rn, t
Rn, t [t0,∞). Под решением
задачи (1.30), (1.31) понимается непрерывная функция x(t), t
[t0,∞). Под решением
задачи (1.30), (1.31) понимается непрерывная функция x(t), t [t0,∞), обладающая
кусочно непрерывной производной.
[t0,∞), обладающая
кусочно непрерывной производной.
Вообще говоря, такой переход (t1→∞ ) требует некоторых
пояснений, связанных, в частности, с тем, что интегралы в (1.32), (1.33)
являются несобственными и их предполагаемое существование фактически означает,
что решения задачи (1.30), (1.31) при произвольных допустимых управлениях имеют
некоторую специфическую асимптотику «на бесконечности». Оказывается, что задачи
вида (1.30)-(1.33) могут иметь ряд интересных особенностей: может оказаться,
например, что замена ∞ на t1 = const < ∞) в
интегралах в (1.32), (1.33) приводит к задаче, неразрешимой в классе конечных
управлений ни для какого конечного t1. Поэтому формальное перенесение
«конечных» результатов на задачи с бесконечными промежутками времени не
сводится к замене t1 на ∞ в формулировках соответствующих теорем.
В связи с этим, а также исходя из содержательной постановки задач вида
(1.30)-(1.33), в подынтегральные выражения в интегралах (1.32), (1.33) вводятся
«дисконтирующие множители»:
 , i =1,2,...,
p , (1.34)
, i =1,2,...,
p , (1.34)
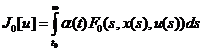 , (1.35)
, (1.35)
где α(t) - «дисконтирующие множители» - достаточно быстро
убывающие на бесконечности функции, описывающие эффект убывания полезности «отложенного»
потребления. В частности, широко используются множители вида α(t) = e-ρt
, ρ
> 0. С учетом
(1.34), (1.35) соответствующим образом видоизменяется задача (1.30)-(1.33).
Оптимизационные задачи с бесконечным горизонтом планирования обычно
являются задачами со свободным правым концом. В оптимизационных задачах с конечным
горизонтом планирования со свободным правым концом для сопряженной функции на
правом конце при t = t1 должно быть выполнено краевое условие. В
случае оптимизационной задачи без ограничений и целевого функционала типа
Лагранжа краевое условие имеет следующий вид:
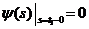 . (1.36)
. (1.36)
При этом сопряженная функция удовлетворяет системе
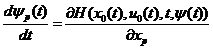 , p = 1, 2, …, n, t
, p = 1, 2, …, n, t [t0 , t1] (1.37)
[t0 , t1] (1.37)
где
H(x, u, t, ψ) =  ψ, f (t, x,
u)
ψ, f (t, x,
u) - F0(t, x, u),
(1.38)
- F0(t, x, u),
(1.38)
а необходимое условие оптимальности запишется в виде
H(x0(t),u(t), t,
ψ(t)) = sup H(x0(t),
u, t, ψ(t)), t [t0 , t1]
[t0 , t1]
u U
U
Формальный переход от такой задачи к оптимизационной задаче с бесконечным
горизонтом планирования подразумевает, в частности, осуществление замены t1
на ∞ и в соотношениях (1.36)-(1.38), так что, например, граничное условие
(1.36) следует «переписать» в виде
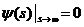 . (1.39)
. (1.39)
Однако, как показывают примеры, условие (1.39) для оптимального
управления в общем случае не удовлетворяется. Это означает, что без
дополнительных предположений о свойствах задачи (1.30)-(1.35) принцип
максимума, получаемый формальной заменой t1 на ∞ не является для
нее обоснованным утверждением.
К счастью, в математических задачах экономической динамики достаточно
естественными являются такие свойства операторов и функционалов, как выпуклость
(вогнутость) интегрантов целевых функций, аддитивная разделенность фазовых
переменных и управлений, специфические свойства правых частей дифференциальных
уравнений, гарантирующие неотрицательность ряда переменных и т.д.
Это позволяет в ряде случаев обосновать достаточные условия оптимальности
в оптимизационных задачах с бесконечным горизонтом планирования в форме
принципа максимума.
Приведем один относительно простой результат для таких задач.
Рассматривается задача максимизации функционала
 (1.40)
(1.40)
на траекториях одномерной управляемой системы
 (1.41)
(1.41)
с краевыми условиями
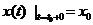 ,
, 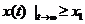 . (1.42)
. (1.42)
Используется кусочно-непрерывное управление u(t),
принимающее значения в множестве U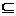 R (допустимые управления).
R (допустимые управления).
Определим гамильтониан задачи формулой
H(x, u, t, ) = ψ f (t,
x, u) + ψ0F(t,
x, u) ,
) = ψ f (t,
x, u) + ψ0F(t,
x, u) ,  =col{ψ0 , ψ}.
=col{ψ0 , ψ}.
Теорема 1.4. Предположим, что при y0 = 1 в задаче (1.40)-(1.42)
допустимая пара {x0(t), u0(t)} удовлетворяет
условиям:
1) H(x0(τ), u, τ,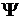 (τ)) ≤ H(x0(τ), u0(τ), τ,
(τ)) ≤ H(x0(τ), u0(τ), τ, 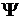 (τ)),
(τ)), 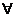 u
u U.
U.
2) , t
, t [t0, ∞).
[t0, ∞).
) Гамильтониан H(x,u,t,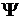 (t)) вогнут по {x,
u}.
(t)) вогнут по {x,
u}.
4) Справедливо соотношение  для любой допустимой пары {x(t),
u(t)}.
для любой допустимой пары {x(t),
u(t)}.
Если рассматривается задача минимизации целевого функционала, то условие
3) следует заменить условием выпуклости гамильтониана.
В общем случае векторных фазовых переменных и управлений вводятся
различные понятия оптимальности на бесконечном интервале времени (слабая
оптимальность, сильная оптимальность, почти оптимальность, совсем оптимальность,
спорадически почти оптимальность и т.д.). Отчасти они вызваны содержательными
постановками оптимизационных задач экономической динамики. Например, спорадически
почти оптимальность пары {x0(t), u0(t)}
(x Rn, u
Rn, u U
U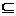 Rm ) означает, что для
любой допустимой пары {x(t), u(t)}
Rm ) означает, что для
любой допустимой пары {x(t), u(t)}
 ,
,
где
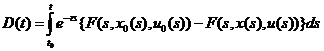 .
.
Оказывается, что для такого управления достаточно справедливости условий
принципа максимума в форме, аналогичной приведенной в теореме 3.4. В этих
условиях существенно условие вогнутости гамильтониана по переменным (x Rn, u
Rn, u U
U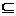 Rm).
Rm).
Выводы
Таким образом, при помощи при помощи данного метода мы смогли вычислить
рентабельность проводимых процессов, использовав при этом следующие методы и
приемы.
При решении вариационных задач классическими методами, как уже отмечалось
выше, серьезные, а иногда и непреодолимые трудности возникают в тех случаях,
когда отыскиваемые управляющие воздействия не принадлежат к классу непрерывных
функций или когда на переменные задачи наложены ограничения типа неравенств.
Для решения таких задач иногда с успехом может быть использован метод,
сформулированный и доказанный в работах Л.С. Понтрягина и его учеников, который
получил название принципа максимума.
Изложенный
выше метод допускает получение более тонких признаков оптимальности для тех
процессов, которые уже удовлетворяют дискретному принципу максимума
<#"879946.files/image054.gif">(I,
N)
Последняя
призвана характеризовать влияние инвестиций I на изменение количества
туристов при заданном уровне террористической угрозы. Сделанные выше
комментарии о характере взаимоотношений величин I и N
делают разумными следующие предположения относительно свойств функции 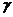 (I,N):
(I,N):
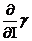 >0,
>0,  <0,
<0,
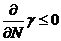 ,
,  ,
, 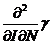 <0
<0
Первое
и третье из данных условий означают, что при заданном уровне N
число туристов является невыпуклой возрастающей функцией инвестиций I. Второе и четвертое неравенства показывают негативный
эффект, который террористы производят в отношении туристической
привлекательности страны, и при заданном I этот
эффект не уменьшается при увеличении количества террористов. Последнее
неравенство утверждает, что положительное воздействие на туриндустрию
дополнительной единицы инвестиции уменьшается с ростом террористической угрозы
(что, в общем-то, интуитивно понятно). Обозначим через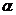 естественный уровень “распада” туриндустрии (моральное
и физическое старение объектов, разрушение инфраструктуры и т.д.), который
предполагается постоянным и положительным. Тогда динамика изменения числа Т(t) иностранных туристов, прибывающих в страну в момент t,
описывается обыкновенным дифференциальным уравнением
естественный уровень “распада” туриндустрии (моральное
и физическое старение объектов, разрушение инфраструктуры и т.д.), который
предполагается постоянным и положительным. Тогда динамика изменения числа Т(t) иностранных туристов, прибывающих в страну в момент t,
описывается обыкновенным дифференциальным уравнением
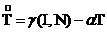 , (1)
, (1)
где
 обозначает производную по времени.
обозначает производную по времени.
Процветающая
туриндустрия формирует привлекательную среду для развития терроризма: теракты в
туристически привлекательных странах(особенно в местах массового скопления
людей) могут затрагивать граждан различных государств и следовательно имеют
большой (зачастую, международный) резонанс. Таким образом, число террористов
можно условно считать пропорциональным количеству Т иностранных туристов.
Предположим для простоты, что число террористов, привлеченных одним туристом,
постоянно. Обозначим эту величину  . Очевидно, что
. Очевидно, что  > 0. Отрицательное воздействие на уровень
террористической угрозы со стороны государства производится путем вложений E
в антитеррористические мероприятия, что формализуется посредством введения
функции φ(Е), относительно которой естественно предполагать
> 0. Отрицательное воздействие на уровень
террористической угрозы со стороны государства производится путем вложений E
в антитеррористические мероприятия, что формализуется посредством введения
функции φ(Е), относительно которой естественно предполагать
φ' > 0, φ'' < 0
(здесь штрих означает производную). Таким образом, число террористов N(t) изменяется со временем в соответствии с обыкновенным
дифференциальным уравнением
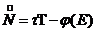 . (2)
. (2)
Целевой функционал
Очевидная цель государства состоит в максимизации суммарной прибыли от индустрии
туризма. Эта прибыль предполагается пропорциональной количеству Т
иностранных туристов, привлеченных в страну. Пусть р - средний доход от
одного туриста (предполагаем этот доход постоянным). Тогда доход за единицу
времени есть рТ.
Пусть задан период планирования [0,T], T ≤ ∞. Критерий качества инвестиционной политики государства формализуется в
виде следующего целевого функционала

подлежащего
максимизации по управлениям (I, E) при естественном с содержательной точки зрения условии
, Е ≥ 0
и динамических ограничениях (1), (2) с некоторыми заданными начальными
данными
Т(0) = T0, N(0) = N0.
В выражение для I, в подынтегральной функции, присутствует e -rt дисконтирующий множитель e , ответственный за деактуализацию дохода рТ - C(I) - bЕ с течением
времени. Здесь r > 0 параметр дисконтирования.
3.2 Исследование задачи оптимального управления
Сосредоточимся на случае конечного периода планирования, т.е.,
предполагаем T < ∞. Переформулируем исследуемую модель в
обозначениях, более привычных для теории оптимального управления, приняв
дополнительно некоторые гипотезы относительно ее структуры.
Положим [7]
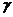 (I,
N) = aI(
(I,
N) = aI( - N),
- N),
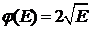
и

где
a  и h
- заданные положительные постоянные (
и h
- заданные положительные постоянные ( отвечает априорному максимальному уровню
террористической угрозы).
отвечает априорному максимальному уровню
террористической угрозы).
После
переобозначения наша экстремальная задача принимает вид:
(P) I =  e-rt
(px - 1/2hu2 - qv) dt → max, (3)
e-rt
(px - 1/2hu2 - qv) dt → max, (3)
ẋ = au( - y) - bx, x(0) = x0, (4)
- y) - bx, x(0) = x0, (4)
ẏ = cx - 2 , y(0) = yo, (5),v
> 0. (6)
, y(0) = yo, (5),v
> 0. (6)
Здесь
x(t),y(t)
E 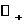 -
состояния (содержательный смысл которых мы пояснили ранее), u,v
- управления (инвестиции) и (r,p,h,q;
a,b,c) - некоторые
параметры.
-
состояния (содержательный смысл которых мы пояснили ранее), u,v
- управления (инвестиции) и (r,p,h,q;
a,b,c) - некоторые
параметры.
Преобразуем
задачу (P) к стандартной форме Майера, для этого введем новую
фазовую переменную:
ż
= e-rt (px - l/2hu2 - qv) , z(0) = 0. (7)
Тогда целевой функционал приобретает вид:
I = z (T). (8)
Далее, удобно перейти к новому управлению w = , w , в терминах которого
уравнения (5), (7) перепишутся следующим образом
ẏ = cx - 2w, y(0) = yo, (9)
ż
= e-rt (px - 1/2hu2 - qw2) , z(0) = 0. (10)
3.2.1 Уравнение состояния
До обращения к задаче оптимизации скажем несколько слов о самой
динамической системе (4), (5). Во-первых, охарактеризуем ее: при заданных
управлениях u,w мы, вообще говоря, имеем дело с
линейной неавтономной неоднородной системой обыкновенных дифференциальных
уравнений. Теперь с прикладной точки зрения: если предположить, что инвестиции
обоих типов в туриндустрию постоянны
u(t) ≡ 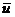 =
const > 0, w(t) ≡
=
const > 0, w(t) ≡ 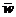 = const > 0,
= const > 0,
чего вполне можно ожидать в реальности, то у системы (4), (5) может
появиться точка динамического равновесия. Допустим, a ≠ 0, x(t) ≡
x0, y(t)≡ y0. Тогда
0 = ẋ = a (ŷ
- y0) - bx0
(ŷ
- y0) - bx0
и
0
= ẏ = cx0 - 2 ,
,
откуда имеем
(x0,y0)
= 
или то же в терминах инвестиций
 (11)
(11)
при
естественном предположении x0 > 0, y0
< y.
Таким
образом, при поступлении в макроэкономическую систему постоянных инвестиций в
размере (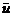 ,
,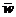 ), определенном в (11), имеем стационарный уровень
туристической активности и террористической угрозы в государстве. Если
начальные условия (x0, y0) отвечают приемлемому с содержательной точки зрения
состоянию, а (a, b, c)
таковы что затраты (
), определенном в (11), имеем стационарный уровень
туристической активности и террористической угрозы в государстве. Если
начальные условия (x0, y0) отвечают приемлемому с содержательной точки зрения
состоянию, а (a, b, c)
таковы что затраты (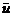 ,
,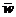 ) не играют существенной роли в бюджете государства,
стратегия, отвечающая подобной инвестиционной политике может быть целесообразна
и без апелляции к задаче оптимизации.
) не играют существенной роли в бюджете государства,
стратегия, отвечающая подобной инвестиционной политике может быть целесообразна
и без апелляции к задаче оптимизации.
3.2.2 Принцип максимума
Запишем для задачи (P) необходимые условия оптимальности в форме принципа максимума
Понтрягина. Введем следующие объекты:
 y
y
· Сопряженная траектория (ψх, ψу, ψz) удовлетворяет следующей системе
А


 (13)
(13)
 = bψх - сψy - e
-rtp, ψх(Т) = 0. (15)
= bψх - сψy - e
-rtp, ψх(Т) = 0. (15)
Для того чтобы избавиться от дисконтирующего множителя применим
стандартный прием: определим функции
λx(t) = еrtψх(t), λy(t) = еrtψy(t),
и положим для замкнутости обозначений λz(t) =ψz(t). Тогда
ψx(t)= е-rt λx(t), ψy(t)= е-rt λy(t),
функция Понтрягина в новых терминах имеет вид
Н(х, y, z, λx, λy, λz, и, w) = e-rt {[au(ŷ - y) - bx] λx+[cx - 2w] λу + px - 1/2hu2 - qw2}
Далее

Мы
заключаем
 ,
,
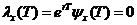
и аналогично
 ,
,
 .
.
Наконец, запишем каноническую систему принципа максимума:
ẋ = au(ŷ - y) - bx, x(0) = x0
ẏ = cx - 2w, y(0) =y0
ż = e-rt (px - 1/2hu2 - qw2),
z(0) = 0
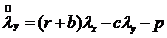 λx(T) =
0
λx(T) =
0
 , λy(T) =
0
, λy(T) =
0
λz ≡ 1. (16)
Пусть a, h, q >0, что отвечает содержанию
рассматриваемой модели. Для того чтобы закончить формулировку принципа
максимума нам осталось решить задачу условной максимизации
H(x, y, z, λx, λy, λz,u, w) → max, u,w >
0.
Последняя разбивается на две независимые подзадачи

и
 ,
,
которые
решаются элементарно:
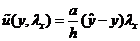
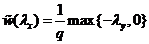 .
.
Формальная подстановка экстремальных отображений (u,w) в каноническую систему (16) приводит нас к
двухточечной краевой задаче
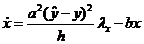 , x(0)
= x0
, x(0)
= x0
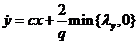 , y(0) =y0
, y(0) =y0
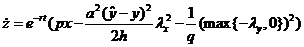 , z(0)=0
, z(0)=0
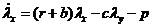 ,
,  (T)=0
(T)=0
 ,
,  (T)=0 (17)
(T)=0 (17)
которая может быть решена численно (с помощью метода “стрельбы” или
какого-нибудь другого приближенного алгоритма; с применением каких-либо
известных программных пакетов-решателей, например Matcad, Mathematica или [9]).
Выводы
Все примеры, приведенные выше служат внедрения инноваций в сфере
оптимального управления инвестициями в макроэкономической модели, описывающей
влияние террористических угроз в индустрии туризма несомненно, благоприятно
влияют на развитие инновационной деятельности, но существуют определенные
недостатки:
отсутствие современных механизмов внедрения технологических нововведений
и выведения их на рынок индустрии туризма;
недостаточное развитие инфраструктурных элементов содействия инновационным
проектам;
отсутствие на внутреннем рынке платежеспособного спроса на передовые
технологии и промышленные нововведения;
недостаточный уровень кадров.
Чтобы поднять уровень исследований и разработок, необходимо проведение
государственной политики стимулирования по следующим направлениям:
целенаправленное изучение и формирование рынка для продукции
инновационных предприятий путем размещения на них государственного заказа;
улучшение информационной базы и создание банков данных о
научно-технических потребностях и разработках.
В настоящее время информация стала одним из основных факторов
производства. Все активнее в повседневную жизнь человека внедряются виртуальные
технологии.
Таким образом, переход экономики в новое качественное состояние увеличил
значимость активизации инновационной деятельности, проблем формирования
инновационного потенциала страны, позволяющего реорганизовать экономику,
ускоренно развивать наукоемкое производство, что должно стать важнейшим
фактором обеспечения условий для экономического роста.
ЗАКЛЮЧЕНИЕ
Международный терроризм превращается в глобальную
военно-политическую проблему, угрожающую существованию человеческой
цивилизации. Именно такое звучание получила эта проблема на прошедшей 60-й
Генеральной Ассамблее ООН (сентябрь 2005 г.). Поэтому развитие международного
туризма в XXI в. зависит от консолидированных усилий всех стран мирового
сообщества в борьбе с международным терроризмом.
Обеспечение безопасности международного туристского
обмена обусловило необходимость международно-правовой регламентации
деятельности специализированных международных организаций и институтов. В этих
целях функционирует ряд международных туристских организаций, которые
определяют основные направления развития индустрии туризма в мире,
разрабатывают основополагающие принципы туристской деятельности, устанавливают
международные нормы и стандарты, способствуют сотрудничеству стран в деле
обеспечения безопасности международного туризма.
В настоящее время существует более 200 таких
международных туристских организаций различного профиля деятельности.
Координатором этой работы является Всемирная туристская организация (ВТО),
которая с октября 2003 г. является специализированным учреждением ООН. В рамках
Исполнительного совета ВТО в 1994 г. был создан Комитет по качеству туристского
обслуживания, в компетенцию которого входит разработка мер по обеспечению
безопасности туризма, уменьшению рисков при путешествиях и защите туристов. В
рамках достижения вышеуказанных целей данный Комитет реализует Программу
качества развития туризма, включающую:
создание системы регулирования в сфере торговли
туристскими услугами, в том числе и меры по либерализации и конкуренции;
безопасность и охрану, включая охрану здоровья;
стандарты качества [3, с. 125].
Важный вклад в обеспечение безопасности международного
туризма вносит деятельность международных организаций нетуристского профиля. В
табл. 1 изложен перечень основных целевых задач, которые решают ряд
непрофильных международных организаций в области обеспечения безопасности
туристских путешествий.
В данной работе рассмотрена макроэкономическая модель, описывающая
влияние террористических угроз на отрасль международного туризма. Цель
дипломной работы состояла в постановке задачи оптимального баланса инвестиций в
туриндустрию и антитеррористические мероприятия. Так же в дипломной
работе дана содержательная интерпретация модели, для поставленной задачи
записан принцип максимума, был изучен базовый аппарат теории оптимального
управления обыкновенными дифференциальными уравнениями. И таким образом, для
анализа экономических процессов и явлений, прогнозирования их дальнейшего
развития применяются логические и формально-математические модели.
Макроэкономические модели - это формализованные логическим, графическим или
алгебраическим способом описания различных макроэкономических процессов и
явлений с целью установить между ними функциональные взаимозависимости. Следует
иметь в виду, что любая модель есть абстрактное упрощение реальности, поэтому
она не может быть всеобъемлющей.
При помощи моделирования можно определить способы управления темпами
инфляции, уровнем занятости, объемами выпуска и потребления продукции,
величиной процентной ставки, валютным курсом. Все эти позиции называются
эндогенными экономическими переменными, т.е. внутренними, формирующимися внутри
модели, являющимися результатами ее построения и определяемыми в ходе
экономических расчетов. Внешними, экзогенными, экономическими переменными, т.е.
исходной информацией, задаваемой до начала построения модели, являются
инструменты, применяемые правительством и центральным банком в осуществлении
фискальной и монетарной политики. Это величина расходов государственного
бюджета, размеры налоговых ставок, объемы денежной массы. Использование
макроэкономических моделей позволяет более правильно сочетать применяемые
методы бюджетно-налоговой и денежно-кредитной, валютной и внешнеторговой
политики для сглаживания цикличности экономики, преодоления кризисов. Модели не
следует оценивать с точки зрения правильности для решения конкретных задач,
стоящих перед национальной экономикой конкретной страны. Их оценка должна
проводиться по критерию полезности при исследовании экономических процессов и
управляемости макроэкономическими показателями. Наряду с делением экономических
переменных на эндогенные и экзогенные существует другая классификация - по
способу их измерения во времени. Выделяют переменные запаса, характеризующие
состояние объекта на определенную дату (начало и конец квартала, года и т.д.).
К таким переменным относятся, к примеру, объем национального богатства страны,
величина государственного долга, совокупный объем капитала в экономике. Помимо
них, существуют переменные потока, характеризующие течение экономических
процессов во времени и измеряемые за единицу времени. Примерами могут служить размеры
валового продукта за год, потребительских расходов за год, объем инвестиций за
год и пр. И те и другие переменные взаимосвязаны, так как потоки вызывают
изменения в запасах. Например, накопление бюджетного дефицита за ряд лет
приводит к увеличению государственного долга. Существует множество видов
макроэкономических моделей. Приведем пять из них. Абстрактно-теоретические и
конкретно-экономические. Статические и динамические. Статические модели
характеризуются заданностью и фиксированностью общего запаса экономических
ресурсов, что может служить для анализа эффективности их распределения.
Динамические - учитывают распределенное по времени решение таких проблем, как
вовлечение ресурсов в производство, накопление сбережений, внедрение достижений
НТП, альтернативность издержек, и некоторых других. Динамические модели
подразделяются на краткосрочные, среднесрочные и долгосрочные, т.е. зависят от
временных периодов, в которых осуществляется анализ. Так, в моделях Дж.М.
Кейнса экономические процессы рассматриваются в краткосрочном периоде;
классические модели являются долгосрочными. Равновесные и неравновесные.
Равновесные модели описывают ситуацию, когда при неизменности внешних условий и
параметров ни у одного из участников хозяйственного процесса нет стимула менять
свое экономическое поведение. Планы экономических субъектов и их реализация
совпадают. При усложнении ряда экономических процессов возникает ситуация,
описываемая неравновесными моделями, например, моменты неопределенности при
отсутствии полной информации, когда различные экономические субъекты стремятся
себя застраховать от возможных рисков или сделки осуществляются по
неравновесным ценам, до того как было установлено равновесие. Равновесные и
неравновесные модели тесно взаимосвязаны. Открытые и закрытые модели
соответствуют открытому или закрытому типам экономики, описанным в параграфе
1.2. Открытые модели предполагают участие национальной экономики в
международной торговле, учитывают основные макроэкономические показатели,
определяющие взаимодействие разных стран. Закрытые модели предполагают
абстрагирование национальной экономики от участия в международных экономических
отношениях.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Алексеев В.М., Тихомиров В.М., Фомин С.В.
Оптимальное управление. М.: Наука. 1979.
. Аркин В.И., Евстигнеев И.В. Вероятностные модели
управления и экономической динамики. М.: «Наука». 1979.
. Ашманов С.А. Введение в математическую экономику.
М.: Наука, 1984.
. Бгатов, А.П., Бойко, Т.В., Зубрева, М.В. Туристские
формальности. М.: Academia, 2004.
. Беллман Р. Динамическое программирование. М.:
Изд-во иностр. литер., 1960.
. Беллман Р., Дрейфус С. Прикладные задачи
динамического программирования. М.: Наука. Гл. ред. физ.-мат. лит., 1965.
. Болтянский В.Г. Математические методы оптимального
управления. М.: Наука. 1969.
. Болтянский В.Г. Оптимальное управление дискретными
системами. М.: Наука. 1973.
. Васильев Ф.П. Численные методы решения
экстремальных задач. М.: Наука. 1988
. Всеобщая декларация прав человека. Мн.:
Представительство ООН в Республике Беларусь, 2000.
. Маринин, М.М. Туристские формальности и
безопасность в туризме. М.: Финансы и статистика, 2002.
. Организация туризма: учебное пособие / А. П.
Дурович [и др.]; под общ. ред. Н.И. Кабушкина и др. Мн.: Новое знание, 2003.
13. Развитие
международного туризма и обеспечение безопасности туристов
<#"879946.files/image103.jpg">
Приложение 2
