Дискетный анализ рисковых активов
Контрольная работа
Дискетный анализ рисковых активов
Содержание
. Возврат и
логарифмический возврат
. Линейный
прогноз
. Гауссовы
модели
.
Стационарные в широком смысле модели
.
Спектральное представление стационарных в широком смысле последовательностей
. Линейный
фильтр
. Линейные
модели финансовых временных последовательностей
. Линейный
прогноз для стационарных в широком смысле последовательностей
.
Статистическое оценивание параметров модели
Литература
. Возврат и логарифмический возврат
логарифмический
возврат статистический линейный
Предположим,
что мы определили единицу измерения времени (один день, один месяц или один
год). Последовательность 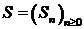 - рыночная стоимость акции, обменный курс двух валют
или что-либо иное. В этом пособии мы будем придерживаться вероятностного
подхода, и следовать общепринятой аксиоматике теории вероятностей. То есть
- рыночная стоимость акции, обменный курс двух валют
или что-либо иное. В этом пособии мы будем придерживаться вероятностного
подхода, и следовать общепринятой аксиоматике теории вероятностей. То есть 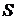 - стохастическая последовательность, которая
определена на некотором вероятностном пространстве
- стохастическая последовательность, которая
определена на некотором вероятностном пространстве 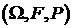 , где
, где  -
пространство элементарных случайных событий (случаев)
-
пространство элементарных случайных событий (случаев) 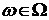 ( в рассматриваемом контексте состояний рынка);
( в рассматриваемом контексте состояний рынка);
F -  -алгебра подмножеств
-алгебра подмножеств  -
совокупность событий наблюдаемых на рынке;
-
совокупность событий наблюдаемых на рынке;
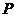 - семейство
вероятностных мер, возможно, параметрическое, на
- семейство
вероятностных мер, возможно, параметрическое, на 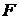 .
.
Для
различных финансовых теорий время и динамика являются неотъемлемой частью
рассуждений, поэтому целесообразно рассмотреть поток  - подалгебр
- подалгебр  . Смысл
введения потока, называемого в литературе также фильтрацией заключается в том,
чтобы в любой момент времени
. Смысл
введения потока, называемого в литературе также фильтрацией заключается в том,
чтобы в любой момент времени 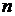 оперировать,
только теми случайными событиями, которые «доступны» наблюдателю до момента
времени
оперировать,
только теми случайными событиями, которые «доступны» наблюдателю до момента
времени 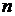 включительно. Например, до момента времени
включительно. Например, до момента времени 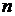 включительно наблюдателю могут быть доступны стоимости
тех или иных активов, начиная с некоторого начального момента до момента
времени
включительно наблюдателю могут быть доступны стоимости
тех или иных активов, начиная с некоторого начального момента до момента
времени 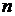 .
.
Таким
образом, базовой вероятностной моделью является
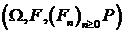 , (1.1)
, (1.1)
называемая фильтрованным стохастическим экспериментом.
Если
рассматривать 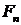 как информацию доступную к моменту времени
как информацию доступную к моменту времени 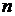 , то естественно считать, что последовательность
, то естественно считать, что последовательность 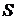 - адаптирована, то есть для любого момента времени
- адаптирована, то есть для любого момента времени 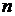
 измеримы. Интерпретация
измеримы. Интерпретация 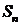 как цены в момент времени
как цены в момент времени 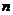 приводит к тому, что
приводит к тому, что  .
.
Существует
два наиболее распространенных способа представления временного ряда 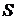 :
:
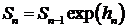 . (1.2)
. (1.2)
Откуда
 , (1.3)
, (1.3)
где
 , и
, и
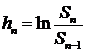 (1.4)
(1.4)
называют возвратом, отдачей, логарифмической прибылью (return).
Другой способ представления
 . (1.5)
. (1.5)
Откуда
 (1.6)
(1.6)
и
 . (1.7)
. (1.7)
Рассмотрим
последовательность  и обозначим через
и обозначим через  ,
,  .
.
Определяемая
этим выражением последовательность называется стохастической экспонентой,
порождаемой  . Формула (1.6) трансформируется в формулу
. Формула (1.6) трансформируется в формулу
 (1.8)
(1.8)
Сопоставление
(1.3) с (1.8) приводит к соотношениям
 (1.9)
(1.9)
При
малых значениях 
 при этом ошибка
при этом ошибка 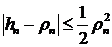 .
.
Таким
образом, представление 1 и представление 2 в одинаковой степени могут быть
использованы для описания последовательности 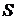 .
.
Далее
мы будем использовать первое представление, поскольку второе представление
накладывает ограничение на 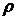 . Из
того, что
. Из
того, что  непосредственно следует, что
непосредственно следует, что 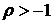 . В тоже время различного рода ограничения могут существенно
отразиться на сложности статистических задач.
. В тоже время различного рода ограничения могут существенно
отразиться на сложности статистических задач.
.
Линейный прогноз
Гильбертовым
пространством вещественно - значных случайных величин с конечным вторым
моментом  называется линейное пространство случайных величин с
называется линейное пространство случайных величин с 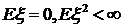 и скалярным произведением
и скалярным произведением
 . (2.1)
. (2.1)
Рассмотрим
совокупность линейно-независимых случайных величин  , обозначим через
, обозначим через  линейную
оболочку, натянутую на случайные величины
линейную
оболочку, натянутую на случайные величины  .
.
Наилучшим
линейным прогнозом случайной величины 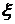 по
совокупности случайных величин
по
совокупности случайных величин  назовем
назовем
 . (2.1)
. (2.1)
Так
как 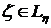 , то
, то  ,
следовательно, наилучший линейный прогноз
,
следовательно, наилучший линейный прогноз
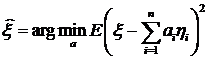 . (2.2)
. (2.2)
Минимум
достигается тогда, когда разность 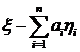 ортогональна
подпространству
ортогональна
подпространству 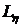 . Таким образом, решение задачи (2.2) сводится к
решению системы линейных алгебраических уравнений
. Таким образом, решение задачи (2.2) сводится к
решению системы линейных алгебраических уравнений 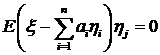 .. В матричных обозначениях система уравнений
представляется в виде:
.. В матричных обозначениях система уравнений
представляется в виде:
 , (2.3)
, (2.3)
где
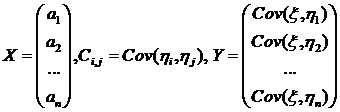 .
.
Дисперсия
ошибки
 .
.
Используем
предыдущие обозначения, в результате получим  .
Откуда
.
Откуда
 . (2.4)
. (2.4)
В
последних выражениях  - скалярное произведение евклидового пространства.
- скалярное произведение евклидового пространства.
Наилучшим
прогнозом случайной величины 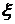 по
совокупности случайных величин
по
совокупности случайных величин  назовем
назовем
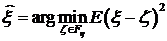 , (2.5)
, (2.5)
где
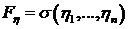 минимальная сигма-подалгебра
минимальная сигма-подалгебра 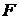 , содержащая события
, содержащая события 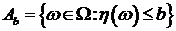 ;
;
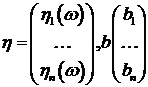 ;
; 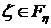 означает,
что
означает,
что  -
-  измерима.
Из телескопического свойства условного математического ожидания
измерима.
Из телескопического свойства условного математического ожидания 
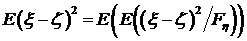 . Из
неравенства
. Из
неравенства  , следует неравенство
, следует неравенство 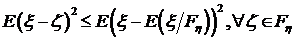 .
Отсюда оптимальный прогноз
.
Отсюда оптимальный прогноз
 . (2.6)
. (2.6)
Если
совместный закон распределения  -
многомерный нормальный закон распределения, то по теореме о нормальной
корреляции [Ширяев, Вероятность] наилучший прогноз совпадает с наилучшим
линейным прогнозом.
-
многомерный нормальный закон распределения, то по теореме о нормальной
корреляции [Ширяев, Вероятность] наилучший прогноз совпадает с наилучшим
линейным прогнозом.
.
Гауссовы модели
Остановимся
на проблеме описания распределения вероятностей последовательности 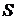 , что сводится к описанию распределения вероятностей
последовательности
, что сводится к описанию распределения вероятностей
последовательности  или последовательности
или последовательности  .
.
С
точки зрения классической теории вероятностей и далеко продвинутой статистики
нормального распределения было бы весьма привлекательным использование
нормального закона распределения для описания поведения последовательности  . Поскольку для задания распределения в этом случае
достаточно задания последовательности математических ожиданий
. Поскольку для задания распределения в этом случае
достаточно задания последовательности математических ожиданий  и ковариационной матрицы
и ковариационной матрицы 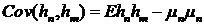 . Принятие такого предположения существенно упрощает
решение задачи прогнозирования
. Принятие такого предположения существенно упрощает
решение задачи прогнозирования  по
по 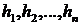 . Как отмечалось выше, наилучший прогноз
. Как отмечалось выше, наилучший прогноз
 . (3.1)
. (3.1)
Коэффициенты
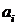 удовлетворяют системе линейных алгебраических
уравнений (2.3).
удовлетворяют системе линейных алгебраических
уравнений (2.3).
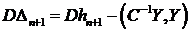 . (3.2)
. (3.2)
Формула для дисперсии ошибки непосредственно следует из (2.4).
Теперь
мы можем говорить о доверительном интервале для  при
заданной доверительной вероятности
при
заданной доверительной вероятности 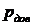 .
Величина
.
Величина  принадлежит доверительному интервалу
принадлежит доверительному интервалу
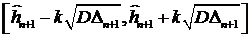 , (3.3)
, (3.3)
где
 находится из уравнения
находится из уравнения 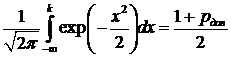 .
.
Зная
доверительный интервал для  , можно
указать доверительный интервал для
, можно
указать доверительный интервал для 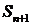 .
.
 . (3.4)
. (3.4)
Пусть
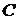 - диагональная матрица, тогда формулы (2.4) и (3.2)
существенно упрощаются. Коэффициенты
- диагональная матрица, тогда формулы (2.4) и (3.2)
существенно упрощаются. Коэффициенты 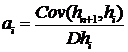 и
дисперсия ошибки
и
дисперсия ошибки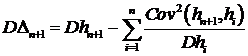 .
.
Равенство
нулю ковариаций для нормального закона распределения равносильно независимости.
В этом случае матрица 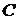 - диагональная матрица, а
- диагональная матрица, а  - нулевой вектор, и наилучший прогноз
- нулевой вектор, и наилучший прогноз 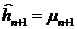 , дисперсия ошибки которого
, дисперсия ошибки которого 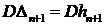 . Если добавить еще более сильное требование
одинаковой распределенности элементов последовательности
. Если добавить еще более сильное требование
одинаковой распределенности элементов последовательности  , то при таких предположении цены
, то при таких предположении цены 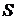 анализируются достаточно просто. В этом случае
прогноз
анализируются достаточно просто. В этом случае
прогноз  и дисперсия ошибки
и дисперсия ошибки 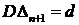 . То есть
теряется возможность какого-либо прогноза будущих значений.
. То есть
теряется возможность какого-либо прогноза будущих значений.
В
реальности ситуация более благоприятна, поскольку многочисленные исследования
временных финансовых последовательностей показывают, что последовательность  не является гауссовой последовательностью. Кроме
этого исследования показывают наличие зависимости между элементами
последовательности
не является гауссовой последовательностью. Кроме
этого исследования показывают наличие зависимости между элементами
последовательности  .
.
Более
емким распределением является смесь гауссовских распределений. В простейшем
случае плотность смеси
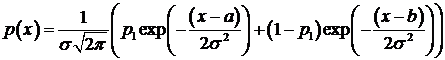 . (3.5)
. (3.5)
Это распределение интерпретируется формулой:
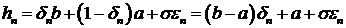 , (3.6)
, (3.6)
в
которой  - последовательность независимых и одинаково
распределенных бинарных случайных величин,
- последовательность независимых и одинаково
распределенных бинарных случайных величин,  -
последовательность независимых стандартных гауссовых величин, независящих от
-
последовательность независимых стандартных гауссовых величин, независящих от  . На рисунке 3.1 представлен график реализации
последовательности
. На рисунке 3.1 представлен график реализации
последовательности  .
.
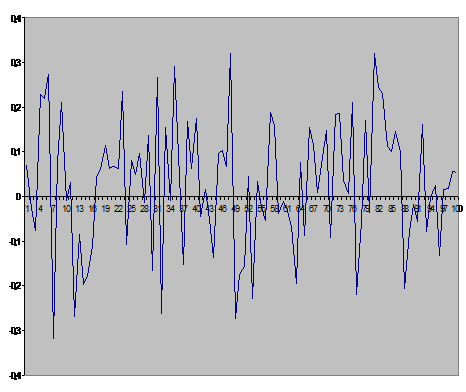
Рис.
3.. График компьютерной реализации последовательности  при
при 
Из (3.6)
следует, что
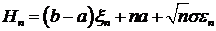 , (3.7)
, (3.7)
где
случайная величина 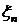 - распределена по закону Бернулли. На рисунке 3.2
представлен график реализации последовательности
- распределена по закону Бернулли. На рисунке 3.2
представлен график реализации последовательности  .
.

Рис.
3.2 График компьютерной реализации последовательности  при
при 
Модель
(3.5)-(3.7) можно рассматривать как модель Кокса-Росса-Рубинштейна с белым
шумом.
Математическое
ожидание и дисперсия 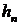
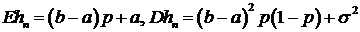 . (3.8)
. (3.8)
Случайные величины в этой модели независимы и одинаково распределены,
поэтому наилучший линейный прогноз
 , (3.9)
, (3.9)
при этом
дисперсия ошибки
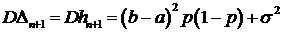 . (3.10)
. (3.10)
Отметим, что в этом случае наилучший линейный прогноз не совпадает с
наилучшим прогнозом.
Модель
(3.5)-(3.7) допускает определенное развитие, в котором учитывается зависимость
в последовательности 
 , (3.11)
, (3.11)
при
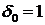 . Для
. Для 

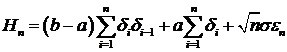 . (3.12)
. (3.12)
В
этой модели  .
.
Рис.
3.3. График компьютерной реализации последовательности  (модель (3.11)-(3.12)) при
(модель (3.11)-(3.12)) при  .
.
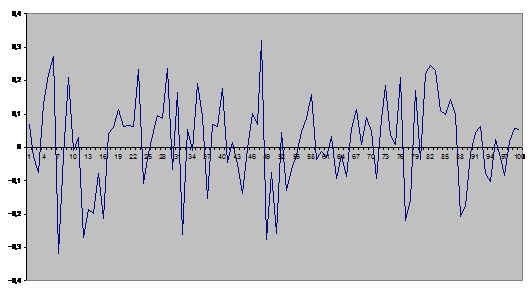
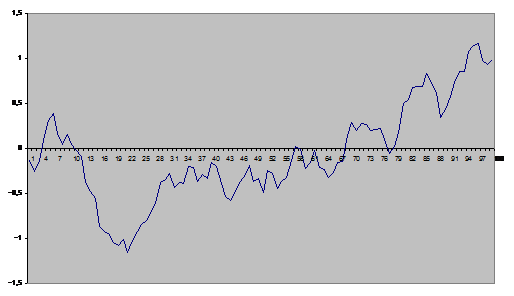
Рис.
3.4 График компьютерной реализации последовательности  (модель (3.11)-(3.12)) при
(модель (3.11)-(3.12)) при 
Математическое ожидание
 . (3.13)
. (3.13)
Ковариация
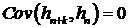 при
при 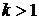 . При
. При 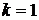
 . (3.14)
. (3.14)
Дисперсия
 . (3.15)
. (3.15)
Введем
обозначения  и
и  . В этих
обозначениях матрица
. В этих
обозначениях матрица  ,
,  .
Представим ковариационную матрицу
.
Представим ковариационную матрицу 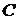 в виде
произведения
в виде
произведения
 , (3.16)
, (3.16)
где
матрица  . Элементы матрицы
. Элементы матрицы  удовлетворяют
уравнениям:
удовлетворяют
уравнениям:
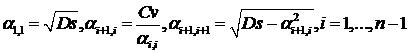 . (3.17)
. (3.17)
Рассмотрим
уравнение (2.3), которое запишем в виде  . Введем
обозначение
. Введем
обозначение 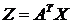 . Уравнение (2.3) распадается на два уравнения:
. Уравнение (2.3) распадается на два уравнения:
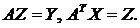 (3.18)
(3.18)
Решение
первого уравнения 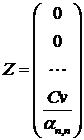 . Решение второго уравнения
. Решение второго уравнения
 . (3.19)
. (3.19)
Таким
образом, наилучший линейный прогноз для модели (3.11),(3.12)
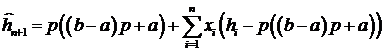 . (3.20)
. (3.20)
При этом дисперсия ошибки
 . (3.21)
. (3.21)
В
модели (3.5)-(3.7) потребуем, чтобы последовательность  была марковской цепью, с независящими от
была марковской цепью, с независящими от 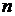 переходными вероятностями
переходными вероятностями  . Обозначим через
. Обозначим через  матрицу
переходных вероятностей.
матрицу
переходных вероятностей.
На
рисунках 3.6 и 3.7 представлены графики машинной реализации последовательности  и последовательности
и последовательности  соответственно.
соответственно.
Математическое
ожидание 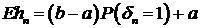 . Вероятность
. Вероятность 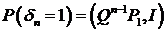 , где
, где  ,
, 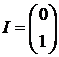 .
Собственные числа матрицы
.
Собственные числа матрицы 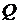 :
: .
Соответствующие собственные векторы
.
Соответствующие собственные векторы  . Таким
образом, для матрицы
. Таким
образом, для матрицы 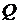 существует сингулярное разложение
существует сингулярное разложение
 , (3.22)
, (3.22)
где
 . Из (3.22) непосредственно следует, что
. Из (3.22) непосредственно следует, что 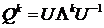 . Матрица
. Матрица  . Отсюда
. Отсюда
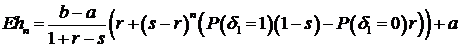 . (3.23)
. (3.23)
Поскольку
 , то
, то  .
Следовательно,
.
Следовательно,
 , (3.24)
, (3.24)
причем скорость сходимости показательная.
Вычислим
ковариацию 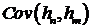 . Не нарушая общности, будем считать, что
. Не нарушая общности, будем считать, что  . Прежде всего, определим математическое ожидание
. Прежде всего, определим математическое ожидание 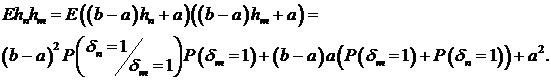
Вероятности
 . Отсюда
. Отсюда 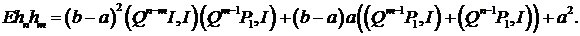
Таким
образом,
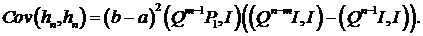 (3.25)
(3.25)
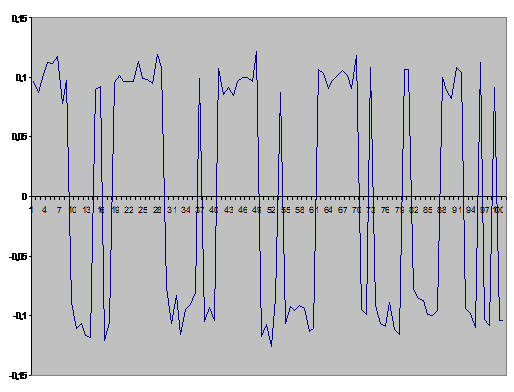
Рисунок
3.6. График машинной реализации последовательности  при
при 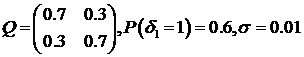 .
.
Далее
будем считать, что последовательность 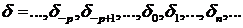 .
Обозначим через
.
Обозначим через 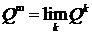 . В рассматриваемом варианте формула (3.25)
преобразуется в формулу
. В рассматриваемом варианте формула (3.25)
преобразуется в формулу 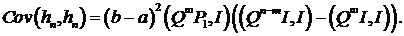 Используем (3.23)
Используем (3.23)  . Так как
. Так как
 , то
, то
 . (3.26)
. (3.26)
Из (3.26) следует
Рисунок
3.6. График машинной реализации последовательности  при
при 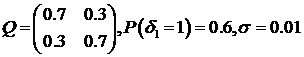
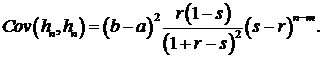 (3.27)
(3.27)
Из (3.27) следует, что дисперсия
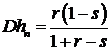 , (3.28)
, (3.28)
Что
выглядит достаточно естественным, если учесть, что в рассматриваемой ситуации  . Отметим также,
. Отметим также,

 , (3.29)
, (3.29)
что хорошо согласуется с (3.24).
Последовательности, обладающие свойством
 (3.30)
(3.30)
называются стационарными в широком смысле.
Отметим, что формулы (3.27) и (3.30) соответствуют определению
стационарной в широком смысле последовательности.
Соединение
стационарности и гауссовости приводит к стационарности последовательности 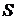 в узком смысле.
в узком смысле.
Последовательность
называется стационарной в узком смысле, если для любых 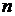 и
и 
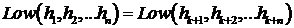 .
.
.
Стационарные в широком смысле модели
Далее
мы будем считать, что последовательность  -
стационарна в широком смысле. Чтобы упростить выкладки будем считать, что
-
стационарна в широком смысле. Чтобы упростить выкладки будем считать, что  . Элементы последовательности принадлежат гильбертову
пространству комплексно-значных случайных величин
. Элементы последовательности принадлежат гильбертову
пространству комплексно-значных случайных величин 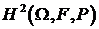 , со скалярным произведением
, со скалярным произведением 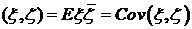 ,
, 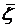 -
комплесно-сопряженное число к
-
комплесно-сопряженное число к  .
Обозначим через
.
Обозначим через
 ,
,
 . (4.1)
. (4.1)
Естественно,
что мы предполагаем, что  .
.
Функция
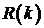 называется ковариационной функцией. Функция
называется ковариационной функцией. Функция  называется корреляционной функцией.
называется корреляционной функцией.
Из
определения следует, что ковариационная функция является неотрицательно
определенной, то есть для любых комплексных чисел 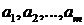 и любых
и любых 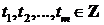 ,
,  ,
,
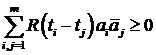 . (4.2)
. (4.2)
В
качестве упражнения доказать следующие свойства ковариационной функции: 
Пример
1. Последовательность 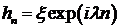 , где
, где 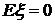 ,
,  и
и 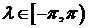 ,
является последовательностью стационарной в широком смысле. Действительно,
,
является последовательностью стационарной в широком смысле. Действительно,  .
.
Пример
2. Последовательность 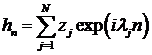 , где
, где 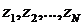 -
ортогональные случайные величины с
-
ортогональные случайные величины с 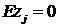 и
и  ,
,  ,
является стационарной.
,
является стационарной.
Действительно,
 .
.
Пример
3. Рассмотрим последовательность.
 , (4.3)
, (4.3)
где
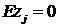 и
и  , причем
, причем  ;
; 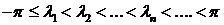 .
Отметим, что ряд
.
Отметим, что ряд 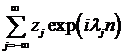 сходится в среднем квадратическом и
сходится в среднем квадратическом и 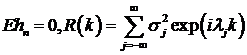 . Следовательно, последовательность стационарна.
. Следовательно, последовательность стационарна.
Рассмотрим
функцию  .
. 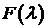 -
неубывающая кусочно-постоянная функция, большая либо равная нуля, имеющая
пределы слева и полунепрерывная справа. Следовательно,
-
неубывающая кусочно-постоянная функция, большая либо равная нуля, имеющая
пределы слева и полунепрерывная справа. Следовательно, 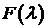 с точностью до нормировки является функцией
распределения. Носитель этой функции сосредоточен на множестве
с точностью до нормировки является функцией
распределения. Носитель этой функции сосредоточен на множестве  . С помощью этой функции ковариационная функция
рассматриваемой последовательности может быть записана в виде интеграла
Лебега-Стилтьеса:
. С помощью этой функции ковариационная функция
рассматриваемой последовательности может быть записана в виде интеграла
Лебега-Стилтьеса:
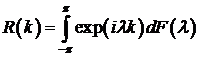 . (4.4)
. (4.4)
Пример
4. Пусть  - последовательность ортонормированных случайных с
нулевыми математическими ожиданиями. Эту последовательность принято называть
белым шумом. Понятно, что белый шум стационарная последовательность с
ковариационной функцией
- последовательность ортонормированных случайных с
нулевыми математическими ожиданиями. Эту последовательность принято называть
белым шумом. Понятно, что белый шум стационарная последовательность с
ковариационной функцией 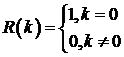 . Эта функция также может быть представлена в виде
интеграла
. Эта функция также может быть представлена в виде
интеграла
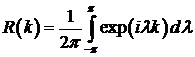 . (4.5)
. (4.5)
Отсюда
 или
или  , то есть
является функцией распределения равномерного закона на интервале
, то есть
является функцией распределения равномерного закона на интервале  .
.
5. Спектральное представление стационарных в широком смысле
последовательностей
Представление последовательности (4.3) и интегральное представление
ковариационной функции в примере 3 наводит на мысль о возможности получения
представления произвольной стационарной последовательности в виде интегрального
обобщения суммы (4.3). Формально это можно сделать следующим образом. Определим
функцию
 . (5.1)
. (5.1)
Использование
функции 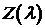 позволяет записать (4.3) в виде:
позволяет записать (4.3) в виде:
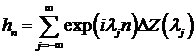 , (5.2)
, (5.2)
где
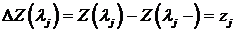 .
.
Правая
часть (5.2) напоминает интегральную сумму для интеграла  . Однако, функция
. Однако, функция 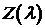 является
случайной функцией. При фиксированном
является
случайной функцией. При фиксированном  функция
функция 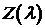 может иметь неограниченную вариацию. Поэтому
понимание интеграла для каждого
может иметь неограниченную вариацию. Поэтому
понимание интеграла для каждого  как
интеграла Римана-Стилтьеса неприемлемо. Процессом с ортогональными приращениями
назовем случайную функцию
как
интеграла Римана-Стилтьеса неприемлемо. Процессом с ортогональными приращениями
назовем случайную функцию 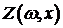 ,
,  если
если
) для
каждого 
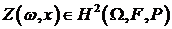 ;
;
) для
каждого 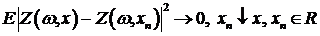 ;
;
) для
любых  .
.
Определим
случайную меру полуоткрытого интервала  :
:
 . (5.3)
. (5.3)
Определим
случайную меру для суммы непересекающихся интервалов 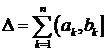 :
:
 (5.4)
(5.4)
Рассмотрим
алгебру  , порожденную полуоткрытыми интервалами
, порожденную полуоткрытыми интервалами  . Соотношение (5.4) определяет элементарную
стохастическую меру на
. Соотношение (5.4) определяет элементарную
стохастическую меру на  . Напомним, что элементарной стохастической мерой
называется комлекснозначная функция
. Напомним, что элементарной стохастической мерой
называется комлекснозначная функция  ,
определенная для
,
определенная для 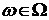 и
и 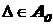 , если
, если
) 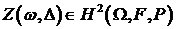 ,
, 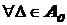 ;
;
) для
любых непересекающихся 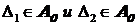
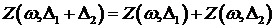 ;
;
) для
любых непересекающихся  , что
, что 
 .
.
)
для любых непересекающихся  и
и 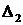
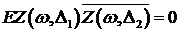 .
.
Задача.
Доказать выполнение 1)-4) .
Определим
функцию
 . (5.5)
. (5.5)
Как
легко показать,  является конечной мерой, и, следовательно, по теореме
Каратеодори может быть продолжена на
является конечной мерой, и, следовательно, по теореме
Каратеодори может быть продолжена на 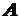 , где
, где 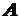 - минимальная
- минимальная  - алгебра,
содержащая
- алгебра,
содержащая  (борелевская
(борелевская  -
алгебра). Эту меру мы будем обозначать
-
алгебра). Эту меру мы будем обозначать  и
называть структурной функцией элементарной стохастической меры
и
называть структурной функцией элементарной стохастической меры  .
.
Итак,
перейдем к построению интеграла. Пусть 
 . (5.6)
. (5.6)
Для каждой такой функции определим интеграл:
 . (5.7)
. (5.7)
Отметим,
если 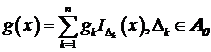 , то
, то
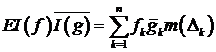 . (5.8)
. (5.8)
Пусть
 - гильбертово пространство комплеснозначных функций
со скалярным произведением
- гильбертово пространство комплеснозначных функций
со скалярным произведением  . Таким
образом, для любых функций вида (5.7) в силу (5.8)
. Таким
образом, для любых функций вида (5.7) в силу (5.8)  . Это соотношение является ключевым при определении
интеграла.
. Это соотношение является ключевым при определении
интеграла.
Пусть
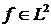 , тогда существует последовательность функций вида
(5.6), что
, тогда существует последовательность функций вида
(5.6), что  при
при  . Тогда
. Тогда  при
при 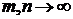 . То есть
последовательность
. То есть
последовательность  является фундаментальной. Из полноты гильбертова
пространства
является фундаментальной. Из полноты гильбертова
пространства  следует существование случайной величины
следует существование случайной величины 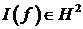 , что
, что 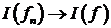 . Ее
естественно назвать интегралом от функции
. Ее
естественно назвать интегралом от функции  по
стохастической мере
по
стохастической мере  . Естественно использовать для этой случайной величины
интегральную запись
. Естественно использовать для этой случайной величины
интегральную запись  .
.
Отметим
основные свойства стохастического интеграла:
)  ;
;
)  , где
, где 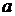 и
и  - константы;
- константы;
) если
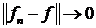 , то
, то  .
.
Задача. Доказать свойства 1)-3).
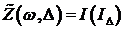 . (5.4)
. (5.4)
Задача. Доказать
1) Если
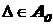 , то
, то 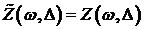 .
.
) Если
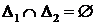 , то
, то  .
.
) 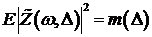 .
.
) Если
 , то
, то  при
при  .
.
) Если
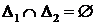 , то
, то  .
.
Пусть
 ковариационная функция стационарной в широком смысле
последовательности
ковариационная функция стационарной в широком смысле
последовательности  . Является справедливой теорема.
. Является справедливой теорема.
Теорема
(Герглотц). Существует конечная мера на  (
(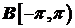 - борелевская
- борелевская  -
алгебра подмножеств интервала
-
алгебра подмножеств интервала  )
)  ,
, 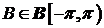 , что для
любого
, что для
любого 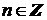
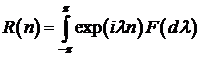 . (5.5)
. (5.5)
Обозначим
через 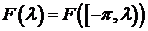 . В этом обозначении
. В этом обозначении
 . (5.6)
. (5.6)
Если
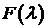 - абсолютно непрерывная функция:
- абсолютно непрерывная функция:  , то
, то
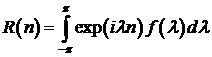 (5.7)
(5.7)
Из
(5.6) следует, что если 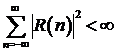 , то
, то
 . (5.8)
. (5.8)
Функция
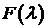 называется спектральной функцией, функция
называется спектральной функцией, функция 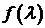 называется спектральной плотностью.
называется спектральной плотностью.
Если
последовательность  - вещественнозначная, то
- вещественнозначная, то
 ,
,
если
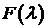 - абсолютно непрерывная функция, то
- абсолютно непрерывная функция, то
 . (5.9)
. (5.9)
Пусть
 - стационарная в широком смысле последовательность, тогда
из теоремы Герглотца существует представление (5.6).
- стационарная в широком смысле последовательность, тогда
из теоремы Герглотца существует представление (5.6).
Пусть
 - гильбертово пространство комплескснозначных функций
со скалярным произведением
- гильбертово пространство комплескснозначных функций
со скалярным произведением  .
.
Обозначим
через  - линейное многообразие, порожденное функциями
- линейное многообразие, порожденное функциями 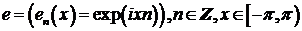 . Отметим, что
. Отметим, что 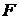 -
конечная мера на
-
конечная мера на 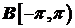 . Отсюда замыкание
. Отсюда замыкание  совпадает
с
совпадает
с  .
.
Рассмотрим
линейное многообразие  , порожденное случайными величинами
, порожденное случайными величинами  , и
, и 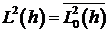 (замыкание
в среднеквадратичном смысле). Построим изоморфизм
(замыкание
в среднеквадратичном смысле). Построим изоморфизм 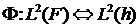 .
.
)
 .
.
)
 (предполагается, что только конечное число
коэффициентов не равно нулю).
(предполагается, что только конечное число
коэффициентов не равно нулю).
Отметим,
что  , аналогично
, аналогично
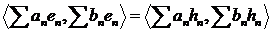 . (5.10)
. (5.10)
В частности,
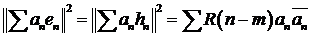 (5.11)
(5.11)
3)
Пусть  , тогда существует последовательность
, тогда существует последовательность  отсюда и из (5.11) следует, что последовательность
отсюда и из (5.11) следует, что последовательность 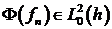 является фундаментальной последовательностью,
следовательно, существует
является фундаментальной последовательностью,
следовательно, существует  . Справедливо и обратное. Положим
. Справедливо и обратное. Положим  , где
, где  и
и  , рассмотренные выше элементы.
, рассмотренные выше элементы.
Задача.
Доказать,
что построенное отображение 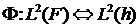 ,
является изоморфизмом, сохраняющим скалярное произведение.
,
является изоморфизмом, сохраняющим скалярное произведение.
Рассмотрим
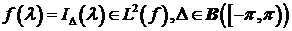 . Определим процесс
. Определим процесс
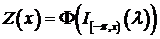 . (5.12)
. (5.12)
Задача. Доказать, что процесс, определенный формулой (5.12) является
процессом с ортогональными приращениями.
Пусть
 . Покажем, что
. Покажем, что  . Рассмотрим
последовательность
. Рассмотрим
последовательность  простых функций, сходящуюся к
простых функций, сходящуюся к  , тогда последовательность
, тогда последовательность  сходится к
сходится к 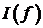 . С
другой стороны
. С
другой стороны  . Кроме этого последовательность
. Кроме этого последовательность  сходится к
сходится к  .
Следовательно,
.
Следовательно,  .
.
Возьмем
функцию 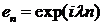 ,
, 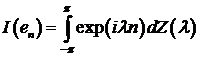 . С
другой стороны
. С
другой стороны  . Следовательно,
. Следовательно,
 . (5.13)
. (5.13)
Формула
(5.13) называется спектральным представлением стационарной в широком смысле
последовательности  .
.
Задача.
Доказать,
что 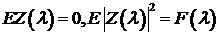 .
.
Пусть
 - стационарная в широком смысле последовательность,
состоящая из действительных случайных величин. Тогда из (5.13) следует, что
- стационарная в широком смысле последовательность,
состоящая из действительных случайных величин. Тогда из (5.13) следует, что 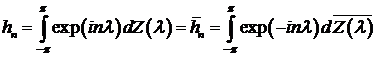 . Отсюда,
. Отсюда,  .
.
Задача.
Представим 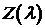 в виде
в виде 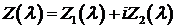 . Пусть
. Пусть  . Доказать, что
. Доказать, что  .
.
Задача.
Доказать
 . (5.14)
. (5.14)
Пусть
 . Структура таких случайных величин определяется
следующей теоремой.
. Структура таких случайных величин определяется
следующей теоремой.
Теорема.
Если  , то найдется такая функция
, то найдется такая функция  , что
, что
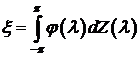 . (5.15)
. (5.15)
Доказательство.
Поскольку  , то найдется последовательность
, то найдется последовательность  , вида
, вида  , предел
которой равен
, предел
которой равен 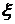 . Рассмотрим последовательность функций
. Рассмотрим последовательность функций  . Поскольку последовательность
. Поскольку последовательность  -фундаментальна, то и последовательность
-фундаментальна, то и последовательность 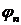 - фундаментальна. Следовательно, существует предел
- фундаментальна. Следовательно, существует предел  . Переходя к пределу в равенстве
. Переходя к пределу в равенстве 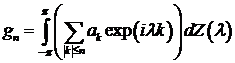 , получим формулу (5.15). Причем
, получим формулу (5.15). Причем
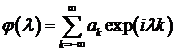 . (5.16)
. (5.16)
Важным
приложением формулы (5.15) является линейное преобразование последовательности  , называемое линейным фильтром.
, называемое линейным фильтром.
.
Линейный фильтр
Предположим,
что на вход системы подается в момент времени 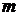 случайный
сигнал
случайный
сигнал  , при этом на выходе системы в момент времени
, при этом на выходе системы в момент времени 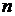 получается сигнал
получается сигнал 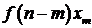 , где
, где  ,
,  -
некоторая комплекснозначная функция, называемая импульсной переходной функцией.
Таким образом, суммарный сигнал на выходе устройства (фильтра)
-
некоторая комплекснозначная функция, называемая импульсной переходной функцией.
Таким образом, суммарный сигнал на выходе устройства (фильтра)
 . (6.1)
. (6.1)
Для
физически реализуемого устройства значение выходного сигнала зависит только от
прошлых значений входного сигнала, то есть от значениями  при
при  . Поэтому
импульсная переходная функция физически реализуемого фильтра
. Поэтому
импульсная переходная функция физически реализуемого фильтра 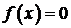 при
при  .
Следовательно, для физически реализуемого фильтра
.
Следовательно, для физически реализуемого фильтра
 . (6.2)
. (6.2)
Подадим
на вход фильтра стационарную в широком смысле последовательность  с ковариационной функцией
с ковариационной функцией  и спектральным представлением (5.13). На выходе
получим случайную последовательность
и спектральным представлением (5.13). На выходе
получим случайную последовательность  .
Вычислим
.
Вычислим 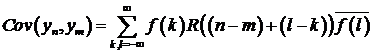 . Сделаем замену переменных
. Сделаем замену переменных  . В результате
. В результате
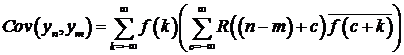 (6.3)
(6.3)
В
частности,  . Следовательно, для того чтобы
. Следовательно, для того чтобы  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
 (6.4)
(6.4)
При
выполнении (6.4) ряд 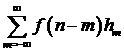 будет сходиться в среднеквадратичном смысле и,
следовательно, последовательность
будет сходиться в среднеквадратичном смысле и,
следовательно, последовательность 
 , (6.5)
, (6.5)
стационарная в широком смысле последовательность.
Из
того, что  , следует, что для последовательности
, следует, что для последовательности  справедливо спектральное представление (5.15) со
спектральной функцией
справедливо спектральное представление (5.15) со
спектральной функцией
 . (6.6)
. (6.6)
Функцию
 (6.7)
(6.7)
называют спектральной характеристикой фильтра.
Задача.
Доказать, что условие (6.4) эквивалентно  , то есть
, то есть
 . (6.7)
. (6.7)
Для
ковариационной функции 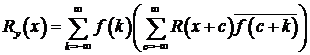 справедливо представление
справедливо представление
 , (6.8)
, (6.8)
которое непосредственно вытекает из спектрального представления (5.15).
В
частности если на вход фильтра подается белый шум 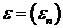 , то есть,
, то есть,
 , (6.9)
, (6.9)
то на выходе будет получаться стационарная последовательность со
спектральной плотностью
 . (6.10)
. (6.10)
По
заданной неотрицательной функции  можно
найти такую функцию
можно
найти такую функцию  , чтобы выполнялось (6.10). Так как
, чтобы выполнялось (6.10). Так как  спектральная плотность, то
спектральная плотность, то  . Следовательно,
. Следовательно,  . Поэтому
функцию
. Поэтому
функцию  можно представить в виде ряда Фурье (6.7), с
коэффициентами
можно представить в виде ряда Фурье (6.7), с
коэффициентами 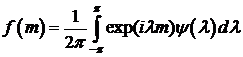 . В частности, если
. В частности, если  ,
то являются справедливыми равенства:
,
то являются справедливыми равенства:
 . (6.11)
. (6.11)
Задача. Доказать (6.11).
Из этих рассуждений вытекает следующая теорема.
Теорема.
Если у стационарной в широком смысле последовательности существует плотность  , то последовательность можно представить в виде:
, то последовательность можно представить в виде:
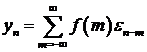 . (6.12)
. (6.12)
Доказательство.
Пусть 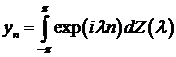 . Рассмотрим процесс
. Рассмотрим процесс 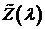 ,
независящий от
,
независящий от 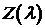 с
с  .
Определим меру
.
Определим меру  , где
, где  , и
процесс
, и
процесс
 (6.13)
(6.13)
Очевидно, что
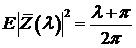 . (6.14)
. (6.14)
Из
(6.14) следует, что  является белым шумом. С другой стороны
является белым шумом. С другой стороны
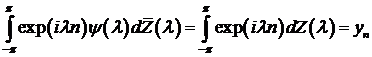 . (6.15)
. (6.15)
Из (6.15) вытекает
 (6.16)
(6.16)
Равенство (6.16) доказывает теорему.
Задача. Доказать равенства (6.14) и (6.16).
Замечание.
Введение процесса 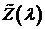 обусловлено возможностью равенства нулю спектральной
плотности
обусловлено возможностью равенства нулю спектральной
плотности  . Если
. Если  (почти
всюду по мере Лебега), то необходимость в процессе
(почти
всюду по мере Лебега), то необходимость в процессе 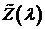 отпадает.
отпадает.
Пусть
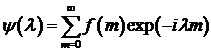 ,
,  , тогда
последовательность
, тогда
последовательность 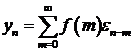 .
.
7. Линейные модели финансовых временных последовательностей
Определение.
Последовательность  , называется последовательностью скользящего среднего,
если она представима в виде
, называется последовательностью скользящего среднего,
если она представима в виде
 . (7.1)
. (7.1)
Если
 при
при  , то
, то
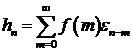 (7.2)
(7.2)
и
последовательность называется односторонней последовательностью скользящего
среднего. Если к тому же  при
при  , то
, то
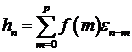 (7.3)
(7.3)
и
последовательность называется последовательностью скользящего среднего порядка 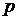 . На рисунке 7.1 представлена машинная реализация
последовательности
. На рисунке 7.1 представлена машинная реализация
последовательности  .
.
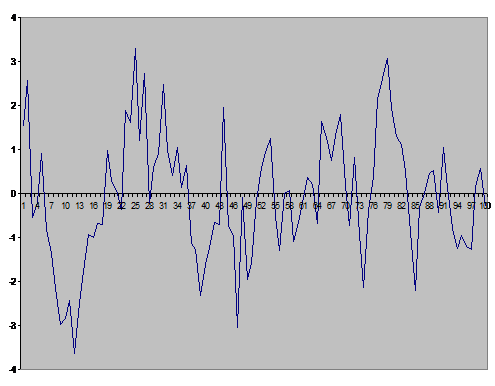
Рисунок
7.1. Машинная реализация последовательности скользящего среднего порядка  , с коэффициентами
, с коэффициентами 
Из результатов предыдущего параграфа следует, что спектральная плотность
последовательности (7.3)
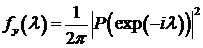 (7.4)
(7.4)
с
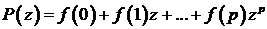 .
.
Задача. Обосновать формулу (7.4).
Определение. Последовательность
 (7.5)
(7.5)
называется
последовательностью авторегрессии порядка 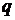 .
.
На
рисунке 7.2 представлена машинная реализация авторегрессионной
последовательности

Рисунок
7.2. Машинная реализация авторегрессионной последовательности:  .
.
Найдем
решение уравнения (7.5). Для этого определим оператор сдвига 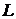
 . (7.6)
. (7.6)
Из
(7.6) следует, что  . С использованием оператора
. С использованием оператора 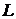 уравнение (7.5) примет вид:
уравнение (7.5) примет вид:
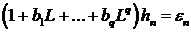 , (7.7)
, (7.7)
где
единица понимается как тождественный оператор. Рассмотрим многочлен 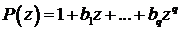 . Тогда
. Тогда 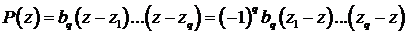 , где
, где  - корни многочлена
- корни многочлена 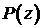 . Отсюда
уравнение (7.7) приобретает вид:
. Отсюда
уравнение (7.7) приобретает вид:
 , (7.8)
, (7.8)
которое превращается в систему рекуррентных уравнений
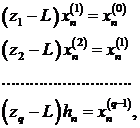 (7.9)
(7.9)
где
 . Рассмотрим
. Рассмотрим  -е
уравнение системы (7.9)
-е
уравнение системы (7.9) 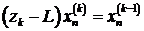 , которое имеет вид:
, которое имеет вид:
 . (7.10)
. (7.10)
Введем
обозначение 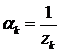 . Решение уравнения (7.10)
. Решение уравнения (7.10)
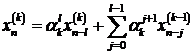 (7.11)
(7.11)
Пусть
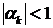 и для любых
и для любых  и
и 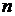
 , тогда
, тогда  при
при  . Тогда решение уравнения представляется в виде :
. Тогда решение уравнения представляется в виде :
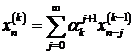 . (7.12)
. (7.12)
Является справедливой теорема.
Теорема.
Если корни многочлена 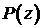 лежат вне единичной окружности, то решение уравнения
(7.10) является односторонним скользящим средним.
лежат вне единичной окружности, то решение уравнения
(7.10) является односторонним скользящим средним.
Доказательство.
Для 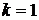 утверждение теоремы очевидно:
утверждение теоремы очевидно: 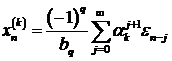 , причем
, причем 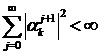 . Пусть
оно справедливо для
. Пусть
оно справедливо для 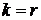 , то есть
, то есть 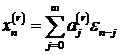 , причем
. Из (7.12) следует, что
, причем
. Из (7.12) следует, что 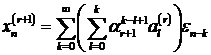 . Следовательно,
. Следовательно, 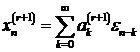 , где
причем Доказательство. Для
, где
причем Доказательство. Для 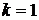 утверждение
теоремы очевидно. Пусть оно справедливо для
утверждение
теоремы очевидно. Пусть оно справедливо для 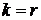 , то есть
, то есть
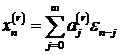 , причем
, причем  . Из
(7.12) следует, что
. Из
(7.12) следует, что  . Следовательно,
. Следовательно, 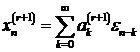 , где
, где 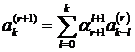 , причем
, причем  .
Последнее справедливо потому, что последовательность
.
Последнее справедливо потому, что последовательность 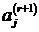 - свертка последовательностей
- свертка последовательностей  и
и 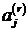 , каждая
из которых принадлежит
, каждая
из которых принадлежит  . Отсюда
. Отсюда
 . (7.13)
. (7.13)
Причем ряд, стоящий в правой части сходится в среднеквадратическом смысле.
Спектральная плотность последовательности
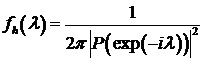 . (7.14)
. (7.14)
Задача. Доказать формулу (7.14).
Пример.
Рассмотрим последовательность  . Нули
многочлена
. Нули
многочлена  :
:  , лежат
вне единичной окружности. Следовательно, последовательность
, лежат
вне единичной окружности. Следовательно, последовательность  представима в виде одностороннего скользящего
среднего. Рассмотрим
представима в виде одностороннего скользящего
среднего. Рассмотрим  , где
, где 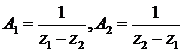 . Тогда
. Тогда  . Отсюда
. Отсюда  .
.
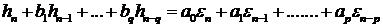 . (7.15)
. (7.15)
Называется смешанной моделью авторегрессии и скользящего среднего.
Теорема.
Если нули полинома 
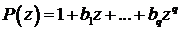 лежат
вне единичной окружности, то последовательность
лежат
вне единичной окружности, то последовательность  представима
в виде скользящего среднего и спектральная плотность последовательности
представима
в виде скользящего среднего и спектральная плотность последовательности  имеет вид:
имеет вид:
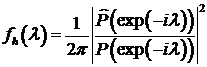 , (7.16)
, (7.16)
где
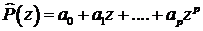 .
.
Задача.
Доказать теорему.
.
Линейный прогноз для стационарных в широком смысле последовательностей
Пусть
 - стационарная в широком смысле последовательность с
ковариационной функцией
- стационарная в широком смысле последовательность с
ковариационной функцией  и нулевым математическим ожиданием. Обозначим через
и нулевым математическим ожиданием. Обозначим через  и через
и через 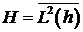 , где
, где 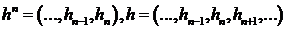 . Пусть
. Пусть 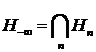 . Для
любого элемента
. Для
любого элемента 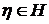 обозначим через
обозначим через  проекцию
проекцию
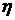 на подпространство
на подпространство  .
Соответственно
.
Соответственно 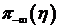 - проекция
- проекция 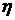 на
на  . Каждый элемент
. Каждый элемент 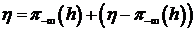 , причем
, причем 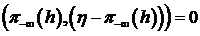 . Таким образом,
. Таким образом,
 , (8.1)
, (8.1)
Где
 состоит из элементов
состоит из элементов  ,
,  из элементов
из элементов 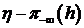 ,
, 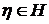 .
.
Определение.
Стационарная последовательность называется регулярной, если
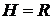 . (8.2)
. (8.2)
Стационарная последовательность называется сингулярной, если
 . (8.3)
. (8.3)
Разложение (8.1) позволяет сформулировать следующую теорему.
Теорема. Всякая стационарная в широком смысле последовательность
представима в виде суммы
 , (8.4)
, (8.4)
где
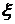 - регулярная ,
- регулярная , -
сингулярная последовательности. При этом
-
сингулярная последовательности. При этом  и
и 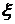 ортогональны (
ортогональны (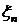 ортогональна
ортогональна 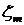 , для любых
, для любых 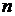 и
и 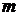 ).
).
Действительно,
поскольку для любого 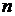
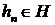 , то
можно использовать (7.17). Причем
, то
можно использовать (7.17). Причем 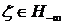 ,
следовательно
,
следовательно  ,
,  ,
следовательно
,
следовательно 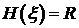 . Ортогональность
. Ортогональность 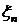 и
и 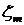 вытекает из ортогональности
вытекает из ортогональности  и
и  .
.
Задача.
Доказать, что разложение (8.4) единственное.
Следующая
теорема устанавливает связь между регулярной последовательностью и
односторонним скользящим средним.
Теорема.
Для того, чтобы невырожденная последовательность  была
регулярной необходимо и достаточно, чтобы она представлялась в виде последовательности
одностороннего скользящего среднего.
была
регулярной необходимо и достаточно, чтобы она представлялась в виде последовательности
одностороннего скользящего среднего.
Доказательство.
Необходимость. Представим  . Поскольку
. Поскольку  порождается
элементами из
порождается
элементами из  и элементами
и элементами 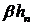 , и
, и  стационарная и регулярная, то размерность
стационарная и регулярная, то размерность 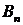 равна единице. Пусть
равна единице. Пусть 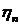 ненулевой
элемент из
ненулевой
элемент из 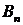 . Положим
. Положим 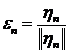 . Теперь
для любых фиксированных
. Теперь
для любых фиксированных 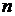 и
и  представим
представим
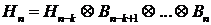 . Отсюда
. Отсюда
 . (8.5)
. (8.5)
Так
как  образуют ортонормированный базис в
образуют ортонормированный базис в  .
.
Рассмотрим
предел 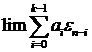 . В силу неравенства
. В силу неравенства 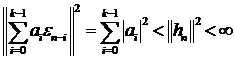 Ряд
Ряд
 сходится в среднеквадратическом смысле. Покажем, что
в том же самом смысле существует предел
сходится в среднеквадратическом смысле. Покажем, что
в том же самом смысле существует предел  . В силу
стационарности достаточно рассмотреть случай
. В силу
стационарности достаточно рассмотреть случай 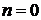 .
Обозначим через
.
Обозначим через  . Поскольку
. Поскольку 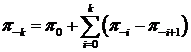 .
Слагаемые ортогональны, поэтому
.
Слагаемые ортогональны, поэтому 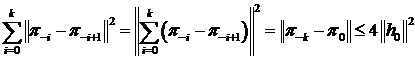 . Поэтому
предел существует. Для каждого
. Поэтому
предел существует. Для каждого 
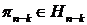 . Следовательно предел
. Следовательно предел  принадлежит
принадлежит
 . Так как
. Так как  -
тривиально по предположению, то
-
тривиально по предположению, то 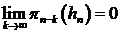 .
.
Необходимость.
Для любого 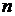
 ,
, 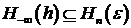 ,
, 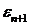 ортогонально
ортогонально 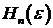 ,
следовательно, ортогонально
,
следовательно, ортогонально  . В тоже
время
. В тоже
время  образуют базис в
образуют базис в  . Отсюда
. Отсюда  тривиально, а значит
тривиально, а значит  -
регулярна.
-
регулярна.
Из
предыдущих теорем вытекает разложение Вольда.
Теорема.
Если  - невырожденная последовательность, то
- невырожденная последовательность, то
 . (8.6)
. (8.6)
Откуда
можно получить наилучший линейный прогноз для 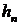 . Как
было показано ранее наилучшим линейным прогнозом для
. Как
было показано ранее наилучшим линейным прогнозом для 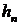 по прошлым значением
по прошлым значением  является
проекция
является
проекция  . Из разложения Вольда следует, что
. Из разложения Вольда следует, что  . Отсюда
. Отсюда
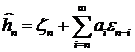 . (8.7)
. (8.7)
Дисперсия ошибки равна
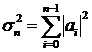 . (8.8)
. (8.8)
Из
(8.8) следует, что если последовательность 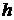 -
сингулярная, то
-
сингулярная, то  и дисперсия ошибки равна нулю (возможно точное
предсказание), если
и дисперсия ошибки равна нулю (возможно точное
предсказание), если 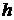 регулярная, то
регулярная, то  и
и 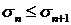 . Причем в случае регулярной последовательности
. Причем в случае регулярной последовательности  , то есть
, то есть 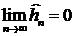 .
.
Интерес
представляет прогноз для регулярной последовательности. Формула
 (8.9)
(8.9)
Дает
решение задачи оптимального линейного прогноза, однако, для того, чтобы ей
можно было бы воспользоваться необходимо решить следующую задачу. Задана
ковариационная функция  или спектральная плотность
или спектральная плотность 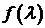 . Требуется вычислить коэффициенты
. Требуется вычислить коэффициенты  и выразить
и выразить  через
через  .
.
Рассмотрим
решение этой задачи. Как было показано выше, если последовательность
представима в виде скользящего среднего, то для такой последовательности
существует спектральная плотность  .
Обратно, если
.
Обратно, если  , то существует представление последовательности в
виде скользящего среднего. Ограничимся рассмотрением важного для приложений
случая
, то существует представление последовательности в
виде скользящего среднего. Ограничимся рассмотрением важного для приложений
случая
 , (8.10)
, (8.10)
где
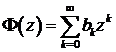 , радиус сходимости степенного ряда
, радиус сходимости степенного ряда 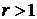 и нули
и нули 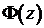 лежат
вне единичной окружности.
лежат
вне единичной окружности.
Рассмотрим
спектральное представление 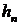 и
и 
 ,
, 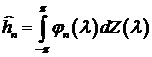 . (8.11)
. (8.11)
Дисперсия ошибки
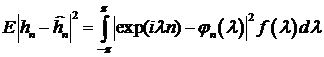 . (8.12)
. (8.12)
Таким
образом, требуется найти минимум правой части (8.12) по  . Покажем, что функция
. Покажем, что функция
 (8.13)
(8.13)
доставляет
минимум правой части (8.12). Во первых,  . Во
вторых, для любого
. Во
вторых, для любого 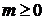 скалярное произведение
скалярное произведение  .
Действительно,
.
Действительно, 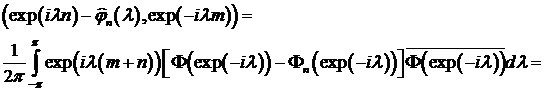
 , так как
, так как
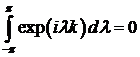 , для любого
, для любого 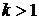 .
.
Разлагая
функцию 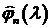 в ряд Фурье
в ряд Фурье
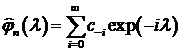 получим
оптимальный линейный прогноз,
получим
оптимальный линейный прогноз,
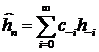 . (8.14)
. (8.14)
Подчеркнем,
что из разложения Вольда регулярной последовательности  следует, что спектральная плотность допускает
представление
следует, что спектральная плотность допускает
представление 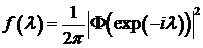 , где
, где 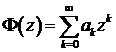 .
Обратно, если спектральная плотность допускает представление
.
Обратно, если спектральная плотность допускает представление 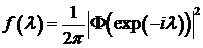 , где
, где 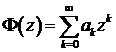 , то
разложение Вольда регулярной последовательности
, то
разложение Вольда регулярной последовательности  .
Таким образом, задача представления спектральной плотности и задача разложения
регулярной последовательности эквивалентны.
.
Таким образом, задача представления спектральной плотности и задача разложения
регулярной последовательности эквивалентны.
Задача.
Доказать, что 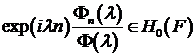 .
.
Пример.
Рассмотрим последовательность
 (8.15)
(8.15)
График
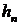 представлен на рисунке 8.1.
представлен на рисунке 8.1.

Рис.
8.1 График машинной реализации последовательности 
Спектральная
плотность последовательности 
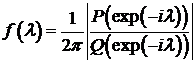 , (8.16)
, (8.16)
где
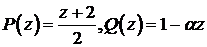 . Функция
. Функция  . Отсюда
. Отсюда 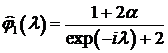 , следовательно, прогноз на один шаг
, следовательно, прогноз на один шаг
 . (8.17)
. (8.17)
На
рисунке 8.2 представлены графики последовательности  и
и  .
.
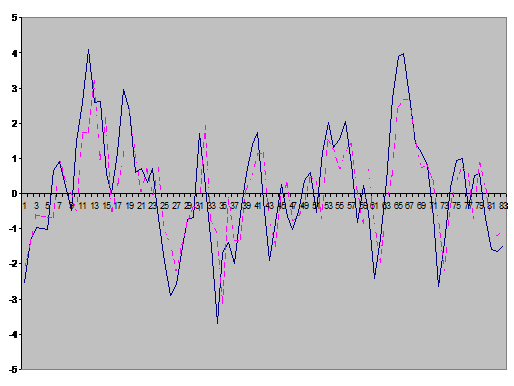
Рис.
8.1. График машинной реализации последовательности  (сплошная линия) и последовательности
(сплошная линия) и последовательности  (пунктирная линия)
(пунктирная линия)
.
Статистическое оценивание параметров модели
Чтобы
решать задачи анализа временных последовательностей, возникающих при описании
эволюции стоимости финансовых активов, необходимо уметь оценивать по наблюдаемым
значениям параметры модели.
Пусть
 - стационарная в широком смысле последовательность с
математическим ожиданием
- стационарная в широком смысле последовательность с
математическим ожиданием 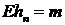 и ковариационной функцией
и ковариационной функцией 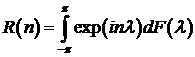 . Возникает задача: как по наблюдениям
. Возникает задача: как по наблюдениям 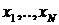 значений
значений 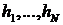 получить
«хорошие» оценки для
получить
«хорошие» оценки для 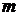 и
и  .
.
Рассмотрим
в качестве оценки 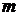
Математическое
ожидание 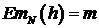 . Следовательно, оценка является несмещенной.
Дисперсия оценки
. Следовательно, оценка является несмещенной.
Дисперсия оценки 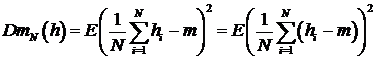 . Отсюда
. Отсюда 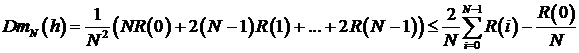 .
Используем спектральное представление ковариационной функции
.
Используем спектральное представление ковариационной функции 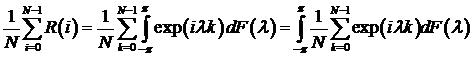 . Так как
. Так как 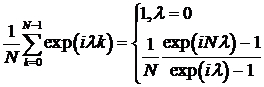 , то
, то  . Если
. Если 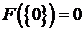 , то
, то 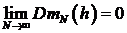 , и оценка
, и оценка  -
состоятельна в среднем квадратическом смысле. Будем считать, что объем выборки
наблюдений достаточно большой, чтобы оценка
-
состоятельна в среднем квадратическом смысле. Будем считать, что объем выборки
наблюдений достаточно большой, чтобы оценка  хорошо
приближала
хорошо
приближала 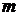 . Поэтому дальше мы будем считать, что
. Поэтому дальше мы будем считать, что 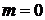 .
.
В
качестве оценки ковариационной функции рассмотрим
 . (9.2)
. (9.2)
Математическое
ожидание 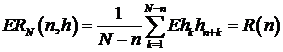 . Следовательно, оценка (2.9) - несмещенная оценка
. Следовательно, оценка (2.9) - несмещенная оценка  . Предположим, что для каждого
. Предположим, что для каждого 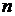 последовательность
последовательность  , с
, с 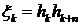 является стационарной последовательностью. Рассмотрим
дисперсию
является стационарной последовательностью. Рассмотрим
дисперсию 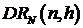 . Аналогично предыдущему для состоятельности оценки в
среднеквадратическом смысле необходимым и достаточным условием является
стремление к нулю
. Аналогично предыдущему для состоятельности оценки в
среднеквадратическом смысле необходимым и достаточным условием является
стремление к нулю 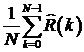 , где
, где  ковариационная
функция последовательности
ковариационная
функция последовательности 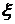 .
Отметим, что
.
Отметим, что  . Если последовательность
. Если последовательность  является гауссовой последовательностью, то [] из
является гауссовой последовательностью, то [] из  следует
следует 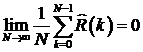 .
.
Для
демонстрации одного из самых эффективных методов метода максимального
правдоподобия [] остановимся на оценке параметров модели авторегрессии 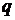 - го порядка
- го порядка  .
Неизвестными параметрами модели являются
.
Неизвестными параметрами модели являются 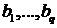 и
и  . Предположим, что
. Предположим, что  независимые
стандартные нормальные случайные величины. Обозначим через
независимые
стандартные нормальные случайные величины. Обозначим через 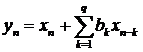 ,
,  .
Логарифм функции правдоподобия
.
Логарифм функции правдоподобия
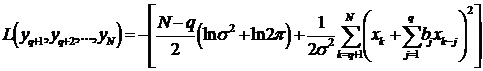 (9.3)
(9.3)
В
соответствии с методом максимального правдоподобия для получения оценок
неизвестных параметров необходимо найти максимум  или
минимум
или
минимум . Таким образом оценки максимального правдоподобия
являются решением системы линейных алгебраических уравнений:
. Таким образом оценки максимального правдоподобия
являются решением системы линейных алгебраических уравнений:
 (9.4)
(9.4)
Литература
1. Г.И.
Белявский, И.В. Павлов. Теория вероятностей. Учебное пособие, Ростов-на-Дону,
РГСУ, 2007. [1-3]
. А.Н.
Ширяев. Вероятность. М.: Наука, 1980. [1-3]
. А.Н.
Ширяев. Вероятность-1. М.: МЦНМО, 2004[1-3]
. А.Н.
Ширяев. Вероятность-2. М.: МЦНМО, 2004[1-3]
. А.Н.
Ширяев. Задачи по теории вероятностей. М.: МЦНМО, 2006[1-3]
. А.Н.
Ширяев. Основы стохастической финансовой математики. Факты. Модели. М.: ФАЗИС,
1998. [1-3]
. А.Н.
Ширяев. Основы стохастической финансовой математики. Теория. М.: ФАЗИС, 1998.
[1-3]
.
А.В. Мельников. Финансовые рынки. Стохастический анализ и расчет ценных бумаг.
ТВП: Москва, 1997. [1]
. Энциклопедия
«Вероятность и математическая статистика» под. Ред.
Ю.В.
Прохорова, М.: ТВП, 1999. [1-3]
. Леман
Э. Теория точечного оценивания, М, Наука,1991
11. Ruey
S. Tsay. Analysis of time series. Jon Wiley and Sons. 2002.
12. Wolberg
J . Data analysis using the method of least squares. Springer. 2006.