Элементы теории вероятностей
Элементы теории вероятностей
Задача 1
Одновременно подбрасывается две
кости. Найти вероятность того, что в сумме выпадет 9 очков.
Решение.
Найдем общее число исходов.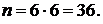 
Найдем число
благоприятствующих исходов. Благоприятных исходов - 4 (3-6,6-3,4-5, 5-4):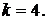 
Находим
вероятность события:
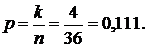
Ответ: 0,111.
Задача 2. Решить задачу, используя теоремы сложения и умножения.
В лотерее выигрывает каждый пятый
билет. Какова вероятность того, что хотя бы один из трех купленных билетов
выиграет?
Решение
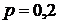- вероятность выигрыша в
лотерее.
Введем события: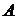 
-
все три билета проиграли,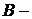 
один
из трех билетов выиграл.
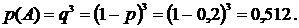
Ответ: 0,488.
Задача 3. Решить задачу, используя формулы полной вероятности или Байеса.
По статистическим данным высокими
потребительскими качествами обладает 90% всех лицензионных и 60% контрафактных
изделий. Вероятность покупки лицензионного изделия составляет 0,7. Зная, что
купленное изделие не обладает высокими потребительскими качествами, найти
вероятность того, что оно лицензионное.
Решение.
Введем в рассмотрение событие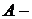 
«купленное изделие не
обладает высокими потребительскими качествами». Введем систему гипотез:
· «изделие
лицензионное»;
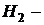· «изделие
контрафактное».
Согласно условию задачи
условные вероятности события 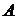равны: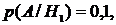 
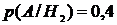.Теперь
найденные значения подставим в формулу Байеса, получим
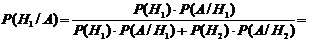
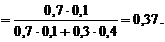
Ответ: 0,37.
Задача 4. Решить задачу, используя схему Бернулли.
Вероятность удачного эксперимента
равна 0,7. Найти вероятность того, что среди 200 проведенных экспериментов
число удачных колеблется от 130 до 160.
Решение. Применим интегральную формулу Муавра-Лапласа,
в которой положим 
=0,7;
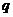=1-0,7=0,3;
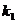=130;
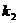=160.
Вычисляем
,
.
Получим согласно (8)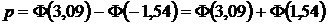 
.
При этом мы учли нечетность функции Лапласа. Далее по таблице находим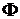 
(3,09)=0,4991,
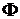(1,54)=0,4382.
Значит,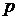 
=
0,4991+0,4382=0,9373. Ответ: 0,9373.
Задача 5. Случайная
величина Х, задана рядом распределения. Найти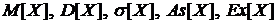 
.
|
X
|
- 2
|
0
|
1
|
2
|
|
p
|
0,2
|
0,5
|
0,2
|
Решение.
Математическое ожидание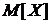 
находим
по формуле:
Для нахождения дисперсии
воспользуемся формулой (16). Для этого предварительно найдем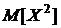 
по
формуле 
.
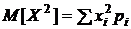Получим
Далее по формуле (16)
находим: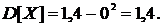 
Среднее квадратическое
отклонение найдем по формуле
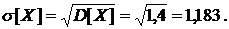
Найдем коэффициент
асимметрии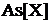 
.
Для этого предварительно найдем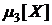 
по формуле
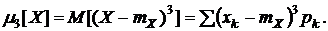
Получим
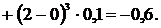
Тогда по формуле (17)
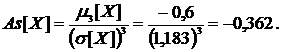
Коэффициент эксцесса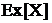 
найдем
по формуле (18). Для этого предварительно найдем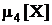 
по формуле
Получим
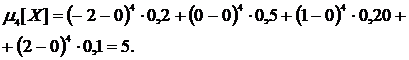
Тогда по формуле (18)
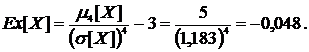
Ответ: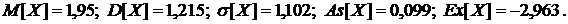 
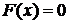при 
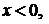
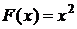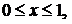
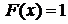при
при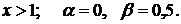 
Решение
Сначала найдем плотность
распределения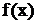 
,
для этого продифференцируем функцию распределения. Получим
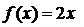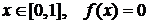при 
при
.
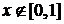Находим вероятность
попадания в интервал. Получим
Математическое ожидание 
найдем
по формуле (13). Получим
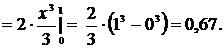
Для нахождения дисперсии
воспользуемся формулой (16). Для этого предварительно найдем .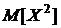
Получим
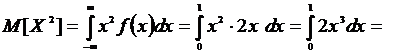
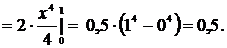
квадратический
отклонение вероятность бернулли
Далее по формуле (16)
находим: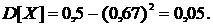 
Среднее
квадратическое отклонение найдем по формуле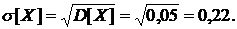 
Ответ: 