Элементы общей теории обыкновенных дифференциальных уравнений первого порядка
Реферат
Элементы
общей теории обыкновенных дифференциальных уравнений первого порядка
Раздел №1.Задачи, приводящие к дифференциальным уравнениям
С проникновением в математику идеи движения и переменных величин, с
развитием понятий производной и первообразной данной функции появился новый вид
уравнений, решение которых дает возможность находить не просто значение тех или
других постоянных величин, а разные виды функциональных зависимостей, законы
тех или иных видов движений и других явлений. Так, например, некоторые процессы
в радиотехнике, кинетика химических реакций, динамика биологических популяций,
движение космических объектов, модели экономического развития исследуются с
помощью уравнений, в которых кроме независимых переменных и неизвестных функций
этих переменных, содержатся производные неизвестных функций (или их
дифференциалы). Такие уравнения называются дифференциальными.
Рассмотрим несколько примеров.
Задача
1. Пусть тело, имеющее температуру 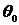 в момент
времени t=0, помещено в среду температуры α (
в момент
времени t=0, помещено в среду температуры α (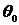 >α). Требуется найти закон, по которому изменяется температура тела в
зависимости от времени.
>α). Требуется найти закон, по которому изменяется температура тела в
зависимости от времени.
Для
математического описания этого процесса нужно выбрать независимую переменную;
таковой в данном случае является время. Будем вести отсчет времени от того
момента, когда тело поместили в среду температуры α и начался процесс его охлаждения. Искомой функцией в
данной задаче является меняющаяся со временем температура тела. Обозначим ее
через 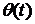 . В начальный момент температура тела была известна,
т.е. известно, что при t=0,
. В начальный момент температура тела была известна,
т.е. известно, что при t=0, 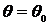 .
.
Из
физики известно, что скорость охлаждения тела пропорциональна разности
температур тела и окружающей среды. Но скорость охлаждения это скорость
изменения (убывания) температуры, а из дифференциального исчисления известно,
что скорость изменения какой-либо функции по сравнению с изменением независимой
переменной есть производная от этой функции по независимой переменной. Таким
образом, учитывая, что функция θ(t) убывающая, сформулированный
выше эмпирический закон можно математически записать следующим образом:
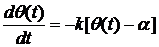 , (1)
, (1)
где
k - коэффициент пропорциональности.
Соотношение
(1) является математической моделью данного физического процесса. Оно
называется дифференциальным уравнением, потому что в него наряду с неизвестной
функцией θ(t)
входит и ее производная. Поскольку в это уравнение входит независимая
переменная, функция и ее первая производная, то это дифференциальное уравнение
первого порядка.
Дифференциальное
уравнение (1) может описывать и другие физические процессы. Например,
радиоактивный распад также описывается уравнением (1) при α=0.
В
данном случае уравнение (1) настолько просто, что нахождение функции θ(t) не
представляет труда. Действительно, перепишем его в виде
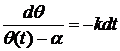 ; (2)
; (2)
В
такой записи мы имеем равенство дифференциалов двух различных выражений, а
именно:
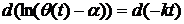 .
.
Но из интегрального исчисления известно, что если производные или
дифференциалы двух функций равны между собой, то сами функции отличаются друг
от друга разве лишь постоянным слагаемым, т.е.
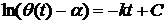 .
.
Отсюда
потенцированием находим:
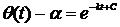 ,
,
или
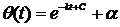 . (3)
. (3)
Формула
(3) и дает выражение температуры как функции времени. Но в эту формулу входит
произвольная постоянная С, которой можно придавать какие угодно числовые
значения, т.е., иначе говоря, формула (3) дает не один ответ на поставленный в
задаче вопрос, а бесконечное множество ответов. Так получилось, потому что
переход от равенства (2) к равенству (3) содержал операцию интегрирования, а с
другой стороны, естественно ожидать, что при решении определенной задачи с
конкретно заданными условиями должен получиться один определенный ответ. Но еще
не были использованы условия: при t=0, 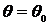 , называемые начальными. Подставим данные начальных
условий в формулу (3):
, называемые начальными. Подставим данные начальных
условий в формулу (3):
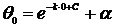 , т.е.
, т.е. 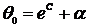 ,
,
откуда
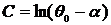 .
.
Таким
образом установлено, что в условиях нашей задачи постоянная С имеет вполне
определенное числовое значение, и, подставляя это значение в формулу (3),
получаем уже только одно выражение для температуры как функции времени, т.е.
получаем один ответ на поставленный в задаче вопрос:
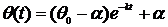 . ■
. ■
Задача
2. Имеется замкнутая электрическая цепь с сопротивлением R и
силой тока I0. В
некоторый момент времени, который мы примем за начальный (t=0),
постоянный ток I0
размыкается. Требуется выяснить, прекратится ли сразу ток в цепи, а если нет,
то как он будет убывать.
Выключение
постоянной электродвижущей силы, поддерживавшей силу тока I0 в цепи, вызывает, вследствие изменения магнитного
поля тока I0,
возникновение электродвижущей силы индукции (явление самоиндукции). Таким
образом в цепи индуцируется ток под действием одной лишь электродвижущей силы
самоиндукции; он называется «экстратоком размыкания». Экстраток размыкания
направлен в ту же сторону, что и основной ток. Известно, что эта
электродвижущая сила самоиндукции пропорциональна скорости изменения силы тока
(коэффициент пропорциональности называется коэффициентом самоиндукции), т.е.
имеет вид:
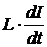 ,
,
где
I - переменная сила экстратока размыкания и L -
коэффициент самоиндукции.
По
закону Ома имеем:
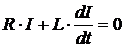 ; (4)
; (4)
это
равенство представляет собой дифференциальное уравнение, из которого надо
определить силу экстратока размыкания как функцию времени. Собираем в уравнении
(4) члены, содержащие переменную I, в левую часть и члены, содержащие переменную t в
правую часть:
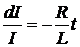 .
.
Как
и в задаче 1, переписываем последнее равенство в виде:
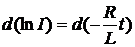 ,
,
откуда
получаем
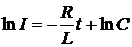
(постоянную
прибавляем в виде логарифма постоянной, так как это удобнее для дальнейших
преобразований). Потенцируя, получаем
 , (5)
, (5)
что
и дает искомое выражение силы экстратока размыкания через t.
Используя начальные условия: при t=0, I=I0 находим
единственное значение С:
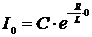 , т.е.
, т.е.  .
.
Подставляя
полученное значение С в формулу (5), имеем:
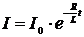 .
.
Эта
формула дает определенный ответ на вопрос, поставленный в задаче: при
размыкании тока сила тока в цепи не сразу падает до нуля, а постепенно спадает
по показательному закону. ■
Аналогичное
исследование с помощью дифференциального уравнения можно провести и для
изучения экстратока замыкания.
Задача
3. Пусть два вещества А и B, находящиеся в растворе, вступают в необратимую
химическую реакцию. Требуется найти формулу, по которой можно было бы
подсчитать в любой момент времени количество вещества, уже вступившего в
реакцию.
Обозначим
через a и b количества этих веществ (в грамм-молекулах на единицу
объема) в начале реакции, т.е. при t=0 (пусть, например, a<b), и
через x - одинаковое количество того и другого вещества, уже
вступившего в реакцию к моменту времени t. В этот момент
времени в единице объема находится a-x грамм-молекул
вещества A и b-x грамм-молекул вещества B. Известно, что
по закону химического взаимодействия масс скорость химической реакции для
некоторых типов реакций пропорциональна произведению (a-x)·(b-x).
Так как скорость химической реакции есть скорость увеличения x, то
она является производной от x по времени, и поэтому закон химического
взаимодействия масс может быть записан следующим образом:
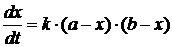 , (6)
, (6)
где
k - коэффициент пропорциональности. Уравнение (6) есть
дифференциальное уравнение первого порядка, где неизвестной является функция x(t).
Для того чтобы найти эту функцию отделим переменные t и x
друг от друга, собрав члены с x в левой части уравнения, а члены с t в
правой:
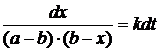 .
.
Последнее
равенство можно переписать в виде
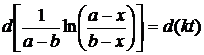 ,
,
откуда
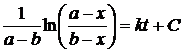 .
.
Умножаем
на (a-b)
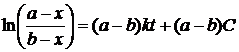
и,
потенцируя, получаем:
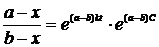 . (7)
. (7)
Обозначим
для простоты второй постоянный множитель одной буквой
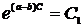
и
найдем из (7) выражение искомой функции x(t)
через время:
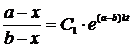 ,
,
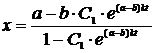 . (8)
. (8)
Конкретное
числовое значение постоянной С для данной задачи можно найти опять-таки с
помощью начальных условий: при t=0, x=0. Подставляем начальные условия в (8):
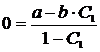 ,
,
Откуда
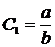 . Подставляем найденное значение С1 в (8):
. Подставляем найденное значение С1 в (8):
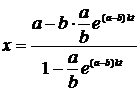 ,
,
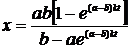 .
.
Эта формула и дает окончательное выражение для количества вещества,
вступившего в реакцию к моменту времени t. Легко видеть, что при возрастании t x приближается к a.
Приведенные задачи показывают, насколько широк и разнообразен круг
вопросов, требующих для своего изучения решения дифференциальных уравнений.
Рассмотрим элементы общей теории обыкновенных дифференциальных уравнений,
введя строгие определения встретившихся нам понятий дифференциального
уравнения, решения дифференциального уравнения, рассмотрев методы и приемы их
решения.
Раздел 2. Элементы общей теории обыкновенных дифференциальных
уравнений первого порядка
Остановимся подробнее на обыкновенных дифференциальных уравнениях первого
порядка.
Определение: Обыкновенным дифференциальным уравнением 1-го порядка называется соотношение вида
F (x, y, y’) = 0, (1)
где F - известная функция своих
аргументов, заданная в некоторой области; x - независимая переменная; y - функция переменной x, подлежащая определению; y’ - ее производная.
Если уравнение (1) можно разрешить относительно y’, то его можно записать в виде
y’ = f (x, y) (2).
Определение: Пусть правая часть уравнения (2), f (x, y) определена на некотором
подмножестве А вещественной плоскости (x, y). Функция y=j(x), определенную в интервале (a, b), называется решением
уравнения (2) в этом интервале, если:
1) Существует производная j’ (x) для всех значений х из интервала (a,b).
2) Функция y = j (x) обращает
уравнение (2) в тождество:
j’ (x) º f [x, j (x)],
справедливое для всех значений х из интервала (a, b).
Процесс нахождения решения называется интегрированием дифференциального
уравнения.
Пример 1. Пусть дано дифференциальное уравнение
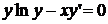 (*)
(*)
или
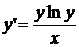 .
.
Проверим,
является ли функция 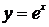 решением уравнения (*), для чего подставим ее в это
уравнение:
решением уравнения (*), для чего подставим ее в это
уравнение:
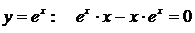 .
.
В
результате подстановки получено верное равенство, следовательно, функция 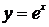 является решением уравнения (*).
является решением уравнения (*).
Проверим
теперь, является ли функция 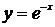 решением
уравнения (*), для чего подставим ее в это уравнение:
решением
уравнения (*), для чего подставим ее в это уравнение:
 .
.
В
результате подстановки снова получено верное равенство, следовательно, функция 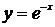 также является решением уравнения (*).
также является решением уравнения (*).
Возьмем
теперь функцию 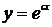 и подставим ее в уравнение (*):
и подставим ее в уравнение (*):
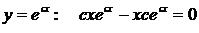 .
.
В
результате подстановки снова получено верное равенство, следовательно, и
функция 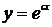 также является решением уравнения (*). ■
также является решением уравнения (*). ■
Таким образом, уравнение (*) имеет не одно, а бесчисленное множество
решений. Это объясняется тем, что на основании теории интегрирования функции
одного переменного все функции, удовлетворяющие уравнению (2) содержат
произвольную постоянную С.
Определение: Семейство решений уравнения (2), зависящее от одной
произвольной постоянной С:
y = j (x, C), (3)
называют общим решением этого уравнения (или Ф(x,y,C)=0 (3’) - общим
интегралом).
То есть при различных значениях постоянной С будут получаться разные
функции, которые будут являться решениями уравнения (2).
Определение: Частным решением дифференциального уравнения (2) называется его решение,
получаемое из общего решения при фиксированном значении С.
В связи с этим одной из важнейших задач в теории дифференциальных
уравнений является так называемая задача Коши. Для уравнения (2)
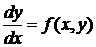 ,
,
задача
Коши ставится следующим образом: среди всех решений уравнения (2) найти такое
решение y = y(x), в котором функция y(x)
принимает заданное числовое значение y0 при заданном числовом значении х0
независимой переменной х, то есть
y(x0) = y0, (4)
где
х0 и y0 заданные
числа, так что решение (4) удовлетворяет условиям
y = y0 при x = x0. (5)
При этом y0
называется
начальным значением искомой функции, а число x0 - начальным значением независимой переменной, а условия (5)
- начальными условиями.
Говорят, что задача Коши с начальными условиями (5) имеет единственное
решение, если существует такое число h > 0, что в интервале Iх - x0I£h определено решение y = y (x) такое, что y (x0) = y0
и не существует
решения, определенного в этом же интервале и не совпадающего с решением y = y (x) хотя бы в одной
точке интервала Iх - x0I £ h, отличной от точки x = x0. В противном случае, то есть когда задача Коши с
начальными условиями (5) имеет не одно решение или же совсем не имеет решений,
говорят, что в точке (x0, y0) нарушается единственность решения задачи Коши.
Замечание. Вопрос о единственности решения задачи Коши представляет
исключительный интерес, как для самой теории дифференциальных уравнений, так и
для ее многочисленных приложений, ибо, зная, что решение задачи Коши
единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям,
уверены, что других решений, удовлетворяющих тем же начальным условиям, нет.
Например, в вопросах естествознания это приводит к тому, что мы получаем вполне
определенный, единственный закон явления, определяемый только дифференциальным
уравнением и начальными условиями.
Пример 1. Материальная точка движется по некоторой прямой, причем так, что
скорость движения представляет собою известную функцию времени f (t). Найти закон движения этой точки, если в заданный момент
времени t0 она занимает положение x0.
Решение.
Примем упомянутую прямую за ось Ох. Принимая во внимание механический
смысл первой производной, получаем дифференциальное уравнение первого порядка
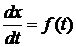 .
.
Предположим,
что f(t) непрерывна в интервале (a, b).
Тогда все решения данного уравнения содержатся в формуле
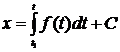 (a
< t < b),
(a
< t < b),
где верхний предел интеграла - переменный, нижний предел - некоторое
фиксированное число из интервала (a, b), а С - произвольная постоянная.
Выделим из семейства движений то движение, при котором движущаяся точка
занимает заданное положение х0 в заданный момент времени t0, т.е. найдем решение x=x (t), удовлетворяющее условиям
x = x0 при t = t0.
 (a
< t < b).
(a
< t < b).
Полученная формула выражает вполне определенный закон движения точки по
оси Ох.
Сформулируем строго утверждение, дающее возможность однозначно решать
вопрос о существовании и единственности решения конкретного дифференциального
уравнения.
Теорема (существования и единственности решения задачи Коши).
Пусть
дано уравнение (2) 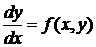 , и поставлены начальные условия (5) y = y0 при x = x0.
Предположим, что функция f (x, y) определена в некоторой замкнутой ограниченной
области R: êx - x0ê£ a, êy - y0ê£ b с точкой (x0, y0) внутри
( a и b - заданные положительные числа) и удовлетворяет в ней
следующим двум условиям.
, и поставлены начальные условия (5) y = y0 при x = x0.
Предположим, что функция f (x, y) определена в некоторой замкнутой ограниченной
области R: êx - x0ê£ a, êy - y0ê£ b с точкой (x0, y0) внутри
( a и b - заданные положительные числа) и удовлетворяет в ней
следующим двум условиям.
1. Функция f (x, y) непрерывна и, следовательно, ограничена, т.е.
êf (x, y)ê< M,
где М - постоянное положительное число, а (x, y) - любая точка
области R.
2. Функция f (x, y) имеет ограниченную частную производную по аргументу y, т.е.:
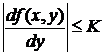 ,
,
где
К - постоянное положительное число, а (x, y) -
любая точка области R.
При
этих предположениях уравнение (2) имеет единственное решение y = y (x),
удовлетворяющее
начальным условиям (5). Это решение определено и непрерывно дифференцируемо в
некоторой окрестности начального значения х0 независимой переменной
х, а именно оно заведомо определено в интервале
Iх - x0I £ h,
где
h есть наименьшее из чисел a и b/M,
h = min (a, b/M).
Данную
теорему мы рассматриваем без доказательства.
Эта
теорема позволяет по виду дифференциального уравнения решить вопрос о
существовании и единственности решения этого уравнения при заданных начальных
условиях, что особенно важно в случае, когда уравнение нельзя решить точно, а
только приближенно.
Если
выполняются условия теоремы, то, подставляя значения x0 и y0 из (5) в
(3), получаем уравнение для определения конкретного значения постоянной С:
(или
 , если в (3’)).
, если в (3’)).
Разрешая
это уравнение относительно С, находим единственное значение С0,
соответствующее заданным начальным условиям (5). Подставляя затем С0 в
общее решение (3) (или общий интеграл (3’)) получаем вид того единственного
решения, которое удовлетворяет и дифференциальному уравнению и заданным
начальным условиям:
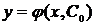
(или
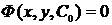 ).
).
Именно
это решение называется частным решением дифференциального уравнения.
Геометрический
смысл основных понятий.
Пусть
дано дифференциальное уравнение
y’=f(x,y).
(6)
Каждой
паре значений x и y соответствует точка M(x,y)
плоскости и по формуле (6) для каждой точки М можно вычислить число y’,
которое будем считать угловым коэффициентом некоторого направления. Таким
образом, каждой точке плоскости ставится в соответствие с помощью уравнения (6)
некоторое направление, которое можно на чертеже изобразить стрелкой, исходящей
из этой точки. В таком случае говорят, что задано поле направлений на
плоскости. Каждое уравнение вида (6) задает свое поле направлений на плоскости.
Каждое
решение y=φ(x) уравнения (6) геометрически изображается кривой на
плоскости. По определению решения производная φ’(x) для данного x, то есть
угловой коэффициент касательной к графику решения y=φ(x) при данном x совпадает с угловым
коэффициентом направления поля в точке плоскости с данной абсциссой x.
График всякого решения дифференциального уравнения обычно называется
интегральной кривой этого уравнения. Таким образом, касательная к интегральной
кривой в любой ее точке совпадает с направлением поля направлений в этой точке
плоскости.
Общее
решение дифференциального уравнения изображается семейством интегральных кривых
на плоскости.
Пример
1. Решить дифференциальное уравнение
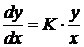 и построить
интегральные кривые этого уравнения.
и построить
интегральные кривые этого уравнения.
Собираем
в данном уравнении члены, содержащие переменную y, в левую часть
и члены, содержащие переменную x в правую часть:
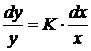 .
.
Так
как  ,
,
то

(постоянную прибавляем в виде логарифма постоянной, так как это удобнее
для дальнейших преобразований). Потенцируя, получаем:
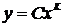 .
.
Построим
семейства интегральных кривых при различных значениях параметра K
(рис. 1).
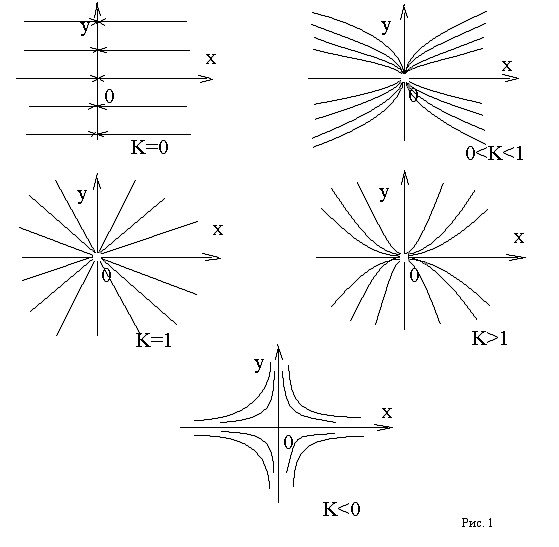
Если в какой-либо задаче требуется выделить из общего решения одно
частное решение, удовлетворяющее заданным начальным условиям:
y=y0 при x=x0, (7)
то геометрически это сводится к тому, что требуется из семейства интегральных
кривых на плоскости выделить одну интегральную кривую, проходящую через
заданную точку плоскости M(x0,y0). Теорема Коши указывает, в каких
случаях через данную точку плоскости проходит только одна интегральная кривая.
Пример 2. Рассмотрим дифференциальное уравнение y’=-ky, где k=const. Правая часть этого уравнения
удовлетворяет условиям теоремы при любых начальных условиях, так как функция f(x,y)=-ky непрерывна в любой точке плоскости и
f’y(x,y)=-k ограничена на всей плоскости. Поэтому можно утверждать, что
через каждую точку плоскости проходит одна и только одна интегральная кривая
этого дифференциального уравнения.
Пример
3. Рассмотрим дифференциальное
уравнение 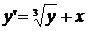 . Здесь функция
. Здесь функция 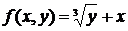 непрерывна
на всей плоскости, но
непрерывна
на всей плоскости, но 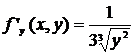 ограничена только в таких точках области R,
которые не лежат на оси Ox (так как y=0 на оси Ox).
Поэтому по теореме Коши можно утверждать, что через каждую точку плоскости, не
лежащую на оси Ox, проходит только одна интегральная кривая этого
уравнения.
ограничена только в таких точках области R,
которые не лежат на оси Ox (так как y=0 на оси Ox).
Поэтому по теореме Коши можно утверждать, что через каждую точку плоскости, не
лежащую на оси Ox, проходит только одна интегральная кривая этого
уравнения.
Особые
решения дифференциального уравнения.
Пусть
дано дифференциальное уравнение
F(x,y,y’)=0.
(8)
Если
в точке М0(x0,y0) плоскости выполняются условия теоремы Коши, то через
нее проходит только одна интегральная кривая этого уравнения.
Если
через точку М0(x0,y0) плоскости проходит не одна интегральная кривая
уравнения (1), то возможны следующие варианты:
1) в точке М0(x0,y0) пересекаются несколько интегральных кривых с разными
касательными (рис. 2). Это может произойти, например, в случае, когда данное
дифференциальное уравнение распадается на несколько уравнений. Тогда точке М0(x0,y0) плоскости соответствует несколько
разных направлений, исходящих из этой точки.
2) Через точку М0(x0,y0) проходят по крайней мере две интегральные кривые с
общей касательной (рис.3).
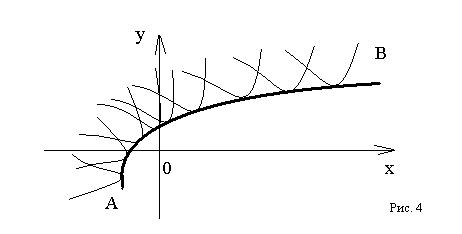
Пусть на плоскости имеется кривая AB, такая, что в каждой точке ее касается какая-нибудь
интегральная кривая уравнения (8) (рис. 4). В таком случае и сама кривая AB является интегральной кривой
уравнения (8). Действительно, в каждой ее точке M(x,y) все три числа x, y и y’
такие же как у некоторой интегральной кривой, и, следовательно, эти три числа
удовлетворяют уравнению (8).
Определение 1. Решение, график которого таков, что через каждую его точку
проходит по крайней мере еще одна касающаяся его интегральная кривая,
называется особым решением дифференциального уравнения.
Очевидно, что в каждой точке особого решения нарушаются условия теоремы
Коши.
Пример
1. Решить дифференциальное уравнение 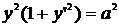 (a=const).
(a=const).
Разрешим
это уравнение относительно y’:
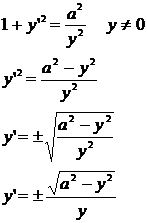
Таким
образом, уравнение распадается на два уравнения, т.е. имеет место первый из
рассмотренных выше случаев. Чтобы решить эти уравнения, отделим в них
переменные x и y друг от друга, обозначив 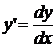 :
:
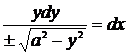 .
.
В такой записи мы имеем равенство дифференциалов двух различных
выражений, а именно:
 ,
,
Откуда
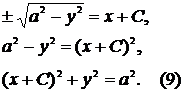
В
такой записи видно, что общий интеграл представляет собой семейство окружностей
радиуса a с центрами в точках (С,0), т.е. с центрами на оси Ox.

Так
как постоянной С можно придавать различные положительные и отрицательные
значения, то центры окружностей расположены сплошь по всей оси Ox.
На рис. 5 видно, что через каждую точку плоскости, лежащую в полосе -a<y<a,
проходят две пересекающиеся в этой точке окружности, т.е. две пересекающиеся в
этой точке интегральные кривые. Это происходит потому, что каждой точке полосы
-a<y<a соответствуют два направления, являющиеся
касательными к двум окружностям в точке их пересечения, в силу того, что данное
уравнение распадается на два уравнения. На рис. 5 видно, что две прямые y=a и y=-a
состоят сплошь из точек касания с окружностями (9). Следовательно, по
определению 1 эти две прямые представляют собой графики особых решений данного
уравнения. Очевидно, что они не могут быть получены из формулы (9) общего
интеграла ни при каком значении постоянной С. Эти два решения были потеряны в
процессе преобразования данного уравнения, а именно в момент деления обеих
частей уравнения на  . Производя деление, мы, естественно предполагали, что
. Производя деление, мы, естественно предполагали, что
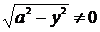 , т.е. что
, т.е. что 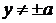 . Прямой
же подстановкой в уравнение убеждаемся в том, что обе функции y=a и y=-a
удовлетворяют уравнению, т.е. являются его решениями.
. Прямой
же подстановкой в уравнение убеждаемся в том, что обе функции y=a и y=-a
удовлетворяют уравнению, т.е. являются его решениями.
Итак,
решениями данного уравнения являются семейство окружностей (9) и две прямые 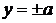 .
.
Таким
образом, иногда особое решение может быть найдено следующим путем: надо найти
те решения уравнения, которые могли быть потеряны в процессе преобразований.
Для этого надо проследить, не происходило ли в процессе преобразований
нарушения равносильности уравнений, и если таковые были, то выявить те
множители, которые могли давать решения исходного уравнения. Полученные таким
путем функции надо подставить в исходное уравнение, чтобы проверить,
действительно ли они являются решениями. После этого надо еще проверить, нельзя
ли получить данные решения из общего решения при каком либо конкретном значении
С. Если это возможно, то найденные решения будут частными решениями исходного
уравнения, если нет - особыми.
Укажем
и другой способ нахождения особых решений, для чего используем понятие
огибающей семейства кривых.
Определение
2. Огибающей семейства кривых
называется такая кривая, которая касается каждой кривой семейства и при том вся
состоит из таких точек касания.
Сравнивая
это определение с определением 1, можно сказать, что если семейство
интегральных кривых, составляющее общий интеграл дифференциального уравнения,
имеет огибающую, то эта огибающая является особым решением дифференциального
уравнения.
Способ
нахождения огибающей семейства кривых состоит в следующем: надо взять уравнение
семейства кривых, то есть в нашем случае общий интеграл дифференциального
уравнения
дифференциальный уравнение коши кривая
Ф(x,y,C)=0
(10)
и
присоединить к нему равенство 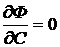 . Из
системы равенств
. Из
системы равенств
Ф(x,y,C)=0,
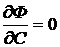
надо
исключить С. Результат исключения даст зависимость вида y=ψ(x). Эта кривая
может быть или огибающей семейства кривых (10), т.е. особым решением уравнения,
или геометрическим местом особых точек кривых (10). В последнем случае функция y=ψ(x) не является
особым решением уравнения.
Литература
1. Балдин,
К.В. Математический анализ: Учебник / К.В. Балдин, В.Н. Башлыков, А.В.
Рукосуев. - М.: Флинта, МПСУ, 2013. - 368 c.
. Боярчук,
А.К. Справочное пособие по высшей математике. Т. 3. Часть 2: Математический
анализ: кратные и криволинейные интегралы / А.К. Боярчук, И.И. Ляшко, Я.Г. Гай.
- М.: ЛИБРОКОМ, 2012. - 256 c.
. Будаев,
В.Д. Математический анализ. Функции одной переменной: Учебник / В.Д. Будаев,
М.Я. Якубсон. - СПб.: Лань, 2012. - 544 c.
. Гаврилов,
В.И. Математический анализ: Учебное пособие для студентов учреждений высшего
профессионального образования / В.И. Гаврилов, Ю.Н. Макаров, В.Г. Чирский. -
М.: ИЦ Академия, 2013. - 336 c.
. Горлач,
Б.А. Математический анализ: Учебное пособие / Б.А. Горлач. - СПб.: Лань, 2013.
- 308 c.
. Лейнартас,
Е.К. Математический анализ: Учебное пособие для бакалавров / А.М. Кытманов,
Е.К. Лейнартас, В.Н. Лукин; Под ред. А.М. Кытманов. - М.: Юрайт, 2012. - 607 c.
.
Лоссиевская, Т.В. Математический анализ: несобственные интегралы: Учебное
пособие / Т.В. Лоссиевская. - М.: МИСиС, 2012. - 61 c.
. Ляшко, И.И.
Справочное пособие по высшей математике.Т. 2. Математический анализ: ряды, функции
векторного аргумента. Часть 1. Радя: Учебное пособие / И.И. Ляшко, А.К.
Боярчук, Я.Г. Гай. - М.: ЛКИ, 2012. - 224 c.
. Просветов,
Г.И. Математический анализ: задачи и решения: Учебное пособие / Г.И. Просветов.
- М.: БИНОМ. ЛЗ, 2011. - 208 c.
. Протасов,
Ю.М. Математический анализ: Учебное пособие / Ю.М. Протасов. - М.: Флинта,
Наука, 2012. - 168 c.
. Шершнев,
В.Г. Математический анализ: сборник задач с решениями: Учебное пособие / В.Г.
Шершнев. - М.: НИЦ ИНФРА-М, 2013. - 164 c.