Численное решение обратных задач по восстановлению граничных условий уравнения параболического типа
Министерство
высшего и среднеспециального образования
Республики
Узбекистан
Самаркандкандский
государственный университет им. А. Навои
На
правах рукописи
УДК
532.546
Диссертация
на
соискание академической степени магистра по специальности "Вычислительная
математика"
Численное
решение обратных задач по восстановлению граничных условий уравнения
параболического типа
Рахмонов Бахтиёр
Научный руководитель:
Заведующий кафедрой
проф. Хужаёров Б.Х.
Самарканд
- 2012
Оглавление
Введение
Глава
1. Основные понятия об обратных и некорректно поставленных задачах
.1
Классификация обратных задач математической физики
.2
Понятие о корректно и некорректно поставленных задачах
.3
Обратные задачи для уравнения теплопроводности
Глава
2. Методы решения граничных обратных задач
2.1 Методы решения граничных обратных задач для
уравнения параболического типа
.2 Решение граничных обратных задач для
уравнения параболического типа прямыми численными методами
.3 Метод квазиобращения
Глава
3. Численные методы решения граничных обратных задач для уравнения
параболического типа
.1
Обратная граничная задача для линейно упругого режима фильтрации
.2
Обратная граничная задача для нелинейно упругого режима фильтрации
.3
Обратная граничная задача для линейно упруго-пластического режима фильтрации
Основные
результаты и выводы
Литература
Введение
Интерес к обратным задачам в последнее время
значительно вырос. Это объясняется двумя причинами. Во-первых, такие задачи
имеют большое практическое значение.
Области использования обратных и некорректных
задач настолько широки и разнообразны, что одно только перечисление названий
отраслей займет много мест.
Отметим некоторые из них:
) математические дисциплины: вычислительная
математика, алгебра, интегральная геометрия, интегральные и операторные
уравнения, дифференциальные уравнения, уравнения математической физики, теория
оптимального управления и др.,
) геофизика,
) квантовая механика,
) акустика,
) электродинамика,
) химия,
) тепло- и массоперенос,
) нефтяное и газовое дело,
) гидрология и гидрогеология,
) медицина,
) экономика,
) экология и др.
Во-вторых обратные задачи являются как правило
некорректными, что создает ряд проблем в процессе их решения.
В связи с созданием эффективных методов решения,
развитием численных методов становится возможным решение достаточно сложных
обратных задач, исследование свойств решения, что в свою очередь требует более
глубокого анализа теоретических проблем, включая вопросы существования и
единственности решений, регуляризации задачи, сходимости регуляризованных
решений и др. Такое обилие задач, достигнутые результаты за последнее время,
практическая важность решения обратных и некорректных задач показывает
актуальность проблемы.
Объем работы. Диссертация состоит из введения,
трех параграфов, основных результатов и выводов, списка использованной
литературы. Общий объем работы включает 92 страницы текста, 44 рисунков, 36
наименований использованной литературы.
Цель и задачи работы. В работе поставлена цель -
решение обратных граничных задач уравнений параболического типа. Исходя из этой
цели, в первой главе рассмотрены общие сведение обратных задач математической
физики. Во второй главе представлены методы решение граничных обратных задач
уравнений параболического типа. Далее, в третей главе, с использованием данных
методов численно решены обратные граничные задачи упругом режиме фильтрации.
При этом, рассмотрены как линейные, так и нелинейные уравнения фильтрации.
Научная новизна. В диссертации решены граничные
обратные задачи фильтрации жидкости при линейном и нелинейном упругом режимах.
Исследованы устойчивости решения к погрешностям исходных данных.
Достоверность полученных результатов. Задачи
фильтрации решены численно с применением метода конечных разностей. При
проведении численных расчетов на ЭВМ проверена устойчивость метода решения.
Специальные численные эксперименты показывают также их устойчивость по
отношению к возмущениям исходных данных.
Практическая ценность работы. Работа посвящена
теоретическому анализу граничных обратных задач для параболического уравнения.
Однако полученные результаты могут быть использованы при анализе процессов
тепло и массообмена, процессов диффузии, фильтрационных процессах нефти и газа
и др.
Положения, выносимые на защиту. На защиту
выносится следующее:
·
решения
граничных обратных задач уравнения параболического типа;
·
решения
граничных обратных задач фильтрации жидкости при линейном упругом режиме;
·
решения
граничных обратных задач фильтрации жидкости при нелинейном упругом режиме.
Основное содержание работы
Во введении обоснована актуальность темы,
сформулированы цель и задачи исследования, показана научная новизна и
практическая значимость результатов работы. Кратко дано основное содержание
диссертации.
В первой главе приведены сведения об обратных и
некорректно поставленных задач математической физики. Даны сведения
классификация обратных задач математической физики.
В второй главе рассмотрены методы решения
граничных обратных задач для уравнения параболического типа.
Во третей главе решены граничные обратные задачи
фильтрации жидкости при линейном и нелинейном упругом режимах, а также для
линейно упруго-пластического режима фильтрации. Восстановлены граничные условия
из решения обратных задач фильтации. Для получения устойчивых решения
использован метод шаговой регуляризации и сглаживание исходных данных.
обратный параболический задача
фильтрация
Глава 1. Основные понятия об обратных и
некорректно поставленных задачах
1.1 Классификация обратных
задач математической физики
Краевая задача для уравнения с
частными производными характеризуется заданием определяющего уравнения,
расчетной области, граничных и начальных условий. Поэтому среди обратных задач
можно выделить коэффициентные, геометрические, граничные и эволюционные
обратные задачи.
Прямые и обратные задачи.
При обработке данных натурных
экспериментов по дополнительным косвенным измерениям делается вывод о
внутренних связях явления или процесса. В условиях, когда структура
математической модели исследуемого процесса известна, можно ставить проблему
идентификации математической модели, например, определение коэффициентов
дифференциального уравнения. Такие задачи мы относим к классу обратных задач
математической физики.
Задачи математической физики
можно классифицировать по различным признакам. Например, можно выделить
стационарные задачи, которые описывают установившиеся, неизменные во времени
процессы и явления. Нестационарные задачи описывают динамические процессы, в
которых решение меняется во времени. Не столь очевидно разделение задач
математической физики на прямые и обратные.
С общей методологической точки
зрения прямыми задачами мы можем назвать задачи, для которых заданы причины, а
искомыми величинами являются следствия. При таких предпосылках обратными будут
задачи, в которых известны следствия, а неизвестными выступают причины. Однако
такое общее разделение не всегда легко провести на практике. Для уравнений с
частными производными в стандартных курсах математической физики формулируются
корректные краевые задачи, которые мы и относим к классу прямых задач. Для
эллиптических уравнений второго порядка дополнительные условия на решение
(первого, второго или третьего рода) задаются на границе области. С точки
зрения причинно-следственных отношений граничные условия являются причинами, а
следствием - решение краевой задачи. Для параболических уравнений задается
начальное условие, а для гиперболических уравнений второго порядка начальное
состояние определяется заданием решения и производной по времени.
Для того чтобы не загромождать
свое рассмотрение терминологическими тонкостями, к прямым задачам мы отнесем
именно эти классические задачи математической физики. Они характеризуются
необходимостью нахождения решения из уравнения с заданными коэффициентами и
правой частью и дополнительных граничных и начальных условий.
Под обратными задачами
математической физики мы будем понимать задачи, которые мы не можем отнести к
прямым. Они связаны часто с необходимостью определения не только решения, но и
некоторых недостающих коэффициентов и (или) условий. Одним из признаков
обратной задачи может служить именно необходимость определения не только
решения, но и некоторых компонент математической модели.
С рассматриваемой точки зрения
обратные задачи характеризуются, прежде всего, тем, чего недостает, чтобы можно
было бы отнести поставленную задачу к классу прямых задач математической
физики. С другой стороны, мы должны компенсировать недостающую информацию.
Поэтому в обратных задачах необходимо выделить дополнительную информацию,
которая позволяет рассчитывать на возможность однозначного определения решения.
По этим отмеченным признакам
можно классифицировать обратные задачи математической физики. Естественно
ориентироваться, прежде всего, на те основные характеристики, которые выделяют
обратную задачу. Для прямых задач математической физики решение определяется
уравнением (коэффициентами и правой частью), граничными и, в нестационарных
задачах, начальными условиями. Классификацию обратных задач удобно провести по
признакам, что какие-то из отмеченных условий не заданы.
Коэффициентные обратные задачи.
Мы выделим коэффициентные
обратные задачи, которые характеризуется тем, что коэффициенты уравнения или
(и) правая часть неизвестны. В качестве характерного примера будем
рассматривать параболическое уравнение
 (1)
(1)
Простейшая прямая задача состоит в
нахождении функции и(х, t), удовлетворяющей уравнению (1) и условиям
 (2)
(2)
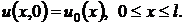 (3)
(3)
В прикладных проблемах часто
свойства среды неизвестны и их нужно определять. В нашем случае можно поставить
задачу идентификации коэффициента  . В простейшем случае однородной
среды неизвестным является коэффициент
. В простейшем случае однородной
среды неизвестным является коэффициент  , для кусочно-однородной среды -
несколько констант. При зависимости свойств среды интерес может представлять
коэффициентная обратная задача по восстановлению
, для кусочно-однородной среды -
несколько констант. При зависимости свойств среды интерес может представлять
коэффициентная обратная задача по восстановлению  .
.
Список возможных постановок
коэффициентных обратных задач не исчерпывается выше отмеченными и легко может
быть продолжен. Характерной является задача для уравнения (1), по нахождению
пары неизвестных функций  . Основная
особенность рассматриваемой обратной задачи состоит в нелинейности
коэффициентной обратной задачи.
. Основная
особенность рассматриваемой обратной задачи состоит в нелинейности
коэффициентной обратной задачи.
Можно выделить как самостоятельную
задачу определения неизвестной правой части  параболического уравнения (1).
Более частные постановки связаны, например, с выбором зависимости
параболического уравнения (1).
Более частные постановки связаны, например, с выбором зависимости
 (4)
(4)
Интерес может представлять
неизвестная зависимость источника (правой части) от времени при известном
распределении по пространству - в представлений (4) функция  неизвестна,
а функция
неизвестна,
а функция  задана.
задана.
Если коэффициенты и (или) правая
часть уравнения (1) неизвестны, то помимо условий (2), (3) необходимо
использовать некоторые дополнительные условия. Этих условий не должно быть
мало, чтобы иметь возможность для однозначного определения решения обратной
задачи. Если ищется коэффициент в классе одномерных функций (функций одной
переменной), то и дополнительные данные должны задаваться в этом же классе.
Пусть, например, рассматривается
обратная задача (1)-(4) по нахождению пары функций  . Помимо
решения краевой задачи (1)-(3) нужно найти зависимость от времени правой части.
В этом случае дополнительная информация может иметь вид
. Помимо
решения краевой задачи (1)-(3) нужно найти зависимость от времени правой части.
В этом случае дополнительная информация может иметь вид
 (6)
(6)
т.е. известно решение на каждый
момент времени не только на границе, но и в некоторой внутренней точке  расчетной
области
расчетной
области  .
.
При рассмотрении обратных задач типа
(1)-(6) особое внимание должно уделяться проблемам единственности решения
обратной задачи. Особенно это важно при рассмотрении нелинейных задач (пример -
задача нахождения пары функций  .
.
Граничные обратные задачи
В условиях, когда прямые измерения
на границе невозможны, мы имеем дело с граничными обратными задачами. В этом
случае недостающие граничные условия идентифицируются, например, по измерениям
внутри области. Приведем пример подобной обратной задачи для параболического
уравнения (1).
Будем считать, что измерения
недоступны на правом конце отрезка  , но зато известно решение во
внутренней точке
, но зато известно решение во
внутренней точке  , т.е.
вместо (2) заданы условия
, т.е.
вместо (2) заданы условия
 (7)
(7)
Типичная постановка граничной
обратной задачи состоит в идентификации потока на части границы, недоступной
измерению (в рассматриваемом примере - при  ). Это соответствует нахождению из
условий (1), (3), (7) функций
). Это соответствует нахождению из
условий (1), (3), (7) функций  .
.
Эволюционные обратные задачи.
Прямая задача для нестационарных
задач математической физики характеризуется заданием начальных условий (см.,
например, (3)). К эволюционным обратным задачам мы будем относить обратные
задачи, в которых идентифицируются начальные условия (их недостает для
формулировки задачи как прямой).
Применительно к рассматриваемой
прямой задаче (1)-(3) простейшая эволюционная обратная задача формулируется
следующим образом. Нам не заданы начальные условия (3), но известно решение на
конечный момент времени 
 (8)
(8)
Необходимо найти решение уравнения
(1) в предшествующие моменты времени (ретроспективная обратная задача).
Можно ставить обратную задачу по идентификации
начального состояния при использовании дополнительной информации о решении во
внутренних точках (дополнительное условие типа (5)).
.2 Понятие о корректно и некорректно
поставленных задачах
Приведем основные понятия теории так называемых
некорректных (или некорректно поставленных) задач и численные методы их решения
при наличии различной априорной информации. Для простоты рассмотрим сначала
только линейные уравнения в нормированных пространствах, хотя, разумеется, все
аналогичные определения могут быть введены и для нелинейных задач в более общих
метрических (и даже топологических) пространствах.
В качестве основного объекта рассматривается
операторное уравнение:
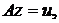
где  - линейный оператор, действующий из
гильбертова пространства
- линейный оператор, действующий из
гильбертова пространства  в
гильбертово пространство
в
гильбертово пространство  . Требуется
найти решение операторного уравнения
. Требуется
найти решение операторного уравнения  , соответствующее заданной
неоднородности (или правой части уравнения)
, соответствующее заданной
неоднородности (или правой части уравнения)  .
.
Такое уравнение является типичной
математической моделью для многих физических, так называемых обратных, задач,
если предполагать, что искомые физические характеристики  не могут
быть непосредственно измерены, а в результате эксперимента могут быть получены
только данные
не могут
быть непосредственно измерены, а в результате эксперимента могут быть получены
только данные  , связанные
с
, связанные
с  с помощью
оператора
с помощью
оператора  .
.
Французским математиком Ж. Адамаром
были сформулированы следующие условия корректности постановки математических
задач, которые мы рассмотрим на примере записанного операторного уравнения.
Задача решения операторного уравнения называется корректно поставленной (по
Адамару), если выполнены следующие три условия:
решение существует  ;
;
1) решение
единственно;
если  то
то  .
.
Второе условие обеспечивается тогда
и только тогда, когда оператор  является взаимно однозначным
(инъективным). Первый и второй условия означают, что существует обратный
оператор
является взаимно однозначным
(инъективным). Первый и второй условия означают, что существует обратный
оператор  , причем его
область определения D(A-1) (или множество значений оператора A, R(A)) совпадает
с U. Третье условие означает, что обратный оператор
, причем его
область определения D(A-1) (или множество значений оператора A, R(A)) совпадает
с U. Третье условие означает, что обратный оператор 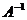 является
непрерывным, т.е. "малым" изменениям правой части u соответствуют
"малые" изменения решения z. Более того, Ж. Адамар считал, что только
корректные задачи должны рассматриваться при решении практических задач. Однако
хорошо известны примеры некорректно поставленных задач, к изучению и численному
решению которых приходится прибегать при рассмотрении многочисленных прикладных
задач. Нужно отметить, что устойчивость и неустойчивость решения связаны с тем,
как определяется пространство решений Z. Выбор пространства решений (в том
числе и нормы в нем) обычно определяется требованиями прикладной задачи. Задачи
могут быть некорректно поставленными при одном выборе нормы и корректно
поставленными при другом.
является
непрерывным, т.е. "малым" изменениям правой части u соответствуют
"малые" изменения решения z. Более того, Ж. Адамар считал, что только
корректные задачи должны рассматриваться при решении практических задач. Однако
хорошо известны примеры некорректно поставленных задач, к изучению и численному
решению которых приходится прибегать при рассмотрении многочисленных прикладных
задач. Нужно отметить, что устойчивость и неустойчивость решения связаны с тем,
как определяется пространство решений Z. Выбор пространства решений (в том
числе и нормы в нем) обычно определяется требованиями прикладной задачи. Задачи
могут быть некорректно поставленными при одном выборе нормы и корректно
поставленными при другом.
Многочисленные обратные (в том числе
и некорректные) задачи можно найти в различных областях физики. Так, астрофизик
не может активно воздействовать на процессы, происходящие на далеких звездах и
галактиках, ему приходится делать заключения о физических характеристиках весьма
удаленных объектов по их косвенным проявлениям, доступным измерениям на Земле
или вблизи Земли (на космических станциях). Прекрасные примеры некорректных
задач можно найти в медицине, прежде всего, нужно отметить вычислительную (или
компьютерную) томографию. Хорошо известны приложения некорректных задач в
геофизике (на самом деле, легче и дешевле судить о том, что делается под
поверхностью Земли, решая обратные задачи, чем заниматься бурением глубоких
скважин), радиоастрономии, спектроскопии, ядерной физике и т.д., и т.п.
.3 Обратные задачи для уравнения
теплопроводности
В этом параграфе будут рассмотрены обратные
задачи для уравнения теплопроводности, представляющие собой задачи определения
либо начального условия, либо граничного условия, либо функции, характеризующей
действие источников тепла по дополнительной информации о решении краевой задачи
для уравнения теплопроводности [5]. Обратные задачи такого типа возникают при
исследовании теплофизических и ряда других процессов [5].
Задача с обратным направлением
времени.
Одной из наиболее известных
обратных задач для уравнения теплопроводности является задача с обратным
направлением времени. Рассмотрим ее постановку в случае первой краевой задачи.
Первая краевая задача для уравнения
теплопроводности с нулевыми краевыми условиями состоит в определении функции  ,
удовлетворяющей уравнению
,
удовлетворяющей уравнению
 (13)
(13)
краевым условиям
 (14)
(14)
начальному условию
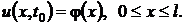 (15)
(15)
Эту задачу можно интерпретировать
следующим образом. Известно распределение температуры в тонком стержне длиной 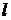 в начальный
момент времени
в начальный
момент времени  . Требуется
найти распределение температуры в стержне в последующие моменты времени
. Требуется
найти распределение температуры в стержне в последующие моменты времени  .
.
Задача с обратным направлением
времени может быть сформулирована так. Известно распределение температуры в
стержне в момент времени 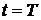 . Требуется
определить распределение температуры в предыдущие моменты времени
. Требуется
определить распределение температуры в предыдущие моменты времени  . Для
определенности поставим задачу более конкретно. Известно распределение
температуры
. Для
определенности поставим задачу более конкретно. Известно распределение
температуры  в момент
времени
в момент
времени 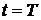
 (16)
(16)
требуется определить распределение  в начальный
момент времени
в начальный
момент времени 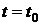 .
.
Приступим к исследованию
поставленной обратной задачи. Как известно, при определенных предположениях
относительно функции  решение
задачи (13)-(15) может быть получено с помощью метода разделения переменных и
имеет следующий вид [3]:
решение
задачи (13)-(15) может быть получено с помощью метода разделения переменных и
имеет следующий вид [3]:

Положив 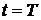 учитывая
(16), имеем
учитывая
(16), имеем
 (17)
(17)
Таким образом, обратная задача
свелась к уравнению (17) относительно неизвестной функции  .
.
Покажем, что уравнение (5) имеет
единственное решение в пространстве  . Так как это уравнение является
линейным, то для доказательства единственности его решения достаточно показать,
что оно имеет только нулевое решение при
. Так как это уравнение является
линейным, то для доказательства единственности его решения достаточно показать,
что оно имеет только нулевое решение при  .
.
Итак, пусть в (17)  при
при  . Так как
система функций
. Так как
система функций  , является
ортогональной в пространстве
, является
ортогональной в пространстве  , а
, а  для
для  , то, умножив (17) на
, то, умножив (17) на  и
проинтегрировав от 0 до
и
проинтегрировав от 0 до 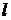 , получим,
что
, получим,
что
 (18)
(18)
Так как система функций  , полна в
, полна в  , то из (18)
следует, что
, то из (18)
следует, что  и уравнение
(17) имеет единственное решение.
и уравнение
(17) имеет единственное решение.
Рассмотрим вопрос о существовании
решения уравнения (17). Обозначим через  скалярное произведение функций
скалярное произведение функций  и
и  в
пространстве
в
пространстве  . Система
функций
. Система
функций  , является
полной ортонормированной системой в
, является
полной ортонормированной системой в  . Пусть уравнение (17) с правой
частью
. Пусть уравнение (17) с правой
частью  имеет
решение
имеет
решение  . Обозначим
через
. Обозначим
через  и
и  коэффициенты
Фурье
коэффициенты
Фурье  и
и  функций
функций  и
и  соответственно.
Тогда из (17) получим, что при
соответственно.
Тогда из (17) получим, что при 



Записывая для функции  равенство
Парсеваля, имеем
равенство
Парсеваля, имеем
 (19)
(19)
Таким образом, для существования
решения уравнения (17) в пространстве  необходимо, чтобы функция
необходимо, чтобы функция  была
такова, что ряд, стоящий в правой части равенства (19), сходился. Так как члены
этого ряда содержат быстро возрастающий множитель
была
такова, что ряд, стоящий в правой части равенства (19), сходился. Так как члены
этого ряда содержат быстро возрастающий множитель  , то
требование сходимости ряда налагает сильное условие на характер убывания
коэффициентов Фурье
, то
требование сходимости ряда налагает сильное условие на характер убывания
коэффициентов Фурье  функции
функции  . Очевидно,
что эти условия выполнены не для всех
. Очевидно,
что эти условия выполнены не для всех  . В качестве примера рассмотрим
бесконечно дифференцируемую на отрезке
. В качестве примера рассмотрим
бесконечно дифференцируемую на отрезке  функцию
функцию

Ряд, стоящий в правой части
равенства (19), для этой функции расходится, так как

 при
при 
Следовательно, уравнение (17) для  решения не
имеет.
решения не
имеет.
Задача решения уравнения (17)
является неустойчивой при  и
и  . Для того
чтобы убедиться в этом, достаточно взять последовательность функций
. Для того
чтобы убедиться в этом, достаточно взять последовательность функций  являющихся
решениями уравнения (17) при
являющихся
решениями уравнения (17) при
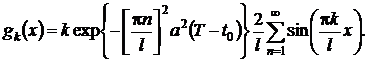
Тогда  , а
, а  при
при  , что и доказывает неустойчивость
задачи.
, что и доказывает неустойчивость
задачи.
Рассматриваемая обратная задача
может быть сведена к интегральному уравнению Фредгольма 1-го рода. Действительно,
поменяв местами порядок суммирования и интегрирования в левой части уравнения
(17), получим уравнение Фредгольма 1-го рода:
 (20)
(20)
с ядром

Так как каждый член этого ряда
содержит быстро убывающий при  множитель, то
множитель, то  является
непрерывной в квадрате
является
непрерывной в квадрате  ,
, 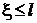 функцией.
Следовательно, интегральный оператор
функцией.
Следовательно, интегральный оператор  , определяемый ядром
, определяемый ядром  , является
вполне непрерывным, если его рассматривать действующим из
, является
вполне непрерывным, если его рассматривать действующим из 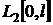 в
в 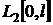 . А значит,
задача решения уравнения (20) в этой паре пространств некорректна.
. А значит,
задача решения уравнения (20) в этой паре пространств некорректна.
Так как ядро  имеет
непрерывные частные производные любого порядка непрерывные в квадрате
имеет
непрерывные частные производные любого порядка непрерывные в квадрате  ,
, 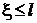 , то
интегральный оператор
, то
интегральный оператор  можно
рассматривать действующим из
можно
рассматривать действующим из  в
в  , где
, где  - произвольное фиксированное
натуральное число. В этом случае задача решения уравнения (20) также будет
неустойчивой. Для доказательства неустойчивости достаточно взять
последовательность
- произвольное фиксированное
натуральное число. В этом случае задача решения уравнения (20) также будет
неустойчивой. Для доказательства неустойчивости достаточно взять
последовательность

тогда
 а
а  при
при 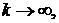
что и доказывает некорректность
задачи решения уравнения (20) в рассматриваемой паре пространств.
Получим оценку устойчивости решения
задачи теплопроводности с обратным течением времени в случае, когда имеется
дополнительная информация о решении задачи.
Будем для упрощения записи считать
далее, что  .
Предположим, что функция
.
Предположим, что функция  непрерывна,
имеет непрерывные производные
непрерывна,
имеет непрерывные производные 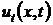 ,
,  и удовлетворяет уравнению (13) при
и удовлетворяет уравнению (13) при  ,
,  , где
, где 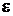 -
произвольное фиксированное положительное число. Предположим также, что
-
произвольное фиксированное положительное число. Предположим также, что  удовлетворяет
граничным условиям (14) при
удовлетворяет
граничным условиям (14) при  и не равна тождественно нулю.
и не равна тождественно нулю.
Рассмотрим при  функцию
функцию
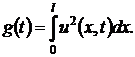
Дифференцируя, имеем

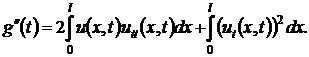
Так как

то

Интегрируя первое слагаемое по
частям и учитывая краевые условия (14), получим


Следовательно,

Рассмотрим функцию  . Покажем,
что
. Покажем,
что  при
при  .
Действительно,
.
Действительно,


Следовательно, используя неравенство
Коши-Буняковского, получим, что  для
для  . Из неотрицательности
. Из неотрицательности 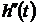 на отрезке
на отрезке  следует,
что при
следует,
что при 

Из этого неравенства имеем

следовательно,
 (21)
(21)
при  .
.
Рассмотрим функции  и
и  ,
удовлетворяющие тел же условиям, что
,
удовлетворяющие тел же условиям, что  , и такие, что
, и такие, что
 (22)
(22)
где  - положительная постоянная.
Обозначив
- положительная постоянная.
Обозначив  , из
неравенства (9) с учетом определения функции
, из
неравенства (9) с учетом определения функции  получим
получим



Положив  , используя
обозначение нормы в пространстве
, используя
обозначение нормы в пространстве  и неравенство (22), имеем
и неравенство (22), имеем
 (23)
(23)
Это неравенство представляет собой
оценку условной устойчивости решения задачи теплопроводности с обратным
направлением времени. Она получена в предположении, что функции  , удовлетворяют
неравенству (22), т.е. их нормы в пространстве
, удовлетворяют
неравенству (22), т.е. их нормы в пространстве  при
при  ограничены заданной постоянной. Эта
оценка может показаться несколько странной, поскольку она получена для решения
некорректной задачи только в предположении (22) об ограниченности решения,
которое не обеспечивает компактность множества в
ограничены заданной постоянной. Эта
оценка может показаться несколько странной, поскольку она получена для решения
некорректной задачи только в предположении (22) об ограниченности решения,
которое не обеспечивает компактность множества в  . Рассмотрим этот вопрос более
детально.
. Рассмотрим этот вопрос более
детально.
В оценке (23) разность решений в
момент времени  оценивается
через разность решений в момент времени
оценивается
через разность решений в момент времени  . Ограниченность же этих решений -
неравенство (22) - предполагается не при
. Ограниченность же этих решений -
неравенство (22) - предполагается не при  , а при
, а при 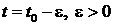 . Обозначим
через
. Обозначим
через  множество
множество

Переход от решения 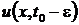 при
при  к решению
к решению  при
при  можно
рассматривать как результат действия интегрального оператора
можно
рассматривать как результат действия интегрального оператора 

с ядром

Так как ядро  непрерывно
при
непрерывно
при  ,
, 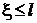 , то
оператор
, то
оператор  , рассматриваемый
действующим из
, рассматриваемый
действующим из  в
в  , является
вполне непрерывным. Следовательно, ограниченное множество
, является
вполне непрерывным. Следовательно, ограниченное множество  в
результате действия оператора
в
результате действия оператора  перейдет в множество
перейдет в множество  , компактное
в пространстве
, компактное
в пространстве  . Таким
образом, неравенство (23) представляет собой оценку устойчивости задачи
теплопроводности с обратным направлением времени на компактном в
. Таким
образом, неравенство (23) представляет собой оценку устойчивости задачи
теплопроводности с обратным направлением времени на компактном в  множестве
множестве  .
.
Приведенная оценка устойчивости
задачи теплопроводности с обратным направлением времени является частным
случаем оценки решения задачи Коши для эволюционного операторного уравнения
первого порядка [6,7].
Задача определения начального
распределения температуры по измерению температуры в точке
Рассмотрим постановку этой обратной
задачи на примере второй краевой задачи для уравнения теплопроводности
 (24)
(24)
 (25)
(25)
 (26)
(26)
Обратная задача ставится так. При  задана
функция
задана
функция  , где
, где  - некоторая
фиксированная точка отрезка
- некоторая
фиксированная точка отрезка  , а
, а  - решение задачи (24)-(26).
Требуется определить
- решение задачи (24)-(26).
Требуется определить  на отрезке
на отрезке  . Физическая
интерпретация этой обратной задачи такова. В течение некоторого интервала
времени в фиксированной точке стержня измеряется температура, и по этим
измерениям требуется определить начальное распределение температуры.
. Физическая
интерпретация этой обратной задачи такова. В течение некоторого интервала
времени в фиксированной точке стержня измеряется температура, и по этим
измерениям требуется определить начальное распределение температуры.
Решение задачи (24)-(26) может быть
получено методом разделения переменных и имеет вид


Положив в этом равенстве  , получим
уравнение для функции
, получим
уравнение для функции 

 (27)
(27)
где  .
.
Исследуем вопрос о единственности,
решения уравнения (27) в случае, когда точка измерения  находится
на конце отрезка.
находится
на конце отрезка.
Теорема 1. Если  , то решение
уравнения (27) единственно в пространстве
, то решение
уравнения (27) единственно в пространстве  .
.
Доказательство.
Из линейности уравнения (27)
следует, что для доказательства единственности решения в  достаточно
показать, что оно имеет только нулевое решение при
достаточно
показать, что оно имеет только нулевое решение при  . Положив в
(27)
. Положив в
(27)  и
и  , получим,
что при
, получим,
что при 
 (28)
(28)
Рассмотрим в комплексной
полуплоскости  , где
постоянная
, где
постоянная  , функцию
комплексной переменной
, функцию
комплексной переменной
 (29)
(29)
Так как при 

то в этой полуплоскости ряд, стоящий
в правой части (29), сходится равномерно. Учитывая то, что каждый член этого
ряда является аналитической функцией при  , и применяя теорему Вейерштрасса
[8]. получаем, что функция
, и применяя теорему Вейерштрасса
[8]. получаем, что функция  является аналитической при
является аналитической при  . Так как из
(28) следует, что
. Так как из
(28) следует, что  на отрезке
действительной оси
на отрезке
действительной оси  , лежащем в
области аналитичности
, лежащем в
области аналитичности  , то из
теоремы единственности для аналитических функций следует, что
, то из
теоремы единственности для аналитических функций следует, что  для всех
для всех  , таких, что
, таких, что
 . Таким
образом, равенство (28) выполнено для всех действительных
. Таким
образом, равенство (28) выполнено для всех действительных  . Переходя в
этом равенстве к пределу при
. Переходя в
этом равенстве к пределу при  , получим последовательно, что
, получим последовательно, что
 (30)
(30)
Так как система функций  ,
,  , является
полной в пространстве
, является
полной в пространстве  , то из
равенств (30) следует, что
, то из
равенств (30) следует, что  . Теорема 1 доказана.
. Теорема 1 доказана.
Покажем, что при измерении
температуры внутри стержня ( ), единственность решения обратной
задачи зависит от выбора точки наблюдения
), единственность решения обратной
задачи зависит от выбора точки наблюдения 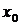 . Действительно, пусть
. Действительно, пусть 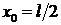 . Возьмем
. Возьмем  . Решение
задачи (24)-(26) имеет вид
. Решение
задачи (24)-(26) имеет вид

Следовательно,  при
при  и решение
обратной задачи не единственно. Пусть теперь
и решение
обратной задачи не единственно. Пусть теперь  . В этом случае
. В этом случае

Тогда, проводя рассуждения, аналогичные
доказательству теоремы 1, получим, что решение уравнения (27) единственно.
Рассматриваемая обратная задача
может быть сведена к интегральному уравнению Фредгольма 1-го рода.
Действительно, поменяв местами порядок интегрирования и суммирования в левой части
уравнения (27), получим уравнение Фредгольма 1-го рода
 (31)
(31)
с ядром

непрерывным в прямоугольнике  ,
,  . Следовательно,
интегральный оператор G, рассматриваемый действующим из
. Следовательно,
интегральный оператор G, рассматриваемый действующим из  в
в  , вполне
непрерывен. Таким образом, задача решения уравнения (31) в этой паре
пространств некорректна.
, вполне
непрерывен. Таким образом, задача решения уравнения (31) в этой паре
пространств некорректна.
Задача определения краевого условия
Рассмотрим обратную задачу,
состоящую в определении зависящей от времени функции, входящей в краевое
условие, по дополнительной информации о решении краевой задачи для уравнения
теплопроводности, представляющей собой функцию, зависящую от времени. Пусть
функция  является
решением краевой задачи
является
решением краевой задачи
 (32)
(32)
 (33)
(33)
 (34)
(34)
 (35)
(35)
Предположим, что функция  задана, а
функция
задана, а
функция  неизвестна,
и требуется определить
неизвестна,
и требуется определить  , если
известна дополнительная информация о решении задачи (32)-(35)
, если
известна дополнительная информация о решении задачи (32)-(35)
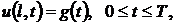 (36)
(36)
где  - заданная функция.
- заданная функция.
Рассмотрим вопрос о единственности
поставленной обратной задачи. Единственность решения этой задачи исследовалась
в более общей постановке целым рядом авторов. Приведем один из результатов,
полученных в этом направлении [9], сформулировав его для случая уравнения
теплопроводности с постоянными коэффициентами (32). Обозначим

Теорема 2. Пусть функция  и удовлетворяет
в
и удовлетворяет
в  уравнению
(32). Тогда если
уравнению
(32). Тогда если  для
для  , mo
, mo 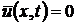 в
в  .
.
Из этой теоремы следует единственность
задачи определения функции  из (32)-(36) при заданных функциях
из (32)-(36) при заданных функциях  и
и  .
Действительно, пусть
.
Действительно, пусть 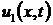 ,
,  удовлетворяют
в
удовлетворяют
в  уравнению
(32) и таковы, что
уравнению
(32) и таковы, что

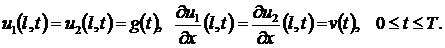
Рассмотрим функцию 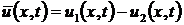 . Эта
функция удовлетворяет условиям теоремы 2. Следовательно,
. Эта
функция удовлетворяет условиям теоремы 2. Следовательно, 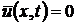 в
в  , а значит,
, а значит,  при
при  .
.
Отметим, что в теореме 2 начальное
условие для функции 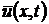 не
задается.
не
задается.
Рассмотрим другую постановку
обратной задачи для краевой задачи (20)-(23). Предположим, что функция  задана, a
задана, a  неизвестна
и требуется определить
неизвестна
и требуется определить  , если
известна дополнительная информация о решении задачи (32)-(35) следующего вида:
, если
известна дополнительная информация о решении задачи (32)-(35) следующего вида:
 (37)
(37)
где  - заданная функция, а
- заданная функция, а 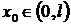 .
Исследование единственности решения этой обратной задачи также можно провести,
используя теорему 2.
.
Исследование единственности решения этой обратной задачи также можно провести,
используя теорему 2.
Теорема 3. Если функции 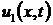 ,
,  ,
удовлетворяют в
,
удовлетворяют в  уравнению
(32), условиям (34), (35), (37) и таковы, что
уравнению
(32), условиям (34), (35), (37) и таковы, что  , при
, при  , mo
, mo при
при  .
.
Доказательство. Рассмотрим функцию 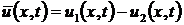 , являющуюся
решением краевой задачи
, являющуюся
решением краевой задачи




Покажем, что  для
для 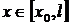 ,
,  . Умножив
уравнение на
. Умножив
уравнение на  и
проинтегрировав, получим
и
проинтегрировав, получим
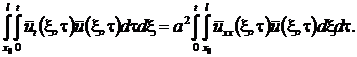
Вычисляя интегралы и используя
краевые и начальные условия, имеем для 

Следовательно,  при
при 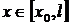 ,
,  , тогда
, тогда  для
для  . Таким
образом, функция
. Таким
образом, функция  удовлетворяет
уравнению (32) при
удовлетворяет
уравнению (32) при 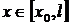 ,
,  , и
, и 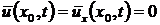 для
для  . Применяя
теорему 2 для прямоугольника
. Применяя
теорему 2 для прямоугольника 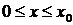 ,
,  , получим, что
, получим, что 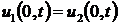 при
при  , т.е.
, т.е.  . Теорема 3
доказана.
. Теорема 3
доказана.
Приведем пример сведения задачи
определения граничного условия к задаче решения интегрального уравнения 1-го
рода. Рассмотрим краевую задачу для уравнения теплопроводности на полупрямой
 (38)
(38)
 (39)
(39)
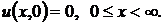 (40)
(40)
Требуется определить функцию  , если
задана дополнительная информация о решении задачи (38)-(40)
, если
задана дополнительная информация о решении задачи (38)-(40)
 (41)
(41)
Решение задачи (38)-(40) имеет
вид [3]
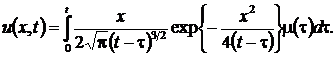
Следовательно, в данном случае
обратная задача сводится к интегральному уравнению Вольтерра 1-го рода

с ядром
 .
.
Глава 2. Методы решения граничных обратных задач
2.1 Методы решения граничных
обратных задач для уравнения параболического типа
Среды обратных задач
математической физики особенно важное прикладное значение имеет граничная
обратная задача [4]. Она связана с проблемами диагностики, когда по
дополнительным измерениям внутри расчетной области необходимо восстановить
граничный режим там, где прямые измерения невозможны. Такая задача принадлежит
к классу условно корректных и для ее приближенного решения разрабатываются
специальные методы регуляризации.
При формулировке общих
постановок и выделении основных классов обратных задач предполагаются
известными постановки прямых задач [2]. Каждая прямая задача в рамках принятой
математической модели может быть сопоставлена некоторым множеством обратных
задач.
Все обратные задачи, вне
зависимости от рассматриваемого физического процесса или технической системы,
можно разделить на три класса [20]:
) обратные задачи, возникающие
при диагностике и идентификации физических процессов;
) обратные задачи, возникающие
при проектировании технических объектов;
) обратные задачи, возникающие
при управлении процессами и объектами.
Математические модели различных
процессов обычно описываются дифференциальными уравнениями с частными
производными. Для этих моделей в общем случае вводится четыре вида обратных
задач - граничные, коэффициентные, ретроспективные и геометрические [2].
Граничные задачи заключаются в нахождении функций и параметров, входящих в
граничные условия; коэффициентные - функций и параметров, входящих в
коэффициенты уравнений; ретроспективные, т.е. обращенные назад по времени - в
нахождении начальных условий; геометрические - в реконструировании
геометрических характеристик области или каких-либо характерных точек, линий,
поверхностей внутри ее (например, в определении координат границы фазового
перехода или контакта сред с различными физическими свойствами). Теоретические
и практические проблемы решения обратных задач математической физики
исследованы в [2-5, 21-24].
Методы решения граничных
обратных задач хорошо исследованы в [1-5]. В работе [1, 4] для решения
граничных обратных задач использованы методы квазиобращения. В работе [2,3,5]
граничные обратные задачи решены прямыми численными методами и в экстремальной
постановке.
.2 Решение граничных обратных
задач для уравнения параболического типа прямыми численными методами
Рассмотрим нелинейную граничную
обратную задачу теплопроводности [2]. Считаем, что тело имеет границы  и на одной
из них
и на одной
из них 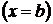 известен
тепловой поток
известен
тепловой поток  . Заданы
температурные измерения
. Заданы
температурные измерения  в некоторой
точке
в некоторой
точке 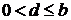 и начальное
распределение
и начальное
распределение  . Требуется
определить температурное поле в теле и условия на границе
. Требуется
определить температурное поле в теле и условия на границе  из условий
из условий
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
где  ,
,  ,
,  ,
,  ,
,  - заданные функции.
- заданные функции.
При использовании прямых методов
решения данной задачи результаты чувствительны к погрешностям в задании
теплофизических характеристики (ТФХ), причем гладкость результатов зависит от
гладкости функций  и
и  . Табличная
форма представления коэффициентов в этом отношении не совсем удачна, поскольку
приводит к дополнительным ошибкам вследствие операции интерполирования между
узловыми точками. Кроме того, значения функций в узлах температурной сетки
далеко не всегда задаются с учетом условий необходимой гладкости. Поэтому при
решении нелинейной обратные задачи теплопроводности (ОЗТ) желательно
представлять теплофизические свойства материала в виде некоторых
аппроксимирующих зависимостей
. Табличная
форма представления коэффициентов в этом отношении не совсем удачна, поскольку
приводит к дополнительным ошибкам вследствие операции интерполирования между
узловыми точками. Кроме того, значения функций в узлах температурной сетки
далеко не всегда задаются с учетом условий необходимой гладкости. Поэтому при
решении нелинейной обратные задачи теплопроводности (ОЗТ) желательно
представлять теплофизические свойства материала в виде некоторых
аппроксимирующих зависимостей  ,
, 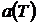 , удовлетворяющих условию
непрерывной дифференцируемости.
, удовлетворяющих условию
непрерывной дифференцируемости.
В этом случае удобно перейти от
уравнения (1) к другой, тождественной форме [2]
 (5)
(5)
где 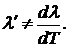
Введением равномерной прямоугольной
сетки 
 можно
записать разностный аналог (5) используя неявную шеститочечную схему при
аппроксимации производной
можно
записать разностный аналог (5) используя неявную шеститочечную схему при
аппроксимации производной  на верхнем
слое [2]
на верхнем
слое [2]
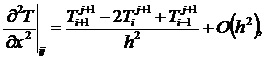


где 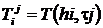 .
.
Откуда, полагая, что ТФХ оцениваются
по температуре предыдущего временного слоя, получено [2]
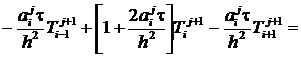
 (6)
(6)
где  ,
,  ,
,  .
.
Для дискретного представления
плотности тепловых потоков 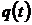 и
и  записаны разностные соотношения
второго порядка точности, учитывающие накопление теплоты в выделенном элементе,
толщиной
записаны разностные соотношения
второго порядка точности, учитывающие накопление теплоты в выделенном элементе,
толщиной  [6]
[6]

 (7)
(7)
где  .
.
Дискретная функция начального
распределения температуры имеет вид
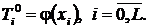 (8)
(8)
Соотношения (6)-(8) позволяют
получить систему линейных алгебраических уравнений для определения неизвестного
теплового потока  , и
неизвестных температур
, и
неизвестных температур  (
( ,
,  - известная
температура в точке
- известная
температура в точке  внутри
тела) [2]
внутри
тела) [2]
 (9)
(9)
Где 
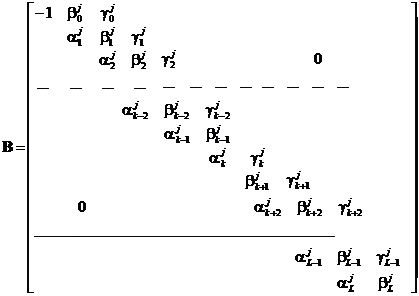

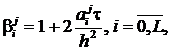








В результате получено 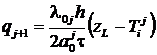 . При
необходимости данный способ численного решения ОЗТ уточняется итерациями по
ТФХ. Из системы (9) можно выделить самостоятельную замкнутую систему с
трехдиагональной матрицей [2]
. При
необходимости данный способ численного решения ОЗТ уточняется итерациями по
ТФХ. Из системы (9) можно выделить самостоятельную замкнутую систему с
трехдиагональной матрицей [2]
 (10)
(10)
Где 
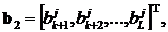

Матричное уравнение (10), по
существу, представляет собой алгебраическую форму неявного конечно-разностного
решения прямой задачи теплопроводности в области  . Вследствие этого система (10)
хорошо обусловлена и эффективно (быстро и точно) решается методом прогонки.
. Вследствие этого система (10)
хорошо обусловлена и эффективно (быстро и точно) решается методом прогонки.
Зная вектор  , можно
представить разностное решение обратной задачи в области
, можно
представить разностное решение обратной задачи в области 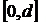 в виде
алгебраической системы с верхней треугольной матрицей, имеющей только три
ненулевые диагонали [2]
в виде
алгебраической системы с верхней треугольной матрицей, имеющей только три
ненулевые диагонали [2]
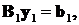 (11)
(11)
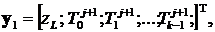


 .
.
Система (11) решается явно -
компоненты вектора  вычисляются
рекуррентным способом, начиная с
вычисляются
рекуррентным способом, начиная с  . При этом большое количество
нулевых коэффициентов приводит к значительному сокращению объема вычислений
[2].
. При этом большое количество
нулевых коэффициентов приводит к значительному сокращению объема вычислений
[2].

Рис. 1. Разностные схемы:  - узлы
сетки с неизвестными значениями температуры;
- узлы
сетки с неизвестными значениями температуры; 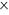 - узел с искомым значениям
- узел с искомым значениям
Замечая, что в случае постоянных ТФХ
( ),
шеститочечная разностная схема (рис. 1, а) вырождается в Т-образную
четырехточечную схему (рис. 1, б).
),
шеститочечная разностная схема (рис. 1, а) вырождается в Т-образную
четырехточечную схему (рис. 1, б).
Т-образной схемой можно было
воспользоваться и для случая переменных свойств тела, аппроксимируя правую
часть уравнения (1) следующим образом [2]


Где 
Желание повысить вязкостные свойства
вычислительных алгоритмов и тем самым расширить область применимости прямых
численных методов приводит к неявной схеме аппроксимации уравнения
теплопроводности в задаче продолжения температурного поля по данным Коши [2]. В
этом случае значения температуры 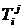 ,
,  на некотором пространственном слое
на некотором пространственном слое 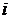 находятся
одновременно из решения алгебраической системы с входными данными в виде двух
временных рядов температур
находятся
одновременно из решения алгебраической системы с входными данными в виде двух
временных рядов температур  и
и  ,
,  .
.
Рассмотрим неявную сеточную
аппроксимацию задачи Коши для уравнения (5) с условиями (2)-(4), считая  [2]. Выбрав
прямоугольную сетку, положим, как и ранее,
[2]. Выбрав
прямоугольную сетку, положим, как и ранее,  ,
,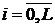 ,
,  ,
,  , где
, где  и
и  - шаги по координате и времени
соответственно.
- шаги по координате и времени
соответственно.
Временной и пространственные
дифференциальные операторы заменены разностными соотношениями (рис. 2) [2]

Чтобы получить возможность расчета
сеточной функции температуры во всех узлах прямоугольной области, необходимо
задать дополнительное условие на ее верхней границе при  .
.
Как показали вычислительные
эксперименты, можно принять одно из следующих априорных условий [2]
 (12)
(12)
 (13)
(13)
Где 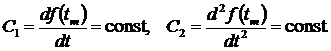
Уклонение решения от искомого,
обусловленное введением ограничений на производные (12) и (13), наблюдается в
некоторой сравнительно небольшой области  , причем условие (13) дает меньшее
искажение результатов [2]. Можно избежать указанного ухудшения решения в
окрестности
, причем условие (13) дает меньшее
искажение результатов [2]. Можно избежать указанного ухудшения решения в
окрестности  , если
значения температуры
, если
значения температуры  известны не
только на интервале времени
известны не
только на интервале времени  , но и при
, но и при  .
.
Другая возможность состоит в
аппроксимации уравнения теплопроводности в граничных узлах сетки ( ) по явной
схеме. Для этого можно воспользоваться следующим соотношением [2]
) по явной
схеме. Для этого можно воспользоваться следующим соотношением [2]
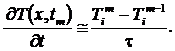 (14)
(14)
Конечно-разностный аналог задачи
(5), (2) - (4) для i-го пространственного слоя соответствует системе нелинейных
алгебраических уравнений с трехдиагональной матрицей ( ) [2]
) [2]
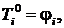 (15)
(15)
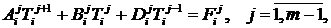 (16)
(16)
 (17)
(17)
Где 
Величины  ,
,  и
и  определяются
видом априорного условия в конце временного интервала. При задании первой
производной в виде соотношения (12) имеем
определяются
видом априорного условия в конце временного интервала. При задании первой
производной в виде соотношения (12) имеем  ,
,  . Для двух других условий
соответствующие выражения получаются с учетом основного разностного уравнения
(16).
. Для двух других условий
соответствующие выражения получаются с учетом основного разностного уравнения
(16).
Условие (13):

 .
.
Условие (14):

 .
.
Коэффициенты и правые части системы
(15)-(17) являются функциями неизвестных температур. Поэтому для каждого шага
по координате х необходимо повторять процесс итерационного приближения до тех
пор, пока в двух последовательных итерационных циклах не исчезнет заметная
разница между сеточными функциями  [2]
[2]

где  - номер итерации,
- номер итерации,  - некоторая
малая величина.
- некоторая
малая величина.
После выполнения условий сходимости
осуществляется переход к следующему пространственному слою. В том случае, когда
функция  задана
таблично, предпочтительнее пользоваться несколько измененным алгоритмом, в
котором производная
задана
таблично, предпочтительнее пользоваться несколько измененным алгоритмом, в
котором производная  аппроксимирована
разностным соотношением [2]
аппроксимирована
разностным соотношением [2]

Тогда в системе (15)-(17)
коэффициенты  и правые
части
и правые
части  запишутся
следующим образом [2]
запишутся
следующим образом [2]

Для начала счета необходимо знать
температуры  и
и  . Первый
временной ряд
. Первый
временной ряд  получается
соответствующей дискретизацией входной функции
получается
соответствующей дискретизацией входной функции  . Температуры
. Температуры  на
фиктивном
на
фиктивном  слое
рассчитываются с помощью выражения для разностной аппроксимации граничного
условия, например, типа (7). Заметим, что если
слое
рассчитываются с помощью выражения для разностной аппроксимации граничного
условия, например, типа (7). Заметим, что если  , значения
, значения  находятся
из решения прямой задачи теплопроводности.
находятся
из решения прямой задачи теплопроводности.
Описанная схема аппроксимации (15) -
(17) имеет второй порядок по времени и первый по пространству. Можно получить
разностные уравнения, имеющие второй порядок также и по пространственной
переменной [7].
Рассмотренный алгоритм, несмотря на
неявную аппроксимацию уравнения теплопроводности, может обладать только слабой
устойчивостью на конечном числе шагов по координате х (подробнее см. [8]).
2.3 Метод квазиобращения
Рассматривается граничная
обратная задача для одномерного параболического уравнения второго порядка
(уравнения теплопроводности), которая состоит в восстановлении граничного
режима по данным измерений внутри расчетной области [4]. Такая задача
принадлежит к классу условно корректных и для ее устойчивого решения
привлекаются методы регуляризации. Как один из известных методов решения таких
задач рассмотрим метод квазиобращения, когда задача рассматривается как
эволюционная по пространственной переменной. Использование метода
квазиобращения ведет, в частности, к известной гиперболической регуляризации
граничной обратной задачи [4]. Он основан на некотором возмущении исходного
уравнения, причем для возмущенного уравнения задача уже корректна. Здесь
параметр возмущения выступает в качестве параметра регуляризации.
При рассмотрении граничной
обратной задачи для одномерного параболического уравнения второго порядка метод
квазиобращения может быть основан на рассмотрении исходной задачи как задачи
для эволюционного уравнения первого порядка. Вторая возможность связана с
рассмотрением исследуемой граничной обратной задачи как задачи с начальными
данными для эволюционного уравнения второго порядка. В качестве эволюционной
переменной выступает пространственная переменная. Поэтому мы и говорим в этом
случае о продолжении по пространственной переменной в граничной обратной
задаче.
Рассмотрим граничную обратную задачу
для параболического уравнения при продолжении решения по пространственной
переменной, которая выступает в качестве временной переменной [4]. Задача
ставится следующим образом. Решение  определяется из уравнения
определяется из уравнения
 (18)
(18)
дополненного начальными условиями по
переменным х и t следующем вида
 (19)
(19)
 (20)
(20)
 .(21)
.(21)
В граничной обратной задаче (18) -
(21) делаем замену переменных: х заменяется на t, t - на х ( ), искомое
решение обозначим
), искомое
решение обозначим  (=
(= ) [4]. Для
нахождения
) [4]. Для
нахождения  получим
задачу [4]
получим
задачу [4]
 (22)
(22)
 (23)
(23)
 (24)
(24)
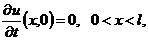 (25)
(25)
где в новых обозначениях функции  соответствует
соответствует
 .
.
Задача (22)-(25) записывается в виде
операторного уравнения [4]
 (26)
(26)
с начальными условиями (24), (25).
Оператор  определяется
выражением [4]
определяется
выражением [4]
 (27)
(27)
с областью определения [4]
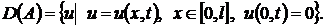
Введенный оператор  не является
самосопряженным и не знакоопределен в
не является
самосопряженным и не знакоопределен в  .
.
Для приближенного решения обратной
задачи (24)-(26) применено метод квазиобращения [1, 4]. Использован один из
вариантов в метода квазиобращения и приближенное решение  определено
из возмущенного уравнения [4]
определено
из возмущенного уравнения [4]
 (28)
(28)
дополненного начальными условиями
 (29)
(29)
 .(30)
.(30)
Сопряженный в  к
к  оператор на
основании (27) определяется выражением [4]
оператор на
основании (27) определяется выражением [4]
 (31)
(31)
Причем

Вариант метода квазиобращения
(28)-(30) с учетом (27), (31) соответствует решению следующей задачи [4]
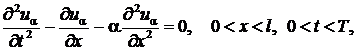 (32)
(32)
 (33)
(33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
Тем самым, метод квазиобращения
приводит к известному в вычислительной практике гаперболическому возмущению
(уравнение (32)) исходного параболического уравнения (22) [4].
Теорема 1. Для решения краевой
задачи (32)-(36) справедлива априорная оценка [4]
 (37)
(37)
Можно использовать и некоторые
другие варианты метода квазиобращения. Например, приближенное решение
определяется из уравнения [4]
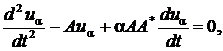 (38)
(38)
дополненного условиями (29), (30).
Поэтому приближенное решение  в
соответствии с (27), (31) определяется из уравнения [4]
в
соответствии с (27), (31) определяется из уравнения [4]
 (39)
(39)
и условий (33)-(36). Аналогично
теореме 1 формулируется следующее утверждение.
Теорема 2. Для решения краевой
задачи (33)-(36), (39) справедлива априорная оценка [4]
 (40)
(40)
Рассмотрим теперь предложенные
варианты метода квазиобращения на сеточном уровне. Для простоты ограничимся
одномерной граничной задачей [4]. Для перехода к разностной задаче вводится
равномерная сетка  где
где  - множество
внутренних узлов, а
- множество
внутренних узлов, а  - множество
граничных узлов [4]. Операторы
- множество
граничных узлов [4]. Операторы  ,
,  вводятся обычным образом. Пусть в
безиндексных, обозначениях [4]
вводятся обычным образом. Пусть в
безиндексных, обозначениях [4]

с областью определения

Скалярное произведение и норма в
сеточном гильбертовом пространстве  задано в виде [4]
задано в виде [4]

Для сопряженного оператора  получено
[4]
получено
[4]

Причем

Для оператора 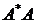 имеем [4]
имеем [4]

Разностное решение задачи (28)-(30)
определено из уравнения [4]
 (41)
(41)
для  , дополненного начальными условиями
, дополненного начальными условиями
 (42)
(42)
 (43)
(43)
При приближенном решении задачи
(41)-(43) используется равномерная сетка по времени с шагом  .
Рассматривается разностная схема [4]
.
Рассматривается разностная схема [4]

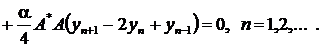 (44)
(44)
Для исследования схемы (44) на
устойчивость вводятся обозначения [4]
 (45)
(45)
Тогда разностная схема (45)
записывается в виде
 (46)
(46)
Умножая разностное уравнение (46)
скалярно на

получено [4]
 (47)
(47)
Правая часть (47) оценивается
следующим образом [4]:


Выберем  и с учетом
последнего это неравенства из (47) получаем [4]
и с учетом
последнего это неравенства из (47) получаем [4]
 (48)
(48)
Используя при  оценку
оценку

и выбирая  из (48)
получена априорная оценка [4]
из (48)
получена априорная оценка [4]
 (49)
(49)
Где 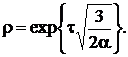 (50)
(50)
Тем самым доказано следующее
утверждение [4].
Теорема 3. Для разностной схемы (44)
при  справедлива
оценка (45), (48).
справедлива
оценка (45), (48).
Вариант метода квазиобращения (38)
соответствует решению уравнения [4]

начальными условиями (42), (43). При
численной реализации используется схема [4]
 (51)
(51)
Теорема 4. Разностная схема (51)  - устойчива
с [4]
- устойчива
с [4]

для нее справедлива априорная оценка
[4]
 (52)
(52)
Приведенные выше результаты
использованы при решении конкретных обратных задач в последующих частях работы.
Глава 3. Численные методы решения граничных
обратных задач для уравнения параболического типа
.1 Обратная граничная задача для линейно
упругого режима фильтрации
Рассмотрим граничную обратную задачу
при упругом режиме фильтрации жидкости в однородной пористой среде [9-11].
Теория упругого режима фильтрации жидкости сформулирована в работах [12, 13].
Для решения задачи используем численные методы [2]. Пористая среда считается
однородным объектом  и на
и на 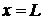 граничные
условия известны (Рис. 3).
граничные
условия известны (Рис. 3).

Рис.
1.3. Схема расположения добывающей (1) и наблюдательной (2) скважин (ДС, НС)
В точке 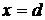 ,
, 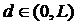 , заданы
значения давления жидкости, т.е. "исходные данные" -
, заданы
значения давления жидкости, т.е. "исходные данные" -  и начальное
распределение давления
и начальное
распределение давления  . Требуется
определить давление в точке
. Требуется
определить давление в точке 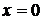 .
.
Данная постановка может быть
интерпретирована как определение характерных параметров в нефтедобывающей
скважине. Задача при этом сводится к определению давления в добывающем скважине
(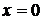 ) на основе
измерений давления в наблюдательной скважине (
) на основе
измерений давления в наблюдательной скважине ( ) и режима изменения давления на
границе пласта.
) и режима изменения давления на
границе пласта.
Таким образом, обратная задача для
теории упругого режима фильтрации ставится так:
уравнение пьезопроводности
 (53)
(53)
дополнительные условия
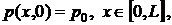 (54)
(54)
 , (55)
, (55)
 (56)
(56)
где  - пьезопроводность пласта,
- пьезопроводность пласта,  -
начальное пластовое давление.
-
начальное пластовое давление.
Требуется найти давление в
добывающей скважине, т.е.  .
.
Для того, чтобы подготовить исходные
данные для решения обратной задачи, т.е.  в (56), сначала решим прямую задачу
для (53). При этом граничные условия имеют вид
в (56), сначала решим прямую задачу
для (53). При этом граничные условия имеют вид
 (57)
(57)
 ,(58)
,(58)
где  - скорость фильтрации,
- скорость фильтрации,  -
проницаемость пласта,
-
проницаемость пласта,  - вязкость
жидкости.
- вязкость
жидкости.
Для решения задачи (53), (54), (57),
(58) применяем метод конечных разностей. В области  вводим
сетку
вводим
сетку
 .
.
Уравнение (53) на сетке  аппроксимируем
неявной конечно-разностной схемой с точностью
аппроксимируем
неявной конечно-разностной схемой с точностью 

Или
 ,(59)
,(59)
где  ,
,  ,
,  .
.
Аппроксимируем начальные и граничные
условия (54), (55), (58)
 (60)
(60)
 (61)
(61)
 ,
,  (62)
(62)
Для решения (59) с (60)-(62)
используем метод прогонки [6]. Решение задачи ищется в виде
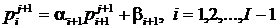 , (63)
, (63)
 ,
,  ,
,  .(64)
.(64)
Так как, при  из (63)
имеем
из (63)
имеем

с дрогой стороны из (62)
 .
.
Поэтому
 ,
,  . (65)
. (65)
Начального условия (60) получается
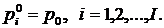
После того, как из (64) и (65)
найдены можно  и
и
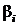 для
всех
для
всех 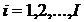 , зная, что
, зная, что  из (63)
можно найти
из (63)
можно найти  .
.
В качестве исходных данных
(дополнительных условии) для обратной задачи принимаются значения давления в
точке  ,
,  ,
,  -
дискретные значения времени.
-
дискретные значения времени.
Погрешность в задании исходных
данных (56) моделировалась следующим образом

 (66)
(66)
где  ,
,  - возмущенные величины
- возмущенные величины  ,
,  -
погрешность,
-
погрешность,  -
равномерно распределенная на
-
равномерно распределенная на 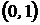 случайная величина,
случайная величина,  - нормально
распределенная случайная величина.
- нормально
распределенная случайная величина.
Теперь уравнение (59) решим в
области 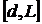 , с
граничным условием
, с
граничным условием
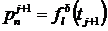 ,
,  .(67)
.(67)
Зная  в области
в области 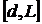 , можно
продолжить решения в область
, можно
продолжить решения в область 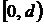 . Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а). Тогда
. Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а). Тогда  можно
определить, используя уравнение
можно
определить, используя уравнение
 . (68)
. (68)
Значения 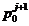 дает нам
искомое граничное условие. Из
дает нам
искомое граничное условие. Из  и
и  можно определить
можно определить  .
.
В расчетах использованы следующие
исходные данные:  м2,
м2,
 м2/с,
м2/с,
 м/с,
м/с,  ,
,  МПа,
МПа,  Па·с.
Па·с.
Результаты расчетов при различном
уровне погрешностей в исходных данных показаны на рис. 4-18. Для получения
устойчивых результатов применяется метод пошаговой регуляризации по времени и
сглаживание "исходных данных" [2, 3]. При  полученные
кривые имеют устойчивый характер (рис. 4-6). С увеличением расстояния
полученные
кривые имеют устойчивый характер (рис. 4-6). С увеличением расстояния  , возникает
неустойчивый характер решения обратной граничной задачи (рис. 7). К тому же,
случайные возмущения исходных данных приводят к существенной неустойчивости
процесса вычисления (рис. 8). Из рис. 9 и 10 видно, что с использованием метода
пошаговой регуляризации по времени получено условно устойчивое решение. При
одновременном использовании метода пошаговой регуляризации и сглаживания исходных
данных улучшается устойчивость решения (рис. 11-18), чем при использовании
только пошаговой регуляризации. Для сглаживания исходных данных использованы
сглаживающие сплайн функции пакета spaps (Spline Toolbox) в среде Matlab 7.6.0
(R2008a).
, возникает
неустойчивый характер решения обратной граничной задачи (рис. 7). К тому же,
случайные возмущения исходных данных приводят к существенной неустойчивости
процесса вычисления (рис. 8). Из рис. 9 и 10 видно, что с использованием метода
пошаговой регуляризации по времени получено условно устойчивое решение. При
одновременном использовании метода пошаговой регуляризации и сглаживания исходных
данных улучшается устойчивость решения (рис. 11-18), чем при использовании
только пошаговой регуляризации. Для сглаживания исходных данных использованы
сглаживающие сплайн функции пакета spaps (Spline Toolbox) в среде Matlab 7.6.0
(R2008a).

Рис. 4. Результаты решения обратной
задачи для точных значений входных данных при  ,
, 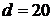 м,
м,  , (
, (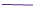 давление, определенное по решению
прямой задачи)
давление, определенное по решению
прямой задачи)

Рис. 5. Результаты решения обратной
задачи для точных значений входных данных при  ,
,  м,
м, 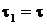 (
( как на Рис.
4)
как на Рис.
4)

Рис. 6. Результаты решения обратной
задачи для точных значений входных данных при  ,
,  м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис.7. Результаты решения обратной
задачи для точных значений входных данных при  ,
,  м,
м,  (─── как на Рис.
4)
(─── как на Рис.
4)

Рис. 8. Результаты решения обратной
задачи для возмущенных значений входных данных при 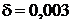 ,
, 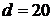 м,
м, 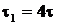 (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 9. Результаты решения обратной
задачи для возмущенных значений входных данных при 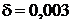 ,
, 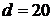 м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 10. Результаты решения обратной
задачи для возмущенных значений входных данных при 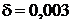 ,
, 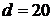 м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 11. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
, 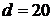 м,
м,  (─── как на Рис.
4)
(─── как на Рис.
4)

Рис. 12. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
, 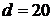 м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 13. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
, 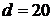 м,
м,  (──
как на Рис. 4)
(──
как на Рис. 4)

Рис. 14. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)

Рис. 15. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по нормальному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)

Рис. 16. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)

Рис. 17. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по нормальному закону) при  ,
,  м,
м,  (─── как на Рис.
4)
(─── как на Рис.
4)

Рис. 18. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по нормальному закону) при  ,
,  м,
м,  (─── как на Рис.
4)
(─── как на Рис.
4)
.2 Обратная граничная задача для нелинейно
упругого режима фильтрации
Рассмотрим граничную обратную задачу при
нелинейно-упругого режиме фильтрации жидкости [14]. В наиболее обобщенном виде
теория нелинейно-упругого режима фильтрации жидкости сформулирована в работах
[15, 16], в которых проницаемость и пористость пласта, плотность и вязкость жидкости
считаются экспоненциально зависящими от давления. В этих работах при
нелинейно-упругом режиме фильтрации жидкости получено уравнение относительно
давления в виде [15, 16]:
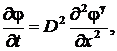 (69)
(69)
где  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 - первоначальное (при давлении
- первоначальное (при давлении  ) значения
проницаемости (м2), пористости и вязкости (МПа·с) соответственно;
) значения
проницаемости (м2), пористости и вязкости (МПа·с) соответственно;  - время, с;
- время, с;
 - линейная
координата, м;
- линейная
координата, м;  - текущее
давление, МПа;
- текущее
давление, МПа;  -
коэффициент сверхсжимаемости жидкости, МПа-1;
-
коэффициент сверхсжимаемости жидкости, МПа-1;  ,
,  ,
,  - коэффициенты изменения
проницаемости, пористости и вязкости соответственно, МПа-1.
- коэффициенты изменения
проницаемости, пористости и вязкости соответственно, МПа-1.
Пористая среда считается однородным
объектом 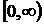 и на
и на  граничные
условия известны. В точке
граничные
условия известны. В точке  ,
,  , заданы
значения давления жидкости, т.е. "исходные данные" -
, заданы
значения давления жидкости, т.е. "исходные данные" -  и начальное
распределение давления
и начальное
распределение давления  . Требуется
определить давление в точке
. Требуется
определить давление в точке  . Данная постановка как и в линейном
случае (§ 1) может быть интерпретирована как определение характерных параметров
в нефтедобывающей скважине (Рис.3). Задача при этом сводится к определению поля
давления в области
. Данная постановка как и в линейном
случае (§ 1) может быть интерпретирована как определение характерных параметров
в нефтедобывающей скважине (Рис.3). Задача при этом сводится к определению поля
давления в области  и скорости
фильтрации в добывающей скважине (
и скорости
фильтрации в добывающей скважине ( ) на основе измерений давления в
наблюдательной скважине (
) на основе измерений давления в
наблюдательной скважине ( ) и режима
изменения давления на границе пласта.
) и режима
изменения давления на границе пласта.
Таким образом, граничная обратная
задача для нелинейно-упругого режима фильтрации ставится так:
уравнение пьезопроводности
 (70)
(70)
дополнительные условия
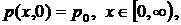 (71)
(71)
 (72)
(72)
 (73)
(73)
Условия (71)-(73) относительно 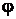 запишем как
запишем как
 (74)
(74)
 (75)
(75)
 (76)
(76)
где  .
.
Требуется найти давление и скорость
фильтрации в добывающей скважине (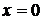 ).
).
Для того чтобы подготовить исходные
данные для решения обратной задачи, т.е.  в (75), сначала решим прямую задачу
для (70). При этом граничное условие имеет вид
в (75), сначала решим прямую задачу
для (70). При этом граничное условие имеет вид
 (77)
(77)
или в обозначениях относительно 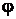 :
:
 (78)
(78)
где 
 - массовый расход на единицу
площади поперечного сечения пласта (т. е.
- массовый расход на единицу
площади поперечного сечения пласта (т. е.  ).
).
Для решения прямой задачи (70),
(73), (76), (78) применим метод конечных разностей. В области  вводим
сетку
вводим
сетку 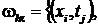
 , где
, где  - некоторая характерная длина
пласта, которая принимается так, чтобы граница возмущенной зоны не доходила до
- некоторая характерная длина
пласта, которая принимается так, чтобы граница возмущенной зоны не доходила до  . Сеточное
решение, соответствующее точке
. Сеточное
решение, соответствующее точке  , обозначим через
, обозначим через  .
.
Нелинейное уравнение (70) на сетке  аппроксимируем
неявной конечно-разностной схемой с точностью
аппроксимируем
неявной конечно-разностной схемой с точностью  [6]:
[6]:

Или
 (79)
(79)
где  ,
,  ,
,  ,
, 
 .
.
Аппроксимируем начальные и граничные
условия (74), (76), (78)
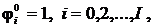 (80)
(80)
 (81)
(81)
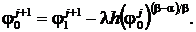 (82)
(82)
Для решения (79) с (80)-(82)
используем метод прогонки [6]. Решение задачи ищется в виде:

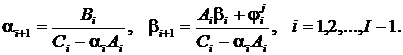
Сеточное решение  определяется
через
определяется
через  следующим
образом
следующим
образом

В качестве исходных данных для
обратной задачи принимаются значения давления в точке  , т.е.
, т.е.  ,
,  -
дискретные значения времени.
-
дискретные значения времени.
Погрешность в задании исходных данных (72)
задается в виде (66).
Теперь в области  решим
прямую задачу (72), (74), (75), (76). Для решения (70), (74)-(76) аналогично
применим метод конечных разностей. Зная
решим
прямую задачу (72), (74), (75), (76). Для решения (70), (74)-(76) аналогично
применим метод конечных разностей. Зная 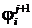 в области
в области  , можно
продолжить решение в область
, можно
продолжить решение в область  . Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а) [2]. Тогда
. Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а) [2]. Тогда  можно
определить, используя уравнение
можно
определить, используя уравнение
 (83)
(83)
Значения  дает нам
искомое граничное условие. Из
дает нам
искомое граничное условие. Из  и
и  можно определить
можно определить  .
.
В расчетах использованы следующие
исходные данные:  м2,
м2,
 м2/с,
м2/с,
 м/с,
м/с,  ,
,  МПа,
МПа,  Па·с,
Па·с,  кг/м3.
кг/м3.
Результаты расчетов при различном
уровне погрешностей в исходных данных показаны на Рис.19-1.32. При  полученные
кривые имеют более устойчивый характер (Рис. 19, 1.20). С увеличением расстояние
полученные
кривые имеют более устойчивый характер (Рис. 19, 1.20). С увеличением расстояние
 , возникает
неустойчивость решения (Рис. 21). Для устранения неустойчивости применяем метод
пошаговой регуляризации, что дает условно устойчивое решение (Рис. 22). Однако
случайные возмущения исходных данных приводят к существенной неустойчивости
процесса вычисления (Рис.23, 1.24). На Рис. 25-1.28 представлены решения с
использованием метода пошаговой регуляризации. Для получения более устойчивых
результатов одновременно применены методы пошаговой регуляризации и сглаживании
исходных данных. Эти результаты показаны на Рис. 29-32.
, возникает
неустойчивость решения (Рис. 21). Для устранения неустойчивости применяем метод
пошаговой регуляризации, что дает условно устойчивое решение (Рис. 22). Однако
случайные возмущения исходных данных приводят к существенной неустойчивости
процесса вычисления (Рис.23, 1.24). На Рис. 25-1.28 представлены решения с
использованием метода пошаговой регуляризации. Для получения более устойчивых
результатов одновременно применены методы пошаговой регуляризации и сглаживании
исходных данных. Эти результаты показаны на Рис. 29-32.

Рис. 19. Результаты решения обратной
задачи для точных значений давления при  ,
, 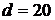 м,
м,  (─── как на Рис.
4)
(─── как на Рис.
4)

Рис. 20. Результаты решения обратной
задачи для точных значений давления при  ,
,  м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 21. Результаты решения обратной
задачи для точных значений давления при  ,
,  м,
м,  (───
как на Рис.4)
(───
как на Рис.4)
Рис. 22. Результаты решения обратной
задачи для точных значений давления при  ,
,  м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 23. Результаты решения обратной
задачи для давления при  ,
,  м,
м,  (
─── как на Рис. 4)
(
─── как на Рис. 4)

Рис. 24. Результаты решения обратной
задачи для давления при  ,
,  м,
м, 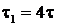 (───
как на Рис. 4)
(───
как на Рис. 4)
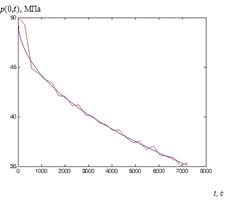
Рис. 25. Результаты решения обратной
задачи для входных данных при  ,
,  м,
м, 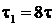 (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 26. Результаты решения обратной
задачи для входных данных при  ,
, 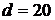 м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 27. Результаты решения обратной
задачи для входных данных при  ,
, 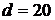 м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 28. Результаты решения обратной
задачи для входных данных при  ,
,  м,
м,  (───
как на Рис. 4)
(───
как на Рис. 4)

Рис. 29. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)

Рис. 30. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)

Рис. 31. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при  ,
,  м,
м,  (── как на Рис. 4)
(── как на Рис. 4)
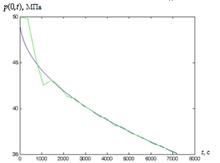
Рис. 32. Результаты решения обратной
задачи для сглаженных значений давления (исходные данные содержали ошибки,
распределенные по равномерному закону) при 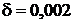 ,
,  м,
м,  (──
как на Рис. 4)
(──
как на Рис. 4)
3.3 Обратная граничная задача для
линейно упруго-пластического режима фильтрации
Рассмотрим граничную обратную задачу при линейно
упруго-пластическом режиме фильтрации жидкости в однородной пористой среде.
Теория упруго-пластического режима фильтрации жидкости сформулирована в работах
[17-19].
Уравнения упруго-пластической фильтрации
жидкости в одномерном случае [17, 18] имеют вид
 (84)
(84)
 (85)
(85)
где  - соответствуют процессам понижения
и восстановления давления,
- соответствуют процессам понижения
и восстановления давления,  - коэффициенты пьезопроводности (
- коэффициенты пьезопроводности ( ),
), 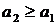 .
.
В режиме понижения давления обратная граничная
задача для уравнения (84) будет аналогичной для уравнения (53), рассмотренная в
параграфе 1.2. Поэтому, предоставляет интерес обратная граничная задача для
уравнения (85) в режиме восстановления давления.
Пористая среда считается однородным
объектом 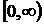 и на
и на  граничные
условия известны. В точке
граничные
условия известны. В точке 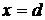 ,
,  , заданы
значения давления жидкости, т.е. "исходные данные" -
, заданы
значения давления жидкости, т.е. "исходные данные" -  и начальное
распределение давления
и начальное
распределение давления  . Требуется
определить давление в точке
. Требуется
определить давление в точке 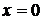 .
.
Таким образом, обратная задача для
теории линейно упругопластического режима фильтрации ставиться так:
уравнение пьезопроводности
 (86)
(86)
дополнительные условия
 (87)
(87)
 (88)
(88)
 (89)
(89)
где  - решение уравнения (84) в
последний момент
- решение уравнения (84) в
последний момент  понижения
давления.
понижения
давления.
Требуется найти кривые
восстановления давления в добывающей скважине, т.е.  .
.
Для того чтобы подготовить исходные
данные для решения обратной задачи, т.е.  в (89), сначала решим прямую задачу
для (86). При этом граничные условия имеют вид
в (89), сначала решим прямую задачу
для (86). При этом граничные условия имеют вид
 (90)
(90)
где  - монотонно убывающая функция
времени,
- монотонно убывающая функция
времени,  - некоторая
постоянная,
- некоторая
постоянная, 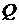 - дебит
скважины.
- дебит
скважины.
Выбор 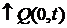 в виде убывающей функции
объясняется тем, что после закрытия скважины происходит остаточный приток
жидкости, в результате чего динамический уровень жидкости в скважине
поднимается до статического. Остаточный приток жидкости, как известно из
практики нефтедобычи, представляет собой монотонно убывающую функцию по
времени.
в виде убывающей функции
объясняется тем, что после закрытия скважины происходит остаточный приток
жидкости, в результате чего динамический уровень жидкости в скважине
поднимается до статического. Остаточный приток жидкости, как известно из
практики нефтедобычи, представляет собой монотонно убывающую функцию по
времени.
Для решения задачи (86), (87), (90)
применяем метод конечных разностей. В области  вводим сетку
вводим сетку
 ,
,
где  - характерная длина пористой среды.
- характерная длина пористой среды.
Уравнение (87) на сетке  аппроксимируем
неявной конечно-разностной схемой с точностью
аппроксимируем
неявной конечно-разностной схемой с точностью  :
:
 ,(91)
,(91)
где 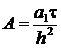 ,
,  ,
,  .
.
Аппроксимируем начальные и граничные
условия (86), (87), (90)
 (92)
(92)
 .(93)
.(93)
Для решения (91) с (92), (93)
используем метод прогонки [6]. Решение задачи ищется в виде:
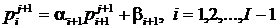 ,(94)
,(94)
 ,
,  ,
,  .(95)
.(95)
Так как, при  из (94)
имеем
из (94)
имеем

и с дрогой стороны из (93)
 ,
,
Поэтому
 ,
,  . (96)
. (96)
После того, как из (95) и (96)
найдены  и
и
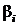 для
всех
для
всех  , зная, что
, зная, что  из (94)
можно найти
из (94)
можно найти  .
.
В качестве исходных данных
(дополнительных условий) для обратной задачи принимаются значения давления в
точке  ,
,  ,
,  -
дискретные значения времени.
-
дискретные значения времени.
Теперь уравнение (86) решим в
области  , с
граничным условием
, с
граничным условием
 ,
,  .(97)
.(97)
Зная  в области
в области  , можно
продолжить решение в область
, можно
продолжить решение в область  . Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а). Тогда
. Для этого можно использовать
Т-образный четырехточечный шаблон (Рис.1 а). Тогда  можно
определить, используя уравнение
можно
определить, используя уравнение
 . (98)
. (98)
Значения 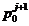 дает нам
искомое граничное условие.
дает нам
искомое граничное условие.
В расчетах использованы следующие
исходные данные:  м2,
м2,
 м/с,
м/с,  ,
,  МПа,
МПа,  Па·с,
Па·с,  .
.
Результаты расчетов восстановления
давления на границе  при
различном уровне погрешностей в исходных данных показаны на Рис33-44. Для
получения устойчивых результатов применялся метод пошаговой регуляризации по
времени [2, 3]. Это приводит к тому, что при
при
различном уровне погрешностей в исходных данных показаны на Рис33-44. Для
получения устойчивых результатов применялся метод пошаговой регуляризации по
времени [2, 3]. Это приводит к тому, что при  полученное решение имеет устойчивый
характер (Рис. 33-36). Из рис 33, 35 видно, что при малых временах возникает
неустойчивый характер решения (Рис 33, 35). Из рисунков 34, 36 видно, что с
увеличением шага по времени
полученное решение имеет устойчивый
характер (Рис. 33-36). Из рис 33, 35 видно, что при малых временах возникает
неустойчивый характер решения (Рис 33, 35). Из рисунков 34, 36 видно, что с
увеличением шага по времени  неустойчивость решения при малых
временах ослабевает. Однако случайные возмущения исходных данных приводят к
существенной неустойчивости решения (Рис. 37-39). Из рисунков 40-44 видно, что
с использованием метода пошаговой регуляризации по времени получено
относительно устойчивое решение.
неустойчивость решения при малых
временах ослабевает. Однако случайные возмущения исходных данных приводят к
существенной неустойчивости решения (Рис. 37-39). Из рисунков 40-44 видно, что
с использованием метода пошаговой регуляризации по времени получено
относительно устойчивое решение.

Рис. 33. Результаты решения обратной
задачи для точных исходных данных при  ,
, 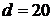 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)

Рис. 34. Результаты решения обратной
задачи для точных исходных данных при  ,
, 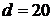 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)

Рис. 35. Результаты решения обратной
задачи для точных исходных данных при  ,
,  м,
м,  ,
,  м2/с,
м2/с,  м2/с
( ── как на Рис. 4)
м2/с
( ── как на Рис. 4)

Рис. 36. Результаты решения обратной
задачи для точных исходных данных давления при  ,
,  м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)

Рис. 37. Результаты решения обратной
задачи для точных исходных данных при  ,
, 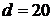 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)

Рис. 38. Результаты решения обратной
задачи для точных исходных данных при  ,
, 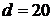 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)

Рис. 39. Результаты решения обратной
задачи для точных исходных данных при 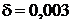 ,
, 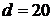 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)
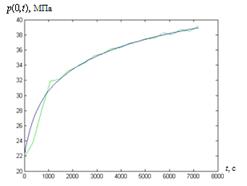
Рис. 40. Результаты решения обратной
задачи для точных исходных данных при 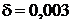 ,
, 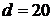 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 4)
м2/с
(── как на Рис. 4)
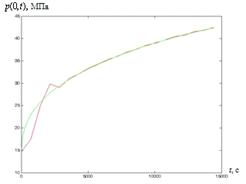
Рис. 41. Результаты решения обратной
задачи для точных исходных данных при 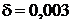 ,
,  м,
м,  ,
, 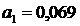 м2/с,
м2/с,  м2/с
(── давление, определенное по решению прямой задачи)
м2/с
(── давление, определенное по решению прямой задачи)
Рис. 42. Результаты решения обратной
задачи для точных исходных данных при 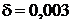 ,
,  м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 41)
м2/с
(── как на Рис. 41)

Рис. 43. Результаты решения обратной
задачи для точных исходных данных при 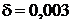 ,
,  м,
м,  ,
,  м2/с,
м2/с,  м2/с
( ── как на Рис. 41)
м2/с
( ── как на Рис. 41)

Рис. 44. Результаты решения обратной
задачи для точных исходных данных при 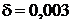 ,
, 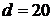 м,
м,  ,
,  м2/с,
м2/с,  м2/с
(── как на Рис. 41)
м2/с
(── как на Рис. 41)
Основные результаты и выводы
Решены обратные задачи по восстановлению
граничного режима при линейном и нелинейном режимах фильтрации жидкости в
пористой среде. Для получения устойчивых решений применен метод пошаговой
регуляризации. Для проверки чувствительности решения на ошибки исходных данных
проводились вычислительные эксперименты с зашумленными исходными параметрами.
Показано, что с увеличением расстояния между точками замера исходных данных и
границы области, где определяется решение обратной задачи, устойчивость решения
ухудшается. К ухудшению устойчивости также приводит зашумление исходных данных.
Для получения условно устойчивых решений исходные данные сглажены. Установлено,
что одновременное применение методов пошаговой регуляризации и сглаживания
исходных данных приводит к улучшению устойчивости решения, чем применение
только метода пошаговой регуляризации. Для сглаживания исходных данных
использована сглаживающая сплайн функция spaps среды Matlab.
Решена обратная граничная задача для
упруго-пластического режима фильтрации жидкости в пористой среде. Физическая
постановка задачи соответствует определению кривой восстановления давления в
нефтедобывающей скважине по данным изменения давления в контрольной скважине. В
режиме восстановления давления (второй этап упруго-пластической фильтрации)
определена динамика давления на границе области. Получена осцилляция решения
при малых временах, что значительно уменьшается при применении пошаговой
регуляризации. Как и при упругом режиме, увеличение расстояния между точками
"замера" исходных данных и определения решения, а также зашумленность
исходных данных приводит к ухудшению устойчивости решения. Условно устойчивое
решение получено при одновременном применении методов пошаговой регуляризации и
сглаживания исходных данных.
Литература
1. Латтес
Р., Лионс Ж.-Л. Метод квазиобращения и его приложения. М.: Мир, 1970. - 336 с.
. Алифанов
О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. - 280 с.
3. Beck
J.V., Blackwell B., St. Clair C.R., Jr. Inverse Heat Conduction. I11-posed
Problems. A Wiley-Interscience Publication, New York,
1985, 308 p.
. Самарский
А.А., Вабищевич П.Н. Численные методы решения обратных задач. - М.: ЛКИ, 2007.
- 480 с.
5. Hao D. Methods for inverse
heat conduction problems. - Peter Lang pub. Inc. 1998. - 249 p.
. Самарский А.А. Теория разностных схем.
- М.: Наука, 1989. - 616 с.
. Алифанов О.М., Артюхин Е.А., Панкратон
Б.М. Решение нелинейной обратной задачи теплопроводности. // Тепломассообмен-V.
Минск: ИТМО АН БССР. 1976. Т. 9. С. 94-103.
. Алифанов О.М. Идентификации процессов
теплообмена летательных аппаратов. М.: Машиностроение, 1979. - 216 с.
. Холияров Э.Ч., Эломов Ф.З. Об одной
обратной граничной задаче при упругом режиме фильтрации // Международная
научно-техническая конференция "Современные проблемы механики" (23-24
сентябрь). - Ташкент, 2009. С. 201-203.
. Хужаёров Б.Х., Холияров Э.Ч., Эломов
Ф.З. Граничная обратная задача при упругом режиме фильтрации однородной
жидкости в пористой среде // Сборник материалов IV-международной конференции
"Проблемы развития инженерных коммуникаций" 17-21.05.2010. г.
Самарканд. С. 48-50.
. Хужаёров Б.Х., Холияров Э.Ч., Эломов
Ф.З., Нурматов Г. Обратная задача по восстановлению граничных условий при
фильтрации жидкости в пористой среде // Сборник материалов Республиканской
научной конференции "Проблемы современной математики" 22-23.04.2011.
г. Карши. С. 547-550.
. Щелкачев В.Н. Основные уравнения
движения упругой жидкости в упругой пористой среде // Докл. АН СССР. Т. 52. №2.
1946. С. 103-106.
. Щелкачев В.Н. Разработка нефтеводоносных
пластов при упругом режиме. - М.: Гостоптехиздат, 1959.
. Хужаёров Б.Х., Холияров Э.Ч., Эломов
Ф.З. Решение обратных граничных задач для нелинейно-упругого режима фильтрации
жидкости // Сборник материалов Республиканской научно-технической конференции "Современное
состояние и перспективы развития информационных технологий" 5-6.09.2011.
г. Ташкент. С. 280-285.
. Николаевский В.Н. К построению
нелинейной теории упругого режима фильтрации жидкости и газа // ПМТФ. 1961. №4.
С. 67-76.
. Николаевский В.Н., Басниев К.С.,
Горбунов А.Т., Зотов Г.А. Механика насыщенных пористых сред. М.: Недра, 1970. -
339 с.
. Баренблатт Г.И., Крылов А.П. Об
упругопластическом режиме фильтрации // Изв. АН СССР. ОТН. 1955. №2. С. 5-13.
. Баренблатт Г.И. О некоторых задачах
восстановления давления и распространения волн разгрузки при
упруго-пластическом режиме фильтрации // Изв. АН СССР. ОТН. 1955. №2. С. 14-26.
19. Barenblatt G.I., Entov V.M.,
Ryzhik V.M. Theory of fluid flows through natural rocks. Kluwer
Academic Publishers. 1990. - 395 p.
. Мишин В.П., Алифанов О.М. Повышение
качества обработки теплонагруженных конструкций и обратные задачи теплообмена.
Ч. II. Практические приложения // Машиноведение. 1986. №6. С. 11-21.
. Тихонов А.Н., Арсенин В.Я. Методы
решения некорректных задач. М.: Наука. 1979. - 288 с.
. Лаврентьев М.М., Романов В.Г.,
Шишатский С.П. Некорректные задачи математической физики и анализа. - М.,
Наука, 1980. - 288 с.
. Романов В.Г. Обратные задачи
математической физики. - М.: Наука, 1984.
. Кабанихин С.И. Обратные и некорректные
задачи. - Новосибирск: Сибирское научное издательство, 2009. - 457 с.
. Хужаёров Б.Х., Холияров Э.Ч. Обратные
задачи упругопластической фильтрации жидкости в пористой среде // ИФЖ. 2007. Т.
80. №3. С. 86-93.
. Желтов Ю.П. Разработка нефтяных
месторождений. М.: Недра, 1986. - 332 с.
. Калиткин Н.Н. Численные методы. М.:
Наука, 1978, - 512 с.
. Сухарев А.Г., Тимохов А.В., Федоров
В.В. Курс методов оптимизации. - М.: ФИЗМАТЛИТ, 2005. -368 с.
29. Бабе
Г.Д., Бондарев Э.А., Воеводин А.Ф., Каниболотский М.А. Идентификация моделей
гидравлики. Новосибирск: Наука, 1980.
. Химмельблау
Д. Анализ процессов статистическими методами. - М.: Мир, 1973.
. Мэтьюз
Джон Г., Финк Куртис Д. Численные методы. Использование MATLAB. - М.:
Издательский дом "Вильяме", 2001. - 720 с.
. Дьяконов
В.П., Круглов В.В. Математические пакеты расширения MATLAB: Специальный
справочник. - СПб.: ПИТЕР, 2001. - 480 с.
. Кетков
Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 7: программирование, численные методы. -
СПб.: БХВ-Петербург, 2005. - 752с.
. Дьяконов
В.П. MATLAB 7.*/R2006/R2007: Самоучитель. - М.: ДМК Пресс, 2008. - 768 с.
. Горбунов
А.Т. Разработка аномальных нефтяных месторождений. М.: Недра, 1981.
. Горбунов
А.Т. Упруго-пластический режим фильтрации жидкости в пористых средах // Изв. АН
СССР. МЖГ. 1973. №5. С. 84-90.