Чисельне інтегрування методом Чебишева
МIНIСТЕРСТВО
ОСВIТИ І НАУКИ
НАЦІОНАЛЬНИЙ
ТРАНСПОРТНИЙ УНІВЕРСИТЕТ
Кафедра
Інформаційних систем і технологій
КУРСОВА
РОБОТА
з
дисципліни «Чисельні методи»
на
тему
«Чисельне
інтегрування методом Чебишева»
Київ
2016
ВСТУП
Актуальність теми роботи. При
дослідженні різноманітних процесів доволі часто виникає необхідність чисельного
інтегрування . В багатьох задачах, що пов’язані з аналізом, ідентифікацією,
оцінкою якості різних засобів та систем автоматики та управління, виникає
необхідність обчислення певних інтегралів.Крім того, часто чисельне
інтегрування стає проміжним етапом розв'язання багатьох складних задач за
допомогою розроблених чисельних методів. Це обумовлено тим, що чисельне
інтегрування вважається найбільш простим математичним об'єктом з добре
розробленою теоретичною базою.
Мета роботи:
продемонструвати
можливості
системи
Mathcad
при вивчені чисельного
інтегрування
методом Чебишева.
Для досягнення поставленої мети в
курсовій роботі сформульовані та вирішені наступні задачі дослідження:
Теоретичний аналіз методу
Чебишева.
Опис алгоритму знаходження інтеграла
методом Чебишева.
Реалізація алгоритму знаходження
інтеграла методом Чебишева за допомогою програми-функції Mathcad.
Об’єктом дослідження є процес
вивчення чисельного інтегрування
методом Чебишева.
Предметом дослідження є використання
СКМ Mathcad під час вивчення чисельного інтегрування
методом Чебишева.
Методи дослідження: Теоретичною
базою для вирішення сформульованого завдання є роботи з вищої математики,
чисельних методів розв’язання математичних задач, теорії алгоритмів. Поряд з
аналітичними розрахунками у роботі використовуються розрахунки виконані за
допомогою комп’ютерного програмного забезпечення.
Достовірність отриманих результатів
підтверджується тим, що вони не суперечать відомим теоретичним положенням, а
також перевіряються шляхом розв’язання поставленої задачі альтернативними
методами з наступним порівнянням результатів.
Особистий внесок. Аналіз теоретичних
матеріалів та практичні розрахунки було виконано автором самостійно, без
сторонньої допомоги.
Обсяг та структура роботи. Курсова
робота складається з вступу, двох розділів, висновків . Загальний обсяг
курсової роботи становить 17 сторінок, 9 формул, 17 рисунків, 1 таблиці, список
використаних джерел містить 3 найменування.
РОЗДІЛ 1. ТЕОРЕТИЧНИЙ
Точне знаходження первісної чи
інтеграла для довільних функцій - справа значно складніша, ніж диференціювання,
тобто пошук похідної. У загальному випадку подати інтеграл довільної функції в
елементарних функціях часто просто неможливо. Тому існує набір методів для
пошуку інтеграла окремих груп функцій.
Якщо функція 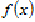 неперервна
на відрізку
неперервна
на відрізку 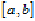 й відома її
первісна
й відома її
первісна 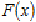 ,
то визначений інтеграл від а до в може бути обчислений за формулою Ньютона -
Лейбніца(1.1,1.2)
,
то визначений інтеграл від а до в може бути обчислений за формулою Ньютона -
Лейбніца(1.1,1.2)
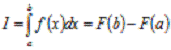 , (1.1)
, (1.1)
де 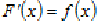 .
(1.2)
.
(1.2)
Графічно інтеграл визначається
площею, що обмежується графіком функції (1.3)
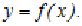 (1.3)
(1.3)
Але часто точно обчислити інтеграл
важко через велику складність аналітичних перетворень, а інколи це взагалі
неможливо (в випадках невласних інтегралів), чи коли підінтегральна функція
задана набором числових даних, наприклад, отриманих з експерименту.
Задача чисельного інтегрування
(numericalintegration) функції полягає в обчисленні значення визначеного
інтегралу на основі ряду значень підінтегральної функції. Формули чисельного
інтегрування часто називають квадратурними.
Найбільш відомими методами
знаходження визначених інтегралів є:
формули прямокутників;
методи Ньютона-Котеса, Гаусса,
Чебишева, які основані на використанні так званих квадратурних формул,
отриманих заміною  інтерполяційними
багаточленами;
інтерполяційними
багаточленами;
методи Монте-Карло, основані на
використанні статистичних моделей.
Особливо важливе значення мають
методи чисельного інтегрування функцій, в яких для знаходження наближеного
значення визначеного інтеграла використовуються значення підінтегральної
функції та її похідних у скінченній кількості точок, що належать переважно
проміжку інтегрування. Такі формули обчислення наближеного значення визначених
інтегралів називають формулами механічних квадратур, або квадратурними
формулами.
Потрібно
знайти
певний
інтеграл
за
квадратурною формулою Чебишева (1.4)
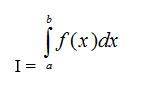 (1.4)
(1.4)
Розглянемо, що
являє
з себе взагалі квадратурна
формула, і як можна за її
допомогою
наближено
обчислити
інтеграл.
Відомо, що певний інтеграл функції
типу(1.5)
 (1.5)
(1.5)
чисельно є площа
криволінійної
трапеції
обмеженою
кривими=
0, y = a, y = b і y = f(x)(Рисунок1.1).

Рисунок 1.1 - Криволінійна трапеція
Якщо f (x) неперервна на відрізку
[a, b], і відома її первісна F (x), то визначений інтеграл від цієї функції в
межах від а до b може бути обчислений за, відомоївсім, формулою Ньютона
-Лейбніца: (1.6)
 (1.6)
(1.6)
де F '(x) = f (x), первісна.
Однак у багатьох
випадках
F (x) не може бути знайдена, або первісна
виходить
дуже
складною для обчислення.
Крім того, функція часто задається
таблично. Тому велике значення
набуває
наближене
і в першу чергу
чисельне
інтегрування.
Завдання чисельного інтегрування
полягає в знаходженні наближеного значення інтеграла по заданих або обчисленими
значеннями підінтегральної функції f (x) в деяких точках (вузлах) відрізка [a,
b].
Чисельне
визначення
однократного інтеграла називається
механічною
квадратурою,
а відповідні формули
чисельного
інтегрування
- квадратурними.
Замінюючи підінтегральної функції
будь-яким інтерполяційним
многочленом, ми отримаємо квадратурні
формули
виду(1.7)
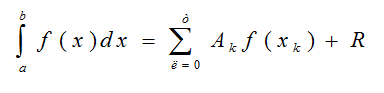 (1.7)
(1.7)
де
 - обрані
вузли
інтерполяції;
- обрані
вузли
інтерполяції;
 - коефіцієнти, що
залежать тільки від вибору вузлів, але не від виду функції (k = 0,1,2,
........, n).- залишковий член, або похибка
квадратурної
формули.
- коефіцієнти, що
залежать тільки від вибору вузлів, але не від виду функції (k = 0,1,2,
........, n).- залишковий член, або похибка
квадратурної
формули.
Відкидаючи
залишковий
член R, ми здійснюємо похибка
усічення.
При розрахунку до неї
додаються
ще
різні
похибки
округлення.
Розіб'ємо відрізок інтегрування [a,
b] на n рівних частин системою точок
 =
=  +
i..h; (I = 0,1,2, ......, n)
+
i..h; (I = 0,1,2, ......, n)
 = a;
= a;  =
b;= (b-a) / n;
=
b;= (b-a) / n;
і обчислимо підинтегральну
функцію
в отриманих вузлах
 = f (
= f ( );
(I = 0,1,2, ......, n).
);
(I = 0,1,2, ......, n).
Квадратурна формула
Чебишева.Розглянемо квадратурну
формулу виду: (1.8)
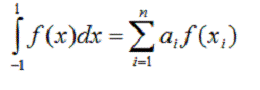 (1.8)
(1.8)
функцію f (x) будем
ошукати
у вигляді коли f (x) багаточлен виду f (x) =  +
+
 +
... +
+
... +  .
.
Проінтегрувавши, перетворивши і
підставивши значення
багаточлена
в вузлах.
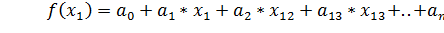
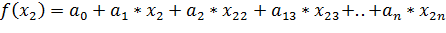
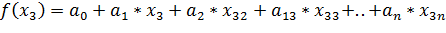
….
Отримаємо формулу Чебишева: (1.9)
 (1.9)
(1.9)
РОЗДІЛ 2. ПРАКТИЧНИЙ
Завдання 1 .
В СКМ Mathcad знайти інтеграл
функції методом Чебишева .(Рисунок 2.1)

Рисунок 2.1- Задана функція
Алгоритм виконання поставленої задачі:


Рисунок 2.2 - Транспонована матриця
Х
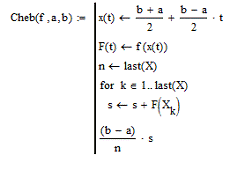
Рисунок 2.3 - Програма -функція
Таблиця 2.1 - Покрокові пояснення
алгоритму методу Чебишева, реалізованого засобами програмування СКМ Mathcad
|
Фрагмент програми-функції
|
Пояснення до фрагменту
програми-функції
|
|

|
Присвоюємо X(t) даний
обрахунок.
|
|
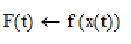
|
Присвоюємо X(t) значення
f(x(t))
|
|
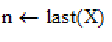
|
Використовуємо функцію last :
last (Х) - обчислення номера останнього елемента вектора Х; Змінній n надаємо
значення last (Х).
|
|

|
Запускаємо цикл, який рахує
кількість ітерацій
|
|
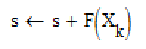
|
Змінній s надаємо значення [
 ] ]
|
|
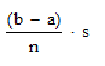
|
Результат
|
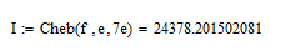
Рисунок 2.4 - Шуканий інтеграл
Тепер, потрібно виконати перевірку
,щоб прослідкувати правильність і точність методу Чебишева.Знаходимо інтеграл
за допомогою панелі Calculus натисканням кнопки зі значком певного
інтеграла.(Рисунок 2.5)

Рисунок 2.5 -Знаходження інтегралу
допомогою панелі Calculus .
Тепер прослідкуємо похибку.
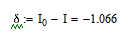
Рисунок 2.6 - Похибка методу
Чебишева
чисельний інтегрування
чебишев
Завдання 2
Аналогічно завданню 1,необхідно
переконатися в неточності метода Чебишева.
Тож ,знаходимо інтеграл функції
методом Чебишева (Рисунок 2.7)
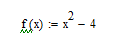
Рисунок 2.7 -Задана функція
Використовуючи програму-функцію
(Рисунок 2.3) знаходимо інтеграл.

Рисунок 2.8 - Шуканий інтеграл
Щоб переконатися в правильності,
зробимо перевірку(Рисунок 2.9)

Рисунок 2.9- Перевірка
І знову бачимо, що відповіді не
співпадають. Маємо похибку(Рисунок 2.10)

Рисунок 2.10 - Похибка методу
Чебишева
Завдання 3
В СКМ Mathcad знайти інтеграл
функції методом Чебишева .(Рисунок 2.11)
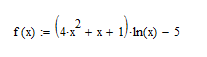
Рисунок 2.11- Задана функція
Задаємо межі інтегрування.(Рисунок
2.12)
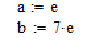
Рисунок 2.12- Межі інтегрування
Задаємо матрицю Xl,яка є
незмінною.(Рисунок 2.13)
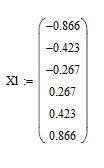
Рисунок 2.13- Матриця Xl.
Оператор collect допомагає в роботі
з дужками - якщо конкретніше, то для винесення через дужок загальних множників
для поліноміальних виразів.
Використавши, саме оператор
collect
записуємо розв’язок.(Рисунок 2.14)

Рисунок 2.14- Знаходження
інтегралу.Розв’язок.
Тепер, потрібно виконати перевірку .
Знаходимо інтеграл за допомогою панелі Calculus натисканням кнопки зі значком
певного інтеграла.(Рисунок 2.15)

Рисунок 2.15- Знаходження інтегралу
допомогою панелі Calculus .
І знову бачимо похибку.(Рисунок
2.16)
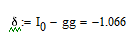
ВИСНОВКИ
Проведено теоретичний аналіз
знаходження інтеграла методом Чебишева.При дослідженні (знаходженні)
першочерговим питанням є питання підбору ,саме методу знаходження інтегралу.
Здійснено опис алгоритму знаходження
інтеграла
методом Чебишева.
Реалізовано алгоритм розв’язання
систем лінійних алгебраїчних рівнянь методом Чебишева за допомогою
програми-функції Mathcad. Можна побачити, що обчислення певних інтегралів з
допомогою квадратурных формул, зокрема за такою формулою Чебишева не дає нам
точного значення, лише близьке. Щоб обчислити інтеграл точніше треба вміти
правильно вибрати метод і формулу, через яку вестиметься розрахунок. Насправді
завжди можна вирішити завдання інтегрування аналітичним способом, тож необхідно
знати чисельні методи, хоч і вони можуть дати точного значення інтеграла.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
Крилов
В. І. Наближені обчислення інтегралів. - М.: Фізмат. Режим
доступу:://ukrbukva.net/print:page,1,34082-Priblizhennoe-vychislenie-opredelennogo-integrala-pri-pomoshi-kvadraturnoiy-formuly-Chebysheva
Самарский
А.А.,ГулинА.В.Численныеметоды: Учеб, пособие для вузов,- М.: Наука. Гл. ред.
физ-мат. лит., 1989.- 432 с.- Режим доступу:://samarskii.ru/books/book1989
Частина
1. Посібник для студентів інженерних спеціальностей НТУ / Укл. В.В. Гавриленко,
К.С. Величко, К.М. Алєксєєнко. - К.: НТУ, 2004. - 127 с.- Режим доступу:
://drive.google.com/folderview?id=0B_rqFBqk2ihkNUZ4ZnpjaExud28&usp=sharing