Топологічні простори та основні означення пов’язані з ними
Зміст
Вступ
. Топологія. Бази топології та
системи околів
. Замикання множини. Аксіоми
численності. Збіжні послідовності
.
Підпростір
топологічного простору. Прямий добуток топологічних просторів
.
Неперервні відображення топологічних просторів
. Компактність
в топологічних просторах
Висновки
Список використаної літератури
Вступ
Топологічний простір є тим
математичним поняттям, яке дає можливість розглянути граничний перехід і
неперервність відображення в найбільш загальному вигляді та узагальнює поняття
метричного простору.
Мета курсової роботи: ознайомитись з
поняттям топологічного простору, розглянути основні означення. Розглянути різні
типи топологічних просторів.
Завдання:
ознайомитись з основними означеннями
в топологічних просторах;
з’ясувати які є типи топологічних
просторів;
розглянути неперервні відображення
топологічних просторів.
Об’єктом курсової роботи є
топологічні простори.
Дана курсова робота складається із
п’яти розділів, вступу, висновків та використаної літератури. В першому розділі
мова йде про замкнені множини, відкриті множини, околи, базиси топології, про
скрізь щільні множини, про ніде не щільні множини. Зокрема, наведені означення
топологічного простору та бази топологічного простору; у другому розділі
наведені означення точок дотику, межових точок. Також наведені аксіоми
численності та розкриті поняття збіжних послідовностей; третій розділ розкриває
нам поняття підпростору топологічного простору. Дано означення прямого добутку
топологічного простору; у четвертому розділі висвітлене поняття неперервного
відображення в точці; п’ятий розділ присвячений компактності топологічних
просторів.
1. Топологія. Бази топології та
системи околів
Якщо  - довільна
непорожня множина, то позначимо через
- довільна
непорожня множина, то позначимо через 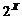 сукупність
всіх підмножин цієї множини,
сукупність
всіх підмножин цієї множини, 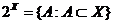 . Очевидно,
. Очевидно, 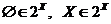 .
.
Означення 1. Клас τ підмножин
непорожньої множини 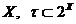 ,
називається топологією на множині
,
називається топологією на множині  , якщо він володіє властивостями
(задовольняє наступні умови):
, якщо він володіє властивостями
(задовольняє наступні умови):
) 
) якщо 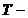 довільна
множина індексів, то
довільна
множина індексів, то
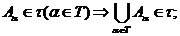
) при кожному справедливе 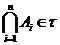 .
.
Впорядкована пара  при цьому
називається топологічним простором (т.п.). Множини із вказаного класу
при цьому
називається топологічним простором (т.п.). Множини із вказаного класу  називаються
відкритими множинами топологічного простору
називаються
відкритими множинами топологічного простору  .
.
Зазначимо, що умови 1 3
називаються інакше аксіомами топологічного простору
3
називаються інакше аксіомами топологічного простору  , який
будемо позначати через
, який
будемо позначати через  , якщо
відомо про яку топологію іде мова.
, якщо
відомо про яку топологію іде мова.
Означення 2. Множина  ,
називається замкнутою в т.п.
,
називається замкнутою в т.п.  , якщо
, якщо 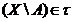 .
.
Спираючись на закони де
Моргана та властивості відкритих множин т.п.  можна довести наступні твердження:
можна довести наступні твердження:
а) 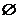 та
та 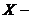 замкнуті
множини;
замкнуті
множини;
б) перетин довільної
сукупності замкнутих множин замкнутий;
в) об’єднання скінченної
сукупності замкнутих множин замкнуте.
Зауваження 1. Якщо задано
деякий клас підмножин множини 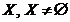 , який володіє вказаними вище
властивостями а), б), в), що характерні для замкнутих підмножин т.п., то на
основі цього класу визначається топологія
, який володіє вказаними вище
властивостями а), б), в), що характерні для замкнутих підмножин т.п., то на
основі цього класу визначається топологія  на
на  , яка
складається, як можна показати, з усіх найможливіших доповнень до
, яка
складається, як можна показати, з усіх найможливіших доповнень до  таких
підмножин.
таких
підмножин.
Приклад 1. Впорядкована пара 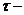 сукупність
всіх найможливіших об’єднань інтервалів разом із множиною
сукупність
всіх найможливіших об’єднань інтервалів разом із множиною 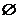 , є
топологічний простір.
, є
топологічний простір.
Виявляється, що на множині  , яка
містить більше одного елемента, можна задати різні топології, отримуючи різні
топологічні простори. Зокрема топологіями на множині
, яка
містить більше одного елемента, можна задати різні топології, отримуючи різні
топологічні простори. Зокрема топологіями на множині  є наступні
класи множин:
є наступні
класи множин: 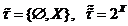 . При цьому
. При цьому  називається
антидискретною топологією, а
називається
антидискретною топологією, а  дискретною топологією. Якщо
дискретною топологією. Якщо 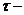 довільна
топологія на множині
довільна
топологія на множині  , вказаній
вище, то, очевидно,
, вказаній
вище, то, очевидно, 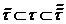 .
.
Якщо на множині 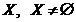 , задані
топології
, задані
топології 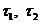 і
і 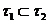 , то
топологія
, то
топологія 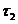 називається
сильнішою за топологію
називається
сильнішою за топологію 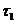 , а
топологія
, а
топологія 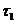 -
слабшою за топологію
-
слабшою за топологію 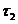 .
.
Означення 3. Підмножина  т.п.
т.п. 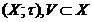 ,
називається околом точки
,
називається околом точки 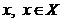 , якщо вона
включає деяку відкриту множину із
, якщо вона
включає деяку відкриту множину із  , що містить точку
, що містить точку  .
.
Сукупність всіх
околів точки  позначимо
через
позначимо
через 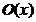
Означення 4. Довільна
відкрита множина 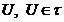 , т.п.
, т.п.  , яка
містить точку
, яка
містить точку 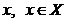 ,
називається відкритим околом точки
,
називається відкритим околом точки  .
.
Сукупність всіх відкритих
околів точки  позначимо
через
позначимо
через 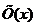 .
.
Очевидно, множина 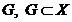 , є
відкритою в т.п.
, є
відкритою в т.п.  тоді і лише
тоді, коли вона є околом кожної своєї точки.
тоді і лише
тоді, коли вона є околом кожної своєї точки.
Теорема 1. Нехай кожному
елементу 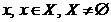 поставлено
у відповідність сукупність підмножин множини
поставлено
у відповідність сукупність підмножин множини  , які володіють властивостями.
, які володіють властивостями.
Тоді існує єдина топологія  на
на  , в якій
, в якій 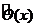 відіграє
роль сукупності всіх околів кожної точки
відіграє
роль сукупності всіх околів кожної точки  із
із  . Вказана топологія задається
рівністю.
. Вказана топологія задається
рівністю.
Доведення сформульованої
теореми можна знайти в підручнику [1].
Зауваження 2. Неважко
переконатися в тому, що сукупність 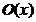 всіх околів довільної точки
всіх околів довільної точки  , т.п.
, т.п.  , володіє
властивостями типу 4)-7), які характерні для сукупностей підмножин множини
, володіє
властивостями типу 4)-7), які характерні для сукупностей підмножин множини  , вказаних в
попередній теоремі. Зазначимо, що теорема 1 дає можливість задати топологію на
множині
, вказаних в
попередній теоремі. Зазначимо, що теорема 1 дає можливість задати топологію на
множині  з допомогою
класів
з допомогою
класів 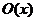 підмножин
множини
підмножин
множини  , про які
іде там мова.
, про які
іде там мова.
Означення 5. Клас 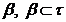 ,
називається базою топології
,
називається базою топології  на множині
на множині  , якщо кожна
відкрита непорожня множина
, якщо кожна
відкрита непорожня множина 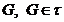 , являє собою об’єднання деякої
сукупності множин із цього класу.
, являє собою об’єднання деякої
сукупності множин із цього класу.
Приклад 2. Базою природної
топології  є сукупність
всіх найможливіших інтервалів разом із множиною
є сукупність
всіх найможливіших інтервалів разом із множиною 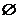 . Роль бази такої топології виконує
також зчисленна сукупність всіх найможливіших інтервалів, разом із множиною
. Роль бази такої топології виконує
також зчисленна сукупність всіх найможливіших інтервалів, разом із множиною 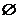 .
.
Теорема 2. Клас 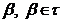 , є базою
топології
, є базою
топології  на множині
на множині  тоді і
тільки тоді, коли
тоді і
тільки тоді, коли 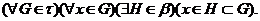
Необхідність. Якщо 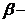 база
топології
база
топології  на
на 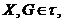 і
і 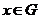 , то
, то 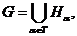 де
де 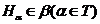 . Тому
. Тому 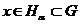 .
.
Достатність. Якщо клас 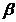 відкритих
множин,
відкритих
множин, 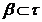 , володіє
властивістю (1), то
, володіє
властивістю (1), то 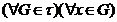
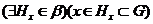 причому
причому . Отже,
. Отже,  , тобто
кожна множина
, тобто
кожна множина 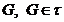 , є
об’єднанням множин із класу
, є
об’єднанням множин із класу 
Зауваження 3. На основі
попередньої теореми можна показати, що клас 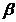 підмножин множини
підмножин множини  є базою
деякої топології
є базою
деякої топології  на
на  тоді і лише
тоді, коли виконуються умови:
тоді і лише
тоді, коли виконуються умови:
) множини  є
об’єднанням множин із класу
є
об’єднанням множин із класу 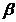 ;
;
) для довільних двох множин 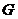 та
та 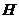 із класу
із класу 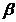 і кожної
точки
і кожної
точки 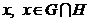 , існує
множина
, існує
множина 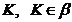 , така, що
, така, що 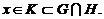 При цьому
вказана топологія
При цьому
вказана топологія  задається
однозначно класом множин
задається
однозначно класом множин 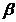 . Дві
топології на
. Дві
топології на  із спільною
базою співпадають.
із спільною
базою співпадають.
Означення 6. Сукупність 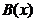 околів
точки
околів
точки 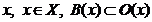 ,
називається базою системи
,
називається базою системи 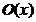 всіх околів
цієї точки із топологічного простору
всіх околів
цієї точки із топологічного простору  , якщо
, якщо 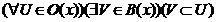 .
.
Приклад 3. В топологічному
просторі із природною топологією  на клас інтервалів утворює базу
системи
на клас інтервалів утворює базу
системи 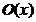 всіх околів
точки х. Ця база складається із зчисленної сукупності околів точки
всіх околів
точки х. Ця база складається із зчисленної сукупності околів точки  .
.
Теорема 3. Нехай в кожній
точці 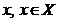 , задано
клас
, задано
клас 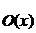 підмножин
множини
підмножин
множини  , який
задовольняє умови:
, який
задовольняє умови:
) 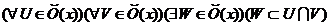 ;
;
) 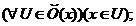
) 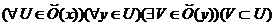 .
.
Тоді існує єдина топологія  на множині
на множині  , для якої
класи
, для якої
класи 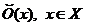 , є базами
системи всіх відкритих околів точки
, є базами
системи всіх відкритих околів точки  , а сукупність всіх множин із усіх
класів
, а сукупність всіх множин із усіх
класів 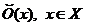 , є базою
, є базою 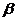 топології
топології  , причому
, причому  .
.
Доведення теореми 3 знову
можна знайти в підручнику  .
.
Зауваження 4. Можна
переконатися в тому, що сукупності всіх відкритих околів довільної
точки  топологічного
простору
топологічного
простору 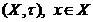 , володіють
властивостями типу 10-12), які характерні для сукупностей
, володіють
властивостями типу 10-12), які характерні для сукупностей 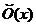 підмножин
множини
підмножин
множини  із
попередньої теореми.
із
попередньої теореми.
Теорема 3 також дає
можливість задати топологію на множині  , з допомогою класів
, з допомогою класів 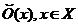 , підмножин
множини
, підмножин
множини  , які
задовольняють умови 10-12) (і які для цієї топології будуть базами системи всіх
відкритих околів кожної точки
, які
задовольняють умови 10-12) (і які для цієї топології будуть базами системи всіх
відкритих околів кожної точки 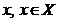 .
.
2. Замикання множини. Аксіоми
численності. Збіжні послідовності
Нехай 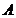 - довільна
непорожня підмножина т.п.
- довільна
непорожня підмножина т.п. 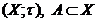 .
.
Означення 1. Перетин усіх найможливіших
замкнутих множин із т.п.  , які
включають множину
, які
включають множину 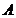 ,
називаються замиканнями цієї множини і позначаються через
,
називаються замиканнями цієї множини і позначаються через 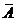 або
або  .
.
Оскільки вказаний вище
перетин є замкнута множина, то і 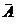 - замкнута множина, причому це
найвужча замкнута множина, що включає
- замкнута множина, причому це
найвужча замкнута множина, що включає 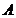 .
.
Очевидно, 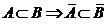 і
і 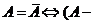 замкнута
множина). Операція замикання володіє властивостями:
замкнута
множина). Операція замикання володіє властивостями: 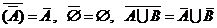 . Вони
доводяться на основі означення замикання.
. Вони
доводяться на основі означення замикання.
Нехай 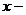 точка т.п.
точка т.п.  , і
, і 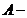 підмножина
множини
підмножина
множини 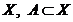 .
.
Означення 2. Точка  називається точкою дотику множини
називається точкою дотику множини 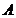 , якщо
, якщо 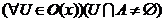 ;
;
точка  називається
ізольованою точкою множини
називається
ізольованою точкою множини 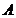 , якщо
, якщо 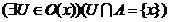 .
.
Очевидно, точка дотику
множини 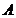 - це або
ізольована точка множини
- це або
ізольована точка множини 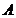 або її
гранична точка. Зрозуміло, що сукупність всіх точок дотику множини
або її
гранична точка. Зрозуміло, що сукупність всіх точок дотику множини 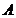 співпадає
із її замиканням.
співпадає
із її замиканням.
Означення 3. Точка 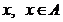 називається
внутрішньою точкою підмножини
називається
внутрішньою точкою підмножини 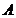 т.п.
т.п.

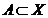 , якщо
, якщо 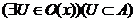 .
.
Сукупність всіх внутрішніх
точок множини 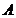 називається
її внутрішністю і позначається
називається
її внутрішністю і позначається  .
.
Множина  називається
межею множини
називається
межею множини 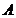 і
позначається
і
позначається 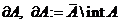 .
.
Означення 4. Говорять, що
т.п.  задовольняє
в точці
задовольняє
в точці 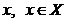 , першу
аксіому з численності
, першу
аксіому з численності 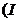 а.з.), якщо
існує база
а.з.), якщо
існує база 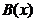 системи
системи 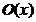 всіх околів
цієї точки, яка складається із зчисленної сукупності околів.
всіх околів
цієї точки, яка складається із зчисленної сукупності околів.
Означення 5. Говорять, що
т.п.  задовольняє
другу аксіому зачисленності (ІІ а.з.), якщо існує база
задовольняє
другу аксіому зачисленності (ІІ а.з.), якщо існує база 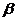 топології
топології 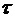 , яка
складається із зчисленної сукупності відкритих множин.
, яка
складається із зчисленної сукупності відкритих множин.
Приклад 2. Із прикладу 3,
§1.1., випливає, що т.п. із природною топологією  задовольняє І а.з. в кожній точці
х.
задовольняє І а.з. в кожній точці
х.
Означення 6. Підмножина 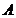 т.п.
т.п. 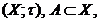 називається
щільною в цьому просторі, якщо
називається
щільною в цьому просторі, якщо 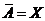 .
.
Означення 7. Якщо існує
зчисленна множина  , яка щільна
в т.п.
, яка щільна
в т.п.  , то цей
простір називають сепарабельним.
, то цей
простір називають сепарабельним.
Приклад 3. Оскільки множина
раціональних чисел зчисленна і вона щільна в т.п. із природною топологією  , то цей
простір сепарабельний.
, то цей
простір сепарабельний.
Теорема 1. Справедливі
твердження:
) якщо т.п.  в точці
в точці 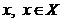 ,
задовольняє І а.з., то існує зчисленна база
,
задовольняє І а.з., то існує зчисленна база  системи
системи 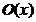 всіх околів
точки
всіх околів
точки  , яка
складається із відкритих множин таких, що
, яка
складається із відкритих множин таких, що 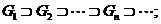
) якщо т.п.  задовольняє
ІІ а.з., то він в кожній точці
задовольняє
ІІ а.з., то він в кожній точці 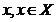 , задовольняє і І а.з.;
, задовольняє і І а.з.;
3) якщо т.п.  задовольняє
ІІ а.з., то він сепарабельний.
задовольняє
ІІ а.з., то він сепарабельний.
Покажемо справедливість
першого твердження. При вказаних в цьому твердженні умовах існує зчисленна база
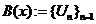 системи
системи 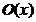 усіх околів
точки
усіх околів
точки  . То множина
. То множина
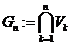 відкрита і
відкрита і . Якщо
. Якщо  , то
, то 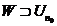 . За
побудовою
. За
побудовою  тобто
тобто 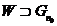 . А це
означає, що
. А це
означає, що 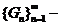 база системи
база системи
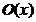 всіх околів
точки
всіх околів
точки  .
.
Якщо виконуються умови
другого твердження, то існує зчисленна база 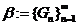 топології
топології  . Тоді роль
бази
. Тоді роль
бази 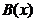 системи
системи 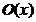 всіх околів
довільної точки
всіх околів
довільної точки 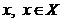 , відіграють
всі ті множини із бази
, відіграють
всі ті множини із бази 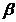 топології
топології  , які
містять точку
, які
містять точку  . Відкриті
околи точки
. Відкриті
околи точки  утворюють
базу всіх околів в цій точці і, отже, клас
утворюють
базу всіх околів в цій точці і, отже, клас 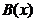 множин із класу
множин із класу 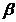 утворює
зчисленну базу системи
утворює
зчисленну базу системи 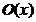 .
.
При виконанні умов третього
твердження існує знову зчисленна база 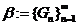 топології
топології  . Вибравши
із кожної множини
. Вибравши
із кожної множини  по одній
точці, утворимо зчисленну множину
по одній
точці, утворимо зчисленну множину 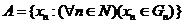 . Неважко показати, що
. Неважко показати, що  . Оскільки
включення
. Оскільки
включення 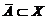 очевидне, то
очевидне, то 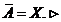
Означення 8. Послідовнсть 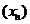 точок т.п.
точок т.п. 
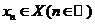 називається збіжною до точки
називається збіжною до точки 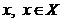 , і пишуть
, і пишуть 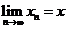 або
або 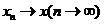 , якщо
, якщо 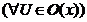 .
.
При цьому точка  називається
границею послідовності
називається
границею послідовності 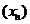 .
.
Виявляється, що збіжна
послідовність точок т.п. може мати кілька і навіть нескінченну сукупність
границь.
Приклад 4. В т.п.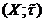 із
антидискретною топологією
із
антидискретною топологією 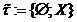 кожна
послідовність його точок збігається до довільної точки
кожна
послідовність його точок збігається до довільної точки 
Означення 9. Топологічний
простір  називається
відокремлюваним або інакше хаусдорфовим, якщо для довільних різних точок
називається
відокремлюваним або інакше хаусдорфовим, якщо для довільних різних точок 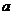 та
та 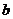 із
із 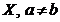 , існують їх околи, що не
перетинаються.
, існують їх околи, що не
перетинаються.
Теорема 2. Справедливі
твердження:
) послідовність 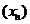 точок т.п.
точок т.п.  збігається
до точки
збігається
до точки 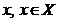 , тоді і
лише тоді, коли для кожного околу
, тоді і
лише тоді, коли для кожного околу  із деякої бази
із деякої бази 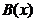 системи
системи 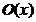 всіх околів
точки
всіх околів
точки  існує номер
п.
існує номер
п.
2) у
відокремлюваному т.п.  збіжна
послідовність має лише одну границю.
збіжна
послідовність має лише одну границю.
Необхідність умов твердження
4) очевидна. Покажемо їх достатність. Якщо ці умови виконуються, то 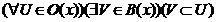 . Тоді
. Тоді 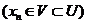 . Отже,
. Отже, 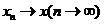 .
.
Твердження 5 доводиться
методом від протилежного з використанням означення границі послідовності.
Зауваження. Можна показати,
що  , де
, де  підмножина
т.п.
підмножина
т.п.  ,
, 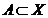 , який
задовольняє в точці
, який
задовольняє в точці  І а.з.,
тоді і лише тоді, коли існує послідовність
І а.з.,
тоді і лише тоді, коли існує послідовність 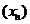 , яка збігається до точки
, яка збігається до точки 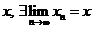 .
.
. Підпростір топологічного
простору. Прямий добуток топологічних просторів
Нехай 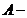 довільна
непорожня підмножина т.п.
довільна
непорожня підмножина т.п.  ,
,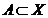 . Покажемо,
що клас множин
. Покажемо,
що клас множин 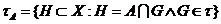 , є
топологією на
, є
топологією на 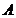 .
.
Такий висновок випливає із наступних
рівностей:
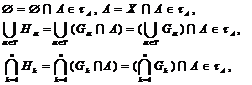
де 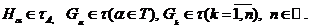
Означення 1. Топологія 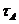 , що вказана
вище, називається індукованою топологією, а т.п.
, що вказана
вище, називається індукованою топологією, а т.п. 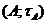 - підпростором т.п.
- підпростором т.п.  .
.
Приклад 1. Якщо
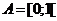 і
і 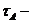 топологія,
яка індукована природною топологією
топологія,
яка індукована природною топологією  , то
, то 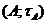 є підпростором т.п. При цьому
множина
є підпростором т.п. При цьому
множина 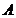 не є ні
відкритою ні замкнутою відносно топології
не є ні
відкритою ні замкнутою відносно топології  . Однак вона є відкритою і замкнутою
відносно топології
. Однак вона є відкритою і замкнутою
відносно топології 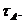
Можна показати, що в
загальному випадку 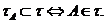
Якщо дано два т.п.  , то
розглянемо прямий добуток
, то
розглянемо прямий добуток 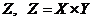 , множин
, множин 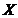 та
та 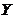 і клас
і клас
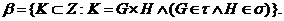
очевидно, 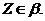
Якщо 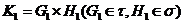 то
то

Тому, згідно із зауваженням
3, §1.1., клас 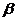 є базою
єдиної топології
є базою
єдиної топології 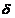 на
на 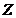 . Топологія
. Топологія 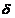 називається
прямим добутком топологій
називається
прямим добутком топологій  та
та 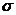 і позначається
і позначається 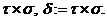
Означення 2. Впорядкована
пара 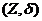 , де
, де 
 називається прямим добутком т.п.
називається прямим добутком т.п. 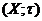 і т.п.
і т.п.  .
.
Якщо дано т.п. 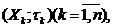 то
сукупність всіх множин виду
то
сукупність всіх множин виду 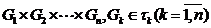 є, як можна показати, базою єдиної
топології на множині
є, як можна показати, базою єдиної
топології на множині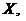
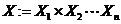 . При цьому
топологія
. При цьому
топологія  , яка
визначається вказаною базою, називається прямим добутком топології
, яка
визначається вказаною базою, називається прямим добутком топології 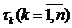 і позначається
і позначається
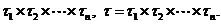
Впорядкована пара 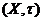 називається
прямим добутком т.п.
називається
прямим добутком т.п. 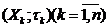 .
.
Приклад 2.
Топологічний простір  (
(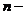 компоненти) і
компоненти) і 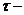 природна
топологія є прямий добуток топологічних просторів. База топології
природна
топологія є прямий добуток топологічних просторів. База топології  складається з усіх найможливіших
складається з усіх найможливіших 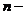 вимірних
відкритих паралелепіпедів та множини
вимірних
відкритих паралелепіпедів та множини 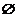 .
.
. Неперервні
відображення топологічних просторів
Нехай дано два т.п. 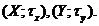
Означення 1. Відображення 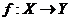 т.п.
т.п. 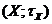 в т.п.
в т.п. 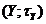 називається
неперервним в точці
називається
неперервним в точці 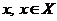 , якщо для
кожного околу
, якщо для
кожного околу 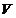 точки
точки 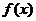 існує окіл
існує окіл 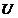 точки
точки  такий, що
такий, що  Відображення
Відображення
 називається
неперервним (неперервним на
називається
неперервним (неперервним на 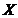 ), якщо воно неперервне в кожній
точці
), якщо воно неперервне в кожній
точці  із
із 
Приклад. Відображення 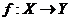 таке, що
таке, що 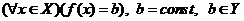 , неперервне, оскільки для кожного
околу
, неперервне, оскільки для кожного
околу 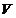 точки
точки 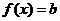 при довільному околі
при довільному околі 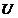 точки
точки  справедливе
справедливе 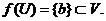
Теорема: Справедливі
твердження:
) вказане в попередньому
означенні відображення 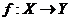 неперервне
тоді і лише тоді, коли прообраз кожної відкритої множини із т.п.
неперервне
тоді і лише тоді, коли прообраз кожної відкритої множини із т.п. 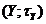 є відкрита
множина т.п.
є відкрита
множина т.п. 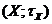 ;
;
) якщо відображення 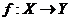 неперервне
в точці
неперервне
в точці 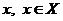 , то для
кожної послідовності такої, що
, то для
кожної послідовності такої, що 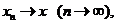 виконується
виконується 
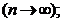
) якщо т.п. 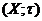 в точці
в точці 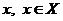 ,
задовольняє І а.з., то попередня вимога є і достатньою для неперервності
відображення
,
задовольняє І а.з., то попередня вимога є і достатньою для неперервності
відображення 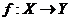 в точці
в точці  ;
;
) якщо відображення 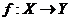 т.п.
т.п. 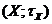 в т.п.
в т.п. 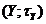 неперервне
і відображення
неперервне
і відображення 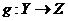 т.п.
т.п. 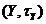 в т.п.
в т.п. 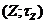 неперервне, то композиція
неперервне, то композиція 
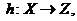 де
де 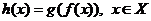 , цих
відображень також неперервна.
, цих
відображень також неперервна.
Зупинимося на доведенні
першого твердження. Якщо відображення  неперервне і
неперервне і 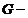 відкрита
підмножина множини
відкрита
підмножина множини 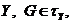 то для
точки
то для
точки 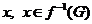 ,
виконується
,
виконується 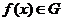 і тому
і тому 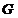 є окіл
точки
є окіл
точки 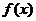 . Існує окіл
. Існує окіл
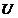 точки
точки  , такий що
, такий що 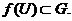 Отже, існує
відкрита підмножина
Отже, існує
відкрита підмножина 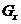 множини
множини 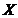 , для якої
, для якої 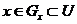 , тобто
, тобто 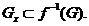 Таким чином
Таким чином
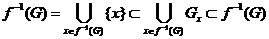
тобто  .
Необхідність умов першого твердження доведено.
.
Необхідність умов першого твердження доведено.
Достатність. Якщо виконуються
умови першого твердження, то для довільної точки 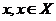 , і довільного околу
, і довільного околу  існує відкрита підмножина
існує відкрита підмножина 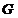 множини
множини 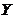 така, що
така, що 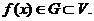 Прообраз
Прообраз 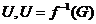 , множини
, множини 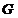 є відкрита
підмножина множини
є відкрита
підмножина множини 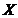 , яка
містить точку
, яка
містить точку  , оскільки
, оскільки  Отже,
Отже,  окіл точки
окіл точки  і
і 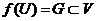 .
Неперервність відображення
.
Неперервність відображення  доведена.
доведена.
Друге твердження доводиться з
допомогою означення неперервності відображення  .
.
Третє твердження доводиться
методом від протилежного.
Справедливість четвертого
твердження випливає із співвідношення 
Означення 2. Бієктивне
відображення 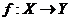 т.п.
т.п. 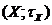 на т.п.
на т.п. 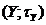 називається
гомеоморфним (або гомеоморфізмом), якщо
називається
гомеоморфним (або гомеоморфізмом), якщо  і обернене до нього відображення
і обернене до нього відображення 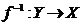 неперервні.
неперервні.
Означення 3. Відображення 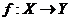 т.п.
т.п. 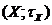 в т.п.
в т.п. 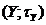 називається
відкритим(замкнутим), якщо образ
називається
відкритим(замкнутим), якщо образ 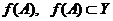 , кожної відкритої (замкнутої)
множини
, кожної відкритої (замкнутої)
множини 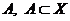 , є відкрита
(замкнута) множина.
, є відкрита
(замкнута) множина.
5.
Компактність в топологічних просторах
Поняття компактності відіграє
важливу роль в різних розділах математики. Зокрема відома з математичного
аналізу лема Бореля-Лебега фактично стверджує компактність відрізка числової
прямої і вона дає можливість довести ряд змінюваних теорем. Ще більш суттєві
застосування має поняття компактності топологічного і зокрема метричного
простору.
Означення 1. Клас 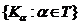 підмножин
топологічного простору
підмножин
топологічного простору  називається покриттям множини
називається покриттям множини 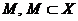 , якщо
, якщо  (у випадку,
коли
(у випадку,
коли  ,
вимагається, щоб
,
вимагається, щоб 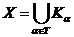 ).
).
Означення 2. Вказане вище
покриття називається скінченним (зчисленним), якщо множина індексів 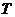 скінченна(зчисленна);
таке покриття називається відкритим, якщо всі множини
скінченна(зчисленна);
таке покриття називається відкритим, якщо всі множини 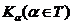 відкриті.
відкриті.
цей простір називається
зчисленно-компактним, якщо кожна нескінченна множина 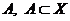 , має в
цьому просторі принаймні одну граничну точку;
, має в
цьому просторі принаймні одну граничну точку;
т.п.  називається
секвенційно компактним, якщо із кожної послідовності, можна виділити збіжну
підпослідовність.
називається
секвенційно компактним, якщо із кожної послідовності, можна виділити збіжну
підпослідовність.
Теорема 1. Якщо т.п.  задовольняє
ІІ а.з., то із кожного нескінченного відкритого покриття його можна виділити
зчисленне покриття (підпокриття).
задовольняє
ІІ а.з., то із кожного нескінченного відкритого покриття його можна виділити
зчисленне покриття (підпокриття).
Якщо 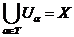 , де
, де 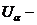 відкриті
множини і
відкриті
множини і  зчисленна
база топології
зчисленна
база топології 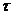 , то
позначимо через
, то
позначимо через 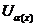 одну із
відкритих множин покриття, яка містить точку
одну із
відкритих множин покриття, яка містить точку 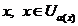 . Позначимо через
. Позначимо через 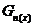 одну із
множин бази, яка містить точку
одну із
множин бази, яка містить точку 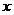 і
включається в
і
включається в 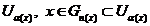 . Зчисленна
сукупність множин
. Зчисленна
сукупність множин 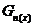 із бази
утворює покриття множини
із бази
утворює покриття множини 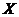 . Для кожної
множини
. Для кожної
множини 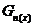 виберемо
одну із множин
виберемо
одну із множин 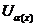 , яка
включає
, яка
включає 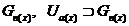 .
.
Теорема 2. Справедливі
твердження:
) якщо т.п.  зчисленно-компакний,
відокремлювний (хаусдорфів) і в кожній точці
зчисленно-компакний,
відокремлювний (хаусдорфів) і в кожній точці 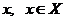 , задовольняє І а.з., то він
секвенційно компактний;
, задовольняє І а.з., то він
секвенційно компактний;
) якщо т.п.  секвенційно
компактний і задовольняє ІІ а.з., то він компактний;
секвенційно
компактний і задовольняє ІІ а.з., то він компактний;
) якщо т.п.  компактний,
то він зчисленно-компактний;
компактний,
то він зчисленно-компактний;
) якщо т.п.  секвенційно
компактний, то він зчисленно-компактний.
секвенційно
компактний, то він зчисленно-компактний.
Якщо виявиться, що множина 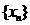 скінченна,
то деякий елемент цієї послідовності, який позначимо через
скінченна,
то деякий елемент цієї послідовності, який позначимо через 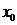 ,
зустрічається в ній нескінченну кількість разів і тому підпослідовність
,
зустрічається в ній нескінченну кількість разів і тому підпослідовність 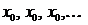 збігається
до точки
збігається
до точки 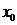 . Якщо
множина
. Якщо
множина 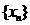 нескінченна, то згідно з умовами першого
твердження вона має граничну точку
нескінченна, то згідно з умовами першого
твердження вона має граничну точку 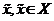 . Оскільки т.п.
. Оскільки т.п.  задовольняє
в точці
задовольняє
в точці 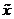 І а.з., то
згідно із відомим твердженням, існує зчисленна база
І а.з., то
згідно із відомим твердженням, існує зчисленна база 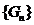 системи
усіх її околів, яка складається із відкритих множин, таких, що
системи
усіх її околів, яка складається із відкритих множин, таких, що 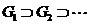 . Позначимо
через
. Позначимо
через 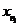 перший член
послідовності
перший член
послідовності 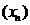 , відмінний
від
, відмінний
від 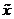 . Оскільки
т.п.
. Оскільки
т.п.  відокремлюваний,
то існують околи точок
відокремлюваний,
то існують околи точок  ,
,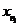 які не
перетинаються. Окіл точки
які не
перетинаються. Окіл точки  включає
окіл
включає
окіл 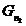 із бази
системи околів. Зрозуміло, що
із бази
системи околів. Зрозуміло, що 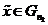 і
і 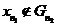 .
.
Позначимо через  перший член
послідовності
перший член
послідовності 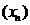 , який
належить околу
, який
належить околу 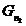 і відмінний
від
і відмінний
від , і т.д. Ми
отримали підпослідовність
, і т.д. Ми
отримали підпослідовність 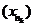 таку, що
таку, що
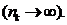
Зупинимося на доведенні
другого твердження. Вважаючи т.п.  секвекційно компактним, і який
задовольняє ІІ а.з., припустимо, що він не є компактним. Тоді існує покриття
його сукупністю
секвекційно компактним, і який
задовольняє ІІ а.з., припустимо, що він не є компактним. Тоді існує покриття
його сукупністю 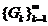 відкритих
множин
відкритих
множин 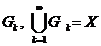 , із якого
не можливо виділити скінченне покриття (підпокриття). Розглянувши тоді
послідовність, що
, із якого
не можливо виділити скінченне покриття (підпокриття). Розглянувши тоді
послідовність, що 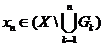 , можемо
стверджувати, що із неї неможливо виділити збіжну підпослідовність. Це тому, що
в протилежному випадку границя
, можемо
стверджувати, що із неї неможливо виділити збіжну підпослідовність. Це тому, що
в протилежному випадку границя 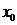 збіжної
підпослідовності належала б деякій множині
збіжної
підпослідовності належала б деякій множині  . Оскільки
. Оскільки  є окіл точки
є окіл точки
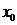 , то
, то 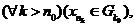 що неможливе
за побудовою послідовності
що неможливе
за побудовою послідовності  Справді, якщо
Справді, якщо  то
то 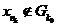 . Отже, із
послідовності
. Отже, із
послідовності 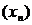 неможливо
виділити збіжну підпослідовність. А це суперечить секвенційній компактності
т.п.
неможливо
виділити збіжну підпослідовність. А це суперечить секвенційній компактності
т.п. 
Покажемо справедливість
третього твердження. Вважаючи т.п.  компактним і взявши довільну
нескінченну множину
компактним і взявши довільну
нескінченну множину  розглянемо
зчисленну її підмножину
розглянемо
зчисленну її підмножину 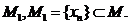 Покажемо,
що множина
Покажемо,
що множина 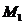 має
граничну точку, яка буде граничною точкою і для множини
має
граничну точку, яка буде граничною точкою і для множини 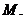 Припустимо
протилежне, тобто, що множина
Припустимо
протилежне, тобто, що множина 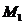 не має жодної граничної точки. Тоді
множина
не має жодної граничної точки. Тоді
множина 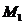 замкнута,
оскільки вона не має точок дотику зовні неї. Отже, кожна множина відкрита,
причому сукупність
замкнута,
оскільки вона не має точок дотику зовні неї. Отже, кожна множина відкрита,
причому сукупність 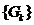 всіх таких
множин утворює відкрите покриття множини
всіх таких
множин утворює відкрите покриття множини 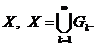 Справді, точка
Справді, точка 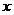 належить
всім множинам
належить
всім множинам 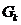 ; якщо
; якщо 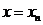 , то
, то  . Вибравши
скінченне відкрите покриття (підпокриття)
. Вибравши
скінченне відкрите покриття (підпокриття) 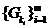 множини
множини 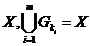 , отримаємо
, отримаємо
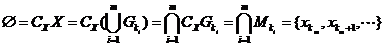
Отримане протиріччя показує
справедливість третього твердження.
Доведемо нарешті четверте
твердження. Якщо виконуються його умови, то, взявши нескінченну множину  , розглянемо
довільну зчисленну її підмножину
, розглянемо
довільну зчисленну її підмножину 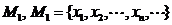 . Із послідовності
. Із послідовності 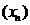 попарно
різних точок множини
попарно
різних точок множини 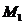 виділимо
збіжну її підпослідовність
виділимо
збіжну її підпослідовність 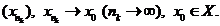 Тоді точка
Тоді точка 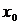 є граничною
точкою множини
є граничною
точкою множини 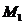 і, отже,
множини М.
і, отже,
множини М.
Наслідок. Якщо
відокремлюваний т.п.  задовольняє
ІІ а.з., то еквівалентні наступні твердження:
задовольняє
ІІ а.з., то еквівалентні наступні твердження:
а) 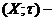 зчисленно-компактний
т.п.;
зчисленно-компактний
т.п.;
б) 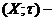 секвенційно
компактний т.п.;
секвенційно
компактний т.п.;
в) 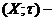 компактний
т.п.
компактний
т.п.
Як відомо, якщо т.п.  задовольняє
ІІ а.з., то він в кожній точці
задовольняє
ІІ а.з., то він в кожній точці 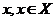 , задовольняє і І а.з.. Якщо окрім
того т.п.
, задовольняє і І а.з.. Якщо окрім
того т.п.  ще є і
відокремлюваним, то, застосовуючи попередню теорему, приходимо до висновку, що
всі імплікації із ланцюга
ще є і
відокремлюваним, то, застосовуючи попередню теорему, приходимо до висновку, що
всі імплікації із ланцюга 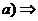 б)
б) в)
в) а) істинні.
А це стверджує вказані вище еквівалентності.
а) істинні.
А це стверджує вказані вище еквівалентності.
Приклад 1. Топологічний
простір із природною топологією 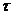 на не є компактним, оскільки із
покриття системою інтервалів неможливо виділити скінченне покриття множини
такими інтервалами.
на не є компактним, оскільки із
покриття системою інтервалів неможливо виділити скінченне покриття множини
такими інтервалами.
Означення 4. Підмножина
 т.п.
т.п.  називається
компактною, якщо із кожного покриття її відкритими множинами цього простору
можна виділити скінченне покриття (під покриття).
називається
компактною, якщо із кожного покриття її відкритими множинами цього простору
можна виділити скінченне покриття (під покриття).
Приклад 2. Згідно із відомою
лемою Бореля-Лебега, кожна обмежена і замкнута підмножина М т.п., 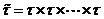
 компонент) і
компонент) і 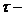 природна
топологія компактна.
природна
топологія компактна.
Теорема 3. Підмножина  т.п.
т.п. 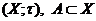 , компактна тоді і лише тоді, коли
т.п.
, компактна тоді і лише тоді, коли
т.п. 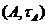 із
індукованою топологією
із
індукованою топологією  на
на  компактний.
компактний.
Необхідність. Якщо 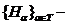 довільне
покриття множини
довільне
покриття множини  відкритими
множинами із топології
відкритими
множинами із топології  , то
розглянемо ті відкриті множини
, то
розглянемо ті відкриті множини  із топології
із топології 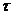 , для яких
, для яких 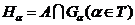 .
.
Клас  утворює покриття множини
утворює покриття множини  відкритими множинами із топології
відкритими множинами із топології 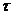 . Оскільки
множина
. Оскільки
множина  компактна
відносно топології
компактна
відносно топології 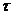 , то і деяка
скінченна сукупність множин
, то і деяка
скінченна сукупність множин 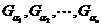 також утворює покриття множини
також утворює покриття множини  . Тоді
множини
. Тоді
множини 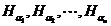 із топології
із топології
 утворюють
скінченне покриття множини
утворюють
скінченне покриття множини  .
.
Достатність. Якщо 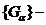 довільне
покриття множини
довільне
покриття множини  відкритими
множинами із топології
відкритими
множинами із топології 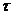 . Якщо
. Якщо 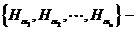 скінчене
покриття множини
скінчене
покриття множини 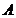 із
топології
із
топології 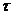 то
то 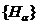 , де
, де 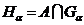 , є
покриттям множини
, є
покриттям множини  відкритими множинами із топології
відкритими множинами із топології  , то
, то 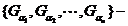 скінченне
покриття множини
скінченне
покриття множини  множинами із топології
множинами із топології 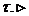
Теорема 4. Довільна замкнута
підмножина 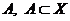 компактного
т.п.
компактного
т.п.  компактна.
компактна.
Якщо 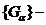 довільне
покриття замкнутої множини,
довільне
покриття замкнутої множини, 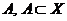 , відкритими множинами із топології
, відкритими множинами із топології 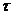 , то
, то 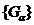 разом із
множиною
разом із
множиною 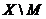 утворюють
відкрите покриття множини
утворюють
відкрите покриття множини 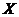 . Виділивши
із останнього покриття скінченне покриття
. Виділивши
із останнього покриття скінченне покриття 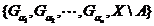 множини
множини 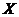 , отримаємо
скінченне покриття
, отримаємо
скінченне покриття  множини
множини 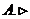
Теорема 5. Компактна
підмножина  відокремлюваного т.п.
відокремлюваного т.п. 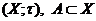 , замкнута.
, замкнута.
Вважаючи 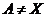 і взявши
довільну точку
і взявши
довільну точку 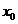 ,
, 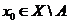 можемо
стверджувати, що для кожної точки
можемо
стверджувати, що для кожної точки 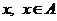 , існують відкриті околи
, існують відкриті околи  та
та 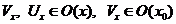 , які не перетинаються. Клас
, які не перетинаються. Клас 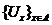 усіх
відкритих околів довільної точки
усіх
відкритих околів довільної точки 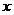 із
із  утворює відкрите покриття множини
утворює відкрите покриття множини  .
.
Згідно з компактністю множини
 , існує
скінченна сукупність
, існує
скінченна сукупність  відкритих околів, що покриває множину
відкритих околів, що покриває множину  . Множина
. Множина 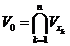 являє собою
відкритий окіл точки
являє собою
відкритий окіл точки 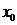 і не перетинається із об’єднанням
і не перетинається із об’єднанням 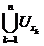 сукупності
околів, які утворюють скінченне покриття множини
сукупності
околів, які утворюють скінченне покриття множини  , причому
, причому 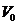 не перетинається з
не перетинається з  . Для кожної
точки
. Для кожної
точки 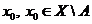 побудуємо таким чином окіл
побудуємо таким чином окіл 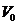 , який не
містить точок множини
, який не
містить точок множини  . Це
означає, що поза множиною
. Це
означає, що поза множиною  не міститься
жодна точка дотику множини
не міститься
жодна точка дотику множини  , тобто
, тобто 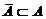 і, отже,
і, отже, 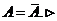
Теорема 6. Справедливі
твердження:
) образ 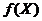 компактного
т.п.
компактного
т.п.  при його
неперервному відображенні
при його
неперервному відображенні 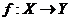 в т.п.
в т.п. 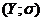 компактний.
компактний.
) неперервне відображення 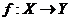 компактного
т.п.
компактного
т.п.  у
відокремлюваний т.п.
у
відокремлюваний т.п. 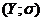 є замкнуте
відображення.
є замкнуте
відображення.
Якщо виконуються умови
твердження 5), то розглянемо довільне покриття 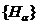 образу
образу
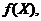
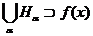 Всі множини
Всі множини 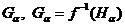 , внаслідок
неперервності відображення
, внаслідок
неперервності відображення  , відкриті,
, відкриті, . Клас
. Клас 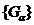 є відкритим
покриттям множини
є відкритим
покриттям множини 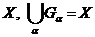 . Виділивши
із останнього покриття скінченне під покриття
. Виділивши
із останнього покриття скінченне під покриття  множини
множини 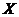 , отримаємо
відповідно скінченне підпокриття
, отримаємо
відповідно скінченне підпокриття 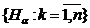 множини
множини 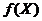 . А це
означає компактність
. А це
означає компактність 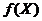 .
.
Якщо виконуються умови
твердження 6), то розглянемо довільну замкнуту множину 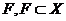 . Ця множина
компактна, внаслідок теореми 4. Її образ
. Ця множина
компактна, внаслідок теореми 4. Її образ 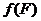 також компактний, внаслідок
твердження 5). Оскільки т.п.
також компактний, внаслідок
твердження 5). Оскільки т.п. 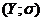 відокремлюваний,
то множина
відокремлюваний,
то множина 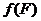 замкнута.
замкнута.
Зауваження. Якщо є неперервне
відображення із природною топологією 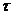 , і
, і 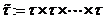 (
(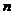 компонент),
то, згідно із попередніми твердженнями, образ
компонент),
то, згідно із попередніми твердженнями, образ 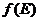 компактної
підмножини
компактної
підмножини 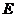 т.п. компактний. Як відомо з математичного
аналізу компактна множина
т.п. компактний. Як відомо з математичного
аналізу компактна множина 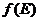 є замкнута і
обмежена в т.п. Ми отримали відому теорему Вейєрштрасса, згідно з якою,
неперервна на замкнутій і обмеженій множині Е числова функція
є замкнута і
обмежена в т.п. Ми отримали відому теорему Вейєрштрасса, згідно з якою,
неперервна на замкнутій і обмеженій множині Е числова функція  обмежена і
досягає на
обмежена і
досягає на 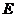 свого найбільшого і найменшого значень. Це тому,
що при неперервному відображенні
свого найбільшого і найменшого значень. Це тому,
що при неперервному відображенні  замкнутої і обмеженої множини Е,
справедливі співвідношення:
замкнутої і обмеженої множини Е,
справедливі співвідношення: 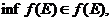
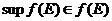 .
.
Означення 5.
Підмножина  т.п.
т.п. 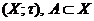 ,
називається перед компактною, якщо її замикання
,
називається перед компактною, якщо її замикання 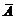 компактне
в цьому просторі.
компактне
в цьому просторі.
Зрозуміло, що кожна компактна
підмножина топологічного простору є перед компактною, але не навпаки.
Висновки
У даній курсовій роботі було
розглянуто топологічні простори та основні означення пов’язані з ними.
В першому розділі мова йшла
про замкнені множини, відкриті множини, околи, базиси топології, про скрізь
щільні множини, про ніде не щільні множини. Зокрема, були наведені означення
топологічного простору та бази топологічного простору.
У другому розділі були
наведені означення точок дотику, межових точок. Також наведені аксіоми
численності та розкриті поняття збіжних послідовностей.
Третій розділ розкрив нам
поняття підпростору топологічного простору. А також ми ознайомились з
означенням прямого добутку топологічного простору. Ознайомились з прикладами.
Поняття неперервного
відображення в точці, та означення гомеоморфізму ми розглянули в четвертому
розділі.
Останній розділ нашої роботи
був присвячений компактності топологічних просторів. В ньому ми розкрили
поняття компактних просторів, зчисленно-компактних та секвенційних. Також
ознайомились з означенням перед компактної множини та підпокриття.
аксіома
математичний простір топологічний
Список використаної
літератури
1. Бурбаки Н. Общая
топология. - М., Наука, 1957.
. Зорич В.А. Математический
анализ. Часть 2. - Изд. 4-е,
испр.- М.,2002. - 664 с.
. Кураторський, Казимир
"Топологія'. Пер. з англ. М.Я. Антоновського. т.1-2, Москва, "Мир'
1966-1969р.
4. Ришард Енгелькинг “Общая топология” - Москва, “Мир”, 1986 р.