Теорема Миттаг–Леффлера (представление мероморфной функции)

Теорема Миттаг-Леффлера (представление мероморфной функции)

1. Вспомогательные сведения

Определение 1.1 Мероморфной функцией будем называть однозначную аналитическую функцию, не имеющую в конечной части плоскости особых точек, отличных от полюсов.

В частности, к мероморфным функциям относятся целые функции, так как они вообще не имеют никаких особых точек в конечной части плоскости, а также рациональные функции.

Другое определение мероморфной функции:

Функция f(z), отличная от тождественного нуля, называется мероморфной, если в окрестности любой конечной точки a для неё имеет место разложение

f(z)=c₀(z-a)^r+c₁(z-a)^r+1+…,

где r-целое число, а с₀≠0.

Число r будем называть порядком нуля функции f(z) в точке a, считая тем самым, что полюс порядка s-это нуль отрицательного порядка -s.

Из определения мероморфной функции вытекают следующие свойства класса мероморфных функций:

. Любая постоянная-мероморфная функция.

. Сумма и разность двух мероморфных функций-мероморфные функции.

. Произведение и частное двух мероморфных функций-мероморфные функции.

. Рациональная функция от мероморфных функций-мероморфные функции.

В частности, отношение двух целых функций-мероморфная функция. Так как 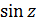 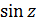и -целые функции, то

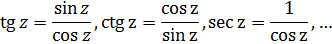
являются мероморфными функциями.

Определение 1.2. Если мероморфная функция f(z) имеет полюсов, то она является целой функцией.

Пусть мероморфная функция f(z) имеет только конечное число полюсов

a₀, a₁, a₂, …, и пусть

главные части в этих полюсах. Тогда

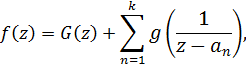
где  - целая функция.

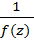
Определение 1.3. Если особая точка z=a однозначной аналитической функции f(z) не является особой точкой для функции 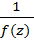, то точка a называется полюсом. Все другие изолированные особые точки однозначных аналитических функций будем называть существенно особыми точками.

Определение 1.4. Выясним поведение функции в окрестности полюса. Если точка a - полюс функции f(z), то в некоторой окрестности этой точки (но не в самой точке a, поскольку значения f(z) в точке a не существует) имеет место равенство

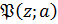
где  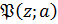- степенной ряд. (Считаем, что 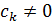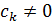.) Согласно равенству (1) в некоторой окрестности точки a можно написать неравенство

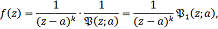
т. е.

Отсюда видно, что 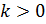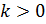, так как при  точка a не была бы особой точкой для функции f(z).

Число k будем называть порядком полюса.

Когда точка z стремится к полюсу a, функции f(z), как видно из формулы(2), стремится к бесконечности, причем

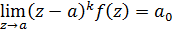
- конечное число, отличное от нуля. Число k показывает, таким образом, с какой скоростью стремится к бесконечности функция в данном полюсе.

Определение 1.5. Используя равенство (2) из определения 1.4, запишем его в виде

Отсюда видно, что разность:

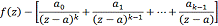
Разлагается в окрестности точки a в степенной ряд, т. е. не имеет особой точки при 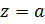 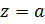. Поэтому будем говорить, что функция имеет в точке a ту же особенность, что и многочлен от  

Этот многочлен от  будем называть главной частью функции f(z) в полюсе a.

Определение 1.6. Точка a называется изолированной особой точкой функции f, если существует такая проколотая окрестность этой точки (то есть множество , если точка a конечна, или множество , если a=∞), в которой функция f голоморфна.

Определение 1.6’. В зависимости от поведения f при приближении к такой точке различают три типа особых точек.

Изолированная особая точка a функции f называется:

. устранимой точкой, если существует конечный

 ;

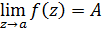
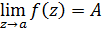. полюсом, если существует

 ;

. существенно особой точкой, если f не имеет ни конечного, ни бесконечного предела при .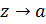

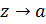Примеры.

1.      ,

точка z=0 является устранимой особой точкой.

2.      , точка z=0 является полюсом.

.        , точка z=0 является существенно особой точкой.

Теорема 1(Лорана). Любую функцию f, голоморфную в кольце , можно в этом кольце представить как сумму сходящегося ряда

Коэффициенты которого определяются по формулам

где .

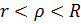
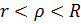Определение 1.7. Функцию, определенную в области D, будем называть регулярной в этой области, если в окрестности каждой точки области D эта функция представляется сходящимся степенным рядом.

. Теорема Миттаг-Леффлера

Если мероморфная функция f(z) имеет бесконечно много полюсов, то они могут иметь предельную точку только в бесконечности. Действительно, предельная точка полюсов - тоже особая точка и притом не полюс (полюс - изолированная особенность), а по определению мероморфная функция не имеет в конечной части плоскости особых точек, отличных от полюсов.

Полюсы мероморфной функции f(z) договоримся нумеровать в порядке возрастания их модулей. Если a₀, a₁, a₂, …- полюсы функции f(z), то наша договоренность означает, что |a₀|≤|a₁|≤|a₂|≤…, а, согласно сделанному выше замечанию,

Заметим, что в последовательности 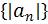 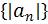в нуль может обращаться только число |a₀|, все следующие положительны.

Главные части функции f(z) в её полюсах будем обозначать

 , , …

Естественно, возникает вопрос, должны ли полюсы мероморфной функции и главные части в этих полюсах удовлетворять каким либо условиям?

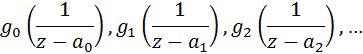
соответственно.

Для доказательства теоремы Миттаг-Леффлера нам понадобится следующая лемма:

Лемма 1. Пусть F₀(z), F₁(z), F₂(z), …-последовательность мероморфных функций. Предположим, что функции F_n(z) (n=0, 1, 2, …) регулярны в кругах |z|≤r_n соответственно, причем

r₀≤r₁≤r₂≤…, .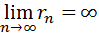

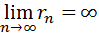Тогда существует такая последовательность  многочленов от z, что ряд

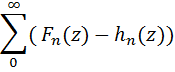
равномерно сходится в круге |z|≤R при любом R<∞ (если отбросить конечное число членов этого ряда, которые могут обращаться в бесконечность).

Доказательство леммы 1. Для доказательства леммы заметим, что ряд

равномерно сходится в круге |z |≤r_n, так как функция F_n(z) по условию леммы регулярна там. Поэтому для любого числа ε_n>0 можно выбрать номер m_n таким образом, чтобы при всех z из круга |z|≤r_n выполнялось неравенство

Выберем последовательность положительных чисел ε₀, ε₁, … так, чтобы сходился ряд ε₀+ε₁+ε₂+…, и обозначим

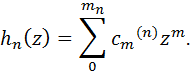
Покажем, что построенные многочлены h_n(z) составляют последовательность, существование которой утверждается в лемме.

Действительно, возьмем любое число R<∞ и выберем номер N таким образом, чтобы выполнялось неравенство r_N≥R. Тогда при |z|≤R ряд

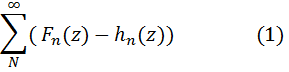
будет мажорироваться сходящимся числовым рядом ε_N+ε_N+1+…, и следовательно, будет равномерно сходиться при |z|≤R. Тем самым лемма доказана.

Перейдем к доказательству теоремы Миттаг-Леффлера.

Доказательство теоремы 1.

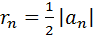
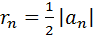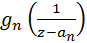
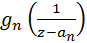Возьмем в качестве последовательности {F_n(z)} последовательность главных частей . Если взять , то условия леммы будут выполнены, так как функции  регулярны в кругах |z|≤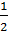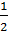|a_n|≤|a_n|. Убедимся, что сумма ряда

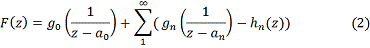
представляет собою мероморфную функцию с заданными полюсами и главными частями в них. Согласно лемме ряд (2) будет равномерно сходиться в круге |z|≤R с любым фиксированным R, если отбросить конечное число его первых членов. По теореме Вейерштрасса сумма равномерно сходящегося ряда регулярных функций-регулярная функция. Поэтому особые точки суммы ряда (2) в этом круге совпадают с особыми точками суммы конечного числа первых членов этого ряда. Эти особые точки-полюсы в заданных точках с заданными главными частями. Теорема доказана.

3. Общий вид мероморфной функции с заданными полюсами

Пусть f(z) - мероморфная функция с полюсами a₀, a₁, …, занумерованными в порядке возрастания модулей. Главные части функции f(z) в этих полюсах обозначим

Согласно теореме Миттаг-Леффлера можно построить функцию

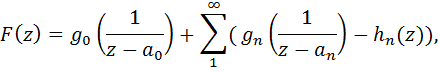
имеющую те же полюсы и те же главные части в этих полюсах, что и функция f(z). Разность G(z)=f(z)-F(z) будет целой функцией, так что

мероморфный функция теорема миттаг

Таким образом:

Любую мероморфную функцию f(z) можно представить в виде суммы целой функции и ряда, членами которого являются рациональные функции, причем каждая из этих функций имеет в конечной плоскости полюсом только один из полюсов функции f(z).

4. Случай простых полюсов

Рассмотрим подробнее часто встречающийся и наиболее простой случай, когда главные части, отвечающие всем точкам a₀, a₁, a₂, …, имеют вид

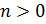
При  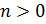имеют место разложения

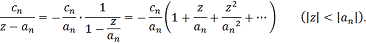
Поэтому, если полюсы простые, то

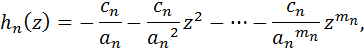
А

Поскольку

формулу (1) можно записать и в виде

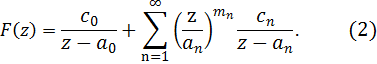
Целые числа  входящие в формулу (1) и (2), следует выбирать так, чтобы написанные ряды равномерно сходились в любом конечном круге (после отбрасывания членов, имеющих в этом круге полюсы). Попытаемся придать этому условию более простую форму.

Возьмем любое 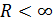 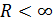и рассмотрим z из круга . При достаточно большом n величина  будет сколь угодно мала. Поэтому можно найти такой номер N, чтобы при всех  выполнялись неравенства

Тогда будут справедливы и неравенства

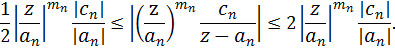
Следовательно:

Ряд (2) для функции F(z) абсолютно сходится в любом конечном круге тогда и только тогда, когда ряд

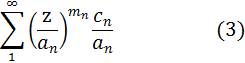
Абсолютно сходится при любом z.

В случае абсолютной сходимости ряда (3) ряд (2) равномерно сходится в любом конечном круге (после отбрасывания членов с полюсами в этом круге). Действительно, выбирая номер N тем же способом, что и выше, видим, что ряд

при  мажорируется рядом

Последний ряд является сходящимся числовым рядом с положительными членами.

Таким образом, мы доказали теорему:

Теорема 1. Если в формуле (2) числа  выбраны так, что ряд

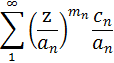
абсолютно сходится при любом z, то ряд в формуле (2) равномерно сходится в любом конечном круге (после отбрасывания конечного числа членов).

Если положить все числа  равными одному и тому же числу m, то

Это дает нам теорему:

Теорема 2. В формуле (2) все числа  можно взять равными одному и тому же числу m, если сходится ряд

Это условие заведомо выполняется, если

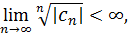
так как 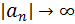 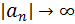при 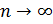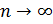. В частности, получаем отсюда:

Если все полюсы простые, а вычеты  в этих полюсах ограничены, то всегда можно взять в формуле (2) .

Список используемой литературы

1. А. Гурвиц, Р. Курант, перевод М.А. Евграфова, Теория функций.-М.: Наука, 1968.

2.      Б.В. Шабат, Введение в комплексный анализ.-М.: Наука, 1976.