Статистическое планирование эксперимента
Практическая
работа 4:
статистическое планирование эксперимента
вариант.
Задача. Планирование эксперимента для описания
зависимости показателя стойкости концевых фрез от геометрических параметров.
Рассмотрим пример применения планирования эксперимента. Поставим задачу
описания зависимости показателя стойкости концевых фрез от заднего угла х1,
переднего угла х2, ширины ленточки х3. В качестве математической модели
принимаем неполную кубическую функцию
М{у} = β0+
β1x1+
β2x2+
β3
x3+
β4
x1x2+
β5
x1x3+
β6
x2x3+
β7x1x2x3.
(5)
Для получения оценок коэффициентов этого
уравнения можно использовать полный факторный эксперимент типа 23. Выберем
основные уровни факторов, близкие к применяемым в практике, а интервалы
варьирования - исходя из реальных пределов колебаний значений факторов (табл.
2). Эксперименты выполняем в соответствии с матрицей планирования (см. табл.1).
Условия испытаний. Испытывали концевые фрезы
диаметром 22 мм, изготовленные из стали Р18. Фрезы были заточены так, чтобы
получить комбинации значений параметров, указанные в строках матрицы плана
эксперимента.
планирование эксперимент показатель
фреза
Таблица 2
Уровни факторов и интервалы варьирования
|
Уровни
факторов
|
Обозначение
|
а°
|
а°
|
f в мм
|
|
|
x1
|
x2
|
x3
|
|
Основной
|
0
|
15
|
16
|
0,06
|
|
Интервал
варьирования
|
Δxi
|
4
|
6
|
0,03
|
|
|
|
|
|
|
Верхний
|
+ 1
|
19
|
22
|
0,09
|
|
Нижний
|
-
1
|
11
|
10
|
0,03
|
В каждой точке факторного пространства опыт
повторялся по 3 раза, поэтому для каждой строки плана изготовляли по 3 фрезы.
Порядок испытаний фрез рандомизирован с помощью таблицы случайных чисел.
Результаты испытаний (стойкость фрез в минутах) приведены в табл. 3 столбцы
2-4.
Таблица 3
Результаты испытаний концевых фрез 22 мм
|
Точки
плана υ
|
y1
|
y2
|
y3
|
 sv2 sv2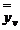  2 2
|
|
|
|
|
1
|
39,46
|
41,15
|
28,81
|
36,47
|
44,76
|
34,3
|
4,71
|
|
2
|
41,74
|
31,06
|
31,42
|
34,74
|
36,78
|
35,8
|
1,12
|
|
3
|
37,14
|
48,48
|
38,15
|
41,26
|
39,39
|
38,3
|
8,76
|
29,14
|
46,44
|
30,85
|
35,48
|
90,88
|
32,1
|
11,42
|
|
5
|
26,11
|
40,06
|
42,42
|
36,20
|
77,70
|
38,5
|
5,29
|
|
6
|
41,11
|
39,35
|
42,30
|
40,92
|
2,20
|
40,7
|
0,05
|
|
7
|
46,61
|
44,00
|
34,18
|
41,60
|
42,96
|
43,4
|
3,24
|
|
8
|
40,00
|
37,18
|
46,21
|
41,13
|
21,34
|
42,4
|
1,62
|
|
|
|
|
y=38,48;
Σsv2=356,1;
Σ36,21
|
Решение. Рассчитаем коэффициенты уравнения для
нашего примера (см. табл. 3).
 .
.
Аналогично рассчитываются значения b2, b3. Расчет b0
выполняется по тому же правилу:
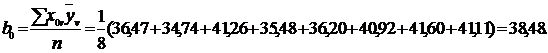
Таким образом, значение b0 равно
среднему значению параметра оптимизации  . Итак получаем: b0 = 38,48; b1 =-3,28, b2 = 2,01, b3 = - 7,64; b12= 0,65; b13= - 0,65, b23 = 0,39, b123 = -0,5.
. Итак получаем: b0 = 38,48; b1 =-3,28, b2 = 2,01, b3 = - 7,64; b12= 0,65; b13= - 0,65, b23 = 0,39, b123 = -0,5.
Уравнение в преобразованных
переменных хiбудет:
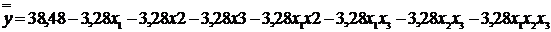 .
.
Для получения уравнения в
натуральных значениях факторов  надо вместо хi подставить
в полученное уравнение их значения согласно формуле преобразования (4):
надо вместо хi подставить
в полученное уравнение их значения согласно формуле преобразования (4):
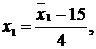
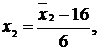
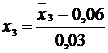 .
.
Для нашего примера из табл.3 имеем,
что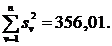 Тогда,
согласно уравнению (8):
Тогда,
согласно уравнению (8):

Пользуясь табл.3 найдем по критерию
Кохрена
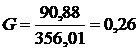 ,
,
По соответствующей таблице в работе
[11] находим для fmax =2, fзнам - N
степеней свободы и уровня значимости 5%. Критическое значение GKP = 0,61.
Гипотеза об однородности дисперсий принимается, если, как в нашем случае,
экспериментальное значение критерия Кохрена не превышает табличного значения.
В нашем случае значимость
коэффициентов модели: 
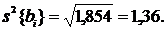
Из формулы видно, что дисперсии всех
коэффициентов равны друг другу, так как они зависят только от ошибки опыта и
числа опытов. Теперь рассчитаем значения tl-критерия по формуле
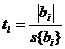 .
.
Получаем:



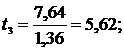
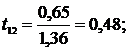

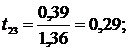
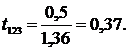
Критическое значение tKP находится
по таблице работы [11] при n(r- 1) = 16 степенях свободы и
заданном уровне значимости α= 5%. В нашем случае tKP> = 1,74. Если
ti>tKP , то гипотеза отвергается и коэффициент bi признается значимым. В
противном случае bi считается статистически незначимым, т. е.βi= 0. В
нашем случае такими незначимыми коэффициентами являются b12, b13, b23, b123.
Теперь можно построить доверительный интервал длиной 2Δbi, где

Коэффициент значим, если его
абсолютная величина больше половины длины доверительного интервала.
Ортогональное планирование позволяет определять доверительные границы для
каждого из коэффициентов регрессии в отдельности, если какой- либо из
коэффициентов окажется незначимым, он может быть отброшен без пересчета всех
остальных. После этого математическая модель объекта составляется в виде уравнения
связи выходного параметра у и переменных xi,
включающего только значимые коэффициенты. Для нашего примера получаем
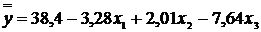 .
.
Чтобы получить модель в натуральных
переменных, надо в уравнение подставить выражения xi из формулы
преобразования.
Получаем

Статистическая незначимость
коэффициента bi может быть обусловлена следующими причинами:
) уровень базового режима xi0
близок к точке частного экстремума по переменной xl, т. е. 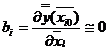 ;
;
) шаг варьирования Δxi выбран
малым;
) велика ошибка эксперимента
вследствие наличия неуправляемых и неконтролируемых переменных.
Если имеет место первая или третья причина,
значение фактора стабилизируется на определенном уровне, во втором случае
увеличивают интервал варьирования. Если имеет место четвертая причина, следует
принять меры к уменьшению ошибки эксперимента.
В нашем случае незначимость коэффициентов,
оценивающих взаимодействие (b12;
b13; b23;
b123), вызвана,
вероятно, отсутствием этих эффектов. В качестве величины, характеризующей вклад
коэффициентов регрессии в уравнение, иногда используют множественный
коэффициент корреляции R:

Где 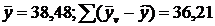 (см. табл.3);
(см. табл.3); 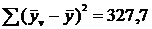 (табл.4).Таблица
4
(табл.4).Таблица
4
Расчет Σ(yv-y)2
|
№точки
v
|
  - -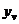 ( ( - -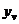 )2 )2
|
|
|
|
1
|
36,47
|
2,12
|
4,49
|
|
2
|
34,74
|
7,33
|
53,73
|
|
3
|
41,26
|
2,34
|
5,48
|
|
4
|
35,48
|
8,62
|
74,30
|
|
5
|
36,20
|
-10,35
|
107,12
|
|
6
|
40,92
|
3,14
|
9,86
|
|
7
|
41,60
|
-8,44
|
71,23
|
|
8
|
41,13
|
-1,22
|
1,49
|
|
У
=
|
38,48
|
|
Σ=327,7
|
Проведем оценку адекватности в нашем примере,
пользуясь данными расчетной табл.3;
Так как в нашем случае s2ад<s2{y} (35,2
<44,50), то адекватность модели очевидна без расчета критерия Фишера. Если
быв нашем случае оказались значимыми также и все коэффициенты при
взаимодействиях и, следовательно, число коэффициентов модели было бы т=8, то
тогда не оставалось бы ни одной степени свободы для оценки адекватности. Тогда
можно было бы прибегнуть к использованию условия b0 - ӯ0-> и таким
образом оценить значимость коэффициентов при членах второго порядка, а именно:
и таким
образом оценить значимость коэффициентов при членах второго порядка, а именно:

Эта величина меньше, чем ошибка
эксперимента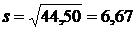 , из чего
следует, что квадратичные эффекты пренебрежимо малы и поэтому линейную модель
можно считать адекватной.
, из чего
следует, что квадратичные эффекты пренебрежимо малы и поэтому линейную модель
можно считать адекватной.