Способы решения функциональных уравнений
Содержание
Введение
. Операции над функциями, которые аналогичны
соответствующим операциям над действительными числами
. Свойства основных операций над функциями, которые
отличаются от свойств одноименных операций над действительными числами
Виды функциональных уравнений
.1 Функциональное уравнение Коши
.1.1 Класс непрерывных функций
.1.2 Класс монотонных функций
.1.3 Класс ограниченных функций
.1.4 Класс дифференцируемых функций
.2 Функциональное уравнение показательной функции
.3 Функциональное уравнение логарифмической функции
.4 Функциональное уравнение степенной функции
.5 Одно обобщение функционального уравнения Коши
. Методы решения функциональных уравнений
.1 Метод сведения функционального уравнения к
известному уравнению с помощью замены переменной и функции
.2 Метод подстановок
.3 Решение функциональных уравнений с применением
теории групп
.4 Применение теории матриц к решению функциональных
уравнений
.5 Применение элементов математического анализа к
решению функциональных уравнений
.5.1 Предельный переход
.6 Дифференцирование
Заключение
Список использованных источников
Введение
Подготовка школьного учителя математики безусловно предполагает, что он
обретет навыки сознательного владения математическими понятиями, которые должен
будет использовать по долгу службы. Однако не все так очевидно и категорично,
ведь некоторые фундаментальные математические понятия (например, понятие
действительного числа) слишком сложны. Что бы аккуратные их определения нашли
себе место в школьном курсе математики. Тем не менее, положение в нем такого
важного математического понятия, как функциональное уравнение, весьма уникально
и даже парадоксально: использование функциональных уравнений в школьном курсе
математики имеет место, а вот самого термина (имени) "Функциональное
уравнение" - нет. Вот и получается, что безымянное понятие (некий
математический аноним!) присутствует на страницах школьных учебников по алгебре
и началу анализа, как какой-нибудь герой невидимка, законспирированный до такой
степени, что даже сам как использования этого понятия, обычно ускользает от
всевидящего учительского ока. Но думается, что подобная не наблюдательность это
- вина не столько учителя, сколько результат некоторых пробелов в его
подготовке. Исправлению сложившегося положения, безусловно, послужили бы чтения
студентам-"математикам" специального курса по функциональным
уравнениям и методам их решения, проведения соответствующих практикумов по
решению математических задач и, наконец, организация занятий соответствующей
математике на курсах повышения квалификации учителей.
Ещё: даже несколько фраз, посвященных функциональных уравнениям и
сказанных на лекциях по методике преподавания математики, так же способствовали
бы исправлению сложившейся ситуации. Тем более, что функциональные уравнения хороший
материал для изучения и иллюстрации некоторых свойств основных операций над
числовыми функциями. Но пока функциональные уравнения забыты, увы, до такой
степени, что уже делаются попытки даже сам термин "функциональные
уравнения" использовать в качестве имени для "обычного"
уравнения вида
f(x)=φ(x),
где f(x) и φ(x)- обозначения для некоторых функций.
В первом разделе курсовой работы рассматриваются операции над
функциями, которые аналогичны соответствующим операциям над действительными
числами.
Во втором разделе курсовой работы рассматриваются свойства основных
операций над функциями, которые отличаются от свойств одноименных операций над
действительными числами
В третьем разделе курсовой работы рассматриваются виды функциональных
уравнений, функциональное уравнение Коши, класс непрерывных функций, класс
монотонных функций, класс ограниченных функций, класс дифференцируемых функций,
функциональное уравнение показательной функции, функциональное уравнение
логарифмической функции, функциональное уравнение степенной функции, одно
обобщение уравнения Коши
В четвертом разделе курсовой работы рассматриваются методы решения
функциональных уравнений, метод сведения функционального уравнения к известному
уравнению с помощью замены переменной и функции, метод подстановок, решение
функциональных уравнений с применением теории групп, применение теории матриц к
решению функциональных уравнений, применение элементов математического анализа
к решению функциональных уравнений, предельный переход, дифференцирование.
1. Операции над функциями, которые
аналогичны соответствующим операциям над действительными числами
Подготовка школьного учителя математики безусловно предполагает, что он
обретет навыки сознательного владения математическими понятиями, которые должен
будет использовать по долгу службы. Однако не все так очевидно и категорично,
ведь некоторые фундаментальные математические понятия (например, понятие
действительного числа) слишком сложны. Что бы аккуратные их определения нашли
себе место в школьном курсе математики. Тем не менее, положение в нем такого
важного математического понятия, как функциональное уравнение, весьма уникально
и даже парадоксально: использование функциональных уравнений в школьном курсе
математики имеет место, а вот самого термина (имени) "Функциональное
уравнение" - нет. Вот и получается,
что безымянное понятие (некий математический аноним!) присутствует на
страницах школьных учебников по алгебре и началу анализа, как какой-нибудь
герой невидимка, законспирированный до такой степени, что даже сам как
использования этого понятия, обычно ускользает от всевидящего учительского ока.
Но думается, что подобная не наблюдательность это - вина не столько учителя,
сколько результат некоторых пробелов в его подготовке. Исправлению сложившегося
положения, безусловно, послужили бы чтения студентам-"математикам"
специального курса по функциональным уравнениям и методам их решения,
проведения соответствующих практикумов по решению математических задач и,
наконец, организация занятий соответствующей математике на курсах повышения
квалификации учителей.
Ещё: даже несколько фраз, посвященных функциональных уравнениям и
сказанных на лекциях по методике преподавания математики, так же способствовали
бы исправлению сложившейся ситуации. Тем более, что функциональные уравнения
хороший материал для изучения и иллюстрации некоторых свойств основных операций
над числовыми функциями. Но пока функциональные уравнения забыты, увы, до такой
степени, что уже делаются попытки даже сам термин "функциональные уравнения"
использовать в качестве имени для "обычного" уравнения вида
f(x)=φ(x),
где f(x) и φ(x)- обозначения для некоторых функций.
Что бы подтвердить сказанное, прежде всего, напомним, что в школьном
курсе математики после рассмотрения понятий функции и определения равных
функций начинают заниматься основными ("арифметическими") операциями
над функциями, в частности изучают свойства этих операций.
Примечательно, что этот процесс изучения "оперативных" свойств
функций в рамках школьного курса математики включает в себя две линии, две
тенденции:
) Главенствующую тенденции - рассмотрения и использование тех свойств
основных операций над функциями, которые аналогичны соответствующим операциям -
"тезкам" над действительными числами;
2) Как бы второстепенную, теневую тенденцию - исследования тех
свойств основных операций над функциями, которые существенно отличаются от
свойств одноименных операций над действительными числами.
Первая линия представлена в школьных учебниках по алгебре и началом
анализа, разбором таких свойств, как ассоциативность и коммутативность сложения
и умножения функций, дистрибутивность умножение относительно сложения, а так же
ещё такими примечательными свойствами, как

 +{(x;0)|
+{(x;0)|
 }=f;
}=f;
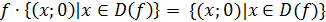
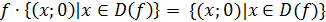 и
и


Эти
последние три свойства показывают, что функции

 +{(x;0)|
+{(x;0)|
 и
и 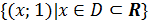
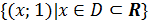
очень
похожи своими свойствами на действительные числа нуль и
единицу,
правда, таких "нулей" и "единиц" столько же, сколько
непустых подмножеств у множества действительных чисел R.
И тем не менее, не мудрствуя лукаво, эти функции обозначили в элементарной
математике соответственно символы 0 и 1, хотя точнее было бы обозначить 
 и
и 
 ведь их
бесконечно много, причем каждая "обслуживает" "свой" набор
функций с общей областью определения
ведь их
бесконечно много, причем каждая "обслуживает" "свой" набор
функций с общей областью определения
D
⊂R.
Аналогичным
образом поступили и с операциями сложения, умножения, вычитания и деления
функции: для обозначения результатов их применения, т.е. частного функции,
взяли "напрокат" знаки их арифметических тезок. То, что это чревато
определенными неприятными последствиями, подтверждают определенные трудности,
возникающие при попытке однозначно "расшифровать" такие записи, как
0+0=0, 1×0=0,
1×1=1.
Подобное
неоднозначность в понимании смысла обозначения уже в полнее может подвигнуть к
проявлению особой осторожности и большего внимания при решении задач на поиск
функции с заданными свойствами. Такая бдительность вдвойне оправдана и наличием
второй линии изучения "оперативных" свойств функции. Увы, но как раз
изучение принципиальных различий в свойствах арифметических операций над
действительными числами и одноименных операций над числовыми функция в школьном
курсе математики уделяют ничтожно мало времени. И в этом случае могли бы помочь
функциональные уравнения, пусть даже без упоминания самого этого термина. Что
бы подтвердить это, приведем несколько простых задач, поиски решения которых,
помогли бы и ученику и учителю более основательно изучить свойства операций над
функциями, возможно даже сделать для себя маленькие, но полезные открытия.
Задача
1.1
Укажите
все функции f(x) и D(x)=R и E(f)⊂R, удовлетворяющие
следующему
условию:
а)
 =
=

б)
 =
= 

в)
 =
= 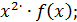
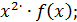
г)
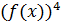
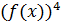 =
= 
 ;
;
д)
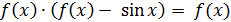
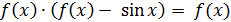
Задача
1.2
Укажите
все функции f(x), удовлетворяющих
следующему условию:
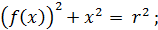
Где
r - произвольное фиксированное положительное число, с 
 и
и 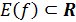
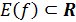 .
.
Естественно,
что решение задач 1.1 и 1.2 можно искать среди функций обладающих некоторыми
дополнительными свойствами (см. задачу 1.3)
Задача 1. 3
Укажите все функции-решения задачи 1.1, а затем задачи 1.2, обладающие
следующими дополнительными свойствами:
а) непрерывностью в каждой точке своей области определения;
б) дифференцируемостью в каждой точке своей области определения;
в) четностью, или нечетностью, или периодичностью.
Первые же попытки решить задачи 1.1 (а) и 1.1 (б) помогают обнаружить
существенное отличие свойств операции умножения функций от свойств
соответствующего арифметического тезки.
Действительно, если из функционального равенства
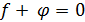
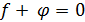
немедленно
следует, что 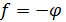
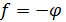 (что
аналогично выводу из арифметического равенства
(что
аналогично выводу из арифметического равенства 
 ), то
сделать вывод из функционального неравенства
), то
сделать вывод из функционального неравенства 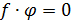
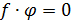 вывод,
аналогичный соответствующему "арифметическо -му" выводу (если
для двух действительных чисел
вывод,
аналогичный соответствующему "арифметическо -му" выводу (если
для двух действительных чисел 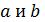
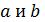 справедливо
равенство
справедливо
равенство 
 , то
, то 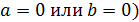
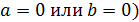 ,
совершенно не правомочно. Без труда можно привести пример двух функций, не
являющихся тождественными нулю, т.е. отличных от нуль-функции, чье произведение
равно нуль- функции.
,
совершенно не правомочно. Без труда можно привести пример двух функций, не
являющихся тождественными нулю, т.е. отличных от нуль-функции, чье произведение
равно нуль- функции.
Например,
таковыми являются функции
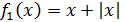
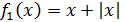 и
и 

с
областью определения R. Вот и получается, что решений у алгебраического
уравнения 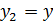
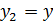 ровно два: 0 и 1, а у задачи 1.1 (а)- бесконечно
много. Приведем пример рассуждений, позволяющих описать все решения задач 1.1 и
1.2.
ровно два: 0 и 1, а у задачи 1.1 (а)- бесконечно
много. Приведем пример рассуждений, позволяющих описать все решения задач 1.1 и
1.2.
Решение
задачи 1.1 (а).
Пусть
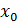
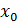 -
произвольное действительное число, тогда число
-
произвольное действительное число, тогда число 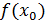
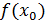 -
значение искомой функции
-
значение искомой функции 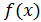
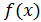 в точке
в точке 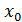
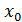 - должно
в соответствии с условием задачи удовлетворять равенству:
- должно
в соответствии с условием задачи удовлетворять равенству:
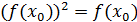
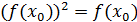 или
или 
 ,
,
а
значит,

 или
или 
 ,
,
т.е.
графику искомой функции (если таковая существует!) принадлежит точка 
 , либо
точка
, либо
точка 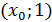
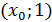 . Однако
было бы грубой ошибкой вывести сюда, что при "конструировании"
искомой функции надо назначить для всех значений аргумента одно и тоже
значение функции - число нуль, или одно и тоже значение - единицу. Можно ведь и
"чередовать" эти возможности при построении того или иного
конкретного решения данной задачи. В частности, её условию удовлетворяет и
знаменитая функция Дирихле
. Однако
было бы грубой ошибкой вывести сюда, что при "конструировании"
искомой функции надо назначить для всех значений аргумента одно и тоже
значение функции - число нуль, или одно и тоже значение - единицу. Можно ведь и
"чередовать" эти возможности при построении того или иного
конкретного решения данной задачи. В частности, её условию удовлетворяет и
знаменитая функция Дирихле
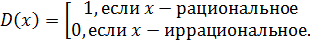
Очевидно
также, что всякая функция 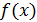
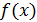 с
с 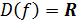
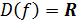 и
и 
 ,
удовлетворяющая условию
,
удовлетворяющая условию 
 или
или 
 для
любого
для
любого 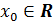
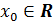 - это
решение задачи пусть и "неконструктивно", но с достаточно
удовлетворяющим ответом.
- это
решение задачи пусть и "неконструктивно", но с достаточно
удовлетворяющим ответом.
Ответ:
условию задачи 1.1 (а) удовлетворяет всякая определённая на R функция,
чей график принадлежит объединению двух прямых декартовой координатной
плоскости с уравнениями 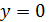
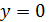 и
и 
 , и
других решений нет.
, и
других решений нет.
Аналогично
и для задачи 1.1 (б): все её решения - определенные на R функции, чьи графики лежат на "кресте", - принадлежат
объединению двух прямых декартовой координатной плоскости, заданной уравнениями
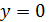
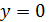 и
и 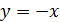
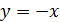 .
.
Так
же легко решить до конца задачу 1.1 и задачу 1.2. Но вот любопытно; и в
студенческой, и в учительской аудитории бывает весьма не просто убедить
слушателей, что у задачи 1.2 бесконечно много решений и наряду с такими
решениями, как функции
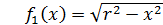
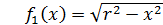 и
и 
 -
-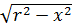
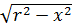 ,
, 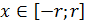
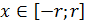 ,
,
будут,
например, такие:

 и
и
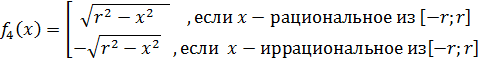
Обратимся
теперь к задачам 1.3 (а) и 1.3 (б). Для их решения удобно использовать
интуитивное представление о графике функции, заданной и непрерывной на
некотором промежутке, как о некоторой "непрерывной" линии, которую
можно вычертить, не отрывая карандаш от бумаги.
Покажем,
как можно получить решение задачи 1.3 (а), когда дополнительные требования
непрерывности накладываются на условие задачи 1.1 (б). Ради краткости примем
для обозначения этой задачи символ 3 (а)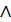
 1 (б).
1 (б).
Решение
задачи 1.3 (а)
 1.1 (б).
Прежде всего, любая, и в частности непрерывная, функция - решение этой задачи
обязана в точке
1.1 (б).
Прежде всего, любая, и в частности непрерывная, функция - решение этой задачи
обязана в точке 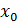
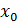 = -3
принимать значение - 3, или 3, так как других точке с абсциссой -3, кроме
(-3;-3) и (-3;3), на объединении графиков функции
= -3
принимать значение - 3, или 3, так как других точке с абсциссой -3, кроме
(-3;-3) и (-3;3), на объединении графиков функции 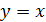
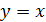 и
и 
 просто
нет.
просто
нет.
Рассмотрим
первый случай, когда график искомой функции (если таковая существует!) проходит
через точку (-3;3). Заставляя аргумент монотонно возрастать от -3 до 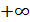
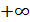 , вначале доберемся до его нулевого значения - абсциссы
общей точки (0;0) графиков функции
, вначале доберемся до его нулевого значения - абсциссы
общей точки (0;0) графиков функции 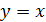
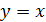 и
и 
 . При
этом переменная точка
. При
этом переменная точка 
 ,
вычерчивая соответствующую часть (от точки (-3;3) до точки (0;0)) графика
искомой непрерывной функции-решения, не сможет (именно потому, что нас
интересует непрерывное решение) покинуть график функции
,
вычерчивая соответствующую часть (от точки (-3;3) до точки (0;0)) графика
искомой непрерывной функции-решения, не сможет (именно потому, что нас
интересует непрерывное решение) покинуть график функции 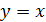
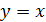 и
"перескочить" на график функции
и
"перескочить" на график функции 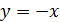
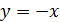 , т.е.
эта переменная точка будет непрерывно скользить по прямой
, т.е.
эта переменная точка будет непрерывно скользить по прямой 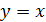
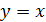 . Однако,
добравшись до точки (0;0), мы окажемся как бы в роли витязя на перепутье: либо
далее двинемся по той же линии - графику функции
. Однако,
добравшись до точки (0;0), мы окажемся как бы в роли витязя на перепутье: либо
далее двинемся по той же линии - графику функции 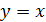
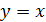 , что
даст нам первое решение задачи - функцию
, что
даст нам первое решение задачи - функцию 
 (заметим,
что для значений аргумента, меньших -3, подобных "развилок" нет!),
либо повернем на линию
(заметим,
что для значений аргумента, меньших -3, подобных "развилок" нет!),
либо повернем на линию 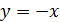
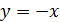 , что
даст нам ещё одно решение задачи:
, что
даст нам ещё одно решение задачи:
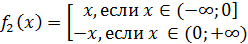
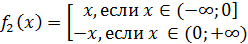 =
= 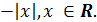
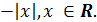
Во
втором случае, когда будем искать непрерывное решение, график которого проходит
через точку (-3;3), аналогичный анализ дает ещё два непрерывных на R решения
- функции 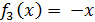
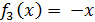 и
и 
 . И
других решений указанного класса нет.
. И
других решений указанного класса нет.
И
наконец, о причинах выбора точки 
 : конечно
же, вместо нее можно было бы взять любое отрицательное число и даже любое
ненулевое (лишь бы не нуль - абсциссу общей точки графиков функций
: конечно
же, вместо нее можно было бы взять любое отрицательное число и даже любое
ненулевое (лишь бы не нуль - абсциссу общей точки графиков функций 
 ).
).
Ответ:
условию задачи 1.3 (а)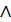
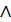 1.1 (б)
удовлетворяют ровно четыре функции, это
1.1 (б)
удовлетворяют ровно четыре функции, это
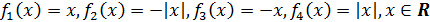
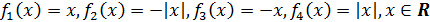
Решение
задачи 1.3 (б) 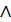
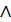 1.1 (б).
Помня о соотношении между непрерывностью и дифференцируемостью функции в точке,
мы должны будем осуществить выбор дифференцируемых на R функций из четырех решений задачи 1.3 (а)
1.1 (б).
Помня о соотношении между непрерывностью и дифференцируемостью функции в точке,
мы должны будем осуществить выбор дифференцируемых на R функций из четырех решений задачи 1.3 (а) 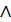
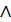 1.1 (б).
Таковыми окажутся
1.1 (б).
Таковыми окажутся
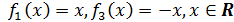
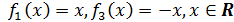 .
.
Ответ:
искомые функции
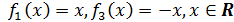
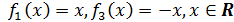 .
.
Для
задач 1.3 (а) 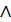
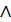 1.1 (а) и
1.3 (б)
1.1 (а) и
1.3 (б) 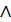
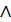 1.1 (а)
аналогичные рассуждения позволяют указать ровно два непрерывных и одновременно
дифференцируемых решения - функции
1.1 (а)
аналогичные рассуждения позволяют указать ровно два непрерывных и одновременно
дифференцируемых решения - функции 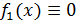
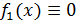 и
и 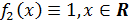
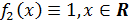 , т.е.
, т.е.

 .
.
2.
Свойства основных операций над функциями, которые отличаются от свойств
одноименных операций над действительными числами
Продемонстрировав некоторые возможности применения функциональных
уравнений в элементарной математике, перейдем теперь к рассказу об их реальном,
хотя и малозаметном присутствии (и уже не один десяток лет!) в школьном курсе
математики. Но прежде чем как узнать разделы и понятия школьного курса, под
сенью которых скрываются функциональные уравнения, напомним, как в математике
определяют это понятие: функциональное уравнение - это уравнение, в котором
неизвестным является функция, связанная при помощи образования сложной функции
с известными функциями.
А вот теперь, помня, что бесконечная числовая последовательность - это
произвольная вещественнозначная функция с областью определения - множеством
натуральных чисел, внимательно присмотримся к определениям бесконечной
арифметической и бесконечной геометрической прогрессий.
Бесконечная
арифметическая прогрессия определяется как последовательность 
 ,
удовлетворяющая условию
,
удовлетворяющая условию
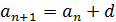
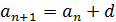 ,
,
где
d - фиксированное
действительное число, а n -любое натуральное.
Иначе
говоря, бесконечная арифметическая прогрессия в школьном курсе математики
определяется как решение следующего функционального уравнения:

 . (2.1)
. (2.1)
Аналогичная
ситуация и с бесконечной геометрической прогрессией. Она определяется в
школьном курсе математики как функциональное уравнение вида:
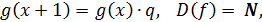
где
q - произвольное фиксированное ненулевое действительное
число.
Далее,
чтобы найти в явном виде выражение для 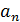
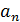 как
аналитически заданную функцию от n, обычно решают эти функциональные
уравнения по традиционной схеме, реализацию которой продемонстрируем на примере
уравнения (1).
как
аналитически заданную функцию от n, обычно решают эти функциональные
уравнения по традиционной схеме, реализацию которой продемонстрируем на примере
уравнения (1).
1. В начале производят накопление "экспериментальных" данных
- находят выражение для f(1), f(2), f(3) и т.д.
2. Затем строят на основе этого "эксперимента" гипотезу,
что
f(x)=
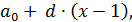
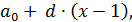
где
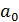
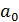 = f(1)
- произвольное, но фиксированное число. И, наконец, последний этап.
= f(1)
- произвольное, но фиксированное число. И, наконец, последний этап.
3. Проверяют справедливость того, что функция f(x) - удовлетворяет условию (1) при любом натуральном x.
И при этом ни слова о функциональных уравнениях!
Далее обычно следует поиск формулы для суммы первых n членов этих последовательностей S(n) (как говорят в математике "в конечном виде").
Для этого в школьных учебниках применяют специальные искусственные методы, а по
сути, опять-таки осуществляют поиск решения функционального уравнения так
называемого разностного типа
F(x+1) - F(x) = φ(x) (2.2)
где φ(x) - известная функция, D(φ) = N, которому очевидно удовлетворяет
функция S(n), если φ(x)-(x+1) -й член суммируемой
последовательности.
Стоит напомнить, что уже давно найдены приемы вычисления сумм вида
φ(1)+φ(2)+…+φ(n),
где
φ(x) - известная функция, x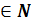
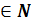 , т.е.
способы решения так называемой основной теории исчисления конечных разностей, в
частности давно и без труда получена общая формула, аналогична формуле Ньютона
- Лейбница:
, т.е.
способы решения так называемой основной теории исчисления конечных разностей, в
частности давно и без труда получена общая формула, аналогична формуле Ньютона
- Лейбница:
φ(1)+φ(2)+…+φ(n)=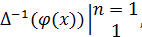
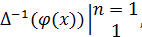
где
символом 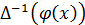
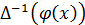 - обозначено любое решение уравнения (2).
- обозначено любое решение уравнения (2).
Действительно,
если 
 любое
конкретное решение уравнения (2),
любое
конкретное решение уравнения (2),
D(f)
= N, то
φ(k) = 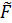
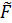 (к+1)
(к+1)

а
значит
φ(1)+φ(2)+…+φ(n)=

=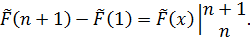
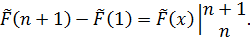
Например,
так как
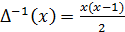
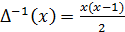 , то 1+2+3+…+n =
, то 1+2+3+…+n =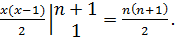
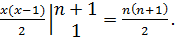
Вспомним
теперь школьную задачу на исследование заданной функции на четность и
нечетность. Легко обнаружить, что ее решение есть ни что иное, как проверка,
является ли исследуемая функция решением функционального уравнения вида:
F(x)=
F(-x) (уравнения четности)
и
функционального уравнения вида:
F(x)=
- F(-x) (уравнения нечетности),
причем
исследуемая функция может удовлетворять обоим уравнениям одновременно. При этом
очевидно, что любое решение системы
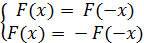
Есть
нуль-функция 
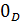 , где D -
произвольное непустое подмножество число вой оси
, где D -
произвольное непустое подмножество число вой оси 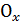
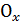 ,
симметричное относительно точки 0.
,
симметричное относительно точки 0.
С
задачей на исследование заданной функции на периодичность ситуация несколько
сложнее, ведь требуется выяснить, существует или нет функциональное уравнение в
классе так называемых уравнений периодичности:
F(x+T)
= f(x),
где Т - любая ненулевая константа, чьим решением является исследуемая
функция. Эта задача, безусловно, сложнее двух предыдущих, ведь даже для наперед
заданного числового множества M,
придумать уравнение или неравенство (используя средства школьной математики),
чьим множеством решений будет именно эта совокупность М, весьма не
просто. Так, например, сообразишь далеко не в считанные мгновения, что для M=N искомым уравнением будет

 или
или 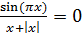
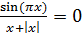
Завершая
рассказ о "невидимках" школьного курса математики по имени
функциональные уравнения, хочется напомнить, что знаменитая
последовательность Фибоначчи 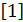
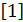 - это
решение функционального уравнения вида:
- это
решение функционального уравнения вида:

 ;
;
что
теорема о существовании и единственности представления всякой функции с
симметричной относительно точки 0 областью определения в виде суммы некоторой
четной и некоторой нечетной функций - это результат системы исследования двух
функциональных уравнений относительно двух неизвестных функций; и наконец, что
простейшие элементарные функции можно определить как решения специальных
"характеристических" функциональных уравнений. Кроме того,
функциональные уравнения и методы их решения (метод подстановки, метод Коши,
метод "сведения на себя" и т.д.) - прекрасная тема для цикла занятий
школьного математического кружка или факультатива, тем более что задачи на
исследование функциональных уравнений - обычные гости математических олимпиад
школьников, причем олимпиад самого высокого уровня.
3. Виды функциональных уравнений
3.1
Функциональное уравнение Коши
Одним из наиболее исследованных в математике является функциональное
уравнение Коши
f(x+y) = f(x) +f(y), D (f) =R (3.1.1)
Теорема 3.1 Линейные однородные функции вида
f(x) = ax (a = const)
удовлетворяют этому уравнению и являются единственными.
Доказательство.
То, что данная функция удовлетворяет уравнению легко проверить:
f(x+y) = a(x+y) = ax + ay = f(x) + f(y)
Вопрос состоит в том, будут ли эти функции единственными.
Прежде всего, выведем несколько общих фактов, не накладывая никаких ограничений
на функцию f (т. е. без всяких предположений о непрерывности,
ограниченности и т. п.).
Положим в уравнении y = x, получим:
f(2x) = 2f(x).
Далее, последовательно полагая y = 2x, y = 3x, y = 4x и т. д.,
имеем:
f(3x) = f(x+2x) = f(x)+f(2x) = f(x)+2f(x) = 3f(x);(4x)
= f(x)+f(3x) = 4f(x);(5x) = f(x)+f(4x) = 5f(x),
и вообще, для любого натурального n
f(nx) = n·f(x) (3.1.2)
(это
легко проверяется по индукции). Заменив здесь x на 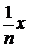 , мы получим
, мы получим
 ,
,
а
затем, если подставить mx (m - натуральное) вместо x и использовать предыдущее
равенство, придём к соотношению
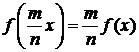 , (3.1.3)
, (3.1.3)
Положим
теперь в основном уравнении (3.1.1) x = y = 0; получим
f(0)
= 2f(0), так что f(0) = 0.
(3.1.4)
Если
же взять y = -x, то:
0 = f(x - x) = f(x) + f(-x)(-x) = -f(x),
так
что функция f(x) является нечётной. А тогда из (3.1.1) легко вывести:
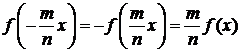 (3.1.5)
(3.1.5)
Полученные
соотношения (3.1.3) - (3.1.5) могут быть объединены в равенстве
f(rx)
= r·f(x),
справедливом
для любого вещественного значения x, каково бы ни было рациональное число r.
Если
взять здесь x = 1, то получим
f(r)
= r·f(1) (3.1.6)
или,
если обозначить f(1) через a,
f(r)
= ar.
Таким
образом, мы, собственно говоря, установили уже вид функции f, но пока
лишь для рациональных значений аргумента. При этом мы использовали только тот
факт, что функция удовлетворяет основному уравнению Коши (3.1.1). Далее в
решении мы будем уже опираться на конкретный класс функций, в котором ищется
решение. Рассмотрим некоторые наиболее общие классы функций, используемых при
решении
3.1.1
Класс непрерывных функций
Для
рациональных x мы установили, что f(x) = ax. Осталось
показать, что это соотношение справедливо и для иррациональных x. Пусть x
будет любое иррациональное число. Тогда существует последовательность
рациональных чисел 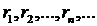 , сходящаяся к этому числу x (это известный факт; можно,
например, взять отрезки соответствующей бесконечной десятичной дроби). По
доказанному
, сходящаяся к этому числу x (это известный факт; можно,
например, взять отрезки соответствующей бесконечной десятичной дроби). По
доказанному
f(rn)
= arn (n = 1,2,3, . . .).
Перейдём
здесь к пределу при 

Справа
мы получим ax, слева же, именно ввиду предположенной непрерывности
функции f, получится
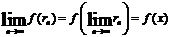
так
что, окончательно,
f(x)
= ax.
Таким
образом, действительно, все непрерывные аддитивные функции являются линейными
однородными. Последняя формула даёт самое общее решение функционального
уравнения (3.1.1).
3.1.2 Класс
монотонных функций
Здесь
мы будем предполагать, что функция f не убывает на всей действительной
оси (случай невозрастания функции рассматривается аналогично). Значит  для любых x1 < x2.
для любых x1 < x2.
Для
рациональных x доказано f(x) = x·f(1). Возьмём произвольное
иррациональное x. Известно, что любое иррациональное число можно сколь
угодно точно приблизить рациональными числами, поэтому для любого натурально q
существует целое p такое, что
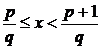 (3.1.2.1)
(3.1.2.1)
и
при достаточно больших q число x расположено между двумя очень
близкими рациональными числами, разность между которыми равна  . Используя монотонность функции f, находим
. Используя монотонность функции f, находим
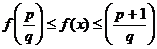
откуда
(воспользовавшись соотношением для рациональных значений функции f)
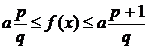 , a
= f(1). (3.1.2.2)
, a
= f(1). (3.1.2.2)
Так
как из (3.1.1.4) f(0) = 0, то , ведь
функция f не убывает, значит,
, ведь
функция f не убывает, значит,
Если
a = 0, то из неравенств 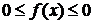 имеем
имеем 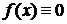 .
.
Если
a = 0, то из (3.1.2.2)
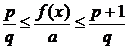 .
(3.1.2.3)
.
(3.1.2.3)
Сравнивая
эти неравенства с (3.1.2.1), получим

Покажем это. Предположим, что это неверно, например,
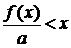
для
выбранного иррационального x. Подберём q настолько большим, чтобы дробь 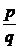 попала между
попала между 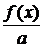 и x
и x

что
противоречиво с (3.1.2.3). Полученное противоречие показывает, что

для
любого заданного иррационального x, поэтому f(x) = ax для всех x.
3.1.3
Класс ограниченных функций
Пусть теперь функция f(x) ограничена с одной стороны (т. е.
ограничена либо сверху, либо снизу) на каком-либо интервале (a, b). Нам
нужно доказать, что линейными однородными функциями исчерпываются все решения
(3.1.1) в данном классе. Мы исследуем решение уравнения (3.1.1), предполагая f
ограниченной сверху (случай, когда f ограничена снизу, сводится к
рассматриваемому случаю заменой f на -f).
Будем
считать, что функция f ограничена сверху константой M, т. е. 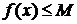 для всех
для всех  .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
g(x) = f(x) - x·f(1).
По доказанному выше g(x) = 0 при любом рациональном x.
Кроме того, функция g(x) также является аддитивной. Действительно,
g(x + y) = f(x + y) - (x + y)·f(1) = f(x) + f(y) - xf(1) -
yf(1) = g(x) + g(y).
Подставим y = r (r - рациональное) в равенство
g(x+y) = g(x)+g(y),
получим, учитывая g(r) = 0,
g(x+r) = g(x)+g(r) = g(x).
Значит, любое рациональное число r является периодом функции g(x).
Покажем теперь, что g(x) ограничена на интервале (a, b).
Имеем

где
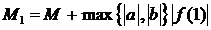 ,
,
поскольку
 при
при  .
.
Отсюда
тогда следует, что g(x) ограничена сверху на всей вещественной оси. В самом
деле, для любого действительного x существует рациональное число r такое, что r
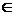 (a-x, b-x),
т. е. a < x+r < b. Поэтому
(a-x, b-x),
т. е. a < x+r < b. Поэтому
g(x)
= g(x+r) < M1,
так
как x + r 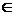 (a, b), а
на интервале (a, b) функция g ограничена числом M1.
(a, b), а
на интервале (a, b) функция g ограничена числом M1.
Сейчас
уже можно утверждать, что g(x) = 0 для любого действительного x.
Допустим это не так, т. е. для некоторого x0
g(x0)
= A, A  0.
0.
Поскольку
для функции g(x), как для любой аддитивной функции, верно соотношение
(4.1.2), то
g(nx0)
= ng(x0) = nA
для
любого целого n. Очевидно, что можно подобрать такое n (может быть, достаточно
большое по абсолютной величине), что
nA
> M1, т.е. g(nx0)
> M1.
Но
функция g ограничена сверху константой M1. Получаем противоречие.
Значит, g(x) 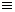 0, откуда f(x)
= x·f(1), что и требовалось.
0, откуда f(x)
= x·f(1), что и требовалось.
3.1.4
Класс дифференцируемых функций
Известно,
что если функция f (х) дифференцируема
в точке х 0, то она непрерывна в этой точке, Как показывает пример
функции f(x)=|x|, обратное утверждение, вообще говоря, неверно. Поэтому
класс дифференцируемых функций уже класса непрерывных функций. Следовательно,
решением уравнения Коши в классе дифференцируемых функций является линейная
однородная функция. Тем не менее, метод решения уравнения Коши в предположении
дифференцируемости f(x)
представляет интерес ввиду его простоты. При фиксированном у 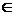 R f (х + у) и f(х)
+ f (у) являются функциями переменной
х
R f (х + у) и f(х)
+ f (у) являются функциями переменной
х 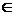 R. Ввиду их равенства, равны и их производные
(по переменной x!). Продифференцировав обе части равенства (3.1.1),
получим
R. Ввиду их равенства, равны и их производные
(по переменной x!). Продифференцировав обе части равенства (3.1.1),
получим
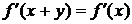 (3.1.4.1)
(3.1.4.1)
( , как производная постоянной). Равенство (3.1.4.1)
выполняется для любых х
, как производная постоянной). Равенство (3.1.4.1)
выполняется для любых х 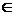 R,
у
R,
у 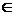 R, так как у можно было выбрать
произвольно, Положив в(3.1.4.1) х = 0, придем к тождеству
R, так как у можно было выбрать
произвольно, Положив в(3.1.4.1) х = 0, придем к тождеству
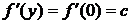
для
всех у 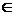 R. Итак,
R. Итак,  - постоянная функция. Поэтому ее первообразная
- постоянная функция. Поэтому ее первообразная
f (х) = сх + b (3.1.4.2)
где
b - некоторое
действительное число. Проверка показывает, что (3.1.4.2) удовлетворяет (3.1.1)
только при b = 0, с 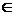 R.
R.
Существуют и другие классы функций, в которых аддитивная функция
неминуемо будет являться линейной однородной, однако найден пример аддитивной
функции и в классе разрывных функций. Этот пример построил Гамель. Построенная
функция обладает следующим свойством: на любом (произвольно выбранном)
интервале (a, b), пусть даже сколь угодно малом, функция f(x) не
ограничена, т. е. среди значений, которые данная функция принимает на этом
интервале, имеется и такое, которое больше любого наперёд заданного
положительного числа. Для построения такой функции Гамель ввёл множество G
действительных чисел, называемое теперь базисом Гамеля, которое обладает
свойством, что любое действительное число x представимо и при том
единственным способом в виде
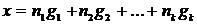 ,
, 
Произвольно
задав значения f(x) в точках множества G, можно однозначно продолжить её
на всю числовую прямую при помощи равенства
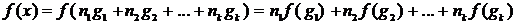
вытекающего
из свойства аддитивной функции. Такими функциями исчерпываются все решения
(3.1.1).
Приведем
пример данной функции.
x = 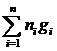 .
.
Покажем,
что функция f(x) = 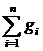 удовлетворяет
нашему уравнению.
удовлетворяет
нашему уравнению.
f(x+y) = f(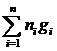 .+
.+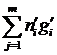 ) =
) = 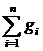 +
+ 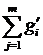 = f(x) + f(y)
= f(x) + f(y)
Очевидно,
что она отлична от уже найденного нами решения. Предыдущее же решение
единственное в классе непрерывных функций, следовательно, это решение является
разрывным.
3.2
Функциональное уравнение показательной функции
Теорема 3.2.1 Все непрерывные на всей действительной прямой функции,
удовлетворяющие функциональному уравнению
f(x+y) = f(x) ·f(y), (3.2.1.1)
задаются формулой
f(x) = ax
(a>0, а ≠ 1)
(если не считать функции, тождественно равной 0).
Доказательство. Пусть f(x) - непрерывная и определённая при всех действительных x
функция, удовлетворяющая (3.2.1.1). Исключим тривиальное решение f(x)
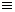 0. Тогда для некоторого значения x
= x0 эта
функция отлична от нуля. Положим y = x0 - x:
0. Тогда для некоторого значения x
= x0 эта
функция отлична от нуля. Положим y = x0 - x:
f(x)
·f(x0-x)
= f(x0)  0;
0;
отсюда
ясно, что f(x) не равна
нулю ни при каком x. Заменяя x и y
в (3.2.1.1) на x/2, получим

так
что f(x) строго
больше 0 для всех x. Тогда равенство (3.1.2.1) можно прологарифмировать,
например, по основанию e:
lnf(x+y) = lnf(x) + lnf(y).
Положив
в этом соотношении φ(x = lnf(x)), придём к
функциональному уравнению Коши (3.1.1):
φ(x+y)
= φ(x) + φ(y).
Учитывая,
что φ - непрерывная функция (как суперпозиция непрерывных
функций), имеем по доказанному:
φ(x) = lnf(x) = cx
(c = const),
откуда находим, что
f(x) = eсx = ax (если положить a = ec).
Таким образом, единственной непрерывной функцией, удовлетворяющей
уравнению Коши (3.2.1.1), является показательная функция (или тождественно
нулевая функция).
В качестве класса функций, в котором искалось решение, мы рассмотрели
лишь класс непрерывных функций. Как и в предыдущем пункте, можно было бы
разобрать решения для монотонных и ограниченных функций, но этого мы делать не
будем, потому что (3.2.1.1), как было подмечено, сводится к (3.1.1), а для него
всё ясно.
3.3
Функциональное уравнение логарифмической функции
Теорема 3.3.1 Все непрерывные решения функционального уравнения
f (xy) = f(x) + f(y), (3.3.1)
справедливого для всех положительных значений x и y,
имеют вид
f(x)
= loga x (a
> 0, a  1).
1).
Доказательство. Для этого введём новую переменную ξ, изменяющуюся в промежутке (- ; +
; +  ), и
положим
), и
положим
x = eξ (ведь x > 0), φ(ξ) = f(eξ),
откуда
ξ = lnx, f(x) = φ(lnx).
Тогда функция φ удовлетворяет функциональному
уравнению (3.1.1):

а
потому
 и f(x)
= clnx.
и f(x)
= clnx.
Если
исключить случай c = 0 (тогда f(x)
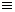 0), то
полученный результат может быть написан в виде
0), то
полученный результат может быть написан в виде
f(x) =
loga x, a = e1/c.
3.4
Функциональное уравнение степенной функции
Теорема 3.4.1 Функциональному уравнению
f(xy) = f(x)·f(y) (x > 0, y > 0)
(3.4.1.1)
удовлетворяют в классе непрерывных функций только функции вида
f(x) = xa.
Доказательство. Прибегая к той же подстановке, что и в п. 3.1.4.1, мы
приведём уравнение (3.4.1.1) к уравнению (3.1.1):
 ,
,
откуда
φ(ξ) = cξ (c >0), и, значит, f(x) = clnx = xa (a = lnc).
Метод
последовательного анализа можно применить к решению других уравнений.
3.5 Одно
обобщение функционального уравнения Коши
Теорема 3.5.1 Пусть n -
фиксированное натуральное число. Рассмотрим функциональное уравнение
 (3.5.1)
(3.5.1)
где
D (f) = R. Решение данного уравнения при n
> 1 является непрерывной функцией.
Доказательство.
При
n = 1 уравнение обращается в уравнение Коши. Как было
показано, в классе непрерывных функций единственным решением уравнения Коши
является линейная однородная функция. Из результатов Гамеля следует, что и
разрывные функции могут удовлетворять уравнению Коши. Покажем, что решение
уравнения (3.5.1) при n > 1 является
непрерывной функцией.
Полагая
х = у = 0, получим f (0) = 0.
Поэтому при х = 0 из (3.5.1) имеем f(уn) = (f(y))n для всех у 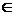 R.
Каждое неотрицательное число z может быть записано в виде z = уn. Отсюда
R.
Каждое неотрицательное число z может быть записано в виде z = уn. Отсюда
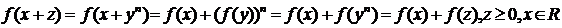

т.е.
f(-z) = - f (z), z 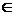 R.
Если
R.
Если  , то
, то

Отсюда
следует что
f(х + w)
= f(х) + f(w)
для
всех х 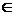 R, w
R, w 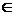 R, т. е.
f(х) -
аддитивная функция. Для аддитивной функции при рациональных t имеет
место соотношение f(tw) = tf (w).
Легко видеть, что
R, т. е.
f(х) -
аддитивная функция. Для аддитивной функции при рациональных t имеет
место соотношение f(tw) = tf (w).
Легко видеть, что
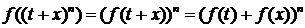 (3.5.2)
(3.5.2)
Воспользовавшись
формулой Ньютона
 ,
, 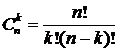
и
аддитивностью f(x), преобразуем отдельно левую и правую части (3.5.2)
при рациональных t:
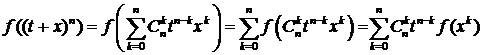 ;
;

Правые
части последних двух равенств представляют собой многочлены от t.
Приравнивая коэффициенты при одинаковых степенях t, получим
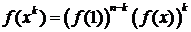 ,
,  .
.
В
частности, для k = 2 имеем
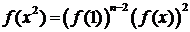 . (3.5.3)
. (3.5.3)
Если
(f(1))n-2 > 0, то f(x)
- неубывающая функция. Действительно, всякое у > 0 представимо в виде
у = х 2, поэтому из (3.5.1.3) имеем f(у) = f(x2) ≥ 0. При х1 > x2, х1 - x2> 0, f(x1 -
x2) ≥
0, или, в силу аддитивности f(х),
f (x1)
- f (х 2) ≥ 0. Если
же (f(1))n
-2 < 0, аналогично доказывается, что функция f(х) - невозрастающая.
Ранее
было доказано, что если аддитивная функция монотонна, то она имеет вид f(х)
= ах.
Полагая
в (3.5.3) х = 1, получим, что f(1) равно 0 или 1 при четном n и f(1) равно 0, 1 или -1 при нечетном n
> 1.
Итак,
f (х) = х либо f(х) = 0 при
четных n; f (x) = х, либо f (х) =
-х, либо f(х) = 0 при нечетных n > 1.
Тем
самым доказана не только непрерывность решения уравнения (3.5.1) при n
> 1, но и получен его вид.
4. Методы решения функциональных
уравнений
4.1 Метод
сведения функционального уравнения к известному уравнению с помощью замены
переменной и функции
Рассмотрим определённые типы функциональных уравнений, которые можно
свести к уравнениям, общие решения которых мы уже знаем. Как правило, такие
уравнения сводятся к основным уравнениям Коши (3.1.1) - (3.4.1). Метод основан
на введении вспомогательной функции, которую следует подобрать таким образом,
чтобы после преобразований было ясно, что она удовлетворяет одному из известных
функциональных уравнений.
Пример 4.1.1 Найти все непрерывные функции f (x), определенные на промежутке (0;∞), для которых
разность f (x1y) - f(x2y) при произвольных допустимых значениях х 1
и х 2 не зависит от у.
Решение. По условию, выражение f (ху) - f (у) (хг = х, х2 = 1) не зависит
от у, Поэтому
f(xy) - f(y) = f(x) - f(1).
Положив
g (х) = f (x) - f (1),
получим функциональное уравнение Коши
g(xy) = g(x) + g(y).
Известно, что в классе непрерывных функций
g (x) = сlnх.
Отсюда
f (х) = cln x+b, где b = f(1).
Проверка показывает, что условию задачи удовлетворяют функции
f (х) = сln х + b
при произвольных b и с.
Рассмотрим пример, считая х 1 и х
2 различными фиксированными числами. Так как f (х1y) - f (х2у) не зависит от у, то
f (х1y) - f (х2у) = с.
Пусть
х2у = х,
тогда
f(ах) = f (x)+c,
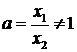
где,
а > 0, с - постоянная. Заменив х на ех, получим

Вычитая
из обеих частей 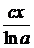 , получим
, получим
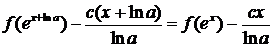 ,
,
или
g(x + lna) = g(x), (4.1.1)
где
 .
.
Уравнению
(4.1.1) удовлетворяют периодические с периодом lnа функции. Отсюда
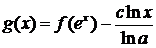
При
проверке убеждаемся, что функции вида
f(х) = g(ln x) + αlnx,
где
α - произвольная константа, а g(х) - непрерывная периодическая с периодом 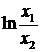 функция, обладают требуемым свойством.
функция, обладают требуемым свойством.
Пример
4.1.2 Известно, что сложение
действительных чисел обладает сочетательным свойством:
(х
+ у) + z = х + (у + z)
для
любых х, y, z  R.
Требуется найти все непрерывные функции f(х), "сохраняющие" сочетательность, т. е.
R.
Требуется найти все непрерывные функции f(х), "сохраняющие" сочетательность, т. е.
f(х + у)
+ f(z) = f(х) + f(у
+ z) (4.1.2.1)
Решение. Перепишем
(4.1.2.1) в виде
f(х + у) - f(x) = f(у + z) - f(z)
Легко видеть, что левая часть не зависит от х,
т.е.
f(х + у) - f(x) = g(y)
При х = 0 имеем
f(у) = g (у) + а, а = f(0).
Пришли к функциональному уравнению Коши
 .
.
Его
непрерывным решением являются функции g(х) = сх. Таким образом,
f (х) =
сх + а,
где
а и с - произвольные константы.
4.2 Метод
подстановок
Заменяя некоторые переменные функционального уравнения либо конкретными
значениями, либо какими-либо другими выражениями пытаемся либо упростить это
уравнение, либо привести его к такому виду, что дальнейшее решение станет
очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде
случаев он позволяет отыскать решения в классе всевозможных функций. Поясним
метод на следующих примерах.
Пример 4.2.1. Найти все функции f(x), заданные на промежутке
 ,
,
для
которых выполнено равенство
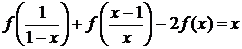
Решение. Выполнив
последовательно две замены  ;
;
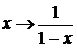 приходим к
системе функциональных уравнений:
приходим к
системе функциональных уравнений:
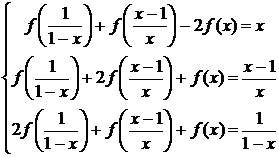
Последнее
уравнение есть сумма первых двух, умноженных на -1, т. е. из данной системы
функция f(x)
однозначно не определяется. Из первых двух уравнений находим

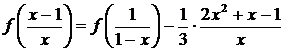
Мы
можем определить f(x)
произвольным образом на одном из интервалов 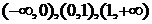 и эти
формулы дадут нам расширение f(x) на всё
множество I.
и эти
формулы дадут нам расширение f(x) на всё
множество I.
Пример
4.2.2 Найти решение системы
функциональных уравнений относительно неизвестных функций f(x) и g(x):

Решение. В первом
уравнении сделаем подстановку 2x = 1/z.
При
этом

и
первое уравнение принимает вид:
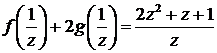
или
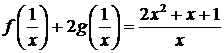
В
результате получаем систему уравнений:

решение которой
g(x) = 1/x, f(x) = x+1.
Пример 4.2.3 Найти все решения функционального уравнения
f(xy)
= yk f(x), k 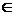 N.
N.
Решение. Положим в
уравнении x = 0: f(0) = yk f(0). Так как y -
произвольно, то f(0) = 0.
Пусть
теперь x ≠ 0. Подставим в уравнение
 ,
,
получим:
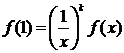 или
или 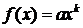 (a=f(1))
(a=f(1))
Функция
f(x) = axk является решением исходного уравнения.
Пример
4.2.4 Пусть 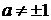 - некоторое действительное число. Найти функцию f(x),
определённую для всех x ≠ 1 и удовлетворяющую уравнению
- некоторое действительное число. Найти функцию f(x),
определённую для всех x ≠ 1 и удовлетворяющую уравнению
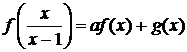 ,
,
где
g - заданная функция, определённая при x ≠ 1.
Решение. При замене 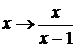 получаем
систему
получаем
систему
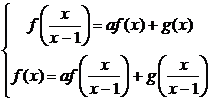 .
.
решением
которой при a2 ≠ 1 является функция

4.3
Решение функциональных уравнений с применением теории групп
В уравнении
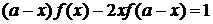
под
знаком неизвестной функции f(x) стоят
функции
g1
= х и g2 = а - х.
В
результате замены х на а - х получено еще одно уравнение,
содержащее те же функции f (х) и f (а - х). Функции g1 и g2
образуют группу относительно композиции функций. Понятие группы позволяет в
ряде случаев выбрать целесообразные подстановки для решения функциональных
уравнений.
Пусть
в функциональном уравнении
 (4.3.1)
(4.3.1)
выражения
f0(x)
= x, f1(x), …, fn-1(x), стоящие
под знаком неизвестной функции g (x), являются элементами конечной
группы порядка n относительно композиции функций. Коэффицненты
уравнения (4.3.1) а0, а1 ..., аn-1, b в общем случае
зависят от x. Некоторые из них могут равняться 0. Предположим, что
уравнение (4.3.1) имеет решение. Заменим х на f1(x).
Эта замена равносильна умножению справа всех элементов группы f1. В результате
последовательность функций f0, f1, …, fn-1
перейдет в последовательность 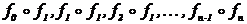 , состоящую
из всех элементов группы.
, состоящую
из всех элементов группы.
Произведенная
замена перевела уравнение (4.3.1) -линейное относительно неизвестных g(f0), g(f1), …,g(fn-1) -
в новое линейное уравнение относительно тех же неизвестных. Заменяя далее x → f2(x), x →
f3(x),…,
x →
fn(x) получим систему
n линейных уравнений с n неизвестными.
Решая
эту систему, находим неизвестную функцию g(f0) = g(x), если, конечно, система имеет решение.
Непосредственной проверкой следует убедиться, что полученная функция
удовлетворяет исходному уравнению. Рассмотренный метод ограничивает область
определения функции, так как приходится отбрасывать те значения аргумента, при
которых элементы группы не имеют смысла.
Пример
4.3.1 Найти функцию f (х),
определенную на множестве действительных чисел, отличных от 0, 1, -1, и
удовлетворяющую уравнению
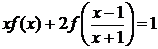 (4.3.2)
(4.3.2)
Решение. Выражения 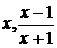 , стоящие под знаком неизвестной функции f,
являются элементами группы, заданной таблицей:
, стоящие под знаком неизвестной функции f,
являются элементами группы, заданной таблицей:
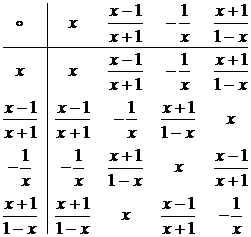
Заменяя
последовательно х на 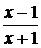 ,
,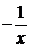 ,
,  , получим
систему
, получим
систему

Последовательно
исключая неизвестные  ,
, ,
, 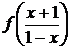 , имеем
, имеем

Рассуждения вытекали из предположения, что решение
уравнения (4.3.2) существует. Подставляя в (4.3.2) полученную функцию,
убедимся, что она удовлетворяет уравнению.
Пример 4.3.2 Найти функцию f(x), х ≠ 0, х ≠ а, удовлетворяющую
уравнению
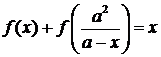
где
а - постоянная, отличная от 0.
Решение. Нетрудно
проверить, что выражения х,  , вместе
с
, вместе
с  составляют группу с таблицей:
составляют группу с таблицей:

Здесь
x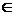 R\{0, а}.
R\{0, а}.
Рассуждая
аналогично решению примера 4.3.1, получим систему
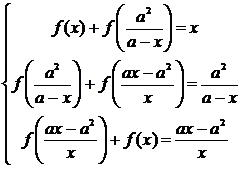
из
нее находим
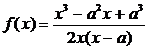 .
.
Проверка
показывает, что эта функция удовлетворяет уравнению.
Иногда
в функциональном уравнении выражения, стоящие под знаком неизвестной функции,
являются значениями элементов некоторой группы от одной и той же функции g.
После замены g(x) на x получаем
уравнение, которое решается изложенным выше методом.
Рассмотрим
функциональные уравнения, в которых под знаков неизвестной функции стоят, кроме
выражений, зависящих от х, и константы.
4.4
Применение теории матриц к решению функциональных уравнений
Под
знаком неизвестной функции могут стоять дробно-линейные выражения вида 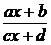 . Такие дроби полностью определяются заданием матрицы
. Такие дроби полностью определяются заданием матрицы 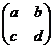 , составленной из коэффициентов a, b, c, d.
, составленной из коэффициентов a, b, c, d.
Пример
4.4.1 Найти функцию f,
определенную при  и
удовлетворяющую уравнению
и
удовлетворяющую уравнению
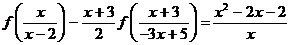 (4.4.1)
(4.4.1)
Решение. Отыщем
подстановку, переводящую выражения, стоящие под знаком неизвестной функции f
в уравнении (4.4.1), друг в друга.
Для
этого положим
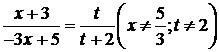 .
.
Отсюда
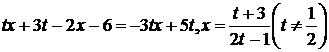 .
.
Кроме
того,
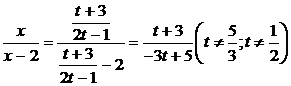 .
.
Следовательно,
подстановка 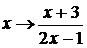 - искомая. Уравнение (4.4.1) примет вид
- искомая. Уравнение (4.4.1) примет вид
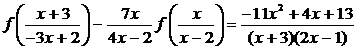 . (4.4.2)
. (4.4.2)
В
уравнении (4.4.1) 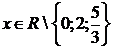 Подстановка
Подстановка  переводит
точки
переводит
точки  соответственно в точки
соответственно в точки 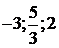 . Кроме
того, из характера подстановки вытекает
. Кроме
того, из характера подстановки вытекает 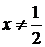 . Поэтому
в уравнении (4.4.2)
. Поэтому
в уравнении (4.4.2) 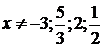 . Область допустимых значений х в системе,
составленной из уравнений (4.4.1) и (4.4.2), является пересечением
соответствующих областей каждого из уравнений (4.4.1) и (4.4.2), т.е.
. Область допустимых значений х в системе,
составленной из уравнений (4.4.1) и (4.4.2), является пересечением
соответствующих областей каждого из уравнений (4.4.1) и (4.4.2), т.е. 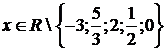 . Исключая из этой системы
. Исключая из этой системы 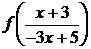 , получим
, получим
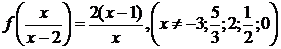
Обозначив
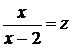 ,
,
получим
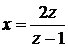 .
.
Из
условия 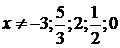 получаем
получаем  , а также
, а также
 , что определяется видом подстановки.
, что определяется видом подстановки.
Подстановка
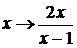 дает
дает
 .
.
Итак,
функция

с
областью определения 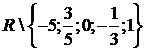 является решением примера 4.4.1, что и подтверждается
проверкой. Сужение области определения искомой функции удалением точек
является решением примера 4.4.1, что и подтверждается
проверкой. Сужение области определения искомой функции удалением точек  вызвано методом решения уравнения. Несложные
вычисления показывают, что функция
вызвано методом решения уравнения. Несложные
вычисления показывают, что функция
 ,
, 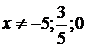 ,
,
удовлетворяет
исходному уравнению.
В
самом деле, полагая в (4.4.1) 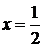 , получим
, получим
 .
.
Значения
функции
 ,
, 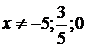 ,
,
в
точках 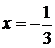 и 1 соответственно равны
и 1 соответственно равны  и удовлетворяют приведенному соотношению.
и удовлетворяют приведенному соотношению.
Более
того, решение уравнения (4.4.1) в классе функций таких, что 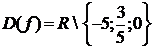 имеет вид
имеет вид
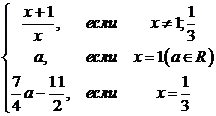
Уравнение
(4.4.1) решено, так как найдена подстановка  переводящая
дробно-линейные функции
переводящая
дробно-линейные функции 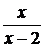 и
и  , получим
друг в друга. На языке матриц это означает, что найдена матрица
, получим
друг в друга. На языке матриц это означает, что найдена матрица 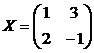 такая, что
такая, что
АХ
= kB; BX =lA,
где 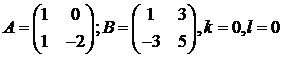 .
.
Возникает
вопрос, для любых ли дробно-линейных функций существует аналогичная
подстановка; другими словами, для любых ли матриц А и В существует матрица X,
удовлетворяющая уравнениям
АХ
= kВ, (4.4.3)
ВХ
= lА (4.4.4)
при некоторых k,
l, отличных от нуля.
Предполагая, что такая матрица существует, из уравнений (4.4.3) и
(4.4.24) получим:
(lА)X = (lk)В, (ВХ)X
= (lk)В,
BX2 = (lk)B (4.4.5)
Предположим, что функции, соответствующие матрицам А и В, отличны от
констант. Тогда, как показано выше, для А и В существуют обратные матрицы.
Умножим обе части равенства (4.4.5) слева на В-1. Получим
B-1BX2= B-1lkB; EX2 = (lk)E; X2 = mE, где m=lk
Найдем общий вид матрицы
 такой,
что
такой,
что 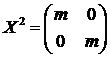 , т.е.
, т.е.
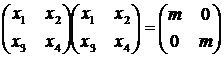 ,
,
при
некотором m ≠
0. Заметим, что х1x4 - х2х3
≠ 0. Из правила умножения и условия равенства матриц имеем:
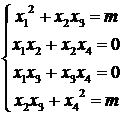
Вычитая
из первого уравнения четвертое, получим 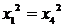 т. е.
т. е. 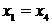 , либо
, либо 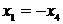 .
.
Если
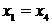 , то
, то 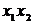 = 0 и
= 0 и 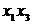 = 0, что приводит к матрицам вида
= 0, что приводит к матрицам вида
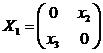 или
или  .
.
Если
же 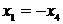 то придем к матрице
то придем к матрице
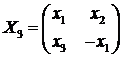
Проверкой
убеждаемся, что матрицы Х2 и Х3 удовлетворяют уравнению X2=mЕ при некотором m. Матрица Х3
при х1 = 0 дает X1.
Итак,
матрицы вида
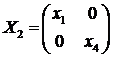 и
и 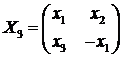
и
только они удовлетворяют уравнению
X2 = mE, m ≠
0.
Из
(4.4.4) имеем
X = lВ-1А.
Поэтому, если матрица В-1А имеет вид Х2 или
Х3, то она удовлетворяет каждому из уравнений (4.4.3), (4.4.4).
Теперь изложим один из способов решения функционального уравнения вида
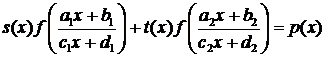 (4.4.6)
(4.4.6)
где
s(x), t(x),
р (х) - некоторые данные функции,
Решая
матричное уравнение вида
А
= ВХ,
где
 ,
,  ,
,
получим
X
= В-1А,
Если
матрица X имеет вид  , то
подстановка
, то
подстановка 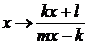 в (4.4.6) даст второе уравнение относительно
неизвестных
в (4.4.6) даст второе уравнение относительно
неизвестных
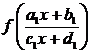 ,
, 
Если
полученная система имеет решение, то из нее найдем выражение для 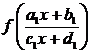 . Последнее дает возможность найти f(x). Как обычно, обязательной частью решения является
проверка. Случай
. Последнее дает возможность найти f(x). Как обычно, обязательной частью решения является
проверка. Случай
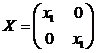
тривиален,
А
= х1В,
т.е.
выражения, стоящие в (4.4.6) под знаком f,
совпадают.
Пример
4.4.3 Найти функцию f,
определенную при 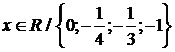 , удовлетворяющую уравнению
, удовлетворяющую уравнению
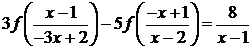 (4.4.7)
(4.4.7)
Решение. Решаем матричное
уравнение
AХ = В,
где
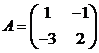 ;
; 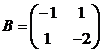 .
.
Для
матрицы A обратной является матрица 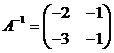 .
.
Тогда
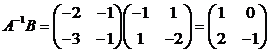 .
.
Матрица
X имеет вид  , поэтому применим к уравнению (4.4.7) подстановку
, поэтому применим к уравнению (4.4.7) подстановку 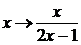 . Последнюю удобно выполнять с помощью матриц. Правой
части уравнения (4.4.7) соответствует матрица
. Последнюю удобно выполнять с помощью матриц. Правой
части уравнения (4.4.7) соответствует матрица 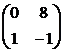 .
Применение к ней подстановки
.
Применение к ней подстановки 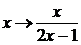 равносильно
умножению
равносильно
умножению 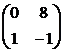 справа на
справа на  . В
результате получим
. В
результате получим 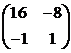 . Таким образом, из уравнения (4.4.7) находим
. Таким образом, из уравнения (4.4.7) находим
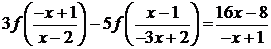 (4.4.8)
(4.4.8)
Исключив
из системы, составленной из уравнений (4.4.7) и (4.4.8) 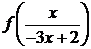 имеем
имеем
 (4.4.9)
(4.4.9)
Из
(4.4.7) видим, что  . Подстановка сохранила эти ограничения. Кроме того,
. Подстановка сохранила эти ограничения. Кроме того, 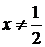 .
.
Положим
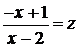 .
.
Так
как 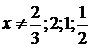 , то
, то  . Отсюда
. Отсюда
 .
.
Заменяя
 , из (4.4.9) получим
, из (4.4.9) получим
 .
.
Проверка
показывает, что эта функция удовлетворяет условию задачи:

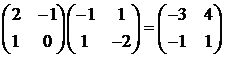

4.5
Применение элементов математического анализа к решению функциональных уравнений
4.5.1
Предельный переход
Идею предельного перехода проиллюстрируем на следующих примерах.
Пример 4.5.1.1 Решить в классе непрерывных функций уравнение
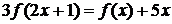 (4.5.1.1)
(4.5.1.1)
где
х 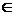 R.
R.
Решение. Заменив х на  , получим
, получим
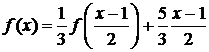 (4.5.1.2)
(4.5.1.2)
Используя
ту же замену, из уравнения (4.5.1.2) последовательно получим
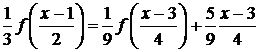 ,
,
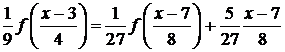
Методом
математической индукции можно доказать, что
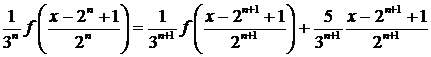 (4.5.1.3)
(4.5.1.3)
Сложив
все уравнения, начиная с (4.5.1.2), получим
 (4.5.1.4)
(4.5.1.4)
Так
как функция f(х)
непрерывна, то при любом фиксированном х
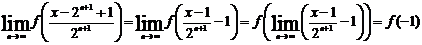
Здесь
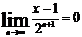 .
.
Из
(4.5.1.1) 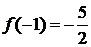 . Тогда
. Тогда
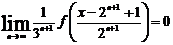
Левая
часть равенства (4.5.1.4) не зависит от n, поэтому
существует ее предел при n →
∞. Переходя к пределу в равенстве (4.5.1.4), при n → ∞ имеем
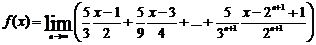 (4.5.1.5)
(4.5.1.5)
Правая
часть (4.5.1.5) является суммой трех бесконечно убывающих прогрессий
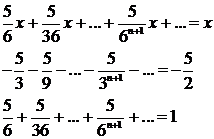
Итак,
 ,
,
что
и подтверждается проверкой.
Пример
4.5.1.2 Функция f:
R→R непрерывна
в точке 0 и для любого x  R
выполнено равенство
R
выполнено равенство
2f(2x) = f(x)+x.
Найти все такие f.
Решение. Пусть функция f удовлетворяет условию. Тогда
Выполняя
подстановку

Тривиальная
проверка показывает, что функция x/3 действительно является искомой.
Пример
4.5.1.3 Решить функциональное
уравнение
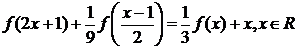 (4.5.1.6)
(4.5.1.6)
в
классе непрерывных функций.
Решение. Выполнив замену 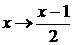 , получим
, получим
 (4.5.1.7)
(4.5.1.7)
Складывая
(4.5.1.6) с уравнением (4.5.1.7), умноженным на  , получим
, получим

Это
уравнение решается аналогично уравнению (4.5.1.1). Найдем подстановку,
переводящую  в
в  . Для
этого положим
. Для
этого положим
 .
.
Отсюда
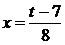 .
.
Выполнив
n раз подстановку 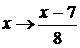 , получим
систему уравнений, из которой находим
, получим
систему уравнений, из которой находим
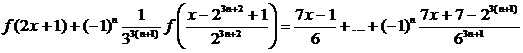
Отсюда
при n → ∞
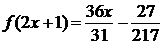 , или
, или  ,
,
что
и подтверждается проверкой.
4.6
Дифференцирование
В некоторых случаях для нахождения решения функционального уравнения
целесообразно продифференцировать обе части уравнения, если, конечно,
производная существует. В результате получим функциональное уравнение, которое
содержит и производную неизвестной функции. Решим это уравнение относительно
производной. Тогда неизвестная функция является одной из первообразных для
найденной производной. Этот метод уже применялся при решении уравнения Коши в
классе дифференцируемых функций.
Пример 4.6.1 Найти в классе функций, имеющих непрерывные производные,
решение уравнения
f(3x+2)
= 3f(x), x 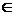 R. (4.6.1)
R. (4.6.1)
Решение. Попытки решить
уравнение методом предельного перехода не приводят к желаемому результату.
Левая и правая части (4.6.2.1) являются функциями от х. Они равны,
следовательно, равны их производные по х. Продифференцируем (4.6.1) и после
сокращения получим
f′(3x+2)
= 3f′(x)
Это
уравнение уже можно решить методом предельного перехода. Выполнив подстановку  , получим цепочку равенств
, получим цепочку равенств
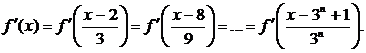
Ввиду
непрерывности 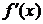 , при n →
∞, имеем
, при n →
∞, имеем
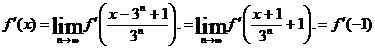
Итак,
 = k, где k=
= k, где k= 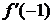 .
Первообразная функция
.
Первообразная функция
f(х) = kx + b.
Подставив в (4.6.1) х = -1, получим f(-1) = 0. Кроме того,
f(-1) = - k + b, т.е. k = b.
Легко проверить, что
f (х) = k (х + 1)
удовлетворяет условию при произвольном k.
Пример 4.6.2 Найти все действительные дифференцируемые функции,
удовлетворяющие функциональному уравнению
 (4.6.2)
(4.6.2)
Решение. Пусть f
удовлетворяет данному уравнению. Тогда

т.е.
f(0)[1+f 2(x)]
= 0,
и,
следовательно, f(0) = 0.
После
преобразований имеем
 , (4.6.3)
, (4.6.3)
откуда,
с учётом 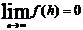 следует, что
следует, что
f(x) = C (1+f 2(x)), (4.6.4)
где C = f′(0). Значит,
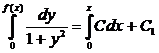 ,
,

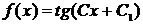
Условие
f(0) = 0
означает, что C1 =
0, т.е.
f(x)
= tg Cx.
Очевидно,
все функции вида tg Cx подходят
под условие задачи.
Заключение
функция уравнение матрица переменная
Список
использованных источников
1. Гомонов, С.А. Математика в школе. [Текст]:[Функциональные
уравнения в школьном курсе математики]/ С.А. Гомонов.-// Издательство "Школа-
Пресс" - 2010.-№10- С. 58-63
2. Лихтарников, Л.М. Элементарное введение в
функциональные уравнения.[Текст]/ Л.М. Лихтарников.- Спб. Лань,1997.-160с.
. Гельфонд, А.О. Исчисление конечных разностей.
[Текст]/А.О. Гельфонд. - М. : Наука,1967г.-376с.
4. Андреев А.А., Кузьмин Ю.Н.., Савин А.Н., Саушкин И.Н.
Функциональные уравнения. - Самара: В мире науки, 2009
. Бродский Я.С., Слипенко А.К. Функциональные уравнения. -
К.: Вища школа. Головное издательство, 2011. - 96 с
. Ильин В.А. Методы решения функциональных уравнений //
Соросовский образовательный журнал, 2009, № 2, с. 116 - 120