Разрешимость одной краевой задачи
Содержание
Введение
Глава 1. Вспомогательные утверждения и конструкции
.1 Основные понятия и определения
.2 Банаховы функциональные пространства
.3 Функция Грина
.4 Задачи, сводящиеся к интегральным уравнениям
Глава 2. Постановка краевой задачи и исследование ее
однозначной разрешимости и отрицательности функции Грина
.1 Признак существования решения краевой задачи для
нелинейного функционально-дифференциального уравнения
.2 Исследование разрешимости краевой задачи
.3 Оценка нормы оператора
.4 Исследование отрицательности функции Грина
.5 Исследование разрешимости двухточечной краевой задачи
Заключение
Список использованных источников
Введение
Математические методы являются важнейшим инструментом анализа
экономических явлений и процессов, построение теоретических моделей,
позволяющих отобразить существующие связи в экономической жизни, прогнозировать
поведение экономических субъектов.
Математика как основа теории принятия решений широко применяется для
управления (планирования, прогнозирования, контроля) экономическими объектами и
процессами. В настоящее время методы математического моделирования находят все
более широкое применение в решение прикладных экономических задач.
Современные модели содержат в себе как настоящие, так и предыдущие
состояния описываемого объекта. Основными методами исследования являются методы
общей теории линейных функционально-дифференциальных уравнений, а также
конструктивные методы исследования краевых задач. Для отображения
функционирования модели ставится краевое условие.
Объектом исследования данной работы является однозначная разрешимость
линейно функционально-дифференциального уравнения второго порядка с
отклоняющимся аргументом и отрицательность функции Грина.
Целью работы является исследование однозначной разрешимости линейно
функционально - дифференциальное уравнения второго порядка с отклоняющимся
аргументом с однородными краевыми условиями и исследование отрицательности
функции Грина. Для достижения поставленной цели решены следующие задачи:
) Введены необходимые понятия и утверждения теории функционального
анализа
) Рассмотрена однозначная разрешимость нелинейной задачи
) Доказана однозначная разрешимость линейной задачи и отрицательность
функции Грина
Структура работы. Работа условно разделена на 2 главы. В первой главе
приводятся необходимые теоретические сведения из специальных разделов
функционального анализа. Во второй главе рассматривается разрешимость
нелинейного функционально-дифференциального уравнения и доказывается
однозначная разрешимость линейной краевой задачи и отрицательность функции
Грина.
Глава 1.
Вспомогательные утверждения и конструкции
.1 Основные
понятия и определения
. Множество X элементов любой
природы называется линейным или векторным пространством, если
а)
для любых 2-х элементов 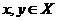 ставится в соответствие элемент
ставится в соответствие элемент 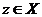 , который называется суммой взятых элементов и
обозначается
, который называется суммой взятых элементов и
обозначается 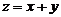
б)
для любого элемента 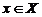 и
и 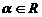 ставится
в соответствие элемент
ставится
в соответствие элемент 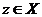 , который называется суммой взятых элементов и
обозначается
, который называется суммой взятых элементов и
обозначается 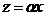 .
.
.
пусть X линейное пространство. Конечный функционал 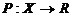 называется нормой, если для любых 2-х элементов
называется нормой, если для любых 2-х элементов 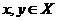 удовлетворяют аксиомы:
удовлетворяют аксиомы:
а)

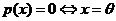
б)
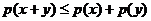
в)
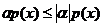
.
Линейное пространство X, в котором определенна некоторая норма, называется
нормированным пространством, норма обозначается 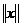 .
.
.
Если пространство X таково, что в нем каждая фундаментальная
последовательность сходиться к элементу этого пространства, то оно называется
банаховым или полным.
.
пусть X -нормированное пространство. Множество 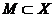 называется относительно компактным, если произвольная
последовательность этого множества содержит подпоследовательность, которая
сходится к элементу пространства X.
называется относительно компактным, если произвольная
последовательность этого множества содержит подпоследовательность, которая
сходится к элементу пространства X.
.
Множество 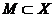 называется компакным, если оно относительно компактно
и замкнуто.
называется компакным, если оно относительно компактно
и замкнуто.
.
Оператор 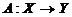 называется ограниченным, если существует такая
константа
называется ограниченным, если существует такая
константа  , такая что
, такая что 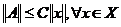
.
Ядро линейного оператора называется множество 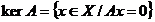
.
Образом оператора A называется множество  подпространство
пространства Y.
подпространство
пространства Y.
.
Совокупность  всех линейных непрерывных функционалов на банаховом
пространстве X образует сопряженное к X линейное
пространство.
всех линейных непрерывных функционалов на банаховом
пространстве X образует сопряженное к X линейное
пространство.
.
пусть X и Y - банаховы пространства, оператор  называется обратным к оператору
называется обратным к оператору  , если
, если 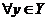 уравнение
уравнение 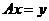 однозначно разрешимо, и это решение представимо в
виде
однозначно разрешимо, и это решение представимо в
виде 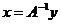
. Число  называется собственным значением оператора A, если существует такой
ненулевой собственный вектор
называется собственным значением оператора A, если существует такой
ненулевой собственный вектор 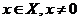 ,
,
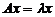
. Точка  называется регулярной, если оператор
называется регулярной, если оператор  непрерывно обратим.
Совокупность регулярных точек называется резольвентным множеством, а оператор
непрерывно обратим.
Совокупность регулярных точек называется резольвентным множеством, а оператор 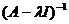 резольвентой оператора A.
резольвентой оператора A.
. Совокупность собственных значений оператора A называется спектром
оператора A.
. Условие Каратеодори: функция 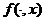 измерима при
измерима при 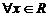 , и функция
, и функция 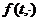 непрерывна
непрерывна 
1.2 Банаховы
функциональные пространства
Пространство L2[a,b].
Через
L2=L2[a,b] обозначим совокупность всех классов интегрируемых
функций по Лебегу с квадратом 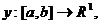 с нормой
с нормой
 Это же пространство будет рассматривать как
действительное гильбертово пространство со скалярным произведением,
определяемым следующим образом:
Это же пространство будет рассматривать как
действительное гильбертово пространство со скалярным произведением,
определяемым следующим образом:

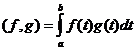

Отметим,
что норма, порождаемая этим скалярным произведением, совпадает с исходной
нормой. [10]
Определение
1. Функция у(t) на [a,b] называется абсолютно непрерывной на [a,b],
если для любого 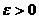 найдётся такое
найдётся такое 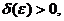 что для
любой конечной системы непересекающихся интервалов
что для
любой конечной системы непересекающихся интервалов 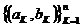 из отрезка [a,b] таких, что
из отрезка [a,b] таких, что 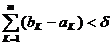 имеет место неравенство
имеет место неравенство

Через
D2=D2[a,b] обозначим пространство абсолютно непрерывных функций
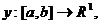 таких, что
таких, что 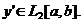 Пространство
D2[a,b] -
является бахановым пространством относительно нормы
Пространство
D2[a,b] -
является бахановым пространством относительно нормы  Пространство H=D2[a,b] можно рассматривать как гильбертово пространство со
скалярным произведением, определяемым следующим образом:
Пространство H=D2[a,b] можно рассматривать как гильбертово пространство со
скалярным произведением, определяемым следующим образом:
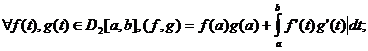
Порождаемая
норма этим скалярным произведением:
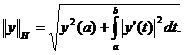
Нормы
 и
и 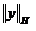 эквиваленты,
т.е. существуют такие константы С1>0, C2>0, что выполняется
эквиваленты,
т.е. существуют такие константы С1>0, C2>0, что выполняется 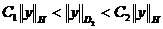 .
.
Обозначим
через C[a,b] пространство непрерывных на отрезке [a,b]
функций 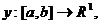 с нормой
с нормой 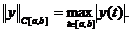
Обозначим
через C1[a,b]
пространство непрерывно - дифференцируемых на отрезке [a,b]
функций 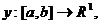 с нормой
с нормой 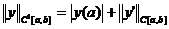 .
.
Справедливо
следующее включение
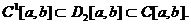
Через
W2=W2[a,b] [5,c.12] обозначим пространство абсолютно непрерывных на
отрезке [a,b] функций 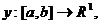 таких, что
таких, что  с нормой
с нормой
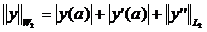
Пространство
H=W2[a,b]
можно рассматривать как гильбертово пространство со скалярным произведением,
определяемым следующим образом:

Порождаемая
норма этих скалярным произведением:
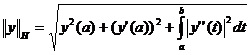
1.3 Функция
Грина
Рассмотрим задачу Штурма-Лиувилля.
Постановка: Найти те значения параметра 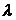 , при которых уравнение
, при которых уравнение
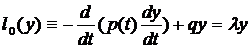 (1)
(1)
имеет нетривиальное решение у (t) 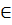 CL2 [a, b],
удовлетворяющее краевым условиям
CL2 [a, b],
удовлетворяющее краевым условиям
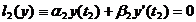 .
.
Краевые условия содержат параметры αi βi которые можно зафиксировать различным образом. Вследствие этого оператор
L в (2.4) должен маркироваться в зависимости от значений α1, β1, α2, β2, (например, 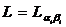 ); с изменением этих значений
меняется область определения оператора, а следовательно, и сам оператор. Задача
Штурма - Лиувилля в зависимости от значений указанных параметров имеет ту или
иную физическую подоплеку, ту или иную специфику. Если β1=β2= 0, то соответствующие условия
); с изменением этих значений
меняется область определения оператора, а следовательно, и сам оператор. Задача
Штурма - Лиувилля в зависимости от значений указанных параметров имеет ту или
иную физическую подоплеку, ту или иную специфику. Если β1=β2= 0, то соответствующие условия
(t1)=0, y(t2)=0
именуются краевыми условиями первого рода; условия
'(t1)=0, y'(t2)=0,
называются краевыми условиями второго рода. Общие условия
(2), записанные в виде
у' (а) - 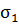 у (а) = 0, у' (а) -
у (а) = 0, у' (а) -  у (а) = 0,
у (а) = 0,
называются краевыми условиями третьего рода. Все
написанные условия есть однородные условия, поскольку в правой части стоит
нуль. В более общем случае справа вместо нуля может стоять произвольное число,
и тогда говорят о неоднородном краевом условии.
Задачу Штурма - Лиувилля называют также задачей на
собственные значения[2,c.326].
Краевые условия (2.6) именуют граничными или предельными условиями (и тогда
говорят о граничной или соответственно о предельной задаче).
Элементарным решением уравнения
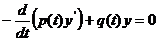 (3)
(3)
с особенностью в точке 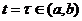 называется функция
называется функция  , определенная в квадрате
, определенная в квадрате
={(t,
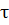 );
); 
 }
}
и обладающая свойствами:
1. 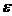 (t,
(t, 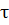 ) непрерывна в Q.
) непрерывна в Q.
. При фиксированном 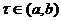 она удовлетворяет уравнению (3) в промежутках [а,
она удовлетворяет уравнению (3) в промежутках [а, 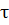 ), и (
), и (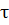 , b] (и, следовательно,
, b] (и, следовательно,  дважды непрерывно дифференцируема в этих промежутках).
дважды непрерывно дифференцируема в этих промежутках).
. Первая производная функции  имеет разрыв первого
имеет разрыв первого
рода в точке 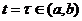 со «.скачком» -1/р(
со «.скачком» -1/р(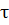 ), т. е.
), т. е.
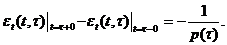
Функцию 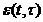 будем
называть функцией Грина оператора L[2,c.332].
будем
называть функцией Грина оператора L[2,c.332].
.4 Задачи,
сводящиеся к интегральным уравнениям
Можно считать общеизвестным, что обыкновенные дифференциальные уравнения
играют исключительно важную роль как математические модели многих реальных
явлений и процессов. Для дифференциального уравнения
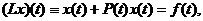
 (1)
(1)
часто
возникает так называемая начальная задача, или задача Коши,
(Lx)(t) = f(t), x(0) = α,
где
требуется найти функцию x(t), удовлетворяющую уравнению (6) и дополнительному
начальному условию x(0) = α. Используя
подстановку
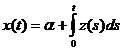 (2)
(2)
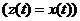 , для
z(t) получаем уравнение
, для
z(t) получаем уравнение
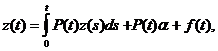

которому
можно придать вид
 (3)
(3)
где
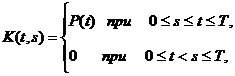
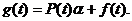
Уравнение
(3) называется линейным интегральным уравнением Фредгольма, а функция двух
переменных K(t, s) - ядром этого уравнения. Для широкого круга прикладных задач
возникает необходимость рассматривать краевую задачу [3, 4], представляющую
собой систему
(Lx)(t)
= f(t),  (4)
(4)
в
которой второе уравнение принято называть краевым условием. В виде lx = α могут быть записаны самые разнообразные случаи краевых
условий. В частности, при соответствующем выборе  и ϕ
в таком виде могут быть записаны: начальное условие
и ϕ
в таком виде могут быть записаны: начальное условие
x(0) = α ( = 1, ϕ(s)
≡ 0);
= 1, ϕ(s)
≡ 0);
периодическое
условие
(T)
= x(0) ( = 0, ϕ(s) ≡ 1, α = 0);
= 0, ϕ(s) ≡ 1, α = 0);
многоточечное
условие

 i=1,2,…,m;
i=1,2,…,m;
в
этом случае
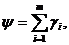
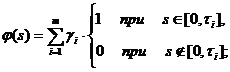
интегральное
условие
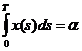 (
( = T, ϕ(s) =T-s).
= T, ϕ(s) =T-s).
Можно
свести задачу (4) к интегральному уравнению: по числу  и функции ϕ можно найти такую функцию u(t),
что u(0)
и функции ϕ можно найти такую функцию u(t),
что u(0)  0, lu =
1 и система уравнений
0, lu =
1 и система уравнений
(t)+B(t)x(0)=z(t), lx= α
где
B(t) = −u(t)/u(0),
однозначно разрешима и ее решение имеет представление
 (5)
(5)
краевой задача грин функция
Здесь

Воспользуемся
W-подстановкой (5) применительно к уравнению (1):
(t)+B(t)x(0)=-P(t)x(t)+B(t)x(0)+f(t).
Получаем
уравнение
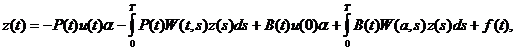
которое
принимает вид (3), если положить K(t, s) = B(t)W(a, s) − P(t)W(t, s), g(t) = f(t) + B(t)u(0)α - P(t)u(t)α. Краевая задача (4) для дифференциального уравнения с отклоняющимся
аргументом

 (6)
(6)
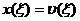 при
при 
для
интегродифференциального уравнения
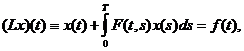
 (7)
(7)
и
многих других классов уравнений тоже сводятся к интегральному уравнению (3) с
помощью W-подстановки (5)[6].
Глава 2.
Постановка краевой задачи и исследование ее однозначной разрешимости и
отрицательности функции Грина
Рассматриваем вопрос об условиях однозначной разрешимости
функционально-дифференциальное уравнения второго порядка с отклоняющимся аргументом
и с однородными краевыми условиями:
 (1)
(1)
 (2)
(2)
Линейный
ограниченный оператор  ,
,  .
.
Функцию
p(t) можно представить в виде разности 2-х функций,
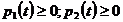 ,
,
 (3)
(3)
Благодаря
равенству (3) исходная краевая задача (1)-(2) запишем следующим образом:

Рассмотрим
вспомогательную задачу
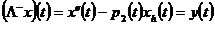 (4)
(4)

Теорема
1:
Если
выполнены следующие условия:
.
Краевая задача (4) однозначно разрешима и функция Грина 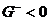 на
на 
. 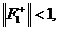 где
где
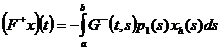
Тогда задача (1)-(2) однозначно разрешима и функция Грина отрицательна.
Доказательство:
Задача
(1)-(2) эквивалента уравнению 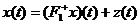 (6), где
(6), где
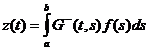
Нужно
отметить, что уравнение (6) мы рассматриваем в пространстве 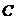 , а решение задачи (1), (2) - элемент пространства
, а решение задачи (1), (2) - элемент пространства 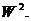 Тем не менее утверждение об эквивалентности верно,
так как в силу свойств функции Грина значение оператора
Тем не менее утверждение об эквивалентности верно,
так как в силу свойств функции Грина значение оператора 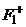 на непрерывной функции является элементом из
на непрерывной функции является элементом из 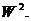
Уравнение
(6) рассматриваем в пространстве непрерывных функций и  , то получаем ряд Неймана[3,с.187].
, то получаем ряд Неймана[3,с.187].
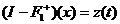
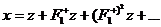
Ряд
Неймана сходится равномерно[3,c.189], его сумма  представляет
решение уравнения (6)
представляет
решение уравнения (6)
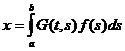 -доказали
однозначную разрешимость.
-доказали
однозначную разрешимость.
Докажем,
что функция Грина отрицательна:
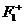 - изотонный
оператор
- изотонный
оператор
Предполагаем, что функция f(t) положительна, 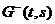 отрицательна из равенства
(6), следовательно, функция
z(t) отрицательная. Каждое
слагаемое в ряде Неймана представляет отрицательно, из этого следует
отрицательность решения уравнения (5):
отрицательна из равенства
(6), следовательно, функция
z(t) отрицательная. Каждое
слагаемое в ряде Неймана представляет отрицательно, из этого следует
отрицательность решения уравнения (5):
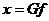 , предполагаем не отрицательность функции f(t), следовательно функция
Грина отрицательна.
, предполагаем не отрицательность функции f(t), следовательно функция
Грина отрицательна.
 Задача
(1)-(2) однозначна разрешима и ее функция Грина отрицательна.
Задача
(1)-(2) однозначна разрешима и ее функция Грина отрицательна.
2.1 Признак
существования решения краевой задачи для нелинейного
функционально-дифференциального уравнения
Рассмотрим нелинейную краевую задачу:
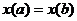 (1)
(1)
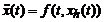 (2)
(2)
Имеет место представление
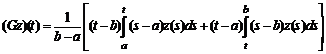
 (3)
(3)
Оператор
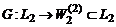
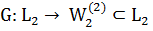 -
линейный ограниченный симметрический; имеет спектр в интервале
-
линейный ограниченный симметрический; имеет спектр в интервале 
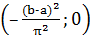 ;
; 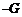 - положителен, т. е. для любого
- положителен, т. е. для любого 
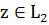 имеет
место неравенство
имеет
место неравенство
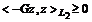 . (4)
. (4)
Введем
следующие обозначения: 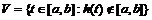 ;
;
 ,
,
где
 - измеримая функция, обладающая свойством
“независания”:
- измеримая функция, обладающая свойством
“независания”:

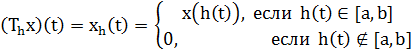
Рассмотрим
краевую задачу (1), (2) в предположениях:

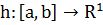 -
измеримая функция;
-
измеримая функция;

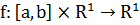 :
: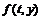
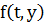 измерима
по
измерима
по  при каждом
при каждом 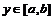
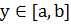 и
непрерывна по
и
непрерывна по 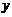
 при
почти всех
при
почти всех 
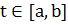 , и для
любого
, и для
любого 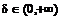
 найдется
такая суммируемая с квадратом на
найдется
такая суммируемая с квадратом на 
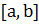 функция
функция 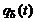
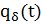 , что
если
, что
если 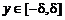
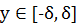 , то
, то 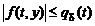
 ;
существуют такие числа
;
существуют такие числа  ,
,  ,
,
 ,
,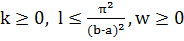 что для почти всех
что для почти всех 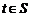
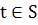 и для
всех
и для
всех 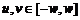
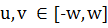 имеют место
неравенства:
имеют место
неравенства: 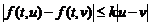
 ;
; 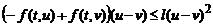
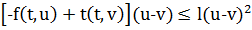 ,
,
где
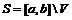
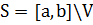 .
.
Решением
задачи (1), (2) будем называть функцию 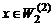
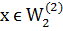 , для
которой выполнены условия (1) и, равенство из (2) выполняется почти всюду на
, для
которой выполнены условия (1) и, равенство из (2) выполняется почти всюду на 
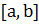 .
.
Рассмотрим
уравнение
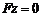 , (5)
, (5)
где
оператор 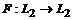
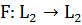 определен равенством
определен равенством 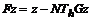
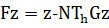 .
.
Лемма1.
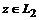
 является
решением уравнения (5) тогда и только тогда, когда
является
решением уравнения (5) тогда и только тогда, когда 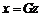
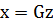 является
решением задачи (1),(2) .
является
решением задачи (1),(2) .
Лемма1
позволяет свести вопрос о разрешимости задачи (1), (2) к изучению уравнения
(5). Поэтому мы предварительно исследуем свойства оператора 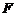
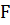 .
.
Пусть
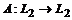
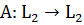 -
линейный ограниченный самосопряженный оператор,
-
линейный ограниченный самосопряженный оператор, 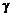 -
положительная константа.
-
положительная константа.
Определение.
Оператор 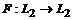
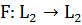 называется
называется
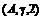
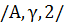 -монотонным[5,c.6],
если для любых
-монотонным[5,c.6],
если для любых 
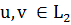 имеет
место неравенство
имеет
место неравенство 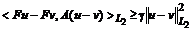
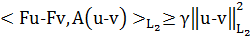 .
.
Лемма2.
Пусть существуют такие константы :
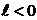

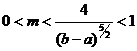
такие,
что
1) 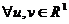 п.в.
п.в. 
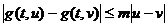
2) 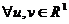 п.в.
п.в. 
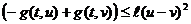
Тогда:
a) оператор
 являются (U,1- m,2)- монотонным
) существует непрерывный обратный оператор
являются (U,1- m,2)- монотонным
) существует непрерывный обратный оператор 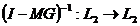 ,
удовлетворяющий уравнению
,
удовлетворяющий уравнению 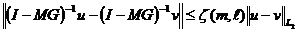 , где
, где 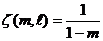 (6)
(6)
Доказательство.
а)
Если 
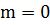 , то
доказываемое непосредственно следует из свойств оператора
, то
доказываемое непосредственно следует из свойств оператора 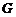

Пусть
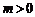
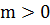 .
Обозначим
.
Обозначим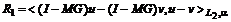
 . Тогда
для любых
. Тогда
для любых 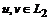
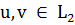 имеем
имеем

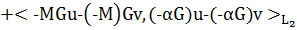 .
.
Ввиду
условия 2) из последнего равенства следует
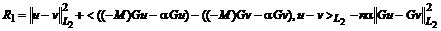
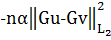 .
.
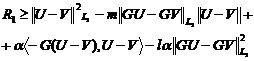
т.к
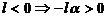 , т.е
, т.е 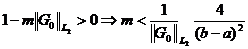
Лемма3:

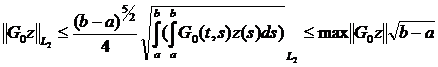
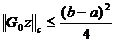
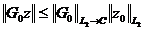
Отсюда
ввиду предположений на m получаем выполнение условия а)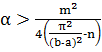
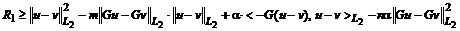 . (7)
. (7)
 (8)
(8)
б)
Из (8), используя неравенство (4), получаем для любых 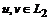
Используя
неравенство Гельдера[10,c.54] и неравенство (4), выводим отсюда

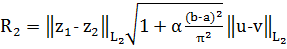 .
.
Из
(9), используя равенство (4) получим 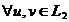
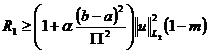
Из
последнего неравенства и теоремы следует существование обратного оператора 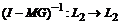
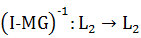 .
.
Обозначим:
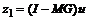 ,
, 
 ,
, 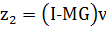
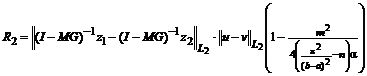
 .
.
Из
(9) имеем 
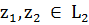 :
: 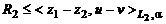
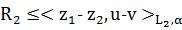 .
.
Используя
неравенство Гельдера и неравенство (4), выводим отсюда

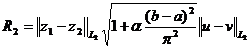
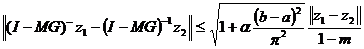 при
при 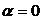
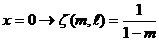
Пусть

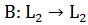 -
непрерывный оператор.
-
непрерывный оператор.
Лемма4.
Пусть: выполнены условия 1), 2) лемме2; для п. в. 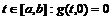
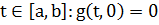 ; оператор
; оператор 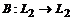
 удовлетворяет
условию Липшица с константой
удовлетворяет
условию Липшица с константой 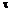
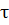 , причем
, причем 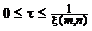
 . Тогда
существует непрерывный оператор
. Тогда
существует непрерывный оператор 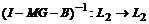
 ,
удовлетворяющий условию Липшица с константой
,
удовлетворяющий условию Липшица с константой 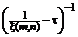
 .
.
Доказательство.
Имеем для любых 
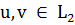 ,
применяя лемму 2, получаем:
,
применяя лемму 2, получаем:
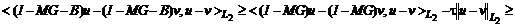
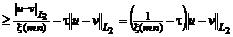
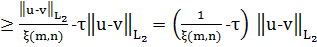 (9)
(9)
Отсюда
по теореме [14] получаем непрерывную обратимость оператора 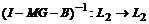
 . Из (7)
для непрерывного оператора
. Из (7)
для непрерывного оператора 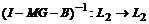 имеем:
для любых
имеем:
для любых  :
: 
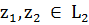
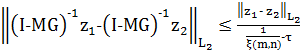
Лемма
5. Для любого 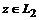
 выполняется
неравенство
выполняется
неравенство
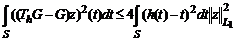 .
.
Теперь
мы можем получить условия, при которых все решения задачи (1),(2) удовлетворяют
априорной оценке, и, одновременно, сама задача (1), (2) однозначно разрешима.
Лемма
6. Пусть выполнены условия:
Существуют
такие константы 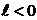

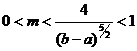 , что:
, что:
) для
любых 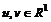
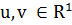 , почти
для всех
, почти
для всех 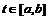
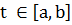 имеет
место неравенство
имеет
место неравенство 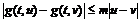 ;
;
) для
любых 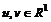
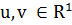 , почти
для всех
, почти
для всех 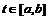
 имеет
место неравенство
имеет
место неравенство 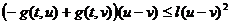
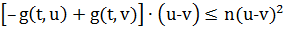 .
.
) выполнено
неравенство 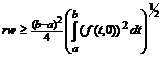
 ,
,
где

Тогда
краевая задача (1), (2) имеет решение 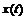
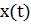 , которое
удовлетворяет оценке
, которое
удовлетворяет оценке 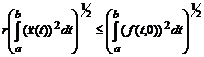
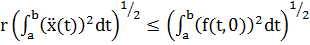 , и
решение, удовлетворяющее такой оценке, единственно.
, и
решение, удовлетворяющее такой оценке, единственно.
Доказательство.
Обозначим 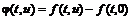
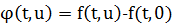 .
.
Построим
функции 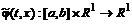
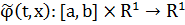 следующим
образом:
следующим
образом:
для
всех 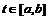
 положим
положим  ;
;

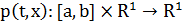 так:
так: 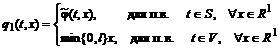 .
.
Обозначим
 ,
,  ,
,  и рассмотрим вспомогательное уравнение
и рассмотрим вспомогательное уравнение
 (10)
(10)
Из
построения функции 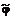
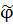 ясно,
что уравнение (10) на множестве
ясно,
что уравнение (10) на множестве 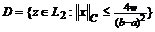 эквивалентно
уравнению (5), множество
эквивалентно
уравнению (5), множество 
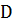 отображается
оператором
отображается
оператором 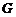
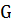 в
множество
в
множество 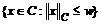
 .
.
Т.
к.  ,
, 
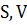 -
измеримые множества, то для любых
-
измеримые множества, то для любых 
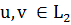 имеем:
имеем:
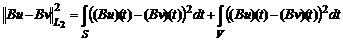 . Из
построения оператора
. Из
построения оператора 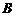
 получим
получим
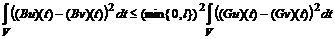 .
.
А
также из построения оператора 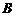
 , условия
1) и теореме 6 получим
, условия
1) и теореме 6 получим
 .
.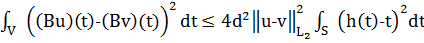
Т.
к. 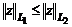
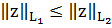 и ввиду
леммы 4 из последних двух равенств получим
и ввиду
леммы 4 из последних двух равенств получим
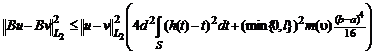 . (11)
. (11)

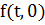 принадлежит
пространству
принадлежит
пространству 
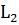 . Поэтому
для однозначной разрешимости уравнения (10) достаточно показать обратимость
оператора
. Поэтому
для однозначной разрешимости уравнения (10) достаточно показать обратимость
оператора 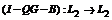
 и
принадлежность решения
и
принадлежность решения 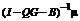
 множеству
множеству
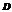
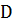 .[4,c.128]
Условия 1) и 2) теоремы 3 выполнены по построению функции
.[4,c.128]
Условия 1) и 2) теоремы 3 выполнены по построению функции 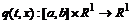
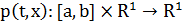 . Ввиду
(11) и того, что
. Ввиду
(11) и того, что 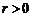
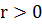 ,
оператор
,
оператор 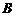
 удовлетворяет
условию теоремы 5.
удовлетворяет
условию теоремы 5.
Итак,
по лемме 4 оператор 
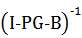 непрерывен
и
непрерывен
и
 , или
, или 
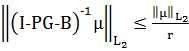 .
.
Отсюда
ввиду условия 2) получим 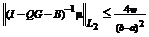 .
.
На
этом доказательство закончено.
2.2
Исследование разрешимости краевой задачи
 ,
, 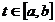 , (4)
, (4)
 ,
, 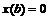 .
.
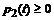 при
почти всех
при
почти всех 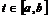 , и введем обозначение
, и введем обозначение
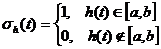
Теорема
3.[14,c.7] Пусть существуют такие константы 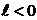

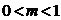
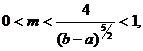 что:
что:
 почти
всюду на
почти
всюду на 
Тогда
задача (4) однозначно разрешима.
.3
Оценка нормы оператора 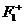
Для
оценки 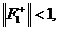 где
где
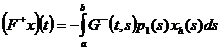 ,
,
применим
следующую лемму
Теорема 4:
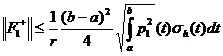
где
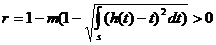
Доказательство:
Оператор Грина для задачи (4) представляет
собой произведение 2-х непрерывных функций.
Из доказательства леммы4 следует, что норма оператора Грина удовлетворяет
неравенству
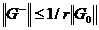 [14,c.5]
[14,c.5]

2.4
Исследование отрицательности функции Грина
Определим
оператор  равенством
равенством
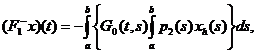
 (2.4.1)
(2.4.1)
Теорема 5. Пусть выполнены условия:
 почти
всюду на
почти
всюду на  , для любого
, для любого 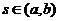 выполнено
неравенство
выполнено
неравенство
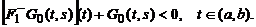
Тогда
функция Грина краевой задачи (1.4)  на
на 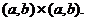
Доказательство.
Рассмотрим
вспомогательную задачу
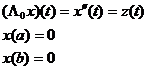 (2.4.2)
(2.4.2)
Краевая
задача (4) эквивалентна уравнению
 (2.4.3)
(2.4.3)
в
пространстве C, где оператор  определен
равенством (2.4.1),
определен
равенством (2.4.1), 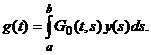 В силу условия
В силу условия  уравнение
(2.4.1), а следовательно, и задача (1.4) однозначно разрешимы. Значит, решение
задачи (4) имеет представление
уравнение
(2.4.1), а следовательно, и задача (1.4) однозначно разрешимы. Значит, решение
задачи (4) имеет представление
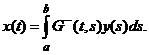
При
любом фиксированном 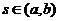 функция
функция  является
решением “импульсной” задачи
является
решением “импульсной” задачи
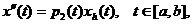
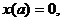

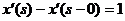
в
пространстве функций 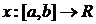 , имеющих на
, имеющих на 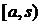 и
и 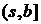 абсолютно непрерывную производную 1-го порядка. Эта
задача эквивалентна уравнению
абсолютно непрерывную производную 1-го порядка. Эта
задача эквивалентна уравнению
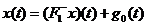 (2.4.4)
(2.4.4)
в
пространстве 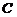 , где
, где 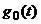 -
решение импульсной задачи
-
решение импульсной задачи



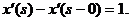
Таким
образом, при фиксированном 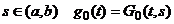 .
.
Для
доказательства неравенства 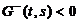 на
на 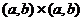 воспользуемся Теорема 6 об уравнении с антитонным
оператором [5,с. 23]. Сформулируем Теорема6 применительно к оператору
воспользуемся Теорема 6 об уравнении с антитонным
оператором [5,с. 23]. Сформулируем Теорема6 применительно к оператору  .
.
Теорема
6. Пусть 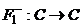 вполне непрерывный, антитонный оператор. Пусть,
далее,
вполне непрерывный, антитонный оператор. Пусть,
далее,  ,
, 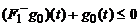 ,
, 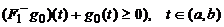 . Тогда уравнение (2.4.4) имеет решение
. Тогда уравнение (2.4.4) имеет решение 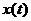 , удовлетворяющее неравенствам
, удовлетворяющее неравенствам
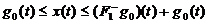 .
.
Условия
указанной теоремы для уравнения (2.4.4) выполнены: 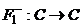 вполне непрерывен, как произведение вполне
непрерывного оператора Грина, действующего из пространства
вполне непрерывен, как произведение вполне
непрерывного оператора Грина, действующего из пространства 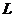 в пространство
в пространство 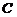 , на
ограниченный оператор
, на
ограниченный оператор 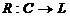 , определяемый равенством
, определяемый равенством
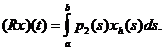
Рассмотрим
оператор следующего вида:
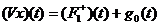 - вполне
непрерывный, антитонный оператор.
- вполне
непрерывный, антитонный оператор.


Данный
оператор отражает порядковый интервал в себя, следовательно, найдется такая
неподвижная точка, что 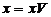 - решение уравнения (2.4.4), при этом
- решение уравнения (2.4.4), при этом  при фиксированном s,
при фиксированном s, 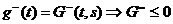 Доказали,
что функция Грина отрицательна для задачи (4).
Доказали,
что функция Грина отрицательна для задачи (4).
2.5
Исследование разрешимости двухточечной краевой задачи
Рассматриваем вопрос об условиях однозначной разрешимости
функционально-дифференциальное уравнения второго порядка с отклоняющимся
аргументом и с однородными краевыми условиями:
 (2.5.1)
(2.5.1)
 (2.5.2)
(2.5.2)
Линейный
ограниченный оператор 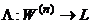 ,
,  .
.
Функцию
p(t) можно представить в виде разности 2-х неубывающих функций, 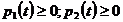 ,
,
 (2.5.3)
(2.5.3)
Благодаря
равенству (2.5.3) исходное уравнение (1) запишем следующим образом:


Рассмотрим
вспомогательную задачу
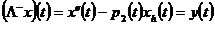 (2.5.4)
(2.5.4)
 (2.5.6)
(2.5.6)
Теорема
7 :
Если
выполнены следующие условия:
)
существуют такие константы 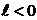

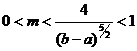 , что:
, что:
 почти
всюду на
почти
всюду на  ,
,
)
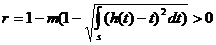
и
оператор  , определяется равенством
, определяется равенством
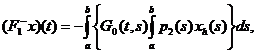
 (2.4.4)
(2.4.4)
для
любого 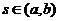 выполнено неравенство
выполнено неравенство
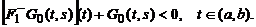
)
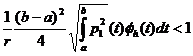
Тогда
задача (1-2) однозначно разрешима и ее функция Грина отрицательна.
Заключение
В дипломной работе рассмотрена краевая задача для
функционально-дифференциального уравнения второго порядка с однородными
краевыми условиями. По схеме Лихачевой Н.Н доказывается однозначная
разрешимость линейной задачи и отрицательность функции Грина.
В зависимости от условий на коэффициенты p(t) и отклонение
аргумента h(t) на основе указанной схемы получен признак однозначной
разрешимости и отрицательности функции Грина такой краевой задачи. В работе
используется метод монотонных операторов в банаховом пространстве.
Список
использованных источников
1. Абдуллаев,
А.Р. Задача Коши для квазилинейного дифференциального уравнения нейтрального
типа/ Абдуллаев, А.Р.., Неволина О.А. // Ярославский педагогический
вестник.-2011.-№3.- C. - 7-13.
. Лизоркин,
П.И. Курс дифференциальных и интегральных уравнений: учеб.пособие/ П.И.
Лизоркин.-М.:Изд-во Наука, 1981-381с.
.Рисс, Ф.
Лекции по функциональному анализу: учеб.пособие/ Ф.Рисс,
Б.Секефальви-Надь.-М.:Изд-во Мир, 1979.-587с.
. Куфнер, А.
Нелинейные дифференциальные уравнения:учеб.пособие/ А.Куфнер, С. Фучик.-М.:
Изд-во Наука, 1988-304с.
.Гусаренко,
С.А. Оптимальное управление : Экстремальные и вариационные задачи:
учебно-методическое пособие/ С.А. Гусаренко.-М.: Изд-во Перм.ун-т, 2001- 87с.
.Азбелев,
Н.В. Введение в теорию функционально-дифференциальных уравнений/ Н.В. Азбелев,
В.П. Максимов, Л.Ф. Рахматуллина.-М.: Наука,1991-280с.
. Азбелев,
Н.В. Функционально-дифференциальные уравнения и их приложения/ Азбелев Н.В,
Максимов В.П., Симонов П.М. // Вестник Удмуртского
университета.-2009.-№1.-С.-1-23.
. Симонов,
В.П. Арифметика рациональных чисел и компьютерное исследование интегральных
уравнений/ Симонов В.П// Соровский образовательный журнал.-1999.-№3.- C.
-121-126.
. Колмогоров,
А.Н./ Элементы теории функций и функционального анализа/ А.Н. Колмогоров,
С.В.Фомин. М.: Наука.1981.С.-40-44.
. Люстерник,
Л.А/ Элементы функционального анализа/ Л.А. Люстерник, В.И. Соболоев. М.:Наука.
1965.519С.
. Абдуллаев,
А.Р./ О разрешимости квазилинейных краевых задач для
функционально-дифференциальных уравнений// Функционально-диффер.
урав.меж-вуз.сб.науч.труд.- Пермь 1992. С.-80-87.
. Треногин,
В.А/ Функциональный анализ.М.:Наука, 1980.С.-496.
. Хелемский,
А.Я./ Лекции по функциональному анализу. М.: 2004.С.-212.