Различные определения интеграла Римана и их сравнения
Министерство образования и науки
Российской Федерации
Институт математики, естествознания и
техники
Кафедра математики и методики её
преподавания
Курсовая работа
Различные определения интеграла
Римана и их сравнения
Елец - 2015
Содержание
Введение
§1. Определение интеграла как предела интегральных сумм Римана
§2. Определение интеграла как единственного числа, разделяющего
верхние и нижние суммы Дарбу
§3. Определение интеграла от непрерывной функции как приращение
первообразной (формула Ньютона-Лейбница)
§4. Равносильность "первого", "второго" и
"третьего" определений интеграла Римана
Заключение
Список литературы
Введение
Целью данной работы является анализ различных определений
интеграла Римана, их сопоставление, сравнение, выявление общего и различного.
Задачи, которые нужно выполнить для достижения цели: изучить
множество литературы по этой теме, отобрать из изученного материла необходимый;
привести примеры использования интеграла Римана.
Иоганн Кеплер (1571-1630), Бонавентура Кавальери (1598-1647),
Эванжелиста Торричелли (1608-1647) и Блез Паскаль (1623-1662) в своих трудах
развивали методы, которые привели к созданию интегрального исчисления в великих
творениях Исаака Ньютона (1643-1727) и Готфрида Вильгельма Лейбница (1646-1716).
Огюстен Луи Коши (1789-1857) дал определение интеграла как
предела интегральных сумм и доказал существование интеграла от непрерывной
функции. Для более широких классов функций определения интегралов дали Георг
Фридрих Бернгард Риман (1826-1866), чье имя носит определенный интеграл
(интеграл Римана), а затем Жан Гастон Дарбу (1842-1917) и Камиль Мари Эдмон
Жордан (1838-1922). Дальнейшее развитие понятие интеграла получило в трудах
Томаса Стилтьеса (1856-1894) и Анри Луи Лебега (1875-1941).
Георг Фридрих Бернхард Риман (17
<https://ru.wikipedia.org/wiki/17_%D1%81%D0%B5%D0%BD%D1%82%D1%8F%D0%B1%D1%80%D1%8F>.09.1826-20.07.1866
<https://ru.wikipedia.org/wiki/20_%D0%B8%D1%8E%D0%BB%D1%8F>) - немецкий
<https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D1%80%D0%BC%D0%B0%D0%BD%D0%B8%D1%8F>
математик
<https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0>,
механик
<https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0>
и физик. За свою короткую жизнь (всего 10 лет трудов) он преобразовал сразу
несколько разделов математики. "Мы склонны видеть в Римане, может быть,
величайшего математика середины XIX века, непосредственного преемника Гаусса
<https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB_%D0%A4%D1%80%D0%B8%D0%B4%D1%80%D0%B8%D1%85>",
- отмечал академик П.С. Александров
<https://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B5%D0%BA%D1%81%D0%B0%D0%BD%D0%B4%D1%80%D0%BE%D0%B2,_%D0%9F%D0%B0%D0%B2%D0%B5%D0%BB_%D0%A1%D0%B5%D1%80%D0%B3%D0%B5%D0%B5%D0%B2%D0%B8%D1%87>
[1].
Понятие интеграла Римана, известное из элементарного курса
анализа, применимо лишь к таким функциям, которые или непрерывны, или имеют
"не слишком много" точек разрыва. Для измеримых функций, которые
могут быть разрывны всюду, где они определены (или же вообще могут быть заданы
на абстрактном множестве, так что для них понятие непрерывности просто не имеет
смысла), римановская конструкция интеграла становится непригодной.
интеграл риман приращение первообразная
§1.
Определение интеграла как предела интегральных сумм Римана
Разбиением множества Mпринято
называть совокупность его подмножеств
 со свойствами:
со свойствами:
) 
 ;
;
) 
 .
.
В дальнейшем роль множества Mу нас будет играть промежуток 
 , а разбиения мы будем рассматривать только некоторого
специального типа. А именно, на
, а разбиения мы будем рассматривать только некоторого
специального типа. А именно, на 
 мы будем выбирать точки
мы будем выбирать точки 
 так, чтобы
так, чтобы

 .
.
Этой совокупности точек, вообще говоря, можно сопоставить
несколько различных разбиений, например, два таких:


(очевидно, можно предложить и другие, поменяв местами круглую и
квадратную скобки у некоторых соседних промежутков).
Поскольку все величины, вводимые ниже, не будут зависеть от
способа расстановки круглых и квадратных скобок в таких разбиениях, обычно любое
из таких разбиений отождествляют с совокупностью точек 
 . Мы так и будем делать в дальнейшем, а чтобы отличать подобного
типа разбиения от произвольного множества точек
. Мы так и будем делать в дальнейшем, а чтобы отличать подобного
типа разбиения от произвольного множества точек 
 , в котором точки
, в котором точки 
 никак не связаны между собой, будем обозначать их символом
никак не связаны между собой, будем обозначать их символом
 .
.
Определение 1.1 Пусть функция fзадана
на отрезке 
 . Тогдадля неё вводятся следующие объекты:
. Тогдадля неё вводятся следующие объекты:
) 
 - разбиение отрезка
- разбиение отрезка
 ;
;
) 
 - отрезок разбиения
- отрезок разбиения 
 ;
;
) 
 - длина отрезка разбиения
- длина отрезка разбиения 
 ;
;
) 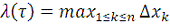
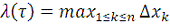 - мелкость разбиения
- мелкость разбиения 
 ;
;
) 
 , где
, где 
 - выборка, соответствующая разбиению
- выборка, соответствующая разбиению 
 ;
;
) 
 - интегральная сумма Римана, соответствующая разбиению
- интегральная сумма Римана, соответствующая разбиению 
 и выборке
и выборке 
 .
.
Определение 1.2. Пусть функция f задана на отрезке 
 . Число Iназывается
пределом интегральных сумм
. Число Iназывается
пределом интегральных сумм
 при мелкости разбиения
при мелкости разбиения 
 , cтремящейся
к нулю, когда выполняется условие:
, cтремящейся
к нулю, когда выполняется условие:
для любого 
 найдется такое
найдется такое 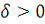
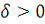 , что для любого разбиения
, что для любого разбиения 
 с мелкостью
с мелкостью 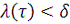
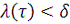 для любых выборок
для любых выборок 
 выполняется неравенство
выполняется неравенство
 .
.
В краткой символической форме то же самое можно записать так:

 .
.
Определение 1.3. В случае, когда существует конечный предел Iинтегральных сумм Римана, говорят, что
функция f интегрируема по Риману на отрезке 
 , а сам этот предел обозначают
, а сам этот предел обозначают 
 и называют (определённым) интегралом Римана (от функции f
по отрезку
и называют (определённым) интегралом Римана (от функции f
по отрезку 
 ).
).
Замечание 1.1. В соответствии с общими принципами определения предела отметим,
что

 .
.
Множество всех интегрируемых по Риману функций на отрезке 
 обозначается
обозначается
 .
.
Докажем необходимое условие интегрируемости:
Теорема 1.1. Если функция f интегрируема по Риману на отрезке 
 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Доказательство. Пусть функция f интегрируема по Риману на отрезке 
 и
и 
 . По определению интеграла для
. По определению интеграла для 
 найдётся такое
найдётся такое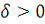
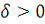 , что для любого разбиения
, что для любого разбиения 
 с мелкостью
с мелкостью
 и для любой выборки
и для любой выборки 
 будет выполняться неравенство
будет выполняться неравенство 
 . Фиксируем разбиение
. Фиксируем разбиение 
 , для которого выполнены неравенства
, для которого выполнены неравенства

 .
.
Предположим противное: Если функция f не ограничена на отрезке 
 , то для этого разбиения найдётся хотя бы один отрезок
, то для этого разбиения найдётся хотя бы один отрезок 
 , на котором она будет не ограничена. Фиксируем все точки
, на котором она будет не ограничена. Фиксируем все точки 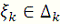
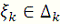 при
при 
 и рассмотрим интегральную сумму
и рассмотрим интегральную сумму

как функцию
 . Так как
. Так как 
 не ограничена на
не ограничена на 
 , очевидно, будет не ограничена и вся сумма
, очевидно, будет не ограничена и вся сумма 
 . А это противоречит неравенствам
. А это противоречит неравенствам 
 . Полученное противоречие доказывает теорему. Подчеркнём, что
ограниченность функции f является только необходимым условием интегрируемости
по Риману, но не является достаточным. Вот простой пример ограниченной функции,
не являющейся интегрируемой по Риману.
. Полученное противоречие доказывает теорему. Подчеркнём, что
ограниченность функции f является только необходимым условием интегрируемости
по Риману, но не является достаточным. Вот простой пример ограниченной функции,
не являющейся интегрируемой по Риману.
Пусть

 - функция Дирихле.
- функция Дирихле.
Очевидно, она ограничена: 
 . Покажем, что она не интегрируема по Риману на отрезке
. Покажем, что она не интегрируема по Риману на отрезке 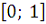
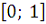 . В самом деле для любого разбиения
. В самом деле для любого разбиения 
 , делая выборку
, делая выборку 
 так, чтобы все
так, чтобы все 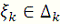
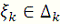 были рациональны (это всегда можно сделать!), получим, что
были рациональны (это всегда можно сделать!), получим, что

 ,
,
а для выборки 
 в которой все
в которой все 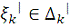
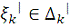 иррациональны (такая выборка тоже всегда возможна), получим
иррациональны (такая выборка тоже всегда возможна), получим

Поэтому не существует числа 
 , для которого независимо от выборки
, для которого независимо от выборки 
 выполнялось бы неравенство
выполнялось бы неравенство 
 . А это противоречит
. А это противоречит
определению интегрируемости по Риману.
Пример 1.1 Задача
(Демидович, № 2185). Вычислить интеграл 
 .
.
Решение. У
нас 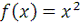
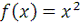 - непрерывная функция, поэтому, для вычисления данного интеграла
можно выбрать произвольную последовательность разбиений
- непрерывная функция, поэтому, для вычисления данного интеграла
можно выбрать произвольную последовательность разбиений 
 и соответствующих выборок
и соответствующих выборок 
 , лишь бы мелкость
, лишь бы мелкость 
 стремилась к нулю, соответствующая последовательность
интегральных сумм
стремилась к нулю, соответствующая последовательность
интегральных сумм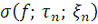
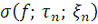 обязана стремиться к значению интеграла.
обязана стремиться к значению интеграла.
Выберем в качестве разбиения 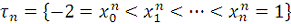
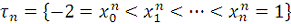 разбиение отрезка
разбиение отрезка 
 на n равных частей. Тогда, очевидно, будем иметь
на n равных частей. Тогда, очевидно, будем иметь 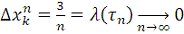
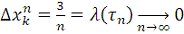 . Далее,
. Далее,
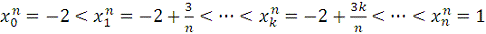
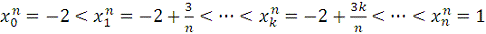 .
.
Выберем 
 . Тогда
. Тогда


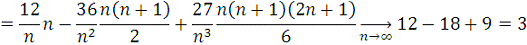
Таким образом, 
 .
.
Пример 1.2 Вычислить
интеграл

 .
.
Решение.


Доопределив эту функцию в точке 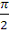
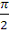 , например, по непрерывности, т.е. полагая
, например, по непрерывности, т.е. полагая 
 , мы получим
, мы получим 
 , и, следовательно, искомый интеграл равен
, и, следовательно, искомый интеграл равен 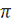
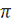 .
.
Свойства интеграла Римана:
1) Невырожденность:
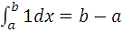
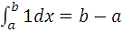 .
.
2) Положительность:
Если интегрируемая функция
 неотрицательна, то её интеграл на отрезке
неотрицательна, то её интеграл на отрезке 
 также неотрицателен.
также неотрицателен.
3) Линейность:
Если функции
 интегрируемы, и
интегрируемы, и 
 , то функция
, то функция
 тоже интегрируема, и
тоже интегрируема, и
 .
.
4) Непрерывность:
Если интегрируемые функции
 равномерно сходятся
<https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B2%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D1%81%D1%85%D0%BE%D0%B4%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D1%8C>
на отрезке
равномерно сходятся
<https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B2%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D1%81%D1%85%D0%BE%D0%B4%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D1%8C>
на отрезке
 к функции
к функции 
 , то
, то 
 интегрируема, и
интегрируема, и
 .
.
5) Аддитивность при разбиениях отрезка:
Пусть 
 . Функция
. Функция 
 интегрируема на отрезке
интегрируема на отрезке 
 , тогда и только тогда, когда она интегрируема на каждом из
отрезков
, тогда и только тогда, когда она интегрируема на каждом из
отрезков 
 и
и 
 , при этом
, при этом

 .
.
6) Непрерывная на отрезке функция интегрируема по Риману
(следствие свойств 1-5). Разрывные функции могут быть как интегрируемы, так и
не интегрируемы.
Примером функции, не интегрируемой по Риману, является всюду
разрывная функция Дирихле. Критерий Лебега интегрируемости функции по Риману:
функция интегрируема по Риману на отрезке
 , если и только если на этом отрезке она ограничена, и множество
точек, где она разрывна
<https://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D1%87%D0%BA%D0%B0_%D1%80%D0%B0%D0%B7%D1%80%D1%8B%D0%B2%D0%B0>,
имеет нулевую меру
<https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%80%D0%B0_%D0%9B%D0%B5%D0%B1%D0%B5%D0%B3%D0%B0>
(то есть может быть покрыто счётным
<https://ru.wikipedia.org/wiki/%D0%A1%D1%87%D1%91%D1%82%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE>
семейством интервалов
<https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D1%80%D0%B2%D0%B0%D0%BB_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)>
со сколь угодно малой суммарной длиной).
, если и только если на этом отрезке она ограничена, и множество
точек, где она разрывна
<https://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D1%87%D0%BA%D0%B0_%D1%80%D0%B0%D0%B7%D1%80%D1%8B%D0%B2%D0%B0>,
имеет нулевую меру
<https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%80%D0%B0_%D0%9B%D0%B5%D0%B1%D0%B5%D0%B3%D0%B0>
(то есть может быть покрыто счётным
<https://ru.wikipedia.org/wiki/%D0%A1%D1%87%D1%91%D1%82%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE>
семейством интервалов
<https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D1%80%D0%B2%D0%B0%D0%BB_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)>
со сколь угодно малой суммарной длиной).
) Если функция 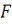
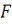 является первообразной
<https://ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BD%D0%B0%D1%8F>
непрерывной функции
является первообразной
<https://ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BD%D0%B0%D1%8F>
непрерывной функции
 , то интеграл функции
, то интеграл функции
 на отрезке
на отрезке
 может быть вычислен по формуле Ньютона-Лейбница
<https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0-%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%D0%B0>:
он равен
может быть вычислен по формуле Ньютона-Лейбница
<https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0-%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%D0%B0>:
он равен
 . (Это - общее свойство любых интегралов, удовлетворяющих
свойствам 1-5, а не только интеграла Римана). Непрерывная на отрезке функция
. (Это - общее свойство любых интегралов, удовлетворяющих
свойствам 1-5, а не только интеграла Римана). Непрерывная на отрезке функция
 всегда имеет первообразную, и каждая первообразная имеет вид:
всегда имеет первообразную, и каждая первообразная имеет вид: 
 , где
, где 
 - произвольная константа
<https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%BD%D0%B0%D1%8F>.
- произвольная константа
<https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%BD%D0%B0%D1%8F>.
Интегральные суммы
 не являются ни последовательностью (хотя
не являются ни последовательностью (хотя 
 присутствует как количество точек разбиения, но уж слишком много
различных разбиений можно предложить при одном и том же количестве точек
присутствует как количество точек разбиения, но уж слишком много
различных разбиений можно предложить при одном и том же количестве точек 
 ), ни функцией какого-нибудь действительного числа.
), ни функцией какого-нибудь действительного числа.
Рассмотрим множество 
 всевозможных разбиений c фиксированными в них выборками
всевозможных разбиений c фиксированными в них выборками 
 .
. 
Таким образом, мы считаем пары 
 и
и 
 разными элементами множества
разными элементами множества 
 , когда отличаются друг от друга или первые или вторые элементы
этих пар или те и другие одновременно. На множестве
, когда отличаются друг от друга или первые или вторые элементы
этих пар или те и другие одновременно. На множестве 
 имеется "естественный" фильтр
имеется "естественный" фильтр 
 , базис которого составляют множества
, базис которого составляют множества 
 , (проверка того, что
, (проверка того, что 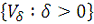
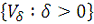 - это действительно базис некоторого фильтра, который мы
обозначили через
- это действительно базис некоторого фильтра, который мы
обозначили через 
 , остаётся в качестве упражнения). Если мы фиксируем функцию
, остаётся в качестве упражнения). Если мы фиксируем функцию 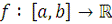
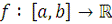 , то интегральную сумму
, то интегральную сумму 
 можно рассматривать как функцию, определённую на множестве
можно рассматривать как функцию, определённую на множестве 
 , и принимающую значения в множестве всех действительных чисел
, и принимающую значения в множестве всех действительных чисел

 :
: 
 .
.
Предел именно этой функции по фильтру 
 и называют пределом интегральных сумм при мелкости разбиения,
стремящейся к нулю, а если он существует и конечен, то интегралом (Римана) от
функции
и называют пределом интегральных сумм при мелкости разбиения,
стремящейся к нулю, а если он существует и конечен, то интегралом (Римана) от
функции 
 по промежутку
по промежутку

 ,
,
 .
.
Замечание 1.2. Чтобы не вводить новых букв, очень часто фильтр 
 (или его базис) обозначают через
(или его базис) обозначают через 
 . При таких обозначениях запись "стандартного"
определения интеграла в точности совпадает с приведённым выше:
. При таких обозначениях запись "стандартного"
определения интеграла в точности совпадает с приведённым выше:
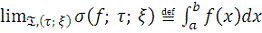
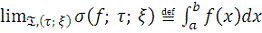 .
.
§2. Определение
интеграла как единственного числа, разделяющего верхние и нижние суммы Дарбу
Определение 2.1 Пусть функция
 определена на отрезке
определена на отрезке 
 и задано разбиение
и задано разбиение 
 отрезка
отрезка 
 . Определим:
. Определим:

 ,
, 

Нижней и верхней интегральными суммами Дарбу функции 
 на
на
 , отвечающими разбиению
, отвечающими разбиению 
 называются соответственно:
называются соответственно:

 ,
, 
 .
.
Лемма 2.1 Если
функция 
 ограничена снизу на
ограничена снизу на 
 , то для любого разбиения
, то для любого разбиения
 -
- 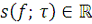
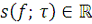 . Если функция
. Если функция 
 неограниченна снизу на
неограниченна снизу на 
 , то для любого разбиения
, то для любого разбиения 
 -
- 
 .
.
Доказательство. Пусть 
 - разбиение отрезка
- разбиение отрезка 
 . Если
. Если 
 ограничена снизу, то
ограничена снизу, то 
 , следовательно,
, следовательно, 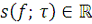
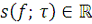 . Если
. Если 
 неограниченна снизу, то она неограниченна снизу на некотором
отрезке
неограниченна снизу, то она неограниченна снизу на некотором
отрезке 
 , следовательно,
, следовательно, 
 и
и 
 .
.
Лемма 2.2 Если
функция 
 ограничена сверху на
ограничена сверху на 
 , то для любого разбиения
, то для любого разбиения
 -
- 
 . Если функция
. Если функция 
 неограниченна сверху на
неограниченна сверху на 
 , то для любого разбиения
, то для любого разбиения

 -
- 
 .
.
Доказательство. Лемма 2.2 доказывается аналогично.
Свойства сумм Дарбу:
1) Для любой выборки 
 и разбиения
и разбиения
 справедливы неравенства
справедливы неравенства
Доказательство.
Так как 
 выполняются неравенства
выполняются неравенства 
 . Домножим все части на
. Домножим все части на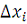
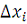 .
.
Получим:

 ,
, 
 .
.
Перейдя к сумме в каждой части неравенства, получаем:

 ,
,
где 
 ,
, 
 ,
, 
 .
.
Согласно определению сумм Дарбу и интегральной суммы 
 , утверждения
, утверждения 
 и
и 
 равносильны.
равносильны.
2) При 
 - фиксированном, справедливы равенства
- фиксированном, справедливы равенства 
 ,
, 
 .
.
Доказательство.
Докажем первое равенство. Необходимо показать, что 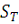
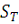 - минимальный предел верхних границ для интегральной суммы, т.е.
нужно показать следующее:
- минимальный предел верхних границ для интегральной суммы, т.е.
нужно показать следующее:
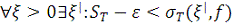
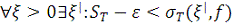 .
.
Так как 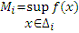
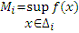 , то
, то 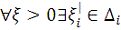
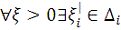
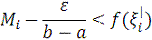

 ,
,
 .
.
Домножим на 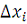
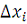 :
: 

Проссумируемые элементы:



Неравенства 
 ,
, 
 и
и 
 равносильны.
равносильны.
Получили, что 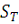
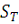 - минимальный предел верхних границ для интегральной суммы
- минимальный предел верхних границ для интегральной суммы 
 . Второе утверждение доказывается аналогично.
. Второе утверждение доказывается аналогично.
3) Существуют числа 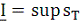
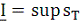 ,
, 
 , называемые верхним и нижним интегралами Дарбу, такие, что для
любых разбиений
, называемые верхним и нижним интегралами Дарбу, такие, что для
любых разбиений 
 отрезка
отрезка 
 :
: 
 .
.
Доказательство.
Существуют 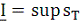
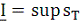 и
и 
 , такие что для всевозможных разбиений отрезка
, такие что для всевозможных разбиений отрезка 
 и для любых разбиений
и для любых разбиений 
 выполняется неравенство:
выполняется неравенство: 
 .
.
Пример 2.1 Найти
суммы Дарбу для функции 
 на отрезке
на отрезке 
 , соответствующие разбиению этого отрезка на
, соответствующие разбиению этого отрезка на
 частей.
частей.
Решение.
В этом случае 
 ,
, 
 ,
, 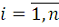
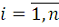 . В силу непрерывности и возрастания этой функции при любом
разбиении отрезка она достигает наименьшего
. В силу непрерывности и возрастания этой функции при любом
разбиении отрезка она достигает наименьшего 
 и наибольшего
и наибольшего 
 значений на левом и правом концах частичного отрезка
значений на левом и правом концах частичного отрезка 
 соответственно. Согласно формулам, находим:
соответственно. Согласно формулам, находим:

 ,
, 

Принимая во внимание, что 
 ,
,
 ,
,
 , в итоге получаем:
, в итоге получаем:

 ,
, 
 .
.
Ответ: 
 ,
, 
 .
.
Пример 2.2 Для
интеграла 
 найти верхнюю и нижнюю интегральные суммы, соответствующие
разбиению отрезка
найти верхнюю и нижнюю интегральные суммы, соответствующие
разбиению отрезка 
 на 3 равные части.
на 3 равные части.
Решение. На отрезке 
 функция
функция 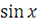
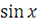 монотонно возрастает, и поэтому для этого отрезка имеем
монотонно возрастает, и поэтому для этого отрезка имеем 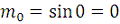
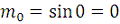 ,
, 
 .
.
На отрезке 
 наименьшим значением функции является
наименьшим значением функции является 
 , а наибольшим
, а наибольшим 
 .
.
На отрезке 
 функция монотонно убывает, и поэтому:
функция монотонно убывает, и поэтому:
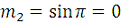
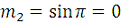 ,
, 
 .
.
Так как все 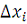
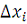 равны
равны 
 , то
, то

 ,
, 
 .
.
Ответ: 
 ,
, 
 .
.
§3.
Определение интеграла от непрерывной функции как приращение первообразной
(формула Ньютона-Лейбница)
Определение 3.1 Функция 
 называется первообразной функцией
называется первообразной функцией 
 на
на
 , если
, если 
 , а на концах отрезка
, а на концах отрезка 
 значения функции
значения функции 
 равны односторонним производным функциям
равны односторонним производным функциям 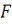
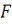 :
:
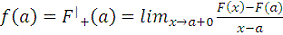
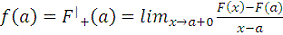 ,
,

 .
.
Теорема 3.1 Если функция 
 непрерывна на
непрерывна на 
 , то функция
, то функция 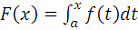
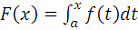 является первообразной функции
является первообразной функции 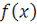
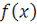 на
на
 .
.
Доказательство.
Пусть 
 .
.
Тогда
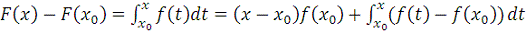
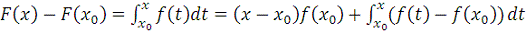 .
.
Следовательно,



 .
.
В силу непрерывности функции 
 на
на


 ,
,
поэтому


то есть 
 , где при
, где при 
 имеется в виду предел справа, а при
имеется в виду предел справа, а при 
 - предел слева.
- предел слева.
Это означает, что 
 . Таким образом, функция
. Таким образом, функция 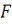
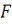 является первообразной функции
является первообразной функции 
 на
на
 .
.
Следствие 3.1 Любая первообразная непрерывной на 
 функции
функции 
 имеет вид
имеет вид 
 , где
, где 
 - произвольная константа.
- произвольная константа.
Следствие 3.2 (Формула Ньютона-Лейбница) Если 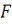
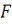 - первообразная непрерывной на
- первообразная непрерывной на 
 функции
функции 
 , то
, то 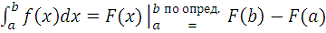
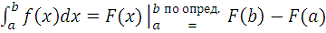
Доказательство.
Воспользуемся следствием 1 и заметим, что
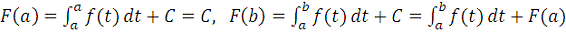
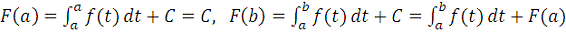 .
.
Следовательно, 
 .
.
Теорема 3.2 (Замена
переменной) Пусть функция
 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 
 , а функция
, а функция 
 непрерывна на отрезке
непрерывна на отрезке 
 . Тогда
. Тогда 
 .
.
Доказательство.
Поскольку функция 
 непрерывна на отрезке
непрерывна на отрезке 
 , то по теореме 3 существует первообразная
, то по теореме 3 существует первообразная 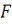
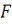 для функции
для функции 
 :
:

 .
.
По формуле Ньютона-Лейбница:

 .
.
Поскольку 
 , то функция
, то функция 
 является первообразной функции
является первообразной функции 
 .
.
Следовательно, по формуле Ньютона-Лейбница:



 .
.
Доказательство.
Пользуясь линейностью интеграла и формулой Ньютона-Лейбница,
получаем:
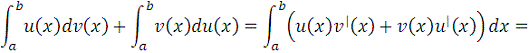

 , откуда следует доказываемое равенство.
, откуда следует доказываемое равенство.
Теорема 3.4 (Интегральная
теорема о среднем) Если функции
 и
и 
 непрерывны на
непрерывны на 
 и
и 
 , то существует точка
, то существует точка 
 такая, что
такая, что 
 .
.
Доказательство. Поскольку функции 
 и
и 
 непрерывны, то по теореме 3 существуют дифференцируемые на
непрерывны, то по теореме 3 существуют дифференцируемые на 
 функции
функции 
 и
и 
 :
:

 ,
, 
 ,
, 
 .
.
По теореме Коши о среднем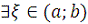
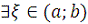 :
:
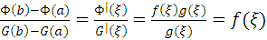
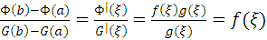 .
.
Так как по формуле Ньютона-Лейбница

 ,
,

 , то
, то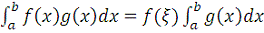
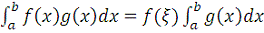 .
.
Пример 3.1 Вычислить
значение определенного интеграла 
 по формуле Ньютона-Лейбница.
по формуле Ньютона-Лейбница.
Решение. Для
начала отметим, что подынтегральная функция 
 непрерывна на отрезке
непрерывна на отрезке 
 , следовательно, интегрируема на нем.
, следовательно, интегрируема на нем.
Для функции 
 множество первообразных для всех действительных значений
аргумента записывается как
множество первообразных для всех действительных значений
аргумента записывается как 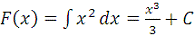
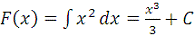 . Возьмем первообразную при
. Возьмем первообразную при 
 :
: 
 .
.
Воспользуемся формулой Ньютона-Лейбница для вычисления
определенного интеграла:

 .
.
Ответ: 
 .
.
Пример 3.2 Вычислить
определенные интегралы 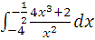
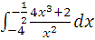 и
и 
 .
.
Решение. На
отрезке 
 подынтегральная функция непрерывна, следовательно, интегрируема.
подынтегральная функция непрерывна, следовательно, интегрируема.
Найдем множество первообразных функции 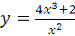
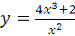 :
:
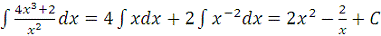
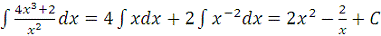 .
.
Возьмем первообразную
 и по формуле Ньютона-Лейбница вычислим требуемый определенный
интеграл:
и по формуле Ньютона-Лейбница вычислим требуемый определенный
интеграл:

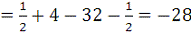
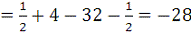 .
.
Переходим ко второму определенному интегралу.
На отрезке 
 подынтегральная функция не ограничена, так как
подынтегральная функция не ограничена, так как 
 , то есть, не выполняется необходимое условие интегрируемости
функции на отрезке.
, то есть, не выполняется необходимое условие интегрируемости
функции на отрезке. 
 не является первообразной функции
не является первообразной функции 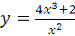
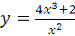 на отрезке
на отрезке 
 , поскольку точка
, поскольку точка 
 , принадлежащая отрезку, не входит в область определения функции.
Следовательно, не существует определенный интеграл Римана и Ньютона-Лейбница
для функции
, принадлежащая отрезку, не входит в область определения функции.
Следовательно, не существует определенный интеграл Римана и Ньютона-Лейбница
для функции 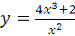
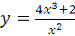 на отрезке
на отрезке 
 .
.
§4.
Равносильность "первого", "второго" и "третьего"
определений интеграла Римана
Теорема 4.1 Если функция 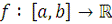
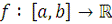 интегрируема по Риману, то для любой последовательности разбиений
интегрируема по Риману, то для любой последовательности разбиений

 отрезка
отрезка
 такой, что
такой, что 
 при
при 
 , и любой последовательности выборок
, и любой последовательности выборок 
 соответствующих разбиениям
соответствующих разбиениям 
 , последовательность интегральных сумм
, последовательность интегральных сумм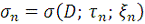
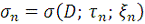 имеет предел равный
имеет предел равный 
 .
.
Доказательство.
По условию функция f интегрируема по Риману на
 . Пусть
. Пусть
 .
.
По определению для любого 
 найдется такое
найдется такое 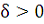
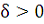 , что для любого разбиения
, что для любого разбиения 
 с мелкостью
с мелкостью 
 для любой выборки
для любой выборки 
 выполняется неравенство
выполняется неравенство 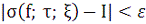
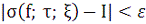 .
.
Но у нас по условию теоремы 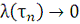
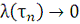 при
при
 . Поэтому найдётся такое N, что при всех
. Поэтому найдётся такое N, что при всех 
 будет выполняться неравенство
будет выполняться неравенство
 .
.
Но тогда для любой выборки 


Таким образом, для произвольного
 , мы нашли такое N, что при всех
, мы нашли такое N, что при всех
 выполняется неравенство
выполняется неравенство 
 . Это и означает, что
. Это и означает, что

 .
.
Теорема 4.2 Если интеграл Римана и определенный интеграл Ньютона-Лейбница
функции 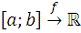
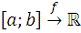 существуют одновременно, то они равны друг другу.
существуют одновременно, то они равны друг другу.
Теорема 4.3 Для ограниченной функции 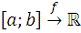
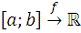 интегралы Римана и Дарбу эквивалентны, то есть они существуют или
не существуют одновременно, а в случае существования их значения совпадают.
интегралы Римана и Дарбу эквивалентны, то есть они существуют или
не существуют одновременно, а в случае существования их значения совпадают.
Теорема 4.4 Пусть на отрезке 
 задана интегрируемая по Риману функция
задана интегрируемая по Риману функция 
 . Тогда функция
. Тогда функция 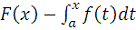
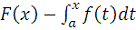 непрерывна на
непрерывна на
 .
.
Доказательство. В силу необходимого условия интегрируемости функция
 ограничена на
ограничена на 
 , то есть
, то есть 
 .
.
Пусть 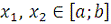
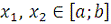 . В силу свойства аддитивности интеграла относительно отрезков
интегрирования
. В силу свойства аддитивности интеграла относительно отрезков
интегрирования 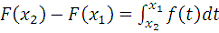
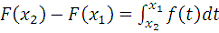 . По теореме об интегрировании неравенств
. По теореме об интегрировании неравенств 
 . Следовательно,
. Следовательно, 


 , то есть
функция
, то есть
функция 
 непрерывна на
непрерывна на
 .
.
Заключение
Интеграл, который мы рассмотрели в данной работе, был введен
Бернхардом Риманом в 1854 г., и является одной из первых формализаций понятия
интеграла и одним из важнейших понятий математического анализа.
Трудно назвать научную область, в которой бы не применялись
методы интегрального исчисления, в общем, и свойства определенного интеграла, в
частности. Также определенный интеграл используется для изучения собственно
самой математики. Например, при решении дифференциальных уравнений, которые в
свою очередь вносят свой незаменимый вклад в решение задач практического
содержания. Можно сказать, что определенный интеграл - это некоторый фундамент
для изучения математики. Отсюда и важность знания методов их решения.
Но вычисление определенных интегралов через предел
интегральных сумм связано с большими трудностями. Поэтому самым простым и
удобным методом вычисления определенного интеграла является формула
Ньютона-Лейбница.
Список литературы
1) Клевчихин,
Ю.А. Лекция 4. Определение интеграла Римана - Владивосток, 2005. - 9 с.
2) Фихтенгольц,
Г.М. Курс дифференциального и интегрального исчисления. Том 3 - Москва, 1966 -
662 с.
) Кудрявцев,
Л.Д. Математический анализ. Том 2 - М.: Высшая школа, 1970. - 424 с.
) Иванов,
Г.Е. Лекции по математическому анализу. Часть 1 - МФТИ, 2000. - 359 с.
5) Свободная
энциклопедия Википедия, статья "Риман, Бернхард". Web: https: // ru.
wikipedia.org/wiki/Риман,_Бернхард <https://ru.wikipedia.org/wiki/Риман,_Бернхард>
) Свободная
энциклопедия Википедия, статья "Интеграл Римана". Web: https: // ru.
wikipedia.org/wiki/Интеграл_Римана
<https://ru.wikipedia.org/wiki/Интеграл_Римана>
) Математический
форум MathHelpPlanet, статья "Интеграл Римана". Web: http://mathhelpplanet.com/static.
php? p=integral-rimana
<http://mathhelpplanet.com/static.php?p=integral-rimana>
8) Савельев,
Л.Я. Элементарная теория вероятностей. Интегралы Римана и Стилтьеса. Часть 3 -
Новосибирск, 2005. - 200 с.