Особенности применения теории графов при решении задач и в практической деятельности

Содержание

Введение

. История возникновения

. Основные понятия графа и их пояснение на примере

. Графический или геометрический способ задания графов. Понятие смежности и инцидентности

. Способы задания графов

. Элементы графа. Маршрут. Цепь. Цикл. Путь и контур. Связный граф. Плоские и планарные графы. Задача о трёх домах и трёх колодцах

.1 Элементы графа: висячая и изолированная вершины

.2 Маршрут графа. Цепь. Цикл

.3 Путь и контур. Длина пути и контура. Длина петли

. Графы - деревья. Корень

. Применение графов в жизни

Заключение

Список литературы

Приложение

Введение

Теория графов находит самое широкое применение в моделировании информационных процессов, в программировании и в решении экономических задач. Она позволяет просто описывать сложные явления и дает им графическую интерпретацию. ”Картинка” графа позволяет быстро понять проблему и на интуитивном уровне разработать рациональный алгоритм решения.

В данной курсовой работе мы рассмотрим: основы теории графов - основные характеристики графа, правила исполнения алгебраических операций и алгоритмы решения некоторых задач на графе.

Нашей целью является выяснить особенности применения теории графов при решении задач и в практической деятельности. И для этого мы поставим некоторые задачи, которые мы рассмотрим позже, такие как: изучить теорию графов, основные понятия графов и как применять их на примере, какие способы существуют, чтобы их применить. Рассмотреть все элементы графа, такие как маршрут, цепь, цель, планарные и не планарные графы.

1. История возникновения

Существуют много различных подходов к определению графа. Отдельные авторы при определении графа исключают возможность введения нескольких ребер, соединяющих одни и те же вершины. Другие исключают наличие петель т.е. ребер соединяющих вершину саму с собой, а потом, чтобы определить графы, вводятся специальные термины типа мультиграф и т.п.. Таким образом, в настоящее время все еще не сложилось единого стандарта терминологии теории графов.

Одним из важнейших разделов дискретной математики является теория графов. С их помощью описывается сложное строение физических, химических, социальных и т.д. объектов. Графы широко используется в градостроительстве при проектировании сетей водо-, газо-, тепло-, электроснабжения.

Датой рождения этой теории можно считать 1736 год, когда была опубликована статья Леонарда Эйлера, посвященная решению головоломки под названием «Задача о кёнисберских мостах». Долгое время методы, аналогичные эйлеровым использовались для исследования подобных развлекательных задач. Но в XIX веке А.Кэли нашел им более достойное определение. С помощью графов он стал описывать химические «цепи».

Существующее название закрепилось за этой наукой с 1936 года, после выхода в свет монографии венгерского математика Д.Кёнига. Термин «граф» происходил от греческого слова «пишу». Он говорит о наглядной графической интерпретации во-первых основных понятий этой теории, во - вторых она тесно связана с геометрией. И действительно, этот раздел дискретной математики находится на стыке геометрии, топологии, комбинаторики и ряда других математических дисциплин и интенсивно использует их методы.

2. Основные понятия графа и их пояснение на примере.

Определение. Графом называется совокупность точек (объектов) и соединяющих их линий. Точки графа при этом называются его вершинами, а связывающие их линии - ребрами.

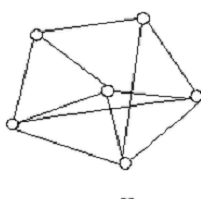
Рис.1

Если для рёбер графа существенно положение соединяемых ими вершин, то оно называется ориентированным. В противном случае - не ориентированным, как это показано на рис.1.

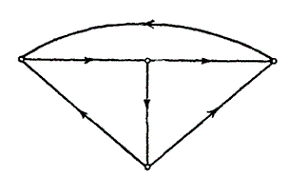
Рис.2

Определение. Ориентированный граф (орграф) - это граф, у которого пары в наборе X являются упорядоченными. У ориентированного графа рис.3 т.е. орграфа или направленного графа, рёбра имеют начало и конец, будем также называть такие рёбра дугами.

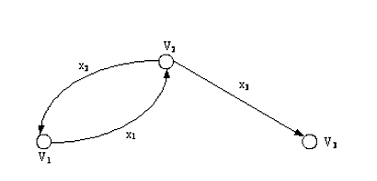
Рис.3

Пример 1.

V = (V1,V2,V3)

X = {x1 = {V1,V2}, x2 = {V2,V1}, x2 = {V2,V3}}

Тогда G = (V,X) - ориентированный граф.

Дуга - это направленное ребро в орграфе . Следовательно в примере для орграфа G = (V,X), дугами являются ребра x1,x2,x3.

Смежные вершины и ребра.

Определение 1. Две вершины называются смежными, если существует ребро, которой им инцидентно.

Определение 2. Два ребра называется смежными, если они имеют общую вершину.

Определение3. Если граф G имеет ребро X(V,V), т.е. его начало и конец совпадает, то это ребро называется петлей.

Для пояснения введенных понятий рассмотрим граф, изображенный на следующем рисунке.

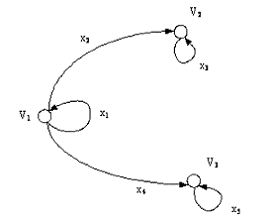
Рис.4

Пусть D = (V,X) - ориентированный граф (рис.4)

V = {V1, V2, V3}

x = {x1 = {V1, V1}, x2 = {V1, V2}, x3 = {V2,V2}, x4 = {V1,V3}, x5 = {V3,V3}},

тогда x1, x3, x5 - петли.

Определение. Полный граф - это граф, каждая пара различных вершин которого, связана лишь одним ребром.

Как выглядит полный граф на самом деле мы увидим на рис.5.

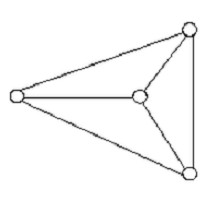
Рис.5

Если вершина Vn является концом ребра Xn , то говорят, что они (ребро и вершина) инцидентны. В то время как смежность представляет собой отношение между однородными объектами (вершинами или ребрами или дугами)

3. Графический или геометрический способ задания графов. Понятие смежности и инцидентности

Важнейший способ задания графа - графический. Его преимущества следует из наглядности всех элементов графа, что позволяет быстро визуально анализировать его строение. Это явное превосходство метода предопределило его широкое использование. В первую очередь это относится к тем сферам применения графов, которые связаны с передачей какой - то информации большому числу людей. Например, схемы движений различных видов транспорта, эвакуаций людей из помещений в чрезвычайных ситуациях, размещения экспозиций, выставок и т.д., даются только в графическом виде, иначе их не сможет воспринять большая масса народа, что, неизбежно, создает очевидные проблемы.

Однако у этого метода представления графов есть и свои недостатки. К ним относятся громоздкость и трудность машинного восприятия. Второе особенно важно при обработке графа с помощью ЭВМ, это в первую очередь относится к задачам управления различными отраслями народного хозяйства страны.

Поэтому в теории графов разработаны и другие способы их задания. Существует несколько достаточно удобных методов аналитического представления графов, из которых наиболее удобными считаются следующие два. Если вершина Vn является концом ребра Xn , то говорят, что они (ребро и вершина) инцидентны. В то время как смежность представляет собой отношение между однородными объектами (вершинами или ребрами или дугами)

4. Способы задания графов

До сих пор мы задавали ориентированные и не ориентированные графы, изображая их с помощью рисунков. Можно задать граф как пару множеств, следуя определению, однако этот способ довольно громоздкий и представляет, скорее, теоретический интерес. Развитие алгоритмических подходов к анализу свойств графов требует иных способов описания графов, более пригодных для практических вычислений, в том числе с использованием ЭВМ.

Рассмотрим самые распространенные способы представления графов: Предположим, что все вершины и все ребра не ориентированного графа или все вершины и все дуги (включая петли) ориентированного графа пронумерованы начиная с единицы. Граф (не ориентированный или ориентированный) может быть представлен в виде матрицы типа n x m, где n - число вершин, m - число ребер (или дуг). Для ориентированного графа и неориентированного (орграфа) элементы этой матрицы задаются следующим образом:

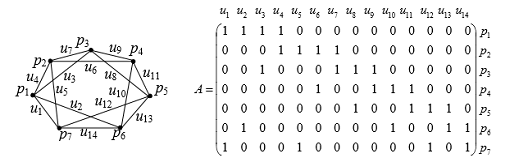
Назовем матрицей инцидентности Таблицу А, состоящую из i строк (вершины) и j столбцов (ребра или дуги), в которой:

)для неориентированного графаi j = 1, если вершина xi инцидентна ребру xj;i j = 0, если вершина xi не инцидентна ребру xj;

)для орграфаi j= 1, если вершина xi является началом дуги xj;i j = 0, если вершина xi не инцидентна дуге xj;i j= - 1, если вершина xi является концом дуги xj.

Так как ребро (дуга) может соединять одну или две конкретные точки графа, то каждый столбец матрицы инцидентности может содержать одну или две 1 (одну 1, или одну 1 и одну -1). Очевидно, если в j-м столбце имеется одна единица, то xi является петлёй, если же имеются одинаковые столбцы, то их число определяет кратность множественного ребра.

Из определения матрицы инцидентности следует, что она учитывает отдельные точки графа нулевыми строками. В строках может быть любое количество единиц или может вообще их не быть. Матрица инцидентности этого графа имеет вид:

5. Элементы графа. Маршрут. Цепь. Цикл. Путь и контур. Связный граф. Плоские и планарные графы. Задача о трёх домах и трёх колодцах

.1 Элементы графа: висячая и изолированная вершины

граф задача теория

Вершина графа имеющая степень равную 1 называется висячей. Вершина графа имеющая степень равную 0 называется изолированная вершина. По рис. 6 мы видим, что изолированными вершинами являются p6, p7 . По определению петля при вершине pnm добавляет 2 в степень соответствующей вершины. Петля в графе тут изображена только одна и это p8.

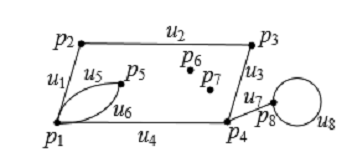
Рис.6

Сумма степеней вершин графа. В графе Г на рис. 6 видно, что сумма степеней вершин графа равна 16 и равна удвоенному числу рёбер 8. Таким образом, сумма степеней вершин графа Г равна удвоенному числу рёбер графа Г и, следовательно, является чётным числом. Пусть граф Г (без петель и изолированных точек) имеет N вершин и M рёбер. Поскольку каждое ребро инцидентно двум вершинам, оно добавляет двойку к сумме степеней вершин графа, поэтому сумма

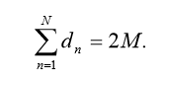
.2 Маршрут графа. Цепь. Цикл

Последовательность попарно инцидентных вершин Vi1, Vi2…Vik неориентированного графа, в котором вторая вершина предыдущего ребра, совпадает с первой вершиной, с последующим ребром называется маршрутом.

Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутым или циклом. Цикл может быть простым, если он содержит отличные друг от друга рёбра, сложным - в противном случае, элементарным, если при обходе по какому-нибудь направлению каждая вершина цикла встречается только один раз.

.3 Путь и контур. Длина пути и контура. Длина петли

Последовательность дуг, при которой конец одной дуги является началом другой, называется путём. Если начальная и конечная точки пути совпадают, образуется контур. Длиной пути (или контура) называют число дуг, которые его образуют. Петля - контур единичной длины. Будем также под длиной пути от одной вершины до другой понимать количество рёбер, входящих в соответствующий маршрут. То есть будем применять термин “длина пути” не только к орграфам. Во всех случаях для орграфов и для неориентированных графов дуги и рёбра будем считать столько раз, сколько раз они входят в путь или маршрут.

Связный граф. Граф называется связным, если любая пара вершин соединена маршрутом. Несвязный граф состоит из нескольких отдельно связных графов.

Полный граф. Граф называется полным, если любая пара его вершин соединена ровно одной дугой или ребром.

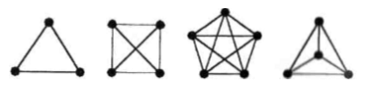
Рис.7

Число рёбер полного графа с N вершинами. Если полный граф Г имеет N вершин, то он обозначится через КN. Легко видеть, что КN имеет N(N-1) / 2 рёбер.

Простым графом называют граф, который не имеет петель или кратных рёбер. Рис.7. Является ли полный граф простым и однородным графом? Полный граф - это простой граф. Он однозначно задаётся числом своих вершин. Полный граф с N вершинами является однородным степени (N-1), так как из каждой его вершины выходит (N-1) рёбер, ведущих к каждой из остальных (N-1) вершин.

.4 Плоские и планарные графы

Граф, который можно начертить на плоскости так, чтобы рёбра его пересекались только в его вершинах, называется планарным графом. Его изображение на плоскости без пересечения рёбер назовём плоским графом. Граф, который не является планарным, называется непланарным. Заметим, что в общем случае рёбра графа могут пересекаться между собой, причём точки пересечения не обязательно являются вершинами графа.

Интегральная микросхема состоит из слоёв миниатюрных микросхем, впечатанных в пластину. В такой ситуации крайне важно исключить пересечение проводов в местах, не предназначенных для соединений. Если изобразить места указанных соединений вершинами графа, то возникнет задача построения графа с непересекающимися рёбрами. Важно отметить, что нас интересует возможность построения графа с непересекающимися рёбрами.

Можно также сказать, что граф, изоморфный плоскому графу, называется планарным. Например, все три изоморфных графа (рис.8) Г1 , Г2 , Г3 на следующем рисунке планарные, но только Г2, и Г3 - плоские.

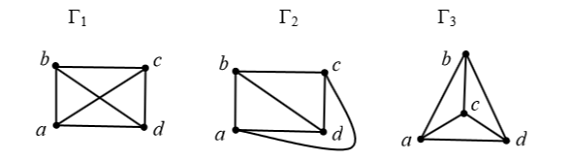
Рис.8

Планарный граф на рис. 9.1 можно изобразить в виде изоморфных плоских графов (рис. 9.2 и рис. 9.3):

Рис.9.1                           Рис.9.2                             Рис.9.3

Естественно поставить следующий вопрос: всегда ли можно изобразить плоский граф так, чтобы все его рёбра были прямолинейными отрезками? Этот вопрос остаётся открытым.

.3 Задача о трёх домах и трёх колодцах

На одном участке земли были построены три дома и вырыты три колодца для их обитателей.

Природа страны и её климат таковы, что колодцы часто пересыхают, поэтому важно, чтобы от каждого из домов имелся доступ к каждому из трёх колодцев. Спустя некоторое время обитатели домов А, В, и С (рис.10) серьёзно поссорились друг с другом и решили проложить дорожки к трём колодцам а, b, с так, чтобы по пути к колодцам и обратно им не приходилось встречать друг друга.

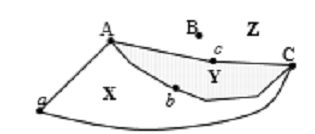
Рис.10

А возможно ли это? Является ли соответствующий граф плоским, т.е. можно ли провести дорожки так, чтобы они не пересекались нигде, кроме вершин графа А, В, С и а, b, с? С помощью непосредственной проверки легко убедиться, что всегда можно провести 8 тропинок, которые, кроме указанных точек, других точек пересечения иметь не будут, а девятая тропинка обязательно пересечёт хотя бы одну из них. На рис. 4 показан один из возможных вариантов проведения тропинок. Решим эту задачу посредством рассуждений.

От домиков А и С проведём требуемые тропинки. Полученный граф разделит плоскость на области: X , Y , Z.

Легко заметить, что домик В может находиться в одной из этих областей. Рассмотрим каждый случай в отдельности.

. Если домик В находится в области Z, как изображено на рисунке, то от него невозможно провести тропинку к b, которая не пересекалась бы ни с одной из уже проведённых тропинок.

. Если домик В находится в области Y , то от него невозможно провести тропинку к объекту а, которая не пересекалась бы ни с одной из уже проведённых.

. Если домик В находится в области X, то от него невозможно провести тропинку к объекту c, которая не пересекалась бы ни с одной из уже проведённых.

Итак, получается, что граф, выражающий ситуацию данной задачи, плоским быть не может. А это значит, что задача неразрешима.

6. Графы - деревья. Корень

Деревом называется связный граф, не содержащий циклов. В частности, дерево не имеет петель и кратных рёбер (поскольку кратные рёбра образуют цикл). Граф без циклов есть граф, связные компоненты которого являются деревьями; иногда такой граф называется лесом.

Любая цепь в графе без циклов является элементарной; любая часть такого графа также будет графом без циклов. Здесь элементарная цепь, как уже определялось ранее, - это цепь, при обходе которой, каждая вершина встречается только один раз.

Корень. Исходная вершина дерева называется его корнем. Заметим, что корнем может служить любая вершина дерева.

Число вершин и рёбер дерева. Для подсчёта числа элементов дерева служит теорема: "Дерево с n вершинами имеет n - 1 рёбер".

Как выглядит дерево рассмотрим следующий рис. 11:

Применение деревьев облегчает разработку и анализ системы, избавляет от необходимости держать в памяти много данных. В последние десятилетия компьютерная наука столкнулась с тем фактом, что деревья обеспечивают удобные структуры для хранения и исправления определённых типов данных - так называемых иерархических баз.

Рис.11

Рассмотрим произвольное дерево с n заданными и пронумерованными в произвольном порядке вершинами. Пусть например, т = 11(левый, рис.12).

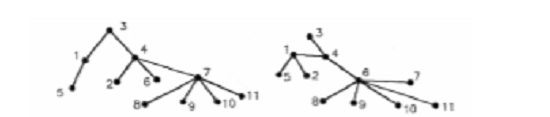
Рис.12

Но ведь те же 11 вершин можно соединить попарно 10 рёбрами и по- другому, чтобы получилось какое-то новое дерево (правый рисунок). У этого нового дерева совпадает с предыдущим только 3 ребра.

Спрашивается: сколько существует таких разных деревьев?

Английскому математику А.Кэлли (1875 г.) опыт, приобретённый в процессе непосредственного подсчёта числа деревьев, помог найти правильный ответ на этот вопрос. Деревьев с n пронумерованными вершинами существует nn-2..

7. Применение графов в жизни

Вот мы рассмотрели все варианты графов, их элементы и теперь мы рассмотрим где и в каких сферах жизни используются графы.

·        В химии (для описания структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия - сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоининформатики. Теория графов позволяет точно определить число теоретически возможных изомеров и углеродов и других органических соединений.

·        В информатике и программировании (граф - схема алгоритма).

·        В коммуникационных и транспортных системах. В частности, для маршрутизации данных в интернете.

·        В экономике.

·        В логистике.

·        В физике или схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф).

·        В биологии.

·        стереохимии

·        В строительстве.

·        В менеджменте.

·        В географии.

·        В социологии.

·        В автоматизации технологических процессов и производств.

·        В психологии.

·        В рекламе.

Графы в биологии.

Графы в биологии большую роль в биологический теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов - размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево. Нас будет интересовать лишь один вопрос: в скольких случаях n - е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под название процесса Гальтона - Ватсона. Его можно рассматривать как частный случай многих общих формул.

Графы в теории массового обслуживания.

Понятие центральной вершины и центра графа появились в связи с задачами оптимального размещения пунктов массового обслуживания, таких как больницы, сберегательные банки, пожарные части, почтамты и т.п., когда важно минимизировать наибольшее расстояние от любой точки населенного пункта до ближайшего пункта.

Графы в математике.

В математике графы применяются для решения логических задач и головоломок. Основной применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Это выявление логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов. Возьмем, к примеру, такую задачу: «Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытство, что один из нас русый, другой - брюнет, а третий - рыжий, но ни кого цвет волос не соответствует фамилии». Какой цвет волос имеет из беседующих?» Решение данной задачи можно изобразить с помощью графа.

Графы в физике.

Недавно в одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем. Печатной схемой называют пластинку из какого - либо диэлектрики (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи. В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках. Итак из всего вышеперечисленного неопровержимо следует практическая ценность теории графов.

Теория графов в психологии.

Теория графов в логистике.

В анализе логических систем основной формы модели, подлежащий совершенствованию и насыщению данными с помощью экспертных оценок, является дерево целей. Экспертам по логистике предлагается оценить структуру логистической модели в целом и дать предложения о включении в нее не учетных связей. При этом используется анкетный метод. Результаты каждого опроса доводятся до сведения всех экспертов по логистике, что позволяет им далее корректировать свои суждения на основе вновь полученной информации. Дерево целей представляет собой связной граф, вершина которого интерпретируется как цели логистической системы, а ребра или дуги - как связи между ними. Это основной инструмент увязки целей верхнего уровня логистической организации с конкретными средствами их достижения на нижнем операционном уровне.

Заключение

В данной курсовой работе были рассмотрены вся теория о графе, что такое граф, какими они бывают и частично рассмотрели все элементы графов. И решили пару интересных задач: задача о трех колодцах и матрицы инцидентности и смежности (восстановили матрицы по графу, и наоборот). Так же применение графов в реальной жизни как мы заметили, очень популярна, так как это помогает решать те или иные задачи. Теория графов в настоящее время является интенсивно развивающимся разделом математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношение между людьми и многое другое.

Список литературы

1.      <#"878354.files/image015.gif">

Задача 2. Условие: Восстановить по графу матрицу инцидентности для неориентированного графа.

Ответ: