Основы математики
1. Направленные отрезки. Прямоугольная
декартовая система координат
Прямоугольная система координат - прямолинейная
система координат с взаимно перпендикулярными осями на плоскости или в
пространстве. Наиболее простая и поэтому часто используемая система координат.
Очень легко и прямо обобщается для пространств любой размерности, что также
способствует ее широкому применению.
Связанные термины: Декартовой обычно называют
прямоугольную систему координат с одинаковыми масштабами по осям, а общей
Декартовой системой координат называют аффинную систему координат (не
прямоугольную).
Прямоугольная система координат на плоскости:

Прямоугольная система координат в пространстве:

- Прямоугольная система координат в многомерном
пространстве:
Прямоугольная система координат может быть
использована и в пространстве любой конечной размерности аналогично тому, как
это делается для трехмерного пространства. Количество координатных осей при
этом равно размерности пространства (в этом параграфе будем обозначать ее n).
Для обозначения координат обычно применяют не
разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:

Для обозначения произвольной i-ой координаты из
этого набора используют буквенный индекс: 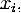
Прямоугольные координаты вектора:
Для определения прямоугольных координат вектора
(применимых для представления векторов любой размерности) можно исходить из того,
что координаты вектора (направленного отрезка), начало которого находится в
начале координат, совпадают с координатами его конца.
Орты:
Прямоугольная система координат (любой
размерности) также описывается набором ортов, сонаправленных с осями координат.
Количество ортов равно размерности системы координат и все они перпендикулярны
друг другу. Такие орты составляют базис, притом ортонормированный.
В трёхмерном случае такие орты обычно
обозначаются: i, j, k \ 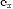

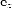
. Уравнение прямой линии с угловым коэффициентом
Если в общем уравнении прямой 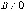 ,
то его можно записать в виде уравнения с угловым коэффициентом
,
то его можно записать в виде уравнения с угловым коэффициентом  где
где
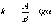 угловой
коэффициент, a - угол, образованный прямой с положительным направлением оси
угловой
коэффициент, a - угол, образованный прямой с положительным направлением оси 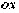 ,
,
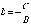 -
свободный член, равный ординате точки пересечения прямой с осью
-
свободный член, равный ординате точки пересечения прямой с осью  .
.
Однозначно определить прямую можно, задав одну
точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку
 с
угловым коэффициентом
с
угловым коэффициентом 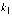 , определяется по
формуле
, определяется по
формуле 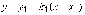 .
.
Пример: Составить уравнение прямой, проходящей
через А(-1,2) с угловым коэффициентом 
Решение: Воспользуемся формулой, подставив
координаты данной точки и угловой коэффициент 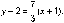 или
общее уравнение
или
общее уравнение 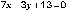 .
.
Ответ: общее уравнение прямой 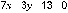 .
.
. Угол между двумя прямыми. Условия
параллельности и перпендикулярности прямых
Условия параллельности двух прямых:
Если прямые заданы уравнениями с угловым
коэффициентом, то необходимое и достаточное условие их параллельности состоит в
равенстве их угловых коэффициентов: k1 = k2.
Для случая, когда прямые заданы уравнениями в
общем виде, необходимое и достаточное условие их параллельности состоит в том,
что коэффициенты при соответствующих текущих координатах в их уравнениях
пропорциональны, т.е


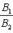
Условия перпендикулярности двух прямых:
В случае, когда прямые заданы уравнениями с
угловым коэффициентом, необходимое и достаточное условие их перпендикулярности
заключается в том, что их угловые коэффициенты обратны по величине и
противоположны по знаку, т. е. 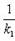
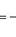
 или
k1k2 = -1.
или
k1k2 = -1.
Если уравнения прямых заданы в общем виде, то
условие их перпендикулярности (необходимое и достаточное) заключается в
выполнении равенства: A1A2 + B1B2 = 0.
Угол между двумя прямыми :
Угол φ между
двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2
= 0, вычисляется по формуле: 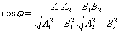
Угол φ между
двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и
y2 = k2x + b2, вычисляется по формуле: 
! Формулы определяют значение тригонометрической
функции одного из двух углов (острого или тупого) между заданными
! прямыми. Для нахождения острого угла между
прямыми выражения в правой части этих формул следует брать по модулю.
. Эллипс и его уравнение. Окружность
1) Окружность - замкнутая плоская кривая, все
точки которой равноудалены от заданной точки (центра окружности). Расстояние от
любой точки окружности P(x, y) до ее центра называется радиусом. Центр
окружности и сама окружность лежат в одной и той же плоскости. Уравнение
окружности радиуса R с центром в начале координат (каноническое уравнение
окружности) имеет вид: x2 + y2 = R2. (Рис 1.)
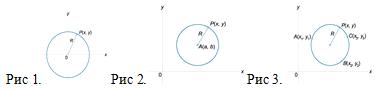
Уравнение окружности радиуса R с центром в
произвольной точке A(a, b) записывается как (x − a)2 + (y − b)2 = R
(Рис 2.)
Уравнение окружности, проходящей через три
точки, записывается в виде:
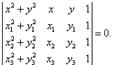
Здесь A(x1, y1), B(x2, y2), C(x3, y3) −
три точки, лежащие на окружности. (Рис 3.)
) Эллипс - плоская кривая, для каждой точки
которой сумма расстояний до двух заданных точек (фокусов эллипса) постоянна.
Расстояние между фокусами называется фокусным расстоянием и обозначается через
2c. Середина отрезка, соединяющего фокусы, называется центром эллипса. У
эллипса есть две оси симметрии: первая или фокальная ось, проходящая через
фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с
эллипсом называются вершинами. Отрезок, соединяющий центр эллипса с вершиной,
называется полуосью эллипса. Большая полуось обозначается через a, малая
полуось − через b. Эллипс, центр которого находится в начале координат, а
полуоси лежат на координатных прямых, описывается следующим каноническим
уравнением:
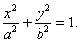
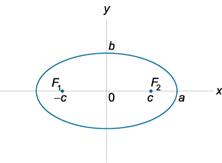
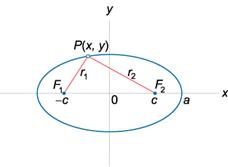
- Сумма расстояний от любой точки эллипса до его
фокусов постоянна: r1 + r2 = 2a, где r1, r2 − расстояния от произвольной
точки P(x, y) до фокусов F1 и F2, a − большая полуось эллипса.
- Соотношение между полуосями эллипса и фокусным
расстоянием : a2 = b2 + c2, где a − большая полуось эллипса, b −
малая полуось, c − половина фокусного расстояния.
Эксцентриситет эллипса: e = c/a < 1
Уравнения директрис эллипса
Директрисой эллипса - прямая, перпендикулярная
его фокальной оси и пересекающая ее на расстоянии a/e от центра. Эллипс имеет
две директрисы, отстоящие по разные стороны от центра. Уравнения директрис
записываются в виде:

- Уравнение эллипса в параметрической форме:

где a, b − полуоси эллипса, t −
параметр.
Общее уравнение эллипса : Ax2 + Bxy + Cy2 + Dx +
Ey + F = 0, где B2 − 4AC < 0.
Общее уравнение эллипса, полуоси которого
параллельны осям координат: Ax2 + Cy2 + Dx + Ey + F = 0, где AC > 0.
Периметр эллипса: L = 4aE(e), где a −
большая полуось эллипса, e − эксцентриситет, E − полный
эллиптический интеграл второго рода.
Приближенные формулы для периметра эллипса:
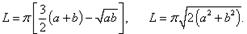 ,
,
где a, b − полуоси эллипса.
Площадь эллипса: S = πab
. Гипербола и ее уравнение
Гипербола - множество точек плоскости, разность
расстояний от каждой из которых до двух заданных (называемых фокусами) есть
величина постоянная. Эта постоянная величина положительна и меньше расстояния между
фокусами. Фокусы гиперболы обозначаются буквами F1,
F2, расстояние между
фокусами - через 2c, постоянную разность между расстояниями от любой точки
гиперболы до ее фокусов - через 2a (2a<2с). Эксцентриситетом гиперболы -
отношение расстояния между фокусами к длине действительной оси:
 или
или 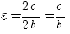
Так как по определению 2a<2c, то
эксцентриситет гиперболы всегда больше единицы.
Прямые L1
и L2 называются
асимптотами. Их уравнения имеют вид: y=
-+b\a
умножить на х
Гипербола не имеет общих точек с осью Oy, а ось
Ox пересекает в двух точках A (a; 0) и B (-a; 0), которые называются вершинами
гиперболы.
Гипербола имеет центр симметрии.
Гипербола имеет две взаимно перпендикулярные оси
симметрии.
Гипербола пересекается с прямой y = kx при  в
двух точках. Если
в
двух точках. Если то общих точек у
прямой и гиперболы нет.
то общих точек у
прямой и гиперболы нет.
. Парабола и ее уравнение
Парабола - множество точек на плоскости,
равноудаленных от заданной точки (называемой фокусом) и данной прямой
(называемой директрисой).
Фокус параболы принято обозначать буквой F,
директрису - буквой d, расстояние от фокуса до директрисы - буквой p (p>0).
Рассмотрим основные случаи расположения параболы
относительно осей координат.
Каноническое уравнение параболы, фокус которой
расположен на оси абсцисс, имеет вид y^{2}=2px или y^{2}=-2px.
7. Линейное (векторное) пространство и его
свойства
Векторным (или линейным) пространством
называется произвольное непустое множество V, на котором заданы операции
сложения векторов и умножения вектора на число, удовлетворяющие следующим
условиям, которые называются аксиомами векторного пространства:
) если x, y ∈
V, то x + y = y + x (сложение векторов коммутативно);
) если x, y, z ∈
V, то (x + y) + z = x + (y + z) (сложение векторов ассоциативно);
) для всякого x ∈
V существует вектор 0 ∈ V (называемый
нулевым вектором) такой, что x + 0 = x;
) для всякого x ∈
V существует вектор y ∈ V (называемый
противоположным к х и обозначаемый через −x) такой, что x + y = 0;
) если x, y ∈
V, а t ∈
R, то t(x + y) = tx + ty (умножение вектора на число дистрибутивно относительно
сложения векторов);
) если x ∈
V, а t,s ∈ R, то (t + s)x = tx + sx
(умножение вектора на число дистрибутивно относительно сложения чисел);
) если x ∈
V, а t,s ∈ R, то t(sx) = (ts)x;
) если x ∈
V, то 1 · x = x. Простейшие свойства векторных пространств: единственность
нулевого вектора:
Укажем ряд простых следствий из аксиом
векторного пространства. Аксиома (3) утверждает существование нулевого вектора,
но не говорит о том, сколько нулевых векторов может быть в пространстве.
Лемма 1:
Векторное пространство содержит только один
нулевой вектор.
Доказательство:
Пусть 0 и 0’ - два нулевых вектора векторного
пространства V. Тогда из аксиомы (3) вытекает, что 0’ + 0 = 0’ , а из аксиом
(1) и (3) - что 0’ + 0 = 0 + 0’ = 0. Следовательно, 0 = 0. Простейшие свойства
векторных пространств: единственность противоположного вектора:
Аксиома (4) утверждает существование вектора, противоположного
к вектору x, но не говорит о
том, сколько таких векторов может быть.
Лемма 2:
Для всякого вектора x
из векторного пространства существует ровно один противоположный к нему вектор.
Доказательство:
Предположим, что векторы y1
и y2 противоположны к x,
т. е. x + y1
= x + y2
= 0. Тогда, с одной стороны, используя аксиомы (1) и (2), имеем y2
+ (x + y1)
= (y2 + x)
+ y1 = (x
+ y2) + y1
= 0 + y1 = y1
+ 0 = y1. С другой стороны
y2 + (x
+ y1) = y2
+ 0 = y2. Следовательно, y1
= y2. Простейшие
свойства векторных пространств: когда произведение числа на вектор равно
нулевому вектору? Лемма 3:
Пусть x - произвольный вектор из векторного
пространства, а t - произвольное число. Равенство tx = 0 выполнено тогда и
только тогда, когда либо t = 0, либо x = 0.
Доказательство: Достаточность:
Проверим, что 0 · x = 0. В силу аксиом (6) и
(8), x = (1 + 0)· x = 1 · x + 0 · x = x + 0 · x для любого вектора x. Учитывая
лемму 1, имеем 0 · x = 0. Аналогичным образом равенство t · 0 = 0 следует из
того, что tx = t(x + 0) = tx + t · 0.
Необходимость:
Пусть tx = 0 и t не равно 0. Тогда, используя
аксиомы (7) и (8),имеем x = 1 · x = (1/t· t) x =1/t · (tx) = 1/t· 0. Из
сказанного в предыдущем абзаце вытекает, что 1/t· 0 = 0. Итак, если tx = 0 и t
не равно 0, то x = 0.
. Пространство со скалярным произведением
Функция F(x)
называется кусочно-непрерывной на отрезке, если она непрерывна на этом отрезке,
за исключением, быть может, конечного числа точек, где она имеет разрывы
первого рода. Такие функции можно складывать и умножать на действительные числа
и получать как результат снова кусочно-непрерывные на  функции.
функции.
Скалярным произведением двух кусочно-непрерывных
на 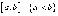 функций
функций
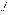 и
и
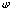 будем
называть интеграл:
будем
называть интеграл:
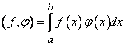
Очевидно, для любых кусочно-непрерывных на  функций
функций
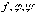 выполняются
свойства:
выполняются
свойства:
) 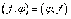
)  и
из равенства
и
из равенства 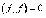 следует, что
следует, что 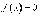 на
на
 ,
исключая, быть может, конечное число точек
,
исключая, быть может, конечное число точек  .
.
) 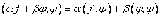 ,
где
,
где 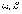 -
произвольные действительные числа.
-
произвольные действительные числа.
Множество всех кусочно-непрерывных функций,
определенных на отрезке  , для которых
введено скалярное произведение по формуле (1), мы будем обозначать
, для которых
введено скалярное произведение по формуле (1), мы будем обозначать  и
называть пространством
и
называть пространством  или
или  .
.
В математике называют пространством  совокупность
функций
совокупность
функций  ,
интегрируемых в лебеговом смысле на
,
интегрируемых в лебеговом смысле на  вместе
со своими квадратами, для которых введено скалярное произведение по формуле
(1). Рассматриваемое пространство
вместе
со своими квадратами, для которых введено скалярное произведение по формуле
(1). Рассматриваемое пространство  есть
часть
есть
часть  .
Пространство
.
Пространство 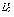 обладает многими
свойствами пространства
обладает многими
свойствами пространства 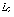 , но не всеми.
, но не всеми.
. Матрицы и действия над ними
Матрица - математический объект, записываемый в
виде прямоугольной таблицы элементов кольца или поля (например, целых,
действительных или комплексных чисел), которая представляет собой совокупность
строк и столбцов, на пересечении которых находятся её элементы. Количество
строк и столбцов матрицы задают размер матрицы. Хотя исторически
рассматривались, например, треугольные матрицы, в настоящее время говорят
исключительно о матрицах прямоугольной формы, так как они являются наиболее
удобными и общими.
Матрицей A=Amn порядка m*n называется
прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Действия над матрицами:
. Сложение матриц - поэлементная операция:

2. Вычитание матриц - поэлементная операция:
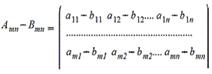
3. Произведение матрицы на число - поэлементная
операция:
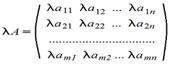
4. Умножение A*B матриц по правилу строка на
столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)mk*Bkn=Cmn
причем каждый элемент сij матрицы Cmn равен сумме
произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го
столбца матрицы B , т.е.

. Определители и их свойства
Каждой квадратной матрице А соответствует число,
которое называется ее определителем, или детерминантом, и обозначается |А|, det
А, или  .
Определителем, или детерминантом, n-го порядка служит число, записываемое в
виде квадратной таблицы
.
Определителем, или детерминантом, n-го порядка служит число, записываемое в
виде квадратной таблицы
det
А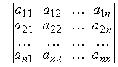
и равное алгебраической сумме n!
произведений вида 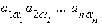 .
.
Итак, det
А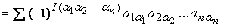 ,
где суммирование распространено на все перестановки из чисел 1, 2, ..., n.
Здесь
,
где суммирование распространено на все перестановки из чисел 1, 2, ..., n.
Здесь 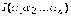 -
число инверсий в перестановке
-
число инверсий в перестановке  . Говорят, что
. Говорят, что
числа 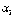 и
и
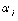 образуют
инверсию в перестановке
образуют
инверсию в перестановке  , если большее из
чисел
, если большее из
чисел  и
и
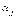 расположено
левее меньшего.
расположено
левее меньшего.
Например, для n
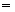 2
2
 ,
для n
,
для n
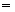 3
3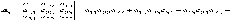
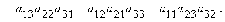
Правило вычисления определителя
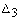 равносильно
правилу треугольников (правилу Саррюса), которое схематически можно записать
как
равносильно
правилу треугольников (правилу Саррюса), которое схематически можно записать
как 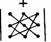 и
и
 .
.
. Решение системы линейных
уравнений по формуле Крамера
!!! Система из двух уравнений с
двумя неизвестными
координата
уравнение перпендикулярность крамер
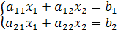
решается с помощью формул
Крамера:
 ,
,  ,где
,где
 и
и
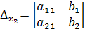 ,
,
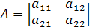 .
.
При решении системы возможны три случая:
. Определитель системы  .
Тогда система имеет единственное решение, определяемое формулами Крамера.
.
Тогда система имеет единственное решение, определяемое формулами Крамера.
. Определитель системы  .
Если при этом хотя бы один из определителей
.
Если при этом хотя бы один из определителей 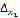 и
и
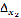 не
равен нулю, то система не имеет решений.
не
равен нулю, то система не имеет решений.
. Если  ,
,
 и
и
 ,
то одно из уравнений есть следствие другого, система сводится к одному
уравнению с двумя неизвестными и имеет бесчисленное множество решений.
,
то одно из уравнений есть следствие другого, система сводится к одному
уравнению с двумя неизвестными и имеет бесчисленное множество решений.
!!! Система из двух уравнений с тремя
неизвестными:
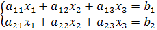
Из основной матрицы  при
помощи поочередного вычеркивания столбцов получаем определители
при
помощи поочередного вычеркивания столбцов получаем определители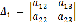 ,
,
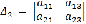 ,
,
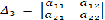 .
.
Дополнительные определители:
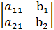 ,
,  .
.
Возможны три случая:
. Если из трех определителей
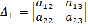 ,
,  ,
,
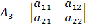
хотя бы один не равен нулю, то система имеет
бесчисленное множество решений, причем одному неизвестному можно дать любое
значение. Пусть, например, отличен от нуля 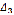 ,
тогда неизвестному
,
тогда неизвестному 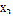 можно придать любое
значение (если
можно придать любое
значение (если 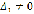 , то
, то  ,
если
,
если  ,
то
,
то  ),
а исходную систему переписать в виде,
),
а исходную систему переписать в виде, 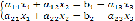 .
Отсюда неизвестные
.
Отсюда неизвестные  определяются по
формулам Крамера.
определяются по
формулам Крамера.
. Все определители 
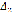
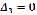 ,
но один из определителей,
,
но один из определителей, 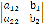 ,
, 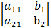 ,
,
 не
равен нулю. В этом случае система несовместна, то есть не имеет решений.
не
равен нулю. В этом случае система несовместна, то есть не имеет решений.
. Все выписанные определители равны нулю.
Система имеет бесчисленное множество решений.
!!! Система из трех уравнений с тремя
неизвестными:
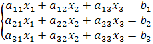
При решении системы из трех уравнений с тремя
неизвестными возможны три случая:
. Определитель системы 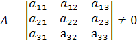 .
Система имеет единственное решение, определяемое формулами Крамера
.
Система имеет единственное решение, определяемое формулами Крамера 
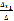 ,
,

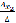 ,
,
 ,где
,где
 и
и
 ,
,
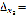
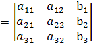 ,
, 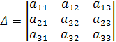 .
.
. Определитель системы равен нулю, 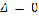 .
Если при этом хотя бы один из определителей
.
Если при этом хотя бы один из определителей 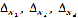 ,
не равен нулю, то система несовместна, решений не имеет.
,
не равен нулю, то система несовместна, решений не имеет.
. Если  и
и
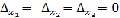 ,
то система имеет бесчисленное множество решений.
,
то система имеет бесчисленное множество решений.
. Матричная запись системы линейных уравнений и
ее решения
Матричный метод решения систем линейных
алгебраических уравнений - вывод формулы.
Пусть для матрицы А порядка n на n существует
обратная матрица 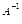 . Умножим обе части
матричного уравнения
. Умножим обе части
матричного уравнения 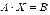 слева на
слева на  (порядки
матриц A ⋅ X и В позволяют произвести
такую операцию, смотрите статью операции над матрицами, свойства операций).
Имеем
(порядки
матриц A ⋅ X и В позволяют произвести
такую операцию, смотрите статью операции над матрицами, свойства операций).
Имеем 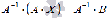 .
Так как для операции умножения матриц подходящих порядков характерно свойство
ассоциативности, то последнее равенство можно переписать как
.
Так как для операции умножения матриц подходящих порядков характерно свойство
ассоциативности, то последнее равенство можно переписать как 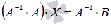 ,
а по определению обратной матрицы
,
а по определению обратной матрицы 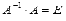 (E
- единичная матрица порядка n на n), поэтому
(E
- единичная матрица порядка n на n), поэтому 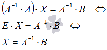
Таким образом, решение системы линейных
алгебраических уравнений матричным методом определяется по формуле  .
Другими словами, решение СЛАУ находится с помощью обратной матрицы
.
Другими словами, решение СЛАУ находится с помощью обратной матрицы 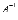 .
.
Мы знаем, что квадратная матрица А порядка n на
n имеет обратную матрицу 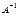 только тогда,
когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только тогда,
когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
. Предел последовательности. Теоремы о пределах
Постоянное число а называется пределом
последовательности {x n }, если для любого сколь угодно малого
положительного числа e существует номер N, что все значения x n ,
у которых n>N, удовлетворяют неравенству : x n - a <
.
Записывают это следующим образом: 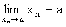 или
x n a.
или
x n a.
Неравенство равносильно двойному неравенству: a-
e < x
n
<
a + e , которое
означает, что точки x n, начиная с некоторого номера n>N, лежат
внутри интервала (a- e , a+ e ), т.е. попадают в какую угодно малую e
-окрестность точки а.
Последовательность, имеющая предел, называется
сходящейся, в противном случае - расходящейся.
Определение:
Постоянное число А называется пределом функции
f(x) при x a, если для всякой последовательности {x n }
значений аргумента, стремящейся к а, соответствующие им последовательности {f(x
n )} имеют один и тот же предел А.
Постоянное число А называется пределом функции
f(x) при x a, если, задав произвольное как угодно малое положительное
число e , можно найти такое d >0 (зависящее от e ), что для всех x, лежащих
в d -окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 < ½
x-a ½ < d , значения функции f(x) будут лежать в
e -окрестности числа А, т.е. ê f(x)-A
ê < e .
ТЕОРЕМЫ О ПРЕДЕЛАХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ :
. Последовательность, имеющая предел,
ограничена.
. Последовательность может иметь только один
предел.
. Любая неубывающая (невозрастающая) и
ограниченная сверху (снизу) последовательность имеет предел.
. Предел постоянной равен этой постоянной:  5.
Предел суммы равен сумме пределов:
5.
Предел суммы равен сумме пределов: 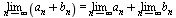
. Постоянный множитель можно выносить за знак
предела:  7.
Предел произведения равен произведению пределов:
7.
Предел произведения равен произведению пределов: 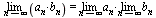 .
.
. Предел частного равен частному пределов, если
предел делителя отличен от нуля: 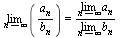
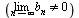
. Если  и
обе последовательности
и
обе последовательности  и
и  имеют
один и тот же предел а, то
имеют
один и тот же предел а, то 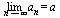 В теоремах 5-8
предполагается, что все пределы в правой части равенств существуют!!!
В теоремах 5-8
предполагается, что все пределы в правой части равенств существуют!!!
Пример.
Найдем предел  .
Имеем
.
Имеем 
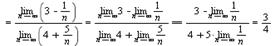
14. Функция и способы ее задания
Понятие функции:
Назовем упорядоченной парой (x, y)
двухэлементное множество {x, y}, в котором элемент x находится на первом месте,
а элемент y - на втором. Элемент x называется первой координатой упорядоченной
пары, а элемент y - второй координатой. Две упорядоченные пары равны, когда
совпадают их координаты: (x, y) = (u,v) <=> x = u, y = v .
Функцией f называется множество упорядоченных
пар чисел (x, y), таких, что x принадлежит X , y принадлежит Y и каждому
элементу x принадлежащему X ставится в соответствие единственный элемент y
принадлежащий Y . Обозначение: f: X → Y. Множество X называется областью
определения функции f, а множество Y - областью значений. Обозначают: Df и Ef.
Если ясно, какие множества X и Y имеются в виду, то пишут y = f (x). Элемент x
называется аргументом, а y - значением функции f.
Способы задания функции:
Табличный:
Используется тогда, когда область определения
состоит из конечного множества чисел. Тогда для задания функции проще всего
указать таблицу, содержащую значения аргумента и соответствующие значения
функции. Например, таблица логарифмов. Другим примером могут быть таблицы,
содержащие данные о числе жителей, населяющих земной шар в отдельные годы,
расписания движения поездов и т.п.
Аналитический:
При аналитическом способе задания функция может
быть задана явно, когда дано выражение у через x, т.е. формула имеет вид y = f
(x); неявно, когда х и у связаны между собой уравнением вида F(x, y) = 0 ;
параметрический, когда соответствующие друг другу значения х и у выражены через
третью переменную величину t, называемую параметром.
Логический:
Если функция описывается правилом ее
составления, например, функция Дирихле: f(x)= 1, если x - рациональное; f(x)=
0, если x - иррациональное.
Графический:
Состоит в изображении графика функции -
множества точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а
ординаты - соответствующие им значения функции y
= f (x). Преимуществом графического задания является его наглядность,
недостатком - его неточность.
. Предел функции. Теоремы о пределах функции
Теорема 1. (о предельном переходе в равенстве)
Если две функции принимают одинаковые значения в
окрестности некоторой точки, то их пределы в этой точке совпадают.
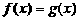
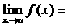
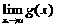 .
.
Теорема 2. (о предельном переходе в неравенстве)
Если значения функции f(x)
в окрестности некоторой точки не превосходят соответствующих значений функции g(x)
, то предел функции f(x)
в этой точке не превосходит предела функции g(x).
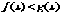 Þ
Þ 
 .
.
Теорема 3.
Предел постоянной равен самой постоянной.
 .
.
Доказательство.(x)=с, докажем, что 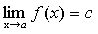 .
.
Возьмем произвольное e>0. В качестве d можно
взять любое положительное число. Тогда при 
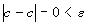 .
.
Теорема 4.
Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
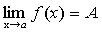 и
и 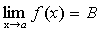 .
.
По теореме о связи предела и бесконечно малой
функции:
f(x)-A=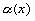 - б.м. при
- б.м. при  , f(x)-B=
, f(x)-B= - б.м. при
- б.м. при 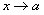 .
.
Вычитая эти равенства, получим:
B-A=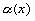 -
- .
.
Переходя к пределам в обеих частях равенства при
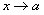 ,
имеем: B-A=0,
т.е. B=A.
Получаем противоречие, доказывающее теорему.
,
имеем: B-A=0,
т.е. B=A.
Получаем противоречие, доказывающее теорему.
Теорема 5.
Если каждое слагаемое алгебраической суммы
функций имеет предел при 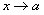 , то и
алгебраическая сумма имеет предел при
, то и
алгебраическая сумма имеет предел при 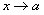 ,
причем предел алгебраической суммы равен алгебраической сумме пределов.
,
причем предел алгебраической суммы равен алгебраической сумме пределов.
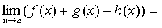


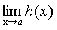 .
.
Доказательство. Пусть 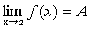 ,
,
 ,
,
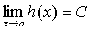 .
.
Тогда, по теореме о связи предела и б.м.
функции:
 где
где  -
б.м. при
-
б.м. при .
Сложим алгебраически эти равенства:
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)=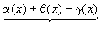 ,
где
,
где 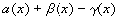 б.м.
при
б.м.
при 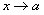 .
.
По теореме о связи предела и б.м. функции:
 А+В-С=
А+В-С=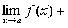

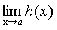 .
.
Теорема 6.
Если каждый из сомножителей произведения
конечного числа функций имеет предел при 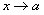 ,
то и произведение имеет предел при
,
то и произведение имеет предел при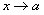 ,
причем предел произведения равен произведению пределов.
,
причем предел произведения равен произведению пределов.
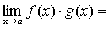
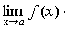
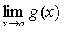 .
.
Следствие:
Постоянный множитель можно выносить за знак
предела.
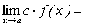

 .
.
Теорема 7.
Если функции f(x)
и g(x)
имеют предел при 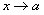 , причем
, причем  ,
то и их частное имеет предел при
,
то и их частное имеет предел при 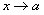 ,
причем предел частного равен частному пределов.
,
причем предел частного равен частному пределов.
 ,
, 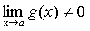 .
.
. Производная функции и ее свойства
Пусть функция 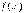 определена
в точке
определена
в точке 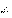 и
в некоторой ее окрестности. Дадим аргументу
и
в некоторой ее окрестности. Дадим аргументу 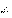 приращение
приращение
 ,
такое, чтобы не выйти из указанной окрестности. Найдем соответствующее
приращение функции
,
такое, чтобы не выйти из указанной окрестности. Найдем соответствующее
приращение функции  и составим
отношение. Если существует предел этого отношения при
и составим
отношение. Если существует предел этого отношения при  стремящемся
к нулю, то указанный предел называют производной функции
стремящемся
к нулю, то указанный предел называют производной функции 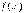 в
точке
в
точке 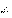 и
обозначают
и
обозначают  . Иначе говоря:
. Иначе говоря:
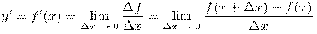 (
( -
приращение функции,
-
приращение функции, 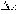 - приращение
аргумента). Если в каждой точке
- приращение
аргумента). Если в каждой точке  из множества
из множества 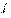 у
функции
у
функции 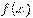 существует
производная, то такая функция называется дифференцируемой на множестве
существует
производная, то такая функция называется дифференцируемой на множестве 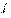 .
.
Геометрический смысл производной:
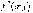 - угловой
коэффициент касательной к графику функции
- угловой
коэффициент касательной к графику функции 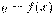 в
точке
в
точке  уравнение
касательной в этой точке
уравнение
касательной в этой точке  .
.
Правила дифференцирования:
Пусть функции  и
и
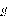 определены
и дифференцируемы на некотором множестве
определены
и дифференцируемы на некотором множестве 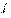 ,
,
 и
и
 -
любые действительные числа. Тогда на множестве
-
любые действительные числа. Тогда на множестве 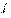 справедливы
соотношения:
справедливы
соотношения:
· 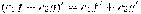 ,
,
·  ,
,
·  ,
,  ,
,
· 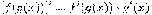
Основные формулы дифференцирования:
· 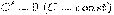
· 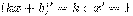
· 
· 
· 
· 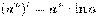
· 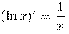
· 
· 
· 
· 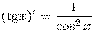
· 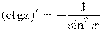
· 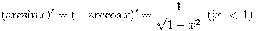
· 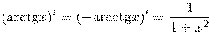
17. Производные и дифференциалы высших порядков
Пусть существует такое множество X, что для  .
Тогда может получиться, что производная
.
Тогда может получиться, что производная  имеет
производную в некоторой точке. Такая производная называется второй производной
или производной второго порядка. Обозначается
имеет
производную в некоторой точке. Такая производная называется второй производной
или производной второго порядка. Обозначается 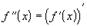 или
или
 .
В общем виде
.
В общем виде 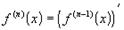 . Переходя к
дифференциалам, получаем:
. Переходя к
дифференциалам, получаем: 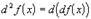 .
. 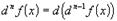 .
.
Не следует путать обозначения: 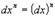 ,
,
 .
.
Второй дифференциал от x равен 0 только тогда,
когда x - независимая переменная или линейная функция от независимой
переменной. В этом случае любой дифференциал 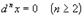 .
То есть для
.
То есть для  .
.
Нарушение инвариантности формул дифференциалов
высших порядков:
Для дифференциалов высшего порядка
инвариантность формул не имеет место, т.е. дифференциал вычисляется по разным
формулам в случае зависимой и независимой переменных.
Вычислим дифференциал от зависимой и независимой
переменных.
Для зависимой переменной: u = u (x) .
.
Для независимой переменной: 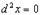 ,
следовательно,
,
следовательно, 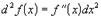 , и, в более общем
случае,
, и, в более общем
случае, 
!!!Теорема (Основные свойства производных и
дифференциалов высших порядков.)
. Если  ,
то
,
то 
2. 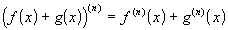 .
.
!!!Теорема (Теорема Лейбница):
Пусть существуют функции 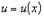 и
и
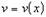 ,
имеющие производные до n-ного порядка включительно. Тогда
,
имеющие производные до n-ного порядка включительно. Тогда
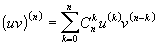 ,
,
где 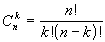 -
число сочетаний из n по k.
-
число сочетаний из n по k.
!!!Теорема (Бином Ньютона):
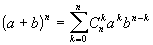 , где
, где 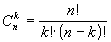 .
.
. Формулы Тейлора и Маклорена
Рассмотрим многочлен 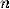 -й
степени
-й
степени 
Его можно представить в виде суммы степеней  , взятых с
некоторыми коэффициентами. Продифференцируем его
, взятых с
некоторыми коэффициентами. Продифференцируем его 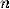 раз
по переменной
раз
по переменной  , а затем найдем
значения многочлена и его производных в точке
, а затем найдем
значения многочлена и его производных в точке  :
:
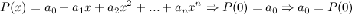
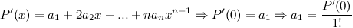
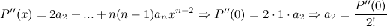
……………………………………………………..
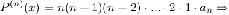

Таким образом, получаем, что
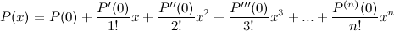
Полученное выражение называется формулой
Маклорена для многочлена 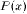 степени
степени 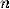 .
.
Рассуждая аналогично, можно разложить многочлен  по
степеням разности
по
степеням разности 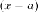 , где
, где  - любое
число. В этом случае будем иметь:
- любое
число. В этом случае будем иметь:
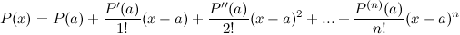
Это выражение называется формулой Тейлора для
многочлена 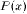 в окрестности
точки
в окрестности
точки  .
.
. Раскрытие неопределенностей 0/0,
бесконечность/бесконечность, 0 х бесконечность. Правило Лопиталя
Теорема (правило Лопиталя):
Пусть функции f(x) и g(x)
дифференцируемы в некоторой окрестности точки a, за исключением, быть может,
самой точки a, и пусть 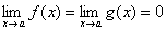 или
или 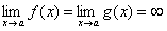 .
Тогда, если существует предел отношения производных этих функций
.
Тогда, если существует предел отношения производных этих функций  ,
то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
,
то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
|

|
(1)
|
Таким образом, коротко правило
Лопиталя можно сформулировать следующим образом: предел отношения двух
бесконечно малых или двух бесконечно больших величин равен пределу отношения их
производных.
Замечание:
Отметим, что формула (1)
справедлива только в том случае, если предел, стоящий справа, существует. Может
случиться, что предел, стоящий слева существует, в то время как предел, стоящий
в правой части равенства, не существует.
Например, найти 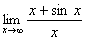 .
Этот предел существует
.
Этот предел существует 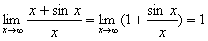 . Но отношение
производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому
пределу.
. Но отношение
производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому
пределу.
Заметим, что если отношение
производных опять представляет собой неопределенность вида 0/0 или ∞/∞,
то можно снова применить сформулированную теорему, то есть перейти к отношению
вторых производных и так далее.
Вспомним, что к этим двум
случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞..

20. Раскрытие неопределенностей 0^0,
1^бесконечность, бесконечность^0

. Общая схема исследования функций
. Нахождение области определения функции.
. Исследование функции на четность и нечетность.
. Установление области непрерывности функции и
точек разрыва. Отыскание вертикальных асимптот.
. Исследование поведения функции при 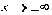 (если
она там определена). Отыскание горизонтальных и наклонных асимптот.
(если
она там определена). Отыскание горизонтальных и наклонных асимптот.
. Нахождение экстремумов и интервалов
монотонности функции. Составление таблицы.
. Нахождение интервалов выпуклости и вогнутости
и точек перегиба графика функции.
. Нахождение точек пересечения графика функции с
осями, интервалов знак постоянства функции. Составление таблицы. Отыскание
дополнительных точек для построения графика.
. Построение графика функции.
22. Функция нескольких переменных. Предел и
непрерывность функции нескольких переменных
Определение 1.
Число А называется пределом функции  в
точке
в
точке  (или
при
(или
при  и
и
 ),
если для любого сколь угодно малого положительного числа
),
если для любого сколь угодно малого положительного числа  найдется
положительное число
найдется
положительное число  такое, что для
всех точек
такое, что для
всех точек  , отстоящих от
точки
, отстоящих от
точки  на
расстояние, меньшее чем
на
расстояние, меньшее чем  , выполняется
неравенство
, выполняется
неравенство
 .
.
Обозначается предел  .
.
Определение 2.
Функция  называется
непрерывной в точке
называется
непрерывной в точке  , если предел
функции в этой точке существует и
, если предел
функции в этой точке существует и  .
.
Tочки, в которых
функция не обладает свойством непрерывности, называются точками разрыва.
На функции нескольких переменных переносятся все
свойства и методы теории пределов функции одной переменной.
. Частные производные. Полный дифференциал
Каждая частная производная (по x и по y) функции
двух переменных представляет собой обыкновенную производную функции одной
переменной при фиксированном значении другой переменной:
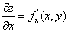 (где
y = const),
(где
y = const), 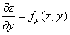 (где
x = const).
(где
x = const).
Поэтому частные производные
вычисляют по формулам и правилам вычисления производных функций одной
переменной, считая при этом другую переменную постоянной (константой).
Если тяжело сосредоточиться,
чтобы отслеживать, где в функции константа, то можно в черновом решении примера
вместо переменной с фиксированным значением подставить любое число - тогда
можно будет быстрее вычислить частную производную как обыкновенную производную
функции одной переменной. Надо только не забыть при чистовом оформлении вернуть
на место константу (переменную с фиксированном значением).
Полный дифференциал :
Произведение частной производной на приращение
соответствующей независимой переменной называется частным дифференциалом.
Частные дифференциалы обозначаются так:
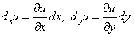
и т.д. Сумма частных
дифференциалов по всем независимым переменным даёт полный дифференциал. Для
функции двух независимых переменных полный дифференциал выражается равенством
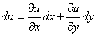
Функция, имеющая полный
дифференциал в каждой точке некоторой области, называется дифференцируемой в
этой области.
Так же как и в случае функции
одной переменной, из дифференцируемости функции в некоторой области следует её
непрерывность в этой области, но не наоборот.
Теорема:
Если функция z = f(x, y) имеет
непрерывные частные производные  и
и 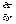 в
данной области, то она дифференцируема в этой области и её дифференциал
выражается формулой.
в
данной области, то она дифференцируема в этой области и её дифференциал
выражается формулой.
Можно показать, что подобно
тому, как в случае функции одной переменной дифференциал функции является
главной линейной частью приращения функции, так и в случае функции нескольких
переменных полный дифференциал является главной, линейной относительно
приращений независимых переменных частью полного приращения функции.
Для функции двух переменных
полное приращение функции имеет вид
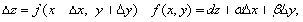 где α
и
β
- бесконечно
малые при
где α
и
β
- бесконечно
малые при 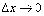 и
и 
. Экстремумы функции нескольких переменных
Понятие точек максимума и минимума:
Пусть функция нескольких переменных u = f(x1,
x2, … , xn) = f(x) определена в некоторой окрестности
точки
0
= (a1, a2, … , an) .
Точка x0 называется точкой локального
максимума (локального минимума) функции u = f(x) , если существует такая
окрестность Oδ(x0)
точки x0 , что для всех точек x О Oδ(x0)
выполняется неравенство f(x) ≤ f(x0) (f(x) ≥ f(x0)).
Если при x ≠ x0 имеет место
неравенство f(x) ≠ f(x0) , то точка x0 называется
точкой строгого локального максимума (минимума).
Точки максимума и минимума функции называются
точками экстремума, а максимумы и минимумы - экстремумами функции.
Необходимое условие экстремума:
Теорема (Необходимое условие экстремума):
Если функция нескольких переменных u = f(x1,
x2, … , xn) имеет экстремум в некоторой точке, то в этой
точке каждая ее частная производная равна нулю или не существует.
Внутренние точки из области определения функции,
в которых выполняются необходимые условия экстремума, называются критическими.
Если в критической точке функция дифференцируема, то такая точка называется
стационарной.
В стационарной точке (x0, y0)
функции f(x, y) существуют частные производные f'x , f'y
и f'x(x0, y0) = 0 , f'y(x0,
y0) = 0
Достаточные условия экстремума:
Достаточным условием экстремума функции
нескольких переменных в ее стационарной точке является знакоопределенность
(положительная или отрицательная определенность) дифференциала 2-го порядка в
этой точке.
Наибольшие и наименьшие значения:
Пусть функция f(x, y) определена в замкнутой
области D , ограниченной линией L , которая задана уравнением F(x, y) = 0 .
Наибольшее значение M функция может принимать в
точках максимума (внутри области D ) и на границе L в точках условного
максимума функции f(x, y) при F(x,y) = 0 , а наименьшее значение m -
соответственно в точках минимума (внутри области D ) и на границе L в точках
условного минимума. Если вычислить значения функции f(x, y) во всех этих
точках, то M и m обязательно окажутся среди вычисленных величин.
Алгоритм отыскания наибольшего значения M и
наименьшего значения m:
1. Находим все точки
экстремума функции f(x, y) внутри области D.
2. Находим все точки
условного экстремумы функции f(x, y) при условии F(x, y) = 0 .
3. Вычисляем значения
функции f(x, y) во всех найденных точках и выбираем среди них наибольшее и
наименьшее. Это и будут M и m .
25. Комплексные числа и действия над ними
Комплексные числа - числа вида x+iy,где
x и y-
вещественные числа,i- мнимая
единица (величина, для которой выполняется равенство: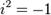 .
Множество всех комплексных чисел с арифметическими операциями является полем и
обычно обозначается С.
.
Множество всех комплексных чисел с арифметическими операциями является полем и
обычно обозначается С.
Стандартная модель:
Комплексное число  можно
определить как упорядоченную пару вещественных чисел
можно
определить как упорядоченную пару вещественных чисел 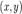 запись
запись
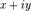 следует
понимать как удобный способ записи пары
следует
понимать как удобный способ записи пары .
.
Введём операции сложения и умножения таких пар
следующим образом:
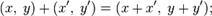
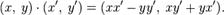
Вещественные числа являются в этой модели
подмножеством множества комплексных чисел и представлены парами вида ,
причём операции с такими парами согласованы с обычными сложением и умножением
вещественных чисел. Ноль представляется парой
,
причём операции с такими парами согласованы с обычными сложением и умножением
вещественных чисел. Ноль представляется парой  единица
-
единица
- 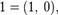 а
мнимая единица
а
мнимая единица 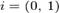 На множестве
комплексных чисел ноль и единица обладают теми же свойствами, что и на
множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен
На множестве
комплексных чисел ноль и единица обладают теми же свойствами, что и на
множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен  ,
то есть
,
то есть 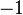 .
Несложно показать, что определённые выше операции имеют те же свойства, что и
аналогичные операции с вещественными числами. Исключением являются только
свойства, связанные с отношением порядка (больше-меньше), потому что невозможно
расширить порядок одиночных чисел, включив в него такие упорядоченные пары
чисел, чтобы операции отношения порядка по-прежнему были согласованы.
.
Несложно показать, что определённые выше операции имеют те же свойства, что и
аналогичные операции с вещественными числами. Исключением являются только
свойства, связанные с отношением порядка (больше-меньше), потому что невозможно
расширить порядок одиночных чисел, включив в него такие упорядоченные пары
чисел, чтобы операции отношения порядка по-прежнему были согласованы.
Матричная модель:
Комплексные числа можно также определить как
подкольцо кольца вещественных матриц 2 x
2
вида  с
обычным матричным сложением и умножением. Действительной единице будет
соответствовать
с
обычным матричным сложением и умножением. Действительной единице будет
соответствовать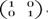 мнимой единице -
мнимой единице -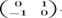
Действия над комплексными числами:
Сравнение  означает,
что
означает,
что  и
и
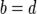 два
комплексных числа равны между собой тогда и только тогда, когда равны их
действительные и мнимые части).
два
комплексных числа равны между собой тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение: :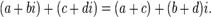
Вычитание: 
Умножение: 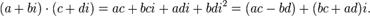
Деление: 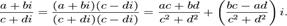 В
частности,
В
частности, 
Геометрическая модель:
Рассмотрим плоскость с прямоугольной системой
координат. Каждому комплексному числу  сопоставим
точку плоскости с координатами
сопоставим
точку плоскости с координатами 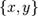 , а также
радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость
называется комплексной (или плоскостью Аргана). Вещественные числа на ней
занимают горизонтальную ось, мнимая единица изображается единицей на
вертикальной оси; по этой причине горизонтальная и вертикальная оси называются
соответственно вещественной и мнимой осями.
, а также
радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость
называется комплексной (или плоскостью Аргана). Вещественные числа на ней
занимают горизонтальную ось, мнимая единица изображается единицей на
вертикальной оси; по этой причине горизонтальная и вертикальная оси называются
соответственно вещественной и мнимой осями.
Часто бывает удобно рассматривать на комплексной
плоскости также полярную систему координат, в которой координатами точки являются
расстояние до начала координат (модуль) и угол радиус-вектора точки
(показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент).
В этом наглядном представлении сумма комплексных
чисел соответствует векторной сумме соответствующих радиус-векторов. При
перемножении комплексных чисел их модули перемножаются, а аргументы
складываются. Если модуль второго сомножителя равен 1, то умножение на него
геометрически означает поворот радиус-вектора первого числа на угол, равный
аргументу второго числа. Этот факт объясняет широкое использование комплексного
представления в теории колебаний, где вместо терминов "модуль" и
"аргумент" используются термины "амплитуда" и
"фаза".
Геометрическая модель комплексных чисел широко
используется в планиметрии: многие планиметрические теоремы можно доказать как
некоторые комплексные тождества. Часто этот метод даёт наиболее простое
доказательство.

Геометрическое представление комплексного числа.
26. Тригонометрическая форма комплексного числа,
форма комплексного числа

Абсцисса a
и ордината b комплексного числа
a + b·i
выражаются через модуль r
и аргумент φ формулами:
. a= r·cos(φ)
. b= r·sin(φ)
Поэтому всякое комплексное число можно представить
в виде: a+b·i=
r·(cos(φ)+
i·sin(φ))
Это так называемая, нормальная
тригонометрическая форма, или просто, тригонометрическая форма комплексного
числа.
В противоположность тригонометрической форме
выражение вида a + b·i
называется алгебраической или координатной формой комплексного числа.
Действия над комплексными числами в
тригонометрической форме:
Умножение:
Произведением двух комплексных чисел  и
и
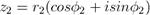 будет
комплексное число вида
будет
комплексное число вида 
Деление:
Частным двух комплексных чисел  и
и

будет комплексное число вида 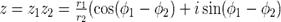
Возведение в степень: 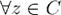
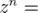
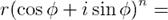
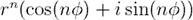
Извлечение корня: 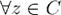
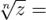
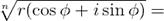
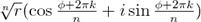

. Формулы
Эйлера
Формула Эйлера названа в честь Леонарда Эйлера,
который её ввёл, и связывает комплексную экспоненту с тригонометрическими
функциями.
Формула Эйлера утверждает, что для любого
действительного и комплексного числа х выполнено следующее равенство: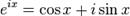 где
где 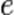 одна
из важнейших математических констант, определяющаяся следующей формулой:
одна
из важнейших математических констант, определяющаяся следующей формулой:  ,
,
 -
мнимая единица.
-
мнимая единица.

Геометрический смысл формулы Эйлера
. Первообразная
и неопределенный интеграл
Первообразной функцией для функции f(x)
называется такая функция F(х),
производная которой равна данной функции F'(x)
= f(x).
Обозначение 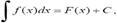 ,
где F'(x)
= f(x).
Функция f(x)
называется подынтегральной функцией, а выражение f(x)dx
- подынтегральным выражением.
,
где F'(x)
= f(x).
Функция f(x)
называется подынтегральной функцией, а выражение f(x)dx
- подынтегральным выражением.
. Свойства
неопределенного интеграла
. Производная неопределенного интеграла равна
подынтегральной функции; дифференциал от неопределенного интеграла равен
подынтегральному выражению, т.е.
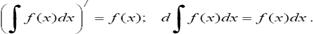
2. Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой функции и произвольной постоянной, т.е 
. Постоянный множитель можно вынести из под
знака интеграла, т.е. если k
= const ≠
0, то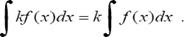
. Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической сумме интегралов от этих функций в
отдельности
. Методы
интегрирования
Метод интегрирования подстановкой заключается во
введении новой переменной интегрирования (то есть подстановки). При этом
заданный интеграл приводится к новому интегралу, который является табличным или
к нему сводящимся. Общих методов подбора подстановок не существует. Умение
правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 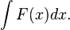 Сделаем
подстановку
Сделаем
подстановку  где
где
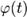 - функция, имеющая
непрерывную производную.
- функция, имеющая
непрерывную производную.
Тогда 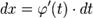 и
на основании свойства инвариантности формулы интегрирования неопределенного
интеграла получаем формулу интегрирования подстановкой:
и
на основании свойства инвариантности формулы интегрирования неопределенного
интеграла получаем формулу интегрирования подстановкой: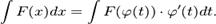
Интегрирование по частям:
Интегрирование по частям - применение следующей
формулы для интегрирования: 
Или: 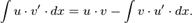
В частности, с помощью n-кратного
применения этой формулы находится интеграл  где
где
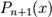 - многочлен
- многочлен  -й
степени.
-й
степени.
. Определённый
интеграл
Определённый интеграл - аддитивный монотонный
нормированный функционал, заданный на множестве пар, первая компонента которых
есть интегрируемая функция или функционал, а вторая - область в множестве
задания этой функции.
Определенный интеграл - это ЧИСЛО, значение
которого вычисляется по формуле Ньютона - Лейбница:
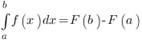
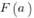 - это значение
первообразной функции
- это значение
первообразной функции 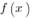 в точке а ,и,
соответственно,
в точке а ,и,
соответственно,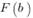 - это значение
первообразной функции
- это значение
первообразной функции 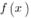 в точке в.
в точке в.
Геометрический смысл определенного интеграла:
Определенный интеграл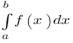 -
это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху
графиком положительной на отрезке
-
это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху
графиком положительной на отрезке 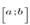 функции
функции
 слева
прямой
слева
прямой 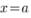 справа
прямой
справа
прямой  ,
и снизу осью ОХ.
,
и снизу осью ОХ.
. Свойства
определенного интеграла
. Величина определенного интеграла не зависит от
обозначения переменной интегрирования, т.е. 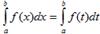 где
х, t - любые буквы.
где
х, t - любые буквы.
II.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
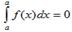
. При перестановке пределов интегрирования
определенный интеграл меняет свой знак на обратный.

. Если промежуток интегрирования [a,b]
разбит на конечное число частичных промежутков, то определенный интеграл,
взятый по промежутке [a,b],
равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

. Постоянный множитель можно выносить за знак
определенного интеграла.
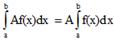
. Определенной интеграл от алгебраической суммы
конечного числа непрерывных функций равен такой же алгебраической сумме
определенных интегралов от этих функций.
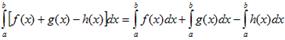
. Определенный интеграл с переменным верхним
пределом
Предварительно заметим, что величина
определенного интеграла зависит от вида подынтегральной функции f (x) , от
пределов интегрирования a, b и не зависит от обозначения переменной
интегрирования. Ее можно обозначить буквами x, u, t, z и т.д Поэтому имеет
место равенство

Рассмотрим интеграл с переменным верхним
пределом 
Он является функцией верхнего предела x . Эта
функция обладает более простыми свойствами, чем подынтегральная, поэтому
операцию интегрирования можно рассматривать как операцию сглаживания функции.
Теорема (о непрерывности интеграла с переменным
верхним пределом):
Если функция f (x) интегрируема по промежутку
[a, b] и x [a, b] , то функция (x) непрерывна в промежутке [a,
b]
Теорема (Барроу, 1630-1677):
Если подынтегральная функция f (x) непрерывна в
промежутке [a, b] , то во всем промежутке [a, b] справедливо равенство (x)
f (x) :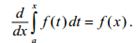
Следствие из теоремы Барроу:
Для всякой непрерывной функции f (x) в
промежутке [a, b] существует в этом промежутке первообразная. Одной из
первообразных для [a, b] является интеграл с переменным верхним пределом (4.2).
Теорема Формула Ньютона - Лейбница:
Определенный интеграл равен разности значений
любой первообразной для подынтегральной функции, взятых на верхнем и нижнем
пределах интеграла:  Здесь F(x)
f (x).
Здесь F(x)
f (x).
Примеры:
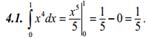
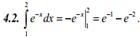
. Формула Ньютона - Лейбница
или основная теорема анализа даёт соотношение
между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Если  непрерывна
на отрезке[a,b]
и Ф- её любая первообразная на этом отрезке, то имеет место равенство
непрерывна
на отрезке[a,b]
и Ф- её любая первообразная на этом отрезке, то имеет место равенство

35. Несобственный
интеграл
Определённый интеграл  называется
несобственным, если выполняется, по крайней мере, одно из следующих условий:
называется
несобственным, если выполняется, по крайней мере, одно из следующих условий:
. Область интегрирования является бесконечной.
Например, является бесконечным интервалом 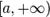
. Функция  является
неограниченной в окрестности некоторых точек области интегрирования.
является
неограниченной в окрестности некоторых точек области интегрирования.
. Если интервал  конечный,
и функция интегрируема по Риману, то значение несобственного интеграла совпадает
с значением определённого интеграла.
конечный,
и функция интегрируема по Риману, то значение несобственного интеграла совпадает
с значением определённого интеграла.
Бесконечные пределы интегрирования:
Пусть f
(x) является
непрерывной функцией в интервале [a,
∞).
Несобственный интеграл определяется через предел
следующим образом: 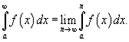
Рассмотрим также случай, когда функция f
(x) непрерывна в
интервале (−∞, b].
В этом случае несобственный интеграл
определяется как:

Если указанные выше пределы существуют и
конечны, то говорят, что несобственные интегралы сходятся. В противном случае
интегралы расходятся.

Если для некоторого действительного числа c
оба интеграла в правой части сходятся, то говорят, что интеграл 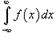 также
сходится; в противном случае он расходится
также
сходится; в противном случае он расходится
Геометрический смысл несобственного интеграла I
рода:
Несобственный интеграл первого рода выражает
площадь бесконечно длинной криволинейной трапеции.
Геометрический смысл несобственных интегралов II
рода:
Несобственный интеграл второго рода выражает
площадь бесконечно высокой криволинейной трапеции
. Площадь плоской фигуры
Площадь плоской фигуры - аддитивная числовая
характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем
случае, когда фигуру можно разбить на конечное множество единичных квадратов,
площадь равна числу квадратов. Также есть такой термин как -РАВНОВЕЛИКИЕ
ФИГУРЫ.
Равновеликие фигуры-это не равные фигуры имеющие
равную площадь .




Произвольный треугольник. a,
b, c
- стороны; a - основание; h
- высота;
A, B,
C - углы,
противоположные сторонам a,
b, c
; p = ( a
+ b + c
) / 2.
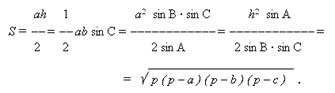
Последнее выражение называется формулой Герона.
Многоугольник, площадь которого нужно
определить, может быть разделён своими диагоналями на несколько треугольников.
Многоугольник, описанный около круга ( рис.67 ), может быть разделён прямыми,
идущими из центра круга к его вершинам. Тогда получаем:

37. Вычисление объема тела по площади
поперечного сечения
Пусть в пространстве 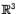 с
декартовой системой координат
с
декартовой системой координат 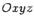 лежит область
лежит область  ,
проектирующаяся на ось
,
проектирующаяся на ось в отрезок
в отрезок  Предположим,
что для каждого
Предположим,
что для каждого  нам известна
площадь
нам известна
площадь сечения
тела
сечения
тела  плоскостью,
проходящей через точку х оси абсцисс перпендикулярно этой оси. Площадь
плоскостью,
проходящей через точку х оси абсцисс перпендикулярно этой оси. Площадь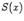 будем
называть площадью поперечного сечения тела
будем
называть площадью поперечного сечения тела  .
.
Для нахождения объёма тела  возьмём
размеченное разбиение отрезка
возьмём
размеченное разбиение отрезка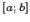 которое образуют
точки деления
которое образуют
точки деления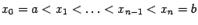 и отмеченные точки
и отмеченные точки  ,
,
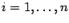 . Плоскости
. Плоскости 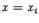 разбивают
тело
разбивают
тело на слои
на слои  объёмы
которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём
слоя
объёмы
которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём
слоя  на
объём цилиндра, высота которого
на
объём цилиндра, высота которого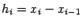 та же, что у слоя
та же, что у слоя а
основание совпадает с сечением тела плоскостью
а
основание совпадает с сечением тела плоскостью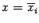 ,проведённой
где-то посередине между основаниями слоя
,проведённой
где-то посередине между основаниями слоя 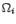 Образующие
этого цилиндра -- отрезки прямых, проходящих параллельно оси
Образующие
этого цилиндра -- отрезки прямых, проходящих параллельно оси  через
точки границы сечения.
через
точки границы сечения.
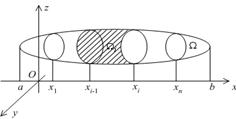
Объём цилиндра равен, очевидно, ,
а подсчитанный приближённо с помощью данного разбиения объём всего тела
,
а подсчитанный приближённо с помощью данного разбиения объём всего тела
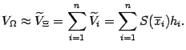
Последняя сумма -- это интегральная сумма,
построенная для функции  по размеченному
разбиению. При неограниченном измельчении разбиения эта сумма стремится к
значению определённого интеграла от
по размеченному
разбиению. При неограниченном измельчении разбиения эта сумма стремится к
значению определённого интеграла от по
по
 .
С другой стороны, задаваемый этой суммой объём будет стремиться к объёму тела
.
С другой стороны, задаваемый этой суммой объём будет стремиться к объёму тела  (этот
предельный объём мы можем по определению считать равным объёму тела
(этот
предельный объём мы можем по определению считать равным объёму тела  ).
Итак, получаем формулу
).
Итак, получаем формулу
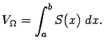
. Объем тела вращения
Вращение вокруг оси x:
Объём тела, образуемого вращением вокруг оси х
фигуры, ограниченной функцией 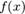 на интервале
на интервале  ,
осью х и прямыми
,
осью х и прямыми  и
и  равен:
равен:
Вращение вокруг оси y:
объём тела, образуемого вращением вокруг оси  фигуры,
ограниченной функцией
фигуры,
ограниченной функцией  на интервале
на интервале 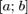 осью
осью
 и
прямыми
и
прямыми  и
и
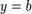 равен:
равен:
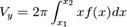
. Длина дуги кривой
Длина кривой (дуги кривой) - это предел, к
которому стремятся длины вписанных в эту кривую (дугу) ломаных при
неограниченном увеличении числа их звеньев, когда длина наибольшего звена
стремится к нулю. Для непрерывных кривых указанный предел - длина дуги -
существует, конечный или бесконечный; в этом случае дуга спрямляема.
Если плоская кривая задана в прямоугольных
декартовых координатах уравнением у = f(x),
где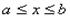 ее
длину можно вычислить по формуле
ее
длину можно вычислить по формуле 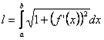
Для параметрически заданной кривой х = х(t),
y = y(t),
где 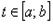 ее
длину можно найти по формуле
ее
длину можно найти по формуле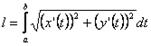
Аналогично можно определить длину
пространственной кривой.
. Приближенное вычисление определенного
интеграла: формула прямоугольников
Пусть требуется найти определенный интеграл от
непрерывной функции ƒ(х). Если
можно найти первообразную 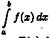 F(x)
функции ƒ(х),
то интеграл вычисляется по формуле Ньютона-Лейбница:
F(x)
функции ƒ(х),
то интеграл вычисляется по формуле Ньютона-Лейбница: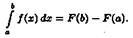 Но
отыскание первообразной функции иногда весьма сложно; кроме того, как известно,
не для всякой непрерывной функции ее первообразная выражается через
элементарные функции. В этих и других случаях (например, функция у = ƒ(х)
задана графически или таблично) прибегают к приближенным формулам, с помощью
которых определенный интеграл находится с любой степенью точности.
Но
отыскание первообразной функции иногда весьма сложно; кроме того, как известно,
не для всякой непрерывной функции ее первообразная выражается через
элементарные функции. В этих и других случаях (например, функция у = ƒ(х)
задана графически или таблично) прибегают к приближенным формулам, с помощью
которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы
приближенного вычисления определенного интеграла - формулу прямоугольников,
формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом
смысле определенного интеграла.
Формула прямоугольников:
Пусть на отрезке [а; b],
а < b, задана
непрерывная функция ƒ(х).
Требуется вычислить интеграл численно равный площади соответствующей
криволинейной  трапеции. Разобьем
основание этой трапеции, т. е. отрезок [а; b],
на n равных частей
(отрезков) длины
трапеции. Разобьем
основание этой трапеции, т. е. отрезок [а; b],
на n равных частей
(отрезков) длины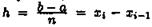 (шаг разбиения) с
помощью точек х0 = а, x1,
х2,..., хn
= b. Можно записать,
что хi=
х0+h• i,
где i = 1,2,..., n
(см. рис. 200).
(шаг разбиения) с
помощью точек х0 = а, x1,
х2,..., хn
= b. Можно записать,
что хi=
х0+h• i,
где i = 1,2,..., n
(см. рис. 200).

В середине  каждого
такого отрезка построим ординату ŷi
=ƒ(сi)
графика функции у = ƒ(х). Приняв
эту ординату за высоту, построим прямоугольник с площадью h
• ŷi.
каждого
такого отрезка построим ординату ŷi
=ƒ(сi)
графика функции у = ƒ(х). Приняв
эту ординату за высоту, построим прямоугольник с площадью h
• ŷi.
Тогда сумма площадей всех n
прямоугольников дает площадь ступенчатой фигуры, представляющую собой
приближенное значение искомого определенного интеграла
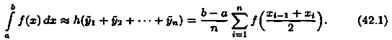
Формула (42.1) называется формулой средних
прямоугольников.
Абсолютная погрешность приближенного равенства
(42.1) оценивается с помощью следующей формулы: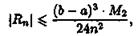 где
М2 - наибольшее значение |ƒ"(х)|
на отрезке [а; b],
где
М2 - наибольшее значение |ƒ"(х)|
на отрезке [а; b], Отметим,
что для линейной функции (ƒ(х)=kх+b)
формула (42.1) дает точный ответ, поскольку в этом случае ƒ"(х)=0.
Отметим,
что для линейной функции (ƒ(х)=kх+b)
формула (42.1) дает точный ответ, поскольку в этом случае ƒ"(х)=0.
. Приближенное вычисление определенного
интеграла формула трапеций
Формула трапеций
Формулу трапеций получают аналогично формуле
прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется
обычной.
Разобьем отрезок [а; b]
на n равных частей
длины Абсциссы
точек деления а = х0, x1,х2,...,b
= хn
(рис. 201). Пусть у0,у1...,уn
-
Абсциссы
точек деления а = х0, x1,х2,...,b
= хn
(рис. 201). Пусть у0,у1...,уn
-
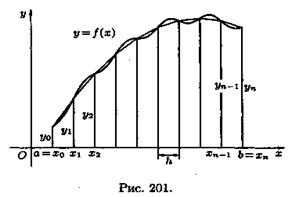
соответствующие им ординаты графика функции.
Тогда расчетные формулы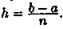 для этих значений
примут вид:
для этих значений
примут вид:
хi =
a+h*i, уi=ƒ(xi),
i= 0,1,2,..., n;
Заменим кривую у=ƒ(х)
ломаной линией, звенья которой соединяют концы ординат yi
и
yi+1
(i = 0,1,2,.. .,n).
Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных
трапеций с основаниями уi,
yi+1
и высотой 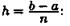
 или
или

Формула (42.2) называется формулой трапеций.
Абсолютная погрешность Rn
приближения, полученного по формуле трапеций, оценивается с помощью формулы
 • М2,
где
• М2,
где 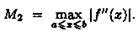
Снова для линейной функции у=kх
+b формула (42.2) -
точная.
. Основные типы дифференциальных уравнений
первого порядка, интегрируемых в квадратурах
Дифференциальное уравнение - уравнение,
связывающее значение производной функции с самой функцией, значениями
независимой переменной, числами (параметрами). Порядок входящих в уравнение
производных может быть различен (формально он ничем не ограничен). Производные,
функции, независимые переменные и параметры могут входить в уравнение в
различных комбинациях или все, кроме хотя бы одной производной, отсутствовать
вовсе. Не любое уравнение, содержащее производные неизвестной функции, является
дифференциальным уравнением. Например,
не является дифференциальным уравнением.
Дифференциальное уравнение порядка выше первого
можно преобразовать в систему уравнений первого порядка, в которой число
уравнений равно порядку исходного уравнения.
Порядок, или степень дифференциального уравнения
- наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального
уравнения порядка n называется
функция y(x),
имеющая на некотором интервале (a,
b) производные 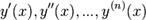 до
порядка n включительно и
удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения
называется интегрированием.
до
порядка n включительно и
удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения
называется интегрированием.
Задача об интегрировании дифференциального
уравнения считается решённой, если нахождение неизвестной функции удается
привести к квадратуре, независимо от того, выражается ли полученный интеграл в
конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить
на обыкновенные (ОДУ), в которые входят только функции (и их производные) от
одного аргумента, и уравнения с частными производными (УРЧП), в которых
входящие функции зависят от многих переменных. Существуют также стохастические
дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций,
независимых переменных дифференциальные уравнения подразделяются на линейные и
нелинейные, с постоянными или переменными коэффициентами, однородные или
неоднородные. В связи с важностью приложений в отдельный класс выделены
квазилинейные (линейные относительно старших производных) дифференциальные
уравнения в частных производных.
Важнейшим вопросом для дифференциальных
уравнений является существование и единственность их решения. Разрешение этого
вопроса дают теоремы существования и единственности, указывающие необходимые и
достаточные для этого условия. Для обыкновенных дифференциальных уравнений
такие условия были сформулированы Липшицем (1864).
Решения дифференциальных уравнений
подразделяются на общие и частные решения. Общие решения включают в себя
неопределенные постоянные, а для уравнений в частных производных - произвольные
функции от независимых переменных, которые могут быть уточнены из
дополнительных условий интегрирования (начальных условий для обыкновенных
дифференциальных уравнений, начальных и граничных условий для уравнений в
частных производных). После определения вида указанных постоянных и
неопределенных функций решения становятся частными.
Поиск решений обыкновенных дифференциальных
уравнений привёл к установлению класса специальных функций - часто
встречающихся в приложениях функций, не выражающихся через известные
элементарные функции. Их свойства были подробно изучены, составлены таблицы
значений, определены взаимные связи и т. д.
Развитие теории дифференциальных уравнений
позволило в ряде случаев отказаться от требования непрерывности исследуемых
функций и ввести обобщённые решения дифференциальных уравнений.
Обыкновенное дифференциальное уравнение:
Обыкновенные дифференциальные уравнения (ОДУ) -
это уравнения, зависящие от одной независимой переменной; они имеют вид  или
или где
где
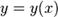 неизвестная
функция (возможно, вектор-функция; в таком случае часто говорят о системе
дифференциальных уравнений), зависящая от независимой переменной х штрих
означает дифференцирование по х. Число
неизвестная
функция (возможно, вектор-функция; в таком случае часто говорят о системе
дифференциальных уравнений), зависящая от независимой переменной х штрих
означает дифференцирование по х. Число  называется
порядком дифференциального уравнения. Наиболее практически важными являются
дифференциальные уравнения первого и второго порядка.
называется
порядком дифференциального уравнения. Наиболее практически важными являются
дифференциальные уравнения первого и второго порядка.
Порядок дифференциального уравнения:
Порядком дифференциального уравнения называют
наивысший порядок производной, входящей в данное уравнение.
Простейшие дифференциальные уравнения первого
порядка:
Простейшие дифференциальные уравнения первого
порядка - класс дифференциальных уравнений первого порядка, наиболее легко
поддающихся решению и исследованию. К нему относятся уравнения в полных
дифференциалах, уравнения с разделяющимися переменными, однородные уравнения
первого порядка и линейные уравнения первого порядка. Все эти уравнения можно
проинтегрировать в конечном виде.
Отправной точкой изложения будет служить
дифференциальное уравнение первого порядка, записанное в т. н. симметричной
форме: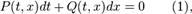 где
функции
где
функции 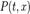 и
и
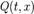 определены
и непрерывны в некоторой области
определены
и непрерывны в некоторой области 
Линейное дифференциальное уравнение:
Как обыкновенные дифференциальные уравнения, так
и уравнения в частных производных можно разделить на линейные и нелинейные.
Дифференциальное уравнение является линейным, если неизвестная функция и её
производные входят в уравнение только в первой степени (и не перемножаются друг
с другом). Для таких уравнений решения образуют аффинное подпространство
пространства функций. Теория линейных ДУ развита значительно глубже, чем теория
нелинейных уравнений. Общий вид линейного дифференциального уравнения n-го
порядка:
 где pi(x)
- известные функции независимой переменной, называемые коэффициентами
уравнения. Функция r(x)
в правой части называется свободным членом (единственное слагаемое, не
зависящее от неизвестной функции) Важным частным классом линейных уравнений
являются линейные дифференциальные уравнения с постоянными коэффициентами.
где pi(x)
- известные функции независимой переменной, называемые коэффициентами
уравнения. Функция r(x)
в правой части называется свободным членом (единственное слагаемое, не
зависящее от неизвестной функции) Важным частным классом линейных уравнений
являются линейные дифференциальные уравнения с постоянными коэффициентами.
Подклассом линейных уравнений являются
однородные дифференциальные уравнения - уравнения, которые не содержат
свободного члена: r(x)
= 0. Для однородных дифференциальных уравнений выполняется принцип
суперпозиции: линейная комбинация частных решений такого уравнения также будет
его решением. Все остальные линейные дифференциальные уравнения называются
неоднородными дифференциальными уравнениями.
Нелинейные дифференциальные уравнения в общем
случае не имеют разработанных методов решения, кроме некоторых частных классов.
В некоторых случаях (с применением тех или иных приближений) они могут быть
сведены к линейным. Например, линейное уравнение гармонического осциллятора  может
рассматриваться как приближение нелинейного уравнения математического маятника
может
рассматриваться как приближение нелинейного уравнения математического маятника 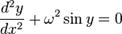 для
случая малых амплитуд, когда y
≈
sin y.
для
случая малых амплитуд, когда y
≈
sin y.
. Линейные дифференциальные уравнения первого
порядка
Линейным дифференциальным уравнением первого
порядка называется уравнение, линейное относительно неизвестной функции и её
производной. Оно имеет вид:
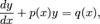 где
где  и
и
 -
заданные функции от х, непрерывные в той области, в которой требуется
проинтегрировать уравнение (1).
-
заданные функции от х, непрерывные в той области, в которой требуется
проинтегрировать уравнение (1).
Если  ,
то уравнение (1) называется линейным однородным. Оно является уравнением с
разделяющимися переменными и имеет общее решение
,
то уравнение (1) называется линейным однородным. Оно является уравнением с
разделяющимися переменными и имеет общее решение 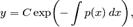 Общее
решение неоднородного уравнения можно найти методом вариации произвольной
постоянной, который состоит в том, что решение уравнения (1) ищется в виде
Общее
решение неоднородного уравнения можно найти методом вариации произвольной
постоянной, который состоит в том, что решение уравнения (1) ищется в виде ,
где
,
где 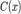 -
новая неизвестная функция от х.
-
новая неизвестная функция от х.
44. Признаки
сходимости числовых рядов
Необходимый признак сходимости числового ряда:
Если ряд 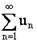 сходится,
то
сходится,
то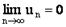 .
Данный признак означает, что если
.
Данный признак означает, что если  то
ряд расходится. Например,
то
ряд расходится. Например,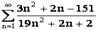 расходится, так как
расходится, так как .
Из выполнения условия
.
Из выполнения условия 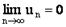 в общем случае не
следует сходимость ряда
в общем случае не
следует сходимость ряда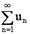 . Например, для
ряда
. Например, для
ряда 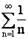 (гармонический
ряд), условие
(гармонический
ряд), условие  выполнено, но
данный ряд расходится.
выполнено, но
данный ряд расходится.
Признак Д’Аламбера:
Если существует 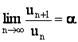 то:
при
то:
при 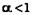 ряд
ряд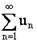 сходится;
при
сходится;
при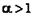 ряд
ряд
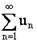 расходится.
расходится.
Радикальный признак Коши:
Если существует то:
при
то:
при  ряд
ряд
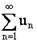 сходится;
при
сходится;
при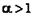 ряд
ряд
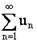 расходится.
расходится.
Интегральный признак Коши:
Пусть задан ряд 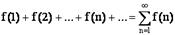 ,
члены которого являются значениями непрерывной, положительной и монотонно
убывающей функции
,
члены которого являются значениями непрерывной, положительной и монотонно
убывающей функции 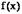 на промежутке
на промежутке 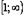 .
Тогда ряд
.
Тогда ряд 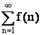 сходится, если
сходится несобственный интеграл
сходится, если
сходится несобственный интеграл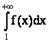 . Если же
. Если же 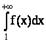 расходится,
то ряд
расходится,
то ряд 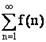 также
будет расходящимся.
также
будет расходящимся.
45. Функциональный
ряд
Ряд, каждым членом которого, в отличие от
числового ряда, является не число, а функция 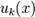 формальное
выражение вида
формальное
выражение вида  называется
функциональным рядом.
называется
функциональным рядом.
Множество Х- область определения ряда. Сумма n
первых членов ряда 
называется n-ой
частичной суммой функционального ряда. Заметим, что 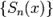 является
функциональной последовательностью, определенной на Х .
является
функциональной последовательностью, определенной на Х .
Пусть точка 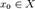 функциональный
ряд
функциональный
ряд  сходится
в точке
сходится
в точке  ,
если числовой ряд
,
если числовой ряд  сходится.
сходится.
Множество D
точек, 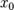 где
где
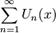 сходится,
называется областью сходимости ряда.
сходится,
называется областью сходимости ряда.
Функциональный ряд  сходится
на множестве D, если
последовательность
сходится
на множестве D, если
последовательность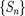 его частичных сумм
сходится на D.
его частичных сумм
сходится на D.
Если функциональный ряд сходится на множестве, D
то его сумма есть функция 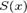
определенная на D,
очевидно, 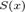 есть предел
функциональной последовательности
есть предел
функциональной последовательности 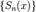
. Степенные ряды и их свойства
Функциональный ряд, членами которого являются
степенные функции аргумента x,
называется степенным рядом: 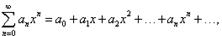 , где a
−
коэффициенты степенного ряда (постоянные действительные числа).
, где a
−
коэффициенты степенного ряда (постоянные действительные числа).
Часто рассматривается степенной ряд,
расположенный по степеням (x
−
x0):
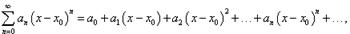 , где точка x0
называется центром степенного ряда.
, где точка x0
называется центром степенного ряда.
Интервал сходимости степенного ряда:
Рассмотрим функции 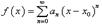 .
Ее областью определения является множество значений x,
при которых ряд сходится. Данная область определения называется интервалом
сходимости.
.
Ее областью определения является множество значений x,
при которых ряд сходится. Данная область определения называется интервалом
сходимости.
Радиус сходимости степенного ряда: Если интервал
сходимости представляется в виде (x0
− R, x0
+ R), где R
> 0, то величина R называется
радиусом сходимости. Степенной ряд сходится абсолютно в каждой точке интервала
сходимости. Сходимость в граничных точках x0
− R и x0
+ R устанавливается
отдельно.
Радиус сходимости по признаку Даламбера:

Радиус сходимости по радикальному признаку Коши:
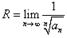
Дифференцирование степенных рядов: Пусть дан
степенной ряд  , имеющий радиус
сходимости R > 0. Функция
, имеющий радиус
сходимости R > 0. Функция  является
непрерывной при |x| < R.
Степенной ряд внутри интервала сходимости можно дифференцировать почленно.
Производная степенного ряда равна
является
непрерывной при |x| < R.
Степенной ряд внутри интервала сходимости можно дифференцировать почленно.
Производная степенного ряда равна
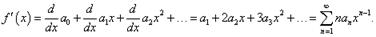
Интегрирование степенных рядов: Степенной ряд
можно почленно интегрировать на отрезке, расположенном внутри интервала
сходимости. Если −R
< b < x
< R, то справедливо
соотношение

Если интегрирование выполняется на отрезке [0, x],
то интеграл выражается формулой:
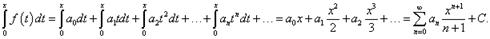
. Ряды
Фурье
Ряд Фурье - в математике - способ представления
произвольной сложной функции суммой более простых. В общем случае количество
таких функций может быть бесконечным, при этом, чем больше таких функций
учитывается при расчете, тем выше оказывается конечная точность представления
исходной функции. В большинстве случаев в качестве простейших используются
тригонометрические функции синуса и косинуса, в этом случае ряд Фурье
называется тригонометрическим, а вычисление такого ряда часто называют
разложением на гармоники.
Ряд Фурье - представление произвольной функции  с
периодом
с
периодом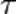 в
виде ряда:
в
виде ряда:

Этот ряд может быть также записан в виде:
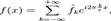 , где
, где  -
амплитуда
-
амплитуда  -го гармонического
колебания,
-го гармонического
колебания, 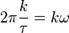 - круговая частота
гармонического колебания,
- круговая частота
гармонического колебания, 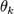 начальная фаза
начальная фаза  -го
колебания,
-го
колебания,  -
- -я
комплексная амплитуда.
-я
комплексная амплитуда.
Тригонометрическим рядом Фурье называют
функциональный ряд вида:
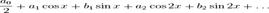 или, более сжато
или, более сжато 
Постоянные числа 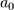 ,
, и
и  (
( )
называются коэффициентами тригонометрического ряда.
)
называются коэффициентами тригонометрического ряда.
Если ряд (1) сходится, то его сумма есть
периодическая функция  с периодом
с периодом  так
как
так
как 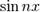 и
и
 являются
периодическими функциями с периодом
являются
периодическими функциями с периодом 