Методы решения систем линейных алгебраических уравнений

Методы решения систем линейных алгебраических уравнений

Методы решения систем линейных алгебраических уравнений

Задание

Решить систему линейных алгебраических уравнений материального баланса относительно неизвестных расходов G_ij

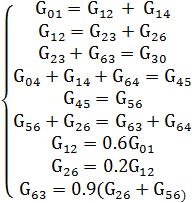
Исходные данные для расчета:

G₀₁ = 5000 кг/c; G₀₄ = 4000 кг/c.

Введение

Системы линейных алгебраических уравнений (СЛАУ) широко используются в инженерных расчетах, в том числе по химической технологии и защите окружающей среды.

С одной стороны, это определяется тем, что уравнения материального и теплового балансов, как правило, линейны или приводятся к линейным при некоторых ограничениях и допущениях.

Тогда при расчете потоков в сложных химико-технологических системах, в балансовых тепловых расчетах, в математических моделях процессов, построенных на базе, например, ячеечной модели гидродинамической структуры потоков возникает необходимость решать системы линейных уравнений высокого порядка. С другой стороны, основным источником знаний о сложных процессах химической технологии по-прежнему является эксперимент, а потому велика доля эмпирико-статистических моделей в инженерных расчетах. Эти модели, полученные на основе обработки результатов наблюдений статистическими методами, чаще всего строятся на базе линейной регрессии, оценка коэффициентов которой также сводятся к решению систем линейных алгебраических уравнений.

Цель работы: рассмотреть некоторые методы решения систем линейных алгебраических уравнений.

1.      История

Идею общего метода решения систем линейных уравнений высказал Лейбниц в 1693 году. Она была реализована швейцарским математиком Крамером в 1752 году. Он сформулировал и обосновал правило, носящее теперь его имя, которое позволяет решать системы n линейных уравнений с n неизвестными и буквенными коэффициентами. По правилу Крамера каждая неизвестная равна отношению двух определителей. Крамер, фактически, заложил основы теории определителей, хотя и не предложил для них удобного обозначения (это сделал в 1841 году А. Кэли). В 1772 году Вандермонд опубликовал обширное исследование определителей, один из которых носит теперь его имя. Систематическое изложение этой теории принадлежит Бине и Коши. Их труды по теории определителей относятся к периоду 1812-1815 гг.

Коэффициенты системы линейных уравнений и свободные члены удобно сводить в таблицы, называемые матрицами системы. Постепенно определители систем стали относить к матрицам систем. Матричный метод решения систем линейных уравнений впервые описан в древнекитайском трактате «Девять книг о математическом искусстве» (II век до н.э.). Система линейных уравнений в этом трактате записывается в виде матрицы, столбцы которой составлены из коэффициентов при неизвестных и свободных членов, и решается методом исключения, впоследствии заново сформулированном Гауссом в 1849 году. Этот метод естественно формулируется в виде правил преобразования так называемой расширенной матрицы системы.

Исследования Вейерштрасса и Фробениуса далеко продвинули теорию матриц, обогатив ее новыми понятиями и задачами. Фробениус, в частности, ввел понятие ранга матрицы (1877 г.). Используя это понятие, Кронекер и Капелли в лекциях 1883-91 гг. (Кронекер) и 1892 г. (Капелли) излагали теорему, дающую исчерпывающий ответ на вопрос о том, при каких условиях система m линейных уравнений с n неизвестными имеет решение.

.        Общие сведения

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛАУ) в линейной алгебре - это система уравнений вида

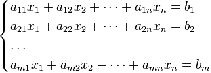                                                           (2.1)

Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.

Здесь 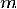 - количество уравнений, а  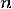- количество неизвестных.₁, x₂, …, x_n - неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn - коэффициенты системы - и b₁, b₂, … b_m - свободные члены - предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (2.1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (2.1) - совокупность n чисел c₁, c₂, …, c_n, таких, что подстановка каждого c_i вместо x_i в систему (2.1) обращает все её уравнения в тождества.

Система (2.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (2.1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (2.1) называются различными, если нарушается хотя бы одно из равенств: ₁⁽¹⁾ = c₁⁽²⁾, c₂⁽¹⁾ = c₂⁽²⁾, …, c_n⁽¹⁾ = c_n⁽²⁾ (2.2)

Совместная система вида (2.1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется недоопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Прямые (или точные) методы решения СЛАУ позволяют найти решение за определенное количество шагов. К прямым методам относятся метод Гаусса, метод Гаусса - Жордана, метод Крамера, матричный метод и метод прогонки (для трёхдиагональных матриц).

Итерационные методы основаны на использовании повторяющегося процесса. Они позволяют получить решение в результате последовательных приближений. К итерационным методам относятся метод Якоби (метод простой итерации), метод Гаусса - Зейделя, метод релаксации и многосеточный метод.

3. Методы решения систем линейных алгебраических уравнений

Матричный метод

Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с 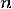 неизвестными (над произвольным полем):

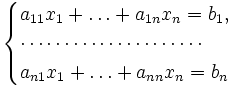 (3.1)

Тогда её можно переписать в матричной форме:

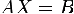, (3.2)

где 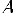 - основная матрица системы,  и 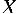 - столбцы свободных членов и решений системы соответственно:

 (3.3)

Умножим матричное уравнение (3.2) слева на  - матрицу, обратную к матрице :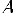

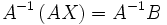 (3.4)

Так как 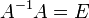, получаем 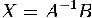. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.

Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.

Невзирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.

Пример решения СЛАУ матричным методом в программе Mathcad

Пример решения СЛАУ матричным методом в программе Mathcad рассмотрен в приложении А.

Метод Крамера

Метод Крамера (правило Крамера) - способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704-1752), предложившего этот метод в 1750 г.

 (3.6)

с определителем матрицы системы 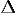, отличным от нуля, решение записывается в виде

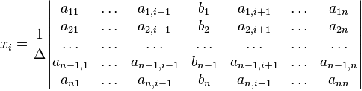 (3.7)

(i-ый столбец матрицы системы заменяется столбцом свободных членов).

В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

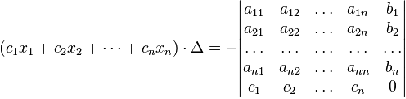 (3.8)

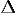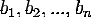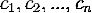В этой форме метод Крамера справедлив без предположения, что  отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы  и , либо набор  состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример решения СЛАУ методом Крамера в программе Mathcad и Delphi

Пример решения СЛАУ методом Крамера в программе Mathcad рассмотрен в приложении Б и в программе Delphi в приложении В.

Пример решения СЛАУ с помощью функции Find в программе Mathcad

Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравнения и неравенства, а последняя формула блока должна выглядеть как

mathcad линейный уравнение алгебраический

Find (х, у,…),

Отметим, что функция Find пытается найти решение в аналитической форме. В том случае, если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.

Пример решения СЛАУ c помощью функции Find в программе Mathcad рассмотрен в приложении Г.

Заключение

В данной работе была поставлена цель: рассмотреть методы решения систем линейных уравнений. Большинство численных методов решения систем линейных алгебраических уравнений предполагает, что исходная система преобразована к стандартному виду: выделены матрица коэффициентов при неизвестных А и вектор свободных членов В.

Цель, поставленная при разработке курсового проекта, достигнута.

Список использованной литературы

1. Википедия [Электронный ресурс] / www.wikipedia.org

2.      Бусыгин Н.Ю. Автоматизированные системы химических расчетов: решение задач в среде Mathcad: учебн. пособие / Н.Ю. Бусыгин. - СПб: СПГУТД, 2009.