|
Ресурсы
|
Норма затрат ресурсов товара
|
Общее количество ресурсов
|
|
1 товар
|
2 товар
|
|
|
1
|
2
|
2
|
12
|
|
2
|
1
|
2
|
8
|
|
3
|
4
|
0
|
16
|
|
4
|
0
|
4
|
12
|
Прибыль от реализации одной единицы
товара первого вида составляет 2 усл. ед., второго вида - 3 - усл. ед.
Найти оптимальный план реализации
товаров, обеспечивающий план реализации товаров. обеспечивающий максимальную
прибыль.
Задание 2. Фирма реализует автомобили двумя способами: через магазин и через
торговых агентов. При реализации x1 автомобилей через магазин расходы на реализацию составляют 4х1 +
х1² усл. ед., а при продаже
х1 автомобилей через торговых агентов расходы составляют х2² усл. ед. Найти
оптимальный способ реализации автомобилей, минимизирующий суммарные расходы,
если общее число предназначенных для продажи автомобилей составляет 200 штук.
. Линейное
программирование. симплексный метод
Геометрическая
интерпретация симплексного метода
Идея последовательного улучшения
решения легка в основу универсального метода решения задач линейного
программирования - симплексного метода.
Геометрический смысл симплексного
метода состоит в последовательном переходе от одной вершины многогранника
ограничений (называемой первоначальной) к соседней, в которой линейная функция
принимает лучшее (по крайней мере, не худшее) значение (по отношения к цели
задачи) до тех пор, пока не будет найдено оптимальное решение - вершина, где
достигается оптимальное значение функции цели (если задача имеет конечный
оптимум).
Впервые симплексный метод был
предложен американским ученым Дж. Джанцингом в 1949 г., однако еще в 1939 г.
идеи метода были разработаны российским ученым Л.В. Кантовичем.
Симплексный метод, позволяющий
решить любую задачу линейного программировании, универсален. В настоящее время
он используется для компьютерных расчетов, однако несложные примеры с
применением симплексного метода можно решать вручную.
Для реализации симплексного метода -
последовательного улучшения решения - необходимо освоить три основных элемента:
· Способ определения
какого-либо первоначального допустимого базисного решения задач;
· Правило перехода к
лучшему (точнее, не худшему) решению;
· Критерий проверки
оптимальности найденного решения.
Для использования симплексного
метода задача линейного программирования должно быть приведена каноническому
виду, т.е. система ограничений должна быть представлена в виде уравнений.
Алгоритм конкретной вычислительной реализации этих элементов рассмотрим на
примерах.
Отыскание
максимума линейной функции
Задача1.
Решить симплексным методом задачу:
F=2x1+3x2 max
при ограничениях:
x1+3x2<=18,
x1+x2<=16, (1)
x2<=5,
x1<=21
x1>=0, x2>=0
Решение. С помощью дополнительных неотрицательных» переменных перейдем к
системе уравнений. В данном случае все дополнительные переменные вводятся со
знаком «плюс», так как все неравенства имеют вид «<=»
Получим систему
ограничений в виде:
x1+3x2+x3=18,
x1+x2+x4=16, (2)
x2+x5=5,
x1+x6=21.
Для нахождения
первоначального базисного решения разобьем переменные на две группы - основные
и неосновные. Так как определитель, составленный из коэффициентов при
дополнительных переменных x3, x4, x5, x6, отличен от нуля, то эти переменные можно взять в качестве
основных на первом шаге |решения задачи. При выборе основных переменных на
первом шаге не обязательно составлять определитель из их коэффициентов и
проверять, равен ли он нулю. Достаточно воспользоваться |следующим правилом:
в качестве основных переменных на
первом шаге следует выбрать (если возможно) такие m переменных, каждая из
которых входит только в одно из т уравнений системы ограничений, при
этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.
Дополнительные
переменные удовлетворяют этому правилу. Если выбранные по этому правилу
переменные имеют те же знаки, что и соответствующие им свободные члены в правых
частях уравнений, то полученное таким образом базисное решение будет
допустимым. В данном случае так и получилось.
1 шаг. Основные переменные: x3, x4, x5, x6.
Неосновные
переменные: x1, x2.
Выразим основные
переменные черезнеосновные:
x3=18-x1-3x2,
x4=16-2x1-x2, (3)
x5=5-x2,
x6=21-3x1.
Положив неосновные
переменные равными нулю, т.еx1=0, x2=0, получим базисное решение x1=(0; 0; 18; 16; 5; 21), которое
является допустимым и соответствует вершине O (0; 0) многогранника OABCDEна рис. 1. Поскольку это
решение допустимое, нельзя отбросить возможность того, что оно оптимально.
Выразим линейную функцию через неосновные переменные: F=2x1+3x2. При решении x1значение функции равно F(x1). Легко понять, что функцию Fможно увеличить за счет увеличения
любой из неосновных переменных, входящих в выражение для F с положительным коэффициентом. Это
можно осуществить, перейдя к такому новому допустимому базисному решению, в
котором эта переменная будет неосновной, т.е. принимать не нулевое, а
положительное значение (если новое решение будет вырождено, то функция цели
сохранит свое значение). При таком переходе одна из основных переменных
перейдет в неосновные, геометрически произойдет переход к соседней вершине
многоугольника, где значение линейной функции «лучше» (по крайней мере «не
хуже»). В данном примере для увеличения Fможно переводить в основные либо x1, либо x2, так как обе эти переменныe| входят в выражение для Fсо знаком «плюс». Для определенности
в такой ситуации будем выбирать переменную, имеющую больший коэффициент, т.е. в
данном случае x2 (такое правило выбора не всегда дает наименее трудоемкое
решение, иногда имеет смысл провести предварительные специальные оценки).
Система (3)
накладывает ограничения на рост переменной x2. Поскольку необходимо сохранять
допустимость решений, т.е. все переменные должны оставаться неотрицательными,
то должны выполняться следующие неравенства (при этом x1=0 как неосновная переменная):
x3=18-3x2>=0, x2<=18/3
x4=16-x2>=0, откуда x2<=16/1
x5=5-x2>=0, x2<=5/1
x6=21
Каждое уравнение
системы (3), кроме последнего, определяет оценочное отношение - границу роста
переменной x2, сохраняющую неотрицательность соответствующей переменной.
Этаграница определяется абсолютной величиной отношения свободного члена к
коэффициенту при xпри условии, что эти числа имеют разные знаки. Последнее уравнение
системы неограничивает рост переменной x2, так как данная переменная в него
не входит (или формально входит с нулевым коэффициентом). В этом случае
условимся обозначать границу символом. Такой же символ будем использовать,
когда свободный член и коэффициент при переменной в уравнении имеют одинаковые
знаки, так как и в этом случае нет ограничений на рост переменной.
Не накладывает
ограничений на рост переменной, переводимой в основные, и такое уравнение, где
свободный член отсутствует (т.е. равен 0), а переводимая переменная имеет положительный
коэффициент. И в этом случае граница обозначается символом. Обратите внимание,
что при нулевом свободном члене и отрицательном коэффициенте при переводимой
переменной уравнение ограничивает рост этой переменной нулем! (любое
положительное ее значение вносит отрицательную компоненту в следующее базисное
решение).
Очевидно, что сохранение
неотрицательности всех переменных (допустимость решения) возможно, если не
нарушается ни одна из полученных во всех уравнениях границ. В данном примере
наибольшее возможное значение для переменной x2 определяется как х2=min {18/3; 16/1; 5/1;}=5.
При х2=5 переменная х5 обращается в нуль и переходит в неосновные.
Уравнение, где
достигается наибольшее возможное значение переменной, переводимой в основные
(т.е. где оценка минимальна), называется разрешающим. В данном случае -
это третье уравнение.
2 шаг. Основные переменные: x2, x3, x4, x6.
Неосновные
переменные: x1, x5.
Выразим новые
основные переменные через новые неосновные, начиная с разрешающего уравнения
(его используем при записи выражения для x2):
x2=5-x5,
x3=18-x1-3 (5-x5), (4)
x4=16-2x1 - (5-x5),
x5=21-3x1,
или
x2=5-x5,
x3=3-x1+3x5,
x4=11-2x1+x5,
x5=21-3x1.
Второе базисное
решение x2=(0; 5; 3; 11; 0; 21) является допустимым и соответствует вершине
A (0; 5)
на рис. 1. Геометрическая интерпретация перехода от x1 к x2 - переход от вершины O к соседней вершине A на многоугольнике решений ОАВСОЕ.
Выразив линейную
функцию через неосновные переменные на этом шаге, получаем:
F=2x1+3x2=2x1+3 (5-x5)=15+2x1-3x5.
Значение линейной
функцииF2=F(X2)=15. Изменение значения линейной функции легко определить
заранее как произведение наибольшего возможного значения переменной,
переводимой в основные, на ее коэффициент в выражении для линейной функции; в
данном случае F1=5*3=15, F2=F1+F1=0+15=15
Однако значение F2 не является максимальным, так как
повторяя рассуждения 1 шага, обнаруживаем возможность дальнейшего увеличения
линейной функции за счет переменной x1, входящей в выражение для Fс положительным коэффициентом.
Система уравнений (4) определяет наибольшее возможное значение для x1: x1=min {3/1 $11/2}=3. Второе
уравнение является разрешающим, переменная x3 переходит в неосновные, при этом F2=3*2=6.
3 шаг. Основные переменные: x1, x2, x4,
Неосновные
переменные: x3, x5.
Как и на 2 шаге,
выражаем новые основные переменные через новые неосновные, начиная с
разрешающего уравнения (его используем при записи выражения для x1_. После преобразований получаем:
x1=3-x3+3x5,
x2=5-x5,
x4=5+2x3-5x5, (5)
x6=12+3x3-9x5.
Базисное решение X3=(3; 5; 0; 5; 0; 12) соответствует
вершине B (3; 5). Выражаем линейную функцию через неосновные переменные: F=2x1+3x2=2 (3-x3+3x5)+3 (5-x5)=21-2x3+3x5, F3=F(X3)=21. Проверяем: F3-F2=21-15=6=F2. Третье допустимое базисное
решение тоже не является оптимальным, поскольку при неосновной переменной x5 в выражении линейной функции через
неосновные переменные содержится положительный коэффициент. Переводим x5 в основную переменную. При
определении наибольшего возможного значения для x5следует обратить внимание на первое
уравнение в системе (5), которое не дает ограничений на рост x5, так как свободный член и
коэффициент при x5 имеют одинаковые знаки. Поэтому x5=min {5; 1; 12/9}=1. Третье
уравнение является разрешающим, и переменная x4 переходит в неосновные; F3=1*3=3.
4 ш а г. Основные переменные: x1, x2, x5, x6
Неосновные
переменные: x3, x4.
После
преобразований получим;
x1=6+(1/5) x3 - (3/5) x4,
x2=4 - (2/5) x3+(1/5) x4,
x5=1+(2/5) x3 - (1/5) x4,
x6=3 - (3/5) x3+(9/5) x4.
Базисное решение X4=(6; 4; 0; 0; 1; 3) соответствует
вершин C (6; 4) на рис. 1.
Линейная функция,
выраженная через неосновные переменные, имеет вид: F=24 - (4/5) x3 - (3/5) x4. Это выражение не содержит
положительных коэффициентов при неосновных переменных поэтому значение F4=F(X4)=24 максимальное. Функцию Fневозможно еще увеличить, переходя к
другому допустимому базисному решению, т.е. решение X4 оптимальное. Вспоминая
экономический смысл всех переменных, можно сделать следующие выводы.
Прибыль предприятия
принимает максимальное значение 24 руб. при реализации 6 единиц продукции Р1
(х1=6) и 4 единиц продукции Р2 (х2=4). Дополнительные переменные х3, х4, х5, х6
показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е.
остатки ресурсов. При оптимальном плане производства х3=х4=0, т.е. остатки
ресурсов S1 и S2 равны нулю, а остатки ресурсов S3 и S4 равны соответственно 1 и 3
единицам.
Теперь можно в
общем виде сформулировать критерий оптимальности решения при отыскании
максимума линейной функции: если в выражении линейной функции через
неосновные переменные отсутствуют положительные коэффициенты при неосновных
переменных, то решение оптимально.
Отыскание
минимума линейной функции
При определении
минимума линейной функции Zвозможны два пути:
) отыскать максимум
функции F, полагая F=-Zучитывая, что Zmin=-Fmax;
) модифицировать
симплексный метод: на каждом шаге уменьшать линейную функцию за счет той
неосновной переменной, которая входит в выражение линейной функции с
отрицательным коэффициентом.
Рассмотрим это на
следующем примере.
Задача2.
Решить симплексным методом задачу
Z=18y1+16y2+5y3+21y4 min
при ограничениях:
y1+2y2+3y4>=2,
y1+y2+y3>=3,
Yi>=0, i=1,2,3,4.
Решение. Введем дополнительные неотрицательные переменные y5 и y6 со знаком «минус», так как
неравенства имеют вид «>=». Получим систему уравнений:
y1+2y2+3y4-y5=2,
3y1+y2+y3-y6=3.
Если на первом шаге
в качестве основных взять дополнительные переменные, то получим недопустимое
базисное решение: (0; 0; 0; 0; -2; -3). В данном случае в качестве основных
удобно взять переменные y3 и y4 (это согласуется с правилом выбора основных переменных,
сформулированным в разд. 2), коэффициенты при у3 и у4 положительны, поэтому в
качестве первоначального получим допустимое базисное решение.
1 шаг. Основные переменные: у3
Неосновные переменные:
у1, у2, у5, у6.
Выражаем основные
переменные через основные:
у3=3-3у1-у2+у6,
у4=(2/3) - (1/3) у1
- (2/3) у2+(1/3) у5.
Y1=(0; 0; 3; 2/3; 0; 0) первое базисное решение, оно допустимое.
Выражаем линейную функцию через неосновные переменные: Z=18y1+16y2+5y3+21y4=18y1+16y2+5 (3-3y1-y2+y6)+21 (2/3 - (1/3) y1 - (2/3) y2+(1/3) y5)=29-4y1-3y2+7y5+5y6.
Z1=Z(Y1)=29 - это значение не является минимальным, так как функцию Zможно уменьшить за счет перевода в
основные любой из переменных у1 или у2, имеющих в выражении для Zотрицательные коэффициенты. Так как y1 имеет больший по абсолютному
значению коэффициент, то начнем с этой переменной.
Для нее наибольшее
возможное значение: y1=min {3/3; 2/3; 1/3}=1, т.е. первое уравнение является разрешающим; y3 становится неосновной переменной, Z1=-4*1=-4
2 шаг. Основные переменные: у1, у4.
Неосновные
переменные: у2, у3, у5, у6.
Получим после
преобразований:
у1=1 - (1/3) у2 -
(1/3) у3+(1/3) у6,
у4=1/3 - (5/9)
у2+(1/9) у3+(1/3) у5 - (1/9) у6,
Z=25 - (5/3) y2+(4/3) y3+7y5+(11/3) y6 - линейная функция. При базисном решении Y2=(1; 0; 0; 1/3; 0; 0) получаем Z2=Z(Y2)=25. Z2-Z1=25-29=-4=Z1. Переменную y2 переводим в основные, так как в
выражение для Z она входит с отрицательным коэффициентом. Наибольшее возможное
значение y2=min {3; 3/5}=3/5, второе уравнение разрешающее и y4 переходит в неосновные переменные;
Z2=3/5
(-5/3) = -1.
3 шаг. Основные переменные: у1, у2.
Неосновные
переменные: у3, у4, у5, у6.
Получим после
преобразований:
у1=4/5 - (2/5)
у3+(3/5) у4 - (1/5) у5+(2/5) у6,
у2=3/5+(1/5) у3 -
(9/5) у4+(3/5) у5 - (1/5) у6,
Z=24+y3+3y4+6y5+4y6. Базисное решение Y3=(4/5; 3/5; 0; 0; 0; 0) оптимальное, так как в выражении для Zнет неосновных переменных с
отрицательными коэффициентами. Поэтому Zmin=Z3=Z(Y3)=24. Z3-Z2=24-25=-1=Z2.
Сформулируем критерий
оптимальности при отыскании минимума линейной функции: если в выражении
линейной функции через неосновные переменные отсутствуют отрицательные
коэффициенты при неосновных переменных, то решение оптимально.
Замечание. На каждом шаге симплексного метода какая-либо неосновная
переменная переводится в основные, при этом каждое уравнений системы
ограничений определяет конечное или бесконечное наибольшее возможное значение
этой переменной - оценочное отношение. В задачах 1 и 2 встречались различные
случаи оценки роста неосновной переменной, которые зависели от знаков и
значений свободного члена и коэффициента при переводимой переменной.
Сформулируем все возможные случаи. Обозначим: Xi - переводимая
неосновная переменная, bj - свободный член, aij - коэффициент при xi.
5. Транспортная задача
линейного программирования
1. Диагональный метод, или метод северо-западного угла. При этом методе на
каждом шаге построения первого опорного плана заполняется левая верхняя клетка
(северо-западный угол) оставшейся части таблицы. При таком методе заполнение
таблицы начинается с клетки неизвестного x11 и заканчивается в
клетке неизвестного xmn, т.е. идет как бы по диагонали таблицы
перевозок.
Пример
Таблица 2
Заполнение таблицы начинается с ее
северо-западного угла, т.е. клетки с неизвестным x11. Первая база A1
может полностью удовлетворить потребность первого заказчика B1
(a1=300, b1=170, a1> b1).
Полагая x11= 170, вписываем это значение в клетку x11 и
исключаем из рассмотрения первый столбец. На базе A1 остается
измененный запас . В оставшейся новой таблице с тремя строками A1, A2,
A3 и четырьмя столбцами B1, B2, B3,
B4; северо-западным углом будет клетка для неизвестного x12.
Первая база с запасом может полностью удовлетворить потребность второго заказчика
B2. Полагаем x12 = 110, вписываем это значение в клетку x12
и исключаем из рассмотрения второй столбец. На базе A1 остается
новый остаток (запас) . В оставшейся новой таблице с тремя строками A1,
A2, A3 и тремя столбцами B3, B4, B5
северо-западным углом будет клетка для неизвестного x13.
Теперь третий заказчик B3 может принять весь запас с базы A1.
Полагаем x13 = 20, вписываем это значение в клетку x13 и
исключаем из рассмотрения первую строку. У заказчика из B3 осталась
еще не удовлетворенной потребность . Теперь переходим к заполнению клетки для
неизвестного x23 и т.д.
Через шесть шагов у нас останется
одна база A3 с запасом груза (остатком от предыдущего шага) и один
пункт B5 с потребностьюb5=200. Соответственно этому
имеется одна свободная клетка, которую и заполняем, положив x35=200.
План составлен. Базис образован неизвестными x11, x12, x13,
x23, x24, x34, x35. Правильность
составленного плана легко проверить, подсчитав суммы чисел, стоящих в
заполненных клетках по строкам и столбцам.
Общий объем перевозок в
тонно-километрах для этого плана составит
2. Метод наименьшей
стоимости. При этом методе на каждом шаге
построения опорного плана первою заполняется та клетка оставшейся части
таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то
заполняется любая из них.
Пример
Таблица3
В данном случае заполнение таблицы
начинается с клетки для неизвестного x32, для которого мы имеем
значение c32 = 10, наименьше из всех значений cij. Эта
клетка находится на пересечении третьей строки и второго столбца,
соответствующим третьей базе A3 и второму заказчику B2.
Третья база A3 может полностью удовлетворить потребность второго
заказчика B2 (a3=250, b2=110, a3>
b2). Полагая x32 = 110, вписываем это значение в клетку x32
и исключаем из рассмотрения второй столбец. На базе A3 остается
изменённый запас . В оставшейся новой таблице с тремя строками A1, A2,
A3 и четырьмя столбцами B1, B3, B4,
B5 клеткой с наименьшим значением cij клетка, гдеc34=11.
Заполняем описанным выше способом эту клетку и аналогично заполняем следующие
клетки. В результате оказываются заполненными (в приведенной
последовательности) следующие клетки:
На пятом шаге клеток с наименьшими
значениями cij оказалось две (c11=c15=70). Мы
заполнили клетку для x15, положив x15 = 180. Можно было
выбрать для заполнения другую клетку, положив x11 = 170, что
приведет в результате к другому опорному плану. Общий объем перевозок в
тонно-километрах для этого плана составит
Понятие потенциала и
цикла.
Для перехода от одного базиса к
другому при решении транспортной задачи используются так называемые циклы.
Циклом пересчета или короче, циклом
в таблице перевозок называется последовательность неизвестных, удовлетворяющая
следующим условиям:
1. Одно из неизвестных
последовательности свободное, а все остальные - базисные.
. Каждые два соседних в
последовательности неизвестных лежат либо в одном столбце, либо в одной строке.
. Три последовательных неизвестных
не могут находиться в одном столбце или в одной строке.
. Если, начиная с какого-либо неизвестного,
мы будем последовательно переходить от одного к следующему за ним неизвестному
то, через несколько шагов мы вернемся к исходному неизвестному.
Второе условие означает, что у двух
соседних неизвестных в цикле либо первые, либо вторые индексы одинаковы.
Если каждые два соседних неизвестных
цикла соединить отрезком прямой, то будет получено геометрическое изображение
цикла - замкнутая ломаная из чередующихся горизонтальных и вертикальных
звеньев, одна из вершин которой находится в свободной клетке, а остальные - в
базисных клетках.
Можно доказать, что для любой
свободной клетки таблицы перевозок существует один и только один цикл,
содержащий свободное неизвестное из этой клетки, и что число вершин в цикле
всегда четно.
Так, например, в таблице перевозок,
составленной по диагональному методу при решения задачи из предыдущего пункта,
неизвестному x21 соответствует цикл x21, x23,
x13, x11, x21 и т.д.
Пусть теперь мы имеем некоторую
свободную клетку с соответствующим ей циклом. Если мы изменим значение свободного
неизвестного, увеличив его на некоторое число x, то, переходя последовательно от
одной вершины цикла к другой, мы должны будем в силу неизменности сумм по
строкам и по столбцам поочередно уменьшать и увеличивать значения неизвестных в
цикле на то же число x. Например, в указанном выше цикле для свободного неизвестного x21
получим:
старые значения: x21= 0,
x23= 80, x13= 20, x11= 170, x21= 0;
новые значения:
Очевидно, если снабдить вершины
цикла поочередно знаками «+» и» -», приписав вершине в свободной клетке знак
«+», то можно сказать, что в вершинах со знаком «+» число x прибавляется к прежнему значению
неизвестного, находящегося в этой вершине, а в вершинах со знаком «-» это число
x
вычитается из прежнего значения неизвестного, находящегося в этой вершине.
Если в качестве x выбрать наименьшее из чисел,
стоящих в вершинах, снабженных знаком «-», то, по крайней мере, одно из прежних
базисных неизвестных примет значение нуль, и мы можем перевести его в число
свободных неизвестных, сделав вместо него базисным то неизвестное, которое было
свободным.
Так, например, в рассмотренном выше
цикле имеем отрицательные вершины x21 и x11;
следовательно, выбрав х = min {80; 170} = 80, мы получаем:
старые значения: x21= 0,
x23= 80, x13= 20, x11= 170, x21= 0;
новые значения:
т.е. вместо прежнего базисного
решения получаем новое базисное решение:
Таблица 4
Выбор в качестве x минимального среди чисел, стоящих в
отрицательных вершинах цикла, обеспечивает допустимость нового базиса.
Если минимальное значение среди базисных
неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной
отрицательной вершине, то свободной оставляют только одну из них, а в других
клетках с тем же минимальным значением пишут нули. В этом случае новое базисное
решение будет вырожденным.
Может случиться, что и само
минимальное значение среди чисел в отрицательных клетках равно нулю. Тогда
преобразование таблицы перевозок сведется к перестановке этого нуля в свободную
клетку. Значения всех неизвестных при этом остаются неизменными, но решения
считаются различными, так как различны базисы. Оба решения вырождены.
Описанное выше преобразование
таблицы перевозок, в результате которого преобразуется базис, называется
пересчетом по циклу.
Заметим, что неизвестные, не
входящие в цикл, этим преобразованием не затрагиваются, их значения остаются
неизменными и каждое из них остается либо в группе базисных, либо в группе
свободных неизвестных, как и до пересчета.
Выясним теперь, как пересчет по
циклу влияет на общий объем затрат на перевозки и при каком условии эти затраты
становятся меньше.
Пусть xpq - некоторое
свободное неизвестное, для которого мы построили цикл и осуществили пересчет по
циклу с некоторым числом x. Если вершине цикла, находящейся в i-й строке и j-м столбце
таблицы перевозок, приписан знак «+», то значение неизвестного xij,
находящегося в этой вершине, увеличивается на x, что в свою очередь вызывает
увеличение затрат на cijx, где cij - тариф,
соответствующий этой клетке; если же указанной вершине приписан знак «-», то
значение неизвестного xij уменьшается на x, что вызывает уменьшение затрат на
cijx.
Сложим тарифы, соответствующие
положительным вершинам цикла, и вычтем из этой суммы сумму тарифов,
соответствующих отрицательным вершинам цикла; полученную разность Spq
назовем алгебраической суммой тарифов для данного свободного неизвестного xpq.
Подсчет алгебраической суммы тарифов можно истолковать и так: припишем тарифам
те же знаки, которые приписаны соответствующим вершинам цикла, тогда
алгебраическая сумма тарифов равна сумме таких тарифов со знаком
(«относительных тарифов»).
Теперь, очевидно, мы можем,
заключить, что в целом при пересчете но циклу, соответствующему свободному
неизвестному xpq общий объем затрат на перевозки изменится на
произведение алгебраической суммы тарифов на x, т.е. на величину Spqx.
Следовательно, если алгебраическая сумма тарифов для некоторого свободного
неизвестного xpq отрицательна (Spq< 0), то пересчет по
циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы
затрат на реализацию плана перевозок. Если же алгебраическая сумма тарифов
положительна (Spq> 0), то пересчет по соответствующему циклу
приведет к увеличению общей суммы затрат. И, наконец, если алгебраическая сумма
тарифов равна нулю (Spq = 0), то пересчет по соответствующему циклу
не изменит общую сумму затрат (два различных базисных плана требуют одинаковых
затрат на их реализацию).
Так, например, для цикла x21,
x23, x13, x11, x21 в рассмотренной
задаче алгебраическая сумма тарифов
.
Значит, пересчет по этому циклу снижает
расходы. И действительно, осуществив такой пересчет, мы получаем план, по
которому объем перевозок в тонно-километрах составляет
тогда как по исходному плану он
составил S1= 30650. Имеем снижение объема перевозок на 1200
тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов
в данном случае равна -15, а пересчет по циклу осуществляется с помощью числа х
= 80 (изменение затрат равно -15*80 = - 1200).
Вычисление алгебраической суммы
тарифов для каждого из свободных неизвестных можно производить без построения
соответствующего цикла, пользуясь, так называемыми, потенциалами. Припишем
каждой базе Ai, некоторое число ui, и каждому потребителю
Bj некоторое число vj:
,
i, + vj = cij,
где cij - тарифы,
соответствующие клеткам, заполненным базисными неизвестными. Эти числа ui,
и vj называются потенциалами соответствующих баз и потребителей.
Зная потенциалы, легко вычислить
алгебраическую сумму тарифов. Действительно, если в алгебраической сумме
тарифов по циклу, соответствующему свободному неизвестному xpq,
заменить тарифы базисных клеток их выражениями через потенциалы по формулам
(3.6), то, в силу чередования знаков при вершинах цикла, все потенциалы, кроме
up и vq сократятся, и мы получим:
pq = cpq - (up + vq).
Так, например, для цикла x21,
x23, x13, x11, x21 в рассмотренной
выше задаче имеем
.
Для базисных клеток сумма
потенциалов строки и столбца, в которых находится эта клетка, равна тарифу,
соответствующему этой клетке; если же клетка для неизвестного xpq
свободная, то сумму потенциалов
называют косвенным тарифом этой
клетки. Следовательно, алгебраическая сумма тарифов для свободной клетки xpq
равна разности ее настоящего («истинного») и косвенного тарифов:
Из (3.8) следует, что если косвенный
тариф для данной свободной клетки больше её истинного тарифа, то алгебраическая
сумма тарифов по циклу, соответствующему этой клетке, будет отрицательна; если
же косвенный тариф меньше истинного, то алгебраическая сумма тарифов
положительна, и, наконец, если косвенный тариф равен истинному, то
алгебраическая сумма тарифов равна нулю.
Потенциалы можно найти из системы
равенств (3.6), рассматривая их как систему (m + n - 1) уравнений с m+n
неизвестными. Так как неизвестных здесь на единицу больше, чем уравнений, то,
по крайней мере, один из потенциалов мы можем выбрать произвольно, положив,
например, u1 = 0; тогда остальные потенциалы легко определяются из
уравнений (3.6).
Например, для плана, полученного по
диагональному методу в рассмотренной выше задаче, имеем
Система содержит семь уравнений с
восемью неизвестными. Выбирая произвольно значение , находим последовательно из
первых трех уравнений значения , затем из четвертого уравнения - , из пятого
уравнения - , из шестого уравнения и, наконец, из седьмого уравнения - .
Положив, например, u1 =
0, получаем значения потенциалов:
Найдем теперь косвенные тарифы для
свободных клеток и сравним их с истинными тарифами:
Для клеток с неизвестными x21
и x32 косвенные тарифы больше истинных. Следовательно, для них мы
будемиметь отрицательные алгебраические суммы тарифов:
Значение S21 = -15 мы уже
имели раньше, вычисляя алгебраическую сумму тарифов для этой клетки
непосредственно по циклу.
Выводы:
Подсчитывая косвенные тарифы как
суммы соответствующих потенциалов, полезно не пропускать и клетки с базисными
неизвестными (заполненные клетки). Для этих клеток сумма потенциалов равна
истинному тарифу; последнее может служить проверкой правильности найденных
значении потенциалов.
Можно показать, что если сумму всех
затрат по данному плану перевозок выразить четырех свободные неизвестные, то
коэффициент при каждом из таких неизвестных будет равен алгебраической сумме
тарифов по циклу, соответствующему ей в таблице перевозок. Это еще раз
подтверждает, что пересчет по циклам является специфической формой применения
симплекс-метода к решению транспортной задачи.
6. Парная регрессия и
корреляция. Аппроксимация функций
Пример. По данным проведенного опроса восьми групп семей известны данные
связи расходов населения на продукты питания с уровнем доходов семьи.
Таблица 5
|
Расходы на продукты питания, 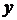 , тыс.
руб.0,91,21,82,22,62,93,33,8 , тыс.
руб.0,91,21,82,22,62,93,33,8
|
|
|
|
|
|
|
|
|
|
Доходы семьи, 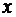 , тыс.
руб.1,23,15,37,49,611,814,518,7 , тыс.
руб.1,23,15,37,49,611,814,518,7
|
|
|
|
|
|
|
|
|
Предположим, что связь между
доходами семьи и расходами на продукты питания линейная. Для подтверждения
нашего предположения построим поле корреляции.
Рис. 2
По графику видно, что точки
выстраиваются в некоторую прямую линию.
Для удобства дальнейших вычислений
составим таблицу.
Таблица 6
|
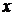 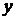 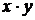 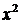 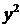 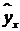 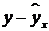 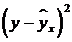  , % , %
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
1,2
|
0,9
|
1,08
|
1,44
|
0,81
|
1,038
|
-0,138
|
0,0190
|
15,33
|
|
2
|
3,1
|
1,2
|
3,72
|
9,61
|
1,44
|
1,357
|
-0,157
|
0,0246
|
13,08
|
|
3
|
5,3
|
1,8
|
9,54
|
28,09
|
3,24
|
1,726
|
0,074
|
0,0055
|
4,11
|
|
4
|
7,4
|
2,2
|
16,28
|
54,76
|
4,84
|
2,079
|
0,121
|
0,0146
|
5,50
|
|
5
|
9,6
|
2,6
|
24,96
|
92,16
|
6,76
|
2,449
|
0,151
|
0,0228
|
5,81
|
|
6
|
11,8
|
2,9
|
34,22
|
139,24
|
8,41
|
2,818
|
0,082
|
0,0067
|
2,83
|
|
7
|
14,5
|
3,3
|
47,85
|
210,25
|
10,89
|
3,272
|
0,028
|
0,0008
|
0,85
|
|
8
|
18,7
|
3,8
|
71,06
|
349,69
|
14,44
|
3,978
|
-0,178
|
0,0317
|
4,68
|
|
Итого
|
71,6
|
18,7
|
208,71
|
885,24
|
50,83
|
18,717
|
-0,017
|
0,1257
|
52,19
|
|
Среднее значение
|
8,95
|
2,34
|
26,09
|
110,66
|
6,35
|
2,34
|
-
|
0,0157
|
6,52
|
|
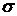 5,530,935------- 5,530,935-------
|
|
|
|
|
|
|
|
|
|
|
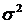 30,560,874------- 30,560,874-------
|
|
|
|
|
|
|
|
|
|
Рассчитаем параметры
линейного уравнения парной регрессии 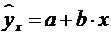 . Для этого
воспользуемся формулами (2.5):
. Для этого
воспользуемся формулами (2.5):
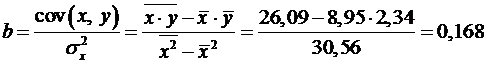 ;
;
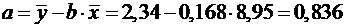 .
.
Получили уравнение: 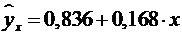 .
Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются
на 168 руб.
.
Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются
на 168 руб.
Как было указано выше,
уравнение линейной регрессии всегда дополняется показателем тесноты связи -
линейным коэффициентом корреляции 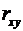 :
:
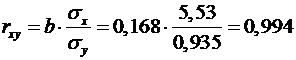 .
.
Близость коэффициента
корреляции к 1 указывает на тесную линейную связь между признаками.
Коэффициент детерминации
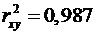 (примерно
тот же результат получим, если воспользуемся формулой (2.7)) показывает, что
уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на
долю прочих факторов приходится лишь 1,3%.
(примерно
тот же результат получим, если воспользуемся формулой (2.7)) показывает, что
уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на
долю прочих факторов приходится лишь 1,3%.
Оценим качество
уравнения регрессии в целом с помощью 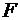 -критерия Фишера.
Сосчитаем фактическое значение
-критерия Фишера.
Сосчитаем фактическое значение 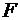 -критерия:
-критерия:
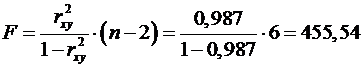 .
.
Табличное значение (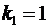 ,
,
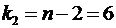 ,
,
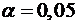 ):
):
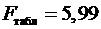 .
Так как
.
Так как 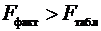 ,
то признается статистическая значимость уравнения в целом.
,
то признается статистическая значимость уравнения в целом.
Для оценки
статистической значимости коэффициентов регрессии и корреляции рассчитаем 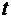 -критерий
Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем
случайные ошибки параметров линейной регрессии и коэффициента корреляции
-критерий
Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем
случайные ошибки параметров линейной регрессии и коэффициента корреляции
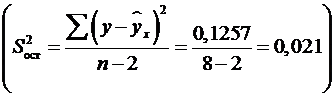 :
:
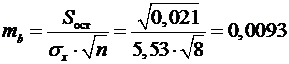 ,
,
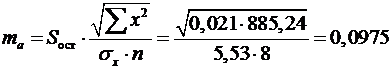 ,
,
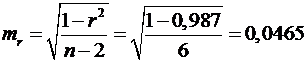 .
.
Фактические значения 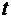 -статистик:
-статистик:
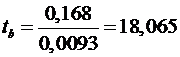 ,
,
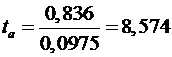 ,
,
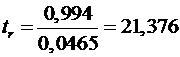 .
Табличное значение
.
Табличное значение 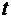 -критерия
Стьюдента при
-критерия
Стьюдента при 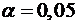 и
числе степеней свободы
и
числе степеней свободы 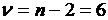 есть
есть
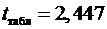 .
Так как
.
Так как 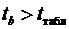 ,
,
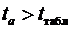 и
и
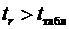 ,
то признаем статистическую значимость параметров регрессии и показателя тесноты
связи. Рассчитаем доверительные интервалы для параметров регрессии
,
то признаем статистическую значимость параметров регрессии и показателя тесноты
связи. Рассчитаем доверительные интервалы для параметров регрессии 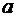 и
и
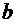 :
:
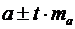 и
и
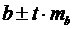 .
Получим, что
.
Получим, что 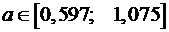 и
и
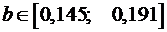 .
.
Средняя ошибка
аппроксимации (находим с помощью столбца 10 таблицы 2.3; 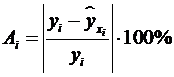 )
)
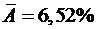 говорит
о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе
модели к исходным данным.
говорит
о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе
модели к исходным данным.
И, наконец, найдем
прогнозное значение результативного фактора 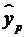 при значении
признака-фактора, составляющем 110% от среднего уровня
при значении
признака-фактора, составляющем 110% от среднего уровня 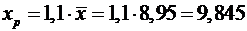 ,
т.е. найдем расходы на питание, если доходы семьи составят 9,85 тыс. руб.
,
т.е. найдем расходы на питание, если доходы семьи составят 9,85 тыс. руб.
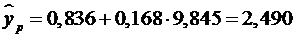 (тыс. руб.)
(тыс. руб.)
Значит, если доходы
семьи составят 9,845 тыс. руб., то расходы на питание будут 2,490 тыс. руб.
Найдем доверительный
интервал прогноза. Ошибка прогноза
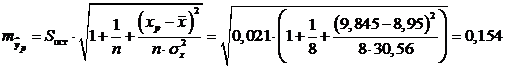 ,
,
а доверительный интервал
(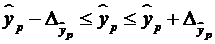 ):
):
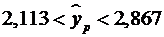 .
.
Т.е. прогноз является
статистически надежным.
Теперь на одном графике
изобразим исходные данные и линию регрессии:
Рис. 3
7. Приложения теории
графов
Пример.
Для графа G построим матрицу смежности А(G) и матрицу инцидентности В(G).
Так как у графа 5
вершин и 6 ребер, то размеры матрицы А(G) будут 5×5, а матрицы В(G) - 5×6.
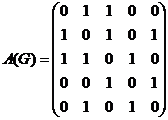
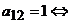 в графе G есть ребро, соединяющее вершины
в графе G есть ребро, соединяющее вершины 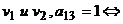 в графе Gесть ребро, соединяющее вершины
в графе Gесть ребро, соединяющее вершины 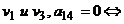 в графе Gнет ребра, соединяющего вершины
в графе Gнет ребра, соединяющего вершины  и т.д.
и т.д.
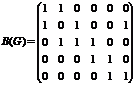
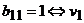 - концевая вершина для
ребра
- концевая вершина для
ребра 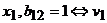 -
концевая вершина для ребра
-
концевая вершина для ребра 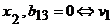 не является концевой
вершиной для ребра
не является концевой
вершиной для ребра 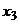 .
и т.д.
.
и т.д.
Пример. Для
орграфа Д построим матрицу смежности А(Д) и матрицу инцидентности В(Д).
Орграф Д содержит 5
вершин и 6 дуг, поэтому размеры матрицы А(Д) будут 5×5,
а матрицы В(Д) - 5×6.

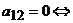 орграф Д не содержит
дуги из
орграф Д не содержит
дуги из 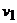 в
в
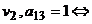 орграф
Д содержит дугу из
орграф
Д содержит дугу из 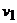 в
в
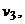 и
т.д.
и
т.д.

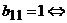 в вершине
в вершине 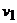 заканчивается
дуга
заканчивается
дуга 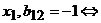 в
вершине
в
вершине 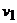 начинается
дуга
начинается
дуга 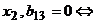 вершина
вершина
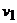 не
является концевой вершиной для дуги
не
является концевой вершиной для дуги 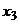 . И т.д.
. И т.д.
8.
Задача определения кратчайшего пути
Задача состоит в
том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до
любой другой вершины.
Задача
1. Узел 7 - склад, остальные узлы - строительные площадки компании.
Показатели на дугах - расстояния в километрах.
Надо найти
кратчайшие расстояния от склада до каждой строительной площадки. Какова длина
кратчайшего пути от склада до строительной площадки 1? Проходит ли кратчайший
путь от склада к строительной площадке 1 через строительную площадку 2? Какова
длина кратчайшего пути от склада до строительной площадки 2? Проходит ли
кратчайший путь от склада к строительной площадке 2 через строительную площадку
4?
Решим эту задачу
методом присвоения меток. Каждому узлу присваиваем метку из двух чисел. Первое
число - это минимальное расстояние от узла 7 до данного узла, второе - номер
предыдущего узла на пути от узла 7 к данному узлу. Узел, для которого мы
определили путь от узла 7, назовем помеченным. Узел, для которого такой путь
еще не определен, назовем непомеченным. Если мы определили кратчайшее
расстояние от узла 7 до данного узла, то соответствующую метку назовем
постоянной и будем обозначать в круглых скобках. Все остальные метки назовем
временными и будем обозначать в квадратных скобках. Узлы с постоянными метками
будем закрашивать.
Итак, узлу 7
присваиваем метку (0, S), где 0 - это расстояние от узла 7, S - обозначение стартового узла.
Узел 7 связан с
узлами 2, 4, 6. Длины соответствующих ребер - 17, 5, 6. Поэтому узлам 2, 4, 6
присваиваем временные метки - [17, 7], [5, 7], [6, 7] соответственно (первое
число - длина пути от узла 7 до данного узла, а второе - это предшествующий
узел).
После выполнения
этой операции можно сделать два следующих шага:
· найти
участок (участки) минимальной длины и соответствующую временную метку (метки)
сделать постоянной;
· узел
(узлы), которому соответствует появившаяся постоянная метка, становится новым
стартом.
После выполнения
этой операции временная метка с наименьшим расстоянием до узла 7 становится
постоянной. Это метка (5, 7) узла 4. Поэтому следующий шаг мы начнем с узла 4.
Узел 4
непосредственно связан с узлами 2 и 5 без постоянных меток. Длина ребра 4-5
равна 4, метка узла 4 - (5, 7) => временная метка узла 5 равна [5+4, 4] =
[9, 4]. Длина ребра 4-2 равна 6, метка узла 4 - (5, 7) => временная метка
узла 2 равна [5+6, 4] = [11, 4]. Таким образом, мы нашли путь от узла 7 до узла
2 длины 11.
Узел 2 пока помечен
меткой [17, 7] (путь длины 17), но 11 < 17 => старую метку [17, 7] узла 2
мы меняем на новую временную метку [11, 4], где 11 - это длина пути от узла 7
до узла 2, а 4 - номер предшествующего узла.
После этого из всех
временных меток [11, 4], [9, 4], [6, 7] выбираем метку с наименьшим первым
числом. Это [6, 7]. Эта метка становится постоянной, а очередной шаг мы начнем
с узла, соответствующего этой метке, - узла 6.
Этот узел связан с
узлом 5 без постоянной метки. Длина ребра 6-5 равна 2, метка узла 6 - (6, 7)
=> метка узла 5 равна [6+2, 6] = [8, 6]. Но узел 5 уже помечен меткой [9,
4]. Так как 8 < 9, то узлу 5 припишем новую метку - [8, 6]. После этого из
всех временных меток [11, 4] и [8, 6] метку с наименьшим первым числом (8, 6)
объявляем постоянной, а следующий шаг начнем с соответствующего ей узла 5.
Узел 5 связан
только с одним узлом без постоянной метки - узлом 3. Длина ребра 5-3 равна 4,
метка узла 5 - (8, 6) => узлу 3 припишем временную метку [8+4, 5] = [12, 5].
Теперь из всех временных меток [11, 4] и [12, 5] метку с наименьшим первым
числом [11, 4] объявляем постоянной, а следующий шаг начнем с соответствующего
ей узла 2.
Узел 2 связан с узлами 1 и 3 без
постоянных меток. Длина ребра 2-1 равна 15, метка узла 2 - (11, 4) => узлу 1
припишем временную метку [11+15, 2] = [26, 2]. Длина ребра 2-3 равна 3, метка
узла 2 - (11, 4) =>мы могли бы пометить узел 3 меткой [11+3, 2] = [14, 2],
но узел 3 уже помечен меткой [12, 5] с меньшим первым числом. Так что метку
узла 3 не меняем. Теперь из временных меток [26, 2] и [12, 5] метка с
наименьшим первым числом становится постоянной (12, 5), а с соответствующего ей
узла 3 начнем следующий шаг. Метку узла 1 меняем на (12+10, 3) = (22, 3). Всем
узлам приписаны постоянные метки. Действие алгоритма прекращается.
Первое число метки
у каждой вершины - это длина кратчайшего пути от узла 7 до данной вершины.
Чтобы восстановить кратчайший путь от узла 7 до какой-то вершины, мы должны из
этой вершины перейти всоседнюю (ее номер - это второе число метки). И т.д. до
вершины 7.
Теперь мы можем
ответить на вопросы задачи. Метка узла 1 - (22, 3) => длина кратчайшего пути
от узла 7 до узла 1 равна 22. Из узла 1 мы идем в узел 3. Метка узла 3 - (12,
5) => идем в узел 5. Метка узла 5 - (8, 6) => идем в узел 6. Метка узла 6
- (6, 7) => идем в узел 7, то есть кратчайший путь 1-3-5-6-7. Он не проходит
через узел 2. Аналогично решаются другие вопросы