Линейное разностное уравнение

Линейное разностное уравнение

Министерство образования Республики Беларусь

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»

Институт информационных технологий

КОНТРОЛЬНАЯ РАБОТА№1

По курсу: Специальные математические методы и функции

Минск, 2013

1. Найти решение 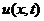уравнения

с граничными усл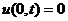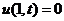овиями ,  и начальными условиями , .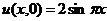

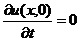Решение:

Будем искать решение в виде ряда:

уравнение фурье функционал экстремаль

.

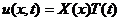Тогда: , .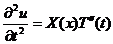

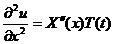Тогда исходное уравнение примет вид:

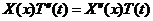или разделяя переменные .

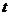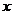Т.к.  и  - независимые переменные, то равенство возможно лишь в том случае, когда левая и правая части являются вещественными числами:

, .

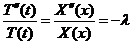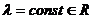В результате для нахождения функци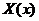йи 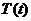 получаем систему дифференциальных уравнений:

Рассмотрим вначале уравнение (2).

В силу нулевых краевых условий имеем:

,

.

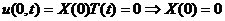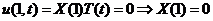Анализ этих уравнений приводит к выводу, что:

, .

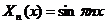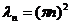Тогда уравнение (1) имеет решение:

.

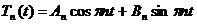Итак, мы нашли подходящие частные решения:

.

Скомбинируем из них общее решение в виде ряда:

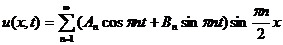. (3)

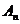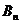Для нахождения чисел  и  почленно продифференцируем ряд по переменной :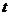

. (4)

Подставим в (3) и (4) 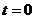. Тогда с учетом начальных условий будем иметь:

,

.

Мы получили разложение функций  и 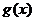 в ряды Фурье по синусам. Поэтому неизвестные коэффициенты определяются по стандартным формулами:

.

.

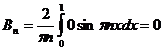Ответ: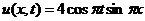

. Найти симметричное преобразование Фурье функции

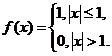
Решение: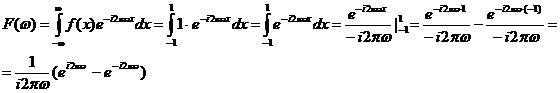

Ответ: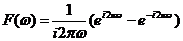

. Решить линейное разностное уравнение

, , , .

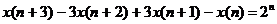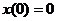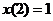Решение:

Пусть .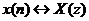

Тогда

.

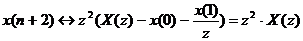
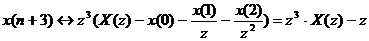Получаем операторное уравнение:

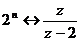
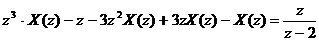
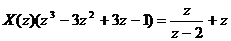
Имеем решение:

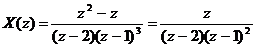
Функция  представляет собой несократимую дробь, знаменатель которой имеет корни 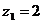,  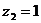кратности 2.

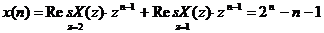
Проверим, выполняются ли начальные условия:

.

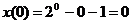
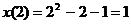Значит, функция  является решением исходной задачи.

Ответ:.

. Найти допустимые экстремали функционала

, , .

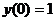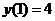Решение:

Приступая к решению задачи, замечаем, что:

, ,

, .

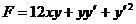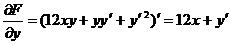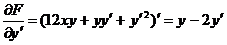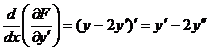Поэтому уравнение Эйлера-Лагранжа выглядит так:

.

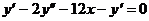
Интегрируя, получаем решение:

.

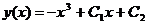Частное решение:

,

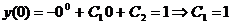Подставим:

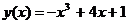- искомая экстремаль.

Ответ: .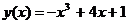

Список используемой литературы

1. Бицадзе, А. В. Уравнения математической физики / А. В. Бицадзе. - М.: Наука, 1976. - 296 с.

. Болгов, В. А. Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: учеб. пособие для втузов / В. А. Болгов, А. В. Ефимов, А. Ф. Каракулин [и др.]; под общ. редакцией Ефимова А. В. и Б. П. Демидовича - 2-е изд. - М.: Наука, 1986. - 368 с.

. Гельфанд, И. М. Вариационное исчисление / И. М. Гельфанд, С. В. Фомин. - М.: Наука, 1961. - 228 с. 3. Жевняк, Р. М. Высшая математика: Дифференциальные уравнения. Уравнения математической физики. Теория функций комплексной переменной: учеб. пособие / Р. М. Жевняк, А. А. Карпук - Минск: ИРФ Обозрение, 1977. - 570 с.

. Жевняк, Р. М. Высшая математика: Операционное исчисление. Теория вероятностей. Математическая статистика. Случайные процессы: учеб. пособие / Р. М. Жевняк, А. А. Карпук. - Минск: ИРФ Обозрение, 1977. - 445с.