Решение нелинейного уравнения методом дихотомии
КУРСОВАЯ РАБОТА
ПО
ДИСЦИПЛИНЕ «программирование и основы алгоритмизации»
НА ТЕМУ
«решение нелинейного уравнения методом дихотомии»
Содержание
Введение
Цель написания и постановка задачи
Метод решения
Блок-схема
Описание программы
Написание текста программы с комментариями
Конечный вид программы (листинг)
Результаты тестовых расчетов
Заключение (вывод)
Список использованной литературы
Введение
Разработанный курсовой проект содержит математическое описание, алгоритм
и программу вычисления нелинейного уравнения методом дихотомии. Программа
написана на языке C++.
Постановка задачи
Существует теорема: Если непрерывная функция на концах некоторого
интервала имеет значения разных знаков, то внутри этого интервала у нее есть
корень (как минимум, один, но м.б. и несколько)". На базе этой теоремы
построено численное нахождение приближенного значения корня функции. Обобщенно
этот метод называется дихотомией, то есть делением отрезка на две части.
Обобщенный алгоритм выглядит так:
1. Задать начальный интервал [Xleft. Xright];
2. Убедиться, что на концах функция имеет разный
знак;
. Повторять
А) выбрать внутри интервала точку X;
Б) сравнить знак функции в точке X со знаком функции в одном из концов;
В) если совпадает, то переместить этот конец интервала
в точку X,
Г) иначе переместить в точку X другой конец интервала;
пока не будет достигнута нужная точность.
Варианты метода дихотомии различаются выбором точки
деления.
Метод половинного деления известен также как метод
бисекции. В данном методе интервал делится ровно пополам.
Такой подход обеспечивает гарантированную сходимость
метода независимо от сложности функции - и это весьма важное свойство.
Недостатком метода является то же самое - метод никогда не сойдется быстрее,
т.е. сходимость метода всегда равна сходимости в наихудшем случае.
Метод половинного деления:
1. Один из простых способов поиска корней функции
одного аргумента.
2. Применяется для нахождения значений
действительно-значной функции, определяемому по какому-либо критерию (это может
быть сравнение на минимум, максимум или конкретное число).
Метод решения
Перед применением метода для поиска корней функции
необходимо отделить корни одним из известных способов, например, графическим
методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке
нужно искать корень.
Будем считать, что корень t функции f(x)=0 отделён на отрезке [a,b]. Задача заключается в том, чтобы найти и уточнить этот
корень методом половинного деления. Другими словами, требуется найти
приближённое значение корня с заданной точностью  .
.
Пусть функция f непрерывна на отрезке [a,b],
(a)•f(b) < 0  - единственный корень уравнения
- единственный корень уравнения 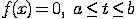 .
.
(Мы не рассматриваем случай, когда корней на отрезке [a,b] несколько, то есть более одного. В качестве  можно взять достаточно малое положительное число,
например, 0.001).
можно взять достаточно малое положительное число,
например, 0.001).
Поделим отрезок [a,b] пополам.
Получим точку c=(a+b)/2 a<c<b и
два отрезка [a,c] и [c,b].
§ Если f(c)=0, то корень t найден (t=c).
§ Если нет, то из двух полученных отрезков [a,c] и [c,b]. надо выбрать один 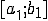 такой, что f(a1) f(b1)<0, то есть
такой, что f(a1) f(b1)<0, то есть
§ 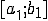 =[a,c], если f(a)f(c)<0 или
=[a,c], если f(a)f(c)<0 или
§ 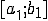 =[c,b], если f(c)f(b)<0.
=[c,b], если f(c)f(b)<0.
Новый отрезок 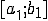 делим пополам. Получаем середину
этого отрезка
делим пополам. Получаем середину
этого отрезка 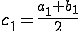 и так далее.
и так далее.
Для того, чтобы найти приближённое значение корня с
точностью до  , необходимо остановить процесс половинного деления на таком
шаге
, необходимо остановить процесс половинного деления на таком
шаге  , на котором
, на котором  и вычислить
и вычислить 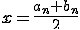
Блок схема

Описание программы
Входными данными для расчета являются:
· a - начальное значение интервала (нижний предел интеграла)
· b - конечное значение интервала (верхний предел интеграла)
· E - требуемая точность
Промежуточными данными для расчета являются:
· с - середина промежутка [a, b]
Выходной величиной для расчета является c - по достижении необходимой точности.
Программа написана для решения нелинейного уравнения вида:
x = x^2
алгоритм программа корень функция
Код программы c комментариями
#include <iostream> #include <math.h> #include
<stdio.h> //Задаем объекты
из библиотеки. Математические
функции и средства ввода/вывода
using namespace std;
double f(double x) //В данной программе будем работать с вещественными числами
{ //типа данных double return x*x-cos(x); //Задаем функцию }
int main() { double a, b, c, sigma, x;
//Вводим промежуток и точность cin
>> a; cin >> b; сin >> sigma;
while (b - a > sigma)
{= (a + b) / 2; //Разбиение промежутка(f(b) * f(c) < 0; //Выяснение знака
a = c;= c;
}<< (a + b) / 2 << endl; //Выводим ответ>>
x;0;
}
Код программы
#include <math.h>
#include <stdio.h>namespace std;f(double x)
{x*x-cos(x);
}main()
{a, b, c, sigma, x;>> a;>> b;>> sigma;(b -
a > sigma)
{= (a + b) / 2;(f(b) * f(c) < 0;= c;= c;
}<< (a + b) / 2 << endl;
cin >> x;0;
}
Результаты тестовых расчетов
|
Номер расчета
|
Значение a
|
Значение b
|
Значение E
|
Результат программы
|
Результат математических
вычислений
|
|
1
|
0
|
2
|
0.01
|
0.820312
|
0.824132
|
|
2
|
0
|
1
|
0.001
|
0.824132
|
0.824132
|
|
3
|
0
|
1
|
0.0001
|
0.820312
|
0.824132
|
|
4
|
-1
|
0
|
0.01
|
-0.820312
|
-0.824132
|
Заключение
Результатом выполнения данной курсовой работы является программа,
позволяющая вычислять корень уравнения x^2=cos(x) в промежутке, который задает
пользователь с необходимой точностью. Программа работает корректно, производя
необходимые вычисления и выводя на экран ответ.
Список использованной литературы
1) Р. Лафоре - Объектно-ориентированное
программирование в С++ // Издательство Москва 2014 год.