Математические методы, применяемые в теории систем массового обслуживания

Математические методы, применяемые в теории систем массового обслуживания

Содержание

Введение

. Математические методы, наиболее часто применяемые в теории систем массового обслуживания

.1 Теория графов

.2 Уравнение Колмогорова

.3 Потоки событий

Заключение

Список использованных источников

Введение

Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного обслуживания потока заявок (требований на обслуживание) при ограничениях на ресурсы системы.

Модели СМО удобны для описания отдельных подсистем современных вычислительных систем, таких как подсистема процессор - основная память, канал ввода-вывода и т.д. Вычислительная система в целом представляет собой совокупность взаимосвязанных подсистем, взаимодействие которых носит вероятностный характер. Заявка на решение некоторой задачи, поступающая в вычислительную систему, проходит последовательность этапов счета, обращения к внешним запоминающим устройствам и устройствам ввода-вывода. После выполнения некоторой последовательности таких этапов, число и продолжительность которых зависит от трудоемкости программы, заявка считается обслуженной и покидает вычислительную систему. Таким образом, вычислительную систему в целом можно представлять совокупностью СМО, каждая из которых отображает процесс функционирования отдельного устройства или группы однотипных устройств, входящих в состав системы.

Совокупность взаимосвязанных СМО называется сетью массового обслуживания (стохастической сетью).

Цель контрольной работы - изучить математические методы, наиболее часто применяемые в теории систем массового обслуживания.

Для достижения заданной цели следует решить следующие задачи:

рассмотреть теорию графов;

изучить уравнение Колмогорова;

охарактеризовать потоки событий.

1. Математические методы, наиболее часто применяемые в теории систем массового обслуживания

1.1 Теория графов

Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Графами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых. С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.

Граф - это средство для наглядного представления состава и структуры системы. Граф состоит из вершин, связанных дугами или ребрами. Вершины могут быть изображены кругами, овалами, точками, прямоугольниками. Связи между вершинами изображаются линиями. Если линия направленная (т.е. со стрелкой), то она называется дугой, если не направленная (без стрелки), то ребром. Принято считать, что одно ребро заменяет две дуги, направленные в противоположные стороны. Граф, в котором все линии направленные, называются ориентированным графом. Две вершины, соединенные дугой или ребром, называются смежными.

Взвешенный (размеченный) граф - это граф, в котором с вершинами или с линиями связана некоторая дополнительная информация. Эта информация называется весом вершины или линии. Чаще всего задается в виде надписи на вершине или линии, но возможны и другие способы: форма или цвет вершины, толщина, цвет и тип линии (например, сплошная или пунктирная).

Вес позволяет отобразить на графе не только структуру системы, но и различные свойства компонент и связей, количественные характеристики.

Размеченный граф состояний строится на основе матрицы перехода системы. Так как в каждой строке содержатся вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими.

Размеченный граф состояний СМО представлен на рисунке 1.1.

Рисунок 1.1 - Размеченный граф состояний СМО

₀ - состояние, когда обе кассы свободны;

S₁ - одна касса занята (любая из двух);

S₂ - обе кассы заняты.

Этот граф представляет собой одну цепочку, в которой каждое из состояний связано прямой и обратной связью с соседними состояниями.

Переход по стрелке, ведущей из состояния в него же, означает задержку системы в данном состоянии.

1.2 Уравнение Колмогорова

Вероятности состояний системы можно найти из системы дифференциальных уравнений Колмогорова, которые составлены по следующему правилу:

В левой части каждого из них стоит производная вероятности i-го состояния. В правой части - сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы p_i (t) в предельном стационарном режиме, которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют. Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии.

Решая подобную систему уравнений, можно получить выражения, определяющие финальные состояния СМО:

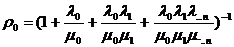, (1)

, (2)

где µ - интенсивность обслуживания покупателей.

массовый обслуживание канал событие

1.3 Потоки событий

Поток событий - последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

Например, это поток вызовов на телефонной станции, поток покупателей в магазине и т.д.

Поток событий можно наглядно изобразить рядом точек на оси времени O t (рисунок 2).

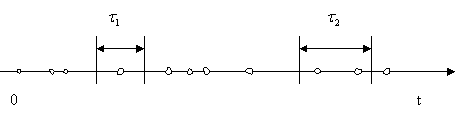
Рисунок 2 - Изображение потока событий на оси времени

Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока.

Интенсивность потока событий (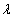) - это среднее число событий, приходящееся на единицу времени.

Рассмотрим некоторые свойства (виды) потоков событий.

Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.

В частности, интенсивность 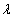 стационарного потока постоянна. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.

Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времен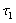и  и 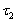 (см. рисунок 2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.

Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.

Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами:

) стационарен;

) ординарен;

) не имеет последствий.

Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

 (4)

где а - это среднее число событий попадающих за данный промежуток времени.

Параметр «а» можно определить через интенсивность потока событий λ.

Размерность интенсивности потока λ - есть среднее число событий в единицу времени.

Заключение

Нами была раскрыта цель контрольной работы - изучены математические методы, наиболее часто применяемые в теории систем массового обслуживания.

Для достижения заданной цели были решены следующие задачи:

рассмотрена теория графов;

изучено уравнение Колмогорова;

охарактеризованы потоки событий.

Таким образом, теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваются вероятностные задачи и математические модели.

Теория систем массового обслуживания (ТСМО) - это область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные действия повторяются многократно (например, на предприятиях бытового обслуживания, в розничных магазинах, на автоматических линиях производства и др.).

Предметом ТСМО - является установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами.

Задачи ТСМО носят оптимизационных характер и в конечном итоге включают экономический аспект по определению такого варианта системы при котором будет обеспечен минимум суммарных затрат, вызванных ожиданием обслуживания, потерями времени и ресурсов на обслуживание, а также простоями каналов обслуживания.

Список использованных источников

1. Вентцель, Е.С. Исследование операций / Е.С. Вентцель, - М: СОЮЗ, 2010. - 213 с.

. Вентцель, Е.С. Теория вероятностей и её инженерные приложения / Е.С. Вентцель, Л.А. Овчаров, - М: ИНФРА-М, 2009. - 147 с.

. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмуран, - М: Высшая школа, 2011. - 122 с.

. Лифшиц, А.Л. Статистическое моделирование СМО / А.Л. Лифшиц, - М.: Дашков, 2008. - 99 с.

. Фомин, Г.П. Математические методы и модели в коммерческой деятельности / Г.П. Фомин, - М: Финансы и статистика, 2010. - 366 с.