Численная интерполяция средствами MathCad
Министерство
образования и науки Российской Федерации Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
«Оренбургский
государственный педагогический университет»
Физико-математический
факультет
Кафедра информатики
и методики преподавания информатики
Курсовая
работа
по
дисциплине «Прикладное программное обеспечение»
Численная
интерполяция средствами Mathcad
Специальность:
230401.65 Прикладная математика
Форма
обучения: дневная
Юртаевой
Ирины Владимировны
Научный
руководитель:
Полищук
О.Б., к.п.н., доцент
Оренбург
2013
ОГЛАВЛЕНИЕ
Введение
Глава 1. Основные понятия численного
интерполирования
.1 Постановка задачи в
численной интерполяции
.2 Основные методы
.2.1 Интерполяционный многочлен
Лагранжа
.2.2 Интерполяционная формула
Ньютона
.2.3 Интерполяция сплайнами
Глава 2. Практическая реализация
методов в среде MathCad
.1 Общие сведения о среде MathCad
.2 Средства MathCad для интерполяции
.3 Примеры
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Актуальность проделанной работы состоит в том,
что система MathCad
- современный программный продукт, который может оказать существенную помощь
при выполнении решения определенной практической задачи на основе заданных
данных.
Объект: прикладное программное обеспечение.
Предмет: реализация численного интерполирования
в среде MathCad.
Цель: изучить возможности математического пакета
MathCad.
Задачи:
1) Провести обзор научно - методической
литературы по теоретическим аспектам интерполяции и практической реализации
методов в среде MathCad.
) Рассмотреть практическую реализацию
численного интерполирования в среде MathCad.
Глава
1. ОСНОВНЫЕ ПОНЯТИЯ ЧИСЛЕННОГО ИНЕТЕРПОЛИРОВАНИЯ
1.1 Постановка
задачи численной интерполяции
Основная задача численной интерполяции
заключается в нахождении значений таблично заданной функции в тех точках внутри
данного интервала, где она не задана. Можно рассчитать искомое значение
исходной функции в любой точке.
Рассматриваются основные проблемы постановки:
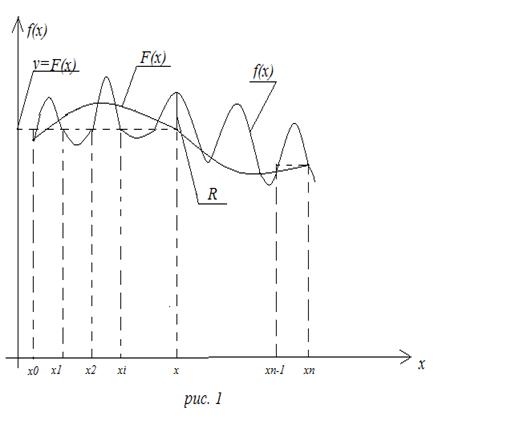
) Выбор интерполяционной функции F(x)
) Оценка погрешности интерполяции R(x)
Специальные методы интерполяции позволяют
определить искомое значение функции без непосредственно прямого построения
интерполяционной функции. В принципе, все интерполяционные методы, базирующиеся
на использование в качестве интерполяционной функции полиномов, дают одни и те
же результаты, на с разными затратами. Это объясняется тем, что полином n,
содержащий n+1 параметр не
проходящий через все заданные N+1
точки - единственный ряд Тейлора, в который расположена исходная
дифференцируемая функция.
Это одно из главных достоинств полинома как
интерполяционной функции. Поэтому чаще первая проблема интерполяции решается
выбором в качестве интерполяционной функции именно полинома, хотя могут
применяться другие функции «например, тригонометрические полиномы, другие
функции выбранные из неформальных условий содержательной задачи». Выбор вида
интерполяционной функции является в общем случае важной задачей, особенно если
помнить, что через заданные точки можно провести любое количество функций
(рис.1).
Следует отметить, что существует очевидный
способ построения интерполяционной функции: из условий прохождения функций
через все точки составляется система уравнений из решения которой находится ее
параметры. Однако этот путь далеко не эффективный, особенно при большом числе
точек.
1.2 Основные методы
.2.1 Интерполяционный
многочлен Лагранжа
Случай глобальной интерполяции, т.е.
построение интерполяционного многочлена, единого для всего отрезка 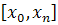
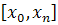 . При этом, естественно, график
интерполяционного многочлена должен проходить через все заданные точки.
. При этом, естественно, график
интерполяционного многочлена должен проходить через все заданные точки.
Запишем искомый многочлен в виде

Из условий равенства значений этого
многочлена в узлах 
 соответствующим заданным табличным
значениям
соответствующим заданным табличным
значениям 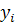
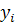 получим следующую систему уравнений
для нахождения коэффициентов
получим следующую систему уравнений
для нахождения коэффициентов 

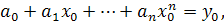
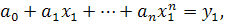
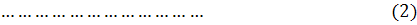

Можно показать, что эта система
имеет единственное решение, если среди узлов интерполяции нет совпадающих, т.е.
если 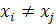
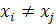 при
при 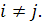
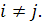 Решив эту систему, найдем
коэффициенты интерполяционного многочлена (1). Заметим вместе с тем, что такой
путь построения интерполяционного многочлена требует значительного объема вычислений,
особенно при большом числе узлов. Существуют более простые алгоритмы построения
интерполяционных многочленов.
Решив эту систему, найдем
коэффициенты интерполяционного многочлена (1). Заметим вместе с тем, что такой
путь построения интерполяционного многочлена требует значительного объема вычислений,
особенно при большом числе узлов. Существуют более простые алгоритмы построения
интерполяционных многочленов.
Будем искать многочлен в виде
линейной комбинации многочленов степени n:

При этом потребуем, чтобы каждый
многочлен 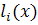
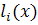 обращался в нуль во всех узлах
интерполяции, за исключением одного (i - го), где
он должен равняться единице. Легко проверить, что этим условиям отвечает
многочлен вида
обращался в нуль во всех узлах
интерполяции, за исключением одного (i - го), где
он должен равняться единице. Легко проверить, что этим условиям отвечает
многочлен вида

Действительно, 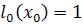
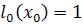 при
при 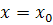
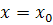 . При
. При 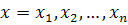
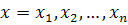 числитель выражения (4) обращается
в нуль. По аналогии с (4) получим
числитель выражения (4) обращается
в нуль. По аналогии с (4) получим
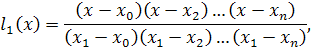
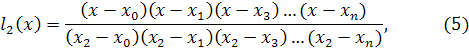

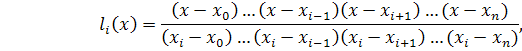

Подставляя в (3) выражения (4), (5),
находим
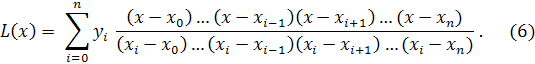
Эта формула называется
интерполяционным многочленом Лагранжа.
Покажем, что этот многочлен является
единственным. Допустим противоположное: пусть существует еще один многочлен 
 степени
степени 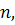
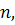 принимающий в узлах интерполяции
заданные значения, т.е.
принимающий в узлах интерполяции
заданные значения, т.е. 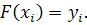
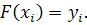 Тогда разность
Тогда разность 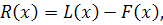
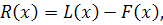 являющаяся многочленом степени
являющаяся многочленом степени 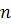
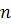 (или ниже), в узлах
(или ниже), в узлах 
 равна
равна
Это означает, что многочлен 
 степени не больше
степени не больше 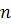
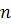 имеет
имеет 
 корней. Отсюда следует, что
корней. Отсюда следует, что 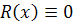
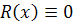 и
и 

Из формулы (6) можно получить выражения
для линейной (
 и квадратичной (
и квадратичной (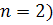
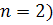 интерполяций:
интерполяций:
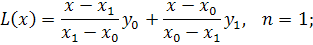
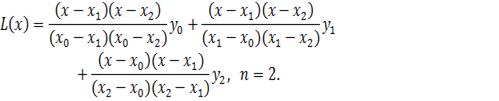
1.2.2
Интерполяционная формула Ньютона
До сих пор не делалось никаких
предположений о законе распределения узлов интерполяции. Теперь рассмотрим
случай равностоящих значений аргумента, т.е. 
 Величина
Величина 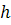
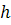 называется шагом.
называется шагом.
Введем также понятие конечных
разностей. Пусть известны значения функций в узлах 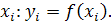
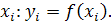
Составим разности значений функции:
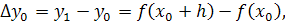
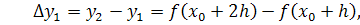


Эти значения называются первыми
разностями (или разностями первого порядка) функции.
Можно составить вторые разности
функции:

Аналогично составляются разности
порядка 

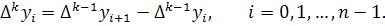
Конечные разности можно выразить
непосредственно через значения функции. Например,
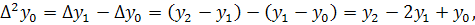

Аналогично для любого 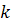
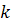 можно записать
можно записать
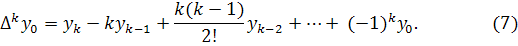
Эту формулу можно записать и для
значения разности в узле 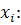
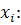

Используя конечные разности, можно
определить 

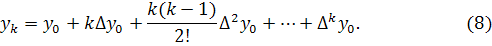
Перейдем к построению
интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем
виде:
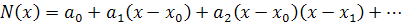
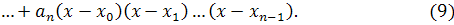
График многочлена должен проходить
через заданные узлы, т.е. 

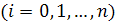
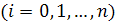 . Эти условия используем для
нахождения коэффициентов многочлена:
. Эти условия используем для
нахождения коэффициентов многочлена:
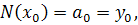
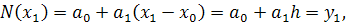

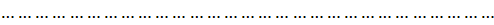
Найдем отсюда коэффициенты 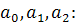
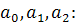
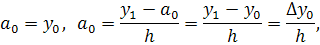
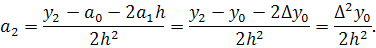
Аналогично можно найти и другие
коэффициенты. Общая формула имеет вид
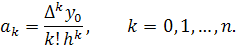
Подставляя эти выражения в формулу
(9), получаем следующий вид интерполяционного многочлена Ньютона:


Конечные разности 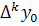
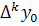 могут быть вычислены по формуле
(7).
могут быть вычислены по формуле
(7).
Формулу (10) часто записывают в
другом виде. Для этого вводится переменная 
 тогда
тогда

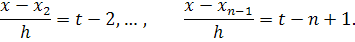
С учетом этих соотношений формулу
(10) можно переписать в виде
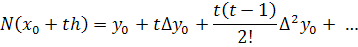
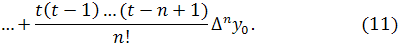
Полученное выражение может
аппроксимировать заданную функцию 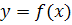
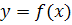 на всем отрезке изменения аргумента
на всем отрезке изменения аргумента
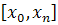
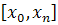 . Однако более целесообразно (с
точки зрения повышения точности расчетов и уменьшения числа членов в (11)
ограничиться случаем
. Однако более целесообразно (с
точки зрения повышения точности расчетов и уменьшения числа членов в (11)
ограничиться случаем 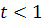
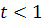 , т.е. использовать формулу (11) для
, т.е. использовать формулу (11) для
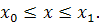
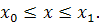 Для других значений аргумента,
например для
Для других значений аргумента,
например для 
 вместо
вместо 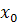
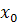 лучше взять значение
лучше взять значение 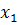
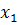 . Таким образом, интерполяционный
многочлен Ньютона можно записать в виде
. Таким образом, интерполяционный
многочлен Ньютона можно записать в виде
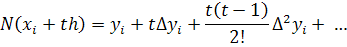
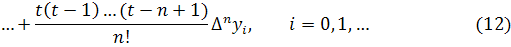
Полученное значение называется
первым интерполяционным многочленом Ньютона для интерполирования вперед.
Интерполяционную формулу (12) обычно
используют для вычисления значений функции в точках левой половины
рассматриваемого отрезка. Это объясняется следующим. Разности 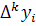
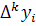 вычисляются через значения функции
вычисляются через значения функции 
 ,
, 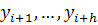
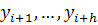 , причем
, причем 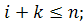
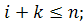 поэтому при больших значениях
поэтому при больших значениях 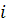
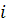 мы можем вычислить разности высших
порядков
мы можем вычислить разности высших
порядков 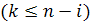
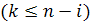 . Например, при
. Например, при 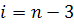
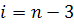 в (12) можно учесть только
в (12) можно учесть только 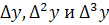
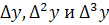 .
.
Для правой половины рассматриваемого
отрезка разности лучше вычислять справа налево. В этом случае

т.е. 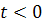
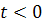 , и интерполяционный многочлен
Ньютона можно получить в виде
, и интерполяционный многочлен
Ньютона можно получить в виде
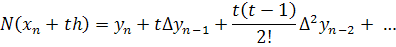
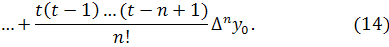
Полученная формула называется вторым
интерполяционным многочленом Ньютона для интерполирования назад.
Рассмотрим пример использования многочленов
Ньютона для интерполирования.
Пример 1. Функция y
= f (x)
задана таблицей значений с шагом h.
а) Запишите первый интерполяционный многочлен
Ньютона второго порядка, используя указанную ниже таблицу разностей.
|
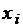 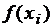 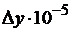  
|
|
|
|
|
|
0,150
0,155 0,160 0,165 0,170 0,175 0,180
|
0,14944
0,15438 0,15932 0,16425 0,16918 0,17411 0,17903
|
494
494 493 493 493 492
|
0
-1 0 0 -1
|
-1
1 0 1
|
Вычислить значения функции при x
= 0,156 при помощи первого многочлена Ньютона
Положим:
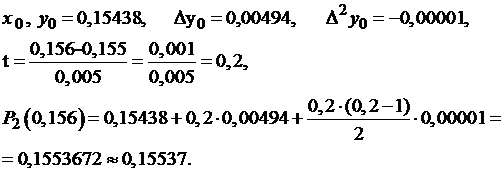
б) Грубую оценку погрешности
полученного значения можно получить, используя формулу (4.13).
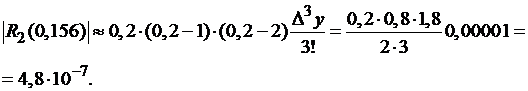
1.2.3 Интерполяция
сплайнами
При большом количестве узлов интерполяции сильно
возрастает степень интерполяционных многочленов, что делает их неудобными для
вычислений. Высокой степени многочленов можно избежать, разбив отрезок
интерполяции на несколько частей с построением на каждой части самостоятельного
интерполяционного многочлена. Такое интерполирование приобретает существенный
недостаток: в точках стыка разных интерполяционных многочленов будет разрывной
их первая производная.
В этом случае удобно пользоваться особым видом
кусочно-полиномиальной интерполяции - интерполяцией сплайнами.
Сплайн - это функция, которая на каждом
частичном отрезке является алгебраическим многочленом, а на всем заданном
отрезке непрерывна вместе с несколькими своими производными. Ниже рассмотрен
способ построения сплайнов третьей степени (кубических сплайнов), наиболее
распространенных на практике.
Пусть интерполируемая функция  задана
своими значениями
задана
своими значениями  в узлах
в узлах 
На отрезке  [
[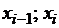 ] функцию
] функцию  запишем в
виде:
запишем в
виде:
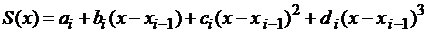 (15)
(15)
где 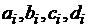 - неизвестные коэффициенты (всего
их 4n).
- неизвестные коэффициенты (всего
их 4n).
Используя совпадение значений  в узлах с
табличными значениями функции
в узлах с
табличными значениями функции  , получаем следующие уравнения:
, получаем следующие уравнения:
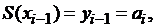 (16)
(16)
 (17)
(17)
Число этих уравнений - 2n. Для
получения дополнительных уравнений используем непрерывность 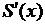 и
и 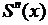 в узлах
интерполяции интервала (
в узлах
интерполяции интервала (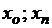 ).
).
Получаем следующие уравнения:
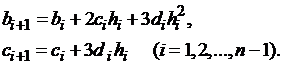 (18)
(18)
Для получения еще двух уравнений
используем условие - равенство нулю второй производной 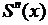 в точках
в точках 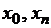 :
:
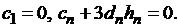 (19)
(19)
Исключив 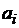 из
полученных выше уравнений, получаем систему, содержащую 3n
неизвестных:
из
полученных выше уравнений, получаем систему, содержащую 3n
неизвестных:
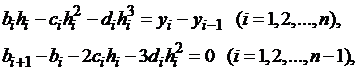
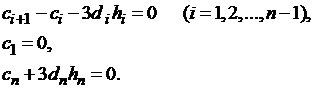 (20)
(20)
Решив данную систему, получаем
значения неизвестных 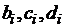 , которые
определяют сплайн
, которые
определяют сплайн  .
.
Рассмотрим пример построения
сплайна.
Пример 2. Интерполирующая функция
задана таблицей, содержащей четыре узла.
|
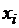 2345 2345
|
|
|
|
|
|
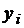 4-26-3 4-26-3
|
|
|
|
|
Используя формулы (15), составляем кубический
сплайн:
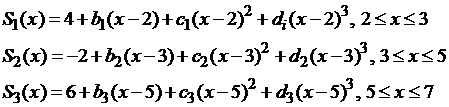
Составляем систему уравнений с
использованием формул (20):
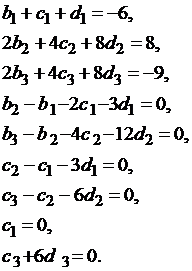
Коэффициенты системы представлены в
таблице 1.
Таблица 1
Коэффициенты, определяющие матрицу
системы примера 2

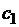



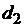
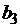

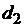 Своб.
Своб.
|
члены
|
|
|
|
|
|
|
|
|
|
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
-6
|
|
0
|
0
|
0
|
2
|
4
|
8
|
0
|
0
|
0
|
8
|
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
4
|
8
|
-9
|
|
-1
|
-2
|
-3
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
-1
|
-4
|
-12
|
1
|
0
|
0
|
0
|
|
0
|
-1
|
-3
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
-1
|
-6
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
6
|
0
|
Система может быть решена с использованием
компьютера, например, методом Гаусса. Получаем решение (результаты округлены до
двух знаков после запятой):

Полученные значения коэффициентов
определяют искомый сплайн:

Глава 2.
ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДОВ С СРЕДЕ MATHCAD
.1
Общие сведенья о среде Mathcad
- система компьютерной алгебры
из класса систем автоматизированного проектирования, ориентированная на
подготовку интерактивных документов с вычислениями и визуальным сопровождением,
отличается легкостью использования и применения для коллективной работы.был
задуман и первоначально написан Алленом Раздовом из Массачусетского
технологического института (MIT), соучредителем компании Mathsoft, которая с
2006 года является частью корпорации PTC (Parametric Technology
Corporation).имеет интуитивный и простой для использования интерфейс
пользователя. Для ввода формул и данных можно использовать как клавиатуру, так
и специальные панели инструментов.
Некоторые из математических
возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве
системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14
версии - использует символьное ядро MuPAD.
Работа осуществляется в
пределах рабочего листа, на котором уравнения и выражения отображаются
графически, в противовес текстовой записи в языках программирования. При
создании документов-приложений используется принцип WYSIWYG (What You See Is
What You Get - «что видишь, то и получаешь»).
Несмотря на то, что эта
программа в основном ориентирована на пользователей-непрограммистов, Mathcad
также используется в сложных проектах, чтобы визуализировать результаты
математического моделирования, путем использования распределённых вычислений и
традиционных языков программирования. Также Mathcad часто используется в
крупных инженерных проектах, где большое значение имеет трассируемость и
соответствие стандартам.достаточно удобно использовать для обучения, вычислений
и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой
технологий .NET иXML позволяют легко интегрировать Mathcad практически в любые
ИТ-структуры и инженерные приложения. Есть возможность создания электронных
книг (e-Book).
Количество пользователей в мире
- около 1.8 млн.содержит сотни операторов и встроенных функций для решения
различных технических задач. Программа позволяет выполнять численные и
символьные вычисления, производить операции со скалярными величинами, векторами
и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad
можно выделить:
Решение дифференциальных
уравнений, в том числе и численными методами и интегрирование.
2.2 Средства Mathcad
для интерполяции
Функции интерполяции определяют кривую, точно
проходящую через заданные точки. Из-за этого результат очень чувствителен к
ошибкам данных. Кроме того, убедитесь, что каждый элемент массива, который
используется в любой из функций, описанных в этом разделе, содержит
определенное значение. Поскольку MathCAD присваивает значение 0 любым
элементам, которые явно не определены.
Линейная интерполяция.
При линейной интерполяции MathCAD соединяет
существующие точки данных прямыми линиями. Это выполняется функцией linterp.
Использует векторы данных 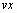 и
и
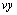 ,
чтобы возвратить интерполируемое значение
,
чтобы возвратить интерполируемое значение 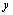 ,
соответствующее третьему аргументу
,
соответствующее третьему аргументу  .
Аргументы
.
Аргументы 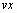 и
и 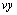 должны
быть векторами одинаковой длины. Вектор
должны
быть векторами одинаковой длины. Вектор 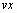 должен
содержать вещественные значения, расположенные в порядке возрастания.
должен
содержать вещественные значения, расположенные в порядке возрастания.
Эта функция соединяет точки данных отрезками
прямых, создавая таким образом ломаную. Интерполируемое значение для
конкретного х есть ордината у соответствующей точки ломаной.
Для значений  ,
расположенных перед первой точкой в векторе
,
расположенных перед первой точкой в векторе 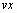 ,
MathCAD продолжает ломаную прямой линией, проходящей через первые две точки
данных. Для значений
,
MathCAD продолжает ломаную прямой линией, проходящей через первые две точки
данных. Для значений  , расположенных за
последней точкой
, расположенных за
последней точкой 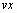 , MathCAD
продолжает ломаную прямой линией, проходящей через последние две точки данных.
, MathCAD
продолжает ломаную прямой линией, проходящей через последние две точки данных.
Для получения наилучших результатов  должно
находится между самыми большими и самыми маленькими значениями
должно
находится между самыми большими и самыми маленькими значениями 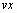 -
маловероятно, что будут полезны значения, вычисленные для
-
маловероятно, что будут полезны значения, вычисленные для  вне
этого диапазона. Функция linterp предназначена для интерполяции, а не для
экстраполяции.
вне
этого диапазона. Функция linterp предназначена для интерполяции, а не для
экстраполяции.
Кубическая сплайн-интерполяция.
Кубическая сплайн-интерполяция позволяет провести
кривую через набор точек таким образом, что первые и вторые производные кривой
непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических
полиномов, проходящих через наборы из трех смежных точек. Кубические полиномы
затем состыковываются друг с другом, чтобы образовать одну кривую.поставляется
с тремя сплайн-функциями: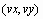
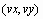
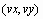
Они возвращают вектор коэффициентов вторых
производных, который мы будем называть 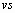 .
Этот вектор
.
Этот вектор 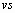 обычно
используется в функции interp, описанной ниже. Аргументы
обычно
используется в функции interp, описанной ниже. Аргументы 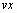 и
и
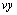 должны
быть вещественными векторами одинаковой длины. Значения вектора
должны
быть вещественными векторами одинаковой длины. Значения вектора 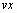 должны
быть расположены в порядке возрастания.
должны
быть расположены в порядке возрастания.
Эти три функции отличаются только граничными
условиями:
· функция lspline генерирует кривую
сплайна, которая приближается к прямой линии в граничных точках;
· функция pspline генерирует кривую
сплайна, которая приближается к параболе в граничных точках.
· функция cspline генерирует кривую
сплайна, которая может быть кубическим полиномом в граничных точках.
2.3 Примеры
Пример 1.
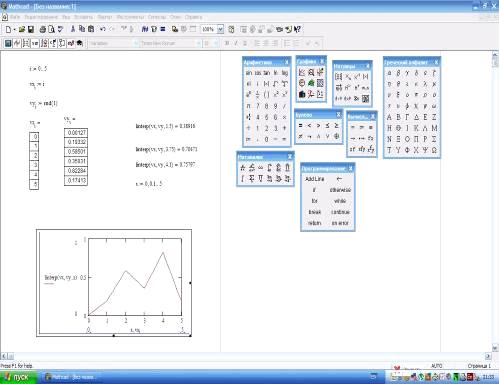
Пример 2.
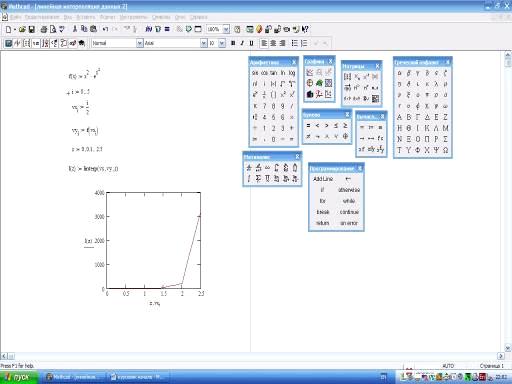
Пример 3.
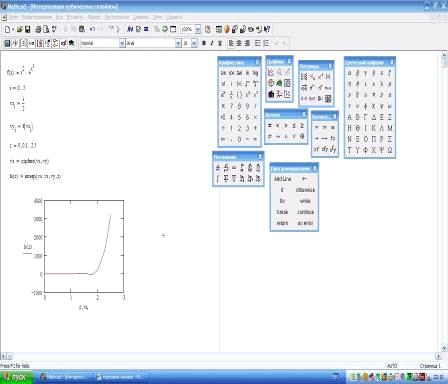
Пример 4.
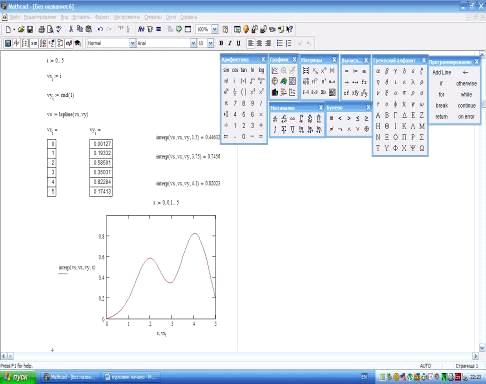
Пример 5.

Заключение
Система MathCad
- современный программный продукт, который может оказать существенную помощь
студентам, инженерам и всем тем, кто выполняет какие - либо расчеты. Основное
достоинство этой системы заключается в отсутствии необходимости MathCad
предельно приближен к обыкновенному математическому языку. Поэтому на решение
поставленных задач затрачивается незначительное время.
Система MathCad
содержит текстовый редактор, мощный вычислитель и очень простой в применении
графический процессор. Это позволяет готовить документы, по виду напоминающие
статьи или разделы книг. Вычислитель системы содержит множество математических
функций - от всем известных элементарных до весьма специфических. Современные
версии MathCad
дают пользователям возможность производить символьные расчеты. В этом случае
результатом вычисления выражения является другое выражение. При этом желаемая
форма этого второго выражения может быть задана. Первоначальное выражение можно
продифференцировать, проинтегрировать, разложить на множители, в ряд и многое
другое.
Возможность производить практически любые
операции с действительными и комплексными числами, большой набор векторных и
матричных операций делают MathCad
незаменимым инструментом в руках студентов всех специальностей при выполнении
контрольных, курсовых и дипломных проектов.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
mathcad интерполяция матрица число
1. Б.В.Соболь, Б.Ч.Месхи, И.М.Пешхоев. Практикум
по вычислительной математике. - Ростов-на-Дону: Феникс, 2008;
. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков.
Численные методы. Изд-во "Лаборатория базовых знаний". 2003;
. Г.С. Шевцов, О.Г. Крюкова, Б.И. Мызникова.
Финансы и статистика. Москва. Издательский дом ИНФРА-М, 2008;
. Ю.Е. Воскобойников. Регрессионный анализ
данных в пакете Mathcad.Москва.
Издательство «Лань», 2011;
. С.В. Поршнев. Компьютерное моделирование
физических процессов с использованием пакета MathCad.
Москва. Горячая линия - Телеком, 2002;
. Ю.В.Васильков, Н.Н. Василькова. Компьютерные
технологии вычислений а математическом моделировании. Москва. Финансы и
статистика, 2002.
. Л.И.Турчак. Основы численных методов: Учеб.
Пособие. - М.: Наука, 1987;
8.
О.Б.Полищук. Практикум по численным методам. Часть 1: Учебное пособие для
студентов физико - математических факультетов педагогических вузов. - Оренбург:
Издательство ОГПУ, 2004.