Основные математические модели твердого тела
Содержание
1.
Основные математические модели твердого тела и их соответствие свойствам
реальных материалов
.
Вывод условия равновесия для осесимметричного напряженного состояния
.
Задача №14
.
Задача №41
.
Анализ операции осадки полосы
Список
используемой литературы
1. Основные математические модели
твердого тела и их соответствие свойствам реальных материалов
Общепринятая математическая модель твердого тела
имеет следующие свойства: непрерывность (сплошность), т.е. предполагается, что
вещество равномерно и непрерывно заполняет весь объем тела; при этом
микропустоты и тем более межатомные пространства атомной решетки во внимание не
принимаются; однородность, т.е. допускается, что во всех точках тело обладает
одинаковыми механическими и химическими свойствами; изотропность, т. е.
предполагается, что свойства твердого тела одинаковы во всех направлениях;
независимость напряжения текучести от гидростатического давления, по крайней
мере, в пределах обычно применяемых для обработки металла напряжений. Следует отметить,
что указанные свойства в равной степени присущи и математической модели
идеальных жидкостей.
Поведение твердого тела в процессе
деформирования определяется диаграммой, выражающей взаимосвязь между
напряжением и деформацией. В зависимости от вида диаграммы могут быть
определены следующие модели.
Так, идеальным жестким называют твердое тело, у
которого независимо от приложенных сил, вызывающих напряженное состояние тела,
находящегося в равновесии, расстояние между любой парой точек в процессе нагружения
остается постоянным. Математическая модель, построенная в координатах
напряжение- деформация, представляет собой прямую линию, совпадающую с осью
ординат.
Идеальным упругим называют твердое тело,
допускающее при наложении напряженного состояния неограниченную величину
упругой (обратимой) деформации при линейном соотношении между напряжением и
деформацией. В координатной системе деформация в - напряжение а модель
идеального упругого тела представлена на.
Математическую модель идеального упругого тела
используют при построении теории упругости и ее приложения - сопротивления
материалов, методы которых применяют для расчета упругонапряженных деталей
машин, конструкций строительной механики, зданий и сооружений. Идеальным
жесткопластическим называют твердое тело, которое ведет себя как жесткое тело
(т. е. не деформируется) до тех пор, пока интенсивность напряжений, приложенных
к телу, не достигнет некоторого определенного значения, равного напряжению
текучести as. После этого тело начинает неограниченно деформироваться
пластически (необратимо) при постоянном напряжении, т. е. деформироваться без
упрочнения.
Развитие технологии холодной обработки металлов
давлением потребовало решения задач для определения усилий деформирования и
напряженно-деформированного состояния материалов, упрочняющихся в процессе
деформирования.
В связи с этим возникла необходимость в
математической модели жесткопластического тела, способного упрочняться. При
этом сначала, пока напряжения не достигли некоторого значения, тело ведет себя как
жесткое, а затем деформируется пластически при непрерывном нарастании
напряжений.
Увеличение напряжений для продолжения деформации
может происходить как по линейному, так и по нелинейному законам.
В связи с созданием крупных и уникальных машин и
агрегатов таких, как корпуса атомных реакторов и роторы сверхмощных турбин и
генераторов, возникла необходимость исследования упругопластических деформаций,
поскольку при высоких средних напряжениях в местах концентрации напряжений
(отверстия, резкие переходы сечений, галтели) наряду с упругими могут иметь
место и пластические деформации.
Соответствие математических моделей твердого
тела свойствам реальных машиностроительных материалов
Поликристаллическая структура образуется уже при
первичном затвердевании жидкого металла во время заливки его в изложницу или
литейную форму. Литой металл, затвердевший в изложницах или литейной форме, в
обычных производственных условиях содержит некоторое количество макро пустот в
виде газовых пузырей и неметаллических включений. В под прибыльной части
отливки располагается усадочная рыхлость, образовавшаяся в результате выделения
газов в процессе затвердевания. Учитывая сказанное, можно сделать вывод, что
литой металл не обладает свойством непрерывности (сплошности).
Однородность. Технические металлы -
многокомпонентные сплавы. Чистейшие металлы, содержащие не более одного атома
примеси на 106 и даже 107 атомов основного металла, применяемые в
радиоэлектронной, радиолокационной, космической технике, выплавляют
специальными методами - зонной плавкой, применением сверхвысоких температур и
т.п. (здесь не рассмотрены). В дальнейшем изложении, применяя термин
технический металл или просто металл, мы будем иметь в виду сплав, содержащий
то или иное количество растворимых и нерастворимых примесей.
Если расплав металла можно считать однородным по
химическому составу, т. е. полагать, что примеси в нем расположены равномерно,
то в процессе кристаллизации однородность металла нарушается. Это происходит в
основном по двум причинам: 1) вследствие характера затвердевания жидкого
металла, имеющего значительно более высокую температуру, чем изложница или
литейная форма; 2) вследствие того, что составляющие расплав химические
вещества (элементы) имеют различную температуру кристаллизации.
Раньше всего затвердевают слои расплава,
непосредственно соприкоснувшиеся со стенками изложницы (или литейной формы).
Процесс кристаллизации первоначально идет с весьма высокой скоростью, в связи с
чем появляются мелкие кристаллиты с осями, перпендикулярными стенкам изложницы.
В результате образуется твердая корка металла - рубашка из мелких кристаллитов.
После этого скорость кристаллизации уменьшается, в связи с чем увеличиваются
размеры вновь образующихся кристаллитов.
Направление отвода теплоты остается прежним - от
периферии к центру; растут шестоватые кристаллиты с осями, перпендикулярными к
оси изложницы, затем постепенно образуются дендриты с осями, несколько
наклоненными к центру слитка.
В центральной зоне слитка оси кристаллитов имеют
произвольную ориентировку, так как поверхность отвода теплоты от вновь
образующихся кристаллитов весьма произвольная.
В связи с тем, что в расплаве присутствуют
компоненты, имеющие различную температуру затвердевания, в первую очередь
кристаллизуются наиболее тугоплавкие составляющие расплава. После образования
металлической корки-рубашки на поверхности слитка и дендритов из тугоплавких
составляющих снижается тепловой градиент между стенками изложницы и расплавом.
Скорость кристаллизации снижается, и менее тугоплавкие составляющие расплава
затвердевают, заполняя пространство между ветвями дендритов. Наконец, примеси
как металлические, так й неметаллические, имеющие наиболее низкую температуру
плавления, располагаются в под прибыльной части отливки.
Таким образом, при затвердевании расплава с
равномерным распределением компонентов образуется твердое тело - металлический
слиток, химически и структурно неоднородный. Кристаллиты - зерна, расположенные
в разных зонах затвердевания, и химически, и структурно неоднородны. Иначе
говоря, слиток или фасонная отливка условию однородности металла не
удовлетворяют.
Изотропность. Металлический расплав изотропен. В
процессе затвердевания расплава в массе жидкого металла возникает бесчисленное
количество центров кристаллизации, вокруг каждого из которых атомы
располагаются упорядоченно, образуя кристаллическую решетку. Процесс
кристаллизации заканчивается, когда границы растущих кристаллитов соприкоснутся
между собой, а между атомами межкристаллического вещества и атомами соседних
кристаллитов возникнут силы взаимодействия. Все это обусловливает неправильную
форму кристаллитов - зерен металла.
Кристаллиты в объеме реального металла
анизотропны. Эта анизотропия усугубляется наличием в реальном металле
растворимых и нерастворимых примесей, распределенных неравномерно по объему.
Таким образом, реальный металл,
кристаллизующийся из расплава, в литом состоянии не обладает свойствами
однородности и изотропности. Следовательно, применение к исследованию его
напряженно деформированного состояния методов и уравнений механики
деформируемого твердого тела не является строгим.
Применяя специальные виды переплава, такие,
например, как зонный, электрошлаковый, электровакуумный с использованием
специальных кристаллизаторов (в частности металлических) с программированным зонным
подогревом, можно существенно повысить сплошность, однородность и изотропность
литого металла. Методами дегазации удается получить металл практически
сплошным, а используя подогреваемые по определенной программе кристаллизаторы,
возможно получить металл высокой химической однородности. Добиться же
абсолютной изотропности литого металла практически чрезвычайно трудно (если не
сказать -невозможно). Подавляющее большинство поковок и проката производится из
слитков, полученных выплавкой из мартеновских печей или электропечей методами
обычной плавки, а также вакуумированных в изложнице.
Обычно (за исключением некоторых особых случаев)
фасонные отливки обработке давлением не подвергаются. Структура металла
отливок, прошедших обработку давлением, претерпевает существенные изменения.
Деформированный металл. В процессе первичной
горячей обработки давлением на прессах и молотах слитки биллетируют, затем
удаляют (отрубают) прибыльную и донную части. Удаляемая прибыльная часть имеет
большое количество пустот, вызванных газовыми пузырями, и неоднородный
химический состав ввиду сосредоточения в ней ликвационной и сегрегационной зон.
Донная часть слитка обычно засорена примесями и также неоднородна по
химическому составу в результате насыщения наиболее тугоплавкими составляющими
расплава, мгновенно затвердевающими в момент соприкосновения горячего металла с
более холодным днищем изложницы. После удаления указанных частей слитка уже
существенно повышаются сплошность и химическая однородность металла,
используемого при последующей обработке давлением.
При первичной ковке происходит повышение
сплошности (непрерывности) металла в результате заварки мелких газовых пузырей
и залечивания трещин и надрывов в теле слитка. На последующих этапах ковки в
зависимости от назначения поковки заготовку или осаживают, или протягивают, или
куют с применением специального инструмента. Во всех случаях, и в особенности
при всесторонней многократной ковке (например, при изготовлении штамповых
кубиков), происходит активное дробление первичной дендритной структуры слитка,
крупных зерен и образование мелкозернистой структуры с беспорядочной
ориентировкой главных осей кристаллитов. После соответствующей термической
обработки (гомогенизации) всесторонне прокованный металл приобретает
равноосную, мелкозернистую структуру и одинаковые механические характеристики
(пределы прочности и текучести, относительное удлинение и сужение) независимо
от направления.
Это означает, что число главных осей
кристаллитов, ориентированных в каком-либо одном направлении, равно числу
главных осей, ориентированных в любом другом направлении. Весь объем металла
состоит из мелких однородных по своему составу равноосных кристаллитов - зерен.
И хотя каждый кристаллит анизотропен, поликристалл ведет себя как однородное
изотропное тело. Таким образом, хорошо прокованный и гомогенизированный металл
является квазиоднородным и квазиизотропным.
Математическая модель непрерывного однородного и
изотропного твердого тела соответствует свойствам реального хорошо прокованного
гомогенизированного металла, нагретого выше температуры рекристаллизации (что
обеспечивает отсутствие упрочнения), и форм изменяемого в изотермических
условиях и с постоянной скоростью деформации.
2. Вывод условия равновесия для
осесимметричного напряженного состояния
Одним из частных случаев объемного напряженного
состояния, весьма часто встречающимся при обработке металлов давлением,
является осесимметричное напряженное состояние.
Под этим видом напряженного состояния
подразумевается напряженное состояние тела вращения, к поверхности или части
поверхности которого приложены распределенные нагрузки, расположенные
симметрично относительно его оси и одинаковые во всех меридиональных сечениях
(рис.1). Примерами могут служить осадка цилиндрической заготовки, ее прошивка,
выдавливание (прессование), волочение и др.
При рассмотрении осесиммстричного напряженного
состояния весьма удобно пользоваться взамен декартовых цилиндрическими
координатами, в которых положение любой точки А определяется радиусом-вектором ρ,
полярным
углом β,
отсчитываемым от оси ρ (x), и
аппликатой z, как представлено на рис.2, где а α
- проекция точки A на плоскость, перпендикулярную к оси z,
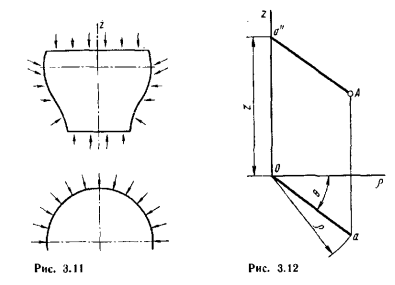
Рис. 1 Рис.
2
проходящую через точку О. Обозначения напряжений
в цилиндрических координатах и форма элемента показаны на рис.3. Тензор
напряжений в цилиндрических координатах запишется так:
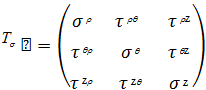
Напряжение называют
радиальным,
называют
радиальным,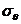 -
тангенциальным, a
-
тангенциальным, a  - осевым.
- осевым.
При осесимметричном напряженном
состоянии компоненты напряжений не зависят от координаты θ, и, следовательно,
все производные по этой координате в дифференциальных уравнениях равновесия
обратятся в нуль. Кроме того, в меридиональных плоскостях (плоскостях,
проходящих через ось z, т. е. плоскостях θ) не могут возникнуть
касательные напряжения вследствие симметричности тела и симметрии внешней
нагрузки.
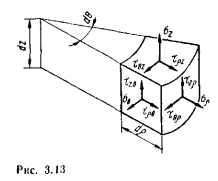
Рис. 3
Поэтому с учетом закона парности касательных
напряжений:

Следовательно, напряжение 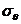 всегда
будет главным, т. е
всегда
будет главным, т. е 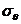 =
= , а ось ρ может иметь
любое направление в плоскости z (т. е. в плоскости, нормальной к оси z).
, а ось ρ может иметь
любое направление в плоскости z (т. е. в плоскости, нормальной к оси z).
Таким образом, компоненты напряжений
при осесимметричном напряжении можно записать так:
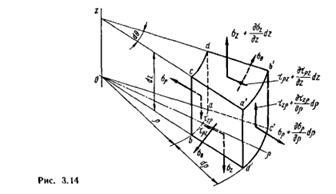
Рис. 4

Всего будет три нормальных и два
равных между собой касательных напряжения.
Применяя тот же метод, который был
использован при рассмотрении объемного напряженного состояния в декартовых
координатах, выведем дифференциальные уравнения равновесия в цилиндрических
координатах для осесимметричного напряженного состояния.
Действующие напряжения показаны на
рис.5. Ось ρ, как
сказано ранее, можно провести в любом направлении на плоскости z. Для удобства
вычисления на рис.5. эта ось проведена так, что плоскость ρz является
плоскостью симметрии выделенного элементарного объема.
Площади элементарных площадок:
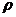 = пл. abcd =ρdθdz;
= пл. abcd =ρdθdz; = пл.
a’b’c’d’ = (ρ+dρ)dθdz;
= пл.
a’b’c’d’ = (ρ+dρ)dθdz;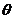 = пл. a’d’bc
= dρdz;
= пл. a’d’bc
= dρdz; = пл. a’cdb’
= пл. ac’d’b = ρ dθdρ.
= пл. a’cdb’
= пл. ac’d’b = ρ dθdρ.
Запишем условие равновесия,
проецируя все действующие на элемент силы на оси ρ и z,
принимая 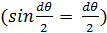 :
:
σ ρdθdz + (σ
ρdθdz + (σ +
+ 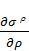 dρ)(ρ + dρ)dθdz - σ
dρ)(ρ + dρ)dθdz - σ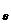 dθdρdz - τ
dθdρdz - τ dθdρ + (τ
dθdρ + (τ +
+ 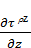 dz)ρdθdρ = 0;
dz)ρdθdρ = 0;
τ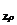 ρdθdz + (τ
ρdθdz + (τ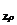 +
+ 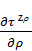 dρ)(ρ + dρ)dθdz - σ
dρ)(ρ + dρ)dθdz - σ ρdθdρ + (σ
ρdθdρ + (σ +
+  dz)ρdθdρ = 0
dz)ρdθdρ = 0
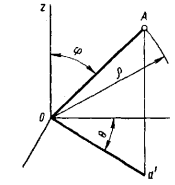
Рис. 5
После алгебраических преобразований и
сокращений, пренебрегая бесконечно малыми высших порядков, получим:
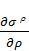 +
+ 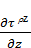 +
+
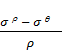 =
0;
=
0;
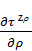 +
+  +
+
 =
0.
=
0.
При решении некоторых осесимметричных задач в
дальнейшем придется встретиться кроме цилиндрических координат со сферическими.
В этой системе (рис.5) положение точки определяется радиусом вектором ρ
и двумя углами θ и φ,
определяющими его положение в пространстве. Угол φ
отсчитывается от оси z (аналогичен географической широте), а угол θ
отсчитывается от некоторой оси в плоскости, нормальной к оси z и проходящей
через центр О системы (аналогичен географической долготе). Обозначения
напряжений в сферических координатах получим, заменив индекс z в обозначениях,
данных для цилиндрической системы, индексом φ.
При осесимметричном напряженном
состоянии напряжения не зависят от координаты θ, а
касательные напряжения, содержащие в индексе эту координату, т. е. τ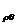 = τ
= τ и τ
и τ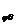 = τ
= τ равны нулю.
равны нулю.
Дифференциальные уравнения
равновесия для осесимметричного напряженного состояния в сферических
координатах приведем без вывода:
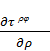 +
+ 
 +
+ 
 .
.
3. Задача №14
В некоторой точке тела задан тензор
напряжений:
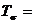
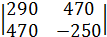 , МПа.
, МПа.
Найти величину напряжений на элементарных
площадках разрезов разного направления, которые можно провести через эту точку.
Направляющие косинусы для этих площадок а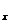 и a
и a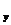 равны, соответственно для N
равны, соответственно для N =(1; 0); N
=(1; 0); N =(1; 0); N
=(1; 0); N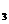 =(0,6; 0,9).
=(0,6; 0,9).
Решение:= 1 2) Ax = 0 3) Ax = 0,6= 0
Ay = 1 Ay = 0,8

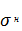 = Sxax + Syay
= Sxax + Syay
σ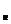 = σxax + σyay2 + 2τxyaxay
= σxax + σyay2 + 2τxyaxay
σ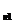 = 290×12 + (- 250×
02) +
2×470×1×0 = 290
= 290×12 + (- 250×
02) +
2×470×1×0 = 290
σ = 290×02 + (- 250×
12) +
2×470×0×1 = -250
= 290×02 + (- 250×
12) +
2×470×0×1 = -250
σ = 290×0,62 + (- 250×
0,82)
+ 2×470×0,6×0,8 = 395,6
= 290×0,62 + (- 250×
0,82)
+ 2×470×0,6×0,8 = 395,6
Полное напряжение= σ12a12 + σ22a22= 2902 ×12 + (-2502×02) = 84100;
S1=290= 2902
×02
+ (-2502×12) = 62500;
S2=250= 2902
×0,62
+ (-2502×0,82) = 84100;
S3=265,1
Нормальное напряжение
σ = σ1a12 + σ2a22
= σ1a12 + σ2a22
σн1 = 290×12 + (-250×02) = 290
σн2 = 290×02 + (-250×12) = -250
σн3 = 290×0,62 + (-250×0,82) =
-55,6
Касательное напряжение
τ = σ12а12 + σ22а22 - (σ1а2 + σ2а22)
= σ12а12 + σ22а22 - (σ1а2 + σ2а22)
τ1 2= 2902×12 + (-2502×02) - (290×12 + (-250×02)) = 84390;
τ1
= 290,5
τ2 2= 2902×02 + (-2502×12) - (290×02 + (-250×12)) = 62750;
τ2
= 250,5
τ3 2= 2902×0,62 + (-2502×0,82) -
(290×0,62 +
(-250×0,82))
= 70331,6;
τ3 = 265.2
4. Задача №41
Напряженное состояние точки деформируемого
тела определяется тензором напряжений:
Тσ =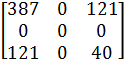 , МПа.
, МПа.
Определить вид деформации: упругая
или пластическая, механическую схему деформации. Максимально возможная величина
главного касательного напряжения при пластической деформации равно 212МПа.
Решение:
σ * = 2K = 2×212 = 424 Мпа
* = 2K = 2×212 = 424 Мпа
 ×σ
×σ = σ
= σ *; σ
*; σ = σ
= σ */
*/  ; σ
; σ = 424/1,154
= 367,4;
= 424/1,154
= 367,4;
σ
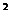 + σ
+ σ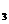
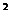 - σ
- σ σ
σ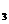 = σ
= σ
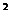 ;
;
3872 + 402 - 387×40
= 367,42;
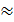 134982,8
134982,8
Исходя из пункта 3, данная деформация является
пластической.
5. Анализ операции осадки полосы
Анализ данного процесса производится с
использованием приближенных уравнений равновесия и условия пластичности.
Для точек контактной поверхности имеется
приближенное уравнение равновесия
 . (1)
. (1)
Принимаем tk = msz, где m - коэффициент трения.
После интегрирования получаем
 . (2)
. (2)
Находим постоянную интегрирования С.
При 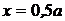 величина
величина  .
.
Тогда 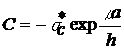 . (3)
. (3)
Окончательно имеем:
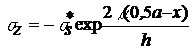 . (4)
. (4)
Эпюра напряжений 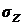 по
уравнению (4) представлена на рис.1 кривой
по
уравнению (4) представлена на рис.1 кривой 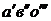 . Эпюра касательных напряжений
. Эпюра касательных напряжений 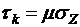 - кривая
dem. Эпюры вычислены при
- кривая
dem. Эпюры вычислены при 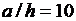 и
и 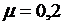 .
.
Напряжения 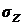 и
и  увеличиваются
к оси симметрии по мере удаления от края полосы. В точке b при
увеличиваются
к оси симметрии по мере удаления от края полосы. В точке b при 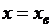 ,
касательное напряжение
,
касательное напряжение 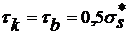 , а
нормальное напряжение
, а
нормальное напряжение  .
.
При пластической деформации
абсолютная величина касательного напряжения не может быть больше  , т. е.
, т. е. 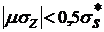 или
или 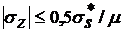 . Необходимо
соблюсти неравенство
. Необходимо
соблюсти неравенство
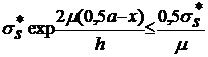 . (5)
. (5)
Решение неравенства (5) относительно
х дает
 . (6)
. (6)
Обозначим ln(2m) / 2m = Y.
Тогда неравенство (6) перепишется
³ 0,5a - Yh.
(7)
Значения Y, в зависимости от m, представлены в табл.1.
Таблица 1
|
m
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,5
|
|
Y
|
23,0
|
4,02
|
2,30
|
1,39
|
0,85
|
0,51
|
0,28
|
0,12
|
0
|
Расстояние точки b от края контактной
поверхности
(0,5а - хв) = Yh. (8)
Чем больше m, тем на меньшем участке
поверхности действительно выражение tk
= msS, и оно
достигает предельного значения 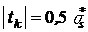 . При m = 0,5 касательное напряжение получает это
предельное на краю заготовки в точке
. При m = 0,5 касательное напряжение получает это
предельное на краю заготовки в точке 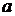 , т. е. при хв = ха = 0,5а.
, т. е. при хв = ха = 0,5а.
В общем случае в точке  , tk = const = - 0,5
, tk = const = - 0,5 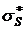 .
.
После подстановки этого выражения в
уравнение (2.1) и интегрирования имеем
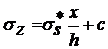 . (9)
. (9)
При x = xв, sz = sв. Следовательно,
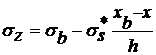 . (10)
. (10)
При tk= const нормальные напряжения изменяются по
линейному закону (линия 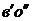 ,
касательная в точке
,
касательная в точке 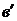 кривой
кривой 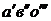 ). Так как tк имеют разные знаки справа и
слева от оси Z, при х = 0 tk
переходит через 0. При tk = 0 и х =
0 имеем
). Так как tк имеют разные знаки справа и
слева от оси Z, при х = 0 tk
переходит через 0. При tk = 0 и х =
0 имеем
 (11)
(11)
Функция sz имеет экстремум. Обе ветви sz плавно перейдут друг в
друга.
На участке ОС
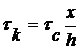 , (12)
, (12)
где tс = - 0,5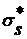 - касательное напряжение в точке х
= хc =
- касательное напряжение в точке х
= хc =  .
.
Нормальное напряжение sz находим из уравнения
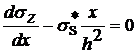 . (13)
. (13)
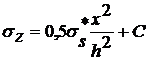 . (14)
. (14)
При x =xc = h, sz = sс. Таким образом
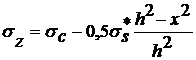 . (15)
. (15)
Нормальное напряжение sz изменяется от sz = sс при хc = h до
sz
= sо = sz = sс - 0,5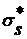
при х = 0 (кривая С¢О¢).
При х = хc = h получим из (15)
 . (16)
. (16)
Если не учитывать падения
касательных напряжений, то при х = 0
 . (17)
. (17)
Сравнивая sо¢¢ = sо = sс, можно установить
sо¢¢ - sо = sо - sс = - 0,5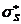 . (18)
. (18)
тело равновесие
напряжение контакт
Таким образом, при осадке полосы
эпюра напряжений разделяется в общем случае на три зоны (А, Б, В):
Участок А (зона скольжения)
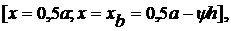
 ,
,
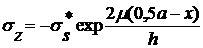 , (19)
, (19)
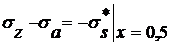 ,
,
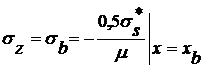 .
.
Участок Б (зона торможения)
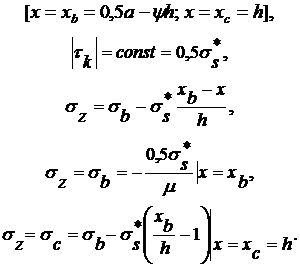 (20)
(20)
Участок В (зона прилипания)
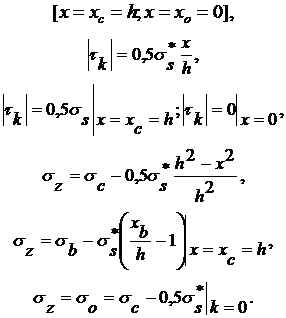 (21)
(21)
Анализ соотношений (19)-(21) дает следующие
выводы по распределению напряжений в зоне контакта при осадке полосы
неограниченной длины:
) при 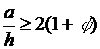 и
и 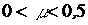 эпюра напряжений состоит из трех
участков А, Б, В (рис. 1). Удельное усилие деформирования находится по формуле:
эпюра напряжений состоит из трех
участков А, Б, В (рис. 1). Удельное усилие деформирования находится по формуле:
 ; (22)
; (22)
) при 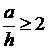 и
и  эпюра напряжений состоит из двух
участков - Б и В (рис. 2).
эпюра напряжений состоит из двух
участков - Б и В (рис. 2).
Удельное усилие деформирования при
этом равно
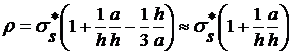 ; (23)
; (23)
) при 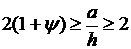 и
и 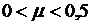 эпюра напряжений состоит из двух
участков - А, В (рис. 3). Удельное усилие находим из соотношения
эпюра напряжений состоит из двух
участков - А, В (рис. 3). Удельное усилие находим из соотношения
 ; (24)
; (24)
) при 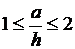 при
при  эпюра напряжений состоит из одного
участка - В (рис. 3). Удельное усилие равно
эпюра напряжений состоит из одного
участка - В (рис. 3). Удельное усилие равно
 ; (25)
; (25)
) при 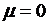 и любом
и любом  существует
один участок:
существует
один участок: 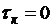 и
и 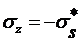 , т. е.
, т. е. 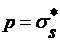 .
.
Влияние роста коэффициента трения 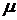 в пределах
малых значений. При
в пределах
малых значений. При 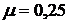 кривые
кривые 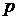 для разных
для разных 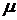 стремятся к
прямолинейной форме и лежат близко к кривой для
стремятся к
прямолинейной форме и лежат близко к кривой для  .
.
Для горячей деформации, когда  , расчётной
формулой для определения удельного усилия деформирования является следующая:
, расчётной
формулой для определения удельного усилия деформирования является следующая:
 . (26)
. (26)
Выражения напряжений sZ в зависимости от координат х
будут те же самые, что и для задачи п. 2.1, но с разницей, что постоянную 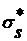 необходимо
заменить на ss из
соотношения
необходимо
заменить на ss из
соотношения 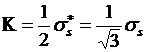 , а размер а
для цилиндра заменить на размер d - диаметр цилиндра.
, а размер а
для цилиндра заменить на размер d - диаметр цилиндра.
Следовательно, как и в п. 1 имеем 5
вариантов распределения контактных напряжений:
) при 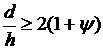 , 0 < m
< 0,5 эпюра
напряжений состоит из трех участков А, Б, В (рис.1). Удельное усилие
деформирования находим по формуле:
, 0 < m
< 0,5 эпюра
напряжений состоит из трех участков А, Б, В (рис.1). Удельное усилие
деформирования находим по формуле:
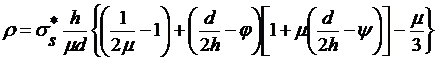 , (27)
, (27)
) при  и
и 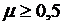 эпюра напряжений состоит из двух участков
- Б и В(рис.2). Удельное усилие деформирования при этом равно:
эпюра напряжений состоит из двух участков
- Б и В(рис.2). Удельное усилие деформирования при этом равно:
 ; (28)
; (28)
) при 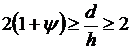 и
и 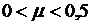 эпюра напряжений состоит из двух
участков - А, В (рис.3). Удельное усилие находим из соотношения:
эпюра напряжений состоит из двух
участков - А, В (рис.3). Удельное усилие находим из соотношения:
Удельное усилие равно:
) при 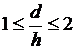 и
и  эпюра напряжений состоит из одного
участка - В (рис.4). удельное усилие равно:
эпюра напряжений состоит из одного
участка - В (рис.4). удельное усилие равно:
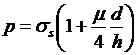 ; (30)
; (30)
) при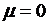 и любом
и любом 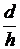 , а также
при
, а также
при 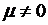 и любом
и любом 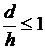 существует
один участок:
существует
один участок:  и
и 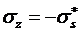 , т.е.
, т.е.
 . (31)
. (31)
Для горячей осадки, когда
коэффициент трения большой и стремится к 0,5, удельное давление можно
рассчитать по приближенной формуле:
 . (32)
. (32)
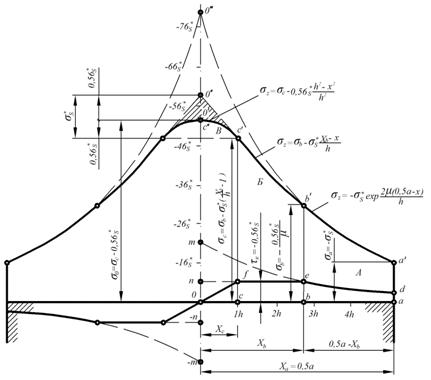
Рис. 6 - Эпюра напряжений (зоны А,
Б, В)
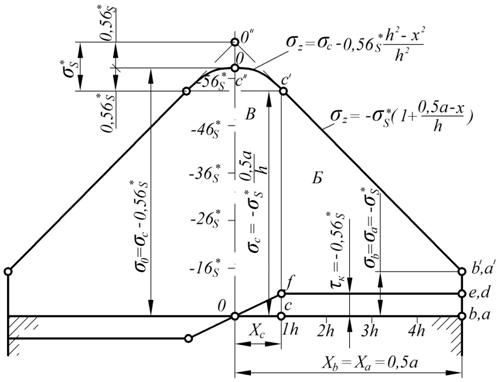
Рис. 7 - Эпюра напряжений (зоны Б, В)
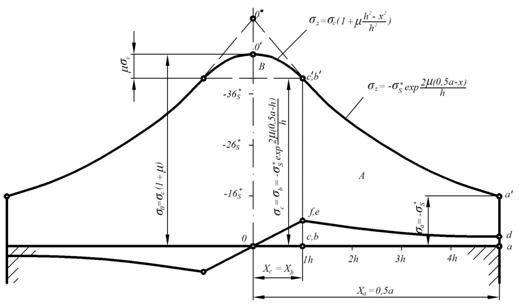
Рис. 8 - Эпюра напряжений (зоны А, В)

Рис. 9 - Эпюра напряжений (зона В)
Список использованной литературы
1.
Сторожев М.В. и Попов Е.А. «Теория обработки материалов давлением»
Машиностроение, 1978 г.
.
Смирнов В.С. «Сборник задач по обработке материалов давлением» Металлургия,
1973 г.
.
Северденко В.П. «Лабораторный практикум по теории машин и технологий обработки
материалов давлением» Минск, Вышэйшая школа, 1975 г.
.
Громов Н.П. «Теория обработки материалов давлением». Металлургия, Москва, 1978
г.