Розфарбування графів як математична модель прикладних задач
КУРСОВА РОБОТА
з інформатики
на тему: Розфарбування графів як
математична модель прикладних задач
рік
Зміст
Вступ
Розділ 1. Задача розфарбування графів: постановка задачі
1.1 Історія виникнення задачі
1.2 Деякі відомості з теорії графів
1.3 Математична модель задачі
2. Задача розфарбування графів як типовий приклад задачі np класу
2.1 Алгоритмічна складність задачі
2.2 Методи отримання точних розв’язків задачі розфарбування графів
2.2.1 Алгоритм мурашиної колонії для розфарбування графів
2.2.2 Алгоритм розфарбування графу методом неявного перебору
3. Комп’ютерна реалізація розв’язку задачі розфарбування графів
3.1 Аналіз типових задач та існуючих програмних продуктів
3.2 Опис програмного продукту
3.3 Машинна реалізація продукту
Висновки
Список використаних джерел
Додатки
Вступ
У даній курсовій роботі розглядаються прикладні
задачі, які зводяться в теорії графів до оптимального розфарбування планарних
графів та знаходження їх хроматичного числа.
Метою роботи є систематизувати та поглибити
знання з дискретної математики, теорії алгоритмів, зокрема застосування теорії
графів у дослідженні прикладних задач, пов’язаних із розфарбуванням графів;
вивчити можливості інформаційних технологій у полегшенні процесу цього
дослідження.
Для досягнення поставленої мети потрібно:
– проаналізувати та систематизувати
теоретичні та практичні досягнення в дослідженні задачі розфарбування графів;
– дослідити типи прикладних задач, що
зводяться до задачі розфарбування графів та існуючи методи їх розв’язання;
– проаналізувати можливості автоматизації
такого роду задач.
Об’єкт дослідження - теорія графів та її
застосування у дослідженні прикладних задач.
Предмет дослідження - методи розв’язання
задач NP класу на прикладі задачі розфарбування графів.
Курсова робота містить Вступ, основну частину
поділену на 3 розділи, Висновки, список використаних джерел та Додатки. Перший
розділ задача розфарбування графів містить: історію виникнення задачі, деякі
відомості з теорії графів та математичну модель задачі.
Другий розділ має назву: задача розфарбування
графів, як типовий приклад задачі NP класу, поділений на два підрозділи,
останній з яких в свою чергу на два пункти, де більш детально описано
алгоритмічну складність задачі та деякі найпоширеніші алгоритми розв'язування.
розфарбування граф програмний продукт
Третій розділ присвячений аналізу типових задач
та існуючих програмних продуктів, машинну реалізацію конкретно наведеного
прикладу.
Розділ
1. Задача розфарбування графів: постановка задачі
1.1
Історія виникнення задачі
В математиці теорема про чотири кольори говорить,
що будь-яку розташовану на сфері карту можна розмалювати чотирма кольорами так,
щоб дві любі області, які мають спільні зони границі, були розмальовані в різні
кольори. Ця теорема була сформульована Ф. Гутрі в 1652 р. але довести її не
могли довгий час.
Теорема Хівуда (полягає в тому, що будь-який граф
можна розмалювати 5 різними кольорами) була доведена в 1890 р. Понизити верхню
планку для хроматичного числа будь-якого планарного графа з 5 до 4, тобто
підтвердити гіпотезу про чотири кольори не вдавалося майже 90 років. У 1969 р.
задача була зведена до розгляду кінцевого, але досить великого числа конкретних
випадків, пізніше їх число було скорочене до "всього лиш" 1482.
Нарешті в 1976 р. К. Аппель і В. Хейкен за допомогою комп’ютерної програми
розібрали всі ці конкретні випадки (витративши на це приблизно 2000 годин
роботи потужного на той час комп’ютера). В результаті вони довели наступну
теорему.
Теорема про чотири кольори.
Хроматичне число будь-якого планарного графа не
перевищує 4.
Доведення цієї теорем стало першим випадком
"комп’ютерного" вирішення важкої і давно суто математичної проблеми.
.2
Деякі відомості з теорії графів
Граф - це
сукупність об'єктів із зв'язками між ними.
Об’єкти - вершини графу, а зв’язки
- дуги та ребра графу. Для різних областей використання видів графів можуть
відрізнятися орієнтованістю, обмеженнями на кількість зв’язків і додатковими
даними про вершини або ребра. Велика кількість структур, які мають практичну
цінність в математиці та інформатиці, можуть бути представленні графами.
Наприклад, будову Вікіпедії можна змоделювати за допомого орієнтованого графа,
в якому статті це вершини, а посилання на інші статті це дуги (орієнтовані
ребра).
граф G - це впорядкована пара G: =
(V,E), для якої виконуються наступні умови:
V - множина
<#"870169.files/image001.gif">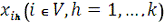 де
де 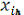
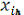 =1 якщо вершині і призначений колір h
=1 якщо вершині і призначений колір h 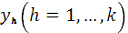
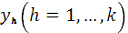 , де
, де 
 =1, якщо колір h використаний в розфарбуванні
=1, якщо колір h використаний в розфарбуванні

 (1)
(1)
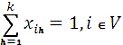
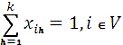 (2)
(2)
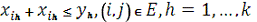
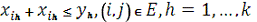 (3)
(3)
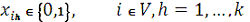
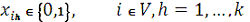 (4)
(4)
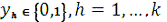
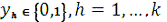 (5)
(5)
Функція (1) мінімізує кількість кольорів, використаних в
розфарбуванні. Обмеження (2) вимагають, щоб кожній вершині був призначений
рівно один колір. Обмеження (3) вимагають, щоб суміжним вершинам були
призначені різні кольори. Нарешті, обмеження (4) і (5) задають можливі значення
змінних - 0 або 1.
2. Задача розфарбування графів як
типовий приклад задачі np класу
2.1
Алгоритмічна складність задачі
Складність алгоритмів вимірюється за необхідними
ресурсами, в основному, це тривалість обчислень або необхідний обсяг пам'яті.
P-задача - це задача, для розв'язку якої існує
поліноміальний алгоритм.
NP-задачею називається задача, яка може бути
розв'язана на детермінованій машині Тьюринга за поліноміальний час O (nm),
де n - розмір задачі.
Якщо ж обмежитися детермінованими алгоритмами, то
для вирішення будь-якої NP-задачі можна використовувати схему перебору з
поверненням або подібні до неї перебірні схеми. Подібні алгоритми є
експоненційними по своїй суті, і задачі, які вимагають застосування таких
алгоритмів, відносяться до класу важко вирішуваних. Втім, це не виключає
існування поліноміальних алгоритмів, і для ряду задач, які мають характер
пошуку на дереві, такі алгоритми дійсно були знайдені. Позначимо через P клас
P-задач, а через NP - клас NP-задач Ясно, що P - підмножина NP. Але питання про
те, чи є це включення строгим, залишається відкритим.
Розфарбування графа мінімальною кількістю
кольорів є комбінаторною задачею, яку відносять до класу NP-складних задач. Ця
задача може бути сформульоване як рекурентне завдання розфарбування графа
мінімальною кількістю кольорів. Спочатку задається певне число кольорів,
(обґрунтоване з точки зору можливості розфарбування, тобто з відповідним
хроматичним числом), а пізніше виконується алгоритм з подальшим зменшенням їх
кількості.
Проблемами цієї задачі є швидкість знаходження
розв’язку, а також точність розв’язання.
Результати тестувань відомого генетичного
алгоритму на складних графах (700-1000) вершин показали, що використання Tabu
Search (метаевристика - назва для стохастичних алгоритмів які використовують
випадковий пошук, або пошук перебором, шлях вирішення цих задач) та певного
кодування істотно покращують виконання генетичного алгоритму розфарбування
графа.
До задач класу складності NP також належать:
· Розв'язність
логічного виразу.;
· Три-кольорове
розфарбування графу.;
· Побудова кліки з 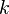 вершин на неорієнтованому
графі;
вершин на неорієнтованому
графі;
· Покриття множин;
· Розбиття множин;
· Існування
гамільтонового циклу на неорієнтованому графі;
· Задача пакування рюкзака
<#"870169.files/image011.gif">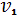 ,,…,. Для виконання цих робіт необхідні механізми
,,…,. Для виконання цих робіт необхідні механізми 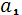
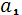 ,,…,. Використання механізмів для кожної з робіт визначається
наступною таблицею:
,,…,. Використання механізмів для кожної з робіт визначається
наступною таблицею:
|
Механізм
|
Робота
|
|
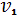
|

|
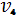
|

|

|
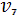
|
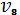
|
|
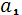
|
+
|
|
+
|
|
|
|
+
|
+
|
|
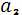
|
|
+
|
|
+
|
|
|
|
|
|

|
|
|
+
|
|
|
+
|
+
|
|
|
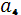
|
+
|
+
|
|
+
|
+
|
|
|
|
|
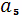
|
|
|
+
|
|
+
|
|
|
+
|
|
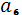
|
|
|
|
|
+
|
+
|
|
+
|
Жоден із механізмів не може бути використаний
одночасно на двох роботах. Виконання кожної роботи займає 1 годину. Як
розподілити механізми так, щоб сумарний час виконання всіх робіт був
мінімальним і який цей час?
Рішення. Розглянемо граф G, вершинами якого є плановані
роботи 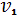
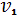 ,,…,, а ребра з'єднують роботи, в яких бере участь хоча б один
загальний механізм (і які, з цієї причини, не можна проводити одночасно). Цей
граф зображений на мал.2. Вершини
,,…,, а ребра з'єднують роботи, в яких бере участь хоча б один
загальний механізм (і які, з цієї причини, не можна проводити одночасно). Цей
граф зображений на мал.2. Вершини 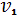
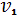 ,,, породжують підграф графа G ізоморфний
,,, породжують підграф графа G ізоморфний 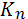
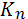 . Отже,
. Отже,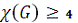
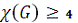
 .
.
Цифри в дужках на мал.3.1 вказують правильну розмальовку
графа G в 4 кольори. Отже, 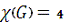
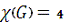
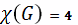 . Таким чином, всі роботи можна виконати
за 4 години. Для цього, відповідно до знайденого розфарбування графа G, треба в
1-у годину виконувати роботи
. Таким чином, всі роботи можна виконати
за 4 години. Для цього, відповідно до знайденого розфарбування графа G, треба в
1-у годину виконувати роботи 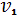
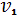 і
і 
 , у 2-й - роботи
, у 2-й - роботи 
 і
і 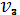
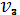 , в 3-й - роботи
, в 3-й - роботи 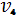
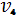 і
і 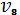
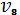 , в 4-й - роботи
, в 4-й - роботи 
 і
і 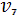
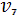 .
.

Мал. 3.1
Задача призначення телевізійних каналів. Передавальні станції зображають
вершинами графа. Якщо відстань між будь-якими двома станціями менша за одиницю,
то відповідно вершини графа з’єднуються ребром. Граф розфарбовують зіставляючи
різним кольорам вершин різні канали. Мінімальна кількість каналів відповідає
розфарбуванню графа мінімальною кількістю кольорів.
Задача складання розкладу. Припустимо, що потрібно прочитати
декілька лекцій у найкоротший термін. Кожна лекція окремо займає одну годину,
але деякі лекції не можна читати одночасно (наприклад, якщо це робить один і
той самий лектор, або лекції читаються одній та тій самій групі студентів).
Побудуємо граф G, вершини якого взаємно однозначно відповідають лекціям, і дві
вершини суміжні тоді й тільки тоді, коли відповідні лекції не можна читати
одночасно. Очевидно, що будь-яке розфарбування цього графа задає можливий
розклад: лекції, які відповідають вершинам одноколірного класу, читають
одночасно. Навпаки, будь-який можливий розклад задає розфарбування графа G.
Оптимальні розклади відповідають розфарбуванням мінімальною кількістю кольорів,
а час, потрібний для читання всіх лекцій, дорівнює χ (G).
Перекладемо це завдання на мову графів. Побудуємо граф G, в
якому вершини відповідають лекціям та дві різні вершини суміжні тоді і тільки
тоді, коли відповідні лекції не можуть читатися одночасно. Очевидно, що
будь-яке правильне розфарбування графа G визначає допустимий розклад (якщо при
цьому розфарбовуванні використано k кольорів, то для всякого i = 1, 2,.,k
вершини, розфарбовані i-м кольором, дають список лекцій, які треба читати на
i-й парі). І навпаки, будь-який допустимий розклад визначає правильне
розфарбування графа G. Таким чином, складання оптимального розкладу зводиться
до знаходження оптимального розфарбування побудованого нами графа.
Розглянемо приклад завдання на складання розкладу. У
студентських групах І-31 і І-32 треба провести заняття з алгебри, дискретної
математики, математичного аналізу та історії України (по одному заняттю з
кожному предмету). Заняття по кожному предмету проводяться з кожною групою
окремо. Заняття з алгебри та з дискретної математики веде викладач X, з
математичного аналізу - викладач Y, з історії України - викладач Z. Знайти
мінімальне число пар, в які можна "укласти" всі заняття, і скласти
відповідний розклад.
Рішення. Побудуємо граф з вершинами А1, А2, Д1, Д2, Ml, М2,
І1 і І2 (літера відповідає предмету, а цифра - номеру групи). З'єднаємо ребрами
вершини, що відповідають парам, які не можна проводити одночасно. Отримаємо
граф, зображений на мал. 1 ліворуч. Вершини А1, А2, Д1 і Д2 цього графа
породжують в цьому графі підграф, ізоморфний графу 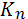
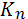 . Отже, хроматичне число нашого графа не менше 4. На мал. 3.2
праворуч вказана правильне розфарбування нашого графа в 4 кольори. Отже,
хроматичне число графа дорівнює 4, тобто всі заняття можна провести за 4 пари.
Відповідний розклад вказано в таблиці.
. Отже, хроматичне число нашого графа не менше 4. На мал. 3.2
праворуч вказана правильне розфарбування нашого графа в 4 кольори. Отже,
хроматичне число графа дорівнює 4, тобто всі заняття можна провести за 4 пари.
Відповідний розклад вказано в таблиці.
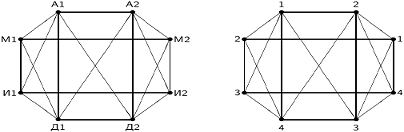
Мал. 3.2
|
І-31
|
І-32
|
|
1 пара
|
Алгебра
|
Математичний
аналіз
|
|
2 пара
|
Математичний
аналіз
|
Алгебра
|
|
3 пара
|
Історія
України
|
Дискретна
математика
|
|
4 пара
|
Дискретна
математика
|
Історія
України
|
Задача комівояжера. Задача комівояжера є
оптимізаційною задачею, що часто виникає на практиці. Вона може бути
сформульована таким чином: на території держави X розташоване n міст, між
деякими парами яких прокладені дороги (не обов'язково двонаправлені). Кожна з
них характеризується числом - своєю довжиною. З одного міста в інше веде не
більше однієї дороги. Бродячий торговець хоче обійти всі міста рівно по одному
разу і повернутися у вихідний пункт (починати рух можна в довільному місті).
Необхідно знайти мінімальну відстань, яку йому доведеться пройти, або
з'ясувати, що шуканого маршруту не існує.
3.2
Опис програмного продукту
В 2 розділі було наведено декілька методів
розфарбування графів. Так як метод перебору є не енергозатратним, саме цей
метод будемо досліджувати та перевіряти. Використовуючи мову програмування
Pascal була написана програма, що дозволяє знаходити оптимальне розфарбування
вершин графа, котрий у свою чергу введений користувачем з клавіатури або ж
використовувати граф що знаходиться у файлі.
Розглянемо алгоритм реалізації розфарбування
графів
GetColor;i: =1 to n do[i]: =1; {Усім кольорам
присвоюємо 1}i: =2 to n do {основний цикл розфарбування графу, де ‘і’ - це
номер вершини, яку ми розфарбовуємо}: =1; {розпочинаємо з першої
вершини}(j<=Graph [i]. Count) and (Graph [i]. List [j] <i) do {ідемо
повним перебором по вершинах всіх}Color [i] =Color [Graph [i]. List [j]]
Then{якщо кольори вершин, що перевіряються співпадають}[i]: =Color [i] +1;
{міняємо колір}: =1; {знову перевіряємо з першої вершини}{якщо кольори різні,
то ми ідемо далі}: =j+1;;;;
3.3
Машинна реалізація продукту
Для демонстрації роботи програмного продукту
розглянемо приклад.
Знайти хроматичне число графа, що зображений на
Мал. 3.3.
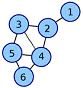
Мал. 3.3.
Якщо ввести в програму заданий планарний граф
(див. мал. 3) и виконати послідовність дій, передбачених програмою (див.
Додатки А, В, С), на моніторі програма виведе нам наступний результат:
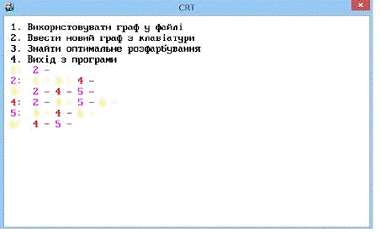
Мал. 3.4
Висновки
У даній курсовій роботі я займався дослідженням
теми розфарбування графів як математичної моделі прикладних задач. Мною було
опрацьовано та проаналізовано список джерел, які допомогли краще освоїти та
зрозуміти тему.
Під час виконання роботи було виконано такі
завдання:
· Проаналізовано та
систематизовано теоретичні та практичні досягнення в дослідженні задачі
розфарбування графів;
· Проаналізовано можливості
автоматизації дослідження такого роду задач.
Список
використаних джерел
1. Андрійчук В.І. Вступ до дискретної математики / В.І.
Андрійчук, М.Я. Команницький, Ю.Б. Іщук. - Львів: Видавничий центр ЛНУ імені
Івана Франка, 2003. - 254 с.
2. Бондаренко М.Ф. Комп’юретна дискретна математика / М.Ф.
Бондаренко, Н.В. Білоус, А.Г. Руткас. - Харків: "Компанія СМІТ",
2004. - 480 с.
. Капітонова М.Ф. Комп’ютерна дискретна математика. / Ю.В.
Капітонова та ін. - Київ: Наукова думка, 2002. - 578 с.
. Кук Д. Компьютерная математика. / Д. Кук, Г. Бейз. - М.:
Наука, 1990. - 384 с.
. Новиков Ф.А. Дискретная Математика для программистов /
Ф.А. Новиков. - Питер: СПб, 2000. - 304 с.
. Карнаух Т.О. Теорія графів у задачах / Т.О. Карнаух, А.Б.
Ставровський: Навчальний посібник. - К.: ВПЦ "Київський університет",
2004. - 76 с.
. Карнаух Т.О., Ставровський А.Б. Теорія графів у задачах
63 с.
. Дискретна Математика:: Планарні графи. Розфарбування
графів
[Електронний
ресурс]: стаття - режим доступу: http://oim. asu.
kpi.ua/files/DM/33_Planar_graphs. pdf
<http://oim.asu.kpi.ua/files/DM/33_Planar_graphs.pdf>
9. К. т. н., доцент Зорін Ю.М., студент Кучук О.М. Алгоритм
мурашиної колонії для розв’язання задачі стійкого розфарбування графу.
[Електронний
ресурс]: http://pmk. fpm. kpi.ua/arhive_2012/56_Kychyk. pdf
<http://pmk.fpm.kpi.ua/arhive_2012/56_Kychyk.pdf>
10. В.Ф. Прокопенков, Ю.Н. Кожин, О.Н. Малых, новый
эвристический алгоритм раскраски графа [Електронний ресурс]: стаття - режим доступу:
http://www.kpi.
kharkov.ua/archive/Науккова_періодика/vestnik/
<http://www.kpi.kharkov.ua/archive/Науккова_періодика/vestnik/> - Загол.
з титул. екрану. Мова: рос.
. Задача
коммивояжёра (поиск минимального гамильтонова цикла) [Електронний ресурс]: стаття
- режим доступу: <http://cybern.ru/zadacha-kommivoyazhyora.html>. -
Загол. з титул. екрану. Мова: рос. Останнє поновлення: 18.01.2012
. Быстрый
алгоритм для решения задачи о раскраске графа с использованием битовых операций
http://itas2014. iitp.ru/pdf/1569941697. pdf
<http://itas2014.iitp.ru/pdf/1569941697.pdf> - Загол. з титул. екрану.
Мова: рос.
. C.Д.
Штовба, к. т. н., доц., О.М. Рудий Мурашині алгоритми оптимізіції [Електронний
ресурс] www.serhiy-shtovba. narod.ru/doc/Visnyk_ANT. pdf <http://www.serhiy-shtovba.narod.ru/doc/Visnyk_ANT.pdf>
. Задача
комівояжера [Електронний ресурс]: стаття - режим доступу: http://uk.
wikipedia.org/wiki/Задача_комівояжера
<http://uk.wikipedia.org/wiki/Задача_комівояжера>. - Загол. з титул.
екрану. Мова: укр. Останнє поновлення: 18.01.2015.
. Клас
складності NP [Електронний ресурс]: стаття - режим доступу:://uk.
wikipedia.org/wiki/Клас_складності_NP
<http://uk.wikipedia.org/wiki/Клас_складності_NP>. - Загол. з титул.
екрану. Мова: укр. Останнє поновлення: 02.08.2013.повна задача [Електронний
ресурс]: стаття - режим доступу: http://uk. wikipedia.org/wiki/NP-повна_задача
<http://uk.wikipedia.org/wiki/NP-повна_задача>. - Загол. з титул. екрану.
Мова: укр. Останнє поновлення: 02.11.2014.
16. П.О. Кравець Ігрова модель хроматичного розфарбовування
графів/ Крапець П.О. - Львів Національний університет "Львівська
політехніка”, 2008.
Додатки
Додаток
А
Задання графу матрицею суміжності:
Uses crt;MS=array [1.10,1.10] of Integer;: MS; n,
i,j: Integer;;('Введіть кількість вершин: ');(n);('Введіть матрицю суміжності:
');i: =1 to n doj: =1 to n do(j*2, i+3);(' ');(a [i,j]);;;;
Задання графу списком суміжності:
Type GList = array [1.10] of record: Integer;:
array [1.10] of Integer; end;=array [1.10] of Byte;Graph: GList; Color: Clist;
ДОДАТОК В
Програмна реалізація алгоритму розфарбування
графів
Procedure GetColor;i: =1 to n do[i]: =1;i: =2 to
n do: =1;(j<=Graph [i]. Count) and (Graph [i]. List [j] <i) doColor [i]
=Color [Graph [i]. List [j]] Then[i]: =Color [i] +1;: =1;: =j+1;;;;
Додаток
С
Повний код програми:
Program algorytmGraf;crt;GList=array [1.10] of
record: Integer;: array [1.10] of Byte;;=array [1.10] of Byte;Graph: GList;
Color: CList; i,j,n: Byte; G: File of GList; s: string;GetColor;i: =1 to n
do[i]: =1;i: =2 to n do: =1;(j<=Graph [i]. Count) and (Graph [i]. List [j]
<i) doColor [i] =Color [Graph [i]. List [j]] Then[i]: =Color [i] +1;: =1;:
=j+1;;;;Vvid_K;('Введіть кількість вершин: ');(n);i: =1 to n do('Введіть
кількість вершин суміжних з ', i,'-ю: ');(Graph [i]. Count);('Введіть номери
вершин суміжних з ', i,'-ю: ');j: =1 to Graph [i]. Count do(j,'-а вершина:
');(Graph [i]. List [j]);;;('Зберегти введений граф у файл? [Y/N] ');ReadKey of
'Y','y': Begin('Введіть назву файлу:
');(s);(G,s);(G);(G,Graph);(G);;
'N','n': Begin;;;Vuvid;i: =1 to n do(Color
[i]);(i,': ');j: =1 to Graph [i]. Count do(Color [Graph [i]. List [j]]);(Graph
[i]. List [j],' - ');;;;;;(15);;('1. Завантажити граф з файлу');('2. Ввести
новий граф з клавіатури');('3. Знайти оптимальне розфарбування');('4. Вихід з
програми');ReadKey of
'1': Begin(' Введіть назву файлу:
');(s);(G,s);(G);(G,Graph);;
'2': Vvid_K;
'3': Begin;;;
'4',#27: Begin;(G);;;False;.