Дискретные методы исследования социальных процессов
Оглавление
Введение
Глава 1. Теоретические аспекты использования дискретных методов в
исследованиях социологических процессах
1.1 Сущность, специфика социологического исследования
1.2 Математическое моделирование социологических исследований
1.3 Система компьютерной математики Mathematica 10 в исследованиях
социологических процессов
Глава 2. Математические модели в социологических исследованиях
2.1 Модели демографических процессов
2.2 Модель военных конфликтов
2.3 Некоторые понятия теории игр и теории принятия решения
Заключение
Список литературы
Введение
Социологическое исследование - это система логически
последовательных методологических, методических и организационно-технических
процедур, связанных между собой единой целью: получить достоверные знания
(данные) об изучаемом явлении или процессе, о тенденциях или противоречиях в их
развитии.
Главной целью социологических исследований является выработка
новых теоретических знаний и/или получение новых эмпирических фактов и их
использование в практике управления различными сферами общественной
жизнедеятельности. Достижение цели исследования обеспечивается четко
разработанной и реализованной структурой процесса исследования,
методологической и технико-методической обеспеченностью.
Важным критерием выделения типа исследования является
дискретность процесса исследования, поскольку, например, мониторинговое
исследование, целью которого является отслеживание и анализ происходящих в
обществе, в объектах исследования изменений, проводятся через определенные промежутки
времени.
Дискретные методы математики наиболее уместны для решения
проблем экологии, биологии, социальных наук, поскольку они имеют дело с
конечными множествами: альтернативные схемы скоростных транспортных систем,
результаты опроса различных социальных групп, демографическая статистика, число
домов, число рабочих и т.д. Дискретное множество может состоять и не из целых
чисел, однако обычно мы не допускаем бесконечно малые различия между его
элементами. Например, количество денег, затраченных на данный проект, можно
измерять в миллионах долларов, сотнях долларов, даже в сотых доллара (т.е. в
центах), но у вас нет более мелкой единицы измерения, чем эта (хотя иногда
приемлемо допущение, что такая единица имеется). Иногда рассматриваемые
проблемы связаны с ситуациями, изменения в которых происходят или
регистрируются только в дискретные моменты времени, например, каждый час или
каждый год. Статистические данные о безработице, используемые для многих целей,
сообщаются раз в месяц. Проблемам социологических исследований в наибольшей
степени соответствует математика конечных, или дискретных, множеств, или же
множеств, изменяющихся только в дискретные моменты времени.
Заметим, что многие разделы и методы
математики, в силу внутренних причин, проявляют свою значимость в прикладных
областях. Например - булева алгебра, которая была использована в вычислительной
технике более чем через пятьдесят лет после своего создания. В ней
предполагается, что сложные сообщения можно закодировать при помощи двух
контактных реле. Простейший поток заявок, например, является математическим
представлением некоторого "идеального" потока, обладающего рядом
замечательных свойств, благодаря которым для многих математических моделей
удаётся получить достаточно простые зависимости, связывающие характеристики
функционирования систем массового обслуживания с исходными параметрами, которые
относятся к классу дискретных систем.
Одна и та же математическая модель может
отображать функционирование совершенно разных по своей природе реальных систем,
описываемых с помощью различных структурно-функциональных и нагрузочных
параметров, состав и перечень которых определяются соответствующей прикладной
областью.
Цель данного исследования - изучение методов и
моделей исследования социальных процессов.
В ходе достижения поставленной цели были решены следующие
задачи:
ü изучены основные методы сбора и обработки
социологической информации;
ü проведен анализ математических моделей
социологических процессов;
ü рассмотрены методы исследования
социологических процессов;
ü решены задачи в системе компьютерной
математики Mathematica 10 и Excel.
Глава 1.
Теоретические аспекты использования дискретных методов в исследованиях
социологических процессах
1.1 Сущность,
специфика социологического исследования
Человеческое общество - это сложная неравновесная
развивающаяся система. Сложность, многофакторность и противоречивость
социальной эволюции приводят исследователей к закономерному выводу о том, что
любое упрощение, редукция, упущение из виду всего многообразия факторов
неизбежно ведет к неверному пониманию изучаемых процессов. Возможно ли описать
его развитие какими-либо достаточно простыми законами? Современные достижения в
области математического моделирования дают однозначный ответ:
"Можно".
Социологическое исследование (наравне с этим термином
используется так же термин социологическое обследование) - это системное
изучение социальных процессов и явлений, характеризующееся: всесторонним
сущностным анализом предмета исследования; эмпирическим способом получения данных
об изучаемом явлении, процессе; статистической обработкой данных об единичных
проявлениях социальной реальности. Это система теоретических и эмпирических
методов обследования социальной реальности с использованием методов
статистической обработки данных.
При проведении социологического исследования пользуются как
общенаучными методами, так и специфическими.
Социологические исследования бывают:
ü теоретическими (то есть основанные на
применении и апробировании определенных социологических теорий) и эмпирическими
(то есть основанные на сборе и обработке данных об объективной реальности,
завершающиеся, как правило, теоретическим осмысливанием);
дискретное исследование социальный процесс
ü фундаментальными (ориентированными на
выявление универсальных связей и отношений) и прикладными (ориентированными на
решение узкого круга практических проблем);
ü сплошными (когда обследуется вся генеральная совокупность [1]
<#"869750.files/image001.gif">
Эта формула называется биноминальным законом распределения
Бернулли. Биноминальное распределение при соответствующих условиях и достаточно
больших значениях n можно заменить подходящим нормальным распределением.
Под вероятностью события в статистическом смысле понимается
почти достоверный предел его относительной частоты (частности) при
неограниченно растущем числе испытаний:
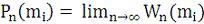
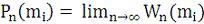 ;
; 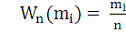
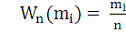 #"869750.files/image004.gif">
#"869750.files/image004.gif">
Абсолютная погрешность не характеризует точности измерения.
Например, при измерении длины стола в 2 м и длины дороги в 200 км допущена
абсолютная погрешность D1= D2=0.1 м. [6]
<#"869750.files/image005.gif">
Следовательно, чтобы определить объем выборочной совокупности
необходимо провести оценивание возможного эмпирического распределения, то есть
извлечь из данных наилучшее статистическое приближение для неизвестных значений
параметров, отвечающих наблюдениям, а также объективную меру этого
распределения. [8] <#"869750.files/image006.gif">
Для обработки эмпирических данных необходимо определить,
доверительный интервал для математического ожидания эмпирической функции
распределения, используя при этом второй метод оценивания, предварительно
вычислив предельную ошибку выборочной средней для максимально возможной
дисперсии D (Xi) = d2= 0.25:

Таким образом, что бы выводы исследования можно было
распространить на исследуемую совокупность, ее объем должен быть в соответствии
закону больших чисел не менее 70 обследуемых для коэффициента доверия, равного
0.9. Обосновав логико-математически требуемое количество респондентов в
выборочной совокупности, необходимо определить логико-структурный состав
выборки, то есть определить в ней представительство конкретных людей
количественно и качественно.
Выборка это процесс формирования выборочной совокупности
путем отбора единиц наблюдения.
Единицы наблюдения включают в себя:
элементы выборочной совокупности (например, респонденты),
подлежащие изучению, это единицы анализа;
элементы (поселения, предприятия, группы респондентов),
отбираемые на каждом этапе выборки по особому плану, это единицы отбора.
Выборочная совокупность это часть генеральной совокупности,
отражающая основные с точки зрения целей исследования свойства, признаки
генеральной совокупности.
Свойство выборочной совокупности воспроизводства
характеристик генеральной совокупности называется репрезентативностью. Ее
критерии: статистический - отражение при расчете объема выборки в выборочной
совокупности параметров генеральной с заданной погрешностью;
ресурсно-экономический - экономичность исследования (оценка кадрового
обеспечения, стоимости, временных затрат и т.д.); аналитический - ограничения
на объем выборки, накладываемые задачами последующего анализа.
Генеральная совокупность это общность людей или социальный
объект, на который распространяются выводы исследования.
Выборка бывает одноступенчатая (на первой ступени объекты
репрезентации совпадают с единицами наблюдения) и многоступенчатая (отбор на
первой ступени объектов репрезентации, на последующих единиц наблюдения).
Случайным называется отбор, при котором каждая единица
генеральной совокупности имеет равную или почти равную вероятность попадания в
выборочную совокупность. Случайные отборы бывают:
Вероятностный отбор - при котором каждая единица генеральной
совокупности сохраняет равную возможность на протяжении всего процесса отбора
быть отобранной в выборочную совокупность (повторный отбор) или вероятность
попадания возрастает, так как отобранная единица не участвует в отборе далее
(бесповторный отбор). Основное требование - достаточно большой объем выборочной
совокупности;
Систематический отбор это случайный отбор, при котором первая
единица наблюдения отбирается случайно, а остальные через один и тот же
интервал (шаг), например из списка. Это псевдослучайный отбор.
Направленным называется неслучайный отбор, при котором
единицы наблюдения отбираются в выборочную совокупность в соответствии с
критериями, заданными исследователем. Направленные отборы бывают:
Гнездовой отбор это направленный многоступенчатый отбор, при
котором на каждой ступени выделяется промежуточный объект репрезентации
("гнездо”), служащий исходной совокупностью для следующей ступени. При его
осуществлении, как правило, в качестве единиц отбора выступают не отдельные
респонденты, а группы с последующим сплошным отбором их. Особенностью является
то, что "гнезда” на каждой ступени неоднородны по внутренней структуре
подобно генеральной совокупности. Респондентом называется лицо
(личность, человек), которое является источником первичной социологической
информации, представляющей собой результат измерения;
Квотный отбор это направленный многоступенчатый отбор, при
котором единицы наблюдения включаются в выборочную совокупность пропорционально
их долям ("квотам”) в генеральной совокупности. Ему предшествует
построение генеральной совокупности, воспроизводящей ее структуру в виде
пропорций (квот) изучаемый признаков, например, если в коллективе количество
мужчин и женщин соотносится как 1: 2, то в выборочной совокупности должны быть
представлены респонденты по этому признаку в таком же соотношении. Это наиболее
сложный метод, применяемый при большой генеральной совокупности и требующий для
отбора респондентов использования не менее четырех признаков;
Районированный отбор это направленный многоступенчатый отбор,
которому предшествует процедура деления совокупности на "районы”, которые
внутри себя относительно однородны, но различаются между собой. Основные
особенности - деление производится на основе признака, коррелирующего с
исследуемыми характеристиками; ошибка выборки обуславливается только вариацией
внутри выделенных типичный групп (районов). Данный отбор требует информации о
генеральной совокупности для определения % -ного представительства признаков
деления в выборочной совокупности, предварительного анализа объекта
исследования;
Основными ошибками социологического исследования
являются: теоретические (связанные с выбранной теорией), статистические (как
правило, это заданная погрешность), наблюдения (полученные при сборе и
первичной обработке информации). Ошибки наблюдения бывают: ошибки регистрации и
ошибки репрезентативности.
Ошибки регистрации возникают в результате неправильного
установления фактов в процессе наблюдения или не точной их записи: случайные -
при заполнении документов, при измерении показателей, при подсчете и т.п.;
систематические - из-за неправильного выбора метода сбора или обработки
первичных данных, неточностью в "инструменте" (анкете, бланке
наблюдения и т.д.), из-за не учета постоянного влияния внешних факторов и т.п.
Ошибки репрезентативности возникают из-за отклонения значений показателей по
выборочной совокупности от их значений по генеральной: случайные - при отборе
единиц наблюдения (как правило, задаются при определении объема выборки);
систематические - из-за неточности соблюдения процедуры выборки, отказа
респондентов, нарушений процедуры обработки.
Таким образом, эмпирическое исследование открывает новые
факты и ставит новые задачи перед теорией. Теоретическое исследование получает
новые возможности объяснения фактов и методологически ориентирует эмпирическое.
В сущности, это два уровня глубины научного исследования социальных процессов и
явлений. Единство и взаимообусловленность эмпирического и теоретического
уровней являются основной теоретико-методологической предпосылкой и условием
достоверности получаемого социологического знания. Социологическое исследование
это система логически последовательных методологических и
организационно-технических процедур, связанных между собой единой целью -
получить объективно-достоверные сведения об изучаемом социальном явлении или
процессе для их последующего использования на практике.
В социологическом исследовании применяются количественный и
качественный способы измерения, сущность которых заключается в выборе
респондентами той или иной категории или цифрового балла из серии предложенных
ответов, с последующей логико-математической обработкой полученных
статистических результатов. При этом основными способами проверки
обоснованности и надежности измерительных шкал являются: логико-математический
и статистический анализ; определение системы независимых критериев, например
сведения документов, результаты экспертиз, апробированных методик и т.д.
1.2
Математическое моделирование социологических исследований
Исходя из вышесказанного строятся
соответствующие математические модели. Выделяются следующие критерии
классификации математических моделей социологических процессов:
тип математического аппарата, посредством
которого осуществляется формализация процесса. Основное различие связано с тем,
является ли модель стохастической вероятностной, случайной, то есть характер
изменения точно предсказать невозможно, или детерминистской (определенной,
причинно-обусловленной). Другие подклассификации относятся к типу используемых
переменных: непрерывное или дискретное время; является ли зависимая переменная
непрерывной, или лее представляет дискретные состояния;
основная функция моделей процессов в
теоретическом и эмпирическом исследовании. В соответствии с этой основной
функцией модели делятся на теоретические эмпирические.
содержание анализируемых процессов:
процессы в малых и больших группах, процессы индивидуального и группового
принятия решений, динамика групповой структуры и т.д.;
тип концептуализации социального процесса:
рассматривается ли данный процесс как процесс без управления или как
управляемый процесс Управляемые процесс можно разделить на процессы
целесообразного поведения рефлексного типа и процессы целенаправленного
поведения не рефлексного типа
Использование компьютерного моделирования
в социальных науках довольно новая идея, хотя первые работы в этом направлении
были осуществлены в 1960х, а широкое использование компьютеров началось в
1990-х. Эта идея имеет огромный потенциал потому, что моделирование
представляет собой превосходный путь прогнозирования и понимания социальных
процессов.
Компьютерное моделирование предоставляет
возможность реализовать идею рождения сложного социального поведения из
сравнительно простых действий индивидов:
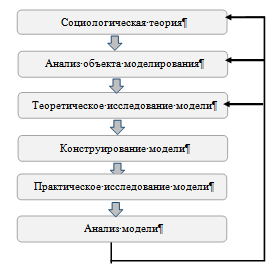
Рис. 1 - Этапы моделирования
Процесс компьютерного моделирования
социальных процессов включает в себя следующие этапы:
. Ознакомление с социологической теорией,
на основе которой строится модель
. Построение информационной модели и
аналитических схем на основе социологической теории объекта моделирования
. Теоретическое изучение готовой
информационной модели и построение математической модели (выбор математического
аппарата, формализация структуры, взаимосвязей и элементов)
Построение компьютерной реализации
математической модели (выбор метода компьютерного моделирования и алгоритма
моделирования)
Практическое изучение готовой компьютерной
модели (работа с компьютерными моделями как с объектами исследования: введение
начальных данных, получение результатов в виде графиков и диаграмм, анализ и
интерпретация полученных данных, изменение начальных условий на основе
имеющихся результатов для нахождения оптимального решения)
В результате анализа компьютерной модели
приходим к выводу об адекватности построенной модели моделируемому социальному
процессу. Далее принимается решение: либо изменить структуру построенной модели
с целью ее совершенствования и улучшения, либо произвести дополнительный анализ
социологического объекта, либо собрать недостающие сведения об исследуемом
социальном процессе.
Взаимосвязи между математикой в любой областью, где она
находит приложение, развиваются двумя путями. Один путь очевиден и состоит
просто в применении математики, которое может осуществляться различными
способами: от решения конкретных практических задач, до развития обширных
теорий. Второй путь, обычно не принимаемый во внимание многими людьми,
заключается в том, что прикладная область может быть "применена к
математики". Такое "применение" либо стимулирует разработку
новых разделов математики, либо помогает при решении известных математических
задач.
Рассмотрим взаимосвязи между математикой и прикладными
проблемами из таких областей, как социология, биология, экология. Эти
взаимосвязи возникли, в основном, значительно позже тех, которые существуют
между математикой и физическими проблемами и затрагивают такие математические
дисциплины, которые до недавних пор не включались в математическое образование.
Применение математики в указанных выше областях, требуется
создание новых математических средств, достаточно мощных, чтобы справиться со
сложными математическими вопросами, возникающими в ряде реальных задач.
Проблемы социологии, экологии, биологи послужили или должны
стать стимулом для развития новой математики. Математика, создаваемая при этом
воздействии, может быть интересна и сама по себе. Ее применимость не
обязательно является критерием оценки, хотя конечно, можно надеяться, что в
конечном счете она окажется полезной. Мы должны иметь в виду, что многие
разделы математики развивались исключительно в силу внутренних причин и
обнаружили свою полезность позднее. Хороший пример - булева алгебра, которая
была использована в вычислительной технике более чем через пятьдесят лет после
свое создания.
Другие разделы математики нередко развивались для одной
единственной цели, и лишь позднее была обнаружена их важность для других
прикладных областей. Значительная часть теории графов имеет такую же историю.
Это наука берет свое начало с известной задачи о кенигсбергских мостах, затем
исследование стимулировались вопросами, относящимися к структурам химических
соединений, анализу игр и головоломок, а сегодня теория применяется для решения
большого числа задач генетики, экологии, анализа транспортных потоков,
коммуникаций и т.д.
Процесс математического моделирования включает четырехэтапный
контур, который в упрощенном виде изображен на рисунке 2.

Рис. 2. Циклическая природа математического моделирования
На первоначальном этапе происходит сбор сведений об изучаемом
явлении. Затем формулируют определенные допущения об этом явлении на строгом
языке - языке математики. Так получается математическая модель. На точном
языке, который обычно используется для описания модели, общие допущения, законы
и теории можно сформулировать таким образом, чтобы изложил" само существо
дела, а не различия, возникающие из-за употребления нечетких терминов. Более
того, становится возможным применить развитые в течение нескольких столетий
точные методы исследований к изучению явлений реального мира.
В любом случае формальная модель строится на математических
допущениях и следующие два блока контура предназначены для испытания
построенной модели, а в случае необходимости и для ее модификации.
Для проверки модели желательно излучить некоторые выводы о
реальном явлении. Такие выводы бывают двух типов: один относятся к ранее
наблюдавшимся ситуациям (и носят объяснительный характер), а другие относятся к
новым, ранее не наблюдавшимся ситуациям (и используются для предсказания или
прогноза). Оба типа выводов важны для проверки математической модели, хотя в
нашем обсуждении целесообразно относиться к ним обоим как к прогнозам. Для
получения таких прогнозов сначала при помощи т математических методов,
разработанных ранее или специально для данной математической модели, составляются
математические прогнозы.
Эти математические прогнозы затем переводятся с языка модели
обратно на язык реального мира и, следовательно, могут интерпретироваться как
прогнозы или выводы для изучаемого явления.
На заключительном этапе прогнозы сверяются с реальными
данными,"ибо известными (в случае проверок объяснительных возможностей
модели) либо новыми (в случае проверок ее предсказывающих возможностей). На
основе новых данных, включающих и сведения о прогнозе, по модели, модель
модифицируется, и процесс исследования циклически повторяется по тому же
контуру.
Таким образом, любая математическая модель признается лишь
временной. Циклический процесс продолжается все время, и новые порции данных
должны повышать объяснительную или предсказывающую способность модели. Следует
иметь в виду, что не всякая математическая модель создается в описанной выше
последовательности, т.е. некоторые шаги могут пропускаться, повторяться и т.п.
Но в качестве некоторой идеализации наша четырехэтапная процедура вполне приемлема.
1.3 Система
компьютерной математики Mathematica 10 в исследованиях социологических
процессов
Сложно представить изучение математики в наше время без
использования программного обеспечения (ПО) различного вида и уровня. ПО берет
на себя большую часть вычислительной и аналитической нагрузки современного
математика. Очевидные плюсы применения ПО выражаются и в повсеместном
требовании повышения компьютерной грамотности, и в экономии времени на
различные промежуточные вычисления, и во всеобщей тенденции компьютеризировать
любую информацию. Поэтому перед сегодняшними исследователями стоят и, главное,
представляются разрешимыми совсем другие задачи, нежели ранее.
Рынок систем компьютерных математик (СКМ) широк, что
позволяет выбрать то или иное ПО по своим критериям. Порой трата времени на
поиск наиболее адаптивной СКМ для самостоятельных исследований с лихвой
окупается ее возможностями.
СКМ Mathematica дает возможность специалистам решать большое
количество достаточно сложных задач, не вдаваясь в тонкости программирования.
Mathematica может быть модернизирована самим пользователем, так как она
является ПО с открытым кодом. Данная СКМ позволяет включать в расчеты все
известные элементарные функции, а также сотни специальных встроенных функций.
Пользователь программы может вводить и свои функции как для применения в
течение одного сеанса работы, так и для постоянного использования. Входной язык
Mathematica содержит большое количество конструкций, позволяющих для каждой
конкретной задачи выбрать оптимальный метод программирования. Помимо обычного
процедурного программирования с применением условных переходов и операторов
цикла, имеется еще несколько методов. В каждой конкретной программе
пользователь может одновременно применять несколько методов или даже все перечисленные.
В то время, когда только начали появляться СКМ, книги по
этому направлению были способны лишь отпугнуть обычного читателя и пользователя
компьютера от изучения возможностей компьютерной алгебры в силу
перенасыщенности их узкоспециальным теоретическим материалом и весьма
специфического языка описания. Несколько периодических изданий и более двухсот
книг посвящено СКМ Mathematica, эти книги способны помочь ознакомиться с
работой в системе, но без знания какой-либо предметной области работа в СКМ не
представляется целесообразной.
В начале 60-х годов XX века обсуждалась задача создания
компьютерных систем, способных осуществлять типовые алгебраические
преобразования, при которых получались бы символьные результаты везде, где это
только возможно. Одни из первых таких систем были Reduce, Derive, Macsyma. На
сегодняшний день существует множество систем компьютерной математики (СКМ) как
коммерческих, так и некоммерческих. Среди коммерческих СКМ наиболее широко
известны такие универсальные системы, как Mathcad, Mathematica, Maple и др.,
т.е. такие системы, которые выполняют как численные, так и символьные
вычисления. Среди свободно распространяемых систем известны Axiom, Eigenmath,
Maxima, Yacas. СКМ Maxima, первоначально носившая имя Macsyma (от MAC's SYmbolic
MAnipulation), была создана в конце 60-х годов в знаменитом MIT (Massachusetts
Institute of Technology) Массачусетском технологическом институте. Macsyma в
течение многих лет использовалась и развивалась в университетах Северной
Америки, где появилось множество вариантов системы. Maxima является одним из
вариантов, созданным профессором Вильямом Шелтером в 1982 году. Принципы,
положенные в основу проекта, позднее были заимствованы наиболее активно
развивающимися ныне коммерческими программами - Mathematica и Maple. Можно
сказать, что Macsyma фактически стала родоначальником всего направления
программ символьной математики.
В конце 80-х Стивен Вольфрам приступил к созданию проекта
математической системы Mathematica. В 80-х годах он основал корпорацию WolframResearch,
для создания компьютерной системы Mathematica.
Первая версия Mathematica была выпущена 23 июня 1988 г. За
все это время Mathematica оптимизировалась, расширялась ее функциональность и
документация. В выпускной работе рассмотрена последняя версия системы.содержит
большую коллекцию высоко оптимизированных алгоритмов, многие из которых были
открыты в WolframResearch. Система поддерживает числа любой точности, причем
для внутренних расчетов часто используются еще более точные значения для повышения
качества результата. Для повышения точности вычисления среда использует
символьные вычисления, т.е. пытается упростить или преобразовать выражение, и
лишь затем производит численный расчет. При этом алгоритм решения выбирается
автоматически из тысяч методов и может быть изменен даже в процессе вычисления,
что ускоряет получение решения и повышает точность больше, чем ручное задание
метода [8].
Начиная с 8-ой версии пакета, можно выделить возможность
ввода вычислительных команд на почти естественном для человека языке. Сами
разработчики называют эту функцию "linguistically controlled
computing" (вычисления с лингвистическим управлением). В систему
интегрирована технология, лежащая в основе онлайн-базы знаний и набора
вычислительных алгоритмов WolframAlpha, благодаря чему в новой версии
Mathematica можно вводить математические выражения на естественном английском
языке и мгновенно получать ответ или переходить к расширенному анализу.
Наглядным примером использования естественного языка в вычислениях является
команда "pi 100 digits". Если ввести ее в стандартное поле команд,
пакет Mathematica преобразует символы в стандартную конструкцию "N [Pi,
100] " (вывод числа Пи до девяноста девятого знака после запятой). Кроме
того, пользователь может ввести целую математическую задачу, например, в форме
системы уравнений вроде "2a - b = 3, a + b + c = 1, c - b = 6".
Интеллекта, вложенного в пакет Mathematica 10, будет достаточно, чтобы
правильно воспринять задачу и вывести решение в понятной форме, в том числе
конкретные значения переменных a, b и c [23].
Пакет Mathematica 10 содержит более 500 новых функций и
инструментов, поддерживает вычисления с использованием ресурсов графического
процессора или многоядерных процессоров. Также Mathematica содержит достаточный
набор управляющих структур для создания условных выражений, ветвления в
программах, циклов и т.д. Таким образом, программирование в совокупности с
символьными, графическими и численными вычислениями, выполняемыми в одном
сеансе использования Mathematica, превращают ее в удобный и мощный инструмент
научных исследований.
Что нового в системе Mathematica 10.
В системе Mathematica 10 были добавлены новые обширные сферы
применения - ещё более расширяя не имеющую себе равных базу алгоритмических,
информационных возможностей и возможностей пользовательского интерфейса системы
Mathematica.
· Полоса с предложениями о
следующих вычислениях. Как только вы закончили вычисления, вам будут предложены
оптимизированные предложения о следующих возможных шагах. Нажатием кнопки можно
выполнить новую функцию или открыть модуль оперативной помощи. Этот новый
подход к интерфейсу пользователя позволяет ориентироваться в функциях системы
Mathematica и открывать для себя новые функциональные возможности.
· Контекстный модуль помощи
ввода. Разумное автозавершение и яркостное выделение для функций, опций и
других элементов системы Mathematica, интегрированное с не имеющей себе равных
документацией системы Mathematica.
· Анализ социальных сетей.
Полный комплект функций для анализа социальных сетей, включая выявление
сообществ, сплочённые группы и меры центральности, а также встроенные каналы
получения данных от Facebook, LinkedIn, Twitter и др.
· Системная поддержка
единиц измерений. Тесно интегрированная поддержка более чем 4500 единиц измерений-в
том числе свободная форма языкового ввода, преобразования, и проверка
согласования размерностей в построении графиков, в численных и символьных
вычислениях.
· Корпоративное
развёртывание вычисляемых документов (Enterprise CDF). Новый вариант Mathematica
Enterprise Edition делает возможным непосредственное развёртывание CDF
документов, использующих оперативные данные во время выполения, и другие
расширенные возможности. Режимы предварительного просмотра имитируют Wolfram
CDF Player и Wolfram Player Pro.
· Обширная поддержка
случайных процессов. Универсальная платформа для моделирования систем, которые
случайным образом изменяются во времени, включая поддержку построения
реализаций, оценивание параметров (калибровку), нахождение распределений
временных срезов, а также ковариационной функции и функции среднего значения.
· Цепи Маркова и теория
массового обслуживания. Автоматизированная поддержка цепей Маркова с дискретным
и с непрерывным временем, и теории массового обслуживания. Нахождение
показателей производительности для построения случайных процессов в прикладных
расчётах, например, для центра телефонного обслуживания или для серверной
архитектуры." Временные ряды и стохастические дифференциальные уравнения.
Автоматическая калибровка моделей временного ряда по данным и прогнозирование
по моделям. Вычисление символьных свойств для стохастических дифференциальных
уравнений, используемых в финансах, обработке сигналов и других дисциплинах.
· Анализ надёжности. Полная
подсистема для анализа надёжности, поддерживающая блок схемы расчёта
надёжности, деревья неисправностей, модели ненагруженного резервирования, и
критерии важности.
· Анализ выживаемости.
Широкая поддержка цензурированных данных, оптимизированные платформы для
параметрического и непараметрического моделирования выживаемости, а также ряд
универсальных функций для проверки гипотез.
· Развёрнутая поддержка
теории вероятностей и статистики. Расширенные возможности по теории
вероятностей и статистике, в том числе критерии статистической независимости, новые
тесты для проверки статистических гипотез, поддержка взвешенных данных, а также
новые параметрические и вторичные распределения вероятностей.
· Расширенная поддержка
графов и сетей. Новые и оптимизированные распределения вероятностей на графах,
функции расчёта транспортных сетей, а также повышенная производительность
подсистемы в целом.
· Встроенная интеграция с
языком R. Использование кода на языке R в процессе работы в системе
Mathematica, обмениваясь данными между системой Mathematica и средой R, и
выполняя R код непосредственно из системы Mathematica. Включает автоматическую
загрузку среды выполнения R.
· Обработка 3D объемных
изображений. Подсистема по обработке изображений теперь поддерживает операции с
трехмерными объемными изображениями, такие как пиксельные операции, локальное
фильтрование, и морфологические операции. Также включает рендеринг трехмерных
поверхностей и объёмов.
· Новые передовые алгоритмы
обработки изображений. Функции определения контура, распознавания лиц, функции
улучшения изображений и другие высоко оптимизированные алгоритмы позволяют
выполнять всесторонний анализ изображений.
· Интерактивный помощник в
работе с изображениями. Новый способ находить функции по работе с
изображениями, используя указательный интерфейс-не покидая среды блокнота
системы Mathematica.
· Поддержка больших
изображений. Работая с внешней памятью, система Mathematica 10 расширяет
масштабы производительности до очень больших двумерных и трехмерных
изображений.
· Поддержка HDR
изображений. Импортирование изображений с высоким динамическим диапазоном (HDR)
и данных цветового профиля, а также улучшенная поддержка форматов JPEG и PNG.
· Интегрированная поддержка
обработки цифровых и аналоговых сигналов. Фильтрование и анализ сигналов-аудио,
изображения, многомерные данные - а также непосредственное создание и
использование интерактивных фильтров. Поддержка SystemModeler.
· Расширенная
функциональность систем управления. Построение моделей с запаздыванием или
алгебраическими уравнениями, и их использование с полным набором функций систем
управления в системе Mathematica. Автоматическое построение ПИД-регуляторов в
соответствии с заданными критериями.
· Значительные расширения в
нахождении численных решений дифференциальных уравнений. Решение
дифференциальных уравнений с разрывными коэффициентами, гибридных
дискретно-непрерывных динамических систем, параметрических дифференциальных
уравнений, а также дифференциально-алгебраических уравнений.
· Встроенная поддержка
символьных тензоров. Эффективная поддержка символьных массивов, от простых
векторов до массивов произвольного ранга, размерности или симметрии. Новые и
улучшенные базовые алгоритмы. Новые специальные функции, улучшения по функциям
линейной и полиномиальной алгебры, а также значительное увеличение быстродействия
по системе в целом.
· Другие новые улучшения.
Поддержка векторного анализа, в том числе векторного исчисления и координатных
систем. Встроенная поддержка производственного и других календарей.
· Расширенные визуализация
и элементы управления. Высоко настраиваемые интерактивные индикаторы для
приборных досок и элементов управления, системная поддержка автоматических
легенд на графиках и диаграммах, а также новые функции визуализации,
специализированные для обработки сигналов.
· Новые форматы для функций
импорта и экспорта. Широкая поддержка новых форматов данных, в таких
дисциплинах как молекулярная биология, обработка изображений с высоким
динамическим диапазоном, химическая спектроскопия.
· Поддержка полного спектра
интернет доступа. Полный доступ к интернету со стороны клиента для обмена
информацией с удалёнными серверами, и для работы с программными интерфейсами
веб-приложений. Асинхронное соединение для программирования в стиле AJAX.
· Перепроектированные
шаблоны слайд-шоу. Обновлённый внешний вид слайд-шоу, использующий новые
стилевые шаблоны, и с поддержкой фоновых изображений.
· Другие новые улучшения.
Низкоуровневая поддержка операций ввода-вывода для потоков данных. Расширенная
документация с рекомендуемыми примерами и учебными ресурсами. Переработанное
стандартное стилевое оформление и новые шаблоны.
Новый проект Mathematica 10 в первую очередь представляет
собой специализированное программное обеспечение для учёных, студентов ВУЗов и
школьников, которые готовятся к экзаменам и решают домашние задания по высшей
математики [7].
Глава 2.
Математические модели в социологических исследованиях
2.1 Модели
демографических процессов
Конструктивный синтез социальных наук и математики требует
введения адекватных способов измерения социальных величин. Одной из наиболее
доступных для непосредственного измерения социальных величин является
численность людей. Поэтому неудивительно, что именно область демографии
привлекает исследователей, давая надежды на успех в построении количественной
теории. Примечательно, что и проникновение математических методов в социальную
сферу во многом проходило под флагом описания популяционной динамики животных.
Численность популяции может меняться во
времени различным образом: расти, совершать колебания, падать и причины этого
могут быть различны. Здесь мы рассмотрим модели роста популяций и
математический аппарат, позволяющий описывать динамику численности разных
популяций.
Однако несмотря на измеримость данных и, более того, на
очевидность формулы, вытекающей из закона сохранения и описывающей
демографическую динамику:
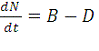
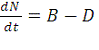 , (4)
, (4)
где N - число людей, B - число рождений и D -
число смертей в единицу времени, на микроуровне оказывается, что и число
рождений, и число смертей зависят от многих других социальных параметров, и в
том числе от "человеческого фактора" - принятия решений отдельными
людьми, слабо поддающегося формализации.
Кроме того, формула (4) не учитывает перемещения людей в
пространстве, а следовательно она должна быть расширена:

 ,
,
где вектор J соответствует миграционному потоку. В этом
случае задача еще больше усложняется, поскольку миграционные процессы еще
сильнее подвержены влиянию внешних факторов.
Поэтому описание демографических процессов на микроуровне
наталкивается на существенные проблемы, связанные, прежде всего, с
неразработанностью формальных социальных законов, увязывающих экономические,
политические, этические и прочие факторы, определяющие поведение малых групп
людей.
Таким образом, единственным пока доступным подходом является
макроописание, не вдающееся в мелкие детали демографического процесса и
описывающее динамику больших людских масс, для которых влияние человеческого
фактора заметно ниже.
Рассмотрим модель, предложенную Мальтусом
в 1798 г. в классическом труде "О законе роста народонаселения".
Томас Роберт Мальтус (1766-1834) - известный английский демограф и экономист,
обратил внимание на тот факт, что численность популяции растет по экспоненте (в
геометрической прогрессии), в то время как производство питания растет со
временем линейно (в арифметической прогрессии), из чего сделал справедливый
вывод, что рано или поздно экспонента обязательно "обгонит" линейную
функцию, и наступит голод. На основании этих выводов Мальтус говорит о
необходимости ввести ограничения на рождаемость, в особенности для беднейших
слоев общества. "Экономический пессимизм", следующий из прогнозов
предложенной им модели, в основу которой положен анализ эмпирических данных,
Мальтус противопоставлял модным в начале IXX века оптимистическим идеям
гуманистов: Жана-Жака Руссо, Уильяма Годвина и других, предсказывающих
человечеству грядущее счастье и процветание. Можно говорить о том, что Мальтус
был первым ученым - "алармистом", который на основании результатов
моделирования "бил тревогу" и предупреждал человечество об опасности
следования развитию по используемым ранее сценариям прогресса.
Динамика популяций в соответствии с моделью Мальтуса
протекает по закону:
где q - некоторое число, большее единицы, а xn
есть численность популяции в n-м году.
Пусть в год Рождества Христова число жителей некоторого
города было равно х0. Через год его численность будет равна x1
= qx0. В году с номером n его численность будет равна xn=
qn x0.
В экономической интерпретации xn - величина
вклада в банке в n-м году, а величина q определена процентной
ставкой.
Удобно рассмотреть вариант q= 1,03, что соответствует
ежегодному 3% -му приросту населения, а в экономической интерпретации
начислению 3% годовых на начальный вклад, график функции на рис.3. Оценим как
происходит рост населения. Через сколько лет удвоится населения города?
Разумеется, что при ежегодном росте в 3 % гарантировано
удвоение через 34 года. Однако эффект начисления процентов на проценты приводит
к тому, что уже через 24 года величина x0 удвоится:
24 = (1,03) 24 · x0 =
2,032793 · x0 > 2 · x0.
Нетрудно посчитать, что через 48 лет население увеличится в 4
раза, через 64 года - в 8 раз, а через 24 n лет - более, чем в 2 nраз.
К 1992 году население увеличилось более, чем в 283 раз, т.к. 1992 =
24*83. Т.е. численность потомства одной пары, жившей во времена Рождества
Христова равна 283*2 = 284 (х0 = 2).
Таким образом посчитали, что при трехпроцентном ежегодном
росте населения количество потомков одной пары современников Христа составит в
среднем более 1025 человек. Это такое количество, что если каждому
человеку выделить на Земле один квадратный сантиметр, то все они на Земле не
поместятся.
Действительно, т.к.210 = 1024, то
84 = (210) 8,4 = 1024 8,4>
(103) 8,4> 10 25.

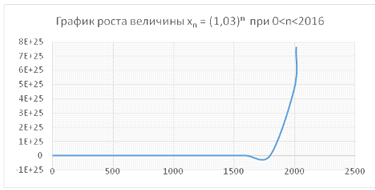
Рис. 3. График роста величины xn = (1,03) n.
Сверху: при n, меняющемся от 0 до 10.
Снизу: при n, меняющемся от 0 до 2016, в измененном масштабе
по обеим осям.
Итогом обсуждения мальтузианской модели является вывод:
Гипотеза постоянного в течение двух тысячелетий ежегодного
трехпроцентного экономического роста (постоянного трехпроцентного роста
практически любой величины) опровергается арифметикой.
Эти соображения заставляют прислушаться к аргументам
сторонников ограничения экономического роста и качественной диверсификации
экономики. Такие идеи высказывались так называемым Римским клубом.
Недостатком модели Мальтуса является то, что она не учитывает
системный характер развития. Производство, например, пищи и воспроизводство
населения взаимообусловлены посредством множества связей. Естественно, что при
слишком большихx: конкуренция за ресурсы (пищу) приводит к уменьшению k.
Поэтому жесткая модель Мальтуса нуждается в уточнении, учитывающем зависимость
коэффициента к от численности населения.
Возвращаясь к модели развития науки, заметим, что дальнейший
экспоненциальный рост по модели Мальтуса привел бы к тому, что в XX в.
исчерпались бы запасы бумаги и чернил, а число ученых достигло бы половины
населения земного шара. Ясно, что общество не может этого допустить и,
следовательно, развитие науки должно быть подавлено, что и наблюдается во
многих странах (в том числе и в России) в виде различного рода реформ
академической науки [2, с. 7-8].
Вместо жесткой модели Мальтуса рассмотрим мягкую модель:
n+1 = kxn
допускающую выбор разных функций k (х). Простейшим примером
является к (х) = а - bх, что приводит к так называемой логистической модели:
n+1 = axn - bxn2 (3.1)
Выбор данной функции может быть обоснован определенными
соображениями. Так как ресурсы ограниченны, то естественно пред и итожить, что
уровень рождаемое тис ростом численности населения будет падать, а уровень
смертности увеличиваться.
Зададим уровень рождаемости функцией:
= r0 - krx
где г0 - первоначальный уровень рождаемости; kr
- скорость падения уровня рождаемости но мере увеличения численности населения х.
Аналогично, уровень смертности может быть найден как:
= d0 +
kdx
где d0
- первоначальный уровень рождаемости; kd - скоростьроста уровня
смертности но мере увеличения численности населения. Тогда для коэффициента к в
уравнении Мальтуса имеем:
= r - d = (r0
- krx) - (d0 + kdx) - = (r0 - d0)
- (kr+ kd) x
Пусть a = (r 0
- d 0), a b = (kr + kd). Подставив приведенные
выражения в уравнение Мальтуса, получим дифференциальное уравнение.
Заметим" что
сделанные выводы справедливы для широкого класса моделей с различными
убывающими функциями к (х). Логистическая модель удовлетворительно описывает
многочисленные явления насыщения. Эмпирический анализ огромного числа
природных, технико-экономических и социокультурных процессов показал, что их
рост, развитие, распространение подчиняются логистическому закону. В книге Ю.М.
Плотинского "Модели социальных процессов" приведено множество
примеров, начиная от развития транспорта и коммуникаций до роста
народонаселения [18, с.184, 191]. S-Образные кривые хорошо описывают замещение
одного вида техники другим, смену технологий, эволюционные процессы в
экономической и социокультурном сферах.
Можно привести
еще немало примеров успешного использования данной модели на практике.
Экспоненциальная
модель с отловом
В этой модели не
учитывается конкуренция, зато предполагается, что на каждом такте происходит
уменьшение численности популяции на фиксированное число. Это фиксированное
число мы обозначим посредством c и будем называть квотой отлова. Модель
определяется формулой:
n+1 = a · xn - c.
(6)
Будем считать, что a > 1.
Вот возможная экономическая интерпретация модели (6):
xn может означать доход
фирмы в n-ый период времени;
a - коэффициент,
демонстрирующий способность работников фирмы увеличивать доход за один период
времени (a > 1). Конкуренция и насыщение рынка в данной модели не
учитываются;
с - постоянные платежи, не
зависящие от n и xn.
На рис.4 отображены результаты расчета
нескольких траекторий (xn) по формуле:
n+1 = 1.1 · xn -
0,06 (7)
при изменении n от 0 до 30.

Рис. 4. Динамика популяции в экспоненциальной модели с
отловом.
Стационарная траектория:
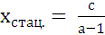
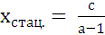 (8)
(8)
в модели (4) является критической: падение популяции ниже этой
величины влечет ее гибель.
В экономической интерпретации это означает, что существует
некоторое критическое значение начального дохода. Если начальный доход фирмы
превышает критическое значение, то доход в дальнейшем неограниченно растет.
Если же начальный доход меньше критического, то в дальнейшем доход сокращается
до нуля.
Формула (8) показывает, что критическое значение дохода зависит от
уровня постоянных платежей: при больших платежах критический уровень дохода
возрастает до опасно высокого уровня, при малых - фирме требуется небольшой
начальный доход, чтобы выжить на рынке. Естественно, формула (8) демонстрирует,
что эффективность работы фирмы, символизированная в коэффициенте а, также
влияет на величину критической величины доход.
Если начальное значение численности популяции станет хотя бы чуть
меньше стационарного значения, то численность резко уменьшается достигая нуля.
Т.о., нерасчетливое назначение квоты может иметь катастрофическое значение для
популяции. Если начальное значение станет больше стационарного, то в дальнейшем
популяция возрастает экспоненциально. Данная модель является неустойчивой
Логистическая модель
Биологические процессы рождения и смерти характерны не только для
людей, но и для любых животных. Поэтому вполне естественным шагом является
попытка описания демографических моделей с применением хорошо зарекомендовавших
себя популяционных моделей, использующихся в биологии [11].
Базовой моделью, описывающей динамику популяции животных, является
логистическая модель, предложенная Ферхюльстом [39]:
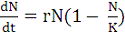
 (9)
(9)
которое можно также представить в виде

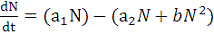 (10)
(10)
где первая скобка соответствует числу рождений B, а вторая - числу
смертей D в формуле (1), а r, K, a1, a2, b -
положительные коэффициенты, связанные соотношениями:
= a1 - a2 и 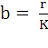
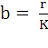
Логика уравнения (6) такова: рождаемость a1 является
постоянной, таким образом, число рождений B = a1N пропорционально
численности популяции, естественная смертность a2 также считается
постоянной, а квадратичная добавка bN2 в выражении для полной
смертности D = a1N+bN2 возникает из-за ограниченности
ресурса, не позволяющей популяции бесконечно расти. Коэффициент b называют
коэффициентом внутривидовой конкуренции [18].
В итоге, динамика популяции, описываемой логистическим уравнением,
имеет следующий вид. Вначале, когда численность животных мала, наблюдается
экспоненциальный рост с показателем r = a1 - a2. Затем,
по мере заполнения экологической ниши, рост замедляется и, в конечном счете,
численность популяции выходит на постоянный уровень K.
Значение параметра K, называемого емкостью экологической ниши
популяции, принципиально. Эта величина определяет равновесное состояние в
динамике популяции при заданных ресурсных ограничениях и определяет пределы ее
роста. Емкость экологической ниши популяции, определяется ограниченностью
пищевых ресурсов, мест для гнездования, многими другими факторами.
Таким образом, емкость экологической ниши представляет собой
системный фактор, который определяет ограниченность роста популяции в данном
ареале обитания.
Таким образом, логистическая модель отражает динамику популяций,
численность которой при любых начальных условиях приближается к некоторой
стационарной величине.
Если численность популяции отклонилась от стационарного значения,
то логистическая модель через некоторое время возвращает ее к стационарному
значению. Это свойство называется устойчивостью как стационарного значения, так
и системы в целом.
Уравнение (6) можно переписать в виде:
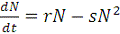
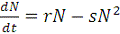 , (11)
, (11)
где s - коэффициент внутривидовой конкуренции.
Аналитическое решение данного уравнения имеет вид:
Эта формула описывает кинетическую кривую, то есть зависимость
численности популяции от времени. Ход кинетических кривых для разных начальных
условий представлен на рис.5.
В случае, если начальная численность
меньше половины максимальной, кривая x (t) имеет точку перегиба с координатами:

Ордината точки перегиба представляет собой
половину максимальной численности, а абсцисса зависит как от емкости популяции
K, так и от константы собственной скорости роста r, чем выше
генетические возможности популяции, тем скорее наступает перегиб на кривой
численности.
Примеры экспериментально наблюдаемой
динамики популяций, развивающихся по логистическому закону, приведены на рис.5,
при малых начальных численностях он имеет S-образный характер.
При изучении более сложных систем мы не
будем искать решение для N (t) в явном виде, а ограничимся исследованием
устойчивости их стационарных состояний. Проведем такое исследование и для
логистического уравнения.
Легко видеть, что уравнение стационарных
состояний f (N`) = 0 в данном случае имеет два корня:
Посмотрим, будут ли эти корни устойчивыми.
Для этого вначале воспользуемся аналитическим методом Ляпунова. Введем новую
переменную x, обозначающую отклонение переменной х от ее стационарного
значения:
= N - N`
Запишем линеаризованное уравнение для (4):
dn /dt = a n,
где 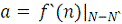
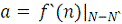
Напомним, что знак величины 
 определяет устойчивость соответствующей особой точки
определяет устойчивость соответствующей особой точки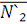
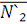 :
:
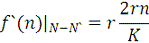 (12)
(12)
Подставив в выражение (12) значение первого корня 
 =0 мы получим
=0 мы получим 
 Будем считать, что величина r - коэффициент естественной
скорости роста популяции положительная
Будем считать, что величина r - коэффициент естественной
скорости роста популяции положительная
 = 0; - неустойчивая особая точка. Если же мы подставим в
выражение (12)
= 0; - неустойчивая особая точка. Если же мы подставим в
выражение (12) 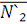
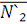 : =K, то получим
: =K, то получим
 - отрицательную величину. Это дает нам право утверждать, что
стационарное решение уравнения
- отрицательную величину. Это дает нам право утверждать, что
стационарное решение уравнения 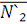
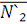 : = K соответствует устойчивому стационарному режиму
существования популяции в ограниченной среде. Проведем теперь исследование
устойчивости стационарных решений этого уравнения, исходя из графика функции
правой части. При переходе от отрицательных к положительным значениям х в точке
: = K соответствует устойчивому стационарному режиму
существования популяции в ограниченной среде. Проведем теперь исследование
устойчивости стационарных решений этого уравнения, исходя из графика функции
правой части. При переходе от отрицательных к положительным значениям х в точке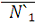
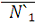 = 0 функция f (n) меняет знак с минуса на плюс, т.е. особая точка
неустойчива. Наоборот, в точке
= 0 функция f (n) меняет знак с минуса на плюс, т.е. особая точка
неустойчива. Наоборот, в точке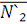
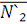 = К имеет место изменение знака f (n) с ростом x с плюса на
минус, следовательно, эта особая точка устойчивая. Несмотря на схематичность
положенных в ее основу представлений, логистическая кривая оказалась очень
хорошим приближением для описания кривых роста численности многих популяций. В
природе внутривидовая конкуренция не удерживает естественные популяции на
строго неизменном уровне, но действует в широком диапазоне начальных значений
плотности и приводит их к гораздо более узкому диапазону конечных значений,
определяя, таким образом, тенденцию к поддержанию плотности в определенных
пределах.
= К имеет место изменение знака f (n) с ростом x с плюса на
минус, следовательно, эта особая точка устойчивая. Несмотря на схематичность
положенных в ее основу представлений, логистическая кривая оказалась очень
хорошим приближением для описания кривых роста численности многих популяций. В
природе внутривидовая конкуренция не удерживает естественные популяции на
строго неизменном уровне, но действует в широком диапазоне начальных значений
плотности и приводит их к гораздо более узкому диапазону конечных значений,
определяя, таким образом, тенденцию к поддержанию плотности в определенных
пределах.
Разность между двумя кривыми (число рожденных минус число
погибших) представляет собой число особей, на которое изменяется численность
популяции в течение какой-либо стадии развития или за какой-нибудь промежуток
времени.
Пополнение популяции невелико при самых низких значениях
плотности, возрастает по мере ее увеличения, снова снижается при достижении
предельной плотности насыщения и становится отрицательным (смертность превышает
рождаемость), когда начальная плотность превышает К.
Логистическая модель с отловом
Данная модель учитывает конкуренцию и предполагает регулярный
отлов. Модель определяется формулой:
 (13)
(13)
Экономическая интерпретация модели (13) также синтезирует
экономические легенды двух предыдущих моделей: она описывает поведение фирмы
или группы фирм в условиях возможного насыщения рынка и при наличии постоянных
платежей, не зависящих от времени, дохода или капитала фирм.
На рис. 5 отображены результаты расчета нескольких траекторий (xn)
по формуле:
n+1 = (1,1 - 0,1 · xn) · xn - 0,02. (14)
при изменении n от 0 до 40.
На рисунке два стационарных состояния. Одно стационарное состояние
устойчиво, к нему притягиваются близкие траектории. Другое стационарное
состояние неустойчиво, близкие к нему траектории отталкиваются от него.
В этой модели небольшой перелов не приводит к катастрофе, поэтому
это есть модель с умеренным отловом.
Для определения двух стационарных значений численности популяции
полагаем 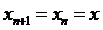 и получаем уравнение:
и получаем уравнение: 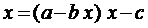 .
.
Имеется один устойчивый стационарный уровень (х = 0,72360) и один
неустойчивый (х =0,27639). Каждая траектория с начальным условием x0 >
0,2764 с течением времени приближается к устойчивому стационарному уровню.
Любое начальное условие x0 < 0,2763 ведет к гибели популяции.
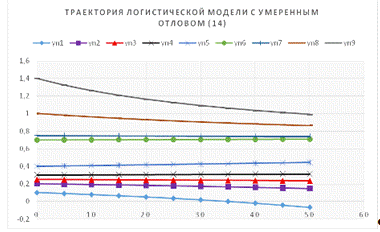
Рис. 5. Траектория логистической модели с умеренным отловом (14).
Модель (13) при малых значениях квоты имеет два стационарных
состояния:
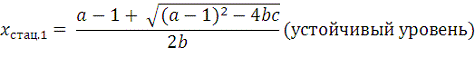

Если в этих формулах положить:
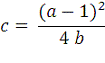
то корни xстац1 и x стац2
сольются.
Некоторые траектории модели (13) в этом критическом случае
изображены на рис. 10. Здесь a = 1,1; b = 0,1; c = 0,025.
Квота отлова c здесь достигла наибольшего уровня, при котором еще теоретически
возможно длительное выживание популяции. Но академик В.И. Арнольд назвал эту
ситуацию так: "оптимизация как путь к катастрофе".
Действительно, как показано на рисунке 6, если численность
популяции оказалась выше единственного стационарного уровня, то теоретически
она и остается выше него сколь угодно долго. Но если в силу какого-либо
"внемодельного" фактора (замора рыбы, очень холодной зимы в лесу,
браконьерства) численность популяции окажется чуть ниже стационарного уровня,
то, как видно на рис.6, популяция гибнет.

Рис. 6. Траектории логистической модели (13) при a =1,1; b
=0,1; c = 0,025. Критический случай. "Оптимизация как путь к
катастрофе".
И, наконец, если значение квоты вылова c станет больше
критического уровня, когда выполняется неравенство:
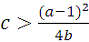
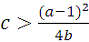 (15)
(15)
популяцию ждет гибель при любых начальных условиях.
Это следует из того, что при условии (15) уравнение для поиска
стационарных значений модели (13) имеет отрицательный дискриминант и поэтому не
имеет действительных корней. Ситуация переловаиллюстрируется рисунком 7,
на котором показаны некоторые траектории модели:
x n+1
= (1,1 - 0,1 · xn) · xn - 0,03 (11)
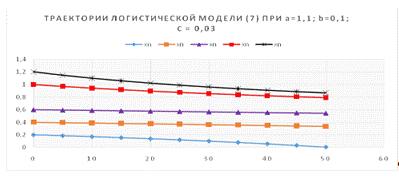
Рис. 7. Траектории логистической модели (7) при a =1,1; b = 0,1; c
= 0,03.
Перелов. При любых начальных условиях популяция гибнет.
То, что в модели динамики популяции мы назвали переловом, в
экономической интерпретации может означать разорение субъекта хозяйствования
под бременем постоянных платежей c, не соразмерных с его динамичностью и с
жесткостью условий рынка, которые характеризуются в формуле (13) коэффициентами
a и b соответственно. Это разорение является универсальным явлением: лучшие
начальные условия только замедляют, но не отменяют его.
2.2 Модель
военных конфликтов
Рассмотрим дискретные модели некоторых социальных явлений:
модели динамики популяций, в том числе модель "хищник - жертва",
модель военных конфликтов и другие. Новизна изложения в том, что
рассматриваются дискретные варианты моделей, которые ранее исследовались на
языке дифференциальных уравнений. Это помогает усвоить основные понятия
математических моделей лицам с невысокой математической подготовкой и поэтому
целесообразно рассматривать дискретные математические модели. В общем не
происходит практически никаких концептуальных потерь при переходе от
дифференциальных уравнений к дискретным. В дискретном варианте достаточно ясны
такие понятия, как начальные условия, траектории системы, стационарные
траектории, устойчивость и неустойчивость, сепаратрисы, оптимальные решения.
Пусть численности армий двух противоборствующих сторон на
некотором n-ом шаге военного конфликта равны xn и yn.
На следующем шаге (через год, неделю, день) армии уменьшаются. Рассмотрим
грубую схему, в которой за один шаг каждый воин армии x убивает в
среднем a
воинов армии y, а каждый воин армии y убивает в среднем b воинов армии x.
Таким образом, на n-ом шаге армия x теряет b · yn
воинов, армия y теряет a · xn воинов. Величины a и b характеризуют
вооруженность сторон. Так мы получаем модель
xn+1 = xn - b · yn
yn+1 = yn - a · xn.
(17)
Вначале численности армий x и y равны x0
и y0 соответственно.
Пара (x0, y0) называется начальным
условием.
Совокупность точек (xn, yn) назовем траекторией
конфликта. Конфликт заканчивается, когда либо xn 0, ноyn
> 0 (победа армии y), либо yn
0, ноyn
> 0 (победа армии y), либо yn  0, но xn
>0 (победа армии x). Рассмотрим модель, в которой вооруженность армии
y вдвое больше вооруженности армии x: в формулах (17) положим α = 0,05; β = 0,1. Получим модель:
0, но xn
>0 (победа армии x). Рассмотрим модель, в которой вооруженность армии
y вдвое больше вооруженности армии x: в формулах (17) положим α = 0,05; β = 0,1. Получим модель:
n+1 = xn - 0,1· ynn+1 = yn
- 0,05 · xn. (18)
Картина траекторий этой системы указана на рис.8. Мы видим,
что существует единственная прямолинейная траектория, заканчивающаяся
"вничью": она стремится к точке (0,0), символизирующей полное
взаимное истребление армий. Конфликт, начавшийся в одной из этих точек прямой,
теоретически будет длиться бесконечно. Упомянутая прямая - сепаратриса
(разделяющая).

Рис. 8. Траектория в модели военных конфликтов, определенной
системой (17).
При любых начальных условиях под сепаратрисой (линия сепаратрисы
проведена красной линией) конфликт завершается победой армии x;
начальные условия над сепаратрисой гарантируют победу армии y.
Найдем сепаратрису траекторий модели (17). Для того, чтобы точка (xn,
yn) лежала на сепаратрисе, требуется, чтобы выполнялось
равенство:
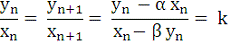
Отсюда,
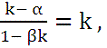
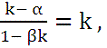 что равносильно
что равносильно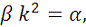
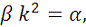 откуда
откуда 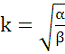
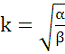 .
.
Получаем условие победы армии y:
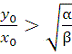
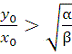 .
.
Этот результат можно трактовать так:
Если вооруженность армии y в n раз больше
вооруженности армии x, то для достижения равновесия численность армии x
должна быть в  раз больше численности армии y.
раз больше численности армии y.
Модель мобилизации
Модель мобилизации описывает динамику изменения численности
организации, вербующей себе сторонников: политических партий или движений,
религиозных групп и т.п. Пусть к началу n-ого периода существования
организации доля ее сторонников в населении равна xn. Тогда к
началу (n+1) - го периода:
. некоторая доля неохваченного населения примкнет к организации
вследствие агитации. Доля неохваченного населения равна (1-xn); доля
примкнувших равна · (1 - xn), где называется
коэффициентом агитируемости. Величина находится в интервале от
0 до 1.
. некоторая доля сторонников отойдет от организации (умрет,
разочаруется, будет исключена). Доля отошедших равна g· (1 - xn).
Числоg называется коэффициентом выбытия. Величина gнаходится в
интервале от 0 до 1.
Таким образом, доля членов организации в начале (n+1) - го
периода определится формулой
n+1
= xn + ¦ · (1-xn)
- g · xn,
илиn+1 = (1 - ¦ - g) · xn + ¦. (19)
Стационарное значение x величины xn, удовлетворяющее
уравнению (19), определяется формулой:
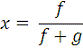
Ввиду неравенств 0 < ¦ < 1, 0 < g < 1 величина коэффициента
(1 - ¦ - g) в
уравнении (19) находится в интервале от (-1) до 1. В этих обстоятельствах при
любых начальных условиях величина xn приближается к
стационарному значению с ростом n. Но если ¦ + g < 1, то xn приближается к
стационарному значению монотонно; если ¦ + g > 1, то приближение идет с колебаниями.
На рис. 9 показаны траектории системы вида (19) при коэффициенте
агитируемости ¦, равном 0,04 и
коэффициенте выбытия g, равном 0,09. Таким образом, рис.9 иллюстрирует динамику
траекторий уравнения
n+1 = 0,09 · xn + 0,04. (20)
На рис.10 показан вариант колебательного приближения величины xn
к своему стационарному значению. Для удобства мы построили только одну
колебательную траекторию.
Здесь коэффициент агитируемости равен 0,6 и коэффициент
выбытия g равен 0,9. Таким образом, рис.12 иллюстрирует динамику одной из
траекторий уравнения
n+1 = 0,9 · xn + 0,6. (21)
Рисунки 9 и 10 демонстрируют устойчивость стационарной величины в
модели и устойчивость модели мобилизации в целом.
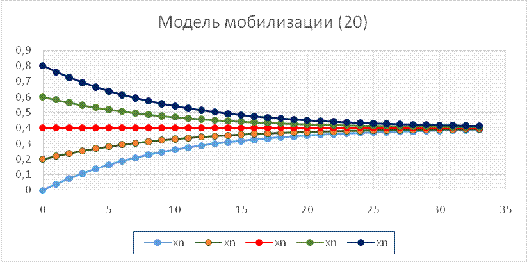
Рис. 9. Модель мобилизации (20). Вариант монотонного приближения к
стационарному значению.
Экономически интерпретация модели мобилизации (уравнения (19))
может быть, например, такой: доходы xn+1 в (n + 1) - м году
некоторого лица поступают из двух источников. Первый источник - величина (1 - f
- g) *xn - часть доходов прошлого года (возможно, весь доход
прошлого года за вычетом налогов). Второй источник - величина ¦ - постоянные поступления, не зависящие от
доходов прошлого года (возможно, пенсия или доходы от ценных бумаг).
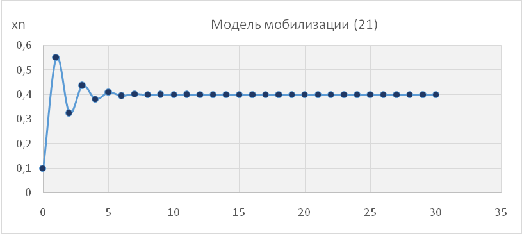
Рис. 10. Модель мобилизации (21). Вариант колебательного
приближения к стационарному значению.
Анализ показывает, что ежегодные доходы в модели со временем
приближаются к некоторой величине, не зависящей от начальных условий.
"Задача Иосифа Флавия".
Это известная математическая задача с историческим подтекстом.
Существует легенда, что Иосиф Флавий - известный историк первого
века - выжил и стал известным благодаря математической одаренности. В ходе
иудейской войны он в составе отряда из 41 иудейского воина был загнан римлянами
в пещеру. Предпочитая самоубийство плену, воины решили выстроиться в круг и
последовательно убивать каждого третьего из живых до тех пор, пока не останется
ни одного человека. Однако Иосиф вместе с одним из своих единомышленников счел
подобный конец бессмысленным. Он быстро вычислил спасительные места в порочном
круге, на которые поставил себя и своего товарища [24]. Задача заключается в
том, чтобы определить номера уцелевших воинов.
Сформулируем задачу на математическом языке для произвольного n.
Натуральные числа от 1 до n записаны в круг. Начиная с 1, вычеркивается
каждое третье число. Процесс продолжается так долго, пока не останется два не
вычеркнутых числа.
Эту задачу также можно решить, используя рекуррентное соотношение.
Однако можно использовать встроенную функциюСКМ Mathematica 10. Список,
вычеркнутых чисел, может быть получен с помощью функции Josephus [n, m],
реализованной в пакете расширения Combinatorica СКМ Mathematica. Данный пакет
включает в себя функции для построения графов и других комбинаторных объектов,
а также функции для работы с ними. Для использования функции Josephus [n,
m], где n - общее количество чисел, а m-е число - номер
вычеркивающего числа, сначала необходимо загрузить пакет Combinatorica с
помощью Needs ["Combinatorica`"] (рис. 11).
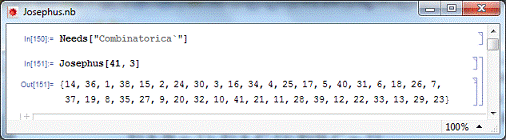
Рис.11. Вычисление функции Josephus [41, 3]
В результате вычисления функции Josephus [41, 3] формируется
список, который показывает, в каком порядке вычеркиваются числа, начиная с 1.
Так, единица будет вычеркиваться на 14-м шаге, двойка - на 36-м, тройка - на
1-м, четверка - на 38-м и так далее.
Обратная перестановка покажет последовательность вычеркнутых
чисел. Последние два числа в списке - искомые числа (рис.12).
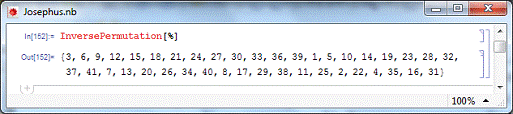
Рис.12. Последовательность вычеркнутых чисел
Представим данное решение более наглядным. Для отображения
порядковых номеров чисел используем функцию EmptyGraph [n] которая
строит пустой граф с n вершинами (рис.13).

Рис.13. Формирование пустого графа
Для визуализации последовательности вычеркивания чисел используем
модуль манипуляций Manipulate (рис.14). Данный модуль позволяет создавать
различные интерактивные средства.
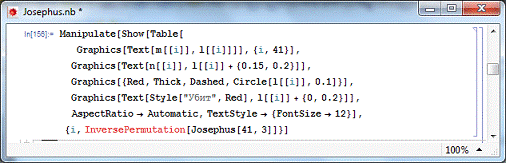
Рис.14. Реализация визуализации решения
Используя данное интерактивное средство, можно узнать для кажого
чила, на каком шаге оно будет вычеркнуто.
2.3 Некоторые
понятия теории игр и теории принятия решения
Теория игр первоначально и рассматривала
экономические модели вплоть до 1950-х она оставалась формальной теорией в
рамках математики. Но уже с 1950-х гг. начинаются попытки применить методы
теории игр не только в экономике, но в биологии, кибернетике, технике,
антропологии, социологии. Во время Второй мировой войны и сразу после нее
теорией игр серьезно заинтересовались военные, которые увидели в ней мощный
аппарат для исследования стратегических решений.
Большим вкладом в применение теории игр
стала работа Томаса Шеллинга, нобелевского лауреата по экономике 2005 г.
"Стратегия конфликта".Т. Шеллинг рассматривает различные
"стратегии" поведения участников конфликта. Эти стратегии совпадают с
тактиками управления конфликтами и принципами анализа конфликтов в
конфликтологии и в управлении конфликтами в организации.
Основные понятиями теории игр.
Математическая модель конфликтной ситуации называется игрой, стороны,
участвующие в конфликте - игроками.
Выбор и осуществление одного из
предусмотренных правилами действий называется ходом игрока. Периоды, в
течение которых игроки делают свои ходы, называются этапами игры.
Выбранные на каждом этапе ходы в конечном счете определяют "платежи"
(выигрыш или убыток) каждого игрока, которые могут выражаться в
материальных ценностях или деньгах. Еще одним понятием данной теории является
стратегия игрока. Стратегией игрока называется совокупность правил,
определяющих выбор его действия при каждом личном ходе в зависимости от
сложившейся ситуации. Обычно в процессе игры при каждом личном ходе игрок делает
выбор в зависимости от конкретной ситуации. Однако в принципе возможно, что все
решения приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это
означает, что игрок выбрал определённую стратегию, которая может быть задана в
виде списка правил или программы. (Так можно осуществить игру с помощью ЭВМ).
Иначе говоря, под стратегией понимаются возможные действия, позволяющие игроку
на каждом этапе игры выбирать из определенного количества альтернативных
вариантов такой ход, который представляется ему "лучшим ответом" на
действия других игроков. Оптимальные стратегии должны также удовлетворять
условию устойчивости, т.е. любому из игроков должно быть невыгодно
отказаться от своей стратегии в этой игре. Если игра повторяется достаточно
много раз, то игроков может интересовать не выигрыш и проигрыш в каждой
конкретной партии, а средний выигрыш (проигрыш) во всех партиях. Целью
теории игр является определение оптимальной стратегии для каждого игрока. При
выборе оптимальной стратегии естественно предполагать, что оба игрока ведут
себя разумно с точки зрения своих интересов.
Рассмотрим задачу, которая введет нас в систему понятий
теории игр и принятия решений.
Постановка задачи: Корпорация "Атлант" выделяет
определенную сумму денег на закупку оборудования для работы в следующем году.
Выбор таков: она может закупить оборудование для производства военного
снаряжения или оборудование для переработки сельхоз продукции.
Эксперты корпорации написали следующий отчет:
"Многое зависит от развития конфликта с соседней страной
Марфией. Мы не знаем, перейдет ли он в войну. Мы не можем даже оценить
вероятность перехода конфликта в фазу военных действий. Но мы оценили
эффективность инвестиций в каждом из двух возможных политических сценариев:
) В случае войны каждый рубль, вложенный в
производство военного снаряжения, даст примерно 5 рублей прибыли; каждый руль,
вложенный в переработку сельхозпродукции, даст 1 рубль прибыли.
2) В случае отсутствия военных действий каждый рубль,
вложенный в производство военного снаряжения, даст 1 рубль убытка; каждый руль,
вложенный в переработку сельхозпродукции, даст 3 рубля прибыли. "
Руководство корпорации должно решить, как получить наибольшую
гарантированную прибыль.
Сразу скажем. Что нет единственно правильного решения для
руководства в условиях поставленной задачи. Можно дать только некоторый анализ
ситуации, которую в математике принято называть игрой.
Представим доступную нам информацию в виде платежной матрицы
(таблицы) игры (рис.15).
|
война мир
|
|
Стратегия №1: инвестиции в военную отрасль
|
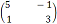
|
|
Стратегия №2: инвестиции в сельское хозяйство
|
|
Рис. 15. Платежная матрица игры
Число в - й строке и в 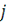
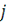 -м столбце (1≤
-м столбце (1≤
 ) матрицы обозначим посредством
) матрицы обозначим посредством 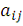
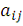 . В нашем случае
. В нашем случае 
 11 = 5,
11 = 5, 
 12 = - 1,
12 = - 1, 
 21 = 1,
21 = 1, 
 22 = 3.
Причем номер строки в матрице есть номер выбранной стратегии, а столбец -
возможная ситуация (война или мир).
22 = 3.
Причем номер строки в матрице есть номер выбранной стратегии, а столбец -
возможная ситуация (война или мир).
Руководство корпорации вольно решать, будет ли корпорация
применять чистые стратегии, то есть все средства вкладывать в одну из отраслей,
или смешанные стратегии, при которых часть средств направляется в одну отрасль,
оставшаяся - в другую.
Чистые стратегии. Выбрав - ю стратегию (1 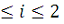
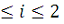 ), корпорация в худшем случае получит прибыль на рубль вложений,
равную
), корпорация в худшем случае получит прибыль на рубль вложений,
равную 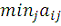
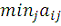 . В нашем случае
. В нашем случае 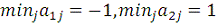
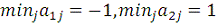 .
.
Если руководство ищет наибольший гарантированный выигрыш, то ему
следует выбрать ту из стратегий, такое значение 
 при котором этот минимум является наибольшим. При котором
достигается
при котором этот минимум является наибольшим. При котором
достигается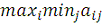
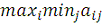 . В нашей игре это стратегия №2. Выигрыш корпорации в этом случае
равен:
. В нашей игре это стратегия №2. Выигрыш корпорации в этом случае
равен:
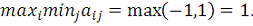
В некотором смысле окончательным решением поставленной задачи
служит вывод: наибольший гарантированный выигрыш при применении чистых
стратегий рамен 1 и достигается при стратегии №2. Этот выигрыш называют
максимином, а указанную стратегию - максиминной стратегией.
Но это не значит, что корпорации следует непременно применять
стратегию №2 (и что в подобных ситуациях на практике именно она выбирается).
Если руководство склонно к риску или имеет основания ожидать военного варианта
конфликта с соседями. То она может выбрать стратегию №1, с возможностью
заработать в случае успеха значительно больше максимина (пять рублей прибыли на
рубль вложений), но и с опасностью получить значительно меньше максимина (рубль
убытков на рубль вложений).
Смешанная стратегия. Теперь рассмотрим более изощренный вариант. Корпорация решила
некоторую часть 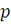
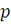 средств (
средств (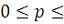
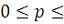 1) направить в военную отрасль, а остальные средства (долю, равную
(1-
1) направить в военную отрасль, а остальные средства (долю, равную
(1-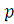
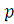 )) направить в сельское хозяйство. Это называется смешанной
стратегией. Вопрос ставится так: как выбрать значение
)) направить в сельское хозяйство. Это называется смешанной
стратегией. Вопрос ставится так: как выбрать значение 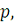
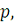 чтобы гарантированный выигрыш был наибольшим.
чтобы гарантированный выигрыш был наибольшим.
Чистые стратегии являются крайними частными случаями смешанной.
Полагая в смешанной стратегии 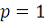
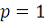 , получим первую чистую стратегию. Полагая
, получим первую чистую стратегию. Полагая 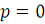
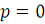 , получим чистую вторую. Решая задачу максимизации гарантированной
прибыли, мы полагаем, что и в смешанной стратегии имеют место прибыли на каждый
рубль инвестиций, указанные платежной матрицей на рис 15. Вначале полагаем, что
нас ждет военный вариант развития конфликта. Вычислим
, получим чистую вторую. Решая задачу максимизации гарантированной
прибыли, мы полагаем, что и в смешанной стратегии имеют место прибыли на каждый
рубль инвестиций, указанные платежной матрицей на рис 15. Вначале полагаем, что
нас ждет военный вариант развития конфликта. Вычислим 
 на каждый рубль инвестиций как функцию от
на каждый рубль инвестиций как функцию от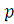
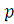 . Она равна
. Она равна

Затем рассмотрим мирный вариант. В этом варианте прибыль 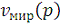
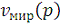 на каждый рубль инвестиций такова:
на каждый рубль инвестиций такова:
На рисунке 16 указаны графики двух функций
 при значениях
при значениях 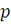
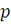 , меняющихся от 0 до 1.
, меняющихся от 0 до 1.

Рис. 16. Зависимость прибылей 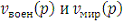
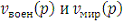 корпорации от доли
корпорации от доли 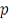
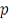 инвестиций в военную отрасль.
инвестиций в военную отрасль.
При изменении 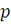
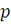 от 0 до 1 гарантированный выигрыш
от 0 до 1 гарантированный выигрыш 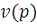
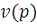 определятся формулой:
определятся формулой:

График 
 показан на рис. 17 жирной ломанной линией. Задача руководства
корпорации - найти максимум гарантированного выигрыша, то есть найти:
показан на рис. 17 жирной ломанной линией. Задача руководства
корпорации - найти максимум гарантированного выигрыша, то есть найти:

Эта задача на максимин решается просто: самая высокая точка на
графике функции 
 и есть требуемый максимин.
и есть требуемый максимин.
Чтобы найти значение 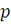
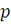 , при котором он достигается, решим уравнение:
, при котором он достигается, решим уравнение:
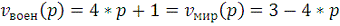
Получаем 
 , при этом
, при этом 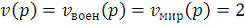
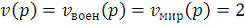 .
.
Вывод таков: наибольшую прибыль, равную двум рублям на рубль
инвестиций, корпорация получит, если четверть средств инвестирует в военную
отрасль и три четверти - в сельское хозяйство.
Впрочем, и здесь готовность к риску или интуитивное понимание
политических перспектив могут сместить оценку в ту или иную сторону.
В нашей задаче был один активный игрок (корпорация) и один
"пассивный" - государство. Государство выбирает военную или мирную
стратегию в конфликте с соседями, но в легенде предыдущей задачи государство не
заинтересовано ни в выигрыше, ни в проигрыше корпорации.
Есть и другой тип игр, в которых явно участвуют два игрока с
противоположными интересами (например, два конкурента на рынке с ограниченным
спросом). Такая игра с нулевой суммой также задается платежной матрицей
(таблицей), и методика поиска оптимальных стратегий в таких играх схожа с
рассмотренной выше.
Заключение
Социологическое исследование - это надежный способ познания
социальной реальности, позволяющий постичь сущность тех или иных явлений и
процессов. Оно дает возможность специалисту в любой области учесть социальные
последствия определенных действий, повысить эффективность деятельности,
уменьшить возможность и последствия ошибок.
Проблемы социальных наук, биологии, экологии часто
оказываются чрезвычайно сложными, они описываются большим числом трудно
определяемых переменных, взаимосвязи между которыми нелегко установить. Нередко
для возможности решения таких задач, приходится делать довольно сильные упрощающие
допущения. Если эти допущения формулируются в математических терминах, то
удается избежать многих двусмысленностей естественного языка и воспользоваться
мощью математических рассуждений.
В работе описаны дискретные модели некоторых социальных
явлений: модели динамики популяций, в том числе модель
"хищник-жертва", модель военных конфликтов и другие, рассматриваются
дискретные варианты моделей, которые ранее исследовались на языке
дифференциальных уравнений. Это помогает усвоить основные понятия математических
моделей без производных и интегралов. Дискретные математические методы
достаточно ясно раскрывают такие понятия, как начальные условия, траектория
системы, стационарные траектории, устойчивость и неустойчивость, сепаратрисы,
оптимальные решения.
Решены задачи теории игр и принятия решения - раздела,
изучающего различные ситуации сделок, относящихся, например, к
землепользованию, созданию угрожающего положения, проблеме очистки воды, а
также к ряду ситуаций голосования, рассмотрения различных групп, члены которых
осуществляют сделку, к группам, пытающимся прийти к совместному решению.
В работу не включены такие методы как графы и задачи
линейного программирования, которые также хорошо подходят для исследования
социологических процессов.
Система компьютерной математики (CKM) Mathematica 10
поддерживает числа любой точности, причем для внутренних расчетов часто в целях
повышения качества результата используются еще более точные значения. Для
повышения точности вычисления среда использует символьные вычисления, т.е.
пытается упростить или преобразовать выражение, и лишь затем производит
численный расчет. В CKM Mathematica 10 решена задача "Иосифа Флавия",
для построения графиков функций в работе использовались также MicrosoftWord,
СКМ Mathcad, Excel.
Список
литературы
1. Альберт
М., Мескон М., Хедоури Ф. Основы менеджмента. - М.: Дело. 2012. С.376-385.
2. Арнольд
В.И. "Жесткие" и "мягкие" модели. Доклад на
научно-практическом семинаре. Аналитика в государственных учреждениях. М. 2009
. Батыгин
Г.С. Лекции по методологии социологических исследований: учеб. для вузов. М.:
Аспект-Пресс, 2009.286 с.
. Бутенко
И.А. Организация прикладного социологического исследования. М.: Тривола,
2014.423 с.
. Власова
М. л. Социологические методы в маркетинговых исследованиях: учеб. пособие для
вузов. М.: Изд. дом ГУВШЭ, 2006.710 с.
. Вольтерра
В. Математическая теория борьбы за существование.М. 2011.
. Горшков
М. к., Шереги Ф.Э. Прикладная социология: учеб. пособие для вузов. М.: Центр
социального прогнозирования, 2013.312 с.
. Девятко
и.Ф. Методы социологического исследования. М.: КДУ, 2013.296 с.
. Добреньков
В.И., Кравченко А.И. Методы социологического исследования: учеб. М.: ИНФРА-М,
2006.768 с.
. Ильин
В.И. Драматургия качественного полевого исследования. СПб.: Интерсоцис,
2006.256 с.
. Квале
С. исследовательское интервью. М.: смысл, 2013.301 с.
. Кипнис
М.М. Модели социальных явлений в коротком курсе математики. Челябинск, ЮУрГУ,
2009.
. Крюгер
Р., Кейси М.С. Фокус-группы: практ. руководство. М.: Изд. дом
"Вильямс", 2012.
. Малхорта
Нэреш К. Маркетинговые исследования: практ. руководство / пер. с англ. М.: Изд.
дом "Вильямc", 2012.960 c.
. Моосмюллер
Г., Ребик Н.Н. Маркетинговые исследования с SPSS: учеб. пособие. М.: ИНФРА-М,
2009.160 с.
. Новиков
Д.А. "Статистические методы в педагогических исследованиях (типовые
случаи)". М.: МЗ-Пресс, 2014. - 67 с.
. Ноэль-Нойман
Э. Общественное мнение. Открытие спирали молчания / пер. с нем.; общ. ред. и
предисл.Н.С. Мансурова. М.: Прогресс-Академия; Весь Мир, 2006.352 с.
. Плотинский
Ю.М. Модели социальных процессов: учеб. пособие для высших учеб. заведений. M.:
Логос, 2001.296 с.
. Плотинский
Ю.М. Математическое моделирование динамики социальных процессов.М., Изд-во МГУ.
2012.
. Робертс
Ф.С. Дискретные математические модели с приложениями к социальным и
экологическим задачам.М. 2011.
. Рогозин
Д.М. Когнитивный анализ опросного инструмента. М., 2012.
. Рой
О.М. Исследования социально-экономических и политических процессов: учеб. для
вузов. СПб.: Питер, 2014.364 с.
. Татарова
Г.Г. Методология анализа данных в социологии (введение): учеб. для вузов. М.:
NOTA BENE, 2009.224 с.
. Толстова
Ю.Н. Анализ социологических данных: Методология, дескриптивная статистика,
изучение связей между номинальными признаками. М.: Научный мир, 2010.352 с.
. Троцук
И.В. Качественное социологическое исследование: предпосылки и логика
проведения: конспект лекций. М.: Изд-во РУДН, 2010.178 с.
. Ядов
В.А. Стратегия социологического исследования: описание, объяснение, понимание
социальной реальности / В.А. Ядов, В.В. Се - менова.6-е изд. М.: Академкнига:
Добросвет, 2013.596 с.
27. http://mzpress.
narod.ru <http://mzpress.narod.ru/>
. http://parlamentchr.ru/legislation
. http://www.mtas.ru/uploads/stat.
zip <http://www.mtas.ru/uploads/stat.zip>
. http://www.myshared.ru.
. <http://www.socioguru.ru/sgurus-776-1.html>