Распространение волн в нелинейных диспергирующих средах

Контрольная работа

Распространение волн в нелинейных диспергирующих средах

Содержание

Нелинейная поляризация

Метод последовательных приближений и ММА

Генерация второй гармоники

Параметрическая генерация и усиление волн

Литература

Нелинейная поляризация

В сильных электрических полях поляризация среды уже не пропорциональна напряженности электрического поля. Для постоянных полей можно записать:

,

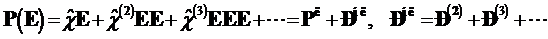где 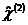 - тензор третьего ранга квадратичной восприимчивости, 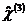 - тензор четвертого ранга кубической восприимчивости. С учетом частотной дисперсии материальные уравнения следует записывать в виде разложения по линейной, квадратичной, кубической и т. д. поляризациям:

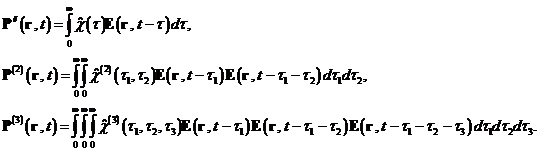
Тогда суперпозиция монохроматических волн

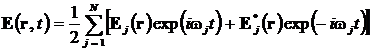 (.1)

возбудит в среде волны линейной и нелинейной поляризации

 (.2)

на комбинационных частотах

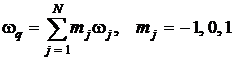. (3)

Каждая частота wj встречается в сумме (3) столько раз, какова степень нелинейности. При этом каждую амплитуду Pq(r), в свою очередь, можно разделить на линейную и нелинейную поляризации. Линейная поляризация возбуждается на каждой частоте независимо:

.

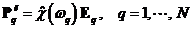Для среды без центра инверсии с квадратичной нелинейностью каждое из полей возбуждает квадратичные поляризации на удвоенной и нулевой частотах:

,

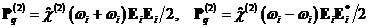то есть имеют место генерация второй гармоники и детектирование волны. Кроме того, две электромагнитные волны с разными частотами wi и wk возбуждают две поляризации среды на суммарной и разностной частотах:

.

Так как в результате взаимодействия двух волн возникает третья волна на комбинационной частоте, то говорят, что на квадратичной нелинейности происходит трехчастотное взаимодействие. В общем случае выражение для тензора квадратичной восприимчивости как функции частоты имеет вид

. (4)

Если одно из полей является постоянным (wk = 0, Ek = E0), то квадратичная поляризация имеет одну частоту:

.

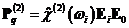Это линейный электрооптический эффект Поккельса, состоящий в изменении диэлектрической проницаемости кристалла под действием постоянного электрического поля, .

Если среда имеет центр инверсии, то P(-E) = -P(E) и нелинейностью низшего порядка является кубическая нелинейность, при которой возможно четырехволновое взаимодействие. Каждая из взаимодействующих волн порождает третью гармонику:

и нелинейную поляризацию на собственной частоте

.

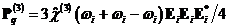Это высокочастотный эффект Керра, благодаря которому диэлектрическая проницаемость кристалла зависит от интенсивности волны:

.

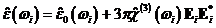Кроме того, диэлектрическая проницаемость среды может меняться под действием другой волны:

, .

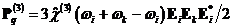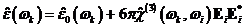Такое воздействие одной волны на другую называется кросс-модуляцией. Если wi = 0, то есть диэлектрическая проницаемость меняется под действием постоянного поля Ei = E0, то . Это квадратичный электрооптический эффект.

В общем случае три волны с частотами wi, wj, wk возбуждают в среде волны кубической поляризации на комбинационных частотах wq = wi ± wj ± wk, соответствующая частотная зависимость тензора кубической восприимчивости имеет вид:

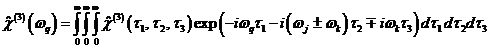. (5)

При наличии нелинейной восприимчивости уравнения Максвелла -можно свести к волновому уравнению вида

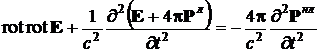. (6)

Подставляя сюда выражение для электрического поля вида (1) и нелинейной поляризации (2) в виде суммы монохроматических волн, можно получить цепочку уравнений Гельмгольца

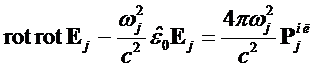, (7)

куда необходимо подставить выражение для нелинейной поляризации, соответствующее исследуемому эффекту. Для решения уравнений Гельмгольца используют приближенные методы.

Метод последовательных приближений и ММА

Пусть среда является слабонелинейной, то есть отношение величины нелинейной поляризации к величине электрического поля на границе среды является малым параметром: |Рнл|/|Е| = m << 1. Пусть

Ej = Ej(0) + mEj(1) + m2Ej(2) + ... , (8)

тогда

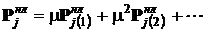. (9)

Подставляя эти разложения в уравнение Гельмгольца (7) и собирая слагаемые одного порядка малости по m, получим:

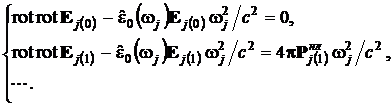 (10)

В нулевом приближении системы уравнений (10) волны, падающие на границу среды, распространяются в ней как бы в отсутствие нелинейности. Для следующего шага нужно задаться видом нелинейности, например Р(2) или Р(3), в зависимости от конкретной задачи, и, выразив с помощью соотношений (8) и (9) нелинейную поляризацию  через Ej(0) и Ej(1), подставить ее во второе уравнение системы (10) и т. д. Например, для квадратичной нелинейности при трехчастотном взаимодействии

,

. (11)

Таким образом, можно найти первое приближение по полю из второго уравнения (10) и первое приближение по поляризации из уравнения (11). Далее по аналогии находится второе и, если нужно, третье приближение. Практический смысл эта процедура имеет только тогда, когда поправки к нулевому приближению малы, то есть амплитуда возбуждаемых в среде волн мала в сравнении с амплитудой падающих волн, и можно ограничиться первыми двумя приближениями. При этом невозможно исследовать эффекты самовоздействия, генерации гармоник и т. д. В подобных случаях применяется метод ММА.

Если среда является слабонелинейной и слабодиссипативной, то амплитуда распространяющейся в ней плоской монохроматической волны будет мало меняться на расстоянии порядка длины волны, тогда пространственные гармоники поля и поляризации в разложениях (1) и (2) соответственно можно представить в виде волн ММА:

Ej(r) = ejAj(mkjr)exp(ikjr), Pq(r) = eqPq(mkpqr)exp(ikpqr), |m| << 1, (12)

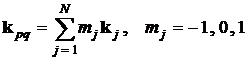. (13)

Отметим, что коэффициенты mj в сумме (13) такие же, как и в сумме (3) для фиксированного номера q гармоники нелинейной поляризации.

Рассмотрим однородное неизотропное полупространство z > 0. Отметим, что ММА-волна (12) совершенно аналогична волне вида (3.14), только в нашем случае амплитуда волны меняется вдоль волнового вектора kj, а не поперек его, как в случае волнового пучка, но для математических выкладок это не существенно. Соответственно, уравнение Гельмгольца (7) отличается от волнового уравнения (3.1) для линейной среды только наличием нелинейной поляризации в правой части. Тогда, полагая 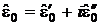, перепишем уравнение (3.12) для случая малых потерь в виде

. (14)

Уравнение (3.17) при этом принимает вид

В силу соотношения (14) выражение в фигурных скобках равно нулю. Домножая уравнение скалярно слева на вектор ej, получим по аналогии с выводом соотношения (3.18):

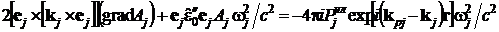. (15)

В п. 3.2 было показано, что вектор [ej ´ [kj ´ ej]] направлен вдоль лучевого вектора sj j-й гармоники. Обозначим bj = [ej ´ [kj ´ ej]] = bjsj/sj. Учитывая, что

sjej = 0, получим bj = bjsj/sj = {kj - ej(kjej)}sj/sj = kjcos(bj), где bj - угол между волновым и лучевым векторами j-й гармоники, kj - волновое число j-й гармоники. В однородном полупространстве амплитуда волны может зависеть только от координаты z. Тогда градиент амплитуды направлен вдоль нормали к поверхности среды и уравнение (15) принимает вид

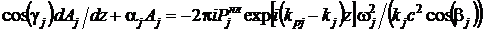, (16)

где 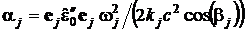 - коэффициент поглощения на частоте wj, gj - угол преломления j-й гармоники, то есть угол между ее лучевым вектором sj и нормалью к поверхности падения.

В правой части укороченного уравнения (16) содержится осциллирующий множитель exp[i(kpj - kj)r], который сильно влияет на характер взаимодействия волн, так как именно он определяет работу внешней силы (волны нелинейной поляризации) по возбуждению поля. Если этот множитель равен единице, то работа имеет постоянный знак на всем протяжении нелинейной среды и взаимодействие наиболее эффективно. С учетом соотношения (14) этот случай имеет место при выполнении условия фазового синхронизма, или фазового согласования:

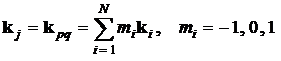, (17)

волна гармоника поляризация частота

Если условие синхронизма (17) заведомо не выполняется, то множитель exp[i(kpj - kj)r] быстро осциллирует при распространении волны в среде, и нелинейная поляризация слабо влияет на распространение волны. В диспергирующей среде условию синхронизма (167) могут удовлетворять 3 - 4 волны, которые и участвуют в нелинейном взаимодействии, амплитудами же других волн на комбинационных частотах можно пренебречь.

В средах без дисперсии с малым затуханием все волны имеют одинаковую скорость и условие синхронизма (17) выполняется для всех гармоник, при этом нелинейные эффекты накапливаются с расстоянием, и даже при малой нелинейности на достаточно больших расстояниях возникают сильные нелинейные искажения исходного профиля волны. В частности, в такой среде гармоническая волна может превратиться в разрывную ударную волну. Этот случай характерен для акустики.

Генерация второй гармоники

Пусть на среду с квадратичной нелинейностью падает нормально плоская монохроматическая волна частоты w. Будем считать, что самовоздействием, генерацией высших гармоник и детектированием можно пренебречь, тогда в среде распространяются только две волны: на основной и удвоенной частоте, w1 = w, w2 = 2w, j = 1, 2. При взаимодействии волн первой и второй гармоник в среде возбуждаются волны квадратичной поляризации. Для изотропной среды с учетом соотношений (3) и (13) получаем:

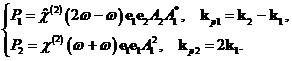 (18)

Подставим эти выражения в укороченные уравнения (16) и, полагая, что волны затухают слабо, пренебрежем слагаемым ajAj в сравнении со слагаемым dAj/dz. Тогда уравнения для комплексных амплитуд основной волны А1 и второй гармоники А2 принимают вид:

 (19)

Здесь Dk = k2 - 2k1 = 2w(n2 - n1)/с - малая расстройка волновых векторов,  - показатель преломления на частоте wj, , .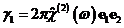

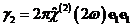При отсутствии затухания (a = 0, e0" = 0) и потока энергии извне полная энергия волны должна сохраняться, то есть s1 + s2 = const. Учитывая формулу (1.36) для потока энергии в плоской волне , получим:

n1|A1|2 + n2|A2|2 = const. (20)

Продифференцировав соотношение (20) по координате z и подставив в него значения производных из уравнений (19), получим, что коэффициенты нелинейности среды должны быть равны: g1 = g2 = g. Кроме того, комплексные амплитуды волн удовлетворяют еще одному закону сохранения

, (21)

которое можно доказать, дифференцируя соотношение (21) по z и учитывая формулы (19).

На входе в нелинейную среду при z = 0 естественно задать граничные условия в виде А1(0) = Е01, А2(0) = 0. Если |А2| << |А1|, то можно пренебречь слабым обратным влиянием второй гармоники на основную волну и положить в первом уравнении системы (19) dA1/dz = 0. Тогда А1(z) = Е01 = const, а второе уравнение системы (19)

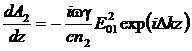
имеет с учетом граничного условия решение в виде

. (22)

Если выполняется условие фазового синхронизма (17), то есть k2 = 2k1,

n2 = n1, Dk = 0, то ,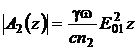

то есть амплитуда второй гармоники растет пропорционально пройденному волной расстоянию, но в силу наложенного ограничения должно выполняться условие |А2| << E01. Это ограничение справедливо на расстоянии

. (23)

При рассогласовании фазовых скоростей, то есть при n2 ¹ n1, уравнение (22) описывает пространственные биения второй гармоники |А2| ~ |sin(Dkz/2)| с первым максимумом на расстоянии длины когерентного взаимодействия

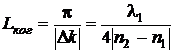. (24)

Соответственно, максимум амплитуды второй гармоники на этой длине равен

,

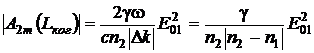и условию малости второй гармоники в сравнении с первой отвечает сильная дисперсия нелинейной среды:

|n2 - n1| >> gE01/n2, Lког << Lнл. (25)

Если условие (25) нарушено, например за счет большой амплитуды поля или слабой дисперсии, возможно эффективное возбуждение второй гармоники с большой амплитудой порядка амплитуды основной волны. Для этого случая введем действительные амплитуды и фазы гармоник:

(z) = A0j(z)exp[ijj(z)], j = 1, 2.

Подставляя это выражение в уравнения (19), (20) и (21) и отделяя мнимую и действительную части, получим:

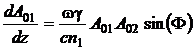, (26)

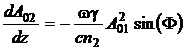, (27)

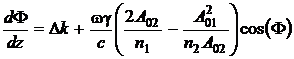, (28)

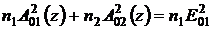, (29)

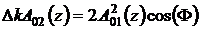, (30)

где Ф = 2j1(z) - j2(z) + Dkz.

При фазовом синхронизме из условия (17) следует, что Dk = 0, в этом случае из уравнения (30) следует, что cos(Ф) = 0, в свою очередь, из уравнения (28) следует, что Ф = const = ±p/2. Из уравнения (27) вытекает, что физический смысл имеет значение Ф = -p/2, sin(Ф) = -1, так как амплитуда второй гармоники А02 должна нарастать при распространении волны вглубь среды. Тогда

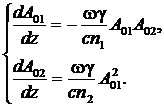 (31)

В условиях фазового синхронизма n2 = n1 и закон сохранения энергии (29) принимает вид 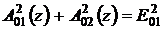, что позволяет легко проинтегрировать систему уравнений (31):

,

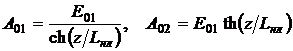где Lнл определена соотношением (23). Нетрудно видеть, что А02(Lнл) = 0,76Е01.

Таким образом, при точном согласовании фазовых скоростей основной волны и второй гармоники можно, в принципе, получить почти полное преобразование энергии волны во вторую гармонику. Обычно такая синхронизация достигается в одноосном отрицательном кристалле, в котором существуют направления синхронизма, вдоль которых скорость обыкновенной волны основной гармоники равна скорости необыкновенной волны второй гармоники.

Параметрическая генерация и усиление волн

Рассмотрим в среде с квадратичной дисперсией трехволновое взаимодействие волн с частотами w1 < w2 < w3. В силу соотношений (3) и (13)

w3 = w2 + w1, kp1 = k3 - k2, kp2 = k3 - k1, kp3 = k2 + k1, соответственно

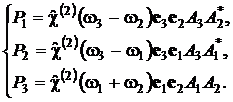 (32)

Подставляя эти выражения в правые части укороченных уравнений (16) для случая нормального падения на плоскую границу изотропной среды без потерь, получим:

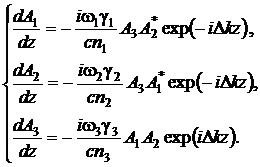 (33)

Здесь обозначено: 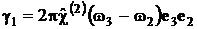, , , Dk = k3 - k2 - k1,.

Закон сохранения энергии для трех волн в бездиссипативной среде имеет вид, аналогичный соотношению (29)

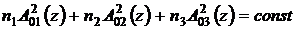. (34)

Продифференцировав это равенство по z и подставив в него производные из уравнений (33), получим, что коэффициенты нелинейности должны быть равны g1 = g2 = g2 = g. С учетом этого умножим первое уравнение системы (33) на 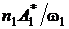, а второе уравнение - на , а затем сложим полученные уравнения друг с другом и со своими комплексными сопряжениями:

.

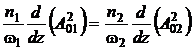Проделав аналогичные операции с первым и третьим уравнениями и учитывая граничные условия А0j(0) = E0j, j = 1, 2, 3, получим соотношения Менли - Роу:

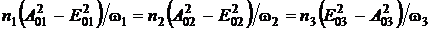. (35)

Из уравнения (35) видно, что если амплитуда волны на высшей частоте w3 уменьшается, то энергия переходит одновременно в обе низкочастотные волны, и наоборот. Рассмотрим случай, когда одна из волн гораздо мощнее двух других. В случае мощной низкочастотной волны из уравнений Менли - Роу (35) следует, что ее плотность энергии (квадрат амплитуды) меняется в пределах 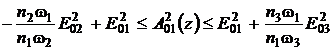. Поскольку по предположению на входе среды E01 >> E02, E03, то амплитуда мощной волны при распространении меняется незначительно.

Аналогично для амплитуд "слабых" волн w2 и w3 получим

, .

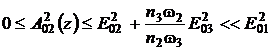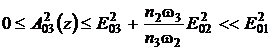Поскольку поле мощной волны w1 можно считать постоянным, а полями волн w2 и w3 можно пренебречь, то, подставляя в правую часть первого уравнения системы (33) значения А2 = А3 = 0, получаем А1(z) = const = Е01. Подставляя это значение во второе и третье уравнения системы (33), легко решаем ее:

|A02,3(z)| = |E02,3cos(z/Lб) + B2,3sin(z/Lб)|,

где константы В2 и В3 определены из граничных условий и введена длина биений

.

Таким образом, в поле мощной низкочастотной волны слабые волны на других частотах не усиливаются, а их амплитуды испытывают пространственные биения с характерным масштабом Lб, причем появление или исчезновение расстройки Dk не влияет на характер процесса, меняется только период биений.

Иное - в случае мощной высокочастотной волны w3. Из соотношений Менли - Роу (35) следует, что , то есть мощная высокочастотная волна может отдать всю свою энергию слабым низкочастотным волнам. Это эквивалентно распадению мощной высокочастотной волны в среде с квадратичной нелинейностью вследствие синхронного трехволнового взаимодействия на две низкочастотные волны - распадная неустойчивость. На начальном этапе взаимодействия ВЧ-поле можно считать заданным, то есть

A03(z) » E03 >> A01(z), A02(z). При этом третье уравнение системы (33) принимает вид dA3/dz = 0, то есть A3(z) = const = E03, а первые два уравнения образуют систему связанных линейных дифференциальных уравнений.

Если дополнительно учесть в левых частях системы уравнений (33) слабую диссипацию по типу уравнения (16), получим

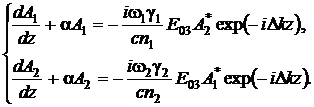
Решение этих уравнений совместно с законом сохранения энергии (34) дает

|A01,2(z)| = |E01,2ch(Гz) + B1,2sh(Гz)|exp(-az),

где введен коэффициент параметрического усиления

, .

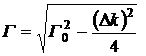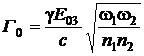Нетрудно видеть, что экспоненциальное нарастание амплитуд низкочастотных волн происходит лишь при условии , то есть если мощность ВЧ-поля превышает порог параметрического усиления

Чем больше потери в среде a и рассогласование волновых векторов Dk, тем выше порог параметрического усиления. Если же условие (36) не выполнено, то имеют место пространственные биения амплитуд низкочастотных волн.

Литература

Гершензон Е.М. и др. Курс общей физики. т.т. 1-2. Механика. М.: Академия, 2007.

Детлаф А.А., Яворский Б.М. Курс общей физики. М. Высшая школа, 2009.

Иродов И.Е. Задачи по общей физике. М.: Бином, 2008.

Иродов И.Е. Механика. Основные законы. М.: Лаборатория базовых знаний, 2009.

Иродов И.Е. Электромагнетизм. Основные законы. М.: Лаборатория базовых знаний, 2009.

Савельев И.В. Курс физики, т.т. 1- М.: Наука, 2006-2008.

Сивухин Д.В. Общий курс физики, т.т. 1- М.: Высшая школа, 2006-2008.

Трофимова Т.И. Краткий курс физики. М.: Высшая школа, 2007.

Яворский Б.М., Пинский А.А. Основы физики, т.т. 1-2. М.: ФИЗМАТЛИТ, 2007.