Основы гидродинамики

Основы гидродинамики

МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРОЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН

ТАШКЕНТСКИЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ ИНСТИТУТ

ФАКУЛЬТЕТ: «УПРАВЛЕНИЕ СТРОИТЕЛЬСТВОМ»

КАФЕРДРА: «ПСЭИК»

Контрольная работа

По предмету «Механика жидкости и газа»

на тему: ОСНОВЫ ГИДРОДИНАМИКИ

Выполнил: Юсупов А.

Проверила: Турсунова Э.А

ТАШКЕНТ 2015

Содержание

Введение

Основные понятия о движении жидкости

Уравнение Бернулли для идеальной и реальной жидкости

Практическое применение уравнения Д. Бернулли

Расходомер. Измерение расхода и количества жидкости

Литература

Введение

В первые попытки исследования сопротивления среды движению тела были сделаны Леонардо да Винчи <https://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%BE%D0%BD%D0%B0%D1%80%D0%B4%D0%BE_%D0%B4%D0%B0_%D0%92%D0%B8%D0%BD%D1%87%D0%B8> и Галилео Галилеем <https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D0%BB%D0%B8%D0%BB%D0%B5%D0%BE_%D0%93%D0%B0%D0%BB%D0%B8%D0%BB%D0%B5%D0%B9>. Принято считать, что Галилео проводил опыты по сбрасыванию шаров различной плотности с пизанской башни, данный опыт описывается в учебной литературе и поэтому известен всем со школьных времен (достоверной информации подтверждающей проведение данного опыта Галилео Галилеем на сегодняшний день не имеется).

В 1628 году Бенедетто Кастелли <https://ru.wikipedia.org/wiki/%D0%91%D0%B5%D0%BD%D0%B5%D0%B4%D0%B5%D1%82%D1%82%D0%BE_%D0%9A%D0%B0%D1%81%D1%82%D0%B5%D0%BB%D0%BB%D0%B8> издал маленькую работу, в которой он очень хорошо для своего времени объяснил несколько явлений при движении жидкости в реках и каналах.

Однако, в работе содержалась ошибка, так как он предполагал скорость вытекания жидкости из сосуда пропорциональной расстоянию отверстия до поверхности воды. Торричелли заметил, что вода, выливающаяся из фонтана поднимается на высоту порядка уровня воды питающего водоема. На основе этого он доказал теорему, о пропорциональности скорости вытекания квадратному корню из расстояния от отверстия до поверхности жидкости. Теорема была экспериментально проверена на воде, вытекающей из различных насадок. Едме Мариотто в труде, который был опубликован после его смерти впервые объяснял несоответствие теории и экспериментов при помощи учета эффектов трения.

В труде Исаака Ньютона «philosophie naturalis principia mathematica» для объяснения снижения скорости проточной воды использовались именно понятия вязкости и трения. Также в работах Ньютона развивались представления Мариотто о потоке воды как о наборе трущихся нитей. Эта теория уже сопоставима с современной теорией переноса движения в жидкостях.

После издания Ньютоном своих работ ученые всего мира начали пользоваться его законами для объяснения различных физических явлений. Спустя 60 лет Эйлер получил аналог второго закона Ньютона для жидкости. В 1738 году Даниил Бернулли издал работу, где объяснялась теория движения жидкостей. Он использовал два предположения: поверхности жидкости, вытекающей из сосуда всегда остается горизонтальной и то, что скорость опускания слоев воды обратно пропорциональна их ширине. В отсутствии демонстраций этих принципов теория доверия не получила.

Основные понятия о движении жидкости

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы - круг (рис.3.1, б); живое сечение клапана - кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

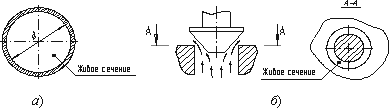
Рис. 3.1. Живые сечения: а - трубы, б - клапана

Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

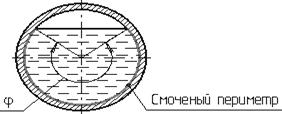
Рис. 3.2. Смоченный периметр

Для круглой трубы

если угол в радианах, или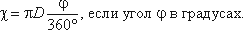

Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R - отношение живого сечения к смоченному периметру

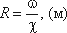
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z)= φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

υ = f₁(x, y, z, t)= φ f₁(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 3.3. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное - течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

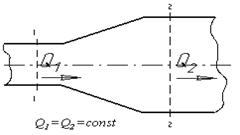
Рис. 3.4. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

ω₁υ₁ = ω₂υ₂

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

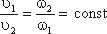
Уравнение Бернулли для идеальной и реальной жидкости

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры - тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 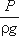. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5). Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова. Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

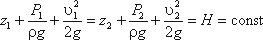
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

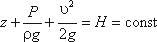
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;

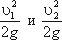 - удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

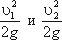Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 - геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения;  - пьезометрические высоты;  - скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

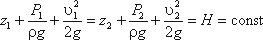
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

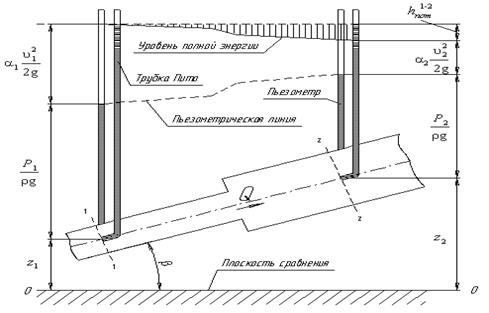
Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются 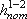 и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ). Потерянная высота 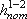 складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

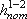 = h_лин + h_мест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω ₁ = υ₂ω₂.

Практическое применение уравнения Д. Бернулли

При применении уравнения Д. Бернулли для решения практических задач гидравлики следует помнить два основных условия:

. уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения. На участках между выбранными сечениями условия плавно изменяющегося движения могут и не соблюдаться;

. гидродинамическое давление 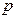 и, следовательно, высоту положения z можно относить к любой точке живого сечения, так как 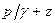 для любой точки живого сечения потока при плавно изменяющемся движении есть величина постоянная. Обычно двучлен 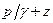 удобно отнести для упрощения решения задач к точкам или на свободной поверхности, или на оси потока.

Разберем применение уравнения Бернулли на примере простейшего водомерного устройства в трубах водомера Вентури (рис. 24.); он представляет собой вставку в основную трубу диаметром D трубы меньшего диаметра d, которая соединена с основной трубой коническими переходами.

В основной трубе сечение 1-1 и в суженном сечении 2-2 присоединены пьезометры, по показаниям которых можно определить расход жидкости в трубе Q.

Выведем общую формулу водомера для определения расхода в трубе. Составим уравнение Бернулли для точек, расположенных в центре тяжести сечений 1-1 перед сужением и 2-2 в горловине, приняв плоскость сравнения по оси трубы о-о. Для наших условий , .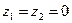

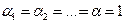Потери напора в сужении ввиду малости расстояния между сечениями считаем равными нулю, т.е. .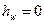

Тогда уравнение Бернулли (74) запишется так:

, или .

Но из рис. 24 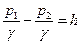, поэтому

. (а)

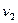В уравнении (а) две неизвестные величины  и . Составим второе уравнение, используя уравнение неразрывности (70)

,

.

Подставляя 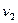 в уравнение (а), получим

.

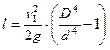Отсюда скорость течения в основной трубе (сечение 1-1) равна

,

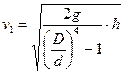расход жидкости в трубе по формуле IV.2:

.

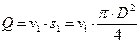
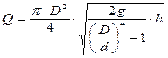Обозначим постоянную величину для данного водомера через К

.

Однако при выводе этой формулы не учитывались потери напора в водомере, которые в действительности будут. С учетом потерь напора формула расхода водомера Вентури запишется так:

где 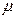- коэффициент расхода водомера, учитывающий потери напора в водомере. Для новых водомеров 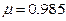; для водомеров, бывших в употреблении, 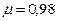. Таким образом, для определения расхода в трубе достаточно замерить разность уровней воды в пьезометрах и подставить ее значение в формулу.

Измерение скорости потока и расхода жидкости

жидкость бернулли гидравлика скорость

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

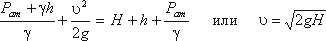
где Н - столб жидкости в трубке Пито.

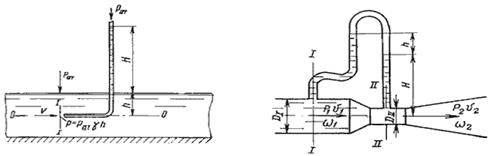
Рис. 3.7. Трубка Пито и pасходомер Вентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

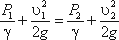
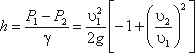
Используя уравнение неразрывности Q = υ₁ω₁ = υ₂ω₂

сделаем замену в получено выражении:

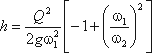
Решая относительно Q, получим

Выражение, стоящее перед 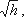, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Литература

<http://gidravl.narod.ru/osnovdin.html>

<http://www.all-fizika.com/article/index.php?id_article=1972>

<http://firing-hydra.ru/index.php?request=full&id=207>

<http://www.kipinfo.ru/info/stati/?id=240>