Оптические свойства материалов и методы их изучения
Лабораторная работа
№ 1
Тема: Измерение
показателя преломления для плоско-параллельной пластинки
Цель работы:
Научиться определять показатель преломления плоскопараллельной пластинки,
смещение падающего луча и оценивать погрешность измерения.
Приборы и материалы;
1. Плексигласовая подставка
. 4 иголки.
. Плоскопараллельная стеклянная
пластинка
. Белая бумага (миллиметровая
или в клетку)
. Карандаш
. Линейка.
. Транспортир.
. Циркуль
Теория:
Пусть на плоскую границу
раздела двух сред падает плоская световая волна.
Волновая поверхность АС
перпендикулярна лучам ОА и ОВ. (рис. 1)
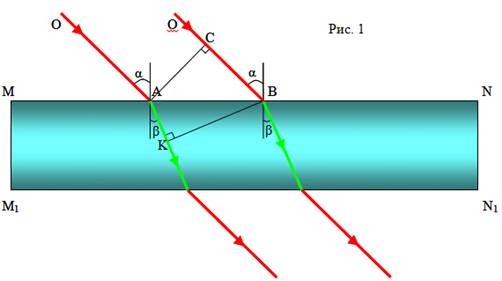
Поверхности МN сначала
достигнет луч ОА. Луч ОB достигнет поверхности спустя время
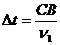 ,
,
где v1 скорость
распространения света в первой среде. Поэтому в момент, когда вторичная волна в
точке В только начнет возбуждаться, волна от точке А уже имеет
вид полусферы радиусом
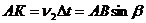 ,
,
v2 - скорость
распространения света во второй среде.
Волновую поверхность преломленной
волны можно получить, проведя поверхность, касательную ко всем вторичным волнам
во второй среде, центры которых лежат на границе раздела сред. В данном случае
это плоскость KВ является огибающей вторичных волн.
Угол падения  равен углу САВ
(стороны одного из этих углов перпендикулярны сторонам другого).
Следовательно,
равен углу САВ
(стороны одного из этих углов перпендикулярны сторонам другого).
Следовательно,
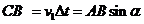
Угол преломления β равен углу
АВК. Поэтому
 (2)
(2)
Разделим почленно (1) на (2)
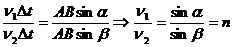 (3),
(3),
где n - постоянная
величина, не зависящая от угла падения, но зависящая от показателей преломления
первой и второй сред, поэтому n называется относительным показателем
преломления и определятся формулой:
 (4)
(4)
Для определения относительного
показателя преломления по формуле (3) необходимо измерить угол падения и
угол преломления.
Можно определить показатель преломления
пластины используя геометрическое построение (рис. 2).
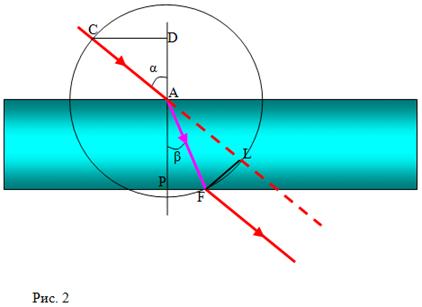
Через т. А границы раздела сред
воздух-стекло проводят перпендикуляр к границе, отмечают углы падения α и
преломления β.
Далее,
с помощью циркуля проводят окружность с центром в точке А радиусом
равным длине луча АF,
Строят прямоугольные треугольники AСD и AFP. Так как

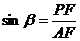 ,
,
то формула (3) примет вид
 (5)
(5)
По формуле (5) для
определения показателя преломления пластинки достаточно измерить расстояния CD и PF.
Надо оценить величину смещения
падающего луча.
В оптических приборах иногда
необходимо сместить лучи на маленькую величину. Для этой цели используется
плоскопараллельная пластинка.
Можно измерить величину смещения
линейкой (длина FL). Можно также вычислить по формуле
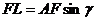 (6),
(6),
где 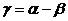
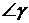 также можно измерить транспортиром.
Стоит заметить, что FP зависит от угла падения.
также можно измерить транспортиром.
Стоит заметить, что FP зависит от угла падения.
Порядок выполнения работы (рис. 3)
. Положить плоскопараллельную
пластинку на миллиметровую бумагу или тетрадный лист в клетку и очертить две
параллельные грани.
. За гранью MN устанавливаем
2 иголки под углом относительно перпендикуляра ОО′, на некотором
расстоянии друг от друга. 1 иголка должна находиться в точке В, а 2
в точке О.
. Со стороны M1N1
рассматриваем обе иголки. Устанавливаем их так, чтобы 1 иголка
"спряталась" за иголку 2, затем на пути луча зрения перед
гранью M1N1
устанавливаем третью иголку, которая находится в точке D так чтобы
она перекрывала 1 и 2 иголки. Иголку 4 ставить на наибольшем
расстоянии от иголки 3.
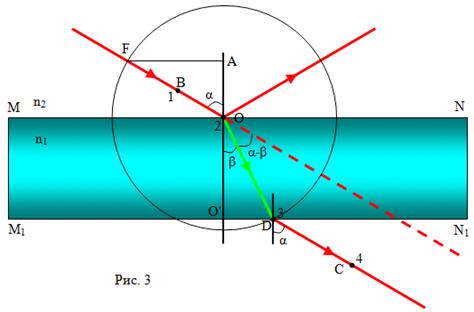
. Сняв иголки и убрав
плоскопараллельную пластинку соединяем при помощи линейки точки O, B, С, D где
находились иголки
. При помощи циркуля строят
окружность с центром в точке О и радиусом OD. Строят
треугольник OFА. Линейкой
измеряют отрезки FА и O'D.
. Углы α и β измеряем при
помощи транспортира.
. Измерения с 1 по 6 пункт
повторить 5 раз
. Вычислить n с помощью
формул (3) и (5)
. Вычислить величину смещения
падающего луча по формуле (6)
. Все измерения и полученные
результаты записать в таблицу. Таблицу заполнить так, как вам удобно.
. Подсчитать среднюю квадратичную
ошибку по формуле
 ,
,
где tan
- коэффициент Стьюдента
N
- число измерений
Занести полученные данные в
таблицу.
Средняя квадратичная ошибка
должна вычисляться по результатам формулы (3) и отдельно по результатам
формулы (5)
. Записать окончательный
результат с учетом доверительного интервала
n=n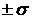 .
.
Окончательных результата должно
быть два по формуле (3) и по формуле (5).
. Построить графика зависимости
n=f(N)
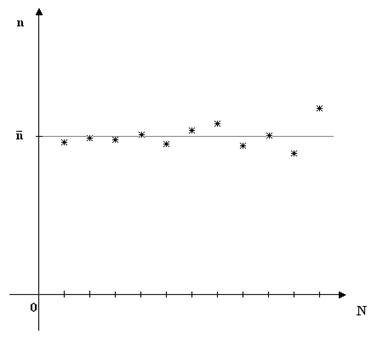
Контрольные
вопросы:
1. Формула определения
относительного показателя преломления?
. Формула определения смещения
падающего луча?
3. Как можно определить показатель преломления,
используя геометрию?
. Что такое волновой фронт и поверхность?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа
№ 2
Тема: Измерение
показателя преломления трехгранной призмы с помощью 4-х иголок
Принадлежности:
1. Плексигласовая плоская
подставка
. 4 иголки
. Трехгранная призма
. Белая бумага (миллиметровая
или в клетку)
5. Карандаш
. Линейка.
. Транспортир.
Цель:
Научиться определять показатель преломления трехгранной призмы оценить
погрешность измерения.
Теория:
Пусть на одну из поверхностей
призмы, показатель преломления которой относительно окружающей среды-n,
падает луч под углом i1.
Исходя из закона преломления, построим ход луча в призме. Угол между
преломляющими поверхностями обозначим через α (преломляющий
угол призмы) линия пересечения преломляющих поверхностей называется
преломляющим ребром. Угол между продолжениями падающего и вышедшего (под углом i2)
лучей обозначим через θ (угол
отклонения луча в призме).
Т.к. θ
есть
внешний угол KРT (рис.1)
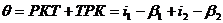
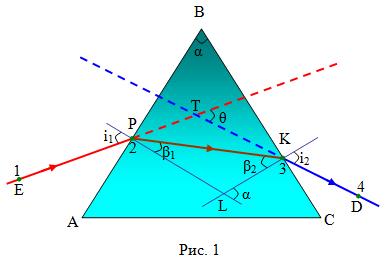
Из треугольника PLK:
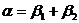
То для угла отклонения имеем

Тогда 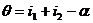
Согласно закону преломления:

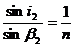
отсюда,

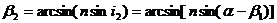
Подставляя значения i1
и β2
в выражение для θ имеем:

Найдем минимальное значение угла
отклонения. Легко доказать, что
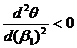
Следовательно,

есть условие минимума. Тогда
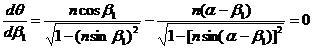
Это равенство имеет место при
 и
и 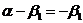 .
.
Поскольку 
 0, то физический смысл имеет
только условие
0, то физический смысл имеет
только условие

откуда следует что
 т.к.
т.к.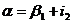 , то,
, то,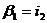
т.е. угол отклонения минимален при
симметричном расположении падающего на призму и вышедшего из нее лучей (когда
луч внутри призмы параллелен ее основанию). Следовательно, для θmin получаем.
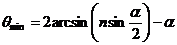
Отсюда
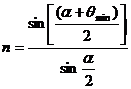 (1)
(1)
(1) - формула для толстой
призмы.
Теперь рассмотрим вывод формулы для
тонкой призмы:
нам дана равнобокая призма АВ=ВС АС, n>nВ
АС, n>nВ
Пусть на призму падает белый свет, АВС= угол
преломления призмы, θ- угол
отклонения призмы.
угол
преломления призмы, θ- угол
отклонения призмы.
Выведем формулу зависимости α,θ,n где n -
показатель преломления среды относительно воздуха.
Рассмотрим ТКР и КРТ для КРТ
- θ внешний,
значит
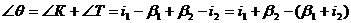 (2)
(2)

т.к. падающий угол очень мал, т.е. i1 и β1, " 1,
Значит

 (3)
(3)
из (3)  (4)
(4)
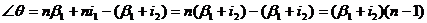 (5)
(5)
из  КBР нам
известен
КBР нам
известен 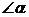
 (6)
(6)
 (7)
(7)

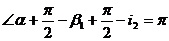 (8)
(8)
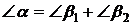 (9)
(9)

(9) 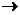 (5), тогда
(5), тогда
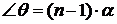 (10)
(10)
Эта формула верна для тонкой призмы.
Порядок выполнения работы:
1. Положить трехгранную призму на
миллиметровую бумагу или тетрадный лист в клетку и очертить ее.
. За гранью АВ призмы АВС
устанавливаем 2 иголки на некотором расстоянии друг от друга.
. Со стороны ВС рассматриваем
через призму обе иголки. Устанавливаем их так, чтобы иголка 1
"спряталась" за иголку 2, затем на пути луча зрения перед
гранью ВС устанавливаем иголку 3 так, чтобы она перекрывала иголки 1
и 2. Иголку 2 ставить на наибольшем расстоянии от иголки 1.
. Затем еще устанавливаем иголку 4,
которая бы перекрывала иголки 1, 2, 3,. Иголку 4
поставить на наибольшем расстоянии от иголки 3.
. Сняв иголки и убрав призму строим
чертеж. Иголки 1, 2, 3 и 4 будут находиться в
точках Р, К, D, Е. Проведем прямые РE, КD и PK. К точкам К
и P построим
нормали к граням призмы обозначив углы между лучом и нормально i1 и β1 на грани АВ
и i2 и β2 на грани ВС.
Измерим их транспортиром.
. Измерения с 1 по 5
пункт повторить 5 раз.
. Вычислив углы  и θ подставим их
в формулы (1) (рекомендовано для физиков) и (10) (для других
специальностей) преломлений призмы.
и θ подставим их
в формулы (1) (рекомендовано для физиков) и (10) (для других
специальностей) преломлений призмы.
. Вес измерения и полученные
результаты занести в таблицу. Таблицу заполнить так как вам удобно.
. Подсчитать среднюю квадратичную
ошибку по формуле

где tan -
коэффициент Стьюдента
N - число измерений
И занести полученные данные в
таблицу. Записать окончательный результат с учетом доверительного интервала
=n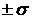
. Построить график зависимости n=f(N).
На ось абсцисс откладывается число измерений, на ось ординат - показатель
преломления. Масштаб выбрать самим.

Контрольные вопросы:
1. Что называется главным
сечением призмы.
. Угол отклонения луча в
призме.
. Формула для тонкой призмы.
. Формула для толстой призмы.
. Единица измерения показателя
преломления. Что он показывает?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа
№ 3
Тема: Изучение
светопропускающих качеств различных материалов с помощью фотоэлемента.
Определение светопропускающих качеств стекла и полиэтиленовой пленки
призма фотоэлемент
микроскоп преломление
Цель работы.
Определение светопропускающей способности различных материалов.
Приборы и
материалы: Фотоэлемент кремниевый,
миллиамперметр, осветитель ГОИ, стеклянная пластинка, два куска чистой и
пожелтевшей полиэтиленовой пленки.
Содержание работы.
Светопропускающие качества
различных прозрачных материалов играют большую роль в технике, науке, сельском
хозяйстве. Полиэтиленовая пленка, покрываемая парники на полях в процессе
длительного использования теряет светопропускающие качества и пропускает меньше
света, чем в начале эксплуатации.
Загрязненные витринные стекла
магазинов, и стекла автомобилей также задерживают большую часть света, что
ухудшает видимость при работе в ночное время. В данной работе определяется
светопропускающая способность различных материалов путем измерения силы фототока,
который возникает под воздействием проходящего через прозрачное тело светового
потока.
Выполнение работы:

1. Высоту фотоэлемента и
источника света установим на одинаковом уровне.
. Направим свет от источника на
фотоэлемент, и передвигая относительно фотоэлемента, чтобы добиться
максимального показателя миллиамперметра Jmax.
. Расположив между источником
света и фотоэлементом чистое стекло, снять показание миллиамперметра и
вычислить светопропускающую способность по процентной формуле.

J0- показания
миллиамперметра при прохождении света через прозрачный материал, J1- через
непрозрачный материал.
. Расположить между источником света
и фотоэлементом поочередно различные полиэтиленовые пленки, снять показание
миллиамперметра J и вычислить светопропускающую
способность по процентной формуле.
J/Jmax*100%
. Все измерения повторить 5 раз.
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа № 4
Тема: Определение увеличения
микроскопа
Цель работы: научиться
определять линейное увеличение микроскопа.
Принадлежности:
1. Микроскоп.
2. Прозрачная линейка.
. Миллиметровая шкала.
Описание прибора: В
устройстве микроскопа простейшего типа можно выделить две основные части:
механическую и оптическую. Механическая часть микроскопа состоит из штатива
(основание, предметный столик), тубуса и приспособления для укрепления зеркала.
Эти приспособления находятся под предметным столиком.
Штатив
микроскопа имеет массивное основание, придающее ему необходимую устойчивость.
Предметный столик квадратной
или круглой формы служит для поддержания препарата и имеет на верхней плоскости
два отверстия, в которые вставляются штифты с пружинами, прижимающих препарат к
столику для предохранения его от передвижения во время наблюдения.
Непосредственно под столиком или на конденсоре укреплена переменная диафрагма,
служащая для регулировки освещенности рассматриваемого изображения. Диафрагмы
бывают двух родов: револьверные и ирисовые. Более простые револьверные состоят
из диска, в котором просверлен ряд отверстий различного диаметра, эти отверстия
могут устанавливаться напротив отверстия в столике микроскопа. Ирисовые
диафрагмы состоят из стальных пластинок особой формы, образующих круглое отверстие,
диаметр которого можно плавно изменять, поворачивая пластинки при помощи
рычажка.
Тубус
представляет собой раздвижную цилиндрическую трубу, длина которой может
изменяться по шкале, нанесенной на боковой поверхности верхней половины. Тубус
в целом связан с колонкой при помощи салазок и может передвигаться при вращении
кремальер винта. Более медленное передвижение тубуса, необходимое для точной
фокусировки объекта, достигается вторым микрометрическим винтом. Нижнее
отверстие тубуса имеет нарезку для привертывания объектива или
"револьвера" - особого держателя, несущего на себе от двух до четырех
объективов и позволяющего быстро менять их. Для того чтобы ось объектива
совпадала с осью микроскопа, револьвер снабжен защелкивающей пружинкой, которая,
попадая в специальную прорезь, удерживает объектив в нужном положении.
Оптическая часть состоит из
осветительного аппарата, состоящего из зеркала и конденсора, сменных объективов
и окуляра.
Приспособление для
установки осветительного аппарата состоит из металлического
держателя для зеркала, вращающегося вокруг двух перпендикулярных осей, и
кремальеры или винта, передвигающих конденсор по оси микроскопа.
Микрометр
служит для точной фокусировки.
Зеркало
служит для направления лучей от источника света вдоль оси прибора сквозь
рассматриваемый объект. Делается оно обычно из стекла.
Действие обеих линз окуляра можно
заменить действием эквивалентной им линзы с фокусным расстоянием  используемой
в качестве лупы (рис. 1).
используемой
в качестве лупы (рис. 1).
Согласно формуле, выражающей
увеличение лупы, имеем
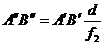 (1)
(1)
где d - расстояние ясного
зрения глаза наблюдателя, f2- фокусное
расстояние линзы L2 А'В'-
увеличенное обратное действительное изображение предмета, А'В'=h
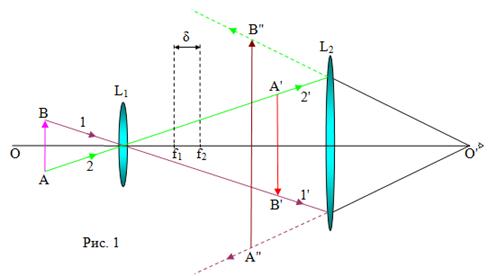
Из формулы (1) следует
 (2)
(2)
А"В"- мнимое, обратное
сильно увеличенное изображение предмета
Линейное увеличение микроскопа
будет:
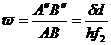 (3)
(3)
Так, изображение А"В"
близко к фокусу окуляра, а фокусное расстояние объектива весьма мало, то с
достаточной степенью точности можно считать 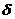 равным расстоянию между задним
фокусом объектива и передним фокусом окуляра. Это расстояние называется
оптической длиной микроскопа.
равным расстоянию между задним
фокусом объектива и передним фокусом окуляра. Это расстояние называется
оптической длиной микроскопа.
Угловое увеличение микроскопа
определяется
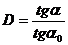 (4)
(4)
где α
и α0
углы зрения изображения А"В" и предмет АВ.
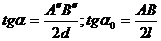
где l - расстояние от объекта
до поверхности А, в которой находится глаз наблюдателя, следовательно
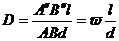
Измерения.
Сбоку от микроскопа на расстояние ясного зрения, равного 25 см, ставят
миллиметровую шкалу. Зеркальце микроскопа ставят наклоненно под углом 45о
к оси прибора и устанавливают глаз и это зеркальце так, чтобы одновременно
видеть как изображение прозрачной линейки, так и миллиметровую шкалу. При этом
для выравнивания освещенности изображений обеих шкал рекомендуется изменение
наклона зеркала предметного столика.
Отсчитывают количество целых
миллиметровых делений шкалы N1
совпадающих с целым числом делений изображения прозрачной линейки N2.
Так как отношение длины делений шкалы и линейки равно 10 мм, то
 (5)
(5)
Зная D по формуле (5) можно
легко найти линейное увеличение.
Контрольные вопросы:
1. Из каких частей состоит
микроскоп?
2. Какую функцию выполняют
объектив и окуляр?
. Сколько лучей
необходимо для объяснения принципа работы микроскопа?
. Как должны
располагаться объектив и окуляр, чтобы получить увеличенное изображение, и
каким оно будет?
. Что называют угловым
увеличением микроскопа?
. Что называется
линейным увеличением микроскопа?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа
№ 5
Тема: Закон Малюса
Цель работы:
ознакомиться с поляризацией света.
Принадлежности:
1. Источник света
. Поляризатор
. Анализатор
. Фотоэлемент
При падении естественного
света, амплитудой Е 0, на поляризатор из последнего выходит
поляризованная волна, интенсивность которой, в соответствии с уравнением
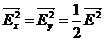 (1)
(1)
равна половине начальной
(точнее - даже меньше, вследствие поглощений и отражений луча на пути).
Чтобы убедиться в том, что
полученная волна поляризована, и выяснить направление поляризации, поставим на
продолжении её пути вторую такую же поляризующую пластинку, называемую в этом
случае анализатором. Если плоскости пропускания поляризатора и анализатора параллельны
друг другу, то поляризованный свет пройдет через анализатор, почти не снижая
своей интенсивности. Если плоскости поляризатора П и А
анализатора перпендикулярны друг другу, то анализатор полностью погасит
падающий на него поляризованный луч. В этом случае говорят, что поляризатор и
анализатор скрещены. В промежуточных случаях интенсивность света, прошедшего
через систему, будет зависеть от ориентации анализатора относительно
поляризатора и имеет значение I, находящееся между I0
и нулем. Разберем этот вопрос несколько подробнее.
Обозначим амплитуду
электрического вектора волны, прошедшей через поляризатор буквой Е.
Плоскость анализатора А повернута относительно плоскости поляризатора Р
на некоторый угол. Разложим вектор Е 0 на две составляющие:
параллельную плоскости анализатора (Е║) и перпендикулярную к
ней (Е┴). Это соответствует разложению волны, колеблющейся в
плоскости Е 0 на две волны, поляризованные во взаимно
перпендикулярных плоскостях и колеблющиеся в одинаковой фазе. Одна из них Е║
пройдет через анализатор, а перпендикулярная Е┴ погасится.
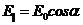 (2)
(2)
отношение интенсивностей
пропорционально отношению квадратов амплитуд
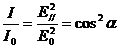 (3)
(3)
и, следовательно
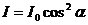 (4)
(4)
уравнение (4) выражает закон Малюса:
Интенсивность света, прошедшего
через анализатор (I), равна интенсивности света,
прошедшего через поляризатор (I0),
умноженной на квадрат косинуса угла (α) между анализатором и
поляризатором.
Порядок выполнения работы:
1. Вращая анализатор (А) на
определенный угол 0°, 30°, 60°, 90°, измерим интенсивность светового потока с
помощью фотоэлемента.
. Для каждого угла измерим 4-5 раз.
. Определим ошибку измерения.
. Составим таблицу.
. Подсчитаем среднеарифметическую
погрешность и запишем результат в виде доверительной ошибки.
. Построим график.
Контрольные вопросы:
1. Что такое поляризатор?
. Что такое анализатор?
. Какой источник света используется
при выполнении работы?
. Какие лучи выходят из поляризатора
и анализатора?
. Что произойдет при вращении
анализатора?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа № 6
Тема: Определение фокусного
расстояния собирающей и рассеивающей линз
Цель работы: ознакомить
с принципом работ линз и определения их фокусного расстояния.
Принадлежности:
1. Оптическая скамья.
2. Лампа накаливания.
. Собирающая и
рассеивающая линзы.
. Экран.
. Масштабная линейка.
. Штангенциркуль.
Теория:
Элементарная теория тонких линз
приводится простым соотношением между фокусным расстоянием тонкой линзы,
расстоянием от линзы до предмета с одной стороны, и до его изображения с
другой.
Простой оказывается также связь
между размерами объекта, его изображения, даваемой линзой, расстоянием от
предмета до линзы. Определяя на опыте названные величины, не трудно упомянутыми
соотношениями вычислить фокусное расстояние тонкой линзы с точностью, вполне
достаточной для большинства случаев.
Рассмотрим три метода
определения фокусного расстояния собирательной линзы.
Описание прибора:
На расположенной горизонтально оптической скамье могут перемещаться на
ползунках следующие приборы: линза, экран, осветитель с предметом. В передней
части осветителя имеется вырез в виде стрелки, освещаемый находящейся внутри
электрической лампочкой. Освещенная стрелка из этого выреза играет роль объекта
(предмета), изображение которого получается с помощью изучаемых линз. Все эти
приборы устанавливается так, чтобы центры их были на одной высоте, а плоскости
экрана и осветителя были перпендикулярны относительно оптической скамьи, а ось
линзы параллельна.
Расстояние между приборами
отсчитываются по линейке.
Для повышения точности
фокусировки нужно добиться четкого изображения стрелки.
Способ №1:
Определение фокусного расстояния относительно расстояния от предмета до линзы (a)
и от линзы до его изображения на экране (b).
Cвязь
между ними выражается формулой
 (1)
(1) 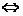
 (2)
(2) 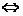
 (3)
(3)
Измерение. (рис. 1)
Поставив экран на достаточно большое расстояние от осветителя, и линзу между
ними, передвигают ее до тех пор, пока не получится на экране отчетливого
изображение стрелки.
Определив по линейке, расположенной
вдоль скамьи, положение линзы, экрана и предмета, передвигают ползунки с
осветителем и экраном в другое положение, получая новое чёткое изображение
предмета на экране, и вновь определяют соответствующее положение линзы и всех
приборов. Измерение повторить не менее пяти раз.
В данном способе полезно производить
часть измерений при увеличенном, а часть при уменьшенном изображении предмета.
Из каждого отдельного измерения по
формуле (3) вычисляют фокусное расстояние линзы и из полученных результатов
находят его среднеарифметическое значение. Оценивают среднеквадратическую
погрешность.
Способ №2: Определение
фокусного расстояния по величине предмета, его изображения и расстояния от
линзы до экрана.
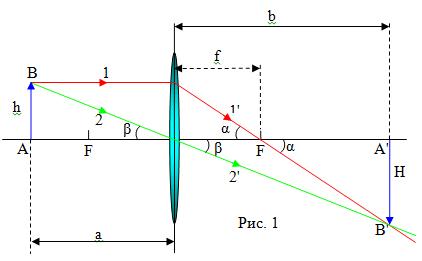
Обозначим величину предмета h, величину
его изображения H и расстояние их от предмета до
линзы, и от линзы до предмета соответственно через a и b(рис. 1).
Эти величина связаны между собой известным соотношением
 (4)
(4)
Определив отсюда a
подставив в формулу (3) легко получить выражение f через эти величины.
 (5)
(5)
Измерения.
Поставим линзу между экраном и предметом так, чтобы на экране получилось сильно
увеличенное отчетливое изображение стрелки, и отсчитаем расстояние линзы и до
экрана.
Измерим при помощи
штангенциркуля величину предмета и величину его изображения на экране. Измерим
расстояние от изображения до линзы, найдем фокусное расстояние линзы по формуле
(5). Изменив расстояние от плоскости стрелки до экрана, повторить опыт 5-6 раз.
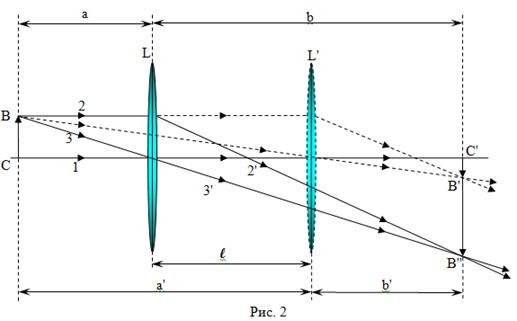
Способ №3.
Определение фокусного расстояния по величине перемещения линзы. Из предыдущих
измерений определяют среднее значение фокусного расстояния собирающей линзы.
Если расстояние от предмета до изображения, которое обозначено через А,
более 4ƒ,
то
всегда найдутся два таких положения линзы, при которых на экране получается
отчетливое изображение предмета, в одном случае уменьшенное, в другом
увеличенное (рис. 2).
При этом оба положения линзы
будут симметричны относительно середины расстоянии между предметом и
изображением.
Действительно, воспользовавшись
уравнением (3) можно написать для первого и второго положений линзы:
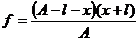 и
и 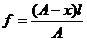
Прировняв правые части этих
уравнений, найдем
х=(A-l)/2
Поставив это значение х в
выражение А- l -х, найдем, что
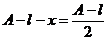
т.е. действительно оба
положения линзы находится на равных расстояниях от предмета и изображения,
следовательно, симметричны относительно середины расстояния между предметом и
изображением. Чтобы получить выражение для фокусного расстояния, рассмотрим
одно из положений линзы, например первое: для него расстояние от предмета до
линзы

а расстояние от линзы до
изображения

Поставляя эти величины в
формулу (3), найдем
 (6)
(6)
Это способ является наиболее общим и
пригодным как для толстых, так и для тонких линз.
Измерение: Установив
осветитель и экран на расстоянии А>4f, помещаем линзу между ними и,
передвигая ее, добиваемся получения на экране вполне отчетливого изображения
предмета. Отсчитав по линейке соответствующее положение линзы, сдвигаем ее в
сторону и вновь устанавливаем. Эти измерения производить несколько раз.
Передвигая линзу, добиваемся
получения второго отчетливого изображения предмета - уменьшенного и вновь
отсчитываем положение линзы по линейке. Повторить опыт и измерения 5 раз.
Измерив расстояние А между экраном и стрелкой, а также среднее значение
перемещения предмета вычисляем фокусное расстояние линзы по формуле (6)
Определение фокусного расстояния
рассевающей линзы
Измерение фокусного расстояния
рассеивающей линзы производится следующим образом (рис. 3).

Если на пути лучей выходящих из
точки В предмета и сходящихся в точке В', после преломления в собирающей линзе L2,поставить
рассеивающую линзу L1,
так, чтобы расстояние L1A'
было меньше её фокусного расстояния, то изображение предмета удалиться от линзы
L1
в точку А". В соответствии с оптическими принципами мысленно рассмотрим
лучи света распространяющееся из В" в обратную сторону. Тогда точка В'
будет её мнимым изображением после преломления лучей через рассеивающую линзу L1.
Обозначим расстояние L1A'
через а, А'А" - b,
причём b будет иметь
отрицательное значение. Тогда получим:
 (7)
(7)
и, следовательно,
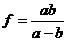 (8)
(8)
Измерение. На
оптической скамье размещают осветитель, собирающую линзу и белый экран.
Передвигая экран, получают на нем отчетливое изображение стрелки осветителя.
Сделав отсчет этого положения экрана на линейке оптической скамей, сдвигают
экран в сторону и вновь находят изображение стрелки.
Таких установок и отсчетов делают
6-8 раз, берут из них среднее арифметическое и среднее квадратическое
отклонение. Это дает положение точки D и погрешности измерении.
Отодвинув экран вправо, ставят на скамью между найденными выше положением
экрана и линзой и вновь находят отчетливое изображение стрелки.
Отсчитывают по линейке положение
линзы и, сдвигая ее (или экран) повторяют установку и отсчеты до 6-8 раз. Из
полученных результатов берут среднее. Отыскав несколько раз второе положение
экрана (точку Е), находят расстояние ЕС и ДС и вычисляют фокусное
расстояние по формуле (8) .
Контрольные вопросы:
1. Что называется главным
фокусом линзы?
2. Что называется
оптической силой линзы?
. В каких единицах
измеряется фокусное расстояние и оптическая сила линзы?
. Как выполняется
построение изображений в линзах?
. Что называется главной
оптической осью?
. Какое изображение
называется действительным, а какое мнимым?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа
№ 7
Тема: Изучение
закона фотометрии
Цель работы:
Электрическим методом изучить законы фотометрии и ознакомить с явлением
внутреннего фотоэффекта.
Принадлежности:
кремневый фотоэлемент, лампа накаливания, микроамперметр, масштабная линейка.
Теория
Интенсивность света
характеризуют величиной переносимой энергии. Это электромагнитная энергия может
быть измерена, по ее превращению в другие формы энергии (тепловую, химическую)
в различных приемниках. Раздел оптики, занимающейся измерением интенсивности
света и его источников, называется фотометрией.
В фотометрии приходится вводить
двойные единицы измерения. Энергетические (оцениваемые по объективным
энергетическим характеристикам) и визуально-оцениваемые воздействием на глаз.
Так как у точечного источника
света размеры малы, то излучение испускается равномерно во все стороны. Фронт
световой волны, испускаемый таким точечным источником, будет сферическим.
Для пространственных задач
распространения света существенно понятие о телесном угле. Мерой телесного угла
является отношение площади, вырезаемой конусом из их поверхности сферы, к
квадрату ее радиуса r т.е.
 (1)
(1)
За единицу телесного угла принят
угол, опирающийся на участок поверхности сферы, площадь которого равна квадрату
её радиуса (dS0=r2). Эта единица называется
стерадиан (стер). Наибольшей телесный угол равен, очевидно, 4 стер,
площадь всей поверхности сферы
стер,
площадь всей поверхности сферы 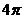 r2, а
безграничная плоскость видна из любой точки пространства под углом 2
r2, а
безграничная плоскость видна из любой точки пространства под углом 2 стер. В
частном случае, когда площадка dS находиться под углом
стер. В
частном случае, когда площадка dS находиться под углом  к dS0, телесный
угол определяется формулой:
к dS0, телесный
угол определяется формулой:
 (2)
(2)
Поток света. Основной
энергетической фотометрической величиной является световой поток Ф. Эта
величина характеризует энергию, проходящую через данную поверхность за единицу
времени, и измеряется соответственно в единицах мощности (Вт).
Сила света. Рассмотрим
точечный источник О. Обозначим световой поток, заключенный, в телесном угле dω через dФ. Тогда
отношение
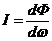 (3)
(3)
называется силой света
точечного источника в данном направлении. Из (3) следует, что сила света
характеризуется величиной потока, заключенного в единице телесного угла.
Если поток, испускающийся
точечным источником, равномерен во всех направлениях, то
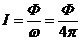 и
и  (4)
(4)
Освещенность.
Понятие освещенности Е численно равно величине потока, падающего на
единицу освещенной поверхности, т.е.
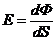 (5)
(5)
измеряются в люкс.
Если произвольно
ориентированная в пространстве площадка освещается точечным источником 0,
то согласно (2)
 (6)
(6)
Где r - расстояние от
источника до площадки, 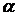 - угол между
нормалью и площадкой, а
- угол между
нормалью и площадкой, а 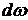 - телесный угол, в
котором видна площадка из точечного источника (рис.1).
- телесный угол, в
котором видна площадка из точечного источника (рис.1).
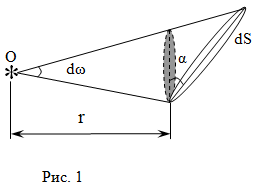
Освещенность этой поверхности
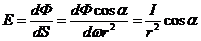 (7)
(7)
Формула (6) выражает три закона
освещенности:
Освещенность площадки обратно
пропорционально квадрату расстояния от точечного источника;
Освещенность площадки прямо
пропорциональна косинусу угла между направлением светового потока и нормалью к
площадке (закон косинуса).
Освещенность площадки прямо
пропорциональна силе света.
Вентильный
фотоэффект
На границе метал -
полупроводник образуется запорный слой
При освещении полупроводника
потоком фотонов, образующий необходимую энергию вырванным из атомов п - полупроводника
электроны, проходит запорный слой в пропускном направлении и, скапливаясь на
внешней границе р - полупроводнике создают постоянную разность
потенциалов  .
.
Если соединить проводником обе
граничные поверхности, то через него потечет ток, измеряемый гальванометром G.
Разность потенциалов  является
электродвижущей силой по отношению к замкнутой цепи.
является
электродвижущей силой по отношению к замкнутой цепи.
Это Э.Д. С. создает в
проводнике фотоэлектрический ток, который в соответствии
 (8)
(8)
пропорционален подающему светлому
потоку Ф. Приборы, в которых фотоэффект используется для превращения
энергии излучения в электрическую, называются фотоэлементами.
Фотоэлементы с запирающим слоем. Эти
фотоэлементы, основанные на внутреннем фотоэлементе и свойствах поверхности
соприкосновения полупроводника - металл, обладают разными достоинствами.
Они обладают чрезвычайно большой
чувствительностью, в особенности к видимым и инфракрасным лучам.
Современные кремниевые фотоэлементы
с запирающим слоем дают мощность свыше 500 мкВт/лм.
Плотность фотометрического тока
определяется из формулы (7) и (8).
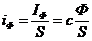
учитывая формулу (6) можно написать:
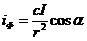 (9)
(9)
Где с - пропорциональность
учитывающая чувствительность фотоэлемента. Формула (8) выражает законы
освещенности:
. Освещенность площадки фотоэлемента
прямо пропорциональна напряжению питанию спиральной лампы, так как I~U.
. Освещенность площадки фотоэффекта
обратно пропорциональна квадрату расстояния от источника света.
. Освещенность площадки фотоэлемента
прямо пропорциональна косинусу угла между направлением светового потока к
нормали площадки.
Порядок выполнения работы:
. Собрать электрическую схему
установки.
. Включить в сеть переменного тока
лампу накаливания.
. Установить напряжение U=180В
с помощью реостата.
. Записать показание микроамперметра,
при различных положениях (α= 0о, 30о,
60о и 90о)
. Переместив лампу на 10 см,
повторить операцию 4 раза.
. Установить напряжение на
вольтметре U=(200В и 220В). Повторить операции 2 - 4 раза.
. На основе полученных данных
построить график.
Запомните, что
показание микроамперметра при α=60о должен быть
меньше, чем α=90о.
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа № 8
Тема: Определение длины волны с
помощью дифракционной решетки
Принадлежности:
1. дифракционная решетка
. держатель для дифракционной
решетки
. линейка со шкалой
. экран с вертикальной щелью со
шкалой
. осветительная лампа с двумя
линзами
. футляр для лампы
. оптическая скамья.
Дифракционная решетка
устанавливается в держателе, который прикреплен к концу линейки. На линейке
располагается экран с узкой вертикальной щелью посередине, лампа
устанавливается в футляре (вся эта установка крепится на оптической скамье).
Лампа, экран и дифракционная решетка должны быть установлены на оптической оси
линзы.
Цель работы: определить
длину волны с помощью дифракционной решетки по опыту Фраунгофера.
Задача дифракции, как и в других
случаях, заключается в нахождении распределения интенсивности света в
зависимости от угла дифракции φ
Фраунгоферова дифракция.
Рассмотрим дифракцию плоской
монохроматической световой волны от щели шириной b.(рис. 1)
Для простоты будем считать, что
плоско-параллельная световая волна некоторой длиной падает нормально к плоской
щели. Параллельная плоская волна, пройдя через щель b на непрозрачный
экран Э дифрагирует под разными углами в правую и левую стороны от
первоначального направления падения волны.
Линза L собирает
параллельные лучи (пучки) дифрагированнные волны в соответствующих токах экрана
расположенного в ее фокальной плоскости. Не дефрагирующие волны соберутся в
точке O, а лучи
дифрагируюшие вправо под углом φ соберутся в
точке φ
(рис.
1).
Задачу дифракции в данном случае можно решить двумя методами - графическим и
аналитическим.

Т.к. параллельный пучок света падает
нормально к плоскости щели, то фронт волны будет совмещен с плоскостью щели,
т.е. все точки фронта волны в плоскости щели будут колебаться с одинаковой
фазой. Разобьем фронт волны в плоскости щели от точки М до точки N
на параллельные по краям плоскости равной ширины. Каждая полоска будет играть
роль вторичного источника. Вследствие идентичности полосок, амплитуды волн в
плоскости щели будут одинаковыми. Равенство фаз во всех точках щели.
Следовательно, и для всех полос, было отмечено выше. Все это упрощает решение
задачи дифракции в обоих случаях (такие условия выполняются и для лазерного
излучения).
Графический метод. Выражая
амплитуду каждой полоски векторами равной длины, найдем результирующую
амплитуду, пользуясь графическим методам сложения амплитуд. Результат при
разных углах дифракции φ.
При φ=0 т.е. в точке
O амплитуда Е
0 будет максимальной, т. к. по величине амплитуды одинаковые,
направлены в одну сторону, поэтому они складываются (рис. 2).
В направлении, при котором крайние
полоски отличаются по фазе на 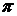 (т.е. разность хода NF между
крайними лучами равна
(т.е. разность хода NF между
крайними лучами равна  ),
результирующая амплитуда равна
),
результирующая амплитуда равна
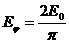
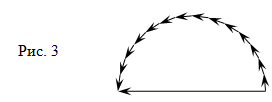
Действительно, как видно из
диаграммы (рис. 3) в этом случае результирующая равна диаметру полуокружности Е
0, т.е.

Это направление определяется из
условия

В случаях, когда разность хода между
крайними волнами (FN) равна λ, т.е. когда фаза крайних полос
вследствие замыкания окружности отличатся на 2π, результирующая
амплитуда обращается в нуль. Это направление определяется как
 .
.
Амплитуда равна нулю во всех
случаях, когда разность хода между крайними волнами равна λ, 2λ, 3λ, 4λ, и т.д.,
наблюдается mах, причем интенсивность их падает с увеличением угла
дифракции.
Аналитический метод. Ширину
элементарной полоски обозначим через dx возмущение, вызванное каждой
полоской в плоскости щели.
Изменение освещённости описывается
уравнением
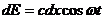
где с - постоянная величина.
Если амплитуду падающей волны соответствующей всей ширине щели обозначим через Е
0, то очевидно что,
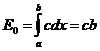 (1)
(1)
откуда
 ,
,
следовательно,
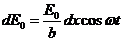
Для нахождения результирующей
амплитуды в любой точке экрана наблюдения, определяемой углом дифракции φ,
необходимо
знать распределение фаз всех колебаний приходящих в эту точку. Поскольку линза
не вносит в добавочном разности хода, то распределение фазы в точке φ
будет таким же, как и в плоскости NF,
образующей с плоскостью щели угол φ.
По этому требуется найти,
распределение для элементарных полос в плоскости NF(рис.
1).
Рассмотрим элементарную
полоску, расположенную на расстоянии от точки М, т.е. от левого края щели МN.
Для лучей дифрагированных под углом φ средняя
точка (X) этой полоски
перемещается в точку X1
полоски NF. Возмущение,
обусловленное произвольной полоской шириной dх расположенной на
расстоянии х от точки N
в плоскости NX1
выражается уравнением
 (2)
(2)
как следует из выражения (2),
вследствие добавочной разности хода волн XX1 возникает
разность фаз между точкой N и точкрй X1 в плоскости
NF, равная
 .
.
Имеем
NX1 = хsinφ,
следовательно:
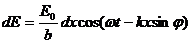 (3)
(3)
Вследствие когерентности возмущений
от всех полосок, нахождение результирующей амплитуды в произвольной точке В, φ сводится к
решению задачи интерференции, т.е. сложения влияний всех полосок с учетом амплитуды
и фазы. Поэтому проинтегрируем выражение (3) по всей ширине щели, т.е. от 0
до b.
 (4)
(4)
Уравнение (4) есть выражение
результирующего возмущения в точке φ с амплитудой

 (5)
(5)
Т.к. интенсивность есть величина
прямо пропорциональная квадрату амплитуды, то распределение интенсивности на
экране наблюдения и зависимости от угла дифракции имеет вид:
 (6)
(6)
Т.е. освещенность на экране
меняется, принимая max и min значения. Здесь Iо
-интенсивность света идущего от всей щели в направлении φ=0, т.е. в
направлении первичного пучка.
Условия min и mах, при
значении угла дифракции φ
удовлетворяющих
условию
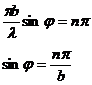 (7)
(7)
где n=1, 2, 3 ...
освещенность равна 0
Дифракция света от двух и многих
щелей. Дифракционная решетка
Дифракция света от дифракционной
решётки (рис.
4). При рассмотрении дифракции плоской световой волны от щели мы видели,
что распределение интенсивности на экране определяется направлением
дифракционных волн. Это означает, что перемещение щели параллельно самой себе
влево и вправо по экрану Э не приводит к какому либо изменению дифракционной
картины.
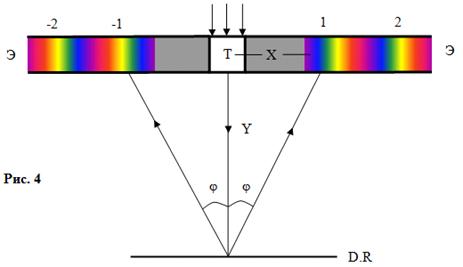
Следовательно, если на экране Э
сделать еще одну щель, параллельно первой такой же ширины b, то картина,
создаваемая на экране Э каждой щелью в отдельности, будет совершенно
одинаковыми. Результирующую картину можно определить путем сложения этих двух
картин с учетом взаимной интерференции волн, идущих от обеих щелей. Направим
параллельный пучок когерентного света на непрозрачный экран с двумя идентичными
щелями шириной b отстоящими друг от друга на расстоянии а.
Очевидно, в тех направлениях, в которых ни одна из щелей не распространяет
свет, будут наблюдаться min с нулевым значением интенсивности. Однако,
что касается mах, то они уже будут наблюдаться не во всех тех
направлениях, в которых мы наблюдали их в одной щели. Вследствие взаимной
интерференции световых волн, двумя волнами, у некоторых направлений они будут
взаимно уничтожаться. Следовательно, в отличие от дифракции от одной щели в
случае двух щелей возникают добавочные min.
Очевидно, что добавочные min
с нулевыми значениями интенсивности будут наблюдаться в тех направлениях,
которым соответствует разность хода 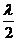 ,
,  ,
,  , … волн посылаемых от соответствующих
точек т.е.
, … волн посылаемых от соответствующих
точек т.е.

где m=0, 1, 2, …
действие одной щели будет
усиливаться другой если

такие mах будем называть
главными.
Обозначив сумму а+b, через d
(рис. 5) перепишем условие добавочных min и главных max в
виде:
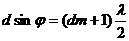 (8) (добавочный min)
(8) (добавочный min)
 (9) (главный maх)
(9) (главный maх)
Как мы знаем, прежние min d
направления определяющие условия:
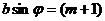 (10) (прежние min)
(10) (прежние min)
Дифракция света от многих щелей.
Дифракционная решетка
Из (8) и (10) видно, что в случаях
двух щелей между соседними главными max наблюдается один добавочный min.
Проведя аналогичные рассуждения, легко убедиться, что для случая N щелей
число добавочных min, наблюдаемых между соседними главными mах
будет N-1.
Система параллельных щелей равной
ширины, разделенных одинаковыми непрозрачными промежутками, называется
дифракционной решеткой. Сумму ширины прозрачной b и непрозрачной а
полос принято называть постоянной решетки d (рис. 5).

=a+b
В
такой решетке прозрачность (амплитудный коэффициент пропускания)  вдоль
решетки будет меняться скачками от τ= 0 до τ = 1.
вдоль
решетки будет меняться скачками от τ= 0 до τ = 1.
Как
в случае фраунгоферовой дифракции от одной щели, распределение интенсивности
для дифракционной решетки в зависимости от угла дифракции можно также
изобразить графически и аналитически. Все колебания идущие от разных щелей в
направлении φ=0
имеют одинаковые амплитуды и фазы колебания. Следовательно, все векторы
амплитуд будут направлены вдоль одной линии и результирующая амплитуда будет
Е
0=NE01,
где
Е 01 - амплитуда колебания соответствующая одной щели.
Интенсивность
в направлении φ=0
будет
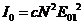 ,
,
где
с - коэффициент пропорциональности. Как видно, в случае дифракции от N
щелей интенсивность в направлении φ=0 растет прямо
пропорционально квадрату числа интерферирующих волн N. min будет
наблюдаться в том случае, еcли колебания идущие от первой и последней щелей,
будут отличаться по фазе на 2π, т.е.
Nδ=2π
(δ- разность
фаз колебаний от соответствующих участков соседних щелей), то

Это
позволяет определить условие добавочных min расположенных между главными
mах.
 ,
,
где р= 1, 2, 3, …
-N.
1, 2, 3, …
-N.
В частности
 (11)
(11)
Т.к. при переходе от главного mах
к соседнему min разность хода меняется на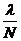 , то имеет место
, то имеет место
 ,
,
отсюда

и условие ширины главного mах

при малых углах дифракции
cosφ≈1 и  .
.
Следовательно, при d = соnst
с увеличением числа щелей помимо роста интенсивности происходит резкое сужение
главных mах в результате чего расплывчатые mах превращаются в
узкие, разделенные темными промежутками.
Порядок выполнения работы.
1. Подготовить таблицу отчета для
записи результатов измерений и вычислений.
. Собрать измерительную установку.
Установить экран, источник света и дифракционную решетку на одной прямой,
строго на горизонтальной плоскости.
. Глядя сквозь дифракционную решетку
и щель в экране на источник света и перемещая экран, установить его так, чтобы
дифракционные спектры располагались параллельно шкале экрана, симметрично
относительно щели экрана Т (рис. 4).
. С помощью шкалы экрана определить
расстояние от центра щели до центра фиолетового, зеленого и красного спектров
для левой и правой стороны щели для спектров 1, 2 и 3 порядка. Каждое измерение
повторить 3-4 раза.
. Определить с помощью линейки
расстояние от экрана до дифракционной решетки.
. При малых углах допустимо
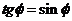 ,
,
поэтому формула (11) примет такой
вид

тогда окончательна формула будет
иметь вид:
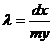
где  - длина данной волны
- длина данной волны
d - постоянная данной решетки
равная 0.01
x -
расстояние от середины щели экрана до середины данного спектра
y -
расстояние от экрана до дифракционной решетки.
. Занести все данные в таблицу и
выполнить все необходимые вычисления
. Сравнить полученные результаты с
длинами волн для данных цветов, взятых из таблицы.
Контрольные вопросы:
1. Что такое длина волны? Единицы ее
измерения.
. Что представляет собой явление
дифракции?
. Что называют дифракционной
решеткой?
. Какая величина характеризует
дифракционную решетку?
. Что такое спектр?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа № 9
Тема: Определение радиуса кривизны
линзы и длины световой волны с помощью колец Ньютона
Цель работы:
Ознакомиться с явлением интерференции в тонких прозрачных изотропных средах.
Принадлежности:
. Кинопроекционная лампа
. Конденсорная линза.
. Вставка для фильтра.
. Установка Ньютона.
. Фокусирующая линза.
. Экран.
. Оптическая скамья
. Штангенциркуль.
. Миллиметровая бумага или белая в клетку.
Теория
Поверхность плоско параллельной
пластинки из прозрачного материала освещается точечным источником
монохроматического света (рис. 1). В произвольную точку А расположенную
по ту же сторону пластинки, что и источник S приходят 2 волны: одна отраженная
от верхней, другая - от нижней поверхности. Обе волны исходят из одного и того
же источника, и являясь когерентными дают нелокализованную интерференционную
картину.
Для объяснения интерференционной
картины на тонкой пластинке можно использовать 2 метода.
. Когда первая волна преломляется, а
вторая отражаясь, встречается с первой.
. Когерентные волны можно получить,
рассматривая ход лучей одной волны. Когда в точку М падает одна волна,
то в ней происходят:
отражение
преломление
т.е. раздвоение одной волны на две.
При этом преломленная волна отражается с другой стороны пластинки доходя до
точки D и выходит из пластинки преломляясь, при этом отраженная волна МQ
и преломленная волна DТ будут параллельными. Эти волны
являются когерентными. В зависимости
от разности хода лучей МА и DА в точке А будет наблюдаться
интерференционная картина. Так как интерференционная картина определяется
оптической разностью хода между интерферирующими волнами, то необходимо найти
эту разность. Вследствие того, что оптические длины всех прошедших через линзу
волн в пределах линзы равны, то любая разность хода между интерференционными
волнами МА и DА возникает от точки М до плоскости DQ:
 (1)
(1)
Где n и n0
- показатели преломления пластинки и окружающей среды. Присутствие последнего
члена 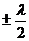 обусловлено
потерей полудлины волны при отражении света от границы раздела оптически более
плотной среды. Если n>n0, то потеря волны произойдет в
точке М, и выше упомянутый член будет иметь знак минус. Если же n<n0
то потеря полудлины произойдет в точке N и последний член будет иметь
знак плюс. В обоих случаях произойдет смещение интерференционной картины на
полполосы в ту или иную сторону относительно предполагаемой интерференционной
картины, полученной без учета потери полуволны.
обусловлено
потерей полудлины волны при отражении света от границы раздела оптически более
плотной среды. Если n>n0, то потеря волны произойдет в
точке М, и выше упомянутый член будет иметь знак минус. Если же n<n0
то потеря полудлины произойдет в точке N и последний член будет иметь
знак плюс. В обоих случаях произойдет смещение интерференционной картины на
полполосы в ту или иную сторону относительно предполагаемой интерференционной
картины, полученной без учета потери полуволны.
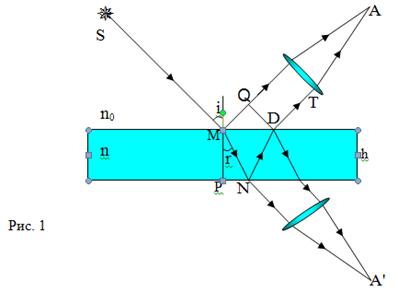
Толщину пластинки, углы падения
и преломления соответственно обозначим через h, i,
r.
Из ∆MPN и ∆MQD
имеем:
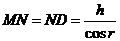 (2)
(2)
 (3)
(3)
Если мы примем во внимание закон
преломления света, согласно которому

Подставляя (2) и (3) в формулу (1),
получим:
 (4)
(4)
Следовательно, с учетом потери волны
для оптической разности хода получим
 (5)
(5)
В точке А будет максимум,
если
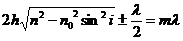 (6)
(6)
и минимум если:
 (7)
(7)
где m=0, 1, 2... - порядок
интерференции. Таким образом, в результате встречи когерентных волн возникает
система интерференционных полос. Как следует из (6) и (7) при данных λ,
h, n,
n0
каждому наклону лучей соответствует своя интерференционная полоса.
Поэтому такие полосы
интерференции называются полосами равного наклона и равной толщины.
Интерференционную картину полос равной толщины
можно наблюдать от воздушной прослойки, образованной плоскопараллельной
пластинкой и соприкасающейся с ней выпуклой или двояко выпуклой линзой большого
радиуса кривизны (рис. 2).
В этом случае геометрическим
местом точек одинаковой толщины является окружность, и поэтому соответствующие
полосы равной толщины будут иметь вид концентрических окружностей с центром в
точке соприкосновения линзы с плоскопараллельной пластинкой. В отраженном свете
в центре интерференционной картины будет наблюдаться минимум. Это обусловлено
тем, что в месте соприкосновения линзы в точке В образуется крайне тонкий
воздушный зазор (толщина его намного меньше длины волны), приводящий к потере
полуволны.
Схема, с помощью которой
наблюдаются кольца Ньютона (рис. 3).
М- источник света; К 1 и
К 2- собирающие конденсорные линзы; Н- прибор для получения колец
Ньютона; Ф- световой фильтр; Э- экран.
Роль пластинки переменной
толщины играет воздушная прослойка между линзой и плоскопараллельной
пластинкой. Границы этой "пластинки" определяются снизу - верхней
поверхностью плоскопараллельной пластинки, сверху - нижней поверхностью линзы.
Параллельный пучок света 1 и 2 выделенный из точечного источника,
расположенного в фокусе конденсорной линзы, направляется на систему линза -
плоско параллельная пластинка. Падающая волна 1 после отражения от
нижнего поверхности воздушной прослойки, выходит из точки D (рис. 2).
Она частично отражается (волна 1’) и частично преломляясь в линзе выходит в
направлении 2’. Волны 1' и 2' являются когерентными при
интерферентном наложении между собой.

Вычисление разности
хода для интерферирующих лучей
Высоту в точке D откуда
выходят волна 2' обозначим через h. т.е.
DЕ=h.
Пусть показатель преломления
пластинки, линзы и прослойки между ними соответственно будут n1,
n2 и n0. Разность хода лучей 1' и 2'
будет (рис. 2)

При нормальном падении луча cosr
≈1.
Считая n0=1 получим:

Вычисление радиусов
для максимумов и минимумов.
Пусть высота DЕ=h
соответствует максимуму m-го порядка, т.е.
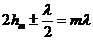 (8)
(8)
где m= 1, 2, 3... и DЕ
=hm. Тогда радиус для максимума m-го прядка будет АB=O'F=rm.
Исходя из формулы (8) и  ОAВ
можно определить rm
(рис. 4).
ОAВ
можно определить rm
(рис. 4).
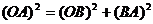 ;
; 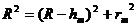
где R - радиус кривизны
линзы. Считая, что hm"R, имеем:
rm=2Rhm (9)
Подставляя выражение hm
из (8) в (9) получим
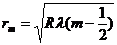 (10)
(10)
Минимумы наблюдаются, если
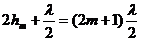
Следовательно, радиусы для минимумов
определяются как
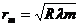 (11)
(11)
При наблюдении интерференции в
прошедшем свете потери полудлины не происходит и разность хода между
интерферирующими лучами будет равна:

Радиусы для минимумов и максимумов
определяют соответственно формулам (10) и (11). Следовательно,
интерференционные картины в отраженном и прошедшем свете, взаимно дополняют
друг друга.

В фокальной плоскости
конденсорных линз К 1 К 2 интерференционная картина
наблюдается в виде колец Ньютона. Максимум и минимум у этих колец зависит от
разности хода лучей 1 и 2. Как следует из (11).
 (12)
(12)
 (13)
(13)
Порядок выполнения работы:
1. Произвести юстировку оптических
систем, т.е. у всех трех линз главная оптическая ось должна лежать на одной
прямой. Линзы должны быть в параллельных плоскостях, чтобы избежать
дополнительной ошибки в измерениях.
. Включить проекционную лампу в
сеть, перемещая установку Ньютона вдоль оптической оси должны получить четкую
картину на экране. Если картина не наблюдается, довести до конца юстировку оптических
приборов.
. Вставить нужный фильтр.
. С помощью штангенциркуля измерить
диаметр цветных колец, при этом диаметр колец нужно измерить в нескольких
направлениях.
. Используя формулу (12) определить
радиус кривизны линзы. Длину волны для данного фильтра взять из таблицы.
. Сменить фильтр и выполнить пункт
4.
. Рассчитать из формулы (13) длину
волны.
. Опыт повторить 5-6 раз.
.Данные занести в таблицу, которую
заполнить так, как вам удобно.
. Подсчитать среднюю квадратичную
ошибку по формуле:
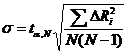
и занеси полученные данные в
таблицу.
. Записать окончательный результат с
учетом доверительного интервала
. Построить 2 графика зависимости R=f(N)
и 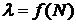
|
№
|
rm-1
|
rm
|
rm-1
|
rm
|
rm-1
|
rm
|
  Rλ Rλ
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|

Контрольные
вопросы:
1. Что представляет собой
явление интерференции?
2. Какие волны называются
когерентными, монохроматичными?
. Опишите установку,
использованную в лабораторной работе?
. Как определялся радиус
кривизны линзы?
Дополнительную информацию можно
найти в электронной версии.
Лабораторная работа
№ 10
Тема:
Фотометрирование источников света
Цель работы:
ознакомление с фотометрическим определением силы света лампы накаливания с
помощью визуального фотометра, оценки коэффициента поглощения стекла,
органического стекла, индикатора рассеивания света вокруг лампы накаливания.
Основными характеристиками излучения источников являются следующие:
Световой поток Ф
- мощность лучистой энергии, оцениваемая по зрительному ощущению. Единицей
светового потока в СИ является люмен (лм)
Опытным путем установлено, что
световому потоку в 1 лм, образованному излучением с длиной волны, 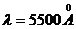 соответствует
поток энергии в 0,0016 Вт.
соответствует
поток энергии в 0,0016 Вт.
Сила света I - световой
поток dФ, приходящийся на телесный угол 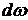
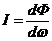 (1)
(1)
Единицей силы света является
кандела (кд). Телесный угол определён формулой:

где R- расстояние
от источника до освещённой поверхности, α- угол между нормалью  поверхности
и направлением источника, dS- освещённая поверхность.
поверхности
и направлением источника, dS- освещённая поверхность.
Если источник точечный, то сила
света одинакова во всех направлениях. В этом случае из (1) следует:
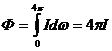
откуда
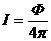 (2)
(2)
Освещенность Е - отношение
светового потока, падающего на поверхность, к площади dS этой
поверхности:
=dФ/dS (3)
Единицей освещенности является люкс
(лк)
Освещенность, создаваемая точечным
источником, можно выразить через силу света I:
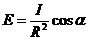 (4)
(4)
Действительно, из формулы (1)
и (3) получаем формулу (4).
Определение силы света
источника практически производится путем сравнения силы света двух источников -
известного и неизвестного. Если создать равенство освещенностей одной пластинки
двумя источниками Е 1=Е 2, то, зная силу света I1,
одного источника и измерив расстояние R1 и R2
от источников до пластинки можно определить силу света другого источника по
формуле:
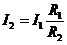 (5)
(5)
Формула (5) справедлива при
условии, что свет от источников падает в поле сравнения, в виде круга С
(рис.1). Остальные лучи испытывают полное отражение от сферической грани призмы
А и уходят в сторону.
Часть лучей от поверхности Е
2, также проходит через оптический контакт и уходит в сторону.
Другая часть лучей на плоскости гипотенузы призмы В испытывает полное
внутреннее отражение и направляется через ту же лупу L,
давая внешнее поле сравнения в виде кольца D
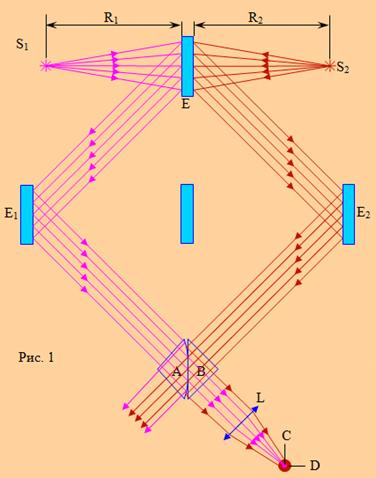
Таким образом, освещённости
обеих сторон экрана Е сравниваются глазом, при помощи освещённых полей С
и D, соприкасающихся
друг с другом и лежащих в одной плоскости. Изменяя расстояние R1
и R2 от источников S1 и S2
до экрана Е добиваясь исчезновения, различия яркости полей сравнения, а,
следовательно, равенства освещенностей. Найдём численное значение I2:
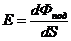 (6)
(6)
Рассмотрим связь между
освещённостью и силой света:
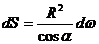


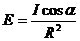
где dФпод -
изменение потока лучей,
R -
расстояние от источника до площадки.
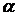 - угол между направлением лучей и
нормалью площадки.
- угол между направлением лучей и
нормалью площадки.
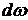 - телесный угол, под которым видна
площадка dS из точечного источника. Если
- телесный угол, под которым видна
площадка dS из точечного источника. Если 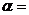 0, тогда для источников S1 и S2 имеем:
0, тогда для источников S1 и S2 имеем:
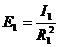 ;
;
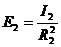
E1=E2 (7) 
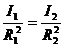 (8)
(8)
Такой метод определения сил света
источника называется фотометрическим. Приборы, применяемые для фотометрических
измерений и служащие для сравнения источников света, называют фотометрами.
В визуальных фотометрах учитывается
особенность глаза, обусловленная тем, что он позволяет достаточно точно
установить равенство освещённости (точнее - яркостей) двух сравниваемых
поверхностей и не может дать количественной оценки соотношений освещённости,
если они различны. Наиболее благоприятное условия для установления равенства
освещённостей двух поверхностей будет в том случае, когда эти поверхности
соприкасаются, и для глаза кажутся лежащими в одной плоскости.
Принципы конструктивного оформления,
обеспечивающего выполнения этого условия, могут быть пояснены из анализа так
называемого кубика Луммера-Бродхуна (рис. 1).
Два сравниваемых источника S1
и S2 силой света I1 и I2
располагаются по обе стороны непрозрачного экрана Е одинаково
рассевающего экрана (матового) и отражающего (белого) с обеих сторон.
Рассеянный экраном свет падает на две вспомогательные белые (иногда зеркальные)
поверхности Е 1 и Е 2 от которых отражается
на кубик. Последний состоит из двух соприкасающихся прямоугольных призм А
и В(рис. 1).
Грань призмы А,
соответствующая гипотенузе, имеет сферическую поверхность, с частично
отшлифованной плоскостью, соприкасающеюся с плоскостью призмы В. При тщательной
шлифовки призмы, в этом месте образуется так называемый оптический контакт, т.
е в этом месте призмы А и В представляют собой один сплошной
кусок стекла. Свет от поверхности Е падая на призмы А и В, в
месте оптического контакта выходит без преломления в другую призму и далее
через лупу L попадает в глаз, давая внутреннюю освещённую область С. В
месте где призмы А и В не соприкасаются, свет отражается от основания призм и
проходя через лупу, попадает в глаз давая внешнюю освещённую область D. Изменяя
расстояния R1 и R2,,добиваемся
одинаковой освещённости областей С и D. Теперь
зная силу света эталонного источника, можно определить силу света испытуемого
источника.
Вследствие невозможности изменять
расстояние R1 и R2 в очень широких
пределах, в некоторых конструкциях фотометров применяют другие способы
ослабления светового потока: вращающееся диски с вырезами, светофильтры и пр.
Определение силы света лампы
накаливания
Принадлежности: оптическая
скамья, две лампы накаливания, визуальный фотометр.
Порядок выполнения работы:
1.Включить в сеть переменного тока
лампу накаливания.
.Передвигая каретку с фотометром,
добиться равенства освещённостей и измерить расстояния R1 и R2,
по шкале скамьи или линейкой.
.Повторить указанные операции
три-четыре различных расстояния между источниками света.
.По известному значению вычислить
для каждого измерения значение I2 по формуле (5), определить
среднее значение силы света исследуемой лампы и определить погрешность
измерения.
Лампы накаливания общего освещения.
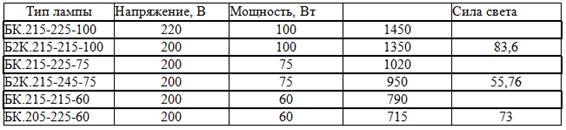
Построение индикатрисы рассеивания
света вокруг лампы накаливания. Индикатрисы рассеивания можно определить с
помощью визуального фотометра.
Порядок выполнения работы.
. Включить в сеть переменного тока
две лампы.
. Повернуть лампы 1 и 2
так, чтобы они были параллельны друг другу и перпендикулярны оси оптической
скамьи.
. Определить силу света исследуемой
лампы в данном положении так же, как и в предыдущем задании.
. Поворачивая лампу 2, определить
силу света через каждые 20о, до поворота на 180°.
. При получении результатов
начертить кривую распределения силы света в зависимости угла поворота лампы,
откладывая по радиусам соответствующие с этим углом значения сила света.
Поглощение света
При прохождении света через
вещество, часть света отражается, часть света проходит через вещество. В случая
поглощение света, его энергия переходит в другие формы энергии и главным
образом в тепловую.
Количественно поглощение света
характеризуется коэффициентом поглощения, который зависит как от природы
вещества, так и от длины волны света, взаимодействующего с веществом. Функцию,
определяющую зависимость коэффициента поглощения от длины волны, называют
спектром поглощения.
Рассмотрим параллельный пучок лучей,
распространяющийся в поглощающей среде.
Обозначим начальную интенсивность
лучистого потока в плоскости х=0 через I0.
Пройдя в среде путь dx, лучистый
поток в результате поглощения и рассеивания света ослабляется и его
интенсивность I(x) становится меньше.
Интенсивность потока, прошедшего путь
x+dx, равным I+dI будет еще
меньше, чем I, т.е. dI<0. Величина dI
представляет собой лучистый поток, поглощенный и рассеянный на участке dx. Это
величина пропорционально толщине участка и интенсивности падающего на этот
участок света I0 т.е.
dI=kI0
dx (9)
где k - коэффициент
ослабления света.
Интегрируя (9), получим:
=I0e-kx (10)
где I0 -
интенсивность света при x=0.
Коэффициент К имеет
размерность обратной длины и может быть определен для данной длины волны из
уравнения:
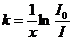 (11)
(11)
Порядок выполнения
работы:
1. Включить в сеть переменного
тока лампу накаливания.
. Передвигая коробку с
фотометром добиться фотометрического равновесия и измерить расстояние линейкой.
. Между лампой L2
и визуальным фотометром поставить стекло или искусственный материал.
. Перемещая лампу добиться
фотометрического равновесия и измерить расстояние линейкой.
. Определить коэффициент
ослабления по следующим алгоритмам:
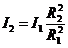
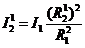

. Измерения повторить для нескольких
участков стекла.
7. Определить среднее значение К и
среднее-квадратическую ошибку.
Дополнительную информацию можно
найти в электронной версии.