Неравновесные системы

Неравновесные системы

Содержание

1. Уравнения баланса тепла и числа частиц

. Броуновское движение. Уравнение Ланжевена

. Уравнение Фоккера-Планка

Уравнение баланса энтропии

. Основные положения линейной неравновесной термодинамики

. Вывод соотношений взаимности Онсагера из теории флуктуаций

. Перекрестные явления в газах

. Ультраразреженные газы

. Диффузия газа в асимметричной мембране

. Термоэлектрические явления

. Электронный ветер

. Уравнение Мастера. Диффузия тяжелого газа в легком

. Причины необратимости в макросистемах

Литература

. Уравнения баланса тепла и числа частиц

В термодинамически равновесных системах температура, давление и химический потенциал одинаковы во всей системе:

, , .

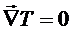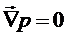Если эти условия не выполняются, то в системе возникают необратимые процессы переноса массы, энергии, электрического заряда и т.д. Большинство же реальных систем не находятся в состоянии равновесия. При этом функции распределения частиц зависят как от координат, так и от времени, а термодинамические параметры принимают различные значения в разных точках пространства.

При обобщении классической термодинамики на неравновесные процессы исходят из представления о локальном равновесии. Известно, что время релаксации растет с увеличением размеров системы, так что отдельные макроскопически малые части системы приходят сами по себе в равновесное состояние значительно раньше, чем устанавливается равновесие между этими частями. Поэтому в неравновесной термодинамике принимают, что, хотя в целом состояние системы неравновесно, отдельные ее малые части равновесны (точнее, квазиравновесны), но имеют термодинамические параметры, медленно изменяющиеся во времени и от точки к точке. Однако в системе локальное равновесие может отсутствовать. Например, это характерное для сильно разреженных газов. Для них часто нельзя ввести такие понятия, как температура, давление и т.д.

Начать с уравнения типа Ланжевена и случайных процессов, а потом на его основе вывести все основные уравнения переноса. Там четко определить Марковский процесс и увидеть, на каком этапе появляется необратимость.

Основы теории переноса тепла были заложены французским математиком Фурье (1768-1830) в первой четверти XIX века. Хотя Фурье и исходил из неправильной теории теплорода, т.е. предполагал, что теплота была каким-то веществом, он получил правильное математическое выражение для плотности теплового потока. Плотностью потока теплоты называется вектор j, совпадающий по направлению с направлением распространения теплоты и численно равный количеству теплоты, проходящему в одну секунду через площадку в один квадратный сантиметр, перпендикулярную к направлению потока теплоты. Закон Фурье для неподвижной среды можно записать в следующем виде:

,

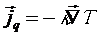где  - коэффициент теплопроводности (Вт/м×К).

Выведем уравнение баланса тепла сначала для одномерного случая.

Пусть имеется неограниченная среда, в которой возникает поток теплоты в направлении, параллельном оси x. В одномерном общем случае свойства среды и величины, характеризующие тепловой поток, могут меняться в том же направлении. Кроме того, они могут меняться во времени. Поэтому плотность потока теплоты j следует рассматривать как функцию координаты x и времени t: j = (x, t). Выделим мысленно в среде бесконечный цилиндр с образующими, параллельными оси x, и рассмотрим бесконечно малый участок такого цилиндра АВ длиной dx (рис. 4.1). Пусть S - площадь поперечного сечения цилиндра. Количество теплоты, поступающее в цилиндр АВ за время dt через основание А с координатой x, равно j (x)Sdt. Количество теплоты, уходящее за то же время через основание В, будет j (x + dx)Sdt. Так как через боковую поверхность цилиндра теплота не поступает, то полное количество теплоты, поступающее за время dt через рассматриваемый участок цилиндра, равно

.

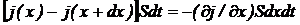Но эту теплоту можно представить в виде dM × c_vdT, где dM = ρSdx - масса цилиндра АВ, c_v - удельная теплоемкость, dТ - повышение температуры. Приравнивая оба выражения и производя сокращение, получим

. (*)

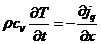Закон Фурье для одномерного случая можно записать в виде:

.

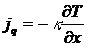Подставляя выражение для плотности потока тепла в (*), получим:

.

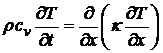Это уравнение называется уравнение теплопроводности. Коэффициент теплопроводности в общем случае зависит от температуры или от координат, но в частном случае, когда эта величина постоянна, имеем:

,

,

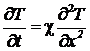где введено обозначение

.

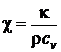Постоянная χ называется температуро-проводностью среды.

Уравнение теплопроводности легко обобщается на случай трехмерного пространства:

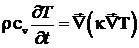, или

.

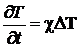Однако тепло может переноситься не только за счет теплопроводности, но и за счет движения среды как целого. В таком случае можно записать для плотности потока тепла:

.

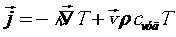Второе слагаемое представляет собой плотность потока тепла, возникающую за счет переноса массы. Покажем для общего случая, что второе слагаемое действительно есть плотность потока тепла, обусловленная движением среды. Рассмотрим аддитивную величину φ, которая переносится вместе со средой в направлении оси x. Обозначим через плотность величины φ (т.е. величина φ, заключенная в единице объема вещества). Рассмотрим цилиндрический объем с площадью поперечного сечения S, по которому движется среда со скоростью v вдоль оси x. Тогда за время dt через поперечное сечение пройдет величина φ, равная:

.

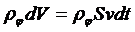Деля на S и dt, получим для плотности потока величины φ выражение:

.

Или в трехмерных координатах:

.

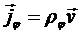Тогда можно записать уравнение баланса тепла в виде

.

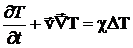Наконец, в среде могут оказаться источники теплоты. Например, теплота может выделяться в результате прохождения электрического тока или радиоактивного распада. Такие источники мы не принимали во внимание. Чтобы их учесть, введем величину q_V, равную количеству теплоты, выделяемому источниками в единице объема среды в одну секунду. Тогда уравнение баланса тепла запишется в виде:

.

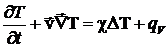Соотношения, во многом аналогичные, можно записать и для переноса частиц. Аналогом закона Фурье для переноса частиц выступает закон Фика:

,

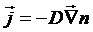где j - вектор плотности потока числа частиц,

D - коэффициент диффузии частиц в среде (м²/с). Вывод уравнения баланса числа частиц во многом аналогичен. Для одномерного случая полное число частиц, поступающее за время dt через рассматриваемый участок цилиндра, равно

.

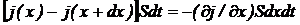Но изменение числа частиц можно представить в виде, где dN = Sdxdn. Приравнивая оба выражения и производя сокращение, получим

. (*)

Закон Фика для одномерного случая можно записать в виде:

.

Окончательно получим:

.

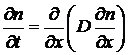Для постоянного коэффициента D имеем:

.

Это уравнение можно аналогичным образом обобщить на случай движущейся среды и источников частиц (например, это могут быть химические реакции или радиоактивный распад):

.

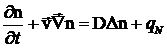Это уравнение называется уравнение баланса числа частиц.

Зависимости коэффициентов переноса от параметров в различных средах!

. Броуновское движение. Уравнение Ланжевена

Частный случай такого движения был описан ботаником Г. Броуном в 1827 году, когда он в микроскоп наблюдал за движением мельчайших частиц пыльцы. Однако характер этого движения был понят только в XX веке.

Рассмотрим движение крупных частиц в термически однородной среде типа газа или жидкости. Термин «крупные частицы» в данном случае означает, что частицы макроскопически наблюдаемы, т.е. размер их порядка R ~ 10^-4 см (для зеленого света l ~ 0,5×10^-4 см). Этот размер и с молекулярной точки зрения является большим.

Например, для воздуха при нормальных условиях среднее расстояние между молекулами ~ 0,5×10^-7 см, для жидкости - на порядок меньше.

Будем считать, что известны форма, размер, масса и т.д. броуновской частицы (БЧ), а также все свойства среды.

Рассмотрим облака БЧ, полагаем, что они не взаимодействуют друг с другом. Поэтому мы вправе рассматривать какую-либо одну БЧ.

Такая крупная частица взаимодействует сразу с большим числом частиц среды и под действием общей равнодействующей совершает два типа случайных блужданий:

а) флуктуации общей величины приводят к трансляционному броуновскому движению,

б) флуктуации момента равнодействующей силы - к вращательному броуновскому движению.

Математически эти процессы во многом эквивалентны, а значит, ограничимся первым типом.

Рассмотрим пространственно однородную систему (потенциал внешней силы 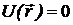) и в ней - одну броуновскую частицу. Т.к. направления x, y, z эквивалентны, исследуем одномерное броуновское движение вдоль оси x.

Выделим из силы F, действующей на броуновскую частицу, ту ее часть, которая существовала бы и в отсутствие флуктуаций. Эта регулярная часть силы F представляет собой не что иное, как силу вязкого трения (которая нам известна).

Например, для сферических частиц радиуса R согласно формуле Стокса:

  ,

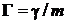h - коэффициент вязкости; v, p - скорость и импульс.

Тогда точное уравнение движения БЧ можно записать в виде:

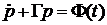
- уравнение Ланжевена (1908 г.),

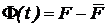 - случайная часть силы, действующей на БЧ. В среднем она равна нулю: <F(t)> = 0.

Проанализируем временные интервалы взаимодействия БЧ с окружением:

время соударения частицы с частицей среды t ~ 10^-12 c(для R ~ 10^-4 см);

время между отдельными взаимодействиями t' ~ 10^-16 ¸ 10^-17 c;

время исчезновения информации (релаксации) о начальном состоянии t_М ~ G^-1 ~ 10^-10 c.

При сравнении величин этих интервалов обращают на себя внимание характерные соотношения: t' << t и t << G ^-1.

3. Уравнение Фоккера-Планка

Теперь рассмотрим трехмерную систему БЧ и будем описывать эволюцию БЧ (или идеального газа БЧ) с помощью функций распределения f в самой грубой временной шкале t >> G^-1.

Распределение по импульсам БЧ в этой шкале является в любой момент времени максвелловским. Поэтому нас будет интересовать только функция распределения по координатам 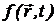, такая, что  - вероятность обнаружить частицу в объеме 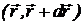, причем

.

Т.к. частицы стабильны (нет их источников), то функция 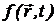 должна удовлетворять уравнению непрерывности

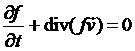, или

Введя грубую шкалу времени (включая dt >> G^-1), t >> G^-1, мы фактически лишим себя возможности использовать микроскопические соображения для превращения этого соотношения в уравнение для одной функции 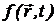. Оставаясь в рамках полуфеноменологического рассмотрения, представим плотность потока  как бы складывающуюся из двух частей

.

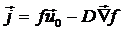Первая из них обусловлена внешними силами, действующими на БЧ, вторая - случайными «флуктуирующими» воздействиями на нее со стороны частиц среды. Второе слагаемое имеет характер диффузионного процесса, а D представляет собой коэффициент диффузии броуновской частицы в среде с заданными свойствами.

Скорость направленного движения частицы можно найти, используя представления гидродинамики (малые скорости, сферические частицы)

_внеш. = gu₀,g = 6pRh,

Поэтому упорядоченную часть плотности потока можно записать в виде

,

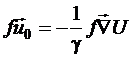где U - потенциал внешнего силового поля.

Величину D можно определить экспериментально, но это сложно сделать во всех случаях жизни. В связи с этим рассмотрим предел , когда система достигнет своего состояния ТД равновесия. В таком состоянии нет потоков (все характеристики постоянны):

.

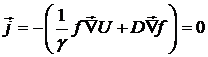Эти уравнения можно записать в виде

, .

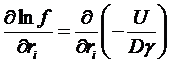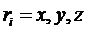Решение этой системы

мы могли бы предсказать заранее, так как идеальный газ БЧ в поле  характеризуется в равновесном случае больцмановским распределением

.

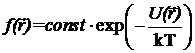Сопоставляя эти выражения, мы получаем, что коэффициент диффузии D просто связан с T, h и R БЧ

.

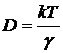Подставляя это выражение в уравнение непрерывности, получим уравнение для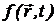

. (4.1)

Это и есть уравнение Фоккера-Планка (1914-1917). Дополненное условием нормировки, начальным (НУ) и граничными (ГУ) условиями, оно полностью определяет решение для искомой функции 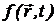. Это решение определяет эволюцию системы на времени t >> G^-1, которая имеет релаксационный характер (к распределению Больцмана) с некоторым временем релаксации t_полн, зависящим уже не только от индивидуальных свойств среды и БЧ, но и от начального распределения, формы и размеров сосуда и т.д.

Рассмотрим случай отсутствия внешнего поля 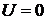 и бесконечной одномерной системы с условием отсутствия потоков на бесконечности и НУ, соответствующим нахождению броуновской частицы в точке :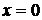

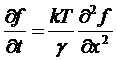, (4.2)

Решение уравнения (4.2), удовлетворяющее начальным и граничным условиям, выглядит следующим образом:

.

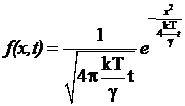Очевидно, что 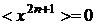 - ввиду симметрии функции :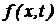

.

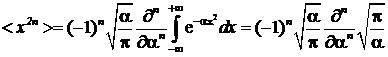В частности, средний квадрат смещения БЧ определяется формулой Эйнштейна

.

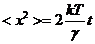Значение полученного решения для 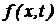не ограничивается только рамками рассмотренного примера. Эта функция может служить основой для получения ряда распределений по другим характеристикам свободного броуновского движения и для проведения оценок.

Оценим время заполнения БЧ сосуда конечных размеров. С математической точки зрения время такой релаксации равно 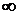. Речь идет о физической оценке эффективного времени релаксации.

Рассмотрим сначала одномерную систему, в которой движение БЧ ограничено стенками, так что 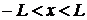. Если бы 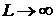, то эффективный размер облака броуновских частиц определялся бы формулой Эйнштейна

.

Если бы на расстоянии 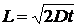 от точки  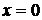по обе стороны стояли стенки, то внутри системы за это время 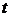 мы получили бы достаточно равномерное распределение броуновских частиц. Поэтому и полагают, что время полной релаксации в слое 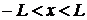 имеет величину.

В двумерном случае (броуновская частица в плоской кювете радиусом 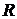) формула Эйнштейна имеет вид:

 ®

.

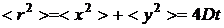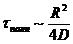Аналогично в трехмерном случае:

,

.

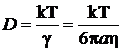Полученная оценка груба, но универсальна, т.к. не зависит от формы сосуда.

Таким образом, эволюцию броуновских частиц можно представить как последовательность характерных ее этапов:

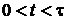)  - механическая шкала времени,  - время корреляции случайного взаимодействия . Описание эволюции системы - задача теоретической механики о столкновении многих частиц. Движение полностью детерминировано.

)  - первая грубая шкала времени, детали воздействия среды на частицу смазаны. В качестве динамических ее параметров выступают усредненные по 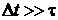 величины.

) При 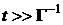 устанавливается максвелловское распределение по импульсам, и . Граничные условия несущественны.

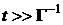 - вторая грубая шкала времени. Случайные блуждания БЧ приобретают характер диффузионного процесса. Частица в этом случае не имеет памяти (в механическом смысле) о своей скорости (распределение - максвелловское).

Такие процессы, в которых будущее системы определяется только настоящим и не зависит от ее предыстории, называются марковскими. Эволюция системы определяется уравнением Фоккера-Планка. Граничные и начальные условия существенны.

4. Уравнение баланса энтропии

Уравнение баланса энтропии в общем виде можно записать следующим образом:

,

где J_S - поток энтропии через границы системы,

Σ - производство энтропии (источник энтропии). Следствием второго начала термодинамики является то, что в изолированной системе энтропия не может убывать. Это означает, что производство энтропии не может быть отрицательно: .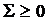

Рассмотрим производство энтропии на примере диффузии газа в сплошной среде. Два объема V₁ и V₂ соединены капилляром и представляют вместе изолированную систему. Поскольку система изолирована, то поток энтропии через ее границы равен нулю. В таком случае производство энтропии может быть определено так:

,

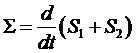где S₁ и S₂ энтропии вещества, находящегося в объемах. Каждую из этих величин можно записать на основе первого начала термодинамики:

,

.

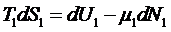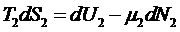Здесь мы пренебрегли изменением объема, а, следовательно, и работой, совершаемой одной системой над другой. Тогда получим:

.

Но ввиду изолированности системы суммарная внутренняя энергия и число частиц сохраняются:

,

.

.

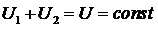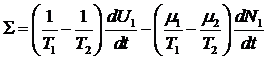Определим производные следующим образом:

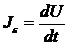 - поток энергии,

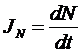- поток числа частиц.

Преобразуем величины в скобках, имея в виде, что отклонение от равновесия в каждой системе мало:

,

.

.

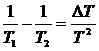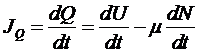В результате получим для производства энтропии:

.

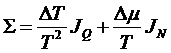Видим, что производство энтропии может быть представлено в виде суммы произведений потоков и соответствующих им сил:

.

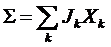Заметим, что выбор потоков (или сил) произволен - можно было выбрать поток энергии.

Поскольку система изолирована, то производство энтропии в ней - величина положительная. В данном случае это можно проиллюстрировать тем, что тепло переходит от более нагретого тела к менее нагретому, или частицы движутся в область с меньшим химическим потенциалом.

В условиях, когда допустимо представление о локальном равновесии можно построить последовательную феноменологическую термодинамику необратимых процессов. Свойства неравновесной системы при этом определяются локальными термодинамическими потенциалами, которые зависят от пространственных координат и времени только через характеристические термодинамические параметры, для которых справедливы уравнения термодинамики.

Рассмотрим теперь в произвольной системе малый объем и запишем аналогично производство энтропии для этого объема. Для простоты примем, что процессы переноса происходят только вдоль оси x. Тогда объем будет представлять собой цилиндр площадью S и длиной Δx. Тогда имеем:

,

где σ - плотность производства энтропии. Преобразуем:

.

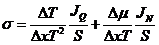Переходя к пределу, имеем:

.

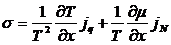Видим, что плотность производства энтропии может быть представлена в виде суммы произведений плотностей потоков и соответствующих им сил. В данном случае силы будут представлять собой градиенты:

,

.

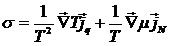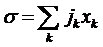5. Основные положения линейной неравновесной термодинамики

В равновесном состоянии термодинамические силы , потоки  и производство энтропии равны нулю. Поэтому при малых отклонениях от равновесия естественно положить линейную связь между потоками и силами:

.

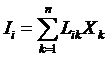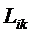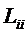Коэффициенты  в этом линейном законе называются кинетическими коэффициентами. Причем диагональные коэффициенты  определяю «прямые» явления переноса, а недиагональные коэффициенты 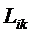 - перекрестные или сопряженные процессы. Эти соотношения можно записать в матрично-векторном виде:

.

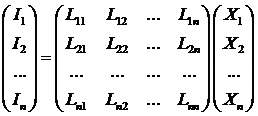Для плотностей потоков можно записать аналогичные выражения:

.

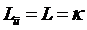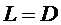Например, по закону теплопроводности Фурье градиент температуры вызывает поток теплоты , по закону Фика градиент концентрации вызывает диффузию , , по закону Ома градиент потенциала вызывает ток ,  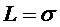и т.д. Наряду с этими прямыми процессами переноса возникают и перекрестные процессы. Например, при существовании градиента температуры кроме переноса теплоты может происходить и перенос массы (термодиффузия). Такие перекрестные процессы характеризуются недиагональными коэффициентами 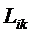. Так, плотность потока массы может быть пропорциональная градиенту температуры и т.д.

Не все коэффициенты 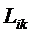 являются независимыми. В 1931 году Ларс Онсагер, исходя из инвариантности микроскопических уравнений движения относительно изменения знака времени (временная симметрия) и из представления о неравновесном состоянии системы, вызванном внешними силами, как крупной флуктуации равновесной системы, установил, что в области линейности необратимых процессов матрица кинетических коэффициентов симметрична: .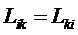

Это соотношение называют соотношение взаимности Онсагера.

Это соотношение приводит к тому, что число независимых величин в матрице кинетических коэффициентов становится меньше. Число диагональных коэффициентов равно n, а число независимых перекрестных коэффициентов равно: .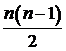

Теорема Пригожина. Рассмотрим систему, в которой имеются два потока и две соответствующие им силы:

,

.

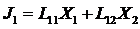Пусть в такой системе реализована ситуация, когда одна из сил (X₁) зафиксирована, т.е. поддерживается каким-либо способом. В результате поток J₂ в стационарном состоянии станет равным нулю, поскольку сила X₂ будет подстраиваться до тех пор, пока два слагаемых в этом потоке не будут компенсировать друг друга. Запишем производство энтропии для такой системы:

.

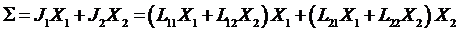Найдем экстремум величины Σ, для чего возьмем производную от Σ по X₂:

.

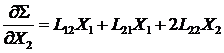Принимая во внимание соотношение взаимности Онсагера, имеем:

.

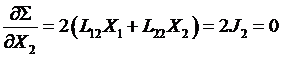Видим, что в стационарном состоянии имеет место экстремум величины Σ. Можно показать, что это минимум, поскольку вторая производная положительна. Таким образом, теорему Пригожина можно сформулировать в следующем виде:

Если хотя бы одна из термодинамических сил зафиксирована, то в стационарном состоянии система стремится к минимуму производства энтропии.

Эта теорема применима только к линейным системам.

Принцип Кюри

В термодинамике существует принцип Кюри для изотропных систем, свойства которых одинаковы во всех направлениях: потоки <#"867921.files/image121.gif">.

Коэффициенты, называемые константами скорости реакции, связаны уравнением детального баланса:

,

где , ,  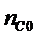концентрации соответствующих веществ в равновесии.

Тогда поток можно записать в виде:

,

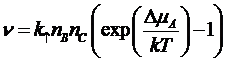где  - разность химических потенциалов исходных веществ и продуктов реакции. Эта величина называется так же «сродство реакции».

В то же время в асимметричных системах запрет на связь потоков разной размерности отсутствует. Это можно продемонстрировать на примере термоэлектрических явлений.

. Вывод соотношений взаимности Онсагера из теории флуктуаций

Докажем важное свойство коэффициентов L_ik, называемое соотношениями взаимности Онсагера. Для доказательства соотношений недостаточно соображений феноменологической термодинамики и следует использовать микроскопическую теорию.

Основная гипотеза, на которой базируется теория Онсагера, заключается в том, что макроскопическое слабо неравновесное состояние системы можно рассматривать как крупную флуктуацию. То есть градиенты температуры, концентрации и других величин, существующие в макроскопической системе, подчиняются тем же законам, что и градиенты, возникающие благодаря флуктуациям.

Будем характеризовать замкнутую систему набором параметров a_i, равных нулю в равновесном состоянии. Так как в состоянии равновесия энтропия системы максимальна, то вблизи от равновесия имеем равенство:

,

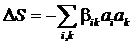где неотрицательно определенная матрица коэффициентов β_ik может быть выбрана симметричной β_ik = β_ki. С другой стороны, вблизи от равновесия скорость изменения параметров 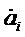так же должна быть малой величиной, так как в состоянии равновесия эта величина должна обращаться в нуль. Допустим, что вблизи от равновесия скорости 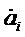 являются малыми первого порядка по a_i:

.

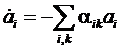Считая энтропию функцией параметров a_i, находим для производной по времени dS/dt, которая для замкнутой системы совпадает с производством энтропии выражение

.

Дальнейшее доказательство основано на том, что первый множитель в правой части отождествляется с потоком, а второй - с сопряженной ему термодинамической силой:

, .

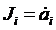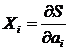Найдем связь между потоками и силами. Из выражения для энтропии имеем:

,

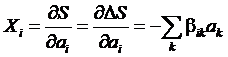Откуда, вводя обратную матрицу, получим

.

Подставим это выражения в формулу для потоков:

.

Для кинетических коэффициентов, следовательно, получим:

.

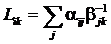Уравнение для потоков можно переписать в виде:

.

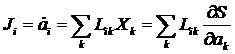Рассмотрим произведение

,

где τ - промежуток времени, малый по сравнению с характерными временами изменения параметров a_k. Тогда эти величины можно разложить в ряд по времени:

.

Задание зачения a_k(t) не определяет однозначно состояния системы в момент времени t+τ, так как существует еще ряд параметров a_l(t) (l≠k), и тем более не определяет значение a_k(t+τ), так как при заданном a_k(t) возможен ряд процессов, ведущих к разным значениям a_k(t+τ).

Найдем среднее значение следующего выражения

.

Для расчета воспользуемся ранее полученной функцией распределения для флуктуаций:

.

.

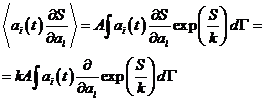Проинтегрируем это выражение по частям. Для этого примем во внимание, что элемент объема в фазовом пространстве для флуктуаций имеет вид:

.

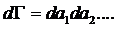Тогда получим:

.

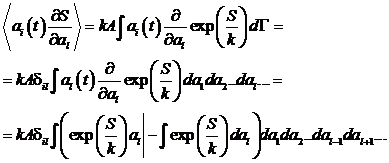Ввиду быстрой сходимости экспоненциальной функции, получим:

.

.

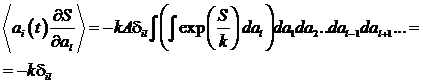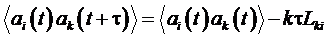Аналогично можно получить соотношение:

.

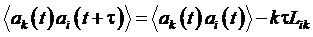Если параметры a_i, a_k таковы, что они не меняются при изменении всех скоростей, то в силу симметрии уравнений механики по отношению к операции отражения времени безразлично, какую из величин мы берем в более ранний, а какую в более поздний момент времени. Следовательно

.

.

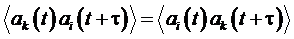Это соотношение справедливо и в том случае, если обе величины и пропорциональны нечетной степени скорости и меняют знак при отражении времени.

. Перекрестные явления в газах

Рассмотрим смешение газов в двух объемах, разделенных диафрагмой с отверстием. Покажем, что разность температур в объемах приводит к возникновению потока частиц. Для этого рассмотрим поток частиц через отверстие:

.

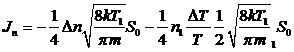Видим, что этот поток содержит два слагаемых. Первое из них отвечает диффузии частиц из одного объема в другой, а второе отвечает потоку частиц, обусловленному разностью температур. Это явление называется термодиффузией.

Термодиффузия (термическая, или тепловая, диффузия), перенос компонент газовых смесей или растворов под влиянием градиента температуры. Если разность температур поддерживается постоянной, то вследствие Т. в объёме смеси возникает градиент концентрации, что вызывает также и обычную диффузию. В стационарных условиях при отсутствии потока вещества Т. уравновешивается обычной диффузией и в объёме возникает разность концентраций, которая может быть использована для разделения изотопов.

Термодиффузия в растворах была открыта нем. учёным К. Людвигом (1856) и исследована швейцарским учёным Ш. Соре (1879-81). Т. в растворах называется эффектом Соре. Термодиффузия в газах была теоретически предсказана английским учёным С. Чепменом и шведским учёным Д. Энскогом (1911-17) на основе кинетической теории газов <#"867921.files/image153.gif">,

.

.

.

,

.

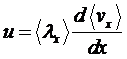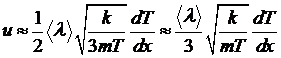Отсюда видно, что тепловое скольжение может быть заметным лишь в разреженных газах, поскольку при больших давлениях длина свободного пробега молекул мала.

Радиометрический эффект. Радиометрический эффект состоит в том, что неравномерно нагретые тела, помещенные в разреженных газах, самопроизвольно приходят в движение в направлении от более нагретой стороны к менее нагретой. При одностороннем освещении тела оно нагревается неравномерно, откуда происходит название эффекта. Силы, приводящие тело в движении имеют двоякое происхождение. Первая сила возникает из-за теплового скольжения газа от менее нагретых участков тела к более нагретым. Из-за вязкости в движение вовлекается и часть газа у поверхности тела. Поскольку импульс системы сохраняется, то тело должно прийти в движение в противоположную сторону. Такой силой объясняется, например, оседание пыли на холодных стенках вблизи батарей центрального отопления. При этом происходит перемещение пыли от нагретых тел к холодным. Вторая сила возникает из-за того, что молекулы газа при отражении от более нагретой части тела, передают ему больший импульс, чем молекулы, отражающиеся от более холодной части. Поэтому возникает радиометрическая сила, направленная от более горячей к более холодной части тела.

Первая сила преобладает в слабо разреженных газах и обратно пропорциональная давлению. Вторая сила играет большую роль в сильно разреженных газах. Она пропорциональна давлению. В промежуточной области существенны обе силы.

Радиометрический эффект при низких давлениях удобно наблюдать с помощью радиометра Крукса. Это прибор состоит обыкновенно из грушеобразного стеклянного сосуда, содержащего алюминиевую вертушку из четырех горизонтальных ветвей, снабженных крыльями из слюды, способную вертеться на острие иголки, как компасная стрелка. Вертикальная стеклянная трубочка, укрепленная сверху, опускается так близко к центральной части вертушки, что последняя не может соскочить с острия.

Из сосуда выкачивают воздух и его запаивают; если слюдяные крылья закопчены с одной лишь стороны, то вертушка приходит в движение, когда на нее падает свет, причем закопченные поверхности как бы отталкиваются лучами света. Радиометр изобретен Вильямом Круксом в 1873 г. Движение его крылышек приписывалось сначала непосредственному давлению света. Было найдено, что скорость вращения пропорциональна силе освещения, что наибольшее действие получается при определенном давлении газа, оставшегося в сосуде (0,304 мм для воздуха, 0,238 для кислорода и 0,380 для водорода), и что оно уменьшается как при крайнем разрежении, так и при упругостях, приближающихся к атмосферному давлению. Потом Шустер, Бертен и Гарбе показали, что сам сосуд начинает вертеться, если его подвесить на волоске или заставить плавать на воде, и что направление его вращения противоположно направлению движения вертушки. При этом скорость во всех частных случаях согласуется с вычисленной на основании закона равенства действия и противодействия. Тогда пришлось заключить, что силы, приводящие в движение вертушку, действуют между ее крылышками и стеклом сосуда, а источник этих сил искать внутри сосуда. Полная теория радиометрического эффекта была создана позднее на основе кинетической теории газов. После того, как Лебедев непосредственно измерил давление света, стало ясно, что сила этого давления значительно меньше, чем силы, действующие на тело со стороны газа. Радиометр может вращаться и под влиянием катодных и рентгеновских лучей, но явление усложняется при этом электризацией самой вертушки.

. Ультраразреженные газы

В случае, когда длина свободного пробега молекул превышает линейные размеры сосуда, говорят, что в сосуде достигнут вакуум. Газ в этом случае называют ультраразреженным. Хотя в буквальном смысле слова вакуум означает «пустоту», в ультраразреженном газе содержится в единице объема большое число молекул. Так, при давлении в 10^-6 мм рт. ст. в 1 м³ находится примерно 10¹⁶ молекул. Более того, в очень малых порах состояние, определяемое как вакуум, может быть достигнуто и при атмосферном давлении. На основе формулы для длины свободного пробега можно получить, что, например, для воздуха для характерного размера 10 см ультраразреженный газ будет иметь место при давлениях, много меньших чем 0.1 Па.

Поведение ультраразреженных газов отличается целым рядом особенностей. В условиях вакуума нельзя говорить о давлении одной части газа на другую. При обычных условиях молекулы часто сталкиваются друг с другом. Поэтому по любой поверхности, которой можно мысленно разграничить газ на две части, будет происходить обмен импульсами между молекулами, и, следовательно, одна часть газа будет действовать по поверхности раздела на вторую с давлением p. Более того, в таком случае вообще нельзя говорить о давлении в термодинамическом смысле, поскольку давление - это скаляр и принципиально, что оно никуда не направлено. В вакууме же силы давления газа не будут изотропны. В вакууме молекулы обмениваются импульсами только со стенками сосуда, так что имеет смысл лишь понятие давление на стенку. Внутреннее давление в газе также отсутствует. Однако тело, движущееся в ультраразреженном газе, будет испытывать действие силы трения, обусловленной тем, что молекулы, ударяясь об это тело, будут изменять его импульс.  Если в ультраразреженном газа температуры стенок различны, то нельзя говорить и о температуре газа, поскольку в объеме будут присутствовать молекулы, отражающиеся от стенок с различной температурой.

Таким образом, в ультраразреженном газе нельзя ввести понятие «локальное равновесие», и, следовательно, все связанные с этим понятием законы, такие как закон Фика, Фурье и т.д. В более общем смысле суперпозиция (с какими-либо весами) распределений Гиббса не является распределением Гиббса со всеми вытекающими из этого факта термодинамическими следствиями.

Поскольку формулами, основанными на локальном равновесии для ультраразреженных систем пользоваться нельзя, то в этом случае необходимо ввести более строгое определение плотностей потоков. Введем понятие односторонней плотности потока молекулярного признака по следующей формуле:

.

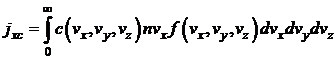Наиболее важными величинами являются:

плотность потока числа частиц (с=1):

,

плотность потока энергии (с = mv²/2):

,

плотность потока тепла

.

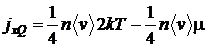Пусть в ультраразреженном газе движутся параллельно друг другу две пластинки.

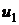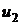Скорости пластинок равны  и . В простейшей модели идеальных пластинок можно считать, что взаимодействие между молекулой и пластинкой в момент удара приводит к тому, что молекула, отскочив от пластинки, имеет в дополнение к тепловой скорости составляющую, равную по величине и направлению скорости пластинки.

Об единицу поверхности верхней пластинки будет ударяться в секунду 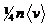 молекул, имеющих составляющую скорости 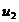, приобретенную при предшествующем ударе о нижнюю пластинку. Каждая из этих молекул имеет составляющую импульса 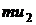. Отразившись от верхней пластинки, молекулы имеют составляющую импульса, равную 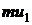. Следовательно, удар каждой молекулы о верхнюю пластинку приводит к уменьшению ее импульса на величину 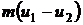. Изменение импульса в единицу времени, отнесенное к единице поверхности пластинки, составит

.

Это выражение есть ни что иное, как плотность потока импульса. ПО второму законю Ньютона это изменение равно силе, действующей на единицу поверхности пластинки:

(мы заменили nm через ρ). Такая же по величине, но противоположно направленная сила действует на единицу поверхности нижней пластинки.

Коэффициент пропорциональности между силой трения и разностью скоростей пластинок естественно назвать коэффициентом трения. Этот коэффициент равен 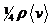, т. е. пропорционален плотности газа, а, следовательно, и давлению газа на пластинку и стенки сосуда (для этого давления сохраняется выражение ).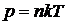

Обратимся теперь к вопросу о передаче тепла газом в условиях вакуума. Рассмотрим две пластинки с температурам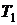и  и , между которыми находится ультраразреженный газ.

Передача энергии внутренних степеней свободы должна рассматриваться отдельно.

Если бы удар молекул о поверхность твердого тела имел абсолютно упругий характер, молекулы отскакивались бы от пластинки с такой же по величине скоростью (а, следовательно, и энергией), какую они имели перед ударом. В результате молекулы не могли бы переносить энергию от пластинки к пластинке. Однако такой вывод находится в противоречии с опытом. Следовательно, взаимодействие между стенкой и одаряющейся о нее молекулой не имеет характера упругого удара. В действительности оно осуществляется так: ударившись о стенку, молекула как бы прилипает к ней на короткое время, после чего покидает стенку в совершенно произвольном направлении со скоростью, величина которой в среднем отвечает температуре стенки. Явление «прилипания» молекул к стенке называется адсорбцией. После ухода молекулы со стенки (десорбция) молекула как бы забывает свое состояние, которое было до падения ее на стенку.

Пользуясь выражением для одностороннего потока тепла, можно получить выражения для рузультирующего потока:

.

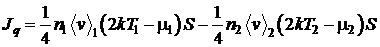Если при этом результирующий поток частиц отсутствует (в стационарном состоянии), то получим:

.

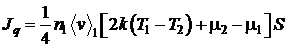Тогда можно ввести коэффициент теплопроводности для данной задачи в виде:

.

Видно, что эта величина прямо пропорциональна конфентрации газа. Следовательно, теплопередача от одной стенки к другой будет с понижением давления уменьшаться, в то время как теплопроводность газа при обычных условиях не зависит от давления.

Сказанное о разреженных газах во многом относится и к газу фотонов. Если фотон сталкивается только со стенками (т.е. не рассеивается по пути) то можно говорить о разреженном газе фотонов. Фотоны, так же, как и классические газы могут переносить энергию, импульс и другие признаки с одной стенки на другую. Отметим, что для фотонов потоки тепла и энергии совпадают, т.к. их химический потенциал равен нулю.

Однако рассеяние фотонов на поверхности имеет свои особенности. Во-первых, как уже было отмечено выше, число фотонов не сохраняется, т.е. часть фотонов может быть необратимо поглощена поверхностью. Во-вторых, нельзя говорить об адсорбции фотонов. Фотоны могут только отражаться или поглощаться.

Отражение фотонов существенным образом зависит от состояния поверхности. Оно может быть зеркальным (когда угол падения равен углу отражения) и диффузным. Во втором случае свет рассеивается на шероховатостях поверхности равномерно во все стороны, тогда говорят о матовой поверхности. Диффузное рассеяние имеет место тогда, когда размер шероховатостей поверхности становится сравнимым (или большим) с длиной волны фотонов, а неровности поверхности расположены беспорядочно. В случае смешанного отражения света часть излучения отражается зеркально, а часть - диффузно. Одна и та же поверхность может быть матовой, диффузно-отражающей для видимого или ультрафиолетового излучения <#"867921.files/image179.gif">.

Перенос энергии излучением в вакууме начинает играть роль при достаточно высоких температурах, поскольку мощность излучения фотонов пропорциональна T⁴. Например, стенки термосов делают зеркальными именно для предотвращения переноса тепла излучением. Если стенки нахотятся при разных температурах, то для фотонного газа так же нельзя ввести локальное равновесие между ними. Например, нельзя говорить о температуре фотонного газа в межстеночном пространстве.

. Диффузия газа в асимметричной мембране

Рассмотрим диффузию газа в асимметричном твердом теле и найдем условия, при которых скалярный источник тепла будет порождать векторный поток частиц.

Рассмотрим твердое тело, потенциальная энергия атомов растворенного газа в котором имеет вид:

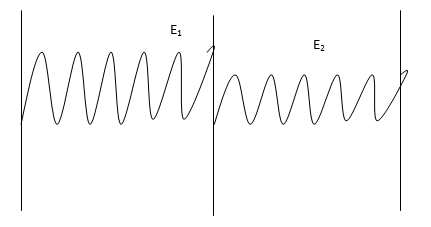
Рисунок 1

Здесь E₁, E₂ - энергии активации диффузии газовых частиц при переходе из одной потенциальной ямы в другую. Предположим, что на стыке двух различных областей находится точечный источник тепла, в результате чего распределение температуры по мембране имеет следующий вид:

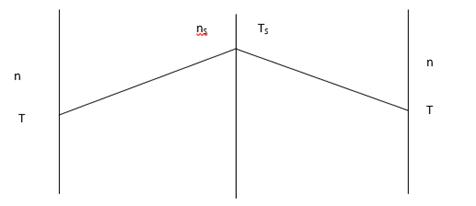
Рисунок 2

уравнение термодинамика флуктуация электронный

Здесь мы предположили, что тепло переносится в основном атомами твердого тела, а не газом. Будем считать так же, что перепады температуры и концентраций малы, т.е. мы находимся в рамках линейной неравновесной термодинамики.

Покажем, что при наличии асимметрии в мембране будет существовать поток атомов газа слева направо или справа налево.

Запишем выражение для плотности потока частиц для двух соседних потенциальных ям:

.

.

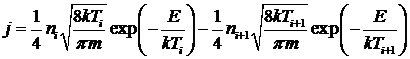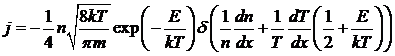Покажем, что распределение температуры в мембране будет линейным. Уравнение теплопроводности для данного случая имеет вид:

.

Тогда и распределение концентрации так же будет линейным. Запишем тогда для каждого потока:

,

.

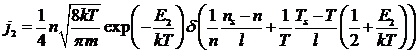Поток в левой части в стационарном состоянии равен потоку в правой части. Тогда получим:

,

.

.

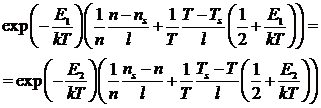
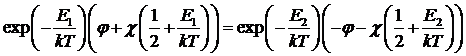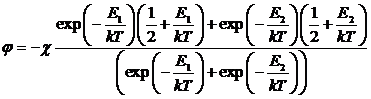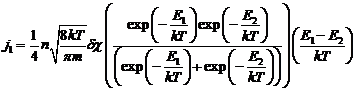При нагреве стыка областей если E₁>E₂, то поток будет идти справа налево, в противном случае - наоборот. При охлаждении направление потока изменится на противоположное.

Видим, что результирующий поток частиц пропорционален разности энергий активации. Очевидно, что в симметричном случае такой поток равен нулю в полном соответствии с принципом Кюри.

В соответствии с равенством перекрестных коэффициентов Онсагера должно существовать (и действительно существует) и обратное явление: в асимметричной системе при наличии потока частиц на стыке двух различных областей будет выделяться тепло. Такой же эффект существует, например, при течении газов в каналах, где роль энергии активации играет шероховатость поверхности.

. Термоэлектрические явления

Одним из важнейших применений линейной термодинамики необратимых процессов является построение теории термоэлектрических явлений. Экспериментально известны три термоэлектрических явления в изотропных средах.

Эффект Зеебека. На стыке двух различных проводников, имеющих разность температур 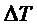, возникает ЭДС  (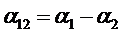- коэффициент термо-ЭДС между данными проводниками,  - коэффициент дифференциальной термо-ЭДС данного проводника). Поэтому из двух различных проводников составить замкнутую цепь и места их контактов поддерживать при различных температурах, то в этой цепи возникает ЭДС. Величина  считается положительной, если возникающий в проводнике ток течет от горячего контакта к холодному.

Эффект Пельтье. При прохождении электрического тока в термически однородной системе в месте соединения двух различных проводников выделяется или поглощается теплота (теплота Пельтье), пропорциональная силе тока.

Эффект Томпсона. При прохождении электрического тока в проводнике с градиентом температуры помимо джоулевой теплоты, выделяется добавочное количество теплоты (теплота Томпсона), пропорциональное градиенту температуры и силе тока.

Рассмотрим простейшую схему для реализации термоэлектрических явлений.

Будем считать, что электрическая цепь составлена из источника ЭДС ΔU и двух разных проводников a и b, спаи которых помещены в термостаты 1 и 2 с температурами , . Явления переноса на обоих спаях и в области между термостатами, где 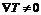, будем считать достаточно медленными, те перепад температур мал, сопротивление проводов достаточно велико, а ΔU достаточно мала.

Запишем общую формулу квазистатической термодинамики для этой системы:

.

Применим эту формулу для каждой из подсистем:

,

.

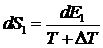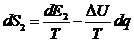
Учитывая, что в изолированной в целом системе , получим с точностью до линейных членов:

.

Относя это изменение к единице времени, для скорости образования энтропии при заданных ΔT и ΔU получим

,

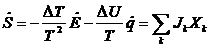где в качестве потоков можно выбрать электрический ток и поток энергии. Тогда выражения для потоков можно записать так:

,

.

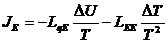Рассмотрим частные случаи и выясним физический смысл кинетических коэффициентов.

А) , .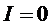

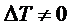Условие 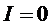 определяет величину термоЭДС, пропорциональную разности температур между спаями 1 и 2:

,

причем коэффициент Z непосредственно измеряется, а если он известен, то полученное устройство (термопара) может служить прибором для измерения ΔT по показанию вольтметра ΔU.

определяет коэффициент теплопроводности участка проводов между термостатами 1 и 2 при условии отсутствия тока. Поскольку материалы, из которых изготовлены провода, известны, то известны и табличные значения их коэффициентов теплопроводности.

Б), ΔT=0, эффект Пельтье

Выражение для тока

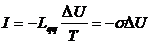
определяет проводимость σ в изотермической системе, а отношения потоков

определяет так называемое тепло Пельтье, которое так же может быть измерено. Из четырех коэффициентов, характеризующих явления переноса А) и Б), независимыми должны быть только три. Мы уже фактически получили связь двух коэффициентов - Зеебека и Пельтье:

.

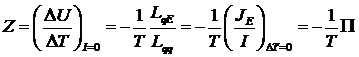Эта связь называется вторым соотношением Томсона. Заметим, что выделяемое на каком-либо спае тепло меняет знак при обращении тока, т.е. если , то

.

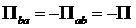В) Эффект Томсона.

Спаи проводников в этом явлении роли не играют. Эффект возникает в однородном проводнике при наличии тока и градиента температуры. Мощность выделяющегося тепла можно записать в виде:

,

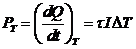где τ- постоянная величина.

Так как работа источника тока за секунду 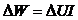должна быть учтена в общем балансе энергии вместе с теплом Томсона на участках проводников с 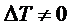и теплом Пельтье на спаях, то согласно первому началу термодинамики с учетом правил знаков имеем (уточнить это правило!):

.

,

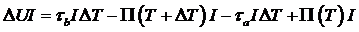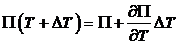и сокращая величину тока, приходим к так называемому «первому» соотношению Томсона:

.

Если подставить сюда соотношение для ΔU, то, сократив на ΔT, получим связь характеристик Томсона и Пельтье:

.

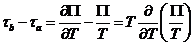Таким образом, характеристики пяти стационарных явлений переноса выражаются с помощью трех экспериментально измеряемых величин σ, æ и Π. Формальные коэффициенты Онсагера выражаются через них следующим образом:

, , .

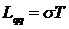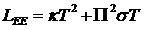Можно записать скорость производства энтропии, учитывая, что потоки можно записать в виде:

,

.

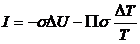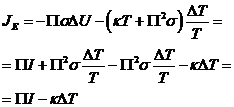Вводя вместо характеристики источника тока

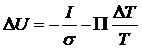
величину самого тока I, получим:

.

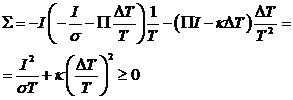Первое слагаемое связано с выделением джоулева тепла в секунду, а второе - с теплопроводностью.

С точки зрения статистической физики объяснение термоэлектрических явлений объясняется тем, что энергия электронов в каждом из металлов разная, поскольку уровень Ферми зависит от концентрации свободных электронов. В таком случае, при переходе из одного металла в другой электроны либо выделяют энергию (передают ее кристаллической решетке) либо поглощают.

Объяснение эффекта в первом приближении заключается в следующем. В условиях, когда вдоль проводника, по которому протекает ток, существует градиент температуры, причём направление тока соответствует движению электронов <#"867921.files/image230.gif">.

В таком случае средняя энергия, приходящаяся на один электрон, будет иметь вид:

.

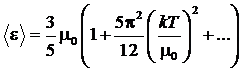Рассмотрим в проводнике объем V и найдем поток энергии в этот объем, обусловленный направленным движением электронов проводимости:

.

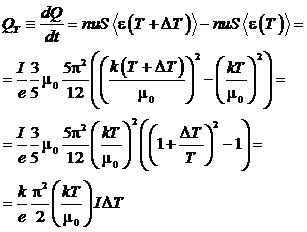Таким образом, видим, что коэффициент Томсона равен:

.

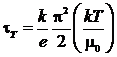Похожее выражение возникает и в других типах проводников (например, в полупроводниках).

11. Электронный ветер

С конца прошлого века ведутся эксперименты по изучению проводимости жидких металлов. В нормальных условиях жидкие металлы встречаются не часто, но многие металлы легко образуют с ртутью жидкие растворы - амальгамы. Проводимость жидких металлов интересна тем, что в электрический ток должны вносить вклад не только электроны проводимости, но и ионы. А с движением ионов связан перенос массы.

Попробуем качественно представить, что произойдёт при подключении к ванночке с чистой ртутью источника напряжения. Ртуть - это смесь электронов проводимости и положительных ионов. Казалось бы, всё ясно - под действием электрического поля электроны будут двигаться от «минуса» к «плюсу», а положительные ионы ртути - в противоположном направлении. Если электроны могут путешествовать по всей электрической цепи, то с ионами дело обстоит иначе. Они, подойдя к отрицательному электроду, вроде бы, должны здесь скапливаться, повысив уровень ртути в этом месте.

Ничего подобного! Эксперименты показали, что уровень чистой ртути практически повсюду один и тот же, а небольшое повышение уровня, если и происходит, то у «плюса», а не у «минуса». В одних амальгамах ионы двигаются, как следует, по полю, а ионы других металлов - против поля! Это удивительно - как могут ионы двигаться не туда, куда их влекут электрические силы?

Причина «странного» поведения ионов - это не учтённая нами непрерывная бомбардировка ионов электронами. Попробуем разобраться в существе дела. Выясним, какое влияние оказывают взаимные соударения электронов и ионов на движение электронов и ионов при наличии внешнего электрического поля.

Для наглядности будем считать ион массивным упругим шаром, на который налетает пучок лёгких частиц - электронов (масса иона в несколько тысяч раз больше массы электрона). Пусть до столкновения пучок частиц имеет среднюю направленную скорость u и соответственно ненулевой импульс. После столкновения пучок рассеивается равномерно во все стороны (рис. 1) (так же равномерно во все стороны зеркальный шар рассеивает направленный пучок света). То есть сразу после соударения все направления движения равновероятны, а значит, суммарный импульс электронов равен нулю.

Раз импульс пучка из-за соударений с ионами меняется, то это означает, что на электроны со стороны ионов действует сила. Если u - средняя скорость электронов в пучке, то mu - средний импульс электрона. Пусть время между столкновениями электрона с ионами - , тогда можно считать, что именно за это время теряется средний импульс mu каждого электрона. Так что средняя сила, отнесённая к одному электрону, равна

.

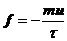Потеря импульса электронами в целом из-за столкновений с ионами и описывается средней тормозящей силой f. Конечно, на отдельный электрон действует не обязательно такая сила, но для движения пучка в целом важна именно эта средняя сила.

Хотя кроме направленного движения со средней скоростью u электронам присуще и хаотическое тепловое движение, это не изменит выражения для силы торможения. Полный импульс большого числа электронов при беспорядочном тепловом движении всё время равен нулю, поэтому изменение суммарного импульса связано только с потерей импульса упорядоченного движения.

При наличии внешнего электрического поля напряжённости Е «рассеянные» электроны «подхватываются» полем, которое вновь упорядочивает их движение, сообщая им некоторый направленный импульс, растрачиваемый при следующем соударении, и т.д. Таким образом, можно сказать, что устанавливается некоторая постоянная средняя скорость движения электронного пучка. Иначе говоря, сумма сил, действующих на электронный пучок, равна нулю. В расчёте на один электрон получаем

еЕ + f = 0.

Итак, при движении с установившейся средней скоростью, когда полная сила равна нулю, тормозящая сила со стороны ионов в расчёте на один электрон равна

f = - eE. (*)

Какие же силы действуют на ионы? Рассмотрим чистый жидкий металл, у которого все ионы одинаковы, причём каждый атом отдал в общее пользование по Z электронов проводимости. Электрическое поле действует на каждый ион с силой 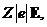где 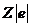 - заряд иона (заряд электрона взят по модулю, ибо ион положителен). Со стороны каждого электрона действует в среднем сила f₁ = - f (по третьему закону Ньютона). Если число ионов N, то на каждый ион со стороны одного электрона приходится сила . Тогда сила, с которой на один ион действуют все электроны (их число ZN), равна Zf₁. Но сумма сил

Чтобы в этом убедиться, подставим значение силы f₁, отличающейся от f только знаком, из выражения (*):

F= Z|e|E+ZeE=0.

Итак, силы, действующие на ионы в чистом металле со стороны электрического поля, компенсируются силами, действующими со стороны «электронного ветра» (движущихся электронов). Равенство полной силы нулю означает либо покой, либо равномерное движение. Но при течении жидкости в сосуде возникает вязкое трение (в конечном счёте из-за взаимодействия со стенками сосуда), оно и обеспечивает покой жидкости относительно сосуда в случае компенсации остальных сил, действующих на жидкость.

А если в металле имеется небольшая примесь «чужих» ионов? Пусть заряд чужака равен . Из-за того, что размеры примесного иона другие, изменится и число ударов электронов об него. Если площадь сечения иона примеси 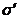, а «своего» иона 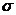, то чужак подвергнется в  раз большему числу ударов, чем свой ион. Во столько же раз изменится и сила, действующая на примесный ион со стороны электронов.

Если 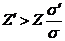, то ионы примеси будут двигаться в направлении этой силы, их скорость будет направлена по полю. Если 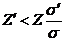, то ионы будут двигаться против поля.

Как же объяснить тот факт, что в чистой ртути ионы движутся по направлению электронного ветра? Мы ведь показали, что в чистом металле ионы должны быть неподвижны! Дело в том, что предполагалась полная одинаковость всех ионов, но это не совсем так. Хотя большинство ионов, действительно, находится в одном и том же «нормальном» энергетическом состоянии, некоторые ионы всегда имеют энергию больше нормальной. Такие ионы называют «активированными». Вероятность столкновений электронов с ионами увеличивается с ростом энергии ионов. Можно сказать, что сечения активированных ионов как бы увеличились по сравнению с нормальными. Таким образом, активированные ионы можно считать чужаками с тем же зарядом, что и нормальный ион, но с бóльшим сечением. Такие ионы увлекаются электронным ветром и сносятся к положительному полюсу источника. На этом основано разделение изотопов ртути в электрическом поле. У ионов разных изотопов заряд и сечение практически одинаковы, но активированные ионы лёгких изотопов сносятся электронным ветром быстрее, чем активированные ионы тяжёлых изотопов, из-за их меньшей массы. Это приводит к увеличению их концентрации у «плюса», то есть, если около положительного полюса отсасывать ртуть, то она будет обогащённой лёгким изотопом.

Впервые «парадоксальный» перенос ионов в амальгамах ртути был обнаружен в 1907 году. Тогда же было и введено представление о взаимном трении ионов и электронов. В последующих теориях, просуществовавших до 1959 года, был сделан шаг назад: движения ионов и электронов считались независимыми. Отчасти это объяснялось неубедительностью результатов экспериментов. В 1953 году был открыт эффект разделения изотопов ртути постоянным током. После этого появился целый ряд работ по исследованию электропереноса ионов. Первые теоретические работы, где был вскрыт физический механизм действия электронного ветра, относятся к началу 1959 года.

С электронным ветром связана целая группа интересных и важных эффектов, как в жидких, так и в твёрдых металлах и полупроводниках. В частности, электронный ветер имеет важное значение для механической прочности электронных схем. Дело в том, что в твердом теле, ввиду того, что оно вцелом неподвижно, при протекании тока возникают механические напряжения. Эти напряжения возникают потому, что в элементах микросхем присутствуют различные ионы. Это означает, что ионы с различным зарядом и сечением взаимодействия с электронами будут подвергаться действию различных сил, сумма которых не равна нулю.

12. Уравнение Мастера. Диффузия тяжелого газа в легком

Простейшим процессом, описывающим причинную связь между событиями, является марковский процесс. Марковский процесс характеризуется тем, что переход из состояния в момент 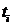времени  в состояние в момент времени 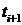 не зависит от предыстории системы. При этом переходы внутри двух последовательных временных интервалов происходят независимо друг от друга.

Для марковских процессов справедливо основное кинетическое уравнение. Рассмотрим некоторое состояние системы 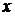. Система может перейти в новое состояние, совершив скачок 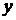. Вероятность прямого перехода из состояния 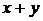 в единицу времени в состояние 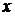 обозначим через , а вероятность обратного перехода из состояния 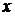 в состояние  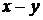будет 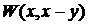. Отсюда сразу следует уравнение

.(*)

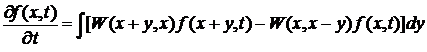Первое слагаемое в (*) характеризует прямые переходы 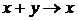, а второе обратные 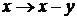. Уравнение (*) называется основным кинетическим уравнением (уравнение Мастера). Основное кинетическое уравнение представляет собой уравнение баланса для плотности вероятности каждого состояния 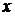. Первый член в правой части уравнения (*) соответствует возрастанию вероятности из-за переходов из других состояний 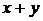, а второй - уменьшению вероятности из-за переходов в другие состояния.

Для дискретных величин аналогом уравнения мастера является уравнение Паули:

.

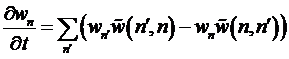В этом уравнении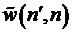 - вероятность перехода из состояния n’ в состояние n в единицу времени, - убыль за секунду вероятности обнаружить систему в состоянии n за счет переходов во все другие состояния системы n’, 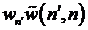- обратный процесс. Это уравнение так же называют уравнением кинетического баланса. Можно показать, что вероятность переходов обладает свойством симметрии:

.

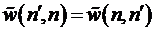Это уравнение еще называется уравнением детального баланса. Оно является следствием законов сохранения.

Заметим, что, вообще говоря, не все случайные процессы в природе являются марковскими. Существуют еще процессы с памятью, в которых информация о прошлых состояниях может сохраняться в системе достаточно долгое время.

Вывод уравнения Фоккера-Планка из уравнения мастера.

Значительную категорию кинетических явлений составляют процессы, в которых средние изменения величин (от которых зависит функция распределения) в каждом элементарном акте малы по сравнению с их характерными значениями. Времена релаксации таких процессов велики по сравнению с временами элементарных актов, составляющих их микроскопический механизм; в этом смысле такие процессы можно назвать медленными.

Типичный пример такого рода дает задача о релаксации по импульсам небольшой примеси тяжелого газа в легком (который сам по себе предполагается находящимся в равновесии). Ввиду малой концентрации тяжелых частиц, их столкновениями друг с другом можно пренебречь и рассматривать их столкновения лишь с частицами основного (легкого) газа. Но при столкновении тяжелой частицы с легкими ее импульс испытывает лишь относительно малое изменение.

Будем для определенности говорить именно об этом примере и выведем кинетическое уравнение, которому удовлетворяет в таком случае функция распределения частиц примеси по импульсам, f(t, p).

Обозначим через ω(р, q) d³q отнесенную к единице времени вероятность изменения импульса р → р-q тяжелой частицы при элементарном акте - ее столкновении с легкой частицей. Тогда кинетическое уравнение для функции f(t, p) запишется в виде

,

где справа стоит разность между числом частиц, поступающих (в 1 с) в заданный элемент импульсного пространства d³p и покидающих его за то же время. Согласно сделанным предположениям, функция ω(р, q) быстро убывает с увеличением q, так что основную роль в интеграле играют значения q, малые по сравнению со средним импульсом частиц. Это обстоятельство позволяет произвести в подынтегральном выражении разложение

,

, .

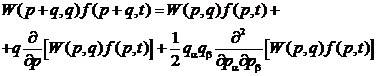
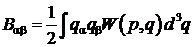Выражение в правой части (21.2) имеет вид дивергенции в импульсном пространстве, 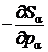, от вектора

.

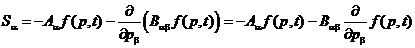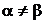Если коэффициент постоянен или почти постоянен, то это откуда-то должно следовать! Превращение из тензора в скаляр тоже не так очевидно, поскольку не совсем ясно, почему при  эта величина должна обращаться в ноль.

Другими словами, полученное уравнение имеет, как и следовало, вид уравнения непрерывности в импульсном пространстве; тем самым автоматически соблюдается сохранение числа частиц при процессе. Вектор же S является плотностью потока частиц в импульсном пространстве.

Согласно приведенным формулам коэффициенты в кинетическом уравнении выражаются через средние характеристики столкновений, и в этом смысле их вычисление представляет собой механическую задачу. Фактически, однако, нет необходимости в раздельном вычислении коэффициентов A_α и B_αβ; они могут быть выражены друг через друга из условия обращения потока в нуль в статистическом равновесии. В данном случае равновесная функция распределения есть

,

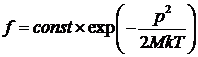где М - масса частиц тяжелого газа, а Т - температура основного (легкого) газа. Подстановка этого выражения в уравнение S = 0 дает

.

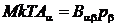Таким образом, кинетическое уравнение принимает вид

. (*)

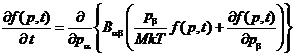Единственный вектор, от которого могут зависеть коэффициенты B_αβ, - импульс тяжелых частиц р. Но если скорости этих частиц, р/М, в среднем малы по сравнению со скоростями легких частиц (при чем тут скорости?), то при столкновениях их можно считать неподвижными; в этом приближении величины В_αβ не будут зависеть от р. Другими словами, тензор В_αβ сведется к постоянному скаляру В:

,

. (**)

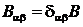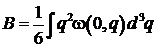
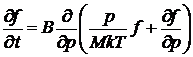Обратим внимание на формальное сходство полученных уравнений (*) с уравнением диффузии во внешнем поле, в особенности наглядное в записи (**), а так же с уравнением Фоккера-Планка. Описываемые уравнением (*) процессы можно назвать диффузией в импульсном пространстве, причем В играет роль коэффициента диффузии.

Ясно поэтому, что уравнение такого же типа будет справедливо и для функций распределения f по другим переменным, если только выполнены условия, лежащие в основе вывода: относительная малость изменения величин в элементарных актах и линейность по f интегрального оператора, выражающего изменение функции благодаря этим актам.

. Причины необратимости в макросистемах

Рассмотрим вопрос о необратимом характере процессов релаксации в макроскопических системах. Как известно, законы, определяющие эволюцию микроскопической системы во времени, инвариантны по отношению к изменению знака времени как в классической, так и в квантовой механике. Это значит, что все микропроцессы принципиально обратимы, т.е. при надлежащем изменении условий (например, при изменении направлений начальных скоростей) любой микропроцесс может протекать, как в прямом, так и в обратном направлении, проходя через одни и те же промежуточные состояния. Возникает вопрос: каким образом статистическая физика, основанная на обратимых во времени законах микропроцессов, может приводить к необратимым законам макроскопических процессов, в частности, к описанию процессов релаксации и к закону возрастания энтропии в замкнутых системах?

Исторически после работ Больцмана по вычислению возрастания энтропии в изолированной газовой системе были сформулированы два наиболее важных возражения против кинетической теории.

Теорема возврата (парадокс Пуанкаре-Цермелло). Теорема возврата утверждает, что за достаточно большое время фазовая траектория в фазовом пространстве, изображающая поведение системы, вернется в область, сколь угодно близкую к некоторой начальной точке этой траектории. Доказательство этой теоремы основано на свойстве несжимаемости газа изображающих точек - теореме Лиувилля.

Таким образом, эволюция состояния макроскопической системы столь же обратима, как и микроскопические процессы. В частности, любое неравновесное макроскопическое состояние рано или поздно должно повториться, как бы ни было велико отклонение от равновесия. Это противоречит представлениям о том, что поведение системы необратимо во времени.

Парадокс Лошмидта. Уравнения движения механики обратимы во времени, поэтому можно представить себе последовательность состояний эволюции системы, и, в равной мере (в силу обратимости уравнений движения), обратную последовательность состояний. Состоянию z_i сопоставляется энтропия S_i. Тогда, если в одной из последовательностей состояний энтропия возрастает, то в другой она убывает. Почему же тогда энтропия в замкнутой системе только возрастает?

Энтропия не изменяется. Докажем, что если вычислить энтропию на основе функции распределения, являющейся решением уравнения Лиувилля, то такая энтропия в замкнутой системе не будет изменяться со временем.

Рассмотрим производную по времени от энтропии изолированной системы и покажем, что она равна нулю

.

Воспользуемся известной формулой для энтропии

.

Будем считать, что функция распределения подчиняется уравнению Лиувилля:

.

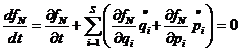Далее будем подразумевать, что по повторяющимся индексам производится суммирование. Найдем производную от энтропии:

.

Частная производная берется, поскольку энтропия не может зависеть от координат и импульсов (интеграл по ним определенный). Далее получим:

.

.

, .

.

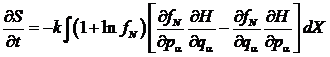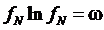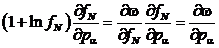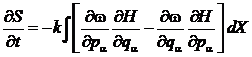Под знаком интеграла мы получили скобку Пуассона от функций ω и H. Теперь заметим, что

.

Следовательно, многомерный интеграл содержит одномерные, которые легко берутся:

Равенство интеграла нулю есть следствие того, что нормированная функция распределения обращается в ноль на бесконечности.

Каким же образом разрешить сформулированные парадоксы?

Рассмотрим два примера:

1.      В сосуде, разделенном перегородкой на две одинаковые части, газ первоначально находится в одной половине. Мы удаляем перегородку и наблюдаем расширение газа в пустоту - происходит релаксация в координатном пространстве.

.        В холодный газ впускается пучок горячих молекул, имеющих почти одинаковые скорости v. Спустя некоторое время благодаря соударениям газ «максвеллизируется», и установится равновесное распределение молекул по скоростям.

В соответствии с теоремой Пуанкаре-Цермелло мы можем утверждать, что спустя некоторое время первоначальное неравновесное состояние должно повторяться со сколь угодно большой точностью, т.е. в первом примере газ вновь собраться в одну половину сосуда, а во втором примере должен снова сформироваться пучок молекул со скоростью v.

Однако такая абстрактно-теоретическая концепция, связанная с теоремой возврата, имеет для больших флуктуаций весьма отдаленную связь с действительностью, так как времена возврата для столь сильных отклонений от равновесия, как в двух рассмотренных примерах, оказываются невообразимо большими, во много раз большими возраста Вселенной.

Грубую оценку времени возврата можно получить следующим образом. Пусть в объеме V находится N молекул газа. Будем понимать под возвратом повторение начального состояния каждой молекулы с точностью до Δv по скорости и Δx по координате. Этой точности соответствует объем ΔГ фазового пространства газа, равный

,

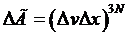в то время как всему набору состояний газа с фиксированной кинетической энергией E соответствует объем

,

.

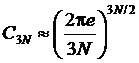Прежде, чем вернуться с заданной точностью в исходное положение, изображающая точка должна пройти число состояний, равное по порядку величины Г/ΔГ. Так как время свободного пробега молекулы τ имеет порядок

,

.

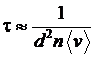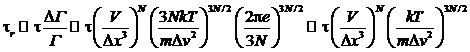Для 1 см³ газа при нормальных условиях эта величина экспоненциально больше возраста Вселенной.

Таким образом, абстрактно теоретическая обратимость сочетается с практической необратимостью макроскопических процессов, если речь идет о сколь-нибудь существенных отклонениях от равновесия.

Уравнения типа Фоккера-Планка, диффузии и другие описывают процессы, идущие только с возрастанием энтропии. Возникает вопрос, на каком этапе вывода уравнений переноса возникает необратимость? В случае уравнения Фоккера-Планка такой гипотезой является предположение о марковском характере процесса (марковским называется процесс, в котором будущие состояния не зависят от прошлых - именно такой процесс был использован ранее при выводе уравнений переноса). Можно сформулировать и другой вариант такого рассмотрения: в равновесии в замкнутой системе равновеликие площади на гиперпространстве постоянной энергии равновероятны. Неравновесные системы таким свойством не обладают. Следовательно, в неравновесных системах должен существовать некоторый механизм перемешивания, т.е. переход к равномерному распределению точек в фазовом пространстве.

Одним из первых ученых, понявших важность такого свойства, был Н.С. Крылов. Проиллюстрируем идеи Крылова на примере идеального газа.

Я.Г. Синай рассмотрел задачу столкновения двух шаров и показал, что эта задача сводится к столкновению материальной точки с выпуклой стенкой. При этом оказалось, что в системе возникает неустойчивость, которая заключается в том, что любое малое начальное отклонение траектории одного из шаров приводит к увеличению этого отклонения после столкновения. В данном случае это означает, что движение такой материальной точки будет необратимо. С течением времени вся фазовая плоскость будет занята траекториями. Поскольку фазовое пространство ограничено, то в нем будет происходить явление, называемое перемешиванием.

Идеи Больцмана по обоснованию кинетической теории были существенно продвинуты Эренфестом. Однако наиболее трудным в проблеме обоснования статистической физики оказался вопрос о том, как возникает близкое к равновесному распределение состояний системы на поверхности постоянной энергии. Анализ, проведенный Крыловым, показал, что в основе понимания природы статистических законов лежит не свойство эргодичности динамической системы, а свойство перемешивания и связанная с ним локальная неустойчивость. Анализ Крылова показал так же, что в уравнениях динамики не содержится какого-либо механизма огрубления (усреднения), даже если динамика является квантовой. Процедура огрубления является дополнительным приемом, который привносится в описание природы извне.

Покажем, как эти парадоксы разрешаются на основе современной теории. Отметим, что проявления статистических свойств в системе вовсе не обязательно, чтобы она состояла из большого числа частиц. Эти свойства могут проявиться в системе, состоящей из двух частиц.

Прежде всего, отметим, что теорема Пуанкаре о возвратах не имеет никакого отношения к появлению статистических свойств в системе. Возвраты существуют как при условно периодическом движении, так и при стохастическом движении. В последнем случае времена последовательных возвратов (циклов) являются случайной последовательностью, а величина их для систем из малого числа частиц также мала. Необратимость проявляется не в том, что система не может вернуться близко к исходному состоянию, а в ином ее свойстве. Рассмотрим фазовую каплю правильной формы и будем следить за изменением формы ее границ со временем. В устойчивом случае (в отсутствии перемешивания) поверхность капли изменяется не очень сильно, в то время как в случае локальной неустойчивости поверхность капли быстро приобретает необычайно сложную и запутанную форму.

Необратимость связана именно с этой формой. Интуитивно ясно, что вероятность возврата капли в свою старую форму столь же мала, как и вероятность возврата для большого числа частиц. Пренебрежение этой вероятностью, эквивалентное некоторому огрублению, и приводит к необратимости.

Теперь проследим за тем, почему нельзя, как заметил Больцман в ответе Лошмидту, повернуть все частицы в обратном направлении, и, тем самым, заставить систему перейти из более вероятного состояния в менее вероятное. Рассмотрим выходящий из малой области Δ₀ пучок траекторий. Рассмотрим так же через некоторое, не слишком большое время область Δ~Δ₀ и те траектории, которые, выйдя из Δ₀, попадают в область Δ. Будем считать, что Δ есть масштаб огрубления в фазовом пространстве. Это означает, что индивидуальный характер траекторий внутри Δ для нас потерян. Поэтому внутри области Δ мы не можем отличить те траектории, которые совершили путь Δ → Δ₀, от траекторий, идущих по другим путям. Следовательно, мы не можем повернуть траектории системы, вышедшие из Δ₀, в обратную сторону. Точнее, мы не можем повернуть только те траектории, которые вышли из Δ₀. Мы поворачиваем все траектории, находящиеся в Δ, т.е. огромное число других траекторий. Именно в этом месте и начинает работать свойство перемешивания системы, которое необходимо для последнего утверждения.

При локальной неустойчивости через короткое время (время перемешивания) в области Δ находится много чужих траекторий, не вышедших из Δ₀. Таким образом, огрубление приводит к потере информации об индивидуальных траекториях в области огрубления Δ в момент их достижения этой области (и тем самым в любой последующий момент времени), а перемешивание приводит к заполнению области огрубления за конечное время траекториями, о которых теряется информация. Наконец, важным является то, что перемешивание заполняет область огрубления траекториями, прошедшими почти из любой области фазового объема. Поэтому в смешении информации участвует доля порядка траекторий, в которых равномерно представлены состояния почти всего фазового объема Δ~Δ₀, а не малой его части. Такая ситуация, обеспечиваемая перемешиванием, делает механизм потери информации экстремальным и устойчивым.

Таким образом, неустойчивость и огрубление являются необходимыми предпосылками для существования необратимых процессов в природе.

Следовательно, энтропия, определенная в статистической физике и энтропия, определенная в термодинамике, не всегда эквивалентны. Энтропия из термодинамики (Клаузиуса) требует понятия «равновесие». Однако, если равновесия нет, то нельзя ввести не только энтропию, но и температуру, а так же другие термодинамические параметры.

Литература

1. Рамм В.М. Абсорбция газов. - М.: Изд-во «Химия», 1976. - 655 с.

. Справочник по пыле- и золоулавливанию / под общ. ред. А.А. Русанова. - М.: Энергия, 1975. - 296 с.

. Шиляев М.И. Контактный тепло- и массообмен в форсуночных и барботажных аппаратах. Моделирование, оптимизация тепломассообмена и абсорбционно-конденсационной пылегазоочистки / М.И. Шиляев, Е.М. Хромова, А.В. Толстых. - Германия: LAP LAMBERT Academic Publishing, 2012. - 273 с.

Дополнительная литература

. Шиляев М.И., Хромова Е.М., Григорьев А.В., Тумашова А.В. Гидродинамика и тепломассообмен в форсуночных камерах орошения // Теплофизика и аэромеханика. - 2011. - Т. 18. - № 1. - С. 15-26.

. Авчухов В.В. Задачник по процессам тепломассообмена: учебное пособие для вузов / В.В. Авчухов, Б.Я. Паюсте. - М.: Энергоатомиздат, 1986. - 144 с.