Анализ динамики ротора транспортной турбины
Федеральное
агентство по образованию
Южно-Уральский
Государственный Университет
Кафедра ПМ и
ДПМ
Курсовой
проект по дисциплине «Динамика машин» на тему:
«Анализ
динамики ротора транспортной турбины»
Челябинск,
2005
Реферат
Курсовой проект «Анализ динамики ротора
транспортной турбины» объёмом 40 листов содержит 9 таблиц, 27 рисунков,
библиография включает 2 наименования.
Ключевые слова: ротор транспортной турбины,
виброактивность, упруго - демпферная опора, оптимизация, «жесткий» ротор, метод
Ритца, метод начальных параметров.
Объект исследования - ротор транспортной
турбины. Цель работы - снижение сил, действующих на опоры, путём выбора
оптимальных податливостей и уровня демпфирования упруго-демпферных опор.
Необходимо определить критические частоты
вращения ротора, собственные частоты невращающегося ротора и ротора,
вращающегося с частотой, равной верхней границе диапазона рабочих оборотов w.
Содержание
Введение
. Задание на курсовой проект
. Расчет упругих и инерционных
характеристик ротора
.1 Характеристики вала
.2 Характеристики диска и ротора
. Определение области допустимых
значений податливостей опор
.1 Определение области допустимых
значений податливостей опор
.2 Ограничение, накладываемое на
первую критическую частоту вращения
. Выбор податливостей опор
. Расчет собственных частот и форм
модели «жесткого» ротора
. Выбор уровня демпфирования в
опорах
. Расчет частот и форм методом Ритца
.1 Разложение по двум координатным
функциям
.2 Разложение по трем координатным
функциям
. Расчет частот и форм методом
начальных параметров
Заключение
Список используемой литературы
Введение
Одним из важнейших показателей качества
транспортной турбины является ее виброактивность, которая определяет
долговечность подшипниковых узлов ротора, вибрационную нагруженность самой
турбины и транспортного средства в целом. Современные транспортные турбины
работают на оборотах, превышающих первые критические частоты вращения их
роторов. Поэтому существует проблема проектирования таких турбин, у которых и
при переходе через критические частоты и в закритической области на рабочих
частотах силы в подшипниковых опорах оказываются минимально возможными, что
значительно повышает долговечность последних, а также уменьшает общую
вибронагруженность транспортного средства.
Существует два пути снижения сил, действующих со
стороны ротора на подшипники. Первый заключается в обеспечении большой
податливости вала, устанавливаемого в жёсткие подшипниковые опоры. Этот путь
имеет ряд недостатков: вал, обладающий большой податливостью, может не
удовлетворять условиям прочности; податливый вал трудно изготовить с высокой
степенью точности; в закритической зоне оборотов внутреннее трение
изгибающегося податливого вала становится фактором, снижающим устойчивость его
движения.
Всех этих недостатков лишён второй путь,
состоящий в максимально возможном повышении податливости опор, в то время как
сам ротор, изготовляемый по условиям прочности, должен быть достаточно жёстким.
Первая критическая частота вращения такого ротора определяется в основном
податливостью опор, сам же ротор практически не изгибается ни на критических
оборотах, ни в закритической области, так что силы внутреннего трения в нём
незначительны и не могут привести к неустойчивости движения. Податливость вала
ротора определяет лишь вторую (и более высокие) критическую частоту, которая
чаще всего лежит гораздо выше верхней границы диапазона рабочих оборотов ω.
В курсовом проекте рассмотрен второй путь
снижения сил в опорах.
1. Задание на курсовой
проект
Рассчитать упруго-демпферные опоры подшипников
ротора одноступенчатой турбины транспортной машины. Определить собственные
частоты ротора и критические частоты его вращения.
Эскиз ротора показан на рисунке 1.
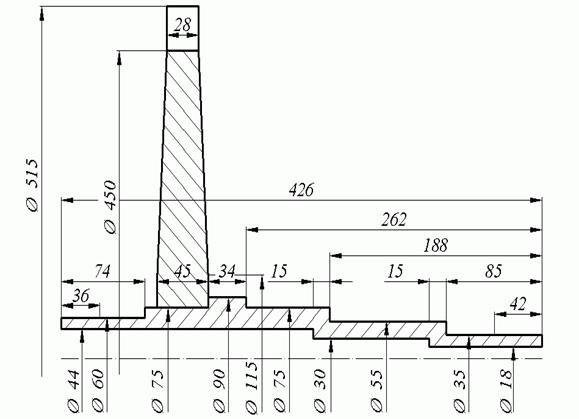
Рисунок 1. Эскиз ротора
Исходные данные приведены в таблице 1.
Таблица 1
|
nmax
|
÷eç×105, рад
|
[W] ≥ ωкр1 / ωраб
|
|
8
|
7
|
0,25..0,3
|
Ротор выполнен из конструкционной стали с
модулем упругости
Е=2,1×105 МПа и
плотностью r=7,8×103 кг/м3.
2. Расчет упругих и
инерционных характеристик ротора
Упругие и инерционные характеристики ротора -
это распределение погонной массы m и жесткости
поперечных сечений EI
вала, масса МD и моменты инерции
диска Ix, Iz
.
2.1 Характеристики вала
Разобьем вал на участки постоянного поперечного
сечения длиной li
(рисунок 2), для которых определяются погонные массы mi
и EIi:


Рисунок 2. Схема разбиения вала на
участки
Таблица 2
|
Номер
участка i
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
Длина
участка li, м
|
0,036
|
0,038
|
0,011
|
0,045
|
0,034
|
0,059
|
0,015
|
0,088
|
0,015
|
0,043
|
0,042
|
|
Координаты
границ участка zi, м
|
0,036
|
0,074
|
0,085
|
0,13
|
0,164
|
0,223
|
0,238
|
0,326
|
0,341
|
0,384
|
0,426
|
|
Di,
м
|
0,06
|
0,06
|
0,075
|
0,075
|
0,09
|
0,075
|
0,075
|
0,055
|
0,055
|
0,035
|
0,035
|
|
di,
м
|
0,044
|
0,044
|
0,044
|
0,044
|
0,044
|
0,044
|
0,03
|
0,03
|
0,018
|
0,018
|
0,018
|
|
mi, кг/м
|
10,194
|
10,194
|
22,599
|
22,599
|
37,761
|
22,599
|
28,946
|
13,018
|
16,547
|
5,520
|
5,520
|
|
EIi
×104, Н×м2
|
9,672
|
9,672
|
29,287
|
29,287
|
64,955
|
29,287
|
32,372
|
8,758
|
9,498
|
1,465
|
1,465
|
Результаты вычислений сведем в таблицу 2.
Масса вала:
 , кг.
, кг.
Положение центра тяжести вала
(Рисунок 2):
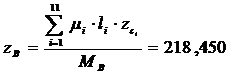 , мм.
, мм.
- положение центра тяжести i-го
участка вала.
2.2 Характеристики
диска и ротора
Разрежем мысленно диск цилиндрическими сечениями
на несколько кольцевых элементов (рисунок 3) таких, что средний радиус каждого
из них rсрi
намного больше толщины кольца (ri-ri-1).
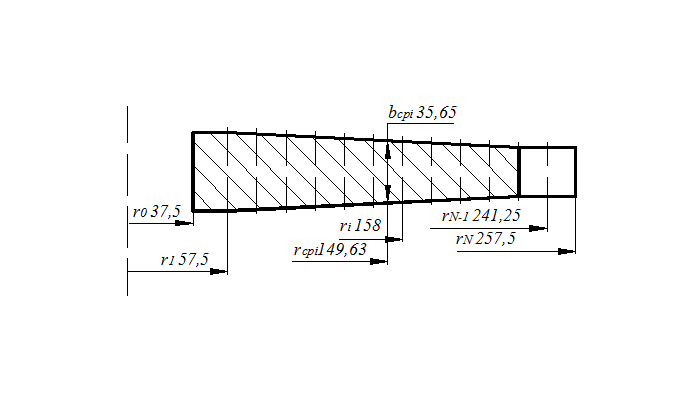
Рисунок 3. Схема разбиения диска на
кольцевые элементы
Массы и моменты инерции относительно оси
вращения можно приближенно определить из выражений:

Объем кольцевых участков,
соответствующих лопаточному венцу, лишь частично заполнен лопатками. Поэтому
для них массы и моменты инерции относительно оси вращения можно приближенно
определить из выражений:

где 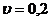 - степень заполнения лопатками
объема кольца.
- степень заполнения лопатками
объема кольца.
Считая диск тонким, примем, что его
момент инерции относительно оси, проходящей через центр тяжести перпендикулярно
оси вращения, есть 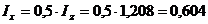 , кг×м2.
, кг×м2.
Результаты вычислений сведем в
таблицу 3 и 4.
Таблица 3
|
Номер колеса i
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
ri×10-3, м
|
37,5
|
57,5
|
57,5
|
74,25
|
74,25
|
91
|
91
|
107,8
|
107,8
|
124,5
|
124,5
|
141,3
|
141,3
|
158
|
|
bср×10-3, м
|
45
|
44,15
|
42,41
|
40,71
|
39,05
|
37,35
|
35,65
|
|
mi,
кг
|
2,095
|
2,387
|
2,877
|
3,321
|
3,723
|
4,074
|
4,379
|
|
Izi,
кг×м2
|
0,005
|
0,010
|
0,020
|
0,033
|
0,050
|
0,072
|
0,098
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4
|
Номер
колеса i
|
8
|
9
|
10
|
11
|
12
|
13
|
S
|
|
ri×10-3, м
|
158
|
174,8
|
174,8
|
191,5
|
191,5
|
208,3
|
208,3
|
225
|
225
|
241,3
|
241,3
|
257,5
|
-
|
|
bср×10-3, м
|
33,95
|
32,25
|
30,55
|
28,85
|
28
|
28
|
-
|
|
mi,
кг
|
4,637
|
4,848
|
5,013
|
5,130
|
1,560
|
1,668
|
45,711
|
|
Izi,
кг×м2
|
0,128
|
0,163
|
0,200
|
0,241
|
0,085
|
0,104
|
1,208
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Масса диска:
 , кг.
, кг.
Положение центра тяжести диска
(Рисунок 2):
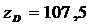 , мм.
, мм.
По найденным инерционным характеристикам диска и
вала можно найти инерционные характеристики ротора:
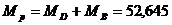 , кг;
, кг;
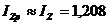 , кг×м2;
, кг×м2;
 , кг×м2.
, кг×м2.
Здесь aD=14,61 мм -
расстояние от центра тяжести ротора до центра тяжести диска, ai -
расстояние от центра тяжести ротора до центра тяжести i-го участка
вала.
Положение центра тяжести ротора
(Рисунок 2):
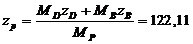 , мм.
, мм.
Результаты вычислений сведем в
таблицу 5.
Таблица 5
|
Ix, кг×м2
|
Iэр, кг×м2
|
IZр, кг×м2
|
Mр, кг
|
|
0,604
|
0,706
|
1,208
|
52,645
|
3. Определение области
допустимых значений податливостей опор
.1 Определение области
допустимых значений податливостей опор
Неравномерность движения транспортной машины
является причиной возникновения значительных ускорений движущейся совместно с
ней турбины. Появляющиеся при этом силы инерции ротора приводят к осадке
податливых опор и изгибу вала, в результате чего лопатки диска смещаются как в
поперечном, так и в осевом направлениях (Рисунок 4). Значение указанных
инерционных сил удобно оценивать перегрузкой nmax,
то есть, отношением их абсолютной величины к собственному весу ротора.
Смещение от податливостей опор и смещение от
прогиба вала будем считать статическими, а амплитудами вынужденных колебаний
ротора пренебрегаем. Обозначим смещения конца лопатки, вызванные податливостью
опор, через DXS и DZS,
а смещения, вызванные прогибом вала, - DXP
и DZP
(Рисунок 4).

Рисунок 4. Схема деформирования
ротора и опор при перегрузках
1- ротор в ненагруженном состоянии; 2- ротор в
нагруженном состоянии; 3- кромки лопаток направляющего аппарата; 4- корпус
турбины
Инерционные силы, действующие на ротор,
сосредоточены в центре тяжести ротора и задаются перегрузкой nmax:
ин=Mр×g×nmax=52,645×9,
81×8=4,131×103,
Н,
где Mр
- масса ротора, g - ускорение
свободного падения, nmax-
максимально возможная перегрузка.
Перемещения DXS
и DZS,
обусловленные податливостью опор, определим, используя представленную на
рисунке 5 расчетную схему.
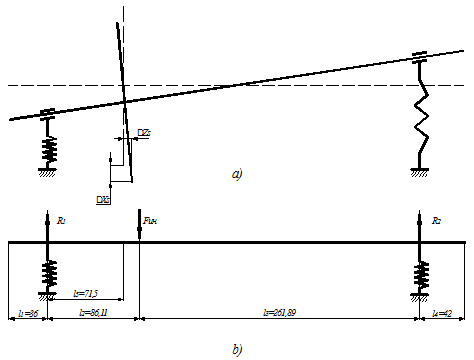
Рисунок 5. Расчетная схема к определению
перемещений DXS и DZS, вызванных
податливостью опор
Усилия, возникающие в опорах, равны:
 Н;
Н;
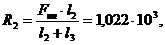 Н.
Н.
Перемещения DXS и DZS:

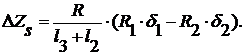
Здесь R
- радиус рабочего колеса.
В свою очередь, перемещения DXР
и DZР,
обусловленные изгибом вала, определим, используя представленную на рисунке 6
расчетную схему.

Рисунок 6. Расчетная схема к
определению перемещений DXР и DZР, вызванных
изгибом вала
Перемещения DXР
и DZР
от изгиба вала вычислим при помощи интеграла Мора. На рисунке 7 представлены
эпюры изгибающих моментов. При этом усилия, возникающие в опорах, равны:

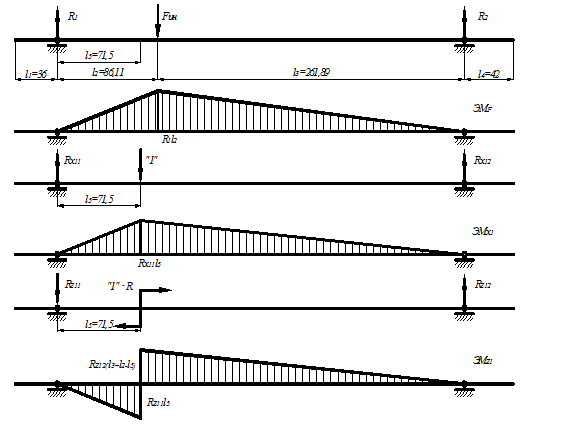
Рисунок 7. Эпюры изгибающих моментов
Перемножая соответствующие эпюры,
получаем:
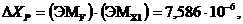 м;
м;
 м.
м.
Промежуточные результаты
перемножения эпюр представлены в таблице 5.
Таблица 6
|
Номер
участка i
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Длина
участка li,, м
|
0,038
|
0,034
|
0,015
|
0,008
|
0,034
|
0,059
|
0,015
|
0,088
|
0,015
|
0,043
|
|
EIi
×104, Н×м2
|
9,672
|
9,672
|
29,287
|
29,287
|
64,955
|
29,287
|
32,372
|
8,758
|
9,498
|
1,465
|
|
Значение
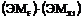 i 10-6,
м0,4670,8730,6750,3770,6191,5480,2302,3320,0850,380 i 10-6,
м0,4670,8730,6750,3770,6191,5480,2302,3320,0850,380
|
|
|
|
|
|
|
|
|
|
|
|
Значение
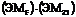 i 10-6,
м-0,435-0,5891,6761,3562,2285,5740,8268,3980,3071,368 i 10-6,
м-0,435-0,5891,6761,3562,2285,5740,8268,3980,3071,368
|
|
|
|
|
|
|
|
|
|
|
Ограничения на перемещения ротора при
перегрузках можно записать в следующем виде:
|DXS+DXP|£[DX]СТ=Dr0/[Kr],
|DZS+DZP|£[DZ]СТ=Dz0/[Kz],
где [DX]СТ,
[DZ]СТ
- допускаемые суммарные статические перемещения, [Kr],
[Kz]
- нормативные коэффициенты запаса, Dr0,
Dz0
- номинальные радиальный и осевой зазоры в турбинах.
Из соображений повышения КПД турбины радиальный
зазор должен быть как можно меньшим, в то время как требования надежности
(отсутствие задевания лопаток за корпус при максимальных нагрузках) не
позволяют сделать его слишком малым. Осевой зазор Dz0
слабее влияет на КПД турбины и может быть большим Δr0.
Необходимые зазоры можно выбрать по следующим формулам:
Dr0=k1×Dmax;
Dz0=k2×b,
где Dmax=515
мм - максимальный диаметр рабочего колеса. Примем k1=0,002,
k2=0,25, [Kz]=[Kr]=1,5
(определяются, в основном, точностью изготовления и сборки деталей турбины и
степенью достоверности величины nmax),
b=28 мм - хорда
лопатки.
Следовательно,
Dz0 = 0,028 ·0,
25 = 7×10-3,
м;
[DX]СТ=0,687×10-3,
м;
[DZ]СТ=4,667×10-3,
м.
Ротор будем считать «жестким», если выполнено
условие:
|DXS|³
20×|DXP|.
Условия (3.1) и (3.2) ограничивают на плоскости
(d1,
d2)
область допустимых значений податливости опор. Поэтому, подставляя полученные
значения DXP, DZP
и DXS,
DZS
в условия (3.1) и (3.2), получим аналитические выражения границ области
допустимых податливостей:
d2= -11,761×d1 +3,235×10-6
d2= 3,040×d1 +2,740×10-8
d2= -11,761×d1 +7,224×10-7
Область допустимых значений податливостей опор
изображена на рисунке 8.
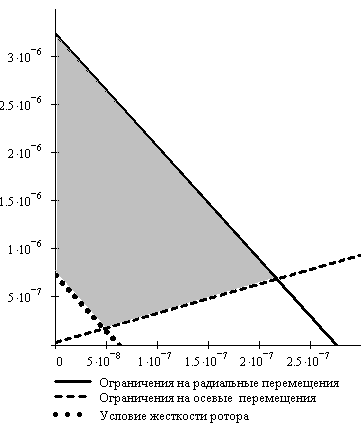
Рисунок 8. Область допустимых
значений податливости опор
3.2 Ограничение,
накладываемое на первую критическую частоту вращения
Выбираемые в дальнейшем податливости опор,
помимо ограничений линией АВ (Рисунок 8), должны обеспечить выполнение
ограничения на критическую частоту ротора, выражаемого следующим неравенством
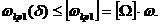
Здесь 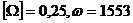 рад/с. - расчетная рабочая частота
ротора, определяемая условиями прочности турбины. Упрощенно ее можно выбрать
такой, чтобы на среднем радиусе лопаток окружная скорость составляла 400 м/с.
рад/с. - расчетная рабочая частота
ротора, определяемая условиями прочности турбины. Упрощенно ее можно выбрать
такой, чтобы на среднем радиусе лопаток окружная скорость составляла 400 м/с.
При определении зависимости первой
критической частоты от податливости опор будем варьировать податливостью первой
опоры, податливость второй опоры будет определять по условию (3.1).
Для получения  представим
ротор абсолютно жёстким.
представим
ротор абсолютно жёстким.
Колебания ротора возбуждаются за счёт
эксцентриситета е центра тяжести (Рисунок 9) по отношению к геометрической оси
ротора z1 и за счёт наклона
главной оси инерции x к геометрической оси на угол e.
Моменты инерции относительно главных центральных осей x
и h
будем считать одинаковыми и равными Iэр.
Ротор вращается с постоянной угловой скоростью w.
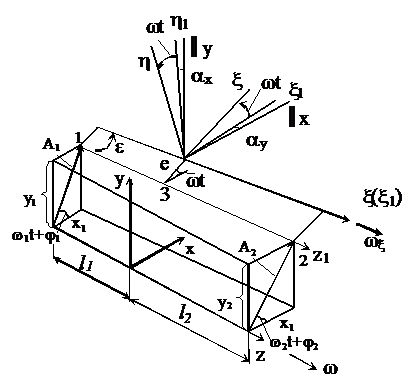
Рисунок 9. Схема к выводу уравнений
движения жесткого ротора
Вывод уравнений движения ротора приведен в
работе [1, стр. 15]. Итоговые уравнения движения имеют вид:
w1×a1
- w1×b1
+ w2×a2 - w2×b2
= Mр×e×w2;
w1×a1
+ w1×b1 + w2×a2
+ w2×b2 = 0;×a1
- w3×b1
+ w4×a2 - w4×b2
= -(Ieр
- Izр)×e×w2;
w3×a1
+ w3×b1 + w4×a2
+ w4×b2 = 0.
Здесь
w1=c1-Mр×w2× ; w1=b1×w;=c2-Мр×w2×
; w1=b1×w;=c2-Мр×w2×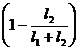 ; w2=b2×w; aj=aj×cosjj;=c1×l1-w2×
; w2=b2×w; aj=aj×cosjj;=c1×l1-w2× ; w3=b1×(l2+l)×w;=-c2×l2+w2×
; w3=b1×(l2+l)×w;=-c2×l2+w2× ; w4=b2×l2×w; bj=aj×sinjj.
; w4=b2×l2×w; bj=aj×sinjj.
Для того, чтобы определить
зависимость  , необходимо
в полученной системе уравнений убрать возбуждение и пренебречь демпфированием.
При этом она распадается на две однородные одинаковые системы, равенство нулю
определителя которых
, необходимо
в полученной системе уравнений убрать возбуждение и пренебречь демпфированием.
При этом она распадается на две однородные одинаковые системы, равенство нулю
определителя которых
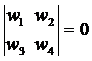
и является условием для нахождения  .
.
Зависимость первой критической
частоты от податливости первой опоры представлена на рисунке 10.
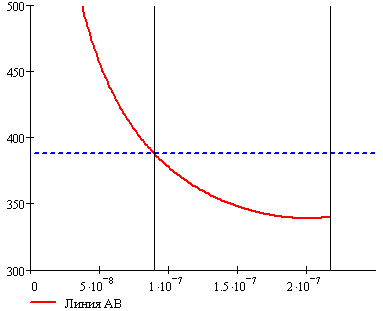
Рисунок 10. Зависимость wкр1 от податливости первой
опоры
Используя полученную зависимость  , определим d1=8,898×10-8, Н/м.
Это значение накладывает дополнительное ограничение на область ABCD (Рисунок
8). В результате получаем новую область допустимых значений податливостей,
представленную на рисунке 11.
, определим d1=8,898×10-8, Н/м.
Это значение накладывает дополнительное ограничение на область ABCD (Рисунок
8). В результате получаем новую область допустимых значений податливостей,
представленную на рисунке 11.
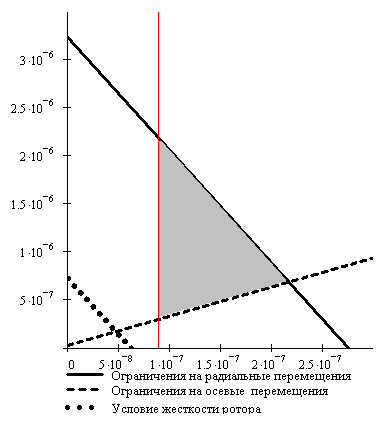
Рисунок 11. Уточненная область
допустимых значений податливости опор
4. Выбор
податливостей опор
При выборе податливости опор в качестве критерия
оптимальности примем минимум максимального значения опорной реакции подшипника
при номинальной рабочей частоте вращения ротора:
Ri, max=min
(i=1, 2).
Каждая из опор может быть схематично
представлена в виде параллельно соединенных упругого элемента жесткостью сj
и демпфера с коэффициентом трения bj
(Рисунок 4). Будем считать, что значения bj
и сj в двух взаимно
перпендикулярных радиальных направлениях одинаковы. Усилие, передаваемое через
такую опору со стороны ротора на основание, состоит из двух составляющих -
упругой (сjхj)
и вязкой (bjх’j).
Здесь хj - радиальное
смещение вала, в котором расположен центр опоры (Рисунок 9). При
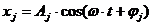
упругая и вязкая составляющие силы Rj изменяются
синхронно, но сдвинуты относительно друг друга по фазе на p/2, так что
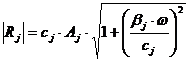 .
.
При умеренном демпфировании вязкое
трение практически не влияет на собственные частоты и критические частоты
вращения ротора, а вязкая составляющая силы Rj мала по
сравнению с упругой
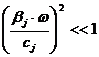 ,
,
так что приближенно можно считать
 .
.
Из анализа динамики жесткого ротора
следует, что амплитуды колебаний его опор Аj при частоте
вращения w можно
определить из системы уравнений:
×a1 + w2×a2
= Mр×e×w2;×a1
+ w4×a2
= - (Ieр
- Izр)
×e×w2.
Модули статической е и динамической e неуравновешенностей ротора
приведены в задании на курсовое проектирование. Однако их знаки могут
совпадать, либо быть противоположными. Поэтому расчет зависимостей сил R1, R2 от
податливости первой опоры следует проводить для случаев еe>0 и ee<0, что
дает четыре кривые, показанные на рисунке 12.
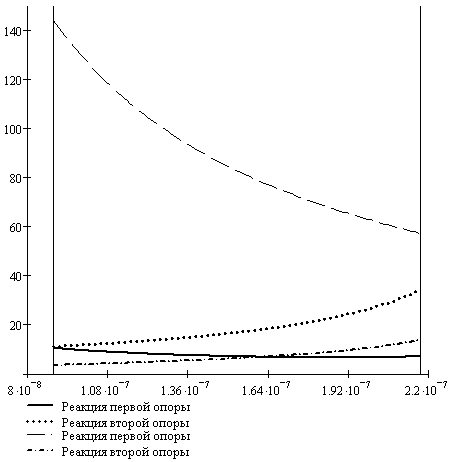
Рисунок 12. Силы в опорах в
зависимости от податливости первой опоры
Поскольку минимум максимального значения опорной
реакции подшипника при номинальной рабочей частоте вращения ротора не
достигается (Рисунок 12), значение податливости первой опоры выберем на границе
интервала d1Î [8,898×10-8;
2,167×10-7], удовлетворяющему
предложенному критерию оптимальности. Примем значение податливости первой опоры
d1=2,167×10-7,
Н/м.
Значение податливости второй опоры определяется
из условия (3.2).
Следовательно, принимаем при последующих
расчетах значения:
d1=2,167×10-7,
Н/м d2=6,864×10-7,
м/Н
с1=4,615×106, Н/м с2=1,457×106,
Н/м.
5. Расчет собственных
частот и форм модели «жесткого» ротора
При d1=2,167×10-7,
м/Н вычислим первую критическую частоту: wkp1=339,605,
рад/с. Форма колебаний на этой частоте определяется из системы уравнений (3.4),
если положить w= wkp1:

Выражение для формы колебаний на
первой критической частоте имеет вид (Рисунок 13):

Собственные частоты невращающегося
ротора определим из частотного уравнения без учета влияния гироскопического
момента (Iz=0): p1 =339,47,
рад/с, и p2 =435,992,
рад/с. Выражения для собственных форм колебаний на частотах р1 и р2 имеет вид
(Рисунок 13):
U1(z) = 0,308×z+0,989;
U2(z) = -11,1×z +1,40.
При этом
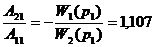 ,
, 
Проведем проверку ортогональности
полученных собственных форм, поскольку она является проверкой правильности
решения задачи:

где zp=122,11, мм
- координата центра тяжести ротора (рисунок 2);
 ;
; =2,411;
=2,411;
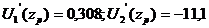 ;
; 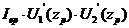 =-2,412.
=-2,412.
жесткий ротор диск
вращение
Полученное значение погрешности D не превышает допустимых 5%.
Форма вынужденных колебаний на
номинальной рабочей частоте
w
=1553, рад/с:
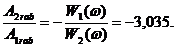
Выражение для формы колебаний на
номинальной рабочей частоте вращения (Рисунок 13):
Urab(z) = -11,6×z +1,42.


Рисунок 13. Формы колебаний
Разложим форму колебаний на номинальной рабочей
частоте w
по собственным формам (выражение можно получить линейной комбинацией
собственных форм):
Urab(z)= ,
,
где k1, k2 -
коэффициенты разложения. Определим эти коэффициенты.
Подставим в соотношение (5.3)
выражения (5.2) и (5.1):
,6×z +1,42=k1(0,308×z+0,989)+k2(-11,1×z +1,40).
Получаем систему из двух уравнений:
,6= 0,308k1 -11,1k2
,42= 0,989k1+1,40k2
k1=0, 05; k2=1, 05.
Итак, Urab(z)=0,05U1(z)+1,05U2(z). Из
разложения формы колебаний ротора, вращающегося на рабочей частоте, по
собственным формам видно, что вторая собственная форма вносит бóльший вклад
в форму колебаний на рабочей частоте, что подтверждается большей близостью
второй собственной формы к форме на рабочей частоте. Это объясняется тем, что
форма колебаний на рабочей частоте ортогональна первой собственной форме, и,
следовательно, первая форма не будет возбуждаться.
6. Выбор
уровня демпфирования в опорах
Введение дополнительного
демпфирования в опоры позволяет снизить динамические силы, передаваемые со
стороны ротора на основание при проходе через критическую частоту вращения. При
этом увеличение демпфирования приводит к некоторому повышению виброактивности
ротора в закритической области. Следовательно, демпфирование должно выбираться
максимально возможным при условии, что оно не повысит существенно
виброактивности ротора на рабочих оборотах. Это практически выполняется, если
 ,
,
где bj - демпфирование в опорах; cj - жёсткость
опор.
с1=4,615×106, Н/м, с2=1,457×106,
Н/м.
b1max
= 990,486 Н×с/м, b2max
= 312,702 Н×с/м.
Предполагается, что специальным демпфером
оснащается лишь одна из опор, рассеянием же энергии в другой опоре будем
пренебрегать. Вопрос о том, какая из опор должна быть упруго-демпферной, а
какая может быть чисто упругой, решается после построения функций Rj(w,
b1,
b2)
в диапазоне частот
,8×wкр1 £
w
£
w.
Реакции определяются из выражения
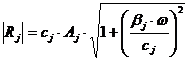 ,
,
где Аj
- амплитуда колебаний, определяемая из системы:
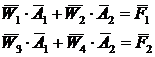 ,
,
где 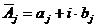 ,
,
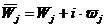 ,
,
 ,
,
 .
.
Реакции определяем для двух
вариантов демпфирования: b1 = 0, b2 = b2max и b1 = b1max, b2 = 0.
Таблица 7
|
Демпфер
установлен на первой опоре
|
Демпфер
установлен на второй опоре
|
|
eе>0
|
eе<0
|
eе>0
|
eе<0
|
|
A1=1,199×10-4
|
A1=1,219×10-4
|
A1=3,597×10-4
|
A1=3,650×10-4
|
|
A2=1,234×10-4
|
A2=1,261×10-4
|
A2=3,692×10-4
|
A2=3,752 ×10-4
|
Расчёт амплитуд для случаев ee
>0 и ee
<0 показал, что большие амплитуды будут в случае ee<0,
поэтому реакции в опорах определяются для этого случая. Графики изменения R1
и R2 от частоты
вращения представлены на рисунке 14.

Рисунок 14. Зависимость динамических
сил в опорах от частоты вращения ротора при различных вариантах демпфирования
Анализируя графики (Рисунок 14), делаем вывод,
что реакции меньше при установке демпфера на первой опоре (турбинной опоре),
поэтому выбираем этот вариант установки демпфера.
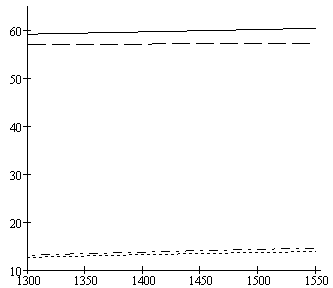
Рисунок 15. Зависимость динамических
сил в опорах от частоты вращения ротора при различных вариантах демпфирования:
1 - реакция в первой опоре (демпфер установлен в первой опоре); 2 - реакция во
второй опоре (демпфер установлен в первой опоре); 3 - реакция в первой опоре
(демпфер установлен во второй опоре); 4 - реакция во второй опоре (демпфер
установлен во второй опоре)
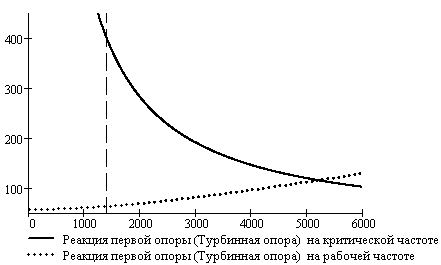
Рисунок 16. Зависимость динамических
сил от уровня демпфирования в турбинной опоре: 1 - реакция в первой опоре на
критической частоте вращения; 2 - реакция в первой опоре на рабочей частоте
вращения
Уточним полученное значение b1max = 990,486 Н×с/м,
поскольку уровень демпфирования должен быть максимально возможным при условии,
что реакции в опорах на рабочих оборотах существенно не повысятся (Рисунок 16).
Этому условию вполне удовлетворяет значение b1=1386,
Н×с/м.
Варьирование коэффициента демпфирования b1
приведено в таблице 8.
Таблица 8
|
b1, Н×с/м
|
R1w, H
|
R2w, H
|
R1wkp1, H
|
R2wkp1, H
|
|
990,486
|
60,351
|
13,839
|
564,069
|
183,738
|
|
1386
|
63,173
|
13,859
|
404,77
|
132,001
|
|
1980
|
68,777
|
13,901
|
285,853
|
93,554
|
Выбрать место расположения демпфера можно по
критерию максимального рассеяния энергии в демпфере. Энергия, рассеиваемая в
демпфере вязкого трения на резонансе за цикл колебаний, есть:
= βjπA2jω,
здесь Аj
- амплитуда колебаний.
Подставив в эту формулу выражение 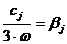 , получим:
, получим:
 .
.
То есть наибольшая энергия, которая
может быть рассеяна в опоре за цикл, пропорциональна упругой энергии 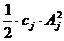 опоры.
Поэтому, демпфер нужно установить на ту опору, где произведение сjA2j больше.
Отношение этих произведений:
опоры.
Поэтому, демпфер нужно установить на ту опору, где произведение сjA2j больше.
Отношение этих произведений:

Отсюда следует, что демпфер необходимо
установить на первой опоре.
Определим декременты колебаний на первой и
второй формах по формуле:
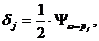
где 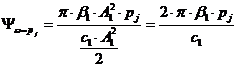 - коэффициент поглощения, рj - j-я
собственная частота ротора. На первой частоте колебаний δ1 =
- коэффициент поглощения, рj - j-я
собственная частота ротора. На первой частоте колебаний δ1 = 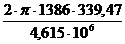 = = 0,64, на
второй - δ2 =
= = 0,64, на
второй - δ2 =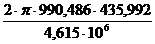 =0,822.
=0,822.
7. Расчет частот и форм
методом Ритца
Формы колебаний зададим в виде ряда
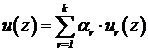 ,
,
где 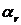 -
коэффициенты перед функциями координат;
-
коэффициенты перед функциями координат;  - известные линейно независимые
функции координат (координатные функции), удовлетворяющие геометрическим
условиям закрепления системы.
- известные линейно независимые
функции координат (координатные функции), удовлетворяющие геометрическим
условиям закрепления системы.
Для консервативной системы имеет место
выражение:
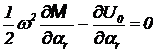 ,
,
где 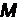 - обобщенная масса,
- обобщенная масса,  -
амплитудное значение потенциальной энергии системы.
-
амплитудное значение потенциальной энергии системы.
7.1 Разложение по двум
координатным функциям
Разложим функции формы по двум координатным
функциям:
 ,
,
здесь 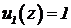 ,
, 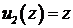 . Тогда
. Тогда 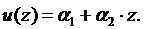
Обобщенная масса:
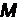
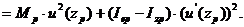
Значение потенциальной энергии:

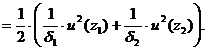
Подставляя 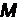 и
и  в выражение
(7.2), получим следующую систему уравнений:
в выражение
(7.2), получим следующую систему уравнений:
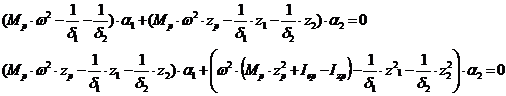
Определитель этой системы
представляет собой частотное уравнение:
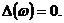
Решая это уравнение, определяем собственные
частоты ротора (Iz=0)
и первую критическую: p1Рц
=339,47, рад/с, p2Рц
=435,992, рад/с, wкр1Рц =339,566, рад/с.
Для построения форм колебаний по
методу Ритца определим коэффициент 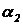 , при этом полагаем
, при этом полагаем 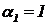 .
Собственные формы (Рисунок 17):
.
Собственные формы (Рисунок 17):
U1Рц(z)
= 0,308×z
+0,989;
U2Рц(z)
= -11,1 ×z
+1,40.


Рисунок 17. Собственные формы
колебаний ротора
Выражение для формы колебаний на первой
критической частоте имеет вид (Форма представлена на рисунке 18):

При w=1553, рад/с, собственные частоты вращающегося
ротора равны:
p1РцВр
=339,592, рад/с, p2РцВр = 2,727×103, рад/с.
Выражение для собственных форм
колебаний на рабочей частоте w
(Формы представлены на рисунке 19):
U1РцВр(z) = 4×10-3z+1;
U2РцВр(z) =-11,68 z +1,418.
Рисунок 18. Форма колебаний ротора
на первой критической частоте
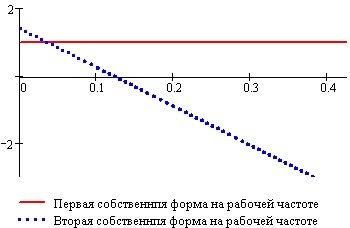
Рисунок 19. Собственные формы
колебаний на рабочей частоте
Анализируя полученные формы (7.5) и (7.6),
видим, что первая и вторая собственные формы (Рисунок 19) совпадают с
собственными формами невращающегося ротора (Рисунок 17).
7.2 Разложение по трем
координатным функциям
Зададим теперь форму колебаний (7.1) в
квадратичном виде:
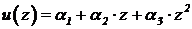 .
.
Для определения обобщенной массы и
амплитудного значения потенциальной энергии проведем разбиение ротора на
участки, представленные на рисунке 2. Жесткость и погонная масса каждого такого
участка постоянны.
Обобщенная масса:
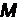
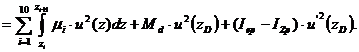
Значение потенциальной энергии:

Подставляя 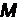 и
и  в выражение
(7.2), получим аналогичную (7.4) систему уравнений. Поскольку система имеет
громоздкий вид, расчеты частот проведем в системе MathCAD.
в выражение
(7.2), получим аналогичную (7.4) систему уравнений. Поскольку система имеет
громоздкий вид, расчеты частот проведем в системе MathCAD.
Определяем собственные частоты ротора (Izp=0)
и первую критическую: p1Рц=338,289
, рад/с, p2Рц =433,534,
рад/с, wкр1Рц
=338,289, рад/с.
Для построения форм колебаний по
методу Ритца определим коэффициенты 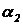 и
и 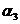 , при этом полагаем
, при этом полагаем 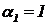 . Выражения
собственных форм (Рисунок 20):
. Выражения
собственных форм (Рисунок 20):
1Рц(z)
= 0,998+0,072z -0,382z2;
U2Рц(z)
= 1,446 -12,459z+0,936z2.

Рисунок 20. Собственные формы
колебаний ротора
Проверка ортогональности собственных форм:
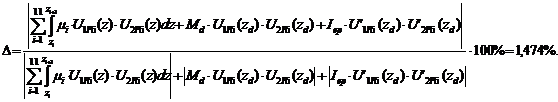
где zd=107,5, мм -
центр тяжести диска (рисунок 2);
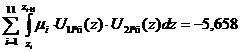 ;
;
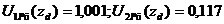 ;
;
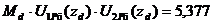 ;
;
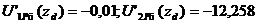 ;
;
 .
.
Полученное значение погрешности D не превышает допустимых 5%.
При w=1553, рад/с, собственные частоты вращающегося
ротора равны:
p1РцВр
=338,288, рад/с, p2РцВр = 2,579×103, рад/с.
Выражение для собственных форм
колебаний на рабочей частоте w
(Формы представлены на рисунке 21):
1РцВр(z)
=0,998+0,082×z-0,383×z2;
U2РцВр(z)
=1,423-11,612 z -3,556×z2.
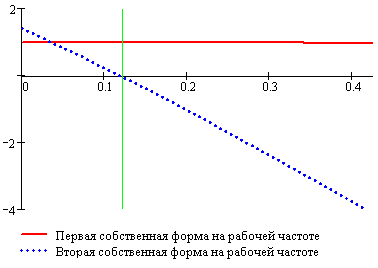
Рисунок 21. Собственные формы
колебаний на рабочей частоте
Выражение для формы колебаний на первой
критической частоте имеет вид (Форма представлена на рисунке 22):
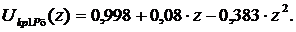

Рисунок 22. Форма колебаний ротора
на первой критической частоте
Сравнивая частоты, полученные в пункте 5 и
методом Ритца с тремя базисными функциями, можно проследить тенденцию к их
снижению. Это обусловлено удержанием трех членов в выражении (7.1), а не двух.
8. Расчет частот и форм
методом начальных параметров
Согласно методу начальных параметров ротор
разбивается на отдельные участки постоянного поперечного сечения, не содержащие
внутри себя никаких дополнительных элементов.
Введем вектор состояния сечения ротора
Vj ={Jj,
J¢j, Mj,
Qj}T,
включающего Jj - перемещение
j-го сечения, J¢j -угол поворота, Mj - изгибающий
момент, Qj - поперечную силу этого сечения. Если задаться частотой вращения
вала ω
и не учитывать инерцию поворота его сечений, то по элементам вектора состояния
на левом краю участка могут быть найдены элементы вектора состояния сечения,
расположенного на его правом краю слева от места присоединения диска и упругих
элементов. Переход от участка к участку осуществляется по соотношению
+1=Rj×Vj,
где Rj
- матрица перехода через j-ый
участок.
 .
.
Здесь обозначено:
Aj= - (Iэрj - IZpj )×w2, Bj=mj×w2-cj, 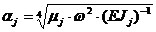 ,
,
где mj- погонная масса j-го участка,
EJj- изгибная
жесткость j-го участка.
Kkj=Kk(aj×lj) -значение k-ой функции
Крылова на правом краю j-го участка.
Функции Крылова (λ = αjlj):

Схема разбиения ротора для МНП
представлена на рисунке 2. При этом разбиении коэффициенты А и В в матрице
перехода имеют следующие значения:
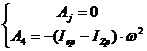 , при j=1..11;
, при j=1..11;
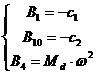 и В = 0 для всех остальных
участков.
и В = 0 для всех остальных
участков.
Здесь Iер и IZр - моменты
инерции диска, Мd - масса диска.
пользуясь рекуррентными соотношениями (8.2),
можно связать векторы состояния правого VN+1
и левого V1 краёв ротора:
 .
.
Система (8.3) может быть
представлена в виде:
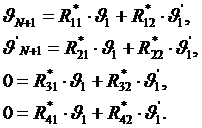
Система, состоящая из двух последних уравнений
(8.4), имеет нетривиальное решение, если ее определитель равен 0:
R*31×
R*42-R*41×
R*32=0,
где R*jk
-элементы матрицы R*.
Решая это уравнение, получаем следующие частоты:
wмнп_кр1 = 332,761, рад/с;
wмнп_кр2 = 1,463×10
4 , рад/с.
Форма колебаний ротора на первой критической
частоте представлена на рисунке 23.
Для нахождения собственных частот невращающегося
ротора примем в матрице перехода:
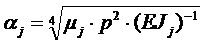
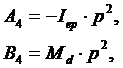
где p-значение
собственной частоты.

Рисунок 23. Формы колебаний ротора
на первой критической частоте
Значения собственных частот невращающегося
ротора:
р1мнп = 332,359, рад/с;
р2мнп = 432,984, рад/с.
Собственные формы невращающегося ротора
представлены на рисунках 24 и 25.
Для нахождения собственных частот ротора,
вращающегося с угловой скоростью w, примем в матрице
перехода:
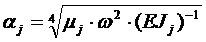 ,
,

где p-значение
собственной частоты ротора, вращающегося с угловой скоростью w.
p1вр_мнп =332,678,
рад/с;
p2вр_мнп = 2432,
рад/с.
Формы колебаний представлены на рисунках 26 и
27.
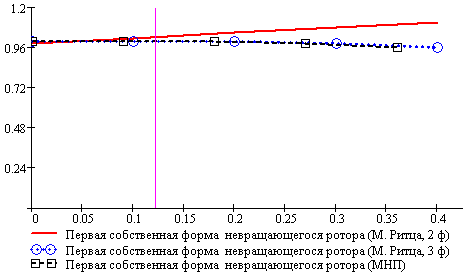
Рисунок 24. Первая собственная форма
невращающегося ротора

Рисунок 25. Вторая собственная форма
невращающегося ротора
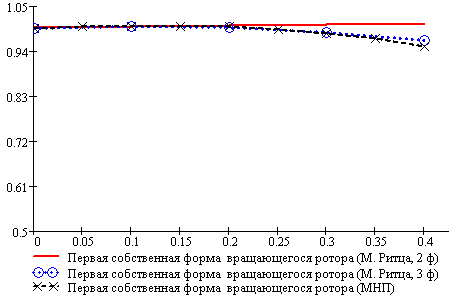
Рисунок 26. Первая собственная форма
ротора на рабочей частоте
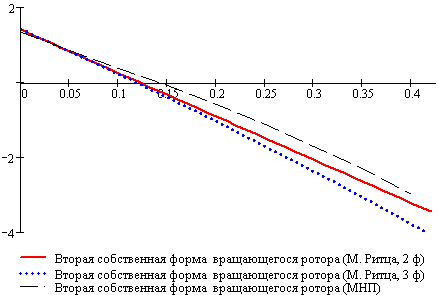
Рисунок 27. Вторая собственная форма
ротора на рабочей частоте
Частоты, полученные по методу начальных
параметров, оказались меньше, чем частоты, полученные другими методами. Это
объясняется тем, что этот метод сравнительно точно учитывает реальную жесткость
системы. Уменьшение жесткости приводит к уменьшению значений частот.
Заключение
В работе рассмотрен вопрос оптимального выбора
упруго-демпферных опор подшипников ротора одноступенчатой турбины транспортной
машины. Для ротора рассчитаны упругие и инерционные характеристики (таблица
2,3,4). Определена область допустимых значений податливостей опор (рисунок 11).
Из условия минимума сил в подшипниках найдены
следующие характеристики:
d1=2,167×10-7,
Н/м, d2=6,864×10-7,
м/Н,
с1=4,615×106, Н/м, с2=1,457×106,
Н/м.
В данной работе определена опора, в которой
устанавливается демпфер (турбинная опора). Коэффициент демпфирования принят:
b = 1386, Н×с/м.
Определены собственные частоты ротора, а также
его критические частоты вращения тремя методами: расчетный метод модели
«жесткого» ротора, метод Ритца и метод начальных параметров (таблицы 8 и 9).
Таблица 8
|
Метод
|
wкр1, рад/с
|
p1, рад/с
|
p2,
рад/с
|
p1Вр, рад/с
|
p2Вр, рад/с
|
|
Расчет
(пункт 5)
|
339,605
|
339,47
|
435,992
|
-
|
-
|
|
метод
Ритца:
2
базисные функции
|
339,566
|
339,47
|
435,992
|
339,592
|
2727
|
|
метод
Ритца:
3
базисные функции
|
338,289
|
338,289
|
433,534
|
338,288
|
2579
|
|
МНП
|
332,761
|
332,359
|
432,984
|
332,678
|
2432
|
Таблица 9
|
Метод
|
fкр1, Гц
|
f1, Гц
|
f2, Гц
|
f1Вр, Гц
|
f2Вр, Гц
|
|
Расчет
(пункт 5)
|
54,077
|
54,056
|
69,425
|
-
|
-
|
|
метод
Ритца:
2
базисные функции
|
54,071
|
54,056
|
69,425
|
54,075
|
|
метод
Ритца:
3
базисные функции
|
53,868
|
53,868
|
69,034
|
53,868
|
410,669
|
|
МНП
|
52,987
|
52,923
|
68,946
|
52,974
|
387,261
|
Исходя из анализа полученных форм колебаний и
частот ротора, можно сделать вывод о том, что на рабочей частоте форма изгиба
ротора не является строго прямолинейной и, следовательно, ротор не является
абсолютно жестким, но его прогибы незначительны по сравнению с перемещениями,
вызванными осадкой опор. Таким образом, полученные оценки параметров
упруго-демпферных опор можно считать корректными.
Список используемой
литературы
1. Пановко
Я.Г. Введение в теорию механических колебаний. - М.: Наука, 1980.
2. Слива
О. К., Ковадло А. А. Анализ динамики ротора транспортной турбины: Учебное
пособие к курсовому проекту по курсу «Динамика машин». - Челябинск: ЧПИ, 1989.
- 33с.