Механика контактного взаимодействия

Механика контактного взаимодействия

Реферат

Механика контактного взаимодействия

Введение

механика контактный шероховатость упругий

Механика контактного взаимодействия является основополагающей инженерной дисциплиной, чрезвычайно полезной при проектировании надёжного и энергосберегающего оборудования. Она будет полезна при решении многих контактных задач, например колесо-рельс, при расчёте муфт, тормозов, шин, подшипников скольжения и качения, передач зубчатыми колесами, шарниров, уплотнений; электрических контактах и др. Она охватывает широкий спектр задач, начиная от расчётов прочности элементов сопряжения трибосистемы с учётом смазывающей среды и строения материала и заканчивая применением в микро- и наносистемах.

Классическая механика контактных взаимодействий связана прежде всего с именем Генриха Герца. В 1882 году Герц решил задачу о контакте двух упругих тел с искривлёнными поверхностями. Этот классический результат и сегодня лежит в основе механики контактного взаимодействия.

1. Классические задачи механики контактного взаимодействия

.        Контакт между шаром и упругим полупространством

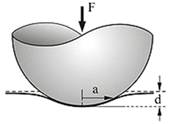
Твёрдый шар радиуса R вдавливается в упругое полупространство на глубину d (глубина проникновения), образуя область контакта радиуса

.

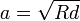Необходимая для этого сила равна

,

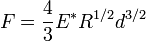где ;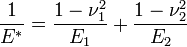

Здесь E1, E2 - модули упругости; ν1, ν2 - коэффициенты Пуассона обоих тел.

2.      Контакт между двумя шарами

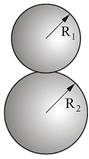
При контакте двух шаров с радиусами R1 и R2 эти уравнения справедливы соответственно для радиуса R

 .

Распределение давления в площади контакта определяется по формуле

с максимальным давлением в центре

.

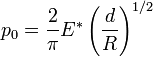Максимальное касательное напряжение достигается под поверхностью, для ν = 0,33 при .

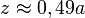3.      Контакт между двумя скрещивающимися цилиндрами с одинаковыми радиусами R

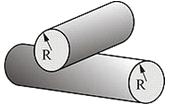
Контакт между двумя скрещенными цилиндрами с одинаковыми радиусами эквивалентен контакту между шаром радиусом R и плоскостью (см. выше).

4.      Контакт между твердым цилиндрическим индентором и упругим полупространством

Если твердый цилиндр радиусом a вдавливается в упругое полупространство, тo давление распределяется следующим образом:

,

причем

.

Связь между глубиной проникновения и нормальной силой определяется

.

5.      Контакт между твердым коническим индентором и упругим полупространством

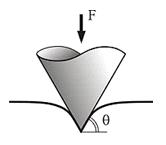
При индентировании упругого полупространства твердым конусообразным индентером глубина проникновения и радиус контакта определяются следующим соотношением:

.

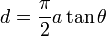Здесь θ − угол между горизонталью и боковой плоскостью конуса.

Распределение давления определяется формулой

 .

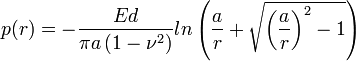Напряжение в вершине конуса (в центре области контакта) изменяется по логарифмическому закону. Суммарная сила рассчитывается как

 .

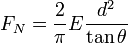6.      Контакт между двумя цилиндрами с параллельными осями

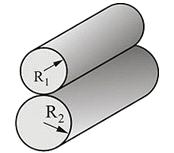
В случае контакта между двумя упругими цилиндрами с параллельными осями сила прямо пропорциональна глубине проникновения

.

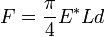Радиус кривизны в этом соотношении вообще не присутствует. Полуширина контакта определяется следующим отношением

,

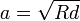с  ,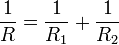

как и в случае контакта между двумя шарами.

Максимальное давление равно

.

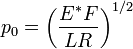7.      Контакт между шероховатыми поверхностями

Когда два тела с шероховатыми поверхностями взаимодействуют друг с другом, то реальная площадь контакта A намного меньше, чем геометрическая площадь A0. При контакте между плоскостью со случайно распределенной шероховатостью и упругим полупространством реальная площадь контакта пропорциональна нормальной силе F и определяется следующим приближенным уравнением:

.

При этом Rq − среднеквадратичное значение неровности шероховатой поверхности и 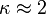. Среднее давление в реальной площади контакта

рассчитывается в хорошем приближении как половина модуля упругости E *, умноженная на среднеквадратичное значение неровности профиля поверхности Rq. Если это давление больше твердости HB материала и таким образом

то микронеровности находятся полностью в пластичном состоянии.

Для ψ <2/3 поверхность при контакте деформируется только упруго. Величина ψ была введена Гринвудом и Вильямсоном и носит название индекса пластичности.

. Учет шероховатости

На основании анализа экспериментальных данных и аналитических методов расчета параметров контактирования сферы с полупространством с учетом наличия шероховатого слоя был сделан вывод о том, что расчетные параметры зависят не столько от деформации шероховатого слоя, сколько от деформации отдельных неровностей.

При разработке модели контактирования сферического тела с шероховатой поверхностью учитывались полученные ранее результаты:

–       при малых нагрузках давление для шероховатой поверхности меньше рассчитанного по теории Г. Герца и распределяется по большей площади (Дж. Гринвуд, Дж. Вильямсон);

–       применение широко используемой модели шероховатой поверхности в виде ансамбля тел правильной геометрической формы, вершины высот которых подчиняются определенному закону распределения, приводит к значительным ошибкам при оценке параметров контактирования, особенно при малых нагрузках (Н.Б. Демкин);

–       отсутствуют пригодные для расчета параметров контактирования простые выражения и не достаточно развита экспериментальная база.

В данной работе предлагается подход, основанный на фрактальных представлениях о шероховатой поверхности как о геометрическом объекте с дробной размерностью.

Модуль упругости шероховатого слоя (а не материала, из которого состоит деталь и, соответственно, шероховатый слой) Eeff, являясь величиной переменной, определяется зависимостью:

, (1)

где Е0 - модуль упругости материала; ε - относительная деформация неровностей шероховатого слоя; ζ - константа (ζ = 1); D - фрактальная размерность профиля шероховатой поверхности.

Действительно, относительное сближение характеризует в определенном смысле распределение материала по высоте шероховатого слоя и, таким образом, эффективный модуль характеризует особенности пористого слоя. При ε = 1 этот пористый слой вырождается в сплошной материал со своим модулем упругости.

Полагаем, что число пятен касания пропорционально размерам контурной площади, имеющей радиус ас:

.

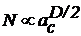Перепишем это выражение в виде

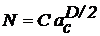. (2)

Найдем коэффициент пропорциональности С. Пусть N = 1, тогда ас=(Smax / π)1/2, где Smax - площадь одного пятна контакта. Откуда

 и .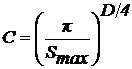

Подставив полученное значение С в уравнение (2), получим:

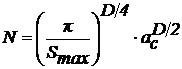. (3)

Полагаем, что кумулятивное распределение пятен контакта с площадью, большей s, подчиняется следующему закону

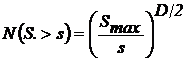. (4)

Дифференциальное (по модулю) распределение числа пятен определяется выражением

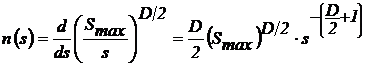. (5)

Выражение (5) позволяет найти фактическую площадь контакта

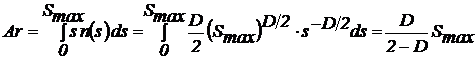. (6)

Полученный результат показывает, что фактическая площадь контакта зависит от структуры поверхностного слоя, определяемой фрактальной размерностью и максимальной площадью отдельного пятна касания, расположенного в центре контурной площади. Таким образом, для оценки параметров контактирования необходимо знать деформацию отдельной неровности, а не всего шероховатого слоя. Кумулятивное распределение (4) не зависит от состояния пятен контакта. Оно справедливо, когда пятна касания могут находиться в упругом, упругопластическом и пластическом состояниях. Наличие пластических деформаций определяет эффект приспосабливаемости шероховатого слоя к внешнему воздействию. Данный эффект частично проявляется в выравнивании давления на площади касания и увеличении контурной площади. Кроме того, пластическое деформирование многовершинных выступов приводит к упругому состоянию этих выступов при небольшом числе повторных нагружений, если нагрузка не превышает первоначального значения.

По аналогии с выражением (4) запишем интегральную функцию распределения площадей пятен контакта в виде

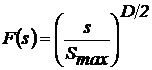. (7)

Дифференциальная форма записи выражения (7) представляется следующим выражением:

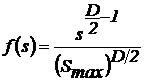. (8)

Тогда математическое ожидание площади контакта определяется следующим выражением:

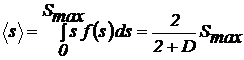. (9)

Так как фактическая площадь контакта равна

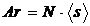
и, учитывая выражения (3), (6), (9), запишем:

.

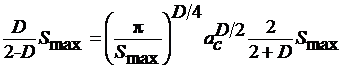Откуда

. (10)

Считая, что фрактальная размерность профиля шероховатой поверхности (1 < D < 2) является величиной постоянной, можно сделать вывод о том, что радиус контурной площади контакта зависит только от площади отдельной максимально деформированной неровности.

Определим Smax из известного выражения

,

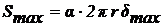где α - коэффициент, равный 1 для пластического состояния контакта сферического тела с гладким полупространством, и α = 0,5 - для упругого; r - радиус закругления вершины неровности; δmax - деформация неровности.

Положим, что радиус круговой (контурной) площади ас определяется модифицированной формулой Г. Герца

. (11)

Тогда, подставив выражение (1) в формулу (11), получим:

. (12)

Приравняв правые части выражений (10) и (12) и решая полученное равенство относительно деформации максимально нагруженной неровности, запишем:

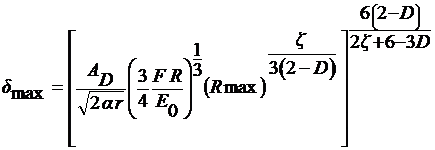. (13)

Здесь 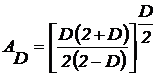, r - радиус закругления вершины неровности.

При выводе уравнения (13) учитывалось, что относительная деформация наиболее нагруженной неровности равна

,

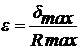где δmax - наибольшая деформация неровности; Rmax - наибольшая высота профиля.

Для гауссовской поверхности фрактальная размерность профиля D=1,5 и при ς = 1 выражение (13) имеет вид:

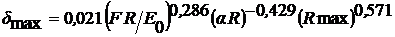. (14)

Считая деформацию неровностей и осадку их основания аддитивными величинами, запишем:

Тогда суммарное сближение найдем из следующего соотношения:

. (15)

Таким образом, полученные выражения позволяют найти основные параметры контактирования сферического тела с полупространством с учетом шероховатости: радиус контурной площади определялся по выражениям (12) и (13), сближение − по формуле (15).

. Эксперимент

Испытания проводились на установке для исследования контактной жесткости неподвижных стыков. Точность измерения контактных деформаций составляла 0,1-0,5 мкм.

Схема испытаний приведена на рис. 1. Методика проведения эксперимента предусматривала плавное нагружение и разгрузку образцов, имеющих определенную шероховатость. Между образцами устанавливались три шарика диаметром 2R=2,3 мм.

Деформации и нагрузка измерялись непрерывно.

Были исследованы образцы, имеющие следующие параметры шероховатости (табл. 1).

При этом верхний и нижний образцы имели одинаковые параметры шероховатости. Материал образцов - сталь 45, термообработка - улучшение (HB 240). Результаты испытаний приведены в табл. 2.

Здесь же представлено сравнение экспериментальных данных с расчетными значениями, полученными на основе предлагаемого подхода.

Таблица 1

Параметры шероховатости

Таблица 2

Сближение сферического тела с шероховатой поверхностью

Сравнение экспериментальных и расчетных данных показало их удовлетворительное соответствие, что говорит о применимости рассмотренного подхода к оценке параметров контактирования сферических тел с учетом шероховатости.

На рис. 2 показана зависимость отношения ас/ас (Н) контурной площади с учетом шероховатости к площади, рассчитанной по теории Г. Герца, от фрактальной размерности.

Как видно на рис. 2, с увеличением фрактальной размерности, отражающей сложность структуры профиля шероховатой поверхности, растет величина отношения контурной площади контакта к площади, рассчитанной для гладких поверхностей по теории Г. Герца.

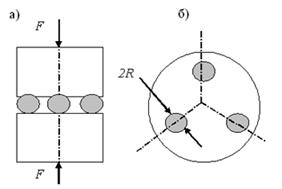
Рис. 1. Схема испытания: а - нагружение; б - расположение шариков между испытуемыми образцами

Приведенная зависимость (рис. 2) подтверждает факт увеличения площади касания сферического тела с шероховатой поверхностью по сравнению с площадью, рассчитанной по теории Г. Герца.

При оценке фактической площади касания необходимо учитывать верхний предел, равный отношению нагрузки к твердости по Бринеллю более мягкого элемента.

Площадь контурной площади с учетом шероховатости найдем, используя формулу (10):

 (16)

Рис. 2. Зависимость отношения радиуса контурной площади с учетом шероховатости к радиусу герцевской площади от фрактальной размерности D

Для оценки отношения фактической площади контакта к контурной разделим выражение (7.6) на правую часть уравнения (16)

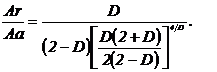 (17)

На рис. 3 показана зависимость отношения фактической площади контакта Ar к контурной площади Ас от фрактальной размерности D. С увеличением фрактальной размерности (увеличением шероховатости) отношение Ar/ Ас уменьшается.

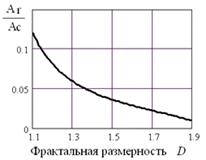
Рис. 3. Зависимость отношения фактической площади контакта Ar к контурной площади Ас от фрактальной размерности

Таким образом, пластичность материала рассматривается не только как свойство (физико-механический фактор) материала, но и как носитель эффекта приспосабливаемости дискретного множественного контакта к внешнему воздействию. Этот эффект проявляется в некотором выравнивании давлений на контурной площади касания.

Список литературы

1.      Мандельброт Б. Фрактальная геометрия природы / Б. Мандельброт. - М.: Институт компьютерных исследований, 2002. - 656 с.

2.      Воронин Н.А. Закономерности контактного взаимодействия твердых топокомпозиционных материалов с жестким сферическим штампом / Н.А. Воронин // Трение и смазка в машинах и механизмах. - 2007. - №5. - С. 3-8.

.        Иванов А.С. Нормальная, угловая и касательная контактные жесткости плоского стыка / А.С. Иванов // Вестник машиностроения. - 2007. - №1. С. 34-37.

.        Тихомиров В.П. Контактное взаимодействие шара с шероховатой поверхностью / Трение и смазка в машинах и механизмах. - 2008. - №9. -С. 3-

.        Демкин Н.Б. Контакт шероховатых волнистых поверхностей с учетом взаимного влияния неровностей / Н.Б. Демкин, С.В. Удалов, В.А. Алексеев [и др.] // Трение и износ. - 2008. - Т.29. - №3. - С. 231-237.

.        Буланов Э.А. Контактная задача для шероховатых поверхностей / Э.А. Буланов // Техника машиностроения. - 2009. - №1(69). - С. 36-41.

.        Ланков, А.А. Вероятность упругих и пластических деформаций при сжатии металлических шероховатых поверхностей / А.А. Лакков // Трение и смазка в машинах и механизмах. - 2009. - №3. - С. 3-5.

8.      Greenwood J.A. Contact of nominally flat surfaces / J.A. Greenwood, J.B.P. Williamson // Proc. R. Soc., Series A. - 196 - V. 295. - №1422. - P. 300-319.

9.      Маджумдар М. Фрактальная модель упруго-пластического контакта шероховатых поверхностей / М. Маджумдар, Б. Бхушан // Современное машиностроение. − 1991. − № − С. 11-23.

10.    Varadi K. Evaluation of the real contact areas, pressure distributions and contact temperatures during sliding contact between real metal surfaces / K. Varodi, Z. Neder, K. Friedrich // Wear. - 199 - 200. - P. 55-62.