Устойчивость нелинейной системы автоматического управления

Устойчивость нелинейной системы автоматического управления

Введение

Анализ и расчет систем управления с обратной связью теснейшим образом связаны с динамикой. Каждый элемент в системе должен рассматриваться как динамический, причем его динамические характеристики задаются либо численно, либо графически, либо в форме уравнения. Довольно часто динамику элементов систем автоматического управления удается описать линейными дифференциальными уравнениями с постоянными коэффициентами. В этом случае работа системы может анализировать посредством хорошо развитого аппарата линейной теории следящих систем.

Фактически можно утверждать, что не существует полностью линейных физических систем или, наоборот, что все физические системы нелинейные. Хорошо известно, что анализ и расчеты, выполненные на основе линейной теории, позволяют создавать совершенные устройства, фактическая работа которых в большей степени согласуется с данными, полученными их линейных расчетов. С другой стороны, для инженера-автоматчика все более очевидно, что ограничение аппарата анализа методами линейной теории не дает удовлетворительного результата в случае высококачественных систем, предназначенных для работ в широком диапазоне рабочих условий. Линейная теория часто полезна на стадии начального изучения; распространенной является практика, при которой предварительный анализ и расчет проводится в линейном плане, а в процессе уточненного расчета рассматривается влияние существенных нелинейностей.

1. Составление уравнений элементов САУ

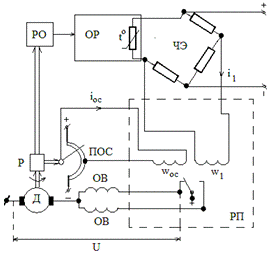
Рис. 1. Система автоматического управления температурой в сушильной камере

В состав нелинейной САУ входят наряду с объектом регулирования (ОР) следующие технические средства автоматизации (см. рис. 1): ЧЭ - чувствительный элемент (измерительный мост с термометром сопротивления), РП - поляризованное реле (усилитель), Д - двигатель, ОВ - обмотки возбуждения двигателя, Р - редуктор, РО - регулирующий орган (заслонка), ПОС - потенциометр обратной связи.

Объектом регулирования (ОР) в рассматриваемой САУ является сушильная камера. Регулируемый параметр - температура греющего агента θ, которая устанавливается поворачивающейся заслонкой (РО), приводимой в движение исполнительным механизмом (электродвигателем Д с редуктором Р). Регулирующий орган - заслонка - изменяет соотношение между количеством холодного воздуха и горячего газа.

Температура теплоносителя - смеси воздуха и газа - измеряется термометром сопротивления, являющимся в системе чувствительны элементом. Измерительный мост является неуравновешенным. Равновесие моста характеризуется отсутствием напряжения и тока на измерительной диагонали. Всякое изменение сопротивления ЧЭ выводит мост из равновесия, т. е. по диагонали моста потечет ток.

Таблица 1. Исходные данные системы

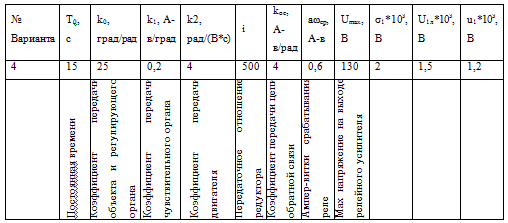
Для заданной принципиальной схеме составим дифференциальные уравнения звеньев системы.

Уравнение регулируемого объекта:

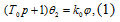
где 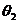 - фактическое значение температуры объекта, 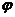 - угол поворота регулирующего органа.

Уравнение чувствительного элемента:

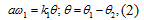
где  - заданное значение температуры объекта, 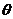 - ошибка рассогласования значений.

Уравнение релейного усиления:

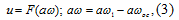
где 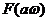 - нелинейная функция, заданная статической характеристикой (см. рис. 2).

Уравнение двигателя постоянного тока:

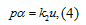
где 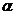 - угол поворота вала двигателя

Уравнение редуктора:

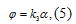
где  - коэффициент передачи редуктора

Уравнение цепи обратной связи:

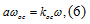
где 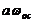 - ампер-витки обмотки обратной связи.

2. Составление структурно-математической схемы САУ

Структурно-математическая схема системы автоматического регулирования температуры изображена на рис. 3.

В соответствии со структурно-математической схемой дифференциальное уравнение линейной части системы можно записать в следующем виде:

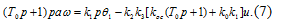
Подставим в уравнение (7) численные значения параметров и получим

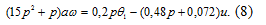
Уравнение линейной части (7) дополняется уравнением нелинейного звена (3).

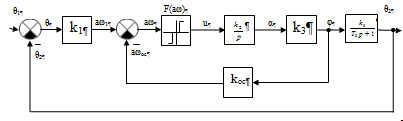
Рис. 2. Структурно-математическая схема САУ температуры

3. Исследование устойчивости САУ температуры в сушильной камере

.1 Исследование устойчивости САУ методом фазового пространства

Исследуем устойчивость САУ температуры методом фазового пространства при отключенной местной обратной связи (см. рис. 1).

В режиме стабилизации температуры можно принять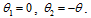

При этом уравнения звеньев системы можно записать в следующем виде:

1)  Уравнение объекта регулирования:

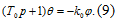
2)  Уравнение чувствительного элемента:

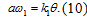
3)      Уравнение усилителя (при ):

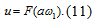
4)  Уравнение двигателя постоянного тока:

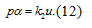
5)  Уравнение редуктора:

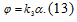
Учитывая, что ток в обмотке поляризованного реле пропорционален отклонению температуры 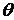, а скорость отклонения регулирующего органа 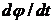 пропорциональна напряжению , в качестве входной величины нелинейного звена (поляризованного реле) можно принять 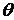, а в качестве выходной - величину 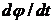 (см. рис. 4).

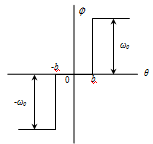
Рис. 3. Статическая характеристика нелинейного звена

На этом рисунке:

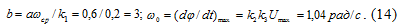
В соответствии с уравнением объекта регулирования (9) и статической характеристикой нелинейного звена (см. рис. 4) уравнения всей системы можно записать в следующем виде:

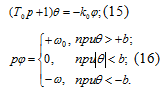
Решив уравнения (15) и (16) совместно, получим:

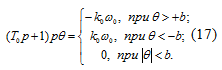
Рассмотрим уравнение (17) при :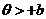

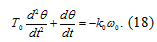
Введем обозначения 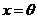,  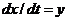и уравнение (18) перепишем следующим образом:

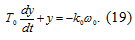
Для исключения времени из уравнения (19) разделим его на 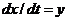. Получим:

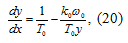
или после разделения переменных:

Проинтегрировав уравнение (21), получим уравнение фазовых траекторий:

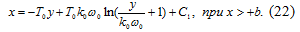
Проделав аналогичные операции с уравнением (17) для остальных условий получим:

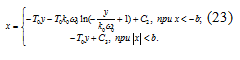
Подставив в уравнения (22) и (23) численные значения параметров, получим:

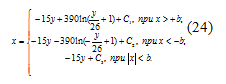
По уравнению (24) построим фазовую траекторию всей системы при соответствующих начальных условиях 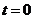, , 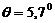 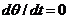((Приложение 1).

Составим таблицы для уравнения (24).

1) ,

Составим таблицу:

2) ,

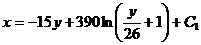C₁=3,047

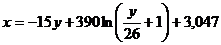
Составим таблицу:

3) ,

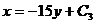C₃=9

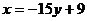
Составим таблицу:

4) ,

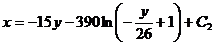С₂=-3,724

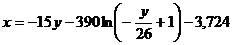
Составим таблицу:

5)

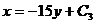
C₃=-19

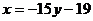
Составим таблицу:

6)

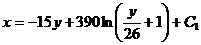
С₁=4,401

Составим таблицу:

3.2 Исследование устойчивости САУ прямым методом Ляпунова

Исследуем устойчивость САУ температуры (см. рис. 1) прямым методом Ляпунова.

В режиме стабилизации температуры можно принять , .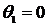

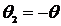Согласно структурно-математической схеме (см. рис.3) САУ температуры описывается следующими дифференциальными и алгебраическими уравнениями:

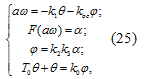
если коэффициент усиления 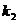 интегрирующего звена относительно к следующему пропорциональному звену.

Приведем систему (25) к нормальному виду. Для этого введем обозначения:

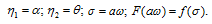
Получим:

Общий вид системы нелинейных уравнений 2-го порядка заданных в нормальной форме, представлен ниже:

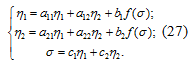
Откуда следует:

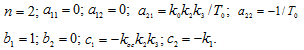
Запишем уравнение (26) в канонической форме. Для этого из коэффициентов уравнения составим определитель:

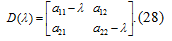
Для нашего случая определитель имеет вид:

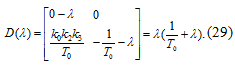
Определим корни характеристического уравнения .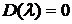

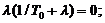
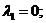
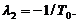
Ввиду того, что в характеристическом уравнении имеется один нулевой корень, канонические уравнения записываются в следующем виде:

Определим постоянные 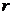,  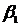и :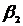

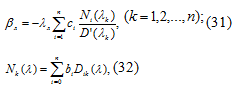
где 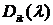 обозначает алгебраическое дополнение элемента 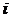-ой строки и 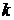-го столбца определителя .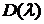

По формуле (32) определим:

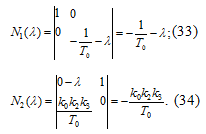
Определим :

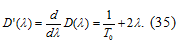
Поскольку 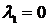, то в соответствии с уравнением (31) .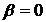

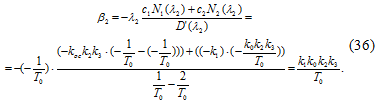
Для класса нелинейных систем, к которому принадлежит рассматриваемая система, достаточные условия устойчивости имеют вид:

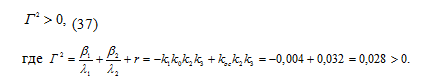
Условие (37) приводит к следующему достаточному условию устойчивости рассматриваемой системы:

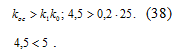
Вывод: Данная система по критерию Ляпунова неустойчивая.

3.3 Исследование устойчивости САУ частотным методом Попова

В режиме стабилизации температуры можно принять: .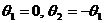

Коэффициент усиления линейной части системы равен:

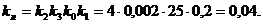
Коэффициент усиления нелинейного звена системы равен:

.

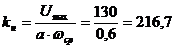Коэффициент усиления линейной части системы и нелинейного звена 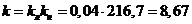 условно отнесем к нелинейному звену.

Необходимо определить, при каких значениях k система будет абсолютно устойчива, если характеристика нелинейного звена расположена в секторе (0, k)

Частотная передаточная функция линейной части системы имеет вид:

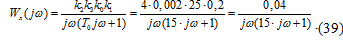
Её вещественная и мнимая части соответственно равны:

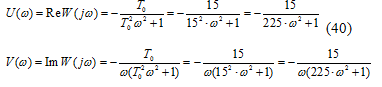
Введем некоторые функции 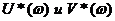 следующим образом:

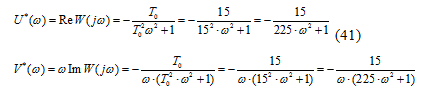
По данным выражениям построим характеристику 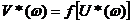 и через точку (-1/k, j0) проведем прямую Попова так, чтобы построенная характеристика целиком лежала справа от этой прямой.

Уравнение прямой Попова, коэффициенты которого получены путем подбора, приведено ниже:

1(ω) = 1∙U(ω) + 0,115

Таблица 2

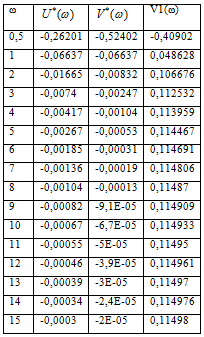
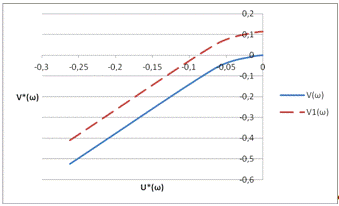
Рис. 4. Характеристика V*(ω) = f [U*(ω)] (сплошная линия) и прямая Попова (пунктирная линия)

Расчетное значение разомкнутой системы равно:

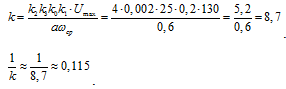
Система абсолютно устойчива для всех нелинейных характеристик, лежащих в секторе 0<k<8,7 и, в частности, для характеристики релейного типа.

3.4 Исследование устойчивости САУ алгебраическим методом

Исследуем устойчивость САУ температуры и определим амплитуду и частоту колебаний алгебраическим методом. По структурно-математической схеме (см. рис. 1) определяем дифференциальное уравнение линейной части системы при отключенной местной обратной связи и :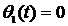

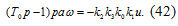
Для нелинейного звена запишем гармонически линеаризованное выражение:

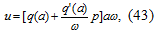
где для нелинейности (см. рис. 2):

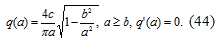
Подставляя значение u из уравнения (43) в уравнение (42), получим линеаризованное уравнение замкнутой нелинейной системы:

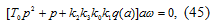
где 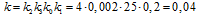 - коэффициент усиления линейной части системы.

Этому дифференциальному уравнению соответствует характеристическое уравнение:

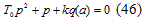
Условие существования в уравнении (45) периодического решения:

будем отыскивать с помощью критерия Михайлова. Для этого в характеристический полином:

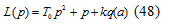
подставим 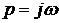, выделим вещественную и мнимую части и приравняем их к нулю:

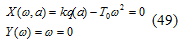
Из второго уравнения системы (49) найдем искомую частоту периодического решения .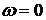

Подставим это решение в первое уравнение (49) и найдем выражение, связывающее амплитуду периодического решения 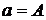 с параметрами системы:

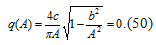
Отсюда получим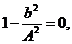

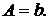
Для исследования устойчивости найденного периодического решения воспользуемся приближенным аналитическим условием, согласно которому периодическое решение устойчиво, если выполняется неравенство:

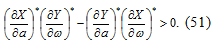
Из выражений (49) находим:

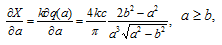
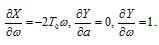
Подставим выражение для частных производных в (49) и одновременно произведем замену .

Получим условие устойчивости периодического решения в виде:

Получаем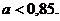

В данном случае условие существования периодического решения имеет вид: . Следовательно, автоколебания отсутствуют, состояние равновесия устойчиво.

Исследуем устойчивость САУ температуры и определим амплитуду и частоту колебаний методом гармонической линеаризации (см. рис. 1) при отключенной местной обратной связи и .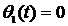

Структурно-математическая схема САУ температуры представлена на рис. 8. Статическая характеристика нелинейного звена изображена на рис. 2.

Введем следующие обозначения:

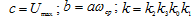 - коэффициент усиления линейной части системы.

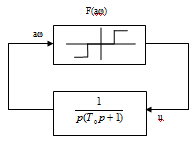
Рис. 5. Структурно-математическая схема САУ температуры

Построим амплитудно-фазовую частотную характеристику линейной части системы  и годограф гармонически линеаризованного нелинейного звена 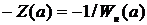. Согласно структурно-математической схеме частотная передаточная функция линейной части системы равна:

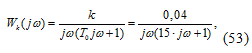
ее модуль:

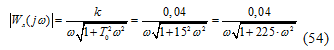
и фаза:

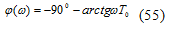
Ее вещественная и мнимая части соответственно равны:

Задаваясь значениями 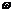от 0 до 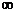, по формулам (56) и (57) строим амплитудно-фазовую характеристику линейной части системы 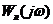(см. рис. 9) :

Таблица 3

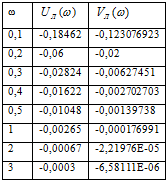
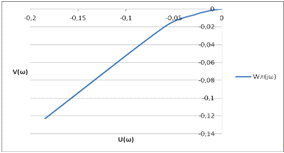
Рис. 6. АФЧХ линейной части системы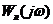

Гармонически линеаризованная передаточная функция нелинейного звена равна:

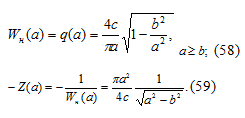
После подстановки численных значений параметров нелинейного звена получим:

.

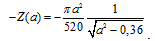Задаемся значениями a от a = b = 0,7 до ∞ и строим годограф нелинейного звена 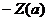 (см. рис. 10):

Таблица 4

В данном случае этот годограф совпадает с отрицательной вещественной полуосью и имеет две ветви:

Рис. 7. Частотные характеристики линейной части системы и нелинейного звена

Минимальное значение модуля функции :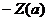

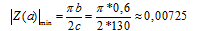
достигается при 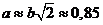. Годографы  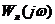и 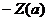 не пересекаются. Это означает, что состояние равновесие системы устойчиво, автоколебания отсутствуют.

3.6 Исследование устойчивости САУ частотным методом

Исследуем переходный процесс в САУ температуры частотным методом.

Коэффициент затухания ξ и частоту колебаний ω переходного процесса в САУ температуры будем отыскивать путем решения гармонически линеаризованного уравнения:

где 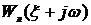 получается из передаточной функции линейной части системы 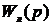 подстановкой , а гармонически линеаризованная передаточная функция нелинейного звена 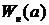 - подстановкой  в выражение:

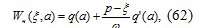
в результате получаем:

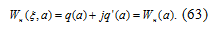
Уравнение (60) будем решать графически. Для этого в передаточной функции линейной части системы:

произведем подстановку . Получим:

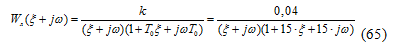
Модуль этой функции:

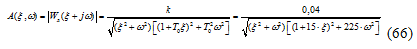
и фаза:

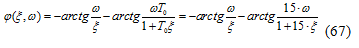
Подставив в выражение (66) и (67) приведенные в исходных данных значения параметров и, задаваясь различными постоянными значениями показателя затухания ξ, построим серию кривых 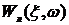 как функции от частоты колебаний ω при ξ = const (см. рис. 10).

На этом же графике нанесем обратную амплитудно-фазовую характеристику нелинейного звена 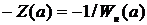 при заданных параметрах b и c. Для нелинейной характеристики релейного типа с зоной нечувствительности имеем:

Отсюда:

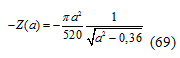
Рис. 8. Частотные характеристики линейной части системы и нелинейного звена САУ температуры

Как видно из графиков, точка пересечения годографов линейной части системы и нелинейного звена отсутствует. Следовательно, САУ температуры находится в устойчивом равновесном состоянии.

3.7 Исследование САУ температуры сушильной камеры в среде Simulink

Согласно рисунку 3, в программном продукте MATLAB в среде Simulink составляется блок-схема математической модели САУ температуры сушильной камеры. После чего проводится анализ САУ: строятся переходная характеристика, ЛАХ и ЛФХ, АФЧХ; определяются характеристики переходного процесса, запасы по фазе и амплитуде.

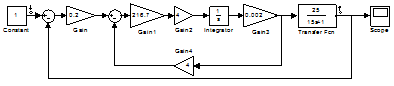
Рис. 9. Структурно-математическая схема системы автоматического регулирования температуры в среде Simulink

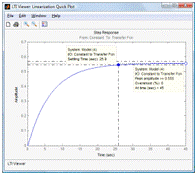
Рис. 10. Переходная (временная) характеристика системы автоматического регулирования температуры

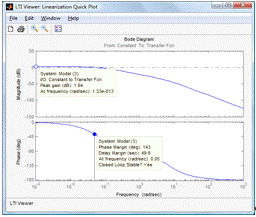
Рис. 11. ЛАХ и ЛФХ нелинейной САУ

Рис. 12. АФЧХ нелинейной САУ

автоматический управление температура сушильный

Заключение

В данном курсовом проекте я исследовал устойчивость нелинейной САУ. Объектом регулирования (ОР) в рассматриваемой САУ является сушильная камера. Регулируемый параметр - температура греющего агента θ, которая устанавливается поворачивающейся заслонкой (РО), приводимой в движение исполнительным механизмом (электродвигателем Д с редуктором Р). Регулирующий орган - заслонка - изменяет соотношение между количеством холодного воздуха и горячего газа.

В процессе выполнения курсовой работы произвел исследование устойчивости и режима автоколебаний нелинейной САУ температуры в сушильной камере с использованием следующих методов:

фазовых траекторий;

прямым методом А.М. Ляпунова;

частотным методом В.М.Попова;

алгебраическим методом;

гармонической реализации;

частотным методом;

с помощью Simulink.

Получили следующие характеристики:

) Время переходного процесса - 25,9 сек;

) Запас по фазе - 143 рад.

) Запас по амплитуде - 49,8 с.

) Частота - 0,05 рад/с.

И сделали вывод, что САУ температуры находится в устойчивом равновесном состоянии, автоколебания отсутствуют.

По разработанной структурно-функционально-математической схеме определил устойчивость нелинейной САУ температуры в сушильной камере при помощи программного пакета Simulink.

Список использованной литературы

1. Щербаков В.С. Конспект лекций по ТАУ

. Щербаков В.С., Сухарев Р.Ю. «Методические указания по выполнению курсовых работ» - 2012г.

. Александров Ю.В. «Основы автоматики и автоматизация производственных процессов в дорожном строительстве». - 1974 г.

. Герман-Галкин С.Г. «Компьютерное моделирование полупроводниковых систем MatLab 6.0»