Комп’ютеризовані системи цифрової обробки сигналів
Міністерство
освіти і науки України
Національний
університет “Львівська політехніка
Кафедра АСУ
Лабораторна
робота з дисципліни:
“Комп’ютеризовані
системи цифрової обробки сигналів”
на
тему: Ряд Фур’є
Львів - 2015
Мета: Вивчити спектри найпростіших сигналів.
Теоретичні відомості:
В ряд Фур’є можуть бути розкладені періодичні
сигнали. При цьому вони представляються у вигляді суми гармонічних функцій або
комплексних експонент з частотами, що утворюють арифметичну прогресію. Для того
щоб такий розклад існував, фрагмент сигналу довжиною в один період повинен
задовольняти умови Дирихлє:
Не повинно бути розривів другого роду (з
відгалуженнями функцій, що уходять в нескінченність);
Число розривів першого роду (скачків) повинно
бути скінченним;
Число екстремумів повинно бути скінченним (в
якості приклада функції, яка на останньому інтервалі має нескінченне число
екстремумів, можна привести sin(1/x) в околі нуля).
В залежності від конкретної форми базисних
функцій розрізняють декілька форм запису ряду Фур’є.
Синусно-косинусна форма:
В цьому варіанті ряд Фур’є має наступний вигляд:
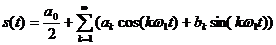(2.1)
Тут 
- кругова
частота, що відповідає періоду повторення сигналу рівному T. Частоти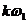
, що входять
до формули і кратні круговій частоті, називаються гармоніки та нумеруються в
залежності від індексу k; частота 
називається k - ою гармонікою
сигналу. Коефіцієнти ряду 
та 
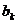розраховуються
за формулами:
,
.
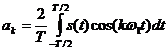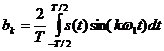Константа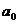 
розраховується
за загальною формулою для . Заради
цієї загальності і введена трохи дивна на перший погляд форма запису постійного
доданку (з діленням на два). Сам же доданок представляє собою середнє значення
сигналу на періоді:
.
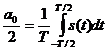Зауваження: Межі інтегрування
не обов’язково повинні бути такими, як в наведених вище формулах (від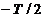 
до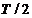 
).
Інтегрування може виконуватися за будь-яким інтервалом довжиною Т - результат
від цього не зміниться. Конкретні межі вибираються для зручності обчислення;
наприклад, може здатися зручніше виконати інтегрування від 0 до Т чи від -Т до
0.
Якщо 
є парною
функцією, то всі 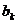будуть
рівними нулю і в формулі ряду Фур’є будуть присутні тільки косинусні складові.
Якщо ж є непарною
функцією, нулю будуть дорівнювати, навпаки, косинусні коефіцієнти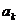 
і в формулі
залишаться тільки синусні складові.
Дійсна форма:
Деяка незручність
синусно-косинусної форми ряду Фур’є полягає в тому, що для кожного значення
індексу додавання 
(тобто для
кожної гармоніки з частотою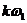 
) в формулах фігурують два доданки -
синус і косинус. Скориставшись формулами тригонометричних перетворень, суму цих
двох доданків можна трансформувати в косинус тієї ж частоти з іншою амплітудою
та деякою початковою фазою:
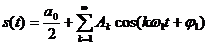(2.2)
Якщо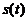
є парною
функцією фази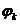 
можуть
приймати тільки значення 0 та 
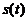, а якщо - функція
непарна, то можливі значення для фази рівні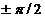 
.
Комплексна форма:
Дана форма представлення ряду
Фур’є найбільш часто використовується в радіотехніці. Вона одержується з
дійсної форми представлення косинуса у вигляді напівсуми комплексних експонент
(таке представлення витікає з формули Ейлера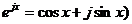 
:
.
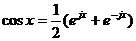Застосувавши дане
перетворення до дійсної форми ряду Фур’є, отримаємо суми комплексних експонент
з додатними та від’ємними показниками:
.
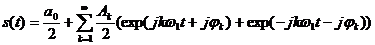А тепер будемо трактувати
експоненти зі знаком «мінус» в показнику як члени ряду з від’ємними номерами. В
рамках цього ж загального підходу постійна складова 
стане
членом ряду з нульовим номером. В результаті отримаємо комплексну форму запису
ряду Фур’є:
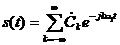(2.3)
Комплексні коефіцієнти ряду
пов’язані з амплітудами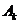 
і фазами 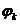, що
фігурують в дійсній формі запису ряду Фур’є (2.2), наступними неважкими
співвідношеннями:
,
, 
.
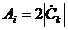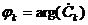Неважко виглядають і формули
зв’язку з коефіцієнтами 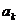та 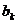синусно-косинусної
форми ряду Фур’є (2.1):
,
, 
.
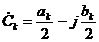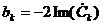Звідси зразу ж слідує формула
безпосереднього розрахунку коефіцієнтів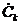 
ряду Фур’є в комплексній формі:
(2.4)
Якщо є парною
функцією, коефіцієнти ряду 
будуть тільки дійсними, а якщо - функція
непарна, коефіцієнти ряду виявляться тільки уявними.
Сукупність амплітуд гармонік
ряду Фур’є часто називають амплітудним спектром, а сукупність їх фаз - фазовим
спектром. Ці поняття не слід плутати з амплітудно- та фазочастотними
характеристиками, які відносяться не до сигналів, а до кіл.
Якщо аналізує мий сигнал є дійсним,
то його амплітудний та фазовий спектри володіють симетрією:
, 
, 
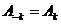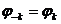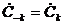
Завдання
. Аппроксимувати стандартний
прямокутний сигнал з частотою, що дорівнює номеру в групі (15), рядом Фур’є з
кількістю гармонік:
а) 2 гармоніки;
б) 4 гармоніки;
в) 8 гармоніки;
. Проробити ті самі
перетворення зі стандартним трикутним сигналом.
. Проробити ті самі
перетворення зі стандартним синусоїдальним сигналом
. В протоколі привести
отримані графіки та математичні залежності.
. Зробити висновки по
проробленій роботі.
Апроксимація стандартного
прямокутного сигналу(2)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=square(x);=1;=(1/T)*trapz(t,y);=
(2/T) * trapz(t, y .* cos(x));= (2/T) * trapz(t, y .* sin(x));= (2/T) *
trapz(t, y .* cos(2*x));= (2/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
фур’є ряд
апроксимація гармоніка
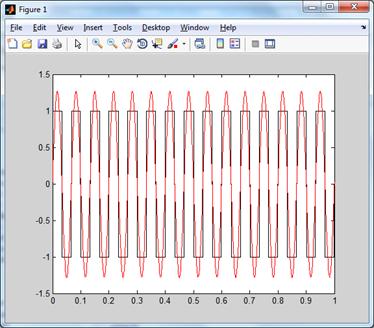
Рис. 1
Апроксимація стандартного
синусоїдального сигналу(2)
Текст програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=sin(x);=1;=(1/T)*trapz(t,y);=
(2/T) * trapz(t, y .* cos(x));= (2/T) * trapz(t, y .* cos(2*x));= (2/T) *
trapz(t, y .* sin(x));= (2/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
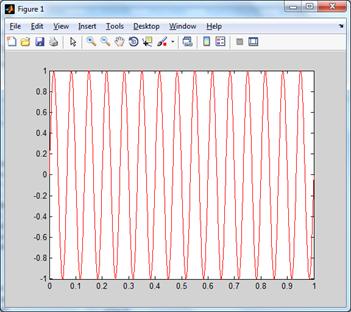
Рис. 2
Апроксимація стандартного
трикутного сигналу(2)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=sawtooth(x);=1;=(1/T)*trapz(t,y);=
(2/T) * trapz(t, y .* cos(x));= (2/T) * trapz(t, y .* cos(2*x));= (2/T) *
trapz(t, y .* sin(x));= (2/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black',
t,s4,'r')(t,y,'black', t,s4,'g')
Отриманий графік:
Рис. 3
гармоніки
Апроксимація стандартного
прямокутного сигналу(4)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=square(x);=1;=(1/T)*trapz(t,y);=
(4/T) * trapz(t, y .* cos(x));= (4/T) * trapz(t, y .* sin(x));= (4/T) *
trapz(t, y .* cos(2*x));= (4/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
Рис. 4
Апроксимація стандартного
синусоїдального сигналу(4)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=sin(x);=1;=(1/T)*trapz(t,y);= (4/T)
* trapz(t, y .* cos(x));= (4/T) * trapz(t, y .* cos(2*x));= (4/T) * trapz(t, y
.* sin(x));= (4/T) * trapz(t, y .* sin(2*x));= a0+ a1*cos(x)+b1*sin(x) +
a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
Рис. 5
гармонік
Апроксимація стандартного
прямокутного сигналу(8)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=square(x);=1;=(1/T)*trapz(t,y);=
(8/T) * trapz(t, y .* cos(x));= (8/T) * trapz(t, y .* sin(x));= (8/T) *
trapz(t, y .* cos(2*x));= (8/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
Рис. 6
Апроксимація стандартного
синусоїдального сигналу(8)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=sin(x);=1;=(1/T)*trapz(t,y);= (8/T)
* trapz(t, y .* cos(x));= (8/T) * trapz(t, y .* cos(2*x));= (8/T) * trapz(t, y
.* sin(x));= (8/T) * trapz(t, y .* sin(2*x));= a0+ a1*cos(x)+b1*sin(x) +
a2*cos(2*x)+b2*sin(2*x);(t,y,'black', t,s4,'r')
Отриманий графік:
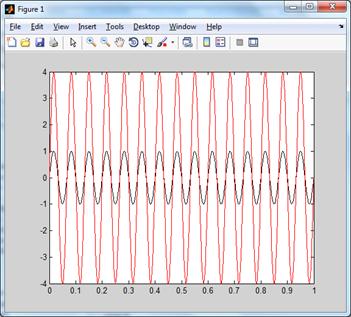
Рис. 7
Апроксимація стандартного
трикутного сигналу(8)
Текст
програми:=15;=1000;=0:1/fs:1;=2*pi*f;=w*t;=sawtooth(x);=1;=(1/T)*trapz(t,y);=
(8/T) * trapz(t, y .* cos(x));= (8/T) * trapz(t, y .* cos(2*x));= (8/T) *
trapz(t, y .* sin(x));= (8/T) * trapz(t, y .* sin(2*x));= a0+
a1*cos(x)+b1*sin(x) + a2*cos(2*x)+b2*sin(2*x);(t,y,'black',
t,s4,'r')(t,y,'black', t, s4,'g')
Отриманий графік:
Рис. 8
Висновок
На даній лабораторній роботі я
навчилася будувати спектр найпростіших сигналів, на прикладі прямокутного,
синусоїдального і трикутного, за допомогою ряду Фур’є. Побудувала графіки для
кожного з цих сигналів відповідно до індивідуального завдання.