Законы электродинамики в четырехмерном пространстве-времени
Реферат
ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ В
ЧЕТЫРЕХМЕРНОМ ПРОСТРАНСТВЕ-ВРЕМЕНИ
1. ЧЕТЫРЕХМЕРНОЕ ПРОСТРАНСТВО-ВРЕМЯ
Уравнения Максвелла в пустоте сводятся к уравнениям Д’Аламбера. В форме
Лоренца для потенциалов электромагнитного поля эти уравнения есть:
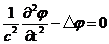 (1)
(1)
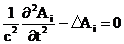
Система (1) в покомпонентной форме записи представляет собой четыре
независимых уравнения, причем каждое из них имеет вид:
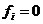 (2)
(2)
где
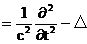 - оператор Д’Аламбера.
- оператор Д’Аламбера.
 -
некоторая функция координат и времени.
-
некоторая функция координат и времени.
Оператор
представляет собой квадратичную форму, инвариантную относительно координат и
времени. Так как уравнения (2) есть закон природы, они должны быть инвариантны
относительно выбора системы координат. Как известно, квадратичные формы могут
быть инвариантны относительно линейных преобразований координат. Таким образом,
возникает идея поиска координатных систем, преобразования которых оставляют
инвариантными квадратичную форму □.
Ранее линейные преобразования от одной системы координат к другой уже
встречались в нерелятивистской физике и имели форму преобразований Галилея
 (3)
(3)

Эти
преобразования зависят от шести параметров - трех пространственных углов Эйлера
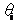 , трех компонент скорости
, трех компонент скорости 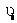 и оставляют инвариантным время
и оставляют инвариантным время 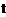 . Однако они нарушают инвариантность преобразования.
Необходимо так обобщить (3) на релятивистский случай, чтобы оставался
инвариантным. Описанное выше временное многообразие
. Однако они нарушают инвариантность преобразования.
Необходимо так обобщить (3) на релятивистский случай, чтобы оставался
инвариантным. Описанное выше временное многообразие 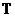 никак не зависит от пространственного многообразия.
Любым возможным обобщением (3) является такое линейное преобразование
координат, когда в формулу изменения каждой компоненты входят все четыре
величины - координаты и время. То есть это должно быть преобразование
четырехмерного пространственно-временного многообразия самого в себя. Поэтому
попытки найти четырехмерное преобразование, обобщающее преобразование Галилея
на релятивистские теории типа электродинамики с необходимостью приводят идее
четырехмерного пространственно-временного многообразия. Единство этого
многообразия отражено в преобразованиях, переводящих его само в себя
затрагивающих все координаты (три пространственных координаты и время). Таким
образом, применение к релятивистской физике (при скоростях волн и частиц
порядка скорости света “
никак не зависит от пространственного многообразия.
Любым возможным обобщением (3) является такое линейное преобразование
координат, когда в формулу изменения каждой компоненты входят все четыре
величины - координаты и время. То есть это должно быть преобразование
четырехмерного пространственно-временного многообразия самого в себя. Поэтому
попытки найти четырехмерное преобразование, обобщающее преобразование Галилея
на релятивистские теории типа электродинамики с необходимостью приводят идее
четырехмерного пространственно-временного многообразия. Единство этого
многообразия отражено в преобразованиях, переводящих его само в себя
затрагивающих все координаты (три пространственных координаты и время). Таким
образом, применение к релятивистской физике (при скоростях волн и частиц
порядка скорости света “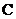 ”) простого математического следствия об
инвариантности квадратичной формы относительно линейных преобразований
координат приводит к возникновению глубокой физической идеи об описании
наблюдаемого мира в терминах четырехмерного многообразия. После возникновения
этой новой заранее неочевидной идеи отпадает необходимость в раздельном
описании пространственных координат и времени. Введем вместо времени
”) простого математического следствия об
инвариантности квадратичной формы относительно линейных преобразований
координат приводит к возникновению глубокой физической идеи об описании
наблюдаемого мира в терминах четырехмерного многообразия. После возникновения
этой новой заранее неочевидной идеи отпадает необходимость в раздельном
описании пространственных координат и времени. Введем вместо времени 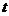 новую четвертую пространственную координату
новую четвертую пространственную координату
 (4)
(4)
Теперь по аналогии с трехмерными четырехмерные координаты объединятся в
единый комплекс, в который войдут три пространственные и временная координаты
 (5)
(5)
Четырехмерная
координата 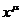 называется контравариантной координатой. Индекс “
называется контравариантной координатой. Индекс “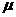 ” выбирается верхним по историческим причинам и
“пробегает” четыре возможные значения
” выбирается верхним по историческим причинам и
“пробегает” четыре возможные значения 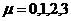 .
.
С
помощью введенных четырехмерных координат оператор Д’Аламбера может быть
переписан в более компактном виде:
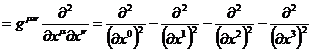 (6)
(6)
Из
формулы (6) вытекает вид матрицы 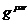
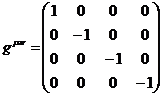 (7)
(7)
Формулу (7) можно переписать также в виде
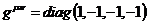 (8)
(8)
Так как выражение (6) есть квадратичная форма, она должна быть
инвариантна относительно преобразований вида:
 (9)
(9)
Причем
в силу однородности и изотропии четырехмерного пространства-времени,
преобразование (9) совпадает с преобразованием дифференциалов координат.
Поэтому справедливо соотношение
 (10)
(10)
где
 .
.
Отметим,
что координаты  ,
, 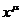 нового и
старого набора, арифметизующие пространство-время не обязаны быть геометрически
эквивалентны друг другу. Поэтому
нового и
старого набора, арифметизующие пространство-время не обязаны быть геометрически
эквивалентны друг другу. Поэтому
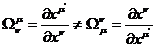
В
то же время физически очевидно, что в нерелятивистском пределе 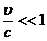 матрица
матрица 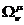 обязана
содержать те же три пространственных угла
обязана
содержать те же три пространственных угла  и три
компоненты скорости
и три
компоненты скорости 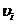 , что и преобразования Галилея (3). Преобразования
(9), переводящие само в себя глобальное четырехмерное многообразие и имеющее
физический смысл преобразования от системы отсчета одного наблюдателя к системе
отсчета другого наблюдателя называются преобразованиями Лоренца. Они с
необходимостью фиксируется требованием инвариантности оператора относительно
преобразований Лоренца, причем во всех системах координат удовлетворяются
равенство
, что и преобразования Галилея (3). Преобразования
(9), переводящие само в себя глобальное четырехмерное многообразие и имеющее
физический смысл преобразования от системы отсчета одного наблюдателя к системе
отсчета другого наблюдателя называются преобразованиями Лоренца. Они с
необходимостью фиксируется требованием инвариантности оператора относительно
преобразований Лоренца, причем во всех системах координат удовлетворяются
равенство
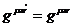 (11)
(11)
Пусть
координаты 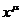 ,
,  нового и
старого набора связаны друг с другом функциональной связью
нового и
старого набора связаны друг с другом функциональной связью 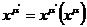 . Пусть
. Пусть 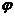 есть
некоторый скаляр, то есть величина, не зависящая от выбора системы отсчета.
есть
некоторый скаляр, то есть величина, не зависящая от выбора системы отсчета.
Выполним
операцию дифференцирования над полем скаляра 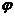 ,
рассматривая его как сложную функцию новых координат
,
рассматривая его как сложную функцию новых координат  от старых
от старых 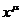 . Тогда
получаем очевидное выражение для производной от сложной функции
. Тогда
получаем очевидное выражение для производной от сложной функции
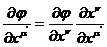 (12)
(12)
Из
(12) следует, что вновь построенный инвариантный оператор дифференцирования  обладает трансформационными свойствами
обладает трансформационными свойствами

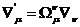 (13)
(13)
где
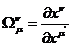 . Индекс
. Индекс 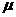 вектора
вектора 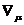 называется ковариантным индексом.
называется ковариантным индексом.
Таким
образом, в законе преобразования (13) проявляется различие верхних и нижних
индексов (контра- и ковариантных компонент тензоров, принадлежащих единому
четырехмерному пространственно-временному многообразию).
Введем
контравариантный оператор дифференцирования 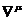 ,
преобразующийся при изменении системы координат как контравариантный вектор
(см. 9). Вычислим его свертку в новой координатной системе, используя законы
преобразования (9),(13)
,
преобразующийся при изменении системы координат как контравариантный вектор
(см. 9). Вычислим его свертку в новой координатной системе, используя законы
преобразования (9),(13)
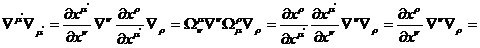
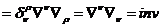
То
есть удалось показать, что величина  есть
инвариант
есть
инвариант
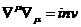 (14)
(14)
Кроме того, из приведенного вывода следует, что свертка фундаментальных
матриц преобразования Лоренца приводит к тензору Кронекера в четырехмерном
пространстве
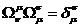 (15)
(15)
Из
соотношений (7), (11), (13), (15) следует инвариантность оператора Д’Аламбера
относительно преобразования системы координат (9), равного по определению

Иначе
говоря 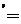 .
.
По аналогии с
матрицей (8) введем матрицу
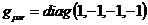 (16)
(16)
обладающую
парой 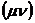 ковариантных индексов. Легко проверить прямым счетом,
что вновь введенная матрица и матрица (8) обладает свойством
ковариантных индексов. Легко проверить прямым счетом,
что вновь введенная матрица и матрица (8) обладает свойством
 , (17)
, (17)
то
есть являются взаимно обратными.
Пользуясь (17) можно определить операции поднятия и опускания индексов
ко- и контравариантных векторов.
Формула опускания индекса контравариантного вектора имеет, в частности,
вид
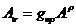 (18)
(18)
Формула
поднятия индекса ковариантного вектора имеет вид
 (19)
(19)
Проверим
(18), (19). Пусть 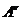 - контравариантный вектор. Тогда из (17) - (19)
следуют равенства
- контравариантный вектор. Тогда из (17) - (19)
следуют равенства

То
есть совместное использование этих формул не приводит к противоречиям.
Отсюда
следует, что квадрат вектора  может
быть записан в нескольких эквивалентных формах
может
быть записан в нескольких эквивалентных формах
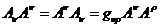 (20)
(20)
Величина
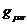 , с помощью которой квадрат вектора
, с помощью которой квадрат вектора 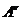 может быть записан в форме (20) называется
метрическим тензором пространства-времени.
может быть записан в форме (20) называется
метрическим тензором пространства-времени.
В
частности, квадрат длины дуги (расстояние между двумя бесконечно близкими
точками четырехмерного пространства) имеет вид
 (21)
(21)
Скалярная
величина  называется бесконечно-малым интервалом четырехмерного
пространства-времени.
называется бесконечно-малым интервалом четырехмерного
пространства-времени.
Из
правил поднятия и опускания индексов (18), (19) и вида матрицы (16) следует,
что в плоском четырехмерном пространстве-времени справедливы простые равенства
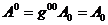 (22)
(22)
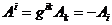
Для
дважды контравариантного тензора этот закон можно получить, составив его в частном
случае из произведения двух векторов
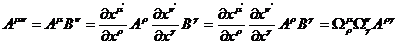
То
есть
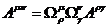 (23)
(23)
Закон
преобразования для l раз ковариантного и l раз
контравариантного тензора следует из соотношения
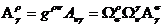 (24)
(24)
с
учетом закона преобразования контравариантного метрического тензора
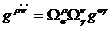 (25)
(25)
Формула
(25) следует, например, из того, что квадрат вектора 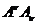 есть инвариант относительно преобразований
четырехмерным пространством самого в себя
есть инвариант относительно преобразований
четырехмерным пространством самого в себя

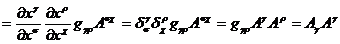 (26)
(26)
Действительно,
из (26) вытекает закон преобразования компонент метрического тензора 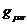 при изменении системы координат
при изменении системы координат
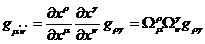 (27)
(27)
Аналогичным
образом строятся и преобразуются четырехмерные тензоры любых рангов.
Точки,
арифметизующие четырехмерное пространство-время, называются событиями.
Интервалом четырехмерного пространства-времени называются расстояния между
событиями. Как и в трехмерной геометрии, эти расстояния представляют собой
квадратичные формы координат.
Построить
все четырехмерные формы координат, сводящиеся к инварианту, не представляет
труда
 (28)
(28)
Используя
правила (22) и вид матрицы 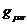 (8)
(8) 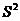 можно упростить до выражения
можно упростить до выражения
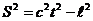 (29)
(29)
где
 - расстояние между точками трехмерного пространства.
- расстояние между точками трехмерного пространства.
В
силу однородности и изотропии четырехмерного пространства-времени как арены
событий электродинамики бесконечно-малый интервал между событиями имеет вид:
 (30)
(30)
Интервалы
четырехмерного пространства-времени допускают следующую классификацию:
 I. .
Времениподобный интервал.
I. .
Времениподобный интервал.
В
этом случае 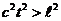 . Для любых бесконечно близких событий это означает
. Для любых бесконечно близких событий это означает 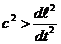 или
или  . Поэтому
вдоль траектории четырехмерного пространства, события которых лежат на
времениподобных кривых может происходить перемещение реальных физических тел с
досветовыми скоростями.
. Поэтому
вдоль траектории четырехмерного пространства, события которых лежат на
времениподобных кривых может происходить перемещение реальных физических тел с
досветовыми скоростями.
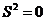 II. .
Изотропный или светоподобный интервал.
II. .
Изотропный или светоподобный интервал.
Если
интервал между событиями - светоподобный, то любым двум точкам, лежащим на
траектории их соединяющей соответствует равенство 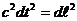 или
или 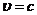 . Вдоль
подобных траекторий может перемещаться только световой сигнал, откуда и
происходит само название интервала.
. Вдоль
подобных траекторий может перемещаться только световой сигнал, откуда и
происходит само название интервала.
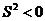 III. .
Пространственно-подобный интервал.
III. .
Пространственно-подобный интервал.
Двум
бесконечно близким событиям, лежащим на данном интервале, соответствует
равенство  . Иначе говоря, скорость перемещения физических тел по
пространственно-подобным кривым должна быть больше световой
. Иначе говоря, скорость перемещения физических тел по
пространственно-подобным кривым должна быть больше световой  . Так как эксперимент показывает, что скорость света
есть предельная скорость распространения взаимодействия, то по
пространственно-подобным кривым не могут перемещаться ни физические частицы, ни
свет. Поэтому области пространства, связанные пространственно-подобными
кривыми, соответствуют событиям, которые не могут быть причиной и следствием
друг друга. Иначе говоря, эти области причинно не связаны и могут быть по отношению
друг к другу лишь абсолютно удаленными.
. Так как эксперимент показывает, что скорость света
есть предельная скорость распространения взаимодействия, то по
пространственно-подобным кривым не могут перемещаться ни физические частицы, ни
свет. Поэтому области пространства, связанные пространственно-подобными
кривыми, соответствуют событиям, которые не могут быть причиной и следствием
друг друга. Иначе говоря, эти области причинно не связаны и могут быть по отношению
друг к другу лишь абсолютно удаленными.
Введенная
таким образом геометрическая конструкция называется световым конусом в
четырехмерном пространстве-времени (Рис. 1.).
В
заключение этого пункта найдем матрицу 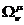 преобразования
Лоренца в явном виде. Сначала для простоты остановимся на так называемом
специальном преобразовании Лоренца. Для этого предположим, что искомые
преобразования связывают две системы координат
преобразования
Лоренца в явном виде. Сначала для простоты остановимся на так называемом
специальном преобразовании Лоренца. Для этого предположим, что искомые
преобразования связывают две системы координат 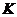 и
и 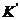 , оси которых ориентированы одинаково, причем начало
системы координат
, оси которых ориентированы одинаково, причем начало
системы координат 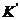 - точка
- точка  движется
со скоростью
движется
со скоростью 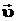 , направленной вдоль оси
, направленной вдоль оси  системы
системы 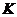 (Рис
2.).
(Рис
2.).
При
таком движении координатные зависимости 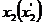 ,
,  должны быть заданы, а
должны быть заданы, а  и
и 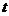 связаны линейным преобразованием (оставляющим
инвариантным интервал
связаны линейным преобразованием (оставляющим
инвариантным интервал 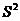 )
)
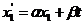 (31)
(31)

где
постоянные  ,
, 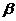 ,
, 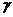 ,
, 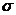 заведомо
связаны инвариантностью интервала (29).
заведомо
связаны инвариантностью интервала (29).
Рассмотрим
движение начала системы 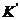 - точки
- точки 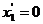 относительно
системы
относительно
системы 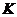 . Тогда из (31) следует
. Тогда из (31) следует  . Но
поскольку скорость этой точки вдоль оси
. Но
поскольку скорость этой точки вдоль оси  , по
предположению равна
, по
предположению равна  , то дифференцируя полученное соотношение, находим
связь между параметрами
, то дифференцируя полученное соотношение, находим
связь между параметрами
 (32)
(32)
Рассмотрим
движение начала системы координат 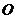 - точки
- точки 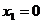 относительно
относительно  . Получим
уравнение
. Получим
уравнение  . Скорости движения начал систем
. Скорости движения начал систем 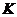 и
и 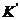 равны по
модулю и противоположны друг другу по направлению. Поэтому
равны по
модулю и противоположны друг другу по направлению. Поэтому
 ;
; 
Требуя
 , находим
, находим
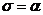 (33)
(33)
То есть исходное линейное преобразование (31) упростилось до
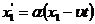 (34)
(34)

Исходя
из (34); требуем инвариантности интервала
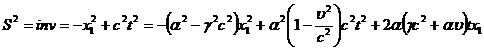 (35)
(35)
Приравнивая
коэффициенты левой и правой части (35), получим выражения для коэффициентов  ,
, 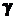 и
тождественно выполняющуюся связь между ними
и
тождественно выполняющуюся связь между ними
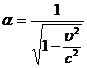
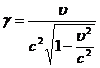 (36)
(36)
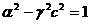
Подставляя
найденные значения коэффициентов (32), (33), (36) в (31) находим формулы
специального преобразования Лоренца, соответствующие рассмотренному
относительному движению систем координат
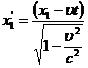 ,
,  (37)
(37)
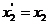 ,
, 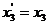
Обобщим
преобразования (37) на случай, когда оси начал координат ориентированы,
по-прежнему, одинаково, и скорость 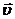 движения
системы
движения
системы 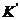 ориентирована относительно
ориентирована относительно 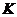 произвольно. Такие преобразования систем координат
носят название преобразований Лоренца без вращения (координатных систем друг
относительно друга). В таком случае, координаты и скорость есть вектор в трехмерном
пространстве
произвольно. Такие преобразования систем координат
носят название преобразований Лоренца без вращения (координатных систем друг
относительно друга). В таком случае, координаты и скорость есть вектор в трехмерном
пространстве
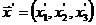
 (38)
(38)


Заметим, что в общем случае (38) формулы специального преобразования
Лоренца (37) можно записать в векторном виде
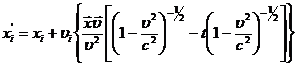 (39)
(39)
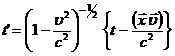
Действительно,
в частном случае 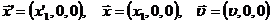 ;
;
Формула
(39) переходит в специальные преобразования Лоренца (37).
Вводя
координату 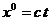 , объединим (39) в четырехмерное преобразование
Лоренца без вращения
, объединим (39) в четырехмерное преобразование
Лоренца без вращения
 (40)
(40)
и
найдем матрицу этого преобразования
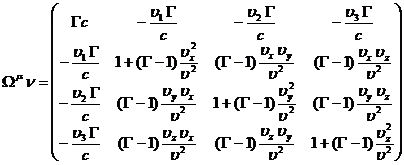 (41)
(41)
Отметим,
что матрица (41) симметрична 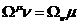 и
содержит в качестве параметров 3 компоненты скорости
и
содержит в качестве параметров 3 компоненты скорости 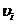 . Кроме того в (41) введено обозначение
. Кроме того в (41) введено обозначение
пространство
время четырехмерный событие
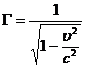
Во
многих задачах находят применение инфинитезимальные (бесконечно - малые)
преобразования Лоренца. Эти преобразования индуцируются бесконечно малым
изменением скорости 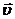 .
.
где
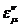 - подлежащие определению инфинитезимальные тензорные
величины.
- подлежащие определению инфинитезимальные тензорные
величины.
Пренебрегая
величинами второго порядка малости по 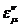 , найдем
интервал
, найдем
интервал  или
или 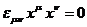 , что
возможно лишь когда
, что
возможно лишь когда 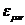 - антисимметричный тензор.
- антисимметричный тензор.
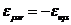 (43)
(43)
Тогда
при бесконечно малых скоростях 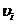 получим
из (41):
получим
из (41):
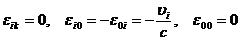 (44)
(44)
Необходимо отметить, что в плоском четырехмерном пространстве существуют
более общие, чем преобразования Лоренца преобразования Пуанкарэ.
 (45)
(45)
Преобразование
(45) включает в себя произвольный постоянный сдвиг начала системы координат -  и поэтому является в общем случае 10-ти
параметрическим (к 3-м компонентам скорости и 3-м пространственным углам общего
преобразования Лоренца добавляются четыре координаты
и поэтому является в общем случае 10-ти
параметрическим (к 3-м компонентам скорости и 3-м пространственным углам общего
преобразования Лоренца добавляются четыре координаты 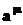 ). Это преобразование, естественно, также оставляет
инвариантным оператор и, поэтому играет важную роль в теории релятивистских
полей.
). Это преобразование, естественно, также оставляет
инвариантным оператор и, поэтому играет важную роль в теории релятивистских
полей.
2.
РЕЛЯТИВИСТСКАЯ КИНЕМАТИКА И ДИНАМИКА СОБСТВЕННОЕ ВРЕМЯ ТОЧЕЧНОЙ ЧАСТИЦЫ
Введенное
в предыдущем разделе понятие интервала  позволяет
обобщить кинематику и динамику точечной частицы на случай четырехмерного
пространства.
позволяет
обобщить кинематику и динамику точечной частицы на случай четырехмерного
пространства.
Пусть
в системе координат К, связанной с некоторым наблюдателем, зависимость
траектории частицы от мирового времени есть 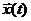 . Разница
между положением частицы в моменты времени
. Разница
между положением частицы в моменты времени 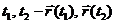 есть
есть  . Для наблюдателя, в системе
. Для наблюдателя, в системе 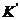 , связанной с движущейся частицей с
, связанной с движущейся частицей с 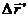 , а текущее по его часам соответственное время есть
, а текущее по его часам соответственное время есть  . То есть, инвариантный интервал с точностью до
постоянной «с» является собственным временем для которого можно ввести
обозначение
. То есть, инвариантный интервал с точностью до
постоянной «с» является собственным временем для которого можно ввести
обозначение
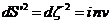 (46)
(46)
Веденный инвариант можно использовать для построения кинематических
величин, связанных с системой отсчета движущегося наблюдателя. Действительно,
по показанием приборов системы отсчета неподвижного наблюдателя интервал между
событиями строится так
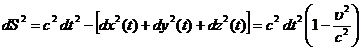 (47)
(47)
где
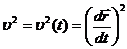 .
.
Вследствие инвариантности интервала между событиями четырех мерного
пространства можно приравнять друг к другу выражения (46), (47):
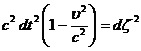 (48)
(48)
и
выразить тем самым дифференциал времени покоящегося наблюдателя 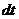 через инвариант
через инвариант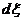 .
.
Ведение инвариантного собственного времени по формулам (46), (48)
позволяет строить четырехмерные динамические величины по аналогии с трехмерными.
По
определению 3 компоненты контравариантной координаты 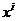 совпадают с координатами в трехмерном пространстве:
совпадают с координатами в трехмерном пространстве:
 (49)
(49)
Это равенство позволяет ввести следующим образом 4-м скорость по аналогии
с трехмерной (3-м)
Трехмерный вектор скорости
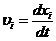
Четырехмерный
вектор скорости
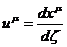 (50)
(50)
Вычислим квадрат четырехмерной скорости, введенной формулой (50).
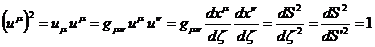 .
.
Результатом этих вычислений является универсальное соотношение для
инварианта скорости:
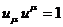 (51)
(51)
Таким образом, компоненты скорости в четырехмерном пространстве всегда
связаны соотношением (51).
Используя
выражение (48) для 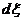 , выпишем компоненты вектора 4- скорости в явном виде
, выпишем компоненты вектора 4- скорости в явном виде
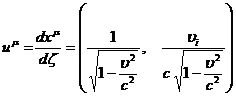 (52)
(52)
Определим
четырехмерное ускорение 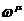 по аналогии с трехмерным
по аналогии с трехмерным 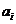 .
.
Трехмерный
вектор ускорения
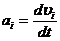
Четырехмерный
вектор ускорения
 (53)
(53)
Дифференцируя
связь (51) по 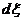 , получаем связь между компонентами 4- м ускорения и
4- м скоростью:
, получаем связь между компонентами 4- м ускорения и
4- м скоростью:
 (54)
(54)
Отметим, что 4- м ускорение, как 4- м скорость, всегда имеет только 3
независимых компоненты. Компоненты 4- ускорения выпишем, пользуясь (48), (52):
 (55)
(55)
Величины, имеющие структуру (55) входят, например, в уравнение движения
заряда в магнитном поле.
 (56)
(56)
где
 .
.
Для
того, чтобы реконструировать в 4- м форме правую часть уравнения (56) надо
найти 4- м аналоги  и сформировать для него уравнения Максвелла в
четырехмерном воде.
и сформировать для него уравнения Максвелла в
четырехмерном воде.
3. УРАВНЕНИЯ
ЭЛЕКТРОДИНАМИКИ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
Для
построения уравнений Максвелла в четырехмерной форме, объединим скалярный 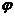 и векторный
и векторный  потенциалы
в единый четырехмерный потенциал. Для этого используем при рассуждении аналогии
и наводящие соображения, используемые при введении 4- м координат и скорости.
Пусть дополнительный индекс (4) обозначает 4- м величину, индекс (3) - 3- м.
Тогда используемое выше равенство (49) примет вид:
потенциалы
в единый четырехмерный потенциал. Для этого используем при рассуждении аналогии
и наводящие соображения, используемые при введении 4- м координат и скорости.
Пусть дополнительный индекс (4) обозначает 4- м величину, индекс (3) - 3- м.
Тогда используемое выше равенство (49) примет вид:
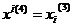 (57)
(57)
По аналоги с ним определим 3 компоненты четырехмерного потенциала:
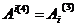 (58)
(58)
Калибровочные преобразования для потенциалов поля имеют вид:
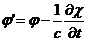 ,
,  (59)
(59)
Четырехмерный потенциал определим как 4- м вектор:
 (60)
(60)
Для упрощения записи в (59) введем дифференциальный оператор:
 (61)
(61)
и
перепишем с его помощью и с учетом (60) соотношения (59). Получим
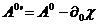 ,
, 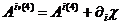 (62)
(62)
опустим индекс у величин (62) с учетом правил (22). В итоге получим два
простых соотношения
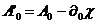 ,
,  (63)
(63)
объединяющихся
в одно 4- м.
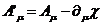 (64)
(64)
Выражение
(64) есть 4- м форма принципа калибровочной инвариантности. Четырехмерная форма
уравнений электродинамики должна с необходимостью допускать преобразование (64).
Для дальнейшего необходимо построить 2- м комбинации, заменяющие 3- м
дифференциальные выражения
 ,
, 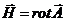 (65)
(65)
С
этой целью введем новое выражение - тензор электромагнитного поля
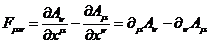 (66)
(66)
Подставляя
калибровочное преобразование (64) в (66) легко доказываем его калибровочную
инвариантность.
По
построению, тензор 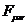 является антисимметричным:
является антисимметричным:
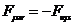 (67)
(67)
поэтому
его диагональные элементы равны нулю
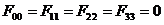 (68)
(68)
Рассчитаем,
к примеру 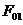 :
:
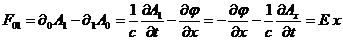 (69)
(69)
где
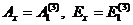 .
.
Аналогично
считаются другие компоненты 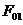 .
Результатом расчета является первое уравнение (65):
.
Результатом расчета является первое уравнение (65):  . Компоненты магнитного поля
. Компоненты магнитного поля 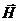 получаются при расчете
получаются при расчете  при
при 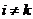 . Рассчитаем, например,
. Рассчитаем, например,  с учетом
связи 3-х и 4-х мерных ковариантных компонент вектор - потенциала
с учетом
связи 3-х и 4-х мерных ковариантных компонент вектор - потенциала 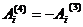 :
:
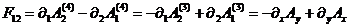 (70)
(70)
В
то же время, прямой расчет по 3- м формулам дает
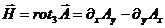 (71)
(71)
Сравнивая
результаты (70), (71), убеждаемся в том, что
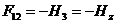 (72)
(72)
Итого
удалось установить явный вид тензора электромагнитного поля:
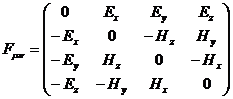 (73)
(73)
Компоненты
контравариантного тензора электромагнитного поля рассчитываются по формуле  , что приводит к результатам
, что приводит к результатам

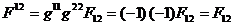

и
так далее
В
результате этих вычислений матрица контравариантного тензора имеет вид:
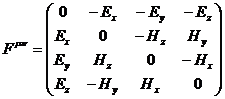 (74)
(74)
Установим
явный вид уравнений Максвелла в четырехмерном пространственно-временном
формализме.
Первая
(вакуумная пара) искомых уравнений представляет собой равенство, полученное с
помощью всевозможных циклических перестановок индексов в выражении 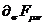 :
:
 (75)
(75)
Уравнение
(75) является следствием определения тензора 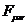 и
обращения в тождество при подстановке в него определения
и
обращения в тождество при подстановке в него определения  .
.
Раскроем
(75) при  получим
получим 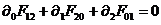 , что
дает
, что
дает

Перебирая
остальные возможные пары индексов 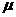 ,
,  , получаем два других уравнения закона индукции
Фарадея:
, получаем два других уравнения закона индукции
Фарадея:
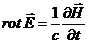
Подставляя
в (75) только пространственные индексы, например  ,
можно получить компоненты уравнения
,
можно получить компоненты уравнения 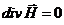 .
.
Для
получения второй пары уравнений Максвелла в 4- м форме введем 4- м вектор тока
в виде:
 (76)
(76)
Последнее
выражение объединяет в единый четырехмерный вектор плотность тока и заряд.
Такое объединение позволяет выписать единое выражение 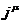 через d-функции точечных
зарядов.
через d-функции точечных
зарядов.
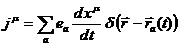 (77)
(77)
Покажем,
что так определенная величина 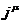 действительно
является 4- вектором. Для доказательства рассмотрим бесконечно малый объем
действительно
является 4- вектором. Для доказательства рассмотрим бесконечно малый объем 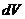 , в котором распределен заряд
, в котором распределен заряд
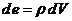 (78)
(78)
Величина
заряда (78) является инвариантом, в том числе и в четырехмерном пространстве.
Построим
4- вектор
 (79)
(79)
Так
как 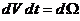 есть 4- объем, из (79) следует, что
есть 4- объем, из (79) следует, что 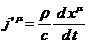 - есть 4- м вектор, связывающий с (77) с точностью до
коэффициента. При подстановке в последнее выражение плоскости точечных зарядов
получаем формулу (77) для
- есть 4- м вектор, связывающий с (77) с точностью до
коэффициента. При подстановке в последнее выражение плоскости точечных зарядов
получаем формулу (77) для 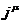 .
.
Для
конструирования уравнений поля в нашем распоряжении имеются:
) Тензор
второго ранга 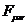 , описывающий электромагнитное поле;
, описывающий электромагнитное поле;
) Вектор
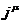 , описывающий источники поля.
, описывающий источники поля.
В соответствии с общей идеологией получения полевых уравнений, развитой в
параграфе 1, необходимо приравнять их друг другу с соблюдением правил
тензорного анализа.
Составим следующее равенство:
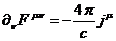 (80)
(80)
и
проверим его покомпонентно для выяснения вопроса о совпадении (80) со второй
парой уравнений Максвелла.
) Пусть
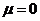 . Получаем уравнение
. Получаем уравнение
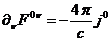 или
или 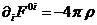
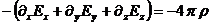

) Пусть
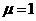 .
.

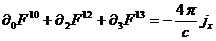
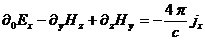
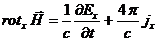 (81)
(81)
Подставляя
в (80) 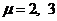 , получим две другие компоненты векторного уравнения
, получим две другие компоненты векторного уравнения

Для
завершения построения электродинамики в 4- м форме необходимо построить
уравнения движения. Для этого используем определенные выше динамические 4- м
величины - скорость 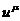 и ускорение
и ускорение 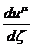 , а также
тензор электромагнитного поля и постулируем соотношение:
, а также
тензор электромагнитного поля и постулируем соотношение:
 (82)
(82)
Вспомним,
что временная компонента скорости 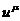 и
ускорения
и
ускорения 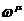 зависит от пространственных (51) и (54).
Проанализируем (82) с учетом тождества
зависит от пространственных (51) и (54).
Проанализируем (82) с учетом тождества  . Умножим
(82) на
. Умножим
(82) на 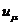 и получим в правой его части тождество:
и получим в правой его части тождество:
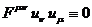 (83)
(83)
которое
следует из свойств симметрии тензора  (67).
Поэтому достаточно убедиться в справедливости (82) для его пространственных
компонент.
(67).
Поэтому достаточно убедиться в справедливости (82) для его пространственных
компонент.
Пусть,
например, 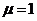 . Тогда получим
. Тогда получим
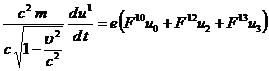 (83)
(83)
где
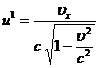 ,
,  ,
, 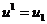 ,
, 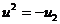 ,
,  .
.
Итого
получили для 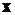 компоненты равенство
компоненты равенство
 ;
;
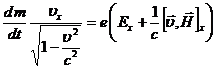 ;
;
 или
или  .
.
В
заключении к 3. выпишем замкнутую систему уравнений Максвелла в 4- м форме
 (84)
(84)
ЛИТЕРАТУРА
Ландау Л.Д.,
Лифшиц Е.М. Электродинамика сплошных сред. (серия «Теоретическая физика», т.
8).- М.: ФИЗМАТЛИТ, 2012.
Ландау Л.Д.,
Лифшиц Е.М. Краткий курс теоретической физики, кн. 1-2.- М.: Наука, 1969, 1972.
Электронная
библиотека студента. Ландау Л.Д. , Лифшиц Е.М. Теоретическая физика. - М.: РХД,
2011.
Гильденбург
В.Б., Миллер М.А. Сборник задач по электродинамике - 2-е изд., дополн. - М.:
ФИЗМАТЛИТ, 2011.
Батыгин В.В.,
Топтыгин И.Н. Сборник задач по электродинамике - М.: НИЦ «Регулярная и
хаотическая динамика», 2012.
Батыгин В.В.,
Топтыгин И.Н. Современная электродинамика. Часть 1.Микроскопическая теория. -
М.: НИЦ «Регулярная и хаотическая динамика», 2003.
Топтыгин И.Н.
Современная электродинамика. Часть 2. Теория электромагнитных явлений в
веществе. - М.: НИЦ «Регулярная и хаотическая динамика», 2005.
Пеннер Д.И.,
Угаров В.А. Электродинамика и специальная теория относительности.- М.:
Просвещение, 1980.
Тамм И.Е.
Основы теории электричества.- М.: Наука, 1976.
Терлецкий
Л.П., Рыбаков Ю.П. Электродинамика: Учеб. пособие. - М.: Высш. шк., 1980. - 335
с.
Мултановский
В.В., Василевский А.С Курс теоретической физики: Классическая электродинамика:
Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. - М.: Просвещение,
1990. - 272 с.
Бредов М.М.,
Румянцев В.В., Топтыгин И.Н. Классическая электродинамика: Учебное псобие / Под
ред. И.Н. Топтыгина. - М.: Наука. гл. ред. физ.-мат. лит., 1985. - 400 с.
Каликинский
И.И. Курс электродинамики. Учебное пособие. Часть 1.- Астрахань: Издательство
АГПИ, 2011.
Каликинский
И.И. Курс электродинамики. Учебное пособие. Часть 1.- Астрахань: Издательство
АГПИ, 2008.- 101 с.