Программная реализация решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта 4-го порядка
ФЕДЕРАЛЬНОЕ
Государственное АВТОНОМНОЕ образовательное учреждение Высшего профессионального
образования
«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»
Институт инженерных технологий и
естественных наук
Кафедра математического и программного
обеспечения информационных систем
программная реализация решения
системы обыкновенных дифференциальных уравнений методом Рунге-кутта 4-го
порядка
Курсовая работа
по дисциплине «Методы вычислений»
студента
очного формы обучения
направления
подготовки 010500.62
«Математическое
обеспечение и администрирование
информационных
систем»
курса группы
07001302
Данькова
Николая Алексеевича
БЕЛГОРОД 2016
Содержание
Введение
. Теоретическая часть
.1 Обыкновенное дифференциальное уравнение первого порядка.
Задача Коши
.2 Суть метода Рунге-Кутта
.3 Выбор среды разработки
. Практическая часть
.1 Программная реализация метода Рунге-Кутта 4-го порядка
. Тестирование
.1 Пример
Заключение
Список использованных источников
Приложение
Введение
При изучении самых разнообразных явлений окружающего мира, имеющих
отношение как к точным, так и к гуманитарным наукам, исследователи сталкиваются
в ряде случаев с тем, что функциональные зависимости между величинами находятся
из уравнений, в которых присутствуют производные от искомых функций. Наиболее
простыми среди них являются те, что содержат только производные первого порядка
и могут быть записаны в виде
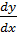 = f(x, y) ,
= f(x, y) ,
где у - искомая функция, х - независимая переменная, f(x,y) - непрерывная
функция от х и у. Однако получить аналитическое решение этого уравнения для
достаточно произвольной функции f не
удается, и только для некоторых частных случаев, с которыми можно ознакомиться
в справочной литературе.
В связи с быстрым развитием электронной вычислительной техники в
последние десятилетия появилась возможность использовать приближенные
математические методы для решения подобного рода задач. Один из таких подходов
называется методом Рунге-Кутты и объединяет целую группу модификаций, связанных
способом их получения.
Цель курсовой работы: изучить метод Рунге - Кутта 4-го порядка для
решения обыкновенных дифференциальных уравнений.
Постановка задачи: необходимо составить программу, позволяющую решать
обыкновенные дифференциальные уравнения методом Рунге - Кутта 4-го порядка.
Курсовая работа состоит из 3 разделов, содержит 6 рисунков, 3 листинга, 1
приложение и 18 страниц.
1. Теоретическая
часть
1.1
Обыкновенное дифференциальное уравнение первого порядка. Задача Коши
Для простоты рассмотрим двумерное пространство переменных х и у
и некоторое открытое множество G, принадлежащее ему. Пусть на этом открытом множестве
определена непрерывно дифференцируемая функция f(х, у) и задано
уравнение
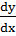 = f(x, y) (1)
= f(x, y) (1)
Согласно теореме существования и единственности для любой точки (x0,y0) ∈G найдется решение у = у(х),
определенное на некотором интервале (х0 -δ, х0 +δ), удовлетворяющее условию y(x0) = y0, такое, что точки (x,y(x)) ∈G и y‘x ≡
f(x, y(x)), причем это решение будет
единственным. Задача для уравнения (1) с начальным условием у(х0) = y0 (задача Коши) состоит в нахождении функции у(х),
обращающей и уравнение (1), и начальное условие в тождество. Допустим, что
значения, которые принимает независимое переменное х, принадлежат интервалу (Х0,
XN ) и запишем задачу Коши:
 (2)
(2)
Разобьём отрезок [Х0, XN ] на N
частей так, что xn+1 - хn = hn ,
n = 0,
… ,N-1. В дальнейшем, не ограничивая
общности, рассмотрим случай, когда разбиение равномерное, т.е. все hn = h =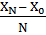 = const,
= const,
n = 0
,… ,N-1.
1.2 Суть
метода Рунге-Кутта
Методы Рунге-Кутта находят широкое применение при решении ДУ. Наибольшее
применение нашел метод 4-го порядка.
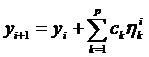 (3)
(3)
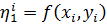 (4)
(4)
 (5)
(5)
 - параметр, который определяет значение функции вблизи точки
- параметр, который определяет значение функции вблизи точки
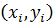 области определения.
области определения.
Общепринятый метод 4-го порядка:
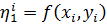 (6)
(6)
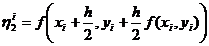 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
Ошибка
формулы (10) пропорциональна h5.
Этот
метод намного более точен, чем методы Эйлера, но требует и большего объема
вычислений: положение точки (xi+1, yi+1)
определяется в результате 4-кратного вычисления значения функции f (x,y). С
появлением ЭВМ этот недостаток перестал быть существенным и метод Рунге-Кутта
4-го порядка применяется на практике чрезвычайно широко.
Число
микроотрезков [xi; xi+1], на
которые разбивается исходный отрезок [x0;xn], определяется требуемой точностью вычислений. Для
достижения нужной точности задача решается несколько раз при последовательно
удваиваемом числе микроотрезков n. Точность считается достигнутой, если при начальном и
удвоенном числе n значения yi и y2i (в
совпадающих точках x) отличаются не более чем на заданную величину:
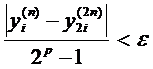 , i =0,
..,n, (11)
, i =0,
..,n, (11)
где
p - порядок точности метода.
Метод
Ругне-Кутта обладает следующими свойствами:
1. Метод является одноступенчатым (чтобы найти 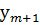 , нужна информация о предыдущей точке
, нужна информация о предыдущей точке ,
,  )
)
. Не требует вычисления производных от f(x,y), а требует вычисления самой функции
. Имеет небольшую погрешность
1.3 Выбор
среды разработки
++ Builder- программный продукт, инструмент быстрой разработки приложений
(RAD), интегрированная среда программирования (IDE), система, используемая
программистами для разработки программного обеспечения на языке
программирования C++. Данный продукт позволяет создавать как консольные
приложения, так и приложения с графическим интерфейсом.Visual Studio - линейка
продуктов компании Microsoft, включающих интегрированную среду разработки
программного обеспечения и ряд других инструментальных средств. С помощью
данного продукта можно разрабатывать консольные приложения, приложения с
графическим интерфейсом, а также веб-сайты, веб-приложения, веб-службы как в
родном, так и в управляемом кодах для всех платформ, поддерживаемых Windows,
Windows Mobile, Windows CE, .NET Framework, Xbox, Windows Phone .NET Compact
Framework и Silverlight.
Для выполнения поставленной задачи был выбран программный продукт C++
Builder. Так как является более простым в использовании и соответствует всем
необходимым требованиям для создания консольного приложения.
2. Практическая
часть
2.1 Программная
реализация метода Ркнге-Кутта 4-го порядка
дифференциальный уравнение программирование коши
Разработка программы начинается с описания функций. Для этого мы
используем оператор switch.
Листинг
1 «описание функций»func(int tip,double x,double y,double a,double b,double c,
double d, double e, double f ) {s=0;(tip){1: {= a+b*(y*c*sin(d*x))-(e*y*f*y);;
}2: {=a*cos(b*x+c*y)+d*(e*x-f*y);; }3: {=((a*cos(b*x)/(x+c))-(d*y*e*y)*f);; }4:
{= a*(b*x+c*y)/(e*f)*d;; }:
{ s =0; }
}s;
}
Когда все нужные данные получены, мы переходим непосредственно к решению
ОДУ методом Рунге - Кутта 4-го порядка.
Листинг 2 «программная реализация решения ОДУ методом Рунге - Кутта
4-го порядка»(i=0;i<=n;i++)
{=func(tip,x[i],y[i],a,b,c,d,e,f)*h;=func(tip,x[i]+h/2,
y[i]+(k1/2),a,b,c,d,e,f)*h;=func(tip,x[i]+h/2,
y[i]+(k2/2),a,b,c,d,e,f)*h;=func(tip,x[i]+h,
y[i]+k3,a,b,c,d,e,f)*h;[i+1]=y[i]+((1.0/6.0)*(k1+2*k2+2*k3+k4));[i+1]=x[i]+h;<<"y"<<i<<"=
"<<y[i]<<endl;
}
3.
Тестирование
Запустив программу, мы увидим уравнения, предлагаемые для выбора.
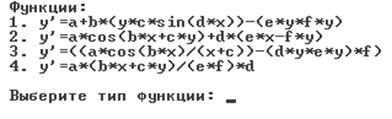
Рис. 1 «выбор уравнения»
Если ввести номер не соответствующий представленным номерам уравнений
программа отреагирует на это.

Рис. 2 «ввод неверного параметра»
Выбрав необходимое уравнение, вводим коэффициенты.

Рис. 3 «ввод коэффициентов»
Далее вводим начало и конец отрезка, на котором будет производиться
расчет, шаг и начальное условие. Выбор последнего параметра необходимо
выполнить пользователю самостоятельно.

Рис. 4 «ввод необходимых параметров»
После окончания вычисления программа выводит решение.

Рис. 5 «вывод результата»
3.1 Пример
Решить задачу Коши:
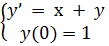
на отрезке [0: 0,4]. Найти решение на равномерной сетке с шагом 0.1
Решение. Так как f(x ,y ) = х + у , то получаем
 =
= 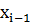 +
+  ,
,
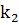 =
= 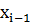 +
+ +
+  ,
,
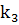 =
= 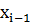 +
+ +
+ 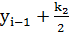 ,
,
 =
= 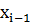 +h+
+h+ 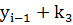 ,
,
 =
=  +
+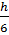 (
(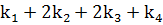 ) ,
) ,
 =
= 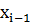 +h ,
+h ,
для значений i = 1, 2, 3, 4.
Полагая  =0,
=0,  = 1, последовательно находим:
= 1, последовательно находим:
при i = 1
 = 0,1(0 +1) = 0,1 ,
= 0,1(0 +1) = 0,1 ,
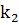 = 0,1(0 + 0,05 +1 + 0,05) = 0,11 ,
= 0,1(0 + 0,05 +1 + 0,05) = 0,11 ,
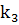 = 0,1(0 + 0,05 +1 + 0,055) = 0,1105 ,
= 0,1(0 + 0,05 +1 + 0,055) = 0,1105 ,
 = 0,1(0 + 0,1 +1 + 0,1105) = 0,121050 ,
= 0,1(0 + 0,1 +1 + 0,1105) = 0,121050 ,
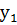 = 1 +
= 1 +  *(0,1 + 2*0,11+2*0,1105 + 0,12105) = 1,110342 ,
*(0,1 + 2*0,11+2*0,1105 + 0,12105) = 1,110342 ,
 = 0+0,1=0.1 ,
= 0+0,1=0.1 ,
при i = 2
 = 0,1*(0 + 1,110342) = 0,121034 ,
= 0,1*(0 + 1,110342) = 0,121034 ,
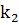 = 0,1*(0,1 + 0,05 +1,110342 + 0,0605171) = 0,1320859 ,
= 0,1*(0,1 + 0,05 +1,110342 + 0,0605171) = 0,1320859 ,
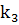 = 0,1*(0,1 + 0,05+1,110342 + 0,06604295) = 0,1326385 ,
= 0,1*(0,1 + 0,05+1,110342 + 0,06604295) = 0,1326385 ,
 = 0,1*(0,1 + 0,1 + 1,110342 + 0,11326385)= 0,1442980 ,
= 0,1*(0,1 + 0,1 + 1,110342 + 0,11326385)= 0,1442980 ,
 = 1,110342 +
= 1,110342 +  *(0,121034 + 2*0,1320859+2*0,1326385 + 0,1442980) = 1,242805
,
*(0,121034 + 2*0,1320859+2*0,1326385 + 0,1442980) = 1,242805
,
 = 0,1+0,1 ,
= 0,1+0,1 ,
Далее получаем:
при i = 3 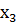 = 0,3,
= 0,3, 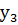 =1,399717,
=1,399717,
при i = 4  = 0.4,
= 0.4, 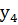 = 1,583648.
= 1,583648.
Погрешность полученного решения не превышает величины
|y4 - φ(x4) | ≈ 0.000001.
Для наглядности в таблице 1 приведены численные решения одной и той же
задачи Коши методами Эйлера, Эйлера-Коши и Рунге-Кутта.
Таблица 1 Численные решения задачи коши разными методами
|
i
|
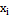
|
Значения  , найденного методом , найденного методом
|
Точное решение φ(xi)=2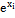 - xi -1 - xi -1
|
|
|
Эйлера
|
Эйлера - Коши
|
Рунге - Кутта
|
|
|
0
|
0
|
1.0
|
1.0
|
1.0
|
1.0
|
|
1
|
0.1
|
1.1
|
1.11
|
1.110342
|
|
2
|
0.2
|
1.22
|
1.24205
|
1.242805
|
1.248805
|
|
3
|
0.3
|
1.362
|
1.398465
|
1.399717
|
1.399718
|
|
4
|
0.4
|
1.5282
|
1.581804
|
1.583648
|
1.583649
|
Теперь сравним полученные результаты с расчетами нашей программы.

Рис. 6 «результат работы программы»
Как мы видим из примера - точность вычисления сохраняется до пятого знака
после запятой.
Заключение
В ходе выполнения курсовой работы была реализована поставленная задача, а
именно составлена программа, позволяющая решать обыкновенные дифференциальные
уравнения методом Рунге - Кутта 4-го порядка.
В ходе тестирования программы были получены результаты, по которым видно,
что результаты решения методом Рунге - Кутта 4-го порядка совпадают, с
достаточной точностью, с аналитическим.
Список
использованных источников
1. Березин
И.С., Жидков Н.П., Методы вычислений: Т.2 - М.: ГИФМЛ, 1960. - 620 с.
. Бахвалов
Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. - М.: Бином, 2001 - с. 363-375.
. Копченова
Н.В., Марон И.А., Вычислительная математика в примерах и задачах - М.: Наука,
1972. - 368 с.
4. <https://ru.wikipedia.org/wiki/Microsoft_Visual_Studio>
. <https://ru.wikipedia.org/wiki/C%2B%2B_Builder>
Приложение 1
#include <iostream.h>
#include <math.h>
#include <locale.h>
#include <windows.h>namespace std;* rus(const char*
text) {*buffRus=new char[strlen(text)];(text, buffRus);buffRus;
}func( int tip,double x,double y,double a,double b,double c,
double d, double e, double f ) {s=0;(tip) {1: {= a+b*(y*c*sin(d*x))-(e*y*f*y);;
}2: {=a*cos(b*x+c*y)+d*(e*x-f*y);; }3: {=((a*cos(b*x)/(x+c))-(d*y*e*y)*f);; }4:
{= a*(b*x+c*y)/(e*f)*d;; }:
{ s =0; }
}s;
}main( ) {tip, i=0, n=0;h=0.0, ot1=1.0, ot2=0.0, k1=0.0,
k2=0.0, k3=0.0, k4=0.0, a=1.0, b=1.0, c=1.0, d=1.0, e=1.0, f=1.0,
res=0.0;flag=0;<<rus(" Функции: ")<<endl;<<" 1.
y'=a+b*(y*c*sin(d*x))-(e*y*f*y)\n 2. y'=a*cos(b*x+c*y)+d*(e*x-f*y)\n 3.
y'=((a*cos(b*x)/(x+c))-(d*y*e*y)*f)\n 4. y'=a*(b*x+c*y)/(e*f)*d\n";(!flag)
{<<endl<<rus(" Выберите тип функции: ");>>tip;((tip == 1) || (tip == 2) || (tip == 3)
|| (tip == 4)){=1; }
else {
cout
<<rus(" Введен неверный параметр!\n");
}
}
cout<<rus(" Введите коэффициенты (a,b,c,d,e,f):
")<<endl;
cout <<" a= ";cin>>a;<<" b=
";cin>>b;<<" c= ";cin>>c;<<" d=
";cin>>d;<<" e= ";cin>>e;<<" f=
";cin>>f;<<rus(" Введите начало (x0) и конец (xn) отрезка")<<endl;
while (ot1>ot2) {<<rus(" x0=
");>>ot1;<<rus(" xn= ");>>ot2;
}<<rus(" Введите
шаг h= ");>>h;=
((ot2-ot1)/h);* x=new double[n];* y=new double[n];(i = 0; i < n; i++)
{[i]=0;[i]=0; } <<rus(" введите начальное условие y(0)= ");
cin>>y[0];<<endl;(i = 0; i <= n; i++)
{=func(tip,x[i],y[i],a,b,c,d,e,f)*h;=func(tip,x[i]+h/2,
y[i]+(k1/2),a,b,c,d,e,f)*h;=func(tip,x[i]+h/2,
y[i]+(k2/2),a,b,c,d,e,f)*h;=func(tip,x[i]+h,
y[i]+k3,a,b,c,d,e,f)*h;[i+1]=y[i]+((1.0/6.0)*(k1+2*k2+2*k3+k4));[i+1]=x[i]+h;<<"y"<<i<<"=
"<<y[i]<<endl;
}("PAUSE");0;
}
Приложение 2