Специальные дискретные случайные процессы

Специальные дискретные случайные процессы

Содержание

1. Системная функция и импульсная характеристика

2.      Авторегрессионный процесс

.        Корреляционная функция и корреляционная матрица

.        Авторегрессионный скользящего среднего процесс (АРСС)

.        Процесс скользящего среднего (СС-процесс)

.        Линейное предсказание

.        Литература

1. Системная функция и импульсная характеристика

Рассмотрим дискретные случайные процессы и системы. Пусть системная функция H(z) имеет вид

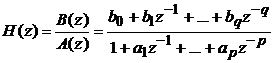
где p<q.

Полагая корни z_k уравнения A(z) = 0 простыми, получим разложение

,

где вычет

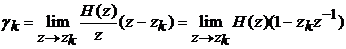
Импульсная характеристика системы принимает вид

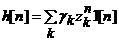
При наличии белого шума с единичной дисперсией на входе системы корреляционная функция отклика R[m] может быть выражена через систему - корреляционную функцию R_h [m]

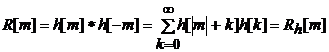
Спектральную плотность мощности S(w) дискретной системы можно разложить

,

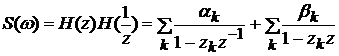где

,

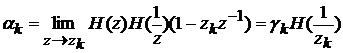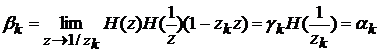
С учетом свойства четности корреляционную функцию можно записать как

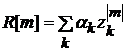
Отклик дискретной системы с системной функцией (1) при белом шуме u[n] на входе описывается разностным уравнением

x[n] +a₁ x[n-1] + … +a_p x[n - p] = b₀ u[n] + … +b_q u[n - q],

которое можно записать в виде

.

2. Авторегрессионный процесс

Случайный процесс x[n] называется авторегрессионным АР-процессом A(p),или процессом авторегрессии порядка p, если

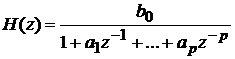
В этом случае случайный процесс удовлетворяет уравнению

x[n] +a₁ x[n-1] + … +a_p x[n - p] = b₀ u[n],

где u[n] - дискретный белый шум, M{u²[n]}=1.

В другой форме записи

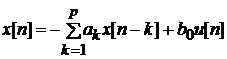
Модель авторегрессии выражает текущее значение процесса через линейную комбинацию предыдущих значений процесса и отсчета белого шума.

Название процесса - термин математической статистики, где линейная комбинация x = a₁y₁ + a₂ y₂ +…+ a_p y_p + z = z + a^Ty, связывающая неизвестную переменную x с отсчетами y = [y₁, y₂, …, y_p]^T, называется моделью регрессии (x регрессирует на y). В рассматриваемых соотношениях x[n] регрессирует на предыдущие отсчеты, поэтому - модель авторегрессии.

Процессы авторегрессии могут быть стационарными, так и нестационарными.

Для стационарности процесса необходимо, чтобы корни l_k характеристического уравнения

l^p + a₁l^p-1 + … + a_p =0

лежали внутри круга единичного круга (| l_I | < 1).

3. Корреляционная функция и корреляционная матрица

Пусть наблюдается вектор

x(n) = [x[n], x[n - 1], x[n - 2],…, x[n - N -1]]^T

Корреляционная матрица процесса R = M{x(n)x^H(n)} запишется как

,

где  - значение автокорреляционной функции дискретного процесса x(n).

Для стационарного процесса

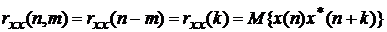
В качестве оценок корреляционных значений используются

-  несмещенная оценка

;

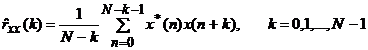-  смещенная оценка

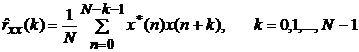
Напомним, что спектральная плотность мощности связана с корреляционной функцией через дискретное во времени преобразование Фурье

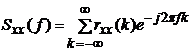
Корреляционная функция асимптотически стационарного АР-процесса АР(p) с нулевым средним

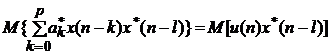, b₀ = 1

Дисперсия процесса

,

где D_z - дисперсия процесса z(n)=b₀ u(n);

r_i = r_xx(i)/r_xx(0) - коэффициент корреляции i -й составляющей процесса.

Для l > 0, текущие значения u(n) некоррелированные с выходными значениями x(n - l), что позволяет получить уравнение Юла - Уокера

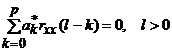, или

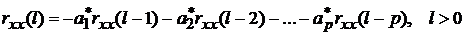
В матричном виде

Или

Параметры авторегрессии могут быть вычислены путем решения системы уравнений 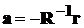, при условии, что инверсная матрица R^-1 существует. Наиболее удобно использовать для этих целей алгоритм Левинсона - Дурбина.

,

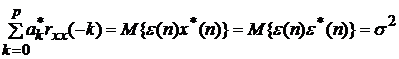где s² - дисперсия инновационного процесса,

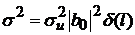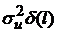,  - дисперсия белого шума;

e(n) = b₀u(n)

В матричном виде получаем

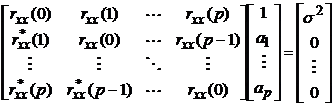, или

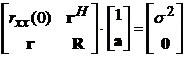
Для расчетов иногда удобна следующая форма записи

Матрица системы уравнений может быть представлена в виде суммы

Пример. Рассмотрим случай p = 2. Уравнения Юла - Уокера имеют вид

r_x(0) + a₁ r_x(1) + a₂ r_x(2) = D_z,_x(1) + a₁ r_x(2) + a₂ r_x(1) = 0,_x(2) + a₁ r_x(1) + a₂ r_x(0) = 0,

Матрица коэффициентов равна

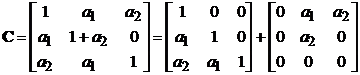
Значения корреляционной функции можно вычислить по формуле

,

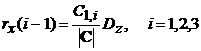где C_1,i алгебраические дополнения первой строки матрицы C; |C| -определитель матрицы.

Значения коэффициентов авторегрессионного процесса могут быть получены следующим образом

,

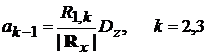_1,k - алгебраические дополнения элементов первой строки корреляционной матрицы.

Примем i = 1, тогда C_1,1 = 1 + a₂; |C| = (1 - a₂)[(1 + a₂)² - a₁²].

Дисперсия равна

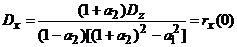
С учетом соотношений

C_1,2 = - a₁; C_1,3 = a₁² - a₂ (1 + a₂)

Определим последующие значения корреляционной функции

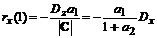
он удовлетворяет уравнению процесса

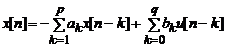
В этом случае, используя равенство

M{x[n - m]} u[n - r]} = 0 при m < r

и умножая на x[n - m] уравнение процесса, получим

R[m] + a₁ R[m - 1] + … + a_p R[m - p] = 0 , m > q ,

где R[n] - значение автокорреляционной функции процесса.

Системная функция формирующего фильтра для такого процесса имеет вид

,

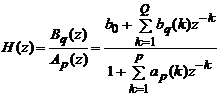где b_q(k) = b_k;

a_p(k) = - a_k.

Функция H(z) имеет p полюсов и q нулей.

При белом шуме на входе с постоянной дисперсией s_u² спектральная плотность мощности на выходе фильтра описывается выражением

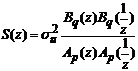
В частотной области

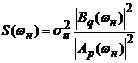
Рассматриваемый процесс часто обозначают как АРСС(p, q)-процессом, который удовлетворяет уравнению

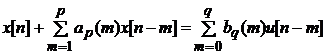
Таким же уравнением связаны друг с другом автокорреляционная функция r_x(k) и взаимная корреляционная функция r_x,u(k)

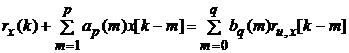
Если p ³ q и известны отсчеты корреляционной функции r_x(0), …, r_x(p-1), тогда значения r_x(k) при k ³ q могут быть вычислены рекуррентно

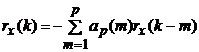
В данном случае уравнения Юла - Уокера нелинейны относительно коэффициентов формирующего фильтра и их решение в общем случае вызывает трудности.

дискретный импульсный случайный авторегрессия

5. Процесс скользящего среднего (СС-процесс)

Процесс скользящего среднего описывается уравнением

x[n] = b₀ u[n] + … + b_q u[n-q].

Другая форма записи

Системная функция представляется как

H(z) = b₀ + b₁ z ^-1 + … + b_q z ^-q.

Импульсная характеристика

h[n] = b₀ d[n]+ b₁ d[n-1]+ … + b_q d[n-q].

В случае использовании белого шума с дисперсией s_u², энергетический спектр процесса на выходе формирующего фильтра равен

S(z) = s_u² B_q(z) B(1/z).

В случае комплексного случайного процесса x[n] корреляционная функция равна

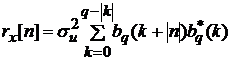
Пример. Найти энергетический спектр при формирующем фильтре первого порядка

Решение. Системная функция равна

H(z) = b₀ + b₁ z ^-1

Z-образ энергетического спектра при s_u² = 1 равен

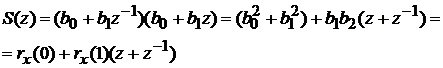
Частотная функция спектра имеет вид

Фильтр, формирующий СС(q)-процесс является нерекурсивным.

6. Линейное предсказание

Рассмотрим оценку отсчета АР(p)-процесса x[n - i] в точке (n - i) при использовании остальных отсчетов от x[n - M] до x[n]

{ x[n], x[n - 1], … , x[n - M]}

В соответствии с уравнением процесса искомую оценку можно записать в виде

,

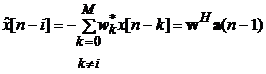где {w_k} - весовые коэффициенты предсказывающего фильтра,

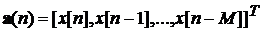- вектор данных

Ошибка предсказания

Найдем оптимальные весовые коэффициенты фильтра, которые минимизируют средний квадрат ошибки

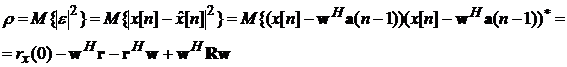
где r и R-соответственно вектор и матрица значений корреляционной функции.

Решение задачи минимизации эрмитовой функции r приводит к результату

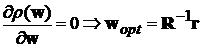
Литература

1. Шахтарин Б.И. Случайные процессы в радиотехнике. М.: Гелиос АРВ, 2006.

2.      Schwardt L. Digital Signal Processing (DSP813). University of Stellenboscgh, 2004