Метод корректировки программных решений близких линейно-квадратичных задач оптимального управления в классе импульсных управлений
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение
образования «Гомельский государственный университет имени Франциска Скорины»
Математический
факультет
Кафедра
вычислительной математики и программирования
Контрольная
работа
Метод
корректировки программных решений близких линейно-квадратичных задач
оптимального управления в классе импульсных управлений
Исполнитель студент
Мережа И.В.
Введение
Линейное программирование (ЛП) представляет
собой наиболее развитый раздел современной теории экстремальных задач. Для
решения таких задач используются численные алгоритмы построения приближенных
решений, которые позволяют получить сколь угодно точные ответы для любых
конкретных наборов параметров.
Создано много программ, более или менее
эффективно решающих общие конечномерные задачи ЛП больших размеров. Однако рост
сложности возникающих на практике задач заставляет непрерывно совершенствовать
и методы, и программы. Совершенствование идет в двух основных направлениях:
а) повышение возможностей универсальных методов
решения общих задач ЛП;
b) создание
специализированных методов, учитывающих особенности конкретных задач.
Грамотная реализация общих принципов ЛП на
специальных задачах позволяет получить программы, эффективность которых во
много раз превосходит эффективность универсальных программ.
При решении практических задач часто приходится
решать выпуклые задачи математического программирования. Особое значение для
теории и методов оптимизации имеют кусочно-линейные задачи. Такие задачи часто
встречаются как самостоятельные при моделировании прикладных задач или и
используются в качестве простейших аппроксимаций при исследовании нелинейных
гладких и негладких задач. Они являются хорошими объектами для выяснения
особенностей теории и методов решения общих негладких задач.
В данном проекте рассматривается решение
линейно-негладкой задачи оптимального управления с ограничениями. Для решения
мы использовали приведение нашей линейно-негладкой задачи к эквивалентной
выпуклой сепарабельной кусочно-линейной задачи, которую можно решить любыми
известными методами, например, прямыми опорными методами (первого или второго
порядка) или двойственными опорными методами (кусочно-линейного или линейного
программирования.
1. Задача минимизации среднеквадратичной интенсивности
управления
.1 Динамическая система управления. Формула Коши
Рассмотрим объект, состояние
которого в момент времени t описывается вектором состояния . На
поведение объекта на фиксированном отрезке времени T=[0,] можно
оказывать влияние с помощью управляющего воздействия u(t), . Объект
будем называть обыкновенной линейной динамической системой, если функции u(t), , связаны
уравнением:
скорость изменения состояния,
A - nЧn-матрица,
характеризующая динамические свойства объекта,
b - n-вектор параметров
входного устройства.
Согласно теории дифференциальных
уравнений, поведение объекта , , будет однозначным, если задать его начальное
состояние(1.2)и управляющее воздействие u(t), , из
класса кусочно-постоянных функций. Функцию u(t), будем
называть кусочно-постоянной, если существует такой набор моментов , что между
соседними моментами t=0; ; t= функция u(t), ,
принимает постоянные значения, причем
Функцию u(t), , будем
называть управлением, функцию , ему соответствующую - траекторией системы (1.1),
(1.2). Получим формулу, выражающую через начальное состояние и .
Для функций , выполняется тождество
, (1.3)
Рисунок 1.1 - Кусочно-постоянное
управление
Умножим обе части (1.3) на
непрерывную - матричную функцию , и проинтегрируем по от 0 до
t:, (1.4)
Проинтегрируем левую часть (1.4) по
частям:
, (1.5)
, (1.6)
Равенство (1.6) называют формулой
Коши, матричную функцию - фундаментальной матрицей решений однородной части:
динамической системы (1.1).Для рассматриваемой нами динамической системы часто
удобнее пользоваться другой фундаментальной матрицей решений системы : ,
которая является решением системы.
, (1.7)
При этом для рассматриваемых систем
справедливы следующие равенства, связывающие фундаментальные матрицы (1.5) и
(1.7):
Поэтому с помощью фундаментальной
матрицы (1.7) формулу Коши (1.6) можно переписать в следующем виде
.2 Управляемость
Пусть на ряду с системой (1.1),
(1.2) имеется выходное устройство
, (1.8)
Система (1.1), (1.2) называется
управляемой на отрезке T по выходу (1.8), если для любого m-вектора g найдется
такое управление u(t), , что
соответствующая ему траектория , системы (1.1), (1.2) порождает выходной сигнал
(1.8), принимающий в конечный момент значение .
Такого вида управляемость называют
относительной управляемостью (управляемостью относительно линейного
многообразия ).
Теорема 1.1 (общий критерий
относительной управляемости) Для управляемости системы (1.1), (1.2) на отрезке T по выходу
(1.8) необходимо и достаточно, чтобы при любом m-векторе , ,
выполнялись соотношение
(1.9)
Доказательство. Необходимость
(доказательство от противного).Пусть система (1.1), (1.2) управляема на отрезке
Т по выходу (1.8), но при некотором
,, (1.10)
Поскольку , то такой, что
, (1.11)
Поскольку система управляема, то
существует управление , , переводящее траекторию системы (1.1), (1.2) из
начального состояния на многообразие ,. Используя формулу Коши (1.6), последнее
равенство запишем в виде
, (1.12)
Умножим равенство (1.12) на :, но из
(1.11) следует, что . Полученное противоречие доказывает
невозможность тождества (1.10). Достаточность. Рассмотрим управления вида
,(1.13). Используя формулу Коши (1.6), условие управляемости на таких
управлениях принимает вид:
, (1.14)
Введем m×m-матрицу
, (1.15)
. (1.16)
Из (1.14)-(1.16) следует, что для
управляемости достаточно, чтобы уравнение ,(1.17) было разрешимо относительно
при любых . Итак, пусть выполняется условие (1.9). Тогда матрица (1.15) -
невырожденная. Действительно, если предположить противное, то при некотором ,
будем иметь . Умножим (1.15) слева и справа на
:
Следовательно, , что противоречит
условию (1.9). В силу не вырожденности матрицы уравнение (1.17) можно
разрешить относительно µ при любых , т.е. управлениями вида (1.13) можно
разрешить задачу управляемости. Теорема доказана. Из теоремы 1.1 вытекают
теоремы 1.2 и 1.3: Теорема 1.2 (вторая форма критерия относительной
управляемости) Для управляемости системы (1.1), (1.2) на отрезке Т по выходу
(1.8) необходимо и достаточно, чтобы rank.
Доказательство. Основываясь на
соотношении (1.9), рассмотрим функцию .(1.18)С учетом (1.5) вычислим
(1.19)
Согласно теореме Гамильтона-Кэли,
каждая квадратная матрица удовлетворяет своему характеристическому уравнению
(1.20)
Следовательно, функция (1.18) является
решением уравнения
(1.21)
получим начальные условия для
(1.21):
(1.22)
Как решение однородного уравнения
(1.21) функция , при фиксированном тогда и только тогда, когда среди начальных
значений (1.22) есть отличные от нуля: (1.23) Поэтому функция , для всех ,
тогда и только тогда, когда соотношения (1.23) выполняются при всех . Последнее
возможно, если .
Теорема 1.3 (опорный критерий
относительной управляемости) Для управляемости системы (1.), (1.2) на отрезке Т
по выгоду (1.8) необходимо и достаточно существования такого множества
изолированных: моментов , для которого не вырождена m×m-матрица
(1.24) со
столбцами .
Доказательство. Необходимость. Пусть
система (1.1), (1.2) управляема на отрезке Т по выходу (1.8). Подсчитаем число
(1.25) Согласно (1.9), α>0.
Из
(1.25) следует:
,(1.26)
, что (1.27)
На отрезке Т возьмем произвольный
момент такой, что . Построим вектор , ортогональный вектору . Используя
(1.27), по вектору найдем момент такой, что . Тогда векторы , будут линейно
независимыми.
Пусть - набор изолированных
моментов, на котором матрица Р (1.24) не вырождена. Поскольку со столбцами.
Рассмотрим управления вида(1.28) считая без ограничения общности, что, т. Тогда
условие управляемости принимает вид
(1.29)
где определяется согласно (1.16).
Уравнение (1.29) разрешимо относительно в силу не вырожденности матрицы M.
Следовательно, управлениями (1.28) можно разрешить задачу управляемости.
.3 Постановка задачи оптимального
управления
Линейно-квадратичную функцию 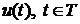 , и
соответствующую ей траекторию
, и
соответствующую ей траекторию 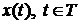 , системы (1.1), (1.2) назовем
допустимым управлениями допустимой траекторией, если на
, системы (1.1), (1.2) назовем
допустимым управлениями допустимой траекторией, если на 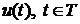 ,
выполняются геометрические ограничения
,
выполняются геометрические ограничения  (1.30)(
(1.30)(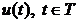 , является
доступным управлением), и в конечный момент на
, является
доступным управлением), и в конечный момент на 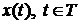 , выполняется терминальное
ограничение
, выполняется терминальное
ограничение
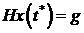 (1.31)
(1.31)
Качество допустимых управлений будем
оценивать по значениям функционала
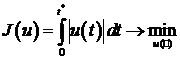 (1.32)
(1.32)
Допустимое управление , и траекторию
, назовем оптимальными, если на них критерий качества (1.32) достигает
минимального значения
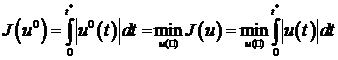 (1.33)
(1.33)
Задача оптимального управления состоит
в построении оптимального управления. Ее компактная форма имеет вид:

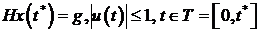 (1.34)
(1.34)
Целью оптимизации может быть
построение -оптимального управления. Допустимым управлением 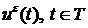 , и
соответствующая траектория
, и
соответствующая траектория 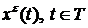 , называются
, называются 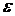 -оптимальными,
если на них значение критерия качества удовлетворяет неравенству
-оптимальными,
если на них значение критерия качества удовлетворяет неравенству
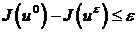 (1.35)
(1.35)
2. Критерий оптимальности
.1 Опора. Опорное управление
Если в задаче (1.34) с помощью
формулы Коши (1.6) исключить ,, то получим задачу линейного программирования в
функциональном пространстве управлений:
, ,(2.1)
где , ; .
Совокупность из m
изолированных моментов , назовем опорой, если не вырождена m×m-матрица , ).
Согласно п. 1.2, в задаче (1.34) опора существует в том и только том случае,
если система (1.1), (1.2) управляема на отрезке Т по выходу (1.8).
Пару из допустимого управления и
опоры назовем опорным управлением. Будем называть его невырожденным, если
, ,(2.2)
.2 Формула приращения критерия
качества
Пусть - опорное управление. На
допустимых управлениях и соответствующих им траекториях подсчитаем приращение
критерия качества (1.32):
(2.3)
для таких вариаций, , для которых ,
(2.4) Поскольку
допустимая вариация траектории , удовлетворяет уравнению
, , , (2.5)
То, используя формулу Коши (1.6)
получим
,(2.6)
, (2.7)
, (2.8)
где у - произвольный m-вектор.
Из (2.8), (1.5) имеем
,
т.е. функция , , является решением
уравнения
, (2.9)
,.(2.10)
+
=
(2.11)
Вектор выберем так, чтобы в формуле
приращения (2.11) коэффициенты при в опорные моменты , были равны нулю (учтем
при этом, что в опорные моменты должны выполняться условия (2.4)):
,
(2.12)
Вектор (2.12) назовем вектором
потенциалов, решение , , системы (2.9), (2.12) (т.е. решение сопряженной
системы (2.9), соответствующее вектору потенциалов (2.12)) - котраекторией в
задаче (1.34).
.3 Критерий оптимальности
Пусть - опорное управление.
Подсчитаем по нему вектор потенциалов (2.12), траекторию , , (2.9), (2.12) и
функцию , (2.10). Теорема 2.1 (критерий оптимальности) Для оптимальности
допустимого управления , , в задаче (1,34) достаточно существования такой опоры
, что для опорного управления выполняются соотношения: при ; при ; при ;при ,
(2.13)
В случае невырожденности опорного
управления соотношения (2.13) являются необходимыми для оптимальности
допустимого управления. , Доказательство. Достаточность. Пусть для опорного
управления соотношения (2.13) выполняются. Тогда (это нетрудно показать) для
любой допустимой вариации управления , , из (2,11) получаем:что и доказывает
достаточную часть критерия оптимальности.
Необходимость (доказательство от
противного). Пусть , -оптимальное управление, а - невырожденное опорное
управление (2.2) задачи (1.34). Предположим, что, вопреки утверждению,
соотношения (2.13) не выполняются, т. е. существует такая точка , в которой эти
соотношения нарушаются (очевидно, ). Для определенности предположим, что для
момента соотношения (2.13) нарушаются следующим образом: , u(.Из
непрерывности функции , , и кусочной непрерывности управления , , следует
существование такого числа , что для всех , выполняются соотношения:
(2.14)
Где , если не является граничной
точкой отрезка и не является точкой разрыва управления , ; в противном случае
заменим здесь и в последующих рассуждениях отрезок на один из отрезков или .
В силу невырожденности опорного управления найдутся такие числа , что для всех
, выполняются соотношения:
(2.15)
Пусть число выбрано так, что для
всех , выполняются и соотношения (2.14), и соотношения (2.15), причем Для
каждого , построим вариацию управления , , следующим образом. Положим
Вариацию управления на отрезках , ,
построим в виде постоянных функций . Из равенства
, (2.16)
Справедливого для каждой допустимой
вариации управления, следует
, (2.17)
Разложив левую часть равенства
(2.17) по степеням в точках
:
, , получим
т.е.
(2.18)
Поскольку , то для достаточно малых
, будем иметь , где . Тогда из (2.18) получаем
,
т.е.(2.19)
В силу линейной зависимости (2.19) и
невырожденности (2.15) опорного управления для достаточно малых и ,
выполняются соотношения:
.
Тогда управление вида
(2.20)
Полученное противоречие доказывает
необходимую часть критерия оптимальности (остальные случаи нарушения
соотношений (2.13) исследуются аналогично).
3. Классы допустимых управлений
.1 Предельный класс допустимых
управлений
Из соотношений (2.13) становится
очевидной структура оптимального управления. Пусть - опорное управление, для
которого выполняются соотношения (2.13). По (оптимальному) опорному управлению
однозначно строятся (оптимальный) вектор потенциалов (2.12), (оптимальная)
траектория , - решение сопряженной системы (2.9), (2.12) и (оптимальная)
функция , (2.10).
Согласно соотношениям (2.13),
оптимальное управление , , полностью определяется с помощью ( оптимальной )
непрерывной функции , : на тех участках , ( критических ), на которых |,, ,
управление принимает критические значения 1 или -1 или , , ); между
критическими участками оптимального управления находятся участки , , на которых
выполняется неравенство |,, , (на них управление тождественно равно нулю: ,, ).
.2 Класс импульсных управлений.
эквивалентная задача линейно-квадратичного программирования
Задачу (1.34) рассмотрим в классе
импульсных управлений, т.е. кусочно-постоянных функций с постоянным периодом
квантования . Для
этого выберем целое число
, и разобьем отрезок на равных частей (рассмотрим сетку с равностоящими
узлами).
.(4.1)
. (4.2)
Тогда, для элементов задачи (1.34)
получим: Для критерия качества
(4.3)
для геометрического ограничения
, :. (4.4)
Используя формулу Коши (для системы
, ). Введем обозначения для множеств, векторов и матриц:
;
задача программа
квадратичный корректировка
Тогда в классе импульсных управлений
(4.2) задача (1.34) эквивалентна следующей выпуклой сепарабельной
кусочно-линейной задаче (постоянный множитель h на минимум
целевой функции не влияет).
4. Корректировка решения близких
задач в классе импульсных управлений
.1 Выбор метода корректировки
Самым легким выходом при поиске
решения задачи (4.6)-(4.8) является сведение линейно-квадратичной задачи к
эквивалентной задаче линейного программирования, и решение этой эквивалентной
задачи известными методами (например, адаптивным методом, двойственным методом
и т.д.). Однако при видимой простате такого подхода, он имеет ряд недостатков.
Во-первых, существенно увеличиваются размеры задачи: число переменных
увеличивается в 3 раза, число основных ограничений увеличивается на n, т.е. их
оказывается m+n (в исходной
задаче основных ограничений было . Во-вторых, стандартные методы ЛП не будут
учитывать специфику полученной эквивалентной задачи ЛП: специальную структуру
матрицы основных ограничений и ее заполненность, специальный вид целевой
функции, зависимость (согласованность) компонент плана.
Все выше сказанное было продемонстрировано в п.
4.Решение конкретной задачи это только первый этап. В жизни приходиться решать
множество близких задач, потому что значение параметров с течением времени
меняется. В классических методах оптимизации для математического программирования
с помощью теории двойственности исследуется проблема чувствительности решения
задачи с малым изменением параметров.
Приходится решать близкие эквивалентные задачи и
ставиться проблема не нахождения решения новой задачи, а только корректировка
решения предыдущей задачи до решения новой измененной задачи. С этой целью
лучше всего использовать двойственный метод, поскольку он в этих условиях
работает лучше всего.
4.2 Использование программы конечного
двойственного метода линейно квадратичного программирования
Программа DMQP-
программа конечного двойственного метода линейно-квадратичного
программирования. Как и прежде рассматриваем задачу линейно -
квадратичного программирования:
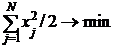 ,
, 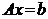 ,
, 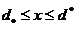 ,
,
где 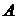 - двумерный
массив основных ограничений размерности
- двумерный
массив основных ограничений размерности 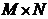 ,
,
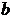 - вектор-столбец размерности
- вектор-столбец размерности
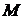 ,
, 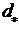 и
и 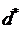 - нижнее и верхнее
ограничениям на переменные,
- нижнее и верхнее
ограничениям на переменные,
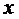 - вектор-столбец размерности
- вектор-столбец размерности  ,
соответствующий начальному плану задачи,
,
соответствующий начальному плану задачи,
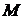 - количество основных ограничений
задачи,
- количество основных ограничений
задачи,  - количество
переменных.
- количество
переменных.
Программа корректировки решений
близких задач линейно-квадратичного программирования написана на языке С. Для
решения задачи используем двойственный метод. Программа конечного двойственного
метода линейно-квадратичного программирования написана на языке фортран и
скомпилирована в файл dmqp.exe.
Запуск этого файла осуществляется с
помощью оператора System. При этом формируются входной и
выходной файлы. Входной файл имеет следующую структуру: В файле: 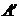 -
транспонированный двумерный массив
-
транспонированный двумерный массив 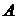 ,
, 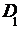 и
и 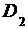 соответственно равны
соответственно равны 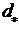 и
и 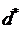 ,
, 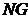 - размер
опоры ограничений начального согласованного опорного плана,
- размер
опоры ограничений начального согласованного опорного плана, 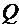 - обратная
матрица к опорной матрице,
- обратная
матрица к опорной матрице, 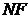 - размер опоры целевой функции
начального согласованного опорного плана,
- размер опоры целевой функции
начального согласованного опорного плана, 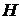 - вектор-столбец, содержащий
элементы верхнего треугольника матрицы, обратной к опорной матрице целевой
функции, записанные по строчкам;
- вектор-столбец, содержащий
элементы верхнего треугольника матрицы, обратной к опорной матрице целевой
функции, записанные по строчкам; 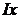 - вектор-столбец размерности
- вектор-столбец размерности 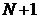 , который
содержит следующую информацию: индексы опорных компонент начального плана,
вошедшие в опору ограничений (их количество
, который
содержит следующую информацию: индексы опорных компонент начального плана,
вошедшие в опору ограничений (их количество 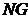 ); индексы опорных компонент
начального плана, вошедшие в опору целевой функции (их количество
); индексы опорных компонент
начального плана, вошедшие в опору целевой функции (их количество 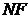 ); индексы
неопорных компонент начального плана (их количество
); индексы
неопорных компонент начального плана (их количество  ).
).
Выходной файл содержит следующую
результирующую информацию: значение параметра 1111. Если он равен нулю,
то построен оптимальный план задачи; размерность опоры ограничений; опору
ограничений; размерность опоры целевой функции; опору целевой функции;
неопорные индексы; оптимальный план задачи.
Заключение
В курсовой работе была
сформулирована линейно-квадратичная задача оптимального управления с ограничениями.
Были сформулированы понятия управляемости, оптимального управления. Были
сформулированы теоремы о достаточном условии оптимальности критерии
управляемости основного ограничения, была выведена формула приращения критерия
качества. На основе полученных сведений был доказан критерий оптимальности. Был
описан класс допустимых управлений для линейно-квадратичной задачи. Были
сформулированы эквивалентные задачи линейного программирования.
Список использованных источников
1. Габасов, Р. Методы линейного
программирования: в 3 ч. Ч. 1. Общие задачи, Ч. 2. Транспортные задачи, Ч. 3.
Специальные задачи / Р. Габасов, Ф. М. Кириллова. - Мн.: БГУ, 1977, 1978, 1980.
- 176 c., 240 c.,
368 c.
2. Габасов, Р. Конструктивные
методы оптимизации: в 5 ч. Ч. 1. Линейные задачи / Р. Габасов, Ф.М. Кириллова,
А.И. Тятюшкин. - Мн.: БГУ, 1983. - 214 с.
. Конструктивные методы
оптимизации: в 5 ч. Ч. 4. Выпуклые задачи / Р. Габасов [и др.]. - Мн.:
Университетское, 1987. - 223 c.
. Альсевич, В.В. Оптимизация
линейных экономических моделей. Статические задачи / В.В. Альсевич, Р. Габасов,
В.С. Глушенков. - Мн.: БГУ, 2000. - 210 с.
. Лубочкин А.В. Методы
решения выпуклых задач оптимального управления: дис. на соиск. уч. cтеп.
канд. физ.-мат. наук / А.В. Лубочкин; БГУ. - Мн., 1987. - 132 с.
. Численные методы
оптимизации: в 2 ч. Ч. 1. Линейные статические задачи: практикум / [М-во образ.
РБ; Гомельск. гос. ун-т им. Ф. Скорины; авторы-составители А.В. Лубочкин, Е.А.
Ружицкая]. - Гомель: ГГУ им. Ф.Скорины, 2001. - 50 с.
. Численные методы
оптимизации: в 2 ч. Ч. 2. Линейные задачи оптимального управления: практикум /
[М-во образ. РБ; Гомельск. гос. ун-т им. Ф. Скорины; авторы-составители А.В.
Лубочкин, Е. Ружицкая]. - Гомель: ГГУ им. Ф. Скорины, 2001. - 55 с.
. Лубочкин, А.В. Оптимизация
выпуклых статических моделей: тексты лекций по спецкурсу / А.В. Лубочкин; М-во
образ. РБ; Гомельск. гос. ун-т им. Ф. Скорины. - Гомель: ГГУ им. Ф.Скорины,
2005. - 74 с.
. Лубочкин, А.В. Оптимальное
управление линейными системами по выпуклым критериям качества: тексты лекций по
спецкурсу / А.В. Лубочкин; М-во образ. РБ; Гомельск. гос. ун-т им. Ф. Скорины.
- Гомель: ГГУ им. Ф. Скорины, 2009. - 55 с.