Математический пакет Maple
Введение
В настоящее время научное программирование претерпевает серьезную
трансформацию: развиваются интегрированные среды, основанные на алгоритмических
языках, и растет применение универсальных математических систем ( Maple, Mathematics, MATLAB. MatCad и
др.). Эти системы имеют дружественный интерфейс, реализуют множество
стандартных и специальных математических операций, снабжены мощными
графическими средствами и обладают собственными языками программирования. Все
это предоставляет широкие возможности для эффективной работы специалистов
разных профилей, о чем говорит активное применение математических пакетов в
научных исследованиях и в преподавании. Система аналитических вычислений Maple -
хороший выбор для проведения любого исследования, где требуется математика - от
курсовой работы до научного открытия. С помощью этих пакетов проще готовить и
выполнять задания, устраивать демонстрации и гораздо быстрее решать
исследовательские и инженерные задачи.
Математический пакет Maple - интеллектуальный лидер в своих классах и образец, определяющий
развитие компьютерной математики. Компьютерная алгебра Maple вошла составной
частью в ряд современных пакетов. Сам пакет постоянно совершенствуются,
развивая аппарат и пополняя ресурсы. Пакет Maple - мощная и хорошо
организованная система, надежная и простая в работе. Освоение даже части его
возможностей даст несомненный эффект, а по мере накопления опыта придет
настоящая эффективность от взаимодействия с ним. Еще одним достоинством пакета
является неизменность набора основных команд и конструкций языка при появлении
новых версий.
Язык Maple - это функции и команды сравнительно небольшого по объему, но
быстрого ядра, написанного на языке Cи, основной библиотеки, содержащей около
500 команд и функций, написанных уже на собственном языке Maple, и большого
количества специализированных библиотек, также написанных на собственном языке
Maple и расширяющих “способности” Maple в различных областях математики.
Пожалуй, наиболее важная особенность системы - открытость архитектуры, т.е.
возможность редактировать и изменять подпрограммы библиотек, а также пополнять
библиотеки собственными подпрограммами. Благодаря этому за короткое время было
создано большое число Maple-подпрограмм, целиком написанных пользователями из
самых разных областей науки и техники. Лучшие подпрограммы пополняют библиотеку
пользователей, так называемую Share-библиотеку, которая распространяется вместе
с пакетом Maple.
К настоящему времени программа Maple превратилась в мощную вычислительную
систему, предназначенную для выполнения сложных проектов. Maple умеет
производить сложные алгебраические преобразования и упрощения над полем
комплексных чисел; находить конечные и бесконечные суммы, произведения, пределы
и интегралы; находить все корни многочленов; решать аналитически и численно
алгебраические (в том числе трансцендентные) системы уравнений и неравенств, а
также системы обыкновенных дифференциальных уравнений и некоторые классы
уравнений в частных производных. В Maple включены специализированные пакеты
подпрограмм для решения задач линейной и тензорной алгебры; евклидовой и
аналитической геометрии; теории чисел; комбинаторики, теории вероятностей и
математической статистики; теории групп; численной аппроксимации и линейной оптимизации
(симплекс-метод); финансовой математики; для выполнения интегральных
преобразований и многих других задач.
Глава I.
Дискретная минимаксная задача с ограничениями на параметры
минимаксный
задача matlab mарle
Минимакс (минимизация максимального уклонения) - принцип оптимального
выбора параметров.
.1 Постановка
задачи
Пусть
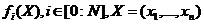 , - функции, заданные и непрерывно дифференцируемые на
некотором открытом множестве
, - функции, заданные и непрерывно дифференцируемые на
некотором открытом множестве 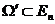 .
Предположим также, что задано выпуклое замкнутое (не обязательно ограниченное)
множество
.
Предположим также, что задано выпуклое замкнутое (не обязательно ограниченное)
множество  .
.
Требуется
найти точку 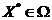 , для которой
, для которой
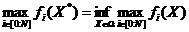 .
.
Введем в рассмотрение функцию
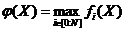 .
.
Эта
функция задана на 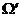 . Поставленная задача сводится к минимизации функции
. Поставленная задача сводится к минимизации функции  на множестве
на множестве 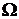 . Функция
. Функция
 является дифференцируемой по всем направлениям в
любой точке множества
является дифференцируемой по всем направлениям в
любой точке множества 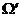 ; в частности, везде на
; в частности, везде на 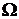 .
.
1.2 Необходимые
условия минимакса
1.
Предположим, что на некотором открытом множестве 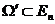 заданы
непрерывно дифференцируемые функции
заданы
непрерывно дифференцируемые функции 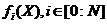 . Как и
ранее, будем использовать обозначения
. Как и
ранее, будем использовать обозначения

Пусть
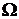 - выпуклое замкнутое множество, содержащееся в
- выпуклое замкнутое множество, содержащееся в 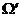 . Рассматривается задача минимизации функции
. Рассматривается задача минимизации функции  на
на  .
.
Теорема
2.1. Для того чтобы точка 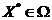 была точкой минимума функции
была точкой минимума функции  на множестве
на множестве  ,
необходимо, а в случае выпуклости
,
необходимо, а в случае выпуклости  на
на 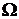 и достаточно, чтобы
и достаточно, чтобы
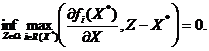
Замечание 1. Нетрудно проверить, что необходимое условие (2.1)
эквивалентно следующему равенству:
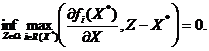 (2.1)
(2.1)
Было
показано, что при фиксированном 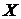 функция
функция

является
непрерывной по  функцией на всем пространстве
функцией на всем пространстве 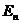 . Поскольку множество
. Поскольку множество  ,
,
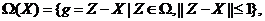
при
любом фиксированном 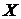 является замкнутым и ограниченным, то отсюда следует,
что функция
является замкнутым и ограниченным, то отсюда следует,
что функция 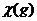 достигает своего минимума на
достигает своего минимума на  .
.
Учитывая
это замечание, заключаем, что инфимум, стоящий в левой части соотношения
(2.1'), достигается, и условие (2.1') может быть переписано в виде
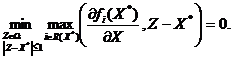
Замечание
2. При 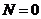 из теоремы 2.1 следует необходимое условие минимума
непрерывно дифференцируемой функции
из теоремы 2.1 следует необходимое условие минимума
непрерывно дифференцируемой функции 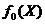 на выпуклом множестве
на выпуклом множестве  : для
того чтобы непрерывно дифференцируемая функция
: для
того чтобы непрерывно дифференцируемая функция 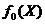 достигала
своего минимального на
достигала
своего минимального на  значения в точке
значения в точке 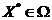 ,
необходимо, а в случае выпуклости
,
необходимо, а в случае выпуклости 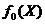 на
на  и достаточно, чтобы
и достаточно, чтобы
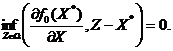 (2.9)
(2.9)
Определение.
Точка 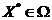 , для которой выполняется соотношение (2.1),
называется стационарной тонкой функции
, для которой выполняется соотношение (2.1),
называется стационарной тонкой функции  на
на  .
.
.
Возьмем любую точку 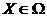 и зафиксируем ее.
и зафиксируем ее.
Рассмотрим
конус 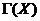 :
:
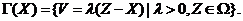
Очевидно,
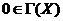 . Замыкание конуса
. Замыкание конуса 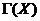 называется
конусом возможных направлений множества
называется
конусом возможных направлений множества  в точке
в точке  и обозначается
и обозначается
Теорема
2.2. Соотношение (2.1) эквивалентно неравенству
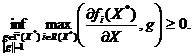 (2.10)
(2.10)
Доказательство
см. Демьянов, стр. 148-149.
Замечание
1. Так как множество

замкнуто
и ограничено, то инфимум в левой части (2.10) достигается, и поэтому
неравенство (2.10) может быть переписано в виде
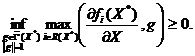 (2.10')
(2.10')
Замечание
2. Рассмотрим случай 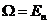 . Для любой точки
. Для любой точки 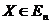 будем
иметь
будем
иметь
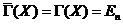 ,
,
так
что условие (2.10') примет вид
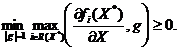
.3
Геометрическая интерпретация необходимых условий
1.
Зафиксируем 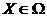 , и пусть
, и пусть 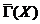 - конус
возможных направлений множества
- конус
возможных направлений множества 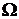 в точке
в точке 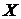 . Введем в рассмотрение сопряженный конус
. Введем в рассмотрение сопряженный конус 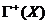 :
:
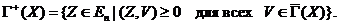
Конус
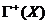 является замкнутым и выпуклым множеством.
является замкнутым и выпуклым множеством.
Пусть,
как и ранее,
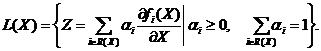
Теорема 3.1. Соотношение (2.1) (или, что то же самое, (2.10))
эквивалентно следующему условию:
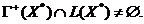 (3.1)
(3.1)
Замечание
1. Если 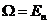 , то
, то 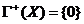 для
любого
для
любого 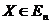 . В этом случае условие (3.1) эквивалентно следующему
включению:
. В этом случае условие (3.1) эквивалентно следующему
включению:
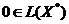 . (3.4)
. (3.4)
Соотношение
(3.4) совпадает с необходимым условием минимакса на всем пространстве 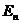 .
.
Замечание
2. Пусть 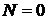 . В этом случае
. В этом случае 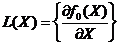 для
любого
для
любого 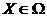 . Учитывая (3.1), получаем следующее геометрическое
условие минимума непрерывно дифференцируемой функции, на множестве
. Учитывая (3.1), получаем следующее геометрическое
условие минимума непрерывно дифференцируемой функции, на множестве  .
.
Для
того чтобы непрерывно дифференцируемая функция 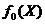 достигала
своего минимального на
достигала
своего минимального на  значения в точке
значения в точке 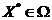 ,
необходимо, а в случае выпуклости
,
необходимо, а в случае выпуклости 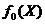 на
на  и достаточно, чтобы
и достаточно, чтобы
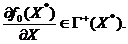
.
Возьмем теперь любую точку  .
Построим для этой точки многогранник
.
Построим для этой точки многогранник 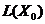 и конус
и конус 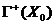 . Положим
. Положим
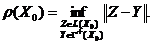 (3.5)
(3.5)
Поскольку
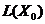 и
и 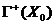 -
замкнутые множества и одно из них (
-
замкнутые множества и одно из них (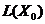 )
ограничено, то инфимум в (3.5) достигается. Таким образом, существуют такие
точки
)
ограничено, то инфимум в (3.5) достигается. Таким образом, существуют такие
точки  и
и  , что
, что
 . (3.6)
. (3.6)
Если
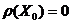 , то точка
, то точка  является
стационарной точкой функции
является
стационарной точкой функции  на множестве
на множестве
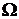 , ибо в этом случае, очевидно, выполняется условие
(3.1).
, ибо в этом случае, очевидно, выполняется условие
(3.1).
Пусть
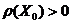 , т.е.
, т.е.  - не
стационарная точка. Нетрудно показать, что в этом случае вектор
- не
стационарная точка. Нетрудно показать, что в этом случае вектор 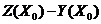 , удовлетворяющий соотношению (3.6), единствен. Введем
обозначение
, удовлетворяющий соотношению (3.6), единствен. Введем
обозначение
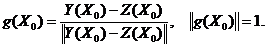
Определение.
Вектор 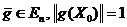 , называется направлением наискорейшего спуска функции
, называется направлением наискорейшего спуска функции
 на множестве
на множестве  в точке
в точке  , если
, если

Теорема
3.2. Если 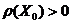 , то направление
, то направление 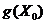 является
направлением наискорейшего спуска функции
является
направлением наискорейшего спуска функции  на
множестве
на
множестве  в точке
в точке  при этом
при этом
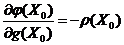 (3.7)
(3.7)
Лемма
3.1. Справедливо равенство
Замечание
1. Направление наискорейшего спуска функции  на
множестве
на
множестве  в точке
в точке  в
случае, если
в
случае, если 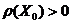 , единственно.
, единственно.
Замечание
2. В теореме 3.2 утверждается лишь, что 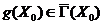 .
.
Может
случиться, что при любых  точки
точки 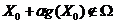 , так что
движение в направлении наискорейшего спуска может оказаться невозможным.
, так что
движение в направлении наискорейшего спуска может оказаться невозможным.
.
В качестве примера рассмотрим функцию

Где 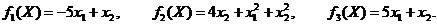
Возьмем
точку 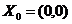 . Как было показано раньше,
. Как было показано раньше, 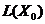 есть треугольник, натянутый на точки (-5, 1), (0, 4),
(5, 1). Так как
есть треугольник, натянутый на точки (-5, 1), (0, 4),
(5, 1). Так как  , то
, то  не
является стационарной точкой функции
не
является стационарной точкой функции  на
на 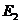 .
.
Введем ограничение


Нетрудно проверить, что в этом случае
 .
.
 .
.
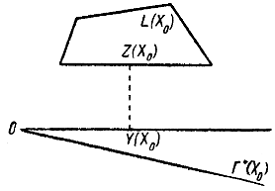
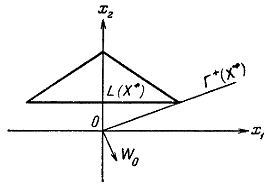
Так
как луч 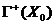 пересекает множество
пересекает множество 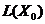 (рис.),
то
(рис.),
то  является стационарной точкой функции
является стационарной точкой функции  на множестве а поскольку
на множестве а поскольку  - выпуклая функция, то
- выпуклая функция, то  - точка
минимума функции
- точка
минимума функции  на
на  .
.

Введем
теперь другое ограничение:
 .
.
В
этом случае 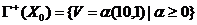 . Так как
. Так как 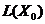 и
и 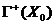 не имеют общих точек, то
не имеют общих точек, то 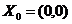 не является стационарной точкой функции
не является стационарной точкой функции  на множестве
на множестве  .
Нетрудно найти направление наискорейшего спуска функции
.
Нетрудно найти направление наискорейшего спуска функции  в точке
в точке  на
множестве
на
множестве  . Это есть вектор
. Это есть вектор
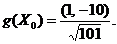
Заметим,
что  при всех
при всех 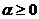 .
.
Положим,
наконец,

Нетрудно
проверить, что в этом случае
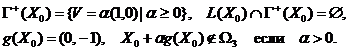
Таким
образом, 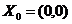 не является стационарной точкой функции
не является стационарной точкой функции  на множестве
на множестве 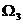 . Вместе
с тем движение вдоль направления наискорейшего спуска невозможно, ибо
направление
. Вместе
с тем движение вдоль направления наискорейшего спуска невозможно, ибо
направление 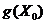 выводит нас из области
выводит нас из области 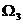 .
.
1.4
Достаточные условия локального минимакса при наличии ограничений
1.
Если  - выпуклая функция, то любая стационарная точка
функции
- выпуклая функция, то любая стационарная точка
функции  на
на  есть
точка минимума
есть
точка минимума  на
на  . Ниже
устанавливаются достаточные условия локального минимакса.
. Ниже
устанавливаются достаточные условия локального минимакса.
Пусть
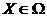 . Введем в рассмотрение функцию
. Введем в рассмотрение функцию
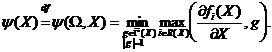
Тогда необходимое условие (2.10) может быть переписано в виде
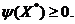
Определение.
Точка 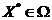 называется точкой локального минимума функции
называется точкой локального минимума функции  на множестве
на множестве  , если
существует такое
, если
существует такое  , что для
, что для 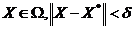 , будет
, будет
 .
.
Если
при тех же условиях для  , выполняется неравенство
, выполняется неравенство
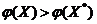 ,
,
то
 называется точкой строгого локального минимума
функции
называется точкой строгого локального минимума
функции  на
на  .
.
Теорема
4.1. Пусть 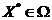 - стационарная точка функции
- стационарная точка функции  на
на  . Если
при этом
. Если
при этом
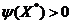 , (4.1)
, (4.1)
то
 является точкой строгого локального минимума функции
является точкой строгого локального минимума функции  на
на  . Выясним
теперь геометрический смысл условия (4.1).
. Выясним
теперь геометрический смысл условия (4.1).
Теорема
4.2. Условие (4.1) эквивалентно тому, что множество 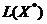 и конус
и конус 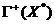 не могут
быть отделены, т.е. не существует ненулевого вектора
не могут
быть отделены, т.е. не существует ненулевого вектора  и числа а таких, что
и числа а таких, что
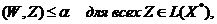 (4.5)
(4.5)
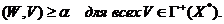 (4.6)
(4.6)
Следствие.
Если 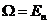 , то
, то 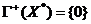 , и
потому условие неотделимости
, и
потому условие неотделимости 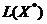 и
и 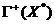 означает, что 0 - внутренняя точка множества
означает, что 0 - внутренняя точка множества 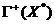 .
.
2. Приведем пример, показывающий, что стационарная точка может и не быть
точкой локального минимума, если не выполнено условие (4.1).
Пример. Пусть
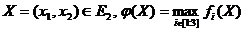
Где

Положим
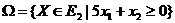 . Возьмем точку
. Возьмем точку 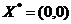 . Ясно, что
. Ясно, что  ;
; 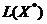 есть треугольник с вершинами в точках (-5, 1), (0,
4), (5, 1);
есть треугольник с вершинами в точках (-5, 1), (0,
4), (5, 1); 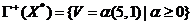 . Нетрудно проверить (рис. 31), что
. Нетрудно проверить (рис. 31), что
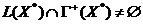 ,
,
так
что 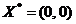 является стационарной точкой функции
является стационарной точкой функции  на
на  .
.
С
другой стороны, условие 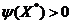 не выполнено, поскольку
не выполнено, поскольку 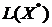 и
и 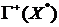 могут
быть отделены прямой
могут
быть отделены прямой

где
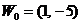 . Действительно,
. Действительно,
 ,
,
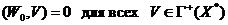 .
.
Таким
образом,  .
.
Покажем,
что  не является точкой локального минимума функции
не является точкой локального минимума функции  на
на  . Возьмем
точку
. Возьмем
точку  . Очевидно,
. Очевидно, 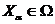 . Имеем
. Имеем

Отсюда
следует, что при малых  будет
будет
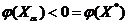 ,
,
т.е.
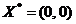 не является точкой локального минимума функции
не является точкой локального минимума функции  на
на  .
.
Заметим,
что этот эффект вызван тем, что функция 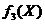 не
является выпуклой, вследствие чего невыпуклой оказалась и функция
не
является выпуклой, вследствие чего невыпуклой оказалась и функция  .
.
*.
Приведем еще одно достаточное условие локального минимума функции  на множестве
на множестве  .
.
Теорема
4.3. Пусть 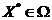 - стационарная точка функции
- стационарная точка функции  на
на  , причем
, причем  . Предположим, что функции
. Предположим, что функции 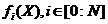 , дважды непрерывно дифференцируемы в некоторой
окрестности
, дважды непрерывно дифференцируемы в некоторой
окрестности 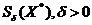 , точки
, точки  . Если
при некотором
. Если
при некотором 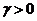 будет
будет

Где

то  является точкой строгого локального минимума функции
является точкой строгого локального минимума функции  на
на 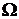 .
.
Глава II.
Применение решений минимаксных задач в экономике с помощью математического
пакета Maple
2.1 Виды
минимаксных задач в экономике
.1.1 Линейное
программирование
Задачи оптимального планирования, связанные с отысканием оптимума
заданной целевой функции (линейной формы) при наличии ограничений в виде
линейных уравнений или линейных неравенств относятся к задачам линейного
программирования.
Линейное программирование - наиболее
разработанный и широко применяемый раздел математического программирования. Это
объясняется следующим:
Ø математические модели очень большого числа экономических
задач линейны относительно искомых переменных;
Ø для них разработаны специальные конечные методы, с помощью
которых эти задачи решаются, и соответствующие стандартные программы для их
решения на ЭВМ;
Ø многие задачи линейного программирования, будучи решенными,
нашли уже сейчас широкое практическое применение в народном хозяйстве;
Ø некоторые задачи, которые в первоначальной формулировке не
являются линейными, после ряда дополнительных ограничений и допущений могут
стать линейными или могут быть приведены к такой форме, что их можно решать
методами линейного программирования.
Линейное программирование - это направление математического
программирования, изучающее методы решения экстремальных задач, которые
характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования
являются ограничения на наличие ресурсов, величину спроса, производственную
мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек
наибольшего или наименьшего значения некоторой функции при определенном наборе
ограничений, налагаемых на аргументы и образующих систему ограничений, которая
имеет, как правило, бесконечное множество решений. Каждая совокупность значений
переменных (аргументов функции F), которые удовлетворяют системе ограничений,
называется допустимым планом задачи линейного программирования. Функция F,
максимум или минимум которой определяется, называется целевой функцией задачи.
Допустимый план, на котором достигается максимум или минимум функции F,
называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями
производства. Задачей линейного программирования (ЗЛП) является выбор из
множества допустимых планов наиболее выгодного (оптимального).
.1.2.
Матричные игры
Матричные игры - игры, в которых участвуют два игрока (I и II) с
противоположными интересами, причём каждый игрок имеет конечное число чистых
стратегий. Если игрок I имеет m стратегий, а игрок II - n стратегий, то игра
может быть задана (m n)-матрицей
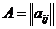
где
 есть выигрыш игрока I, если он выберет стратегию
есть выигрыш игрока I, если он выберет стратегию  , а игрок II - стратегию
, а игрок II - стратегию 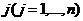 . Следуя общим принципам поведения в антагонистических
играх (частным случаем которых являются Матричные игры), игрок I стремится
выбрать такую стратегию
. Следуя общим принципам поведения в антагонистических
играх (частным случаем которых являются Матричные игры), игрок I стремится
выбрать такую стратегию 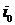 , на которой достигается
, на которой достигается
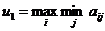 ;
;
игрок
II стремится выбрать стратегию  , на
которой достигается
, на
которой достигается
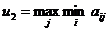 ;
;
Если
 , то пара
, то пара 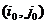 составляет
седловую точку игры, то есть выполняется двойное неравенство
составляет
седловую точку игры, то есть выполняется двойное неравенство
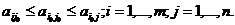
Число
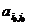 называется значением игры; стратегии
называется значением игры; стратегии 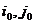 называются оптимальным и чистыми стратегиями игроков
I и II соответственно. Если
называются оптимальным и чистыми стратегиями игроков
I и II соответственно. Если 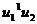 , то
всегда
, то
всегда 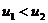 ; в этом случае в игре седловой точки нет, а
оптимальные стратегии игроков следует искать среди их смешанных стратегий (то
есть вероятностных распределений на множестве чистых стратегий). В этом случае
игроки оперируют уже с математическими ожиданиями выигрышей.
; в этом случае в игре седловой точки нет, а
оптимальные стратегии игроков следует искать среди их смешанных стратегий (то
есть вероятностных распределений на множестве чистых стратегий). В этом случае
игроки оперируют уже с математическими ожиданиями выигрышей.
Основная
теорема теории Матричные игры (теорема Неймана о минимаксе) утверждает, что в
любой Матричные игры существуют оптимальные смешанные стратегии 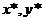 , на которых достигаемые «минимаксы» равны (общее их
значение есть значение игры). Например, игра с матрицей
, на которых достигаемые «минимаксы» равны (общее их
значение есть значение игры). Например, игра с матрицей 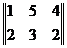 имеет седловую точку при
имеет седловую точку при 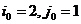 , а значение игры равно 2; игра с матрицей
, а значение игры равно 2; игра с матрицей 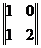 не имеет седловой точки. Для неё оптимальные
смешанные стратегии суть
не имеет седловой точки. Для неё оптимальные
смешанные стратегии суть  ; значение игры равно
; значение игры равно 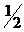 .
.
Для
фактического нахождения оптимальных смешанных стратегий чаще всего используют
возможность сведения Матричные игры к задачам линейного программирования. Можно
использовать так называемый итеративный метод Брауна - Робинсон, состоящий в
последовательном фиктивном «разыгрывании» данной игры с выбором игроками в
каждой данной партии своих чистых стратегий, наилучших против накопленных к
этому моменту стратегий оппонента. Игры, в которых один из игроков имеет только
две стратегии, просто решить графически.
Матричные
игры могут служить математическими моделями многих простейших конфликтных
ситуаций из области экономики, математической статистики, военного дела,
биологии. Нередко в качестве одного из игроков рассматривают «природу», под
которой понимается вся совокупность внешних обстоятельств, неизвестных принимающему
решения лицу (другому игроку).
.1.3
Транспортная задача
Классическая транспортная задача - задача о наиболее экономном плане
перевозок однородного продукта или взаимозаменяемых продуктов из пунктов
производства в пункты потребления, встречается чаще всего в практических
приложениях линейного программирования. Линейное программирование является
одним из разделов математического программирования - области математики,
разрабатывающей теорию и численные методы решения многомерных экстремальных
задач с ограничениями.
В зависимости от способа представления условий транспортной задачи она
может быть представлена в сетевой (схематичной) или матричной (табличной)
форме. Транспортная задача может также решаться с ограничениями и без
ограничений.
.1.4 Потоки в
сетях
Потоки в сетях - функция, сопоставляющая дугам данной сети
(ориентированного графа) некоторые числа.
Сетью
называется связный граф (обычно, не орграф и не мультиграф), в котором заданы
«пропускные способности» ребер, т. е. числа  . Это
числа большие или равные нулю, причем
. Это
числа большие или равные нулю, причем 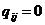 , тогда и
только тогда, когда нет ребра, соединяющего вершины
, тогда и
только тогда, когда нет ребра, соединяющего вершины  и
и 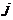 . Таким
образом, можно считать, что пропускные способности ребер заданы для любой пары
вершин. В дискретной математике пропускные способности ребер, как и все
возникающие константы, считаются целыми числами (или рациональными, что одно и
то же, так как рациональные числа отличаются от целых только единицами
измерения). Заметим, что сети имеют огромные приложения, в частности, «сети
планирования» (имеется в виду планирование производства некоторых новых,
достаточно сложных изделий), где «пропускные способности» ребер - это время, за
которое нужно из нескольких узлов изделия (вершин графа) получить другой (более
сложный) узел. Сетевое планирование здесь не исследуется, так как гораздо
больший интерес представляет сеть связи, где пропускные способности ребер - это
обычно «количество одновременных разговоров», которые могут происходить между
телефонными узлами (вершинами графа).
. Таким
образом, можно считать, что пропускные способности ребер заданы для любой пары
вершин. В дискретной математике пропускные способности ребер, как и все
возникающие константы, считаются целыми числами (или рациональными, что одно и
то же, так как рациональные числа отличаются от целых только единицами
измерения). Заметим, что сети имеют огромные приложения, в частности, «сети
планирования» (имеется в виду планирование производства некоторых новых,
достаточно сложных изделий), где «пропускные способности» ребер - это время, за
которое нужно из нескольких узлов изделия (вершин графа) получить другой (более
сложный) узел. Сетевое планирование здесь не исследуется, так как гораздо
больший интерес представляет сеть связи, где пропускные способности ребер - это
обычно «количество одновременных разговоров», которые могут происходить между
телефонными узлами (вершинами графа).
Потоком
в сети между вершиной 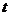 (источником) и
(источником) и 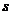 (стоком)
называется набор чисел
(стоком)
называется набор чисел 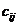 , (т.е. количество условного «груза», перевозимого из
вершины
, (т.е. количество условного «груза», перевозимого из
вершины 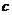 номером
номером  в
вершину с номером
в
вершину с номером 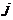 ), удовлетворяющих четырем условиям:
), удовлетворяющих четырем условиям:
)
числа 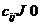 , причем если
, причем если 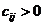 , то
, то 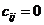 (нет встречных перевозок);
(нет встречных перевозок);
)
числа 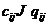 (соответствующих пропускных способностей ребер);
(соответствующих пропускных способностей ребер);
)
если вершина с номером 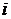 - промежуточная (не совпадает с источником и стоком),
то
- промежуточная (не совпадает с источником и стоком),
то
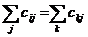 ,
,
т.е.
количество «груза», вывозимого из вершины 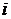 , равно
количеству «груза», ввозимого в эту вершину;
, равно
количеству «груза», ввозимого в эту вершину;
)
количество «груза», вывозимого из источника 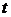 , должно
быть равно количеству груза, ввозимого в сток
, должно
быть равно количеству груза, ввозимого в сток 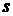 :
:
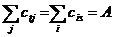 .
.
Число
 называется величиной данного потока или просто
потоком между
называется величиной данного потока или просто
потоком между 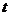 и
и 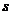 .
.
.1.5 Сетевое
планирование
Сетевое планирование и управление - это совокупность расчётных методов,
организационных и контрольных мероприятий по планированию и управлению
комплексом работ с помощью сетевого графика (сетевой модели).
Под комплексом работ мы будем понимать всякую задачу, для выполнения
которой необходимо осуществить достаточно большое количество разнообразных
работ.
Для того чтобы составить план работ по осуществлению больших и сложных
проектов, состоящих из тысяч отдельных исследований и операций, необходимо
описать его с помощью некоторой математической модели. Таким средством описания
проектов является сетевая модель.
Сетевая модель - это план выполнения некоторого комплекса взаимосвязанных
работ, заданного в форме сети, графическое изображение которой называется
сетевым графиком.
Главными элементами сетевой модели являются работы и события.
Термин работа в СПУ имеет несколько значений. Во-первых, это
действительная работа - протяжённый во времени процесс, требующий затрат
ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая
действительная работа должна быть конкретной, чётко описанной и иметь
ответственного исполнителя.
Во-вторых, это ожидание - протяжённый во времени процесс, не требующий
затрат труда (например, процесс сушки после покраски, старения металла,
твердения бетона и т.п.).
В-третьих, это зависимость, или фиктивная работа - логическая связь между
двумя или несколькими работами (событиями), не требующими затрат труда,
материальных ресурсов или времени. Она указывает, что возможность одной работы
непосредственно зависит от результатов другой. Естественно, что
продолжительность фиктивной работы принимается равной нулю.
Событие - это момент завершения какого-либо процесса, отражающий
отдельный этап выполнения проекта. Событие может являться частным результатом
отдельной работы или суммарным результатом нескольких работ. Событие может
свершиться только тогда, когда закончатся всё работы, ему предшествующие.
Последующие работы могут начаться только тогда, когда событие свершится. Отсюда
двойственный характер события: для всех непосредственно предшествующих ему работ
оно является конечным, а для всех непосредственно следующих за ним - начальным.
При этом предполагается, что событие не имеет продолжительности и свершается
как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно
быть полно, точно и всесторонне определено, его формулировка должна включать в
себя результат всех непосредственно предшествующих ему работ.
Основные элементы сетевой модели

При составлении сетевых графиков (моделей) используют условные
обозначения. События на сетевом графике (или, как ещё говорят, на графе)
изображаются кружками (вершинами графа), а работы - стрелками (ориентированными
дугами):
¡ - событие,
- работа (процесс),
фиктивная работа - применяется для упрощения сетевых графиков
(продолжительность всегда равна 0).
Среди событий сетевой модели выделяют исходное и завершающее события.
Исходное событие не имеет предшествующих работ и событий, относящихся к
представленному в модели комплексу работ. Завершающее событие не имеет последующих
работ и событий.
Существует и иной принцип построения сетей - без событий. В такой сети
вершины графа означают определённые работы, а стрелки - зависимости между
работами, определяющие порядок их выполнения. Сетевой график «работы-связи» в
отличие от графика «события-работы» обладает известными преимуществами: не
содержит фиктивных работ, имеет более простую технику построения и перестройки,
включает только хорошо знакомое исполнителям понятие работы без менее
привычного понятия события.
Вместе с тем сети без событий оказываются значительно более громоздкими,
так как событий обычно значительно меньше, чем работ (показатель сложности
сети, равный отношению числа работ к числу событий, как правило, существенно
больше единицы). Поэтому эти сети менее эффективны с точки зрения управления
комплексом. Этим и объясняется тот факт, что в настоящее время наибольшее
распространения получили сетевые графики «события-работы».
Если в сетевой модели нет числовых оценок, то такая сеть называется
структурной. Однако на практике чаще всего используют сети, в которых заданы
оценки продолжительности работ, а также оценки других параметров, например
трудоёмкости, стоимости и т.п.
2.1.6
Целочисленное программирование
Целочисленное программирование -разновидность линейного программирования,
подразумевающая, что искомые значения должны быть целыми числами.
2.2
Математические пакеты Maple и MATLAB
Сколь значителен спектр задач, которые решаются при помощи пакета Maple видно из следующего
перечисления:
o проведение математических исследований, требующих вычислений
и аналитических выкладок;
o разработка и анализ алгоритмов;
o математическое моделирование, компьютерный эксперимент;
o анализ и обработка данных;
o визуализация, научная и инженерная графика,
o разработка графических и расчетных приложений.
Пакет предоставляет удобные среды для компьютерных экспериментов, когда
пробуются различные подходы к задаче, анализируются частные решения, при
необходимости программирования отбираются требующие особой скорости фрагменты.
Он позволяет создавать интегрированные среды с участием систем
программирования. Когда расчеты проведены и требуется оформить результаты,
опять-таки можно использовать эти пакеты для визуализации данных и подготовки
иллюстраций. Работа с системой проходит интерактивно - пользователь вводит
команды и видит на экране результат их выполнения. Квалификация пакета
обеспечивает выбор подходящих типов переменных и выполнение операций, так что в
общем случае не требуется описания переменных.
Система Maple создавалась
как пакет компьютерной алгебры, то есть основным объектом здесь являются
формулы и операции с ними. Без дополнительных указании символ, например х,
считается фактически математической переменной, как х в формуле Т(х). Такая
специфика систем компьютерной алгебры позволяет проводить точные вычисления.
Система имеет развитые средства программирования, аналогичные
распространенным алгоритмическим языкам, но при этом и здесь сохраняется
специфика. обусловленная направленностью пакетов.
Пакет Maple -
интерактивная программа, позволяющая проводить анали тические выкладки и
вычисления, снабженная средствами двумерной и трехмерной графики, имеющая
мощный язык программирования и богатую библиотеку математических формул и
сведений. Работа с Maple заключается в том, что пользователь вводит
математические выражения и инструкции (команды), а система пытается их
выполнить и представить ответ. Получив (или не получив) ответ, пользователь
вводит новые инструкции и так далее - взаимодействие с пакетом происходит в
диалоговом режиме. Благодаря собственному язык программирования высокого уровня
введенные выражения и инструкции, а также результаты выполнения команд -
формулы, графики, таблицы и числа - запоминаются в едином документе (worksheet).
Это обеспечивает уникальную технологию работы, когда чуть ли не все этапы
математического исследования можно отразить в одном документе, и итоговый
документ становится (быть может, с минимальными дополнениями) научной статьей,
разделом в учебнике, отчетом.
Основы Maple.
В данной главе рассмотрен ряд общих вопросов: интерфейс (системы меню,
значков и справки), кратко описана организация документа Maple, изложены общие сведения об
основных объектах (переменных, константах, выражениях) и синтаксисе, а также
дан обзор базовых типов Maple и основных математических функций.
Работа с Maple и интерфейс
Графический интерфейс Maple аналогичен имеющемуся в системах редактирования и подготовки текста
и использует обычные средства работы с файлами и редактирования (мышь и
клавиатура). После запуска выполняемого модуля wmapte или xmaple в среде Unix появляется
оболочка с новым документом (worksheet). В верхней части окна расположено меню
(пункты File, Edit и т. д.), чуть ниже - строка значков Toolbar для ряда часто
выполняемых операций, еше ниже - строка значков Context Ваг, организующих
представление данных в сеансе. Затем следует одно или несколько окон с
документами, в которых размешаются формулы, рисунки, сопровождающий текст и др.
В нижней части окна находится полоса Status Une, которая содержит информацию о
системе. Работа в Maple проходит в режиме сессии (session) - пользователь
вводит команды. математические выражения, процедуры, которые воспринимаются и
интерпретируются Maple. Каждая команда должна завершаться точкой с занятой (;)
или двоеточием (:). В первом случае в строке под предложением будет выведен
результат исполнения команды или сообщение об ошибке, во втором случае
результат не выводится. Для отмены всех сделанных назначений и начала нового
сеанса без выхода из Maple используется команда restart.
Кроме того, в Maple
можно вводить таблицы и текстовые параграфы, структурировать текст и документ,
добавлять гиперссылки, объединяющие несколько документов в подобие электронной
книги. В документ также можно вставлять объекты (рисунки и таблицы) из других
программ, используя интерфейс OLE2.
Отметим, что различные документы, открытые в одном сеансе, используют
общую область памяти, и значение, присвоенное переменной в одном документе,
сохраняется при переходе к другому локумету. Для реализации многозадачной
работы имссгся программа Parallel
Server Maple 6. Ее интерфейс идентичен основной программе wmaple, но при работе
назначения переменных действительны только в пределах «родного документа».
Оболочка
Результаты работы могут быть сохранены в файлах различных форматов.
Текущий документ (области ввода и вывода, комментарии, текст, графика)
записываются в файл с расширением .mws. При записи в файлы с другими расширениями сохраняются
только области ввода и тексты комментариев. Кроме того, весь документ или его
часть могут быть сохранены в форматах, допускающих их использование в других
программах.
Пакет Maple постоянно развивается, приобретая новые команды и,
соответственно, возможности для проведения математических выкладок, вычислений,
графического отображения информации. При этом происходят изменения в синтаксисе
и оболочке. Для хранения преемственности с документами, подготовленными в
старых версиях, фирма снабжает свой продукт специальными конверторами, при
загрузке файла устаревшей версии Maple предлагает преобразовать нотацию файла
согласно новым правилам.
.3 Средства
решения минимаксных задач в среде Мар1е-языка
Задачи
на определение минимума и/или максимума (минимакса)
функции имеют не только чисто теоретическое значение в качественных аспектах
целого ряда математических разделов, но в большей мере в многочисленных
приложениях математического анализа. Для решения задач данного типа Maple-язык.
предоставляет ряд средств различного уровня. К средствам первого уровня
относятся функции min и max, имеющие идентичные форматы кодирования вида
{min|max}(V1,V2,…,Vn) и возвращающие {минималъное|максималъное} значение среди
результатов вычисления выражений Vk, указанных фактическим аргументом {Vk} - последовательности
(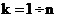 ). В качестве выражений Vk допускаются выражения,
результаты вычисления которых могут быть как числовыми, так и символьными. В
случае определения минимакса над последовательностью как числовых, так и
символьных значений, возвращается {min|max}-конструкция, в которой произведены
выбор числового минимакса и вычисления символьных выражений. При этом, если для
символьных значений используется assume-механизм, то в выборе минимакса могут
принимать участие и символьные значения, в ряде случаев возвращая символьный
результат. Пустые вызовы функций {min, max} возвращают
). В качестве выражений Vk допускаются выражения,
результаты вычисления которых могут быть как числовыми, так и символьными. В
случае определения минимакса над последовательностью как числовых, так и
символьных значений, возвращается {min|max}-конструкция, в которой произведены
выбор числового минимакса и вычисления символьных выражений. При этом, если для
символьных значений используется assume-механизм, то в выборе минимакса могут
принимать участие и символьные значения, в ряде случаев возвращая символьный
результат. Пустые вызовы функций {min, max} возвращают 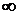 -значения, а именно: [min(),max()];
-значения, а именно: [min(),max()]; , что по логике вещей должно быть с точностью до
наоборот. Функции {min, max} могут
использоваться совместно с функцией convert({min|max},piecewise), определяй
минимаксные области для значений символьных выражений. Однако в таком случае
операции возведения в степень в аргументе {min|max} функции convert должны быть
представлены в терминах произведения. Следующий простой фрагмент иллюстрирует
вышесказанное:
, что по логике вещей должно быть с точностью до
наоборот. Функции {min, max} могут
использоваться совместно с функцией convert({min|max},piecewise), определяй
минимаксные области для значений символьных выражений. Однако в таком случае
операции возведения в степень в аргументе {min|max} функции convert должны быть
представлены в терминах произведения. Следующий простой фрагмент иллюстрирует
вышесказанное:

Приведенное описание функций {min,max} делает примеры фрагмента вполне прозрачными, как и
применение рассмотренных функций минимакса в целом. Здесь же следует отметить
то обстоятельство, что в виду градиентного характера понятий минимума и
максимума на множестве числовых значений, в частности, и с помощью функции sort
возможно решать минимаксные задачи уровня, не ниже рассмотренного. Так
последний пример фрагмента представляет простую процедуру MinMax, реализованную
на основе функции sort и возвращающую трехэлементный список, элементы которого
представляют соответственно: количество переданных процедуре в качестве ее
фактических аргументов числовых выражений, а также минимальное и максимальное
среди них значение. На основе функции sort можно создавать и полезные
нечисловые минимаксные процедуры, для которых стандартные средства языка АРМа
не применимы.
На втором уровне
Maple-язык АРМа предлагает функции minimize и maximize, допускающие следующие
идентичные для обоих функций форматы кодирования:
{minimize|maximize}(V{,<Переменная>{,<Диапазон>|`infinite`}})
и возвращающие в случае простейшего формата соответственно {минимум|максимум} указанного первым
фактическим аргументом алгебраического выражения V либо последовательность
значений выражения V в качестве кандидатов для искомого минимакса. При
кодировании второго фактического аргумента он определяет ведущую переменную
либо их множество, относительно которых должен отыскиваться минимакс выражения
V. При отсутствии второго фактического аргумента (простейший формат кодирования
с одним формальным аргументом) минимакс отыскивается относительно всех
идентификаторов исходного выражения V, т.е. <Переменная>=indets(V,name).
Необязательный третий аргумент функции (указывается только при наличии
второго аргумента) определяет интервал или их множество для ведущих переменных
выражения V, в рамках которых отыскивается его минимакс; при этом анализируются
и граничные точки интервалов. В случае указания в качестве третьего
фактического аргумента минимаксной функции `infinite` -значения минимакс отыскивается для
действительных значений по всем ведущим переменным выражения V, определяемым
вторым фактическим аргументом функции.
В качестве границ интервалов (третий фактический аргумент) для
минимаксных функций
{minimize,maximize} допускаются только выражения, результаты вычисления которых
имеют {integer|fraction|float}-тип, в противном случае идентифицируется
ошибочная ситуация «Error», {minimize|maximize} expects its 3rd argument,
ranges». В случае одной ведущей переменной интервал можно указывать без ее
идентификатора. На неопределенных функциях в качестве первого фактического
аргумента минимаксной {minimize,maximize}-функции возвращаются значения NULL.
В ряде случаев минимаксные функции возвращают результаты в терминах
алгебраических чисел вместе со вторым фактическим аргументом функции, если их
порядок выше двух. Данная ситуация во многих случаях исключаема путем указания
интервалов для ведущих переменных либо определения `infinite`-значения для
третьего аргумента функции. Следующий простой фрагмент иллюстрирует применение
рассмотренных минимаксных функций Maple-языка АРМа:


Примеры фрагмента с учетом сказанного достаточно прозрачны и особых пояснений не требуют. Таким
образом, по минимаксной {minimize,maximize}-функции можно отыскивать как
глобальные, так и локальные минимаксы функций нескольких переменных; при этом,
при необходимости исследуется их бесконечная асимптотика. Завершает фрагмент
процедура MiniMax, имеющая не менее двух формальных аргументов: тип искомого
минимакса `{mini|maxi}` анализируемое на минимакс выражение V, а также,
возможно, интервалы по ведущим переменным, определяющие область отыскания
минимакса выражения. Для случая одной ведущей переменной процедура возвращает
список, содержащий как тип и значение минимакса, так и точку, в которой он
получен; для многомерного случая возвращается тип минимакса и его значение.
В модуле student наряду
с рядом средств для решения базовых задач анализа содержатся определения
функций минимакса (аналогичные рассмотренным выше или более ограниченные по
возможностям) и функция extrema, имеющая формат:
(V,<Условия>{,<Множество переменных>{,'h'}})
Функция extrema возвращает
условный экстремум алгебраического выражения V от нескольких ведущих переменных
(определенных множеством их идентификаторов в третьем фактическом аргументе) согласно
заданным вторым фактическим аргументом условиям. Второй аргумент функции
обязателен и задается в виде множества уравнений либо выражений, связывающих
ведущие переменные; в случае выражений они по умолчанию полагаются в качестве
левых частей уравнений с нулевой правой частью. В случае отсутствия таких
ограничений кодируется пустое {}-множество.
В случае отсутствия третьего фактического аргумента, определяющего
множество ведущих переменных,относительно которых должен отыскиваться экстремум
выражения V, в качестве их по умолчанию выбираются все идентификаторы выражения V и
уравнений-условий. В качестве результата функция ехtreта возвращает множество
экстремумов, а также, возможно, вложенное множество экстремальных точек,
включая и кандидаты на принадлежность к экстремальным; последнее возвращается в
качестве значения невычисляемого идентификатора `h` - четвертого фактического
аргумента функции. В случае невозможности получить выражение для экстремальных
точек в качестве значения переменной h возвращается система уравнений, решение
которой и определяет такие точки. Для вычисления условных экстремумов функция
ехtrета использует метод неопределенных множителей Лагранжа. Следующий фрагмент
иллюстрирует применение функции ехп-ета для вычисления условных экстремумов:

В
приведенном фрагменте вычисляются экстремумы для двух функций А(х,у) и Z(x,y) с проведением анализа результатов, полученных
на основе функции extrema. Наряду с этим, для функции g(x)=(x+2)*sin(x), не
имеющей конечного глобального экстремума на открытом интервале 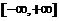 , но имеющей бесконечное множество локальных
экстремумов, применение функции extrema позволяет
получать ближайший справа от начала координат базовый локальный экстремум (С;
максимум) и в качестве экстремальной точки-кандидата (h-nepeменная) ближайший
слева от начала координат локальный экстремум (.3093012857; максимум).
Представленный график иллюстрирует поведение исследуемой функции g(x) в области
полученных функцией extrema локальных экстремумов. В качестве полезного
упражнения читателю рекомендуется на основе рассмотренных выше средств
дифференцирования, отыскания пределов и минимакса написать общего типа
процедуру, позволяющую производить полный анализ функций одной переменной с
выводом графика в области экстремальных точек.
, но имеющей бесконечное множество локальных
экстремумов, применение функции extrema позволяет
получать ближайший справа от начала координат базовый локальный экстремум (С;
максимум) и в качестве экстремальной точки-кандидата (h-nepeменная) ближайший
слева от начала координат локальный экстремум (.3093012857; максимум).
Представленный график иллюстрирует поведение исследуемой функции g(x) в области
полученных функцией extrema локальных экстремумов. В качестве полезного
упражнения читателю рекомендуется на основе рассмотренных выше средств
дифференцирования, отыскания пределов и минимакса написать общего типа
процедуру, позволяющую производить полный анализ функций одной переменной с
выводом графика в области экстремальных точек.
При
вычислении условных экстремумов во многих
случаях для получения строго численных результатов рекомендуется использовать
функцию evalf, как это продемонстрировано в примерах фрагмента. Возвращаемые
функцией extrema результаты следует проверять на предмет типа экстремума
{минимум|максимум} и анализировать экстремальные точки, возвращаемые h-переменной,
ибо среди них могут находиться как точки, определяющие возвращаемый функцией
экстремум, так и точки-кандидаты в качестве экстремальных. В случае выражения V
от нескольких переменных и корректного определения условий по функции extrema во
многих случаях возвращается искомый экстремум, а через h-переменную -
координаты экстремальной точки, в остальных же случаях требуется дополнительное
исследование поведения выражения V.
Наконец,
третий уровень средств по обеспечению решения минимаксных задач составляют средства модуля пакета simplex, содержащего
определения как минимаксных, так и ряда других функций для решения задач
линейного программирования симплексным методом. Детальнее со средствами simpleх-модуля
можно ознакомиться в [74, 84, 85, 94], здесь же мы остановимся на двух базовых
минимаксных функциях, решающих проблему минимакса для линейной целевой функции
(ЦФ) и имеющих формат:
{minimize|maximize}(<Целевая
функция>{,<ЛО>{,<ТВП>{'а'{,'b'}}})
где
в качестве первого фактического аргумента функции выступает линейная целевая функция (ЦФ), для которой отыскивается
соответственно {минималъное максималъное} значение на определенных вторым
фактическим аргументом линейных ограничениях (ЛO) и типах ведущих переменных
(ТВП), определяемых третьим фактическим аргументом функции. Второй фактический
аргумент записывается в виде списка/множества линейных неравенств по ведущим
переменным целевой функции. Третий необязательный аргумент функции определяет
тип знака для ведущих переменных, относительно которых отыскивается минимакс
ЦФ; для него допустимыми являются только два значения: NONNEGATIVE (по
умолчанию; все ведущие переменные полагаются неотрицательными) и UNRESTRICTED (ограничений
на знак ведущих переменных не накладывается). Наконец, необязательные четвертый
и пятый аргументы функции определяют невычисляемые переменные 'а' и 'b', через
которые возвращаются описание оптимизирующего решения минимаксной задачи и
использованные для его получения преобразования ведущих переменных
соответственно.
При
этом для тестирования корректности задания системы ограничений, определяемых
вторым и третьим фактическими аргументами минимаксной функции, служит
логическая функция feasible(<ЛО>{,<ТВП>{'а'{,'b'}}}), смысл аргументов которой полностью соответствует выше
сказанному и которая возвращает значение true в случае корректности системы
условий и значение false - в противном случае. Более того, два последних
необязательных аргумента функции в этом случае возвращают соответственно
значение для окончательной системы корректных ЛO (которая может также включать
глобальные переменные _AR, _SLk и/или _negk, _posk ядра пакета) и использованные
для ее получения преобразования ведущих переменных ЦФ.
При
этом модульная функция convert(LO,std) возвращает
множество/список линейных ограничений для целевой функции, полученных путем
переноса всех констант левых частей LO-списка/множества ограничений в их правые
части. Модульная функция convert(LO,stdle) производит конвертацию всех
неравенств LO-ограничений в неравенства (<=)-типа, упрощая решение задач
симплекс-методом. Для использования обоих функций требуется выполнение
предложения with(simplex).
Минимаксная
функция {minimize|maximize} возвращает
результат оптимизации исходной ЦФ в виде множества уравнений по ее ведущим
переменным, на которых ЦФ достигает соответственно {минимума|максимума}.
Последующая подстановка их в ЦФ возвращает само минимаксное значение. В случае
отсутствия оптимизирующего решения возвращается пустое {}-множество, а для
неограниченного решения возвращается значение NULL. Следующий фрагмент
иллюстрирует применение рассмотренных средств для решения простых задач
линейного программирования:

С учетом сказанного примеры фрагмента представляются достаточно
прозрачными. В частности, для целевой функции определяется система линейных
ограничений, после проверки которой на корректность производится вычисление
максимизирующего функцию QR решения на указанных линейных ограничениях.
Полученное в виде множества уравнений оптимизирующее решение R посредством
функции subs подставляется в функцию QR, возвращая искомое значение QR_max:=
1588872, максимальное для заданной системы линейных ограничений. С остальными
примерами фрагмента рекомендуем разобраться читателю в качестве упражнения.
Таким образом, рассмотренные и ряд других функций simplex-модуяя можно
рассматривать в качестве базового средства решения задач линейного
программирования в среде Maple-языка.
Минимаксные задачи составляют весьма обширный класс математических
проблем, использующих для своего решения разнообразные методы. Прямые средства
языка АРМа позволяют успешно решать только наиболее простые из них, однако
имеющие весьма широкие приложения. Вместе с тем, на основе их и ряда других
рассмотренных средств
Maple-языка пользователь может создавать собственные средства оптимизации и
решения минимаксных задач различного назначения. Более того, имеется достаточно
широкий набор средств такого типа, поставляемых по выбору или содержащихся в
многочисленных пользовательских приложениях пакета Maple.
Вывод
В данной курсовой работе были рассмотрены примеры решения минимаксных
задач при помощи пакета программ Maple.
Благодаря повышению функциональности редактора повысилась надежность
аналитических вычислений, написание программ и оформление рабочего документа
Maple стали более удобными.
Особенно важно то, что Maple - не просто калькулятор, способный аналитически
решать многие задачи, а легко обучаемая система. Совершенно ясно, что как бы ни
была совершенна программа, всегда найдется много специальных задач, которые
оказались за пределами интересов разработчиков. Усвоив несложный, но
эффективный язык Maple, пользователь может изменить существующие процедуры или
пополнить систему новыми, приспособленными для решения нужных ему задач. Эти
процедуры можно включить в одну из библиотек, снабдить подсказками, так что они
гармонично впишутся во всю систему. Мне кажется, что именно по этой причине
система приобрела большую популярность.
Следует заметить также, что далеко не все задачи поддаются аналитическому
расчету и приходится применять численные методы. Несмотря на то что язык
программирования Maple позволяет решать и такие задачи, программы будут
выполняться медленнее, чем на компилируемых языках. Так что решение задач,
требующих большого объема численных вычислений, в среде Maple неэффективно.
Именно поэтому в системе имеются средства перекодировки программ с языка Maple
на Си и Фортран.
Пакет Maple удобен при оформлении отчета, дипломной работы, диссертации
или подготовке материала для публикации. Он с высоким полиграфическим качеством
изобразит математические формулы, построит красивые графики, а если вам потребуется
профессиональное качество оформления, то вы сможете, используя встроенную в
систему процедуру, преобразовать рабочий лист в формат LaTeX - стандартный
формат научно-технических публикаций.несложно приспособить для учебных целей. С
ее помощью легко проверить любой математический расчет, наглядно представить
результат вычислений или проиллюстрировать закон природы, выраженный формулой.
Обучаться математике, другим техническим дисциплинам, а также методам
программирования с помощью Maple не только легко, но и приятно.подтверждает
лидерство корпорации Maple Waterloo среди разработчиков программ символьной
математики и дает специалистам новые превосходные возможности для повышения
производительности и комфортности труда. Отмечу, что разработчики некоторых
известных математических пакетов, таких, как MathCad и MatLab, приобрели
лицензию на использование основной библиотеки Maple в своих программах для
обеспечения отдельных аналитических расчетов.
Список
использованной литературы
1. Аладьев
В.З., Шишаков М.Л. Автоматизированное рабочее место
математика. Лаборатория базовых знаний, 2000. - 752 c.
2. Алексеев
Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple
9/Алексеев Е.Р., Чеснокова О.В. - М.: НТ Пресс, 2006. -496 с.
. Гарнаев
А.Ю. Использование MS Excel и VBA в экономике и финансах. СПб.: БХВ - Санкт-Петербург,
2000. - 336.
. Говорухин
В., Цибулин В. Компьютер в математическом исследовании. Питер, 2001. - 624 с.
. Говорухин
В.Н., Цибулин В.Г. Введение в Maple.
Математический пакет для всех. М.: Мир, 1997.
. Демьянов
В.Ф., Малоземов В.Н. Введение в минимакс, Главная редакция
физико-математической литературы издательства «Наука», 1972, с.368.
. Дьяконов
В. Maple 7. Учебный курс. - Питер, 2002. - 672 с.
. Иллюстрированный
самоучитель по Maple 9.
. Калихман
И.Л. Сборник задач по математическому программированию. Изд. 2-е, доп. и
перераб. М., «Высшая школа», 1975.
. Матричные
игры. [Сборник переводов], под редакцией Н. Н. Воробьева, М., 1961; Нейман Дж.
фон, Моргенштерн О., Теория игр и экономическое поведение, перевод с
английского, М., 1970; Оуэн Г., Теория игр, перевод с английского, М., 1971.
. Матросов
А. Maple 6. Решение задач высшей математики и механики. BHV - Санкт - Петербург
Мастер. Руководство для профессионалов, 2003, - 528.
. Рабкин
Е.Л., Фарфоровская Ю.Б. Дискретная математика. Булевы функции и элементы теории
графов: Методические указания и контрольные задания. Кафедра высшей математики
СПбГУТ им. проф. М.А. Бонч-Бруевича.
. Сдвижков
О.А. Математика на компьютере: Maple
8. - М.: СОЛОН-Пресс, 2003. - 176 с.
. Черняк
А.А., Новиков В.А., Мельников О.И., Кузнецов А.В. Математика для экономистов на
базе Mathcad. - СПб.: БХВ-Петербург, 2003. - 496.
Приложения
. Решить задачу линейного программирования
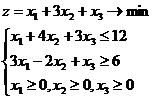
Решение.
>
with(simplex);
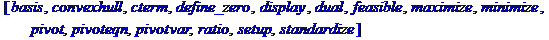
> z:=x1+3*x2+x3;
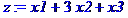
> minimize(z,{x1+4*x2+3*x3<=12,3*x1-2*x2+x3>=6},NONNEGATIVE);
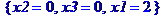
> subs(%,z);
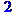
Ответ:
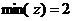 .
.
.
Решить транспортную задачу по следующим исходным данным: 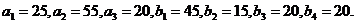

Символ
 в матрице
в матрице  указывает,
что для данной коммуникации нет ограничений по пропускной способности.
указывает,
что для данной коммуникации нет ограничений по пропускной способности.
>
with(simplex);
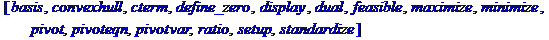
> x:=matrix(3,4);

> C:=matrix([[9,5,3,10],[6,3,3,2],[3,8,4,8]]);

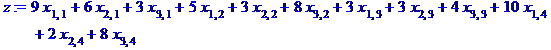
>
minimize(z,{sum(x[1,j],j=1..4)=25,sum(x[2,j],j=1..4)=55,sum(x[3,j],j=1..4)=20,sum(x[i,1],i=1..3)=45,sum(x[i,2],i=1..3)=15,sum(x[i,3],i=1..3)=20,sum(x[i,4],i=1..3)=20,x[1,3]<=15,x[2,1]<=15,x[2,4]<=10},NONNEGATIVE);
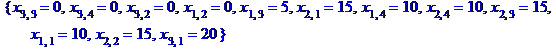
> v:=matrix([[10,0,5,10],[15,15,15,10],[20,0,0,0]]);
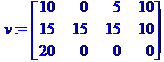
. Задача на поток в сетях.
Пусть задана ориентированная 2-полюсная сеть, один полюс - вход, другой -
выход, весовые коэффициенты дуг - максимальные пропускные способности дуг.
Требуется определить максимальную пропускную способность сети. Геометрическое
решение данной задачи основано на теореме Форда-Фалкерсона, согласно которой
максимальная пропускная способность сети равна минимальной пропускной
способности сечений сети. Аналитическая задача решается сведением ее к задаче
линейного программирования.
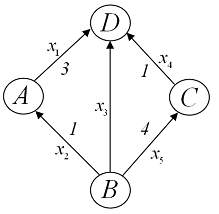
Цифры
рядом с дугами - максимальные пропускные способности дуг,  - планируемые потоки в дугах. Аналитическая
постановка задачи о максимальном потоке для данной сети имеет вид:
- планируемые потоки в дугах. Аналитическая
постановка задачи о максимальном потоке для данной сети имеет вид:
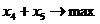
при
условиях
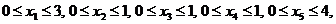
а
также

так
как входящие и выходящие потоки в каждом транзитивном узле  и
и  должны
быть равны.
должны
быть равны.
>
with(simplex);
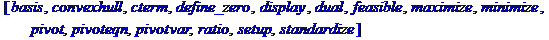
>
maximize(x4+x5,{0<=x1,x1<=3,0<=x2,x2<=1,0<=x3,x3<=1,0<=x4,x4<=1,0<=x5,x5<=4,x1+x3=x4,x2=x3+x5});
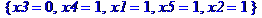
. Задача по планированию производства.
Небольшая фабрика выпускает два типа красок: для внутренних (1) и
наружных (2) работ. Продукция обоих видов поступает в оптовую продажу. Для
производства красок используется два исходных продукта А и В. Максимально
возможные суточные запасы этих продуктов составляют 6 и 8 тонн, соответственно.
Расходы продуктов А и В на 1 т. соответствующих красок приведены в таблице
|
Исходный продукт
|
Расход исходных продуктов
на тонну краски, т
|
Максимально возможный
запас, т
|
|
краска 1
|
краска 2
|
|
|
А
|
1
|
2
|
6
|
|
В
|
2
|
1
|
8
|
Изучение рынка сбыта показало, что суточный спрос на краску 1 никогда не
превышает спроса на краску 2 более чем на 1 т. Кроме того, установлено, что
спрос на краску 1 никогда не превышает 2 т в сутки. Оптовые цены одной тонны
красок равны: 3 000 грн. для краски 2 и 2 000 грн. для краски 1. Какое
количество краски каждого вида должна производить фабрика, чтобы доход от
реализации продукции был максимальным?
> with(simplex);
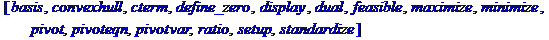
> z:=3000*x1+2000*x2;
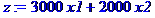
>
maximize(z,{x1+2*x2<=6,2*x1+x2<=8,x2-x1<=1,x2<=2},NONNEGATIVE);
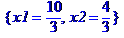
>
> subs(x1=10/3,x2=4/3,3000*x1+2000*x2);
