Плоские волны в однородной изотропной среде

Реферат

Плоские волны в однородной изотропной среде

Содержание

Плоские волны

Плоские электромагнитные волны в однородной изотропной среде

Поток энергии в плоской волне

Поляризация электромагнитной волны

Отражение и преломление плоских волн на плоской границе раздела

Литература

Волна - это распространение колебания в пространстве, происходящее с конечной скоростью. Волновой процесс включает зависимость не только от времени, но и от пространственных переменных, поэтому он описывается уравнениями в частных производных. Основную роль в теории волн играет линейное дифференциальное уравнение в частных производных второго порядка гиперболического типа - волновое уравнение

, (1)

где D - оператор Лапласа, с - скорость волны. При наличии в системе внешних сил или источников и диссипации уравнение (1) принимает вид:

. (2)

Плоские волны

Простейшим решением волнового уравнения (1) является плоская волна

u = u(x, t), x = rm = xm_x + ym_y + zm_z. (3)

Для таких волн уравнение (1) становится одномерным

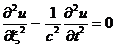 - (4)

первая каноническая форма или

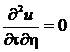 - (5)

вторая каноническая форма,

t = t - x/c, h = t + x/c. (6)

Общее решение уравнения (5) с учетом замены переменных (6) имеет вид

u = u₁(t) + u₂(h) = u₁(t - x/c) + u₂(t + x/c), (7)

где u₁ и u₂ - произвольные функции, их конкретный вид определяется граничными условиями, t и h - фазы. В любой фиксированный момент времени t функ­ции u₁ и u₂ имеют постоянное значение во всех точках плоскости, определяемой соотношением

x = rm = const. (8)

Рассмотрим функцию u₁(t) и найдем условия, при которых t = const. Из соотношений (3) и (6) следует, что в этом случае mdr/dt = c. С учетом условия (8) это означает, что поверхность t = const является плоскостью, которая перемещается со скоростью с в направлении вектора m. Аналогично плоскость, на которой h = const, перемещается со скоростью с в направлении вектора -m. Таким образом, функция u₁(t - rm/c) описывает плоскую волну, бегущую в направлении вектора m со скоростью с, а это значит, что поверхность постоянной фазы t = const является плоской.

Плоскую волну (7) можно представить интегралом Фурье вида

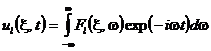, (9)

где 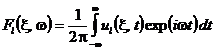, l = 1, 2. Подставляя соотношение (9) в волновое уравнение (4), получим уравнение Гельмгольца

, (10)

общее решение которого можно записать в виде

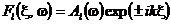, (11)

где k = w/c - волновое число.

Подставляя соотношение (11) в интеграл Фурье (9), получим

, (12)

при этом подынтегральное выражение Aexp(±ikx - iwt) является плоской гармонической волной в смысле определения (7), то есть произвольную плоскую волну можно представить как суперпозицию гармонических плоских волн.

Если ввести волновой вектор k = km, то фазу плоской гармонической волны можно представить в виде t = kr - wt, уравнение kr = const определяет плоскость постоянной фазы. Подставляя соотношение (11) в уравнение (10), получим связь между волновым вектором и частотой (дисперсионное соотношение) для среды без поглощения

|k|² = w²/c². (13)

В общем случае волновой вектор может быть комплекснозначным k = k' + ik", тогда из дисперсионного соотношения (13) следует связь между его действительными и мнимыми частями

|k'|² - |k"|² = w²/c², k'k" = 0. (14)

Соответственно, общий вид гармонической плоской волны

u(r, t) = Aexp[-rk" - i(wt - k'r)] (15)

описывает неоднородную плоскую волну. Поверхности равных фаз k'r = const и равных амплитуд k"r = const - плоские и перпендикулярные друг другу в силу соотношения (14).

Плоские электромагнитные волны в однородной изотропной среде

Запишем для поляризующейся и проводящей среды уравнения Максвелла

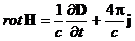, (16)

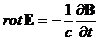, (17)

, (18)

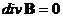. (19)

Для замыкания системы уравнений необходимо дополнить ее материальными уравнениями D(E), B(H), j(E). В простейшем случае линейной изотропной и однородной среды они имеют вид D = eE, B = mH, j = sE, где e, m и s - константы. Тогда из уравнений (16) и (17) получаем

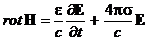, (20)

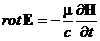. (21)

Будем считать, что свободных зарядов в среде нет (при s ¹ 0 они должны рассасываться), то есть div E = 0. Возьмем ротор от правой и левой частей уравнения (21) и, учитывая, что rot rot E = grad div E - DE = -DE, получим с учетом уравнения (20)

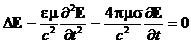. (22)

При s = 0 (диэлектрик) уравнение (22) для каждой из компонент вектора E имеет вид волнового уравнения (1) для среды без потерь. Легко показать, что такому же уравнению удовлетворяет и вектор Н. В плоской волне вида (3) векторы E и Н зависят только от одной пространственной координаты x = rm и волновое уравнение (22) принимает вид

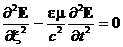, (23)

описывающий распространение в направлениях ±m двух плоских векторных волн

E = E(t ± x/v), H = H(t ± x/v). (24)

Для плоских волн вида (24), распространяющихся в направлении +m,

,

и уравнения Максвелла (16) - (19) принимают вид

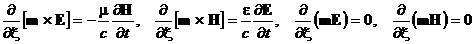. (25)

Умножая первые два уравнения системы (25) на m, получим ¶Е_x/¶t = 0,

¶H_x/¶t = 0, ¶Е_x/¶x = 0, ¶H_x/¶x = 0, то есть продольные компоненты векторов Е и Н не зависят ни от времени, ни от координат. Таким образом, переменная составляющая продольных компонент электрического и магнитного полей в волне равна нулю, то есть электромагнитная волна является поперечной.

В проводящей среде второе уравнение системы (25) принимает вид

.

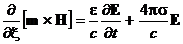После скалярного умножения на m получим

, Е_x(t) = Е_x(0)exp(-4pst/e),

то есть в проводящей среде продольная компонента электрического поля быстро затухает, и волна остается поперечной.

Для плоской волны u₁(t),t = t - x/v, частные производные принимают вид

. (26)

Константа интегрирования здесь положена равной нулю, так как мы рассматриваем как волну только переменные составляющие полей. Из уравнения (26) следует, что векторы Е, Н и m образуют правую ортогональную тройку, причем

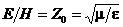 - (27)

импеданс среды.

Для проводящей среды рассмотрим распространение гармонической волны E = E₀(x)exp(-iwt), подставляя это выражение в уравнение (22), получим уравнение Гельмгольца в виде

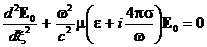. (28)

В отличие от уравнения (10) в соотношение (28) входит комплексная величина

.

Общее решение уравнения (28) имеет вид

, , то есть

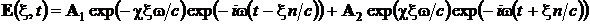 (29)

две плоские волны, амплитуда которых экспоненциально убывает по мере распространения. Здесь c - показатель поглощения, характеризует скорость убывания амплитуды волны, n = c/v - показатель преломления, определяет фазовую скорость волны. Обозначим

 - (30)

тангенс угла потерь, тогда 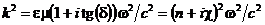, то есть n² - c² = me, 2nc = metg(d), откуда получаем

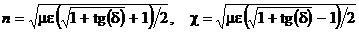. (31)

Из формул (30) и (31) следует, что в проводящей среде фазовая скорость (показатель преломления) и показатель затухания зависят от частоты, то есть среда является диспергирующей. При распространении плоской волны произвольной формы происходит искажение ее профиля, так как затухание и фазовые скорости ее гармонических компонент вида (9) разные.

Для малых потерь (слабозатухающая волна) tg(d) << 1, тогда из формулы (31) получаем . В случае сильных потерь, когда tg(d) >> 1, получаем . При этом амплитуда волны убывает в е раз на расстоянии d = c/(wc) = l/(2pc) << l. Нетрудно показать, что в проводящей среде

. (32)

Поток энергии в плоской волне

Запишем для однородной линейной непроводящей среды закон сохранения электромагнитной энергии в форме

¶W/¶t + div S = 0, (33)

где W - плотность электромагнитной энергии, S - ее поток. Умножим уравнение (16) скалярно на Е, а уравнение (17) - на Н и вычтем их, полагая s = 0:

,

.

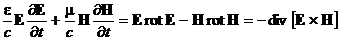Сравнивая это уравнение с уравнением (33), получим

. (34)

Вектор S в такой форме называется вектором Умова - Пойтинга.

Для гармонической электромагнитной волны в рамках метода комплексной амплитуды, полагая E(r, t) = Re[E₀(r)exp(iwt)], H(r, t) = Re[H₀(r)exp(iwt)], можно найти средний за период поток энергии

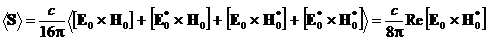. (35)

С учетом соотношений (26) и (34) для плоской волны получаем

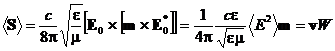, (36)

здесь  - скорость волны и учтено, что в силу соотношения (26) в волне eЕ² = mН², а .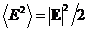

Поляризация электромагнитной волны

плоский волна электромагнитный

Для полного описания поперечной волны необходимо кроме ее амплитуды, фазы и частоты указать поляризацию, то есть направление векторов Е и Н. Пусть волновой вектор k направлен вдоль оси z, тогда векторы Е и Н лежат в плоскости ху

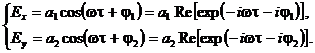 (37)

Исключим из уравнений (37) переменную t = t - z/v и получим уравнение эллипса в осях Е_х, Е_у:

.

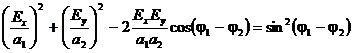Если D = j₁ - j₂ = ±p/2, то оси эллипса совпадают с осями координат х, у, а при а₁ = а₂ эллипс вырождается в окружность. Если D = j₁ - j₂ = pn, то эллипс вырождается в прямую Е_х/а₁ - (-1)ⁿЕ_у/а₂ = 0 с углом наклона tg(c) = ±а₂/а

Можно ввести множитель поляризации

. (38)

При комплексном значении Р волна имеет эллиптическую поляризацию, при

Р = ±i поляризация круговая. При действительном значении Р волна имеет линейную поляризацию. Знак мнимой части Р определяет направление вращения вектора Е в плоскости фронта, если Im(P) > 0, поляризация правая, а если Im(P) < 0 - левая. Правая поляризация соответствует вращению вектора Е по часовой стрелке для наблюдателя, смотрящего в направлении прихода волны. При Im(P) = 0 получаем Р = ctg(c).

Если отношение а₁/а₂ и D в волне не меняются, то есть компоненты Е_х и Е_у когерентны, то волна называется поляризованной. Если же a₁(t), a₂(t) и D(t) - случайные функции, то все положения вектора Е в плоскости фронта равноправны и волна является неполяризованной. Пример - естественный свет, излучение ламп накаливания и т. д. В более общем случае волна может быть смесью поляризованной и неполяризованной волн и описываться (в заданной точке пространства) как колебание с медленно меняющейся амплитудой

E(t) = a(t)exp(-iwt - ij(t)).

Состояние таких волн можно охарактеризовать матрицей когерентности

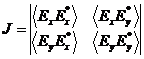. (39)

Пусть I = |E|² - интенсивность волны. Тогда для неполяризованной волны , |E_х|² = |E_у|² = I/2, поэтому |J| = I²/4. Для поляризованной волны |J| = 0, а sp(J) = I. Для частично поляризованной волны 0 £ |J| £ I²/4. Подставляя уравнение (37) в формулу (39), получим

, (40)

где .

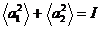Кроме того, в оптике широко используются параметры Стокса

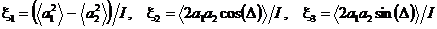. (41)

В этих переменных матрица когерентности (39) принимает вид

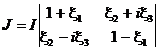. (42)

Для неполяризованной волны x₁ = x₂ = x₃ = 0, для полностью поляризованной 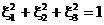. Соответственно, сумма квадратов параметров Стокса (41) характеризует степень р поляризации волны . Интенсивность поляризованной составляющей при этом равна pI, а неполяризованной (1 - p)I.

В курсе оптики показывается, что величина x₁I равна разности интенсивностей линейно поляризованных компонент с c = 0 и c = p/2, а x₂I - соответственно с c = p/4 и c = 3p/4. Величина x₃I равна разности интенсивностей волн с правой и левой поляризациями. Таким образом, коэффициенты Стокса можно легко измерить и, тем самым, построить матрицу поляризации (39).

Отражение и преломление плоских волн на плоской границе раздела

Из опыта известно, что при падении волны на границу раздела двух сред с разными свойствами, например коэффициентом преломления, возникает преломление и отражение волн. Пусть на плоскую границу раздела z = 0 между двумя полубесконечными средами с однородными параметрами e₁, m₁, s₁ для z > 0 и e₂, m₂, s₂ для z < 0 падает из первой среды плоская монохроматическая волна с частотой w под углом q₀ к оси z (рис. 1). Обозначим k₀ = k₁m₀ - волновой вектор падающей волны. Здесь учтено, что волновое число  одинаково и для падающей, и для отраженной волны, поскольку обе они распространяются в среде 1, а частота волны в линейном приближении сохраняется.

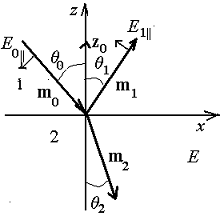
Рис. 1. Плоскость падения

Пусть плоскость xz (плоскость падения) проходит через вектор k₀, k₁ - волновой вектор отраженной волны, а k₂ - волновой вектор преломленной волны. Запишем электрические и магнитные поля в падающей, отраженной и преломленной волнах соответственно в виде (29) с учетом соотношения (32):

Здесь 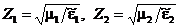 - импеданс первой и второй сред соответственно.

В плоскости z = 0 должны выполняться условия непрерывности тангенциальных компонент Е и Н суммарного волнового поля

 (43)

Поскольку граничные условия (43) должны выполняться во всех точках плоскости z = 0, то фазовые множители всех компонент должны быть одинаковы, 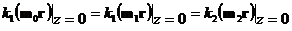, то есть k₁sin(q₀) = k₁sin(q₁) = k₂sin(q₂), откуда, в свою очередь, получаем

q₀ = q₁, (44)

sin(q₁)/sin(q₂) = k₂/k₁ - (45)

закон Снелиуса. Если s₁ = s₂ = 0, то q₂ - угол между нормалью к фронту преломленной волны и осью z.

Рассмотрим теперь две различные поляризации - горизонтально поляризованную волну с E_x = E_z = 0, E_y ¹ 0 и вертикально поляризованную волну с E_у = 0, E_z ¹ 0, E_x ¹ 0. Произвольную эллиптическую поляризацию можно получить как линейную комбинацию этих двух волн. Для горизонтальной поляризации из соотношения (43) получаем

E₀ + E₁ = E₂, E₀cos(q₀) - E₁cos(q₁) = E₂cos(q₂)Z₁/Z₂,

откуда следуют выражения для коэффициентов Френеля

Для вертикально поляризованной волны расчет удобнее проводить через вектор Н, который в этом случае перпендикулярен плоскости падения xz:

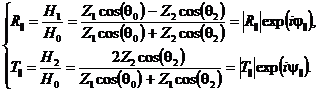 (47)

При нормальном падении q₀ = 0 и

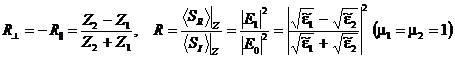. (48)

При отражении от границы двух диэлектриков с s₁ = s₂ =0, m₁ = m₂ = 1 с учетом соотношений (45), (46) и (47) получим при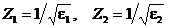

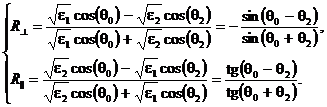 (49)

Поскольку коэффициенты Френеля (49) действительные, фазовый сдвиг между падающей и отраженной волнами равен 0 или p. При e₂ > e₁ из соотношения (45) получаем, что q₂ < q₀, то есть j_|| = p. При e₂ = e₁ соответственно q₂ = q₀ и R_|| = 0, а при q₂ + q₀ = p получаем R_^ = 0. Таким образом, при выполнении условия

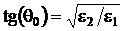 (50)

отраженная волна будет полностью вертикально поляризована. Угол падения, удовлетворяющий условию (50), называется углом Брюстера или углом полной поляризации.

При отражении от менее плотного диэлектрика с e₂ < e₁ q₂ > q₁, если при этом 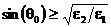, то из условия (45) следует, что sin(q₂) > 1, а 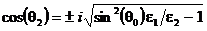. Угол  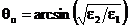называется углом полного внутреннего отражения. Если угол падения q₀ больше угла полного внутреннего отражения q_п, получаем , то есть пре­ломленная волна представляет собой плоскую неоднородную волну, экспоненциально затухающую вглубь второй среды. Найдем плотность потока энергии во вторую среду в этом случае. С учетом соотношений (35) и (27) получим 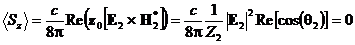, то есть средняя плотность потока энергии во вторую среду при полном отражении равна нулю.

Легко видеть, что при полном отражении |R_^| = |R_||| = 1, для фаз же коэффициентов Френеля (49) получаем

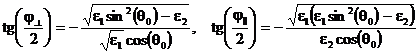. (51)

Из формулы (51) следует, что полное отражение сопровождается изменением фазы волны, различным для горизонтально и вертикально поляризованных волн. Поэтому, если полное отражение испытывает волна, плоскость поляризации которой наклонена к плоскости падения под некоторым углом, отраженная волна оказывается эллиптически поляризованной.

Рассмотрим теперь отражение и преломление падающей волны на границе диэлектрик - проводник. Пусть m₁ = m₂ = 1, e₁ = 1, s₁ = 0. Тогда из соотношения (45) следует, что k_1x = k₁sin(q₁) = k_2x = k₂sin(q₂) = k₁sin(q₀), а поскольку 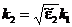, то

.

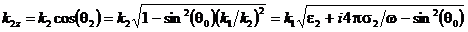Обозначая

 (52)

где 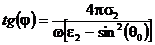, и учитывая, что k₁ = w/c, получим:

k_2z = (q + ip)w/c, E_T = E₂exp(-k₁p|z|)exp[i(k₁xsin(q₀) + qk₁z)]. (53)

Таким образом, преломленная волна (53) плоская и неоднородная, плоскости равной амплитуды pz = const параллельны границе раздела. Для плоскости равной фазы xsin(q₀) + qz = const нормаль направлена под углом y к оси z, где

. (54)

Соответственно, относительный показатель преломления второй среды относительно первой 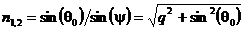 зависит не только от свойств среды, но, в отличие от соотношения (45), и от угла падения.

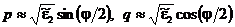Если проводимость среды достаточно велика, так что , то в формуле (52) можно положить , . Если при этом e₂ не слишком велика, так что tg(d) >> 1, то j » p/2, 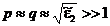, а из соотношения (54) следует cos(y) ® 1, sin (y) ® 0, то есть y ® 0.

Тот факт, что для сильно проводящей среды преломленная волна независимо от угла падения распространяется почти перпендикулярно границе раздела, позволяет сформулировать приближенные граничные условия Леонтовича. Заметим, что в этом случае соотношение (26) принимает вид

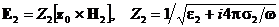. (55)

Так как при нормальном падении тангенциальные компоненты полей на границе равны и в первой, и во второй среде полным значениям самих полей, то из условия непрерывности Е₁ = Е₂, Н₁ = Н₂ и уравнение (55) можно переписать в виде

E₁ = Z₂[z₀ ´ H₁]. (56)

Распространяя соотношение (56) на случай падения под произвольными углами, получим приближенные граничные условия Леонтовича

[z₀ ´ E₁] = Z₂[z₀ ´ [z₀ ´ H₁]]. (57)

Литература

Основная

1. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 2009. - 384 с.

. Рабинович М.И., Трубецков Д.М. Введение в теорию колебаний и волн. Учебное пособие для вузов. М.: Наука, 2004. - 320 с.

Дополнительная

3. Ланда П.С. Нелинейные колебания и волны. М.: Наука, 2007. ­- 496 с.

. Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука, 2009. - 544 с.

. Вайштейн Л.А. Электромагнитные волны. М.: Радио и связь, 2008. - 440 с.