Задача о минимизации стоимости перегона транспортных средств

Пояснительная записка к курсовой работе

Задача о минимизации стоимости перегона транспортных средств

Аннотация

Пояснительная записка содержит 22 страницы, в том числе 9 рисунков, 4 таблицы, 6 источников.

В данной работе рассматривается один из разделов математического программирования - линейное программирование, в частности, одна из задач данного раздела - транспортная задача.

Кроме того, после представлено практическое применение данной теории к решению конкретной задачи.

Курсовой работой предусмотрено применение Microsoft Office Excel 2010.

Содержание

Введение

. Теоретическая часть

1.1 Математические методы решения задачи

.2 Математическая модель

1.2.1 Постановка задачи

.2.2 Экономико-математическая модель

2. Практическая часть

2.1 Компьютерная модель

.2 Компьютерный эксперимент

Заключение

Список использованных источников

Введение

В настоящее время множество задач планирования и управления в отраслях народного хозяйства, а также большой объем частных прикладных задач решаются методами математического программирования. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования.

Эти методы позволяют описать с достаточной точностью широкий круг задач коммерческой деятельности, таких, как:

планирование товарооборота;

размещение розничной торговой сети города;

планирование товароснабжения города, района;

прикрепление торговых предприятий к поставщикам;

организация рациональных перевозок товаров (транспортная задача);

распределение работников торговли по должностям (задача о назначении);

организация рациональных закупок продуктов питания (задача о диете);

распределение ресурсов;

планирование капиталовложений; оптимизация межотраслевых связей;

замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади;

установление рационального режима работы.

Математическая наука сформировала методологию решения таких задач. Основным (наиболее часто используемым) способом решения задач оптимизации является так называемый симплекс-метод.

Универсальность применения симплекс-метода связана с самой природой таких задач, ведь оптимизация заключается в максимизации или минимизации значения какой-либо целевой функции (например максимизации прибыли/дохода или минимизации затрат) в условиях выполнения различных ограничений (например по количеству или стоимости доступных ресурсов).

В рамках курсовой работы по математическим методам были поставлены задачи:

.        рассмотреть суть транспортной задачи, ее применение и назначение;

.        найти способы решения транспортной задачи и разработать компьютерную модель.

1. Теоретическая часть

Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителей этих ресурсов.

На автомобильном транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:

.        прикрепление потребителей ресурса к производителям;

.        привязка пунктов отправления к пунктам назначения;

.        взаимная привязка грузопотоков прямого и обратного направлений;

.        отдельные задачи оптимальной загрузки промышленного оборудования;

.        оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

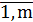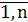Рассматривается экономико-математическая модель прикрепления пунктов отправления к пунктам назначения. Имеются m пунктов отправления груза и объемы отправления по каждому пункту а1, а2 ,…, аm. Известна потребность в грузах b1, b2, …, bn по каждому из n пунктов назначения. Задана матрица стоимостей доставки по каждому варианту сij, i=, j=. Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го пункта отправления (от поставщика) в каждый j-й пункт назначения (до потребителя) xij с минимальными транспортными издержками.

В общем виде исходные данные представлены в таблице 1. Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнений.

Таблица 1 - Исходные данные

Все грузы из i пунктов должны быть отправлены, т.е.:

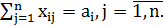 (1.1)

Все j пункты (потребители) должны быть обеспечены грузами в плановом объеме:

(1.2)

Суммарные объемы отправления должны равняться суммарным объемам назначения:

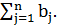 =  (1.3)

Должно выполняться условие неотрицательности переменных: xij≥0, i=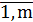, j=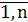. Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):

Zmin=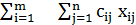. (1.4)

В модели (1.1) - (1.4) вместо матрицы стоимостей перевозок (сij) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматриваются минимум суммарной транспортной работы. Как видно из выражения (1.3), уравнение баланса является обязательным условием решения транспортной задачи.

Транспортным задачам присущи следующие особенности:

.        распределению подлежат однородные ресурсы;

.        условия задачи описываются только уравнениями;

.        все переменные выражаются в одинаковых единицах измерения;

.        во всех уравнениях коэффициенты при неизвестных равны единице;

.        каждая неизвестная встречается только в двух уравнениях системы ограничений.

Виды транспортных задач:

.        Транспортная задача называется закрытой, если суммарный объем отправляемых грузов 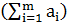 равен суммарному объему потребности в этих грузах по пунктам назначения :

 = .

.        Транспортная задача называется открытой, если суммарный объем отправляемых грузов не равен суммарному объему потребности в этих грузах по пунктам назначения (потребности выше запасов или наоборот), т.е.:

 ≠ .

Когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае если

.        потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;

.        запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.

Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.

.1 Математические методы решения задачи

Методы решения транспортных задач.

Метод северно-западного угла (диагональный).

Сущность метода заключается в том, что на каждом шаге заполняется левая верхняя (северо-западная) клетка оставшейся части таблицы, причем максимально возможным числом: либо полностью выносится груз из аi, либо полностью удовлетворяется потребность bj. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы аi и не удовлетворяются все потребности bj. В заключении проверяют, удовлетворяют ли найденные компоненты плана xij горизонтальным и вертикальным уравнениям.

Метод наименьшего элемента.

Сущность метода в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьшую оценку; в случае наличия нескольких таких равных оценок заполняется та, в которую производится наибольшая доставка груза. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы аi и не удовлетворяются все потребности bj. В заключении проверяют, удовлетворяют ли найденные компоненты плана xij горизонтальным и вертикальным уравнениям.

Метод аппроксимации Фогеля.

При определении опорного плана транспортной задачи методом аппроксимации Фогеля находят разность по всем столбцам и по всем строкам между двумя записанными в них минимальными оценками. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальную стоимость. Если минимальная стоимость одинакова для нескольких клеток столбца (строки), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными стоимостями, находящимися в данном столбце (строке).

Метод потенциалов.

Решение задачи методом потенциалов включает следующие этапы:

.        разработку начального плана (опорного решения);

.        расчет потенциалов;

.        проверка плана на оптимальность;

.        поиск максимального звена неоптимальности (если условие п.3 не было достигнуто);

.        составление контура перераспределения ресурсов;

.        определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру;

.        получение нового плана.

Описанная процедура повторяется несколько раз (итераций), пока не будет найдено оптимальное решение. Вычислительный алгоритм для каждой итерации не меняется.

.2 Математическая модель

.2.1 Постановка задачи

Четыре овощехранилища каждый день обеспечивают картофелем три магазина. Магазины подали заявки на 17, 12 и 32 т. Овощехранилища имеют соответственно 20, 20, 15 и 25 т. Тарифы (в д. е. за 1 т.) указаны в таблице 2.

Таблица 2 - Исходные данные задачи

Составить план перевозок, минимизирующий суммарные транспортные расходы.

.2.2 Экономико-математическая модель

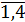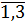Пусть xij, i=, j= - количество картофеля, поставляемого от i-ого овощехранилища к j-ому магазину.

Целевая функция:

F= 2x11+7x12+4x13+3x21+2x22+x23+5x31+6x32+2x33+3x41+

+4x42+7x43 ->min

Ограничения:

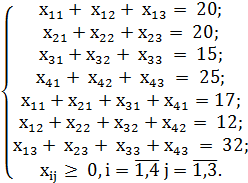
2. Практическая часть

Решение задачи методом северо-западного угла представлено в таблице 3.

Таблица 3 - Метод северо-западного угла

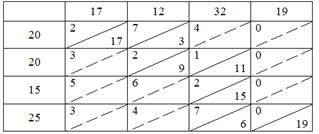
=2*17+7*3+2*9+1*11+2*15+7*6=156

Метод минимальной стоимости дает другой первоначальный план поставок груза и в соответствии с названием метода наименьшие суммарные затраты на доставку. Решение задачи методом минимальной стоимости представлено в таблице 4.

Таблица 4 - Решение методом минимальной стоимости

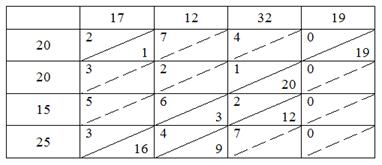
=2*1+1*20+6*3+2*12+3*16+4*9=148

2.1 Компьютерная модель

В результате решения задачи методом северо-западного угла и методом минимальной стоимости были составлены первоначальные планы поставок, которые не являются оптимальными.

Задачи оптимизированного моделирования можно решать с помощью надстройки электронных таблиц "Поиск решения". Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке и получить оптимальный план поставок.

В книге Математические методы на листе Транспортная задача вводятся в соответствующие ячейки исходные данные задачи (рис. 1).

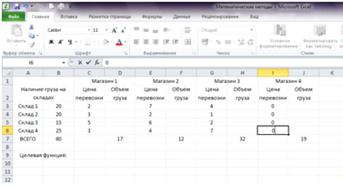
Рисунок 1 - Исходные данные

В ячейку С9 заносится целевая функция (единственная функция в таблице) (рис. 2).

Общая стоимость всех "элементарных" перевозок вычисляется как сумма произведений цены доставки одной тонный груза на объем груза, перевозимого в данном направлении:

Общая стоимость =C3*D3 + C4*D4 + C5*D5 + C6*D6 + E3*F3 + E4*F4 + E5*F5 + E6*F6 + G3*H3 + G4*H4 + G5*H5 + G6*H6 + I3*J3 + I4*J4 + I5*J5 + I6*J6.

Рисунок 2 - Компьютерная модель задачи

2.2 Компьютерный эксперимент

математический оптимизация транспортный программирование

В Excel имеется надстройка Поиск решения, которая помогает решить задачи линейного программирования. Необходимо воспользоваться меню Данные, Поиск решения. Если в меню Данные отсутствует команда Поиск решения, необходимо выполнить команду Файл, Параметры, Надстройки. Найти элемент Поиск решения и поставить "галочку" рядом с ним. Если в окне Надстройки нет элемента Поиск решения, необходимо доустановить Excel.

Выделить ячейку С9, в которой находится целевая функция. Выбрать команду Данные, Поиск решения (рис. 3).

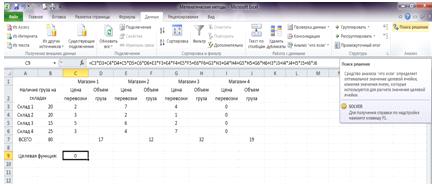
Рисунок 3 - Поиск решения

В диалоговом окне в поле ввода Оптимизировать целевую функция уже содержится $С$9 (при необходимости эту ссылку можно изменить). Установить переключатель До Минимума.

Рисунок 4 - Окно поиска решения

Щелкнуть кнопку Предложить, и в поле ввода Изменяя ячейки переменных появится $C$2:$C$4;$E$2:$E$4;$G$2:$G$4;$I$2:$I$4;$K$2:$K$4 (рис. 5).

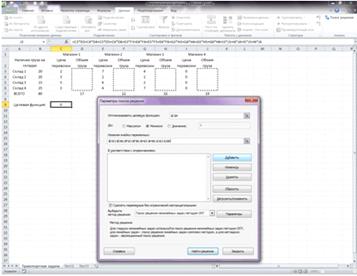
Рисунок 5 - Изменяемые ячейки

Щелкнуть кнопку Добавить, чтобы ввести первое ограничение задачи. В диалоговом окне Добавление ограничения в поле ввода Ссылка на ячейку указать $B$3. Правее в выпадающем списке с условными операторами выбрать =. В поле ввода Ограничение вводят $D$3+$F$3+$H$3+$J$3. Щелкнуть кнопку Добавить и ввести другие ограничения. Щелкнуть кнопку Ок. Добавление первого ограничения представлено на рисунке 6.

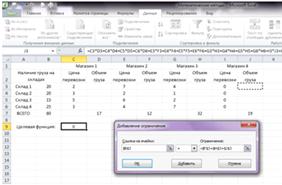
Рисунок 6 - Добавление ограничения

Оказавшись в диалоговом окне, можно наблюдать введенные ограничения. С помощью кнопок Изменить и Удалить можно изменить и удалить ограничения. Все введенные ограничения представлены на рисунке 7.

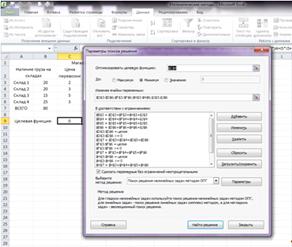
Рисунок 7 - Ограничения

В выпадающем списке Выберите метод решения выбрать Поиск решения линейных задач симплекс-методом и нажать кнопку Найти решение (рис. 8).

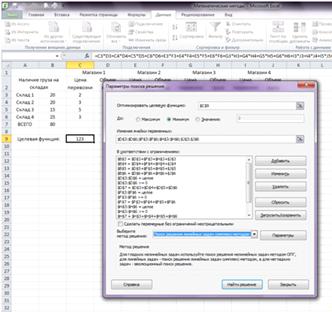
Рисунок 8 - Запуск Поиска решения

Установив кнопку Сохранить найденное решение, можно сохранить предложенные значения. С помощью этого диалогового окна (рис. 9) можно сформировать отчет.

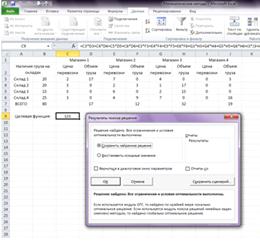
Рисунок 9 - Решение задачи

Первое овощехранилище поставит первому магазину 17 т. картофеля, третьему магазину - 3 т. картофеля. Второе овощехранилище поставит второму магазину 3 т. картофеля, третьему магазину - 17 т. картофеля. Третье овощехранилище поставит третьему магазину 15 т. картофеля. Четвёртое овощехранилище поставит второму магазину 9 т. картофеля, четвертому магазину - 16 т. картофеля. Суммарные затраты составят 123 д.е.

Заключение

В рамках курсовой работы была рассмотрена транспортная задача, ее применение и назначение.

Найдены и рассмотрены методы решения транспортной задачи: метод северо-западного угла, метом минимальной стоимости, метод потенциалов.

На основе этих методов, в частности методе потенциалов, построен Поиск решения, который позволяет решать не только транспортные задачи, но и многие другие, например: составление плана производства изделий; задача о назначениях; задача о диете (о смесях); задача о раскрое материала; задача о снабжении предприятий сырьем и другие.

Список использованных источников

1.      Могилев А.В. и др. Информатика: Учеб. пособие для студ. пед. вузов / А.В. Могилев, Н.И. Пак, Е.К. Хённер; Под ред. Е.К. Хённера. - М., 2009. - 816 с. - ISBN 5-7695-0330-0

2.      Просветов Г.И. Математические методы в экономике: Учебно-методическое пособие. - М.: Издательство РДЛ, 2004. - 160 с. - ISBN5-9340-047-3

.        Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2010. - 432 с.: ил. - ISBN5-279-02940-8

.        Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2012. - 616 с.: ил. - ISBN5-279-02828-2

.        Партыка Т.Л., Попов И.И. Математические методы: учебник. 2-е изд., испр. и доп. - М.: ФОРУМ: ИНРФА-М, 2007. - 464 с.: ил. - ISBN978-5-91134-152-7 (ФОРУМ) ISBN978-5-16-003157-6 (ИНФРА-М)

.        http://ru.wikipedia.org/Транспортная_задача