Основная теорема алгебры

Основная теорема алгебры

Всякий многочлен с любыми комплексными коэффициентами , степень которого не меньше единицы имеет хотя бы один корень, в общем случае комплексный.

                                                  

План доказательства.

Лемма №1. Многочлен  f(x) является непрерывной  функцией комплексного переменного x.

Лемма №2. Если данн многочлен  n-ой степени, n>0,

                           f(x)=a₀xⁿ+a₁x^n-1+…+a_n

с произвольными комплексными коэффициентами и если  k- любое положительное действительное число, то для достаточно больших  по модулю значений

                           |a_nxⁿ|>k|ax^n-1+a_nx^n-2+….+a₀|

Лемма №3.

Лемма №4.(Лемма  Даламбера).

 

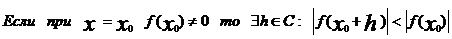
Лемма №5.

Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.

 

Лемма №6.

Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге  Е достигает своего минимума и максимума.

 

Доказательство основной теоремы.

                          

Лемма  №1.

Надо доказать, что   |f(x₀+x)-f(x₀)|<e.

Докажем Лемму №1 сначала для многочлена без свободного члена и при  x₀=0

Если      A=max(|a₀ |,|a₁|,…,|a _n-1|) и 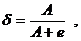 (1)

то |f(x)|=|a₀xⁿ+…+a_n-1x|

                       ,

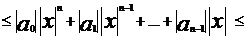
т.к |x|<б ,и из (1) б<1, то

т.к. a₀=0 то f(0)=0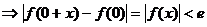

Что и требовалось доказать.

Теперь докажем непрерывность любого многочлена.

f(x₀+x)=a₀(x₀+x)ⁿ+…+a_n  

pаскрывая все скобки по формуле бинома и собирая вместе члены с

одинаковыми степенями x  получим

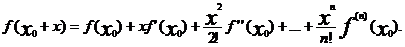
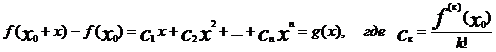Многочлен g(x)-это многочлен от x при x₀ =0  и а₀=0 |f(x₀+x)-f(x)|=|g(x)|<e

Лемма доказана.

Лемма №2

Если дан многочлен  n-ой степени, n>0,

                           f(x)=a₀xⁿ+a₁x^n-1+…+a_n

с произвольными комплексными коэффициентами и если  k- любое положительное действительное число, то для достаточно больших  по модулю значений x верно неравенство:

                           |a₀xⁿ|>k|a₁x^n-1+a₂x^n-2+….+a_n| (2)

                          

Доказательсво.

Пусть А=max(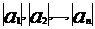), тогда

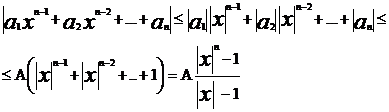
пологая |x|>1, получим

                          

откуда

  

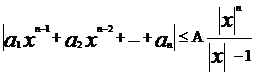
следовательно неравенство (2) будет выполняться если |x|>1 и

  

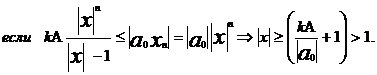
Лемма №2 доказана.

 Лемма №3.

Доказательство.

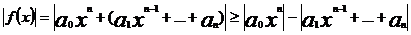  (3)

применим лемму 2: при k=2 существует такое N₁ , что при |x|> N₁

|a₀xⁿ|>2|a₁x^n-1+a₂x^n-2+….+a_n|

откуда

               |a₁x^n-1+a₂x^n-2+….+a_n|<|a₀xⁿ|/2

тогда из (3)

              

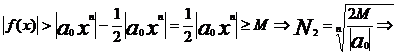
при |x|>N=max(N₁ ,N₂)   |f(x)|>M что и тебовалось доказать.

              

Лемма №3(Лемма Даламбера).

Если при x=x₀ многочлен f(x) степени n,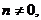 не обращаеться в нуль, то существует такое приращение h, в общем случае комплексное, что

                           |f(x₀+h)|<|f(x)|

                          

Доказательство.

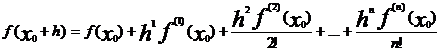По условию f(x₀) не равно нулю, случайно может быть так, что x₀ является корнем f’(x),..,f^(k-1) (x). Пусть k-я производная будет первой, не имеющей x₀ своим корнем. Такое k существует т.к.

                           f⁽ⁿ⁾( x₀)=n!a₀

Т.к f(x₀) не равно нулю то поделим обе части уравнения на f(x₀)

и обозначим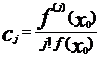

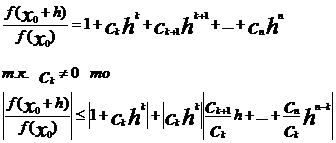
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его аргумент.

По лемме№1: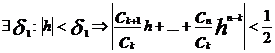  

С другой стороны при

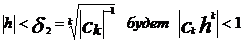                 (4)

Пусть |h|<min(б₁, б₂), тогда

             

Теперь выберем аргумент h так, чтобы c_kh^k было действительным отрицательным числом.

При таком выборе c_kh^k=-| c_kh^k| следовательно учитывая (4) получим

  

Что доказывает лемму Даламбера.

Лемма №5.

Если действительная функция комплексного переменного  f(x) непрерывна в замкнутом круге Е, то она ограничена.

Доказательство.

Предположим, что это не верно тогда

                                      

получена бесконечная ограниченная последовательность x_n,

из нее можно выбрать сходящуюся подпоследовательность 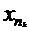, пусть ее предел равен x₀. Так как круг Е замкнут, то x₀ пренадлежит Е. Тогда так как f(x) непрерывна

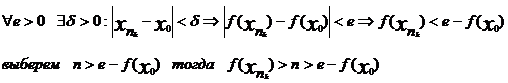
получено противоречие, следовательно неверно, предположение о неограничености f(x).

Лемма №6.

Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге  Е достигает своего минимума и

максимума.

Доказательство.

Докажем это утверждение для максимума.

 Так как f(x) непрерывна в Е, то она ограничена и следовательно существует M=sup{ f(x)}. Рассмотрим функцию .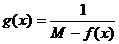

Если f(x) не достигает своего максимума, то M> f(x) следовательно M-f(x)>0 , следовательно g(x) непрерывна в Е.

  

Полученое противоречит тому, что M=sup{ f(x)}. Следовательно функция достигает свего максимума. Аналогично доказывается достижение минимума.

 

Доказательство основной теоремы.

Пусть дан многочлен f(x), очевидно что если a_n-свободный член, то f(0)= a_n. Теперь применим лемму№3: возьмем М=|f(0)| =|a_n| тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Е ограниченный окружностью с центром в нуле и радиусом N, включая границы круга. Так как (по лемме №1) многочлен f(x)-непрерывен, то и |f(x)|-непрерывен внутри замкнутого круга Е, следовательно(по лемме №6), существует такая точка x₀, что для всех x из E выполняется неравенство |f(x)|>=|f(x₀)|. x₀ является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N |f(x)|>M>|f(0)|>|f(x₀)| точка x₀ является точкой минимуа |f(x)| на всей комплексной плоскости.

|f(x₀)|=0 т.к по лемме Даламбера если |f(x₀)|¹0 то x₀ не точка минимума для |f(x)|Þ x₀-корень многочлена f(x).

Теорема доказана.