Ответы экзамен начертательная геометрия

Ответы экзамен начертательная геометрия

1.В основе правил построения изображений в нач.геом лежит метод проекций.Изучать его начинают с построения проекции точки,так как при построении изображения любой пространственной формы объект рассматривается ряд точек,принад.этой форме.проекцией фигуры наз-ся совокупность проекций всех её точек

2. Существует два вида проецирования: центральное и параллельное.

3. 5. Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.дПравила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов

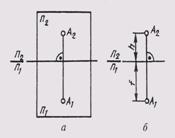
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 ... и называть горизонтальными проекциями (точки, прямой, плоскости).Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.Спроецируем точку А ортогонально на обе плоскости проекций:АА1_|_ П1;AА1 ^П1=A1; АА2_|_ П2;AА2 ^П2=A2;Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.

4.Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения ( см. рис. 2.3, 2.4) .(следствие 1). Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций, т. е. перпендикулярную третьей, называют прямой частного положения.

a) Прямая АВ параллельна плоскости П1 ( ее называют горизонтальной прямой - горизонталь); фронтальная проекция a2b2 параллельна оси x; длина горизонтальной проекции равна длине самого отрезка(a1b1 =AB);

b) Прямая АВ параллельна плоскости П2 ( ее называют фронтальной прямой - фронталь); горизонтальная проекция a1b1 параллельна оси x; длина фронтальной проекции отрезка равна длине самого отрезка (а2b2=AB);

c) Прямая АВ параллельна плоскости П3( ее называют профильной прямой - профиль); длина профильной проекции отрезка равна длине самого отрезка (a3b3= AB) ;

Эти прямые называют прямыми уровня

a) Прямая перпендикулярна плоскости П1, ее проекция a2b2 перпендикулярна оси x; проекции а1 и b1 совпадают;

b) Прямая перпендикулярна плоскости П2, ее проекция a1b1 перпендикулярна оси x, проекции a2 и b2 совпадают;

c) Прямая перпендикулярна плоскости П3, ее проекции a1b1, a2b2 параллельны оси x; проекции a3 и b3 совпадают;

Эти прямые называют проецирующими ( следствие 3).

Как уже указывалось, если точка принадлежит прямой, то ее проекции принадлежат одноименным проекциям этой прямой ( см. рис. 2.3 , 2.4) . Обратное положение: если две проекции точки принадлежат одноименным с ними проекциям прямой в системе П1, П2, то точка принадлежит прямой, - справедливо для проекций всех прямых, кроме профильной. Для профильных прямых обратное положение справедливо только в системах П1, П2, П3, или П2, П3, или П1, П3.

5.см.4

6. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла).

Если проекция угла представляет угол 900, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций

Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 

Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

7. Свойства и признаки

Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны

Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны

Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

8.Например на П1 проведем через заданную прямую а1 вспомогательную горизонтально проецирующую плоскость s1: а s и s П1. Построим m1 - линию пересечения вспомогательной плоскости s1 с заданной плоскостью b1. Отметим точки 11 и 21 - точки пересечения прямой m1 и отрезков А1В1 и В1С1 соответственно. Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС. Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2. По линии связи находим первую проекцию точки К - точку К1.

Определяем видимость прямой а с помощью метода конкурирующих точек. На П2, правая часть прямой а2 (относительно точки К2) - видима, а левая часть прямой а2 - невидима. На П1, левая часть прямой а1 (относительно точки К1) - невидима, а правая часть прямой а1 - видима.

9. Для построения линии пересечения плоскостей строят точки пересечения прямых одной плоскости с другой и через них проводят искомую линию.Пример такого построения на чертеже приведен на рисунке 4.2. Одна из плоскостей задана треугольником с проекциями a1b1c1, a2b2c2. Вторая - параллельными прямыми с проекциями.d2e2, d1e1 и f1g1, f2g2.

Для построения проекций линии пересечения определены проекции m2, m1 и n2, n1 двух ее точек пересечения прямых с проекциями d2e2, d1e1 и f2g2, f1g1, с плоскостью треугольника. Проекции m2, m1 , n2, n1 точек пересечения построены с помощью фронтально - проецирующих плоскостей, заданных следами Q2 и P2 . Плоскость Q проходит через прямую DE и пересекает плоскость треугольника по линии с проекциями 11 21, 12 22. Пересечение горизонтальных проекций 11 21 и d1e1 является горизонтальной проекцией m1 искомой точки . По ней построена фронтальная проекция m2, на фронтальной проекции d2e2. Аналогично с помощью плоскости Р (Р 2 ) построены проекции n2, n1 второй точки. Через построенные точки m2, n2 и m1, n1 проведены проекции m2 n2 и m1, n1 отрезка, по которому пересекаются заданные пластины.Анализ видимости участков пластин на фронтальной проекции выполнен с помощью конкурирующих точек с проекциями 42, 41 и 52, 51, лежащих на скрещивающихся прямых gf и bc. Их фронтальные проекции 42 и 52 совпадают. На горизонтальной проекции видно, что при взгляде по стрелке K точка 52 закрывает точку 42. Видимость участков пластин на горизонтальной проекции определена так же с помощью конкурирующих точек с проекциями 62, 61 и 72, 71, лежащих на скрещивающихся прямых ed и ac. Их горизонтальные проекции 61 и 71 совпадают. Из фронтальной проекции видно, что при взгляде по стрелке S точка 71 закрывает точку 61

10.построить перпендикуляр

11.Строится перпендикуляр из точки K на плоскость s (АВС) : m1 h1, m2 f2.

Находится точка N - точка пересечения перпендикуляра m с плоскостью s (АВС).

Определяется расстояние от точки K до точки N с помощью прямоугольного треугольника K1N1M0. Длина гипотенузы N1M0 – это искомое расстояние: |KN| = N1M0.

12.

13. Видимость объектов на плоскостях проекций определяют по конкурирую-

щим точкам: точкам, принадлежащим различным объектам ( в данной задаче -

перпендикуляру n и плоскости Σ ).

   Для определения видимости на плоскости П1 необходимо на этой же

плоскости взять конкурирующие точки, принадлежащие перпендикуляру и

плоскости и совпадающие на плоскости П1. Обычно, такие точки выбирают в

месте наложения проекций перпендикуляра и прямых, задающих плоскость.

Выбрав, например, в качестве конкурирующих точек точки 101 ≡ 111,если 10n,

а 11 Σ, по проекциям точек 102 и112 определим, точка какого объекта выше.

Этот объект и будет видимым на плоскости П1.

   Для определения видимости на плоскости П2 необходимо взять точки,

принадлежащие перпендикуляру n и плоскости Σ, и совпадающие на этой же

плоскости проекций. По горизонтальным проекциям конкурирующих точек

определим, какая точка ближе к наблюдателю (имеет большую глубину), и,

следовательно, объект, видимый на плоскости П2.

   Проекции объекта, невидимого на плоскости проекций, показывают

штриховыми линиями (линиями невидимого контура).

14. Строим на проекциях действительную длину прямой АВ.

Пересечение действительной длины с проекциями прямой дают действительные углы наклона прямой к плоскостям проекций.

Угол α является углом наклона данной прямой к горизонтальной плоскости проекций, а угол β – к вертикальной.

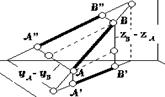
15. Графически натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, у которого одним катетом будет любая из проекций отрезка, вторым катетом будет глубина одного из катетов отрезка относительно другого. Попутно здесь же решается задача определения угла наклона прямой и плоскостям проекций H и V.

16.множество послед.положений движущейся линии или другой пов-ти в пространстве

18. КОНИЧЕСКИЕ СЕЧЕНИЯ, плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка. За исключением вырожденных случаев, рассматриваемых в последнем разделе, коническими сечениями являются эллипсы, гиперболы или параболы.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.

19. Натуральную величину фигуры сечения можно определить уже известными нам способами замены плоскостей проекций или вращения В данном случае проще применить второй метод Для этого повернем фигуру сечения вокруг стороны 3—4 (фронтально-проецирующая прямая) до наложения на плоскость Н. При этом фронтальные проекции вершин фигуры сечения

         перемешаются по дугам окружности, а горизонтальные — по прямым, перпендикулярным к проекции оси вращения i = 3—4 Натуральная величина фигуры сечения — 3-4-2 i-l i.

22.23.В начертательной геометрии для образования поверхностей как объектов инженерного исследования преимущественно используются кинематический и каркасный способы.

Кинематический способ.

Поверхность рассматривается как совокупность всех последовательных положений некоторой линии – образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей.

Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих.

Каркасный способ.

Поверхность рассматривается как совокупность некоторого числа линий, образующих каркас. Основное отличие каркасных поверхностей от кинематических состоит в том, что для первых задается определенное число линий каркаса – дискретный каркас, а у вторых в любой точке поверхности может быть построена линия каркаса, т.е. поверхность имеет непрерывный каркас. Каркасные поверхности задают на чертеже проекциями линий каркаса. Точки и линии каркасной поверхности, не лежащие на линиях каркаса, могут быть построены только приближенно. Поэтому поверхность, заданная каркасом, не вполне определена. Могут существовать и другие поверхности с тем же каркасом, но несколько отличающиеся одна от другой в промежутках между каркасными линиями.

На эпюре Монжа поверхность задается проекциями ее репера.

Построение недостающей проекции точки, принадлежащей поверхности, осуществляется с помощью простейших линий каркаса поверхности, проходящих через эту точку. Для построения таких линий каркаса используют закон образования данной поверхности.

Следует отметить, что, умея строить одну точку поверхности, можно построить проекции любой линии, принадлежащей заданной поверхности, рассматривая эту линию, как совокупность отдельных точек.

24.опред.пов. совокупность независимых услов. Зад.поверх. (геом часть-точки линии повти и закон образования аоверх геом частью опред).

27.  Для того чтобы построить линию пересечения двух поверхностей нужно найти ряд

общих точек, принадлежащих им, и затем эти точки соединить в определенной

последовательности.

     Линия пересечения двух поверхностей в общем виде представляет собой

пространственную кривую, которая может распадаться на две части и более.

     Для того чтобы найти произвольную точку линии пересечения поступают так

(рис.2.1):

     1. Вводится вспомогательная секущая поверхность. На рис. 2.1. введена плоскость

Г⊥ П2 (Г2).

     2. Строится линия пересечения вспомогательной поверхности с каждой из заданных.

В данном примере окружность m есть линия пересечения плоскости Г с поверхностью Ф,

а окружность n - линия пересечения с поверхностью Λ, т.е.

                                        m = Г П Ф;

                                        n = Г П Λ.

     3. На пересечении линий m и n отмечается общая точка К, принадлежащая линии

пересечения.

                                        Кj = m п n.

     Последовательно вводя ряд вспомогательных секущих поверхностей находим

необходимое число точек, принадлежащих искомой линии пересечения заданных

поверхностей.

     Определение проекций линии пересечения обычно начинают с построения опорных

точек, т.е. точек расположенных на очерках поверхности (точки, определяющие границы

видимости проекций кривой), точек, удаленных на экстремальные (min и max)

расстояния от плоскости проекций. Затем определяют произвольные или случайные

точки кривой.

28.29 Сечение - изображение фигуры, получающееся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости.

Сечения, не входящие в состав разреза, разделяют на:

вынесенные (рис. 70);

наложенные (рис. 71).

Вынесенные сечения являются предпочтительными и их допускается располагать в разрыве между частями одного и того же вида (рис. 72). Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями, а контур наложенного сечения – сплошными тонкими линиями, причем контур основного изображения в месте расположения наложенного сечения не прерывают (см. рис. 71).

Ось симметрии наложенного или вынесенного сечения указывают штрихпунктирной тонкой линией без обозначения буквами и стрелками и линию сечения не проводят (см. рис. 70, 71).

Для несимметричных сечений, расположенных в разрыве (рис. 73) или наложенных (рис. 74) линию сечения проводят со стрелками, но буквами не обозначают.

Вынесенные сечения располагают:

на любом месте поля чертежа;

на месте основного вида;

с поворотом с добавлением знака «повернуто»

Если секущая плоскость проходит через ось поверхности вращения, ограничивающие отверстие или углубления, то их контур в сечении показывают полностью, т.е. выполняют по правилу разреза (рис. 75).

Если сечение получается состоящим из двух и более отдельных частей (рис. 76, а), то следует применить разрез, вплоть до изменения направления взгляда (рис. 76, б).

Секущие плоскости выбирают так, чтобы получить нормальные поперечные сечения (рис. 77).

Для нескольких одинаковых сечений, относящихся к одному предмета, линию сечения обозначают одной буквой и вычерчивают одно сечение (рис. 78).В теории пространственных построений выделим основные операции:

1.Задать положение точки в пространстве

2.Провести прямую через две данные точки

3.Провести плоскость через три точки, не лежащие на одной и той же прямой

4.Найти точку пересечения прямой с плоскостью

5.В каждой плоскости производить все планиметрические построения.

30. Если сечение вынесенное и расположено на свободном поле  чертежа, то оно обозначается прописными буквами алфавита типа А-А, Б-Б, а секущая плоскость изображается штрихами разомкнутой линии, длина которых равна приблизительно 10 мм. К штрихам подводят стрелки, указывающие направление взгляда. С внешних сторон которых одну и туже прописную  букву. Если сечение располагается в разрыве между частями одного и того же вида, то оно не обозначается, а показывается только секущая плоскость разомкнутой линией и направление взгляда стрелками букв при этом рядом не ставится.

31. Аксонометрические проекции в зависимости от направления проецирования разделяют на:

косоугольные, когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;

прямоугольные, когда направление проецирования перпендикулярно плоскости аксонометрических проекций.

В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:

изометрия — все три коэффициента искажения равны между собой (u = v = w);

диметрия — два коэффициента искажения равны между собой и отличаются от третьего (и не равно v = w или и= v не равно w);

триметрия — все три коэффициента искажения не равны между собой (u не равно v не равно w).

Основное предложение аксонометрии сформулировано немецким геометром К. Польке: три произвольной длины отрезка прямых, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных координатных осях от начала.

Согласно этой теореме любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые произвольной длины отрезки этих прямых, отложенные от точки их пересечения, можно принять за аксонометрические масштабы.

Эта система аксонометрических осей и масштабов является параллельной проекцией некоторой прямоугольной системы координатных.

32. В зависимости от взаимного положения плоскостей П1, П2 и П3, аксонометрической плоскости проекций и направления проецирования s в пространстве координаты точки будут проецироваться с различными искажениями.

Отношения XA'/XA, YA'/YA, ZA'/ZA называют натуральными коэффициентами искажения. Условимся обозначать эти коэффициенты:

m = XA'/XA - коэффициент искажения по оси х;

n = YA'/YA - коэффициент искажения по оси у;

р = ZA'/ZA - коэффициент искажения по оси z.

В тех случаях, когда коэффициенты искажения являются дробными числами, для построения аксонометрических проекций требуются большие вычислительные операции. Но вычислительную работу можно уменьшить, если хотя бы один из коэффициентов искажения привести к более удобному для расчета числу - например, к единице.

Приведем к единице коэффициент искажения р. Разделив единицу на р (1/р), получим коэффициент k, называемый коэффициентом приведения. Умножив коэффициенты искажения m, n и р на k, получим значения приведенных коэффициентов искажения. Приведенные коэффициенты искажения, в отличие от натуральных, обозначим через M, N, P. Тогда М = km; N = kn; Р = kp = 1.

33. Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.

В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же оси: 2a = 1,22d и 2b = 0,71 d. На рис. 159 показано построение осей такого овала для изометрии окружности диаметра d.

Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс— аксонометрию окружности