Ответы на экзамен электроника электротехника
1.
Основные элементы электрической цепи (активные,
пассивные). Обозначение тока, потенциалов и напряжения в электрической цепи.
Электрическая цепь– совокупность
источников, приёмников электрической энергии и соединяющих их проводов. Кроме
этих элементов, в Э. ц. могут входить выключатели, переключатели,
предохранители и другие электрические аппараты защиты и коммутации, а также
измерит, и контрольные приборы.
Активные
элементы
– источники электрической энергии, в которых неэлектрические виды энергии
преобразуются в электрическую.
Различают
два основных активных элемента: источник напряжения (ЭДС) и источник тока.
Пассивные
элементы
– приемники электромагнитной энергии. Электрическая энергия в них преобразуется
в неэлектрические виды энергии – активное сопротивление (проводимость), либо
накапливается в виде энергии электрического поля (емкость) или энергии
магнитного поля (индуктивность). Емкость и индуктивность являются реактивными
приемниками энергии или реактивными элементами.
Ток
обозначается
через I с направлением
течения.
На
схемах рядом с точкой более высокого потенциала ставится знак +, а рядом с
точкой более низкого – знак -. Разность потенциалов обозначается через U. Разность потенциалов
в двух точках a и b обозначается через Uab.
Напряжение
обозначается
U.
2.
Идеальные источники тока и ЭДС, обозначение и
основные характеристики.
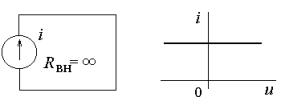
Идеальный
источник
тока
(I),
величина тока, протекающего через который, не зависит от напряжения на его
зажимах. Внутреннее сопротивление такого источника можно условно принять равным
бесконечности. Обозначение идеального
источника
тока и его
вольт-амперная характеристика приведены на рис.
Идеальный
источник
напряжения (E),
напряжение на зажимах которого не зависит от величины протекающего через
него тока .
Внутреннее сопротивление идеального
источника
напряжения можно условно принять равным нулю. Обозначение такого источника и
его вольт-амперная характеристика приведены на рис.
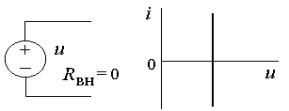
1.
Закон Ома для участка цепи без источника ЭДС и закон
Ома для замкнутой цепи. Рисунок. 4. Закон Ома для участка цепи, содержащий
ЭДС. Рисунок.




5.
Первый закон Кирхгофа. Пример его применения. 6.
Второй закон Кирхгофа. Пример его применения.
Кроме простых цепей существуют
сложные цепи. Сложной электрической цепью называют цепь, которая не может быть непосредственно
рассчитана по закону Ома.
Сложная
цепь обычно содержит несколько источников ЭДС в разных ветвях. Число ветвей
электрической цепи обозначают через q, число узлов — через q, а число независимых контуров —
через п, где п = р - q + 1.
Для расчета сложных
цепей используют законы Кирхгофа, которые формулируются для разветвленных и
сложных электрических цепей; при их рассмотрении используют понятия ветви,
узла и контура.
Ветвью называют часть электрической
цепи, состоящую только из последовательно соединенных источников ЭДС (или тока)
и сопротивлений и имеющую два зажима для подключения ее к остальной
части цепи. На схемах электрических цепей каждую ветвь обычно изображают в виде
последовательного соединения одного эквивалентного источника ЭДС (или тока) и
одного эквивалентного сопротивления. Ветвь непосредственно соединяет два узла.
В ветви через все элементы протекает один и тот же ток.
Узлом называют точку электрической цепи, в которой соединено не
менее трех ветвей. На схемах узел обозначают точкой.
Контуром называют последовательность ветвей электрической цепи,
образующей замкнутый путь, в котором один из узлов одновременно является
началом и концом пути, а остальные встречаются только один раз.
Первый закон Кирхгофа выражает тот факт, что ни в одной точке цепи
не происходит накопление электрических зарядов. Согласно этому закону (закону
Кирхгофа для токов) алгебраическая сумма токов в любом узле электрической цепи
равна нулю:

где со
знаком плюс записывают токи с положительными направлениями от узла, со знаком
минус — с положительными направлениями к узлу или наоборот. Иначе: сумма
токов, направленных от узла, равна сумме токов, направленных к узлу. Так,
например, для узла 1
(рис. 1.4) получим уравнение
I1-I2+I3-I4=0,
Второй
закон Кирхгофа устанавливает
связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре. Согласно
этому закону (закону Кирхгофа для напряжений), алгебраическая сумма напряжений
участков любого контура электрической цепи равна нулю:


где т
— число участков контура.
Со
знаком плюс записывают напряжения, положительные направления которых
совпадают с произвольно выбранным направлением обхода контура, со знаком минус
— противоположно направленные или наоборот. В частности, для контура схемы
замещения цепи, содержащего только источники ЭДС и резистивные элементы,
алгебраическая сумма напряжений на резистивных элементах равна алгебраической
сумме ЭДС:

Где
т
—
число резистивных элементов; п — число ЭДС в контуре.
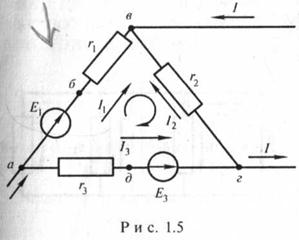
Со
знаком плюс записывают ЭДС и токи, положительные направления которых совпадают
с произвольно выбранным направлением обхода контура, со знаком минус —
противоположно направленные или наоборот. Так, например, для контура, приведенного
на рис. 1.5,

7.
Баланс мощностей в цепях постоянного тока.

8.
Преобразование схем с последовательным, параллельным
и смешанным соединением сопротивлений.



9.
Преобразование треугольника сопротивлений в звезду и
наоборот.
Элементы цепи часто соединяют
или треугольником, или звездой (рис. 1.11).
Для упрощения
расчета электрических цепей в ряде случаев целесообразно применять
преобразование треугольника сопротивлений в эквивалентную звезду или звезды в
эквивалентный треугольник.
Условия
эквивалентного преобразования требуют, чтобы преобразования, производимые в
одной части цепи, не вызывали изменений в распределении токов и напряжений в
остальной части цепи. Согласно этим условиям, потенциалы одноименных точек
треугольника и звезды и подходящие к узлам токи должны быть одинаковы.
Формулы
перехода от сопротивлений треугольника к сопротивлениям звезды и наоборот в
соответствии с обозначениями на рис. 1.11 имеют вид:

Используя эквивалентные
преобразования, сложную цепь иногда можно свести к простой. Часто
преобразования приводят к уменьшению числа ветвей и узлов сложной цепи и,
следовательно, к упрощению ее расчета.

6.
Метод контурных токов. Пример его применения.
Ме́тод ко́нтурных то́ков — метод
сокращения размерности системы уравнений, описывающей электрическую цепь.
Основные принципы
Любая электрическая цепь, состоящая из Р
рёбер (ветвей, участков) и У узлов, может быть описана системой
уравнений в соответствии с 1-м
и 2-м законами Кирхгофа. Число уравнений в такой системе равно Р, из
них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов,
кроме одного; а остальные Р–У+1 уравнений – по 2-му закону
Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в
цепи считаются токи рёбер, число независимых переменных равно числу уравнений,
и система разрешима.
Существует несколько методов сократить число
уравнений в системе. Одним из таких методов является метод контурных токов.
Метод использует тот факт, что не все токи в рёбрах
цепи являются независимыми. Наличие в системе У–1 уравнений для узлов
означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1
независимых токов, то систему можно сократить до Р–У+1 уравнений.
Метод контурных токов основан на очень простом и удобном способе выделения в
цепи Р–У+1 независимых токов.
Метод контурных токов основан на допущении, что в
каждом из Р–У+1 независимых контуров схемы циркулирует некоторый
виртуальный контурный ток. Если некоторое ребро принадлежит только одному
контуру, реальный ток в нём равен контурному. Если же ребро принадлежит
нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с
учётом направления обхода контуров). Поскольку независимые контура покрывают
собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в
любом ребре можно выразить через контурные токи, и контурные токи составляют
полную систему токов.
Построение системы уравнений
Для построения системы уравнений необходимо выделить
в цепи P – У + 1 независимых контуров. По
каждому из этих контуров будет составлено одно уравнение по 2-му закону
Кирхгофа. В каждом контуре необходимо выбрать направление обхода (например, по
часовой стрелке).
Ток во всех рёбрах схемы необходимо представить как
сумму (с учётом знаков) контурных токов, которые протекают по этим рёбрам.
При наличии в цепи источников тока, их
предварительно преобразовывают в источники напряжения.
Правило построения уравнения таково. Обходя контур в
соответствии с выбранным направлением, записываем в левую часть уравнений сумму
(с учётом знаков) токов в рёбрах, умноженных на сопротивление ребра. В правой
части уравнения записываем все источники ЭДС, имеющиеся в контуре (со знаком
«плюс», если направление обхода контура совпадает с направлением ЭДС, и
наоборот).
Составив уравнения для всех независимых контуров,
получаем совместную систему P – У + 1
уравнений относительно P – У + 1 неизвестных
контурных токов.
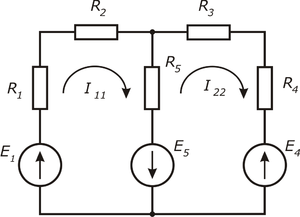
Пример
Метод
контурных токов
Положим, что в левом контуре по часовой стрелке
течет контурный ток I11, а в правом (также по часовой
стрелке) — контурный ток I22. Для каждого из контуров
составим уравнения по второму закону
Кирхгофа.
При этом учтем, что по смежной ветви (с сопротивлением R5)
течет сверху вниз ток I11–I22. Направления
обхода контуров примем также по часовой стрелке.
Для первого контура
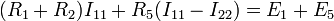
или
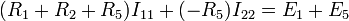
Для второго контура
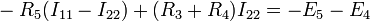
или
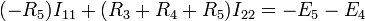
Перепишем эти уравнения следующим образом:
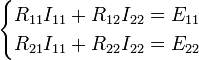
Здесь
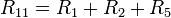 — полное сопротивление первого контура;
— полное сопротивление первого контура;
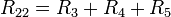 — полное сопротивление второго контура;
— полное сопротивление второго контура;
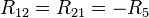 — сопротивления смежной ветви между первым и вторым
контурами, взятые со знаком минус;
— сопротивления смежной ветви между первым и вторым
контурами, взятые со знаком минус;
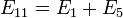 —
контурная ЭДС первого контура;
—
контурная ЭДС первого контура;
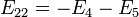 — контурная ЭДС второго контура.
— контурная ЭДС второго контура.
7. Метод
эквивалентного генератора. Пример его применения.


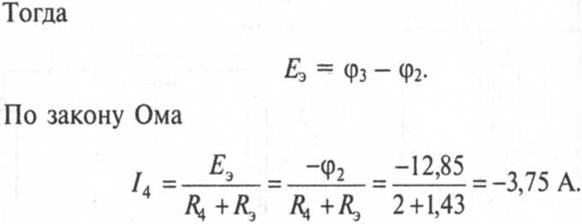
8.
Метод эквивалентного сопротивления. Пример его
применения.

9.
Закон Джоуля-Ленца. Пример его применения.
Закон
Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймсом Джоулем и Эмилием Ленцом.
При прохождении электрического
тока через металлический проводник электроны сталкиваются то с нейтральными
молекулами, то с молекулами, потерявшими электроны. Движущийся электрон либо отщепляет
от нейтральной молекулы новый электрон, теряя свою кинетическую энергию и
образуя новый положительный ион, либо соединяется с молекулой, потерявшей
электрон (с положительным ионом), образуя нейтральную молекулу. При столкновении
электронов с молекулами расходуется энергия, которая превращается в тепло.
Любое движение, при котором преодолевается сопротивление, требует затраты
определенной энергии. Так, например, для перемещения какого-либо тела
преодолевается сопротивление трения и работа, затраченная на это, превращается
в тепло.
Электрическое сопротивление проводника играет ту же
роль, чтя и сопротивление трения. Таким образом, для проведения тока через
проводник источник тока затрачивает некоторую энергию, которая превращается в
тепло. Переход электрической энергии в тепловую отражает закон Ленца — Джоуля
или закон теплового действия тока.
Русский ученый Ленц и английский физик Джоуль
одновременно и независимо один от другого установили, что при прохождении
электрического тока по проводнику количество теплоты, выделяемое проводником,
прямо пропорционально квадрату тока, сопротивлению проводника и времени, в
течение которого электрический ток протекал по проводнику. Это положение
называется законом Ленца — Джоуля.
Если обозначить количество теплоты,
создаваемое током, буквой Q, силу тока, протекающего по
проводнику,— I, сопротивление проводника r и время, в
течение которого ток протекал по проводнику, t, то
закону Ленца — Джоуля можно придать следующее выражение:

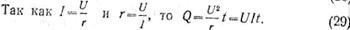
Пример 1. Определить
количество теплоты, выделенное в нагревательном приборе в течение 0,5 ч, если
он включен в сеть с напряжением 110 в и имеет сопротивление 24 ом.
Решение. Время прохождения в секундах:
t=0,5 ч =30 мин
=30х60=1800 сек.
Количество теплоты, выделенное в приборе,
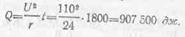
Примеры 2. В электрическом
кипятильнике вода, потребляя количество теплоты 400 000 дж,
закипает через 15 мин. Определить сопротивление нагревательного
элемента этого кипятильника, а также мощность, если кипятильник работает под
напряжением 220 в и его к. п. д. равен 80%.
Решение. Так как к. п. д. кипятильника равен 80%,
выделенное нагревательным элементом количество теплоты
Q = 400 000 : 0,8 = 500 000 дж.
Силу тока, протекающего через кипятильник, найдем из
слёлующей формулы
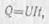
откуда
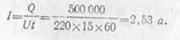
Сопротивление нагревательного элемента

Мощность, потребляемая кипятильником,
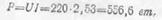
10.
Выделяемая и потребляемая мощность.
Зная работу,
совершаемую током за некоторый промежуток времени, можно рассчитать и мощность
тока, под которой, так же как и в механике, понимают работу, совершаемую за
единицу времени. Из формулы A=UIt, определяющей работу постоянного тока,
следует, что мощность его
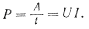 (58.1)
(58.1)
Таким образом, мощность постоянного тока на любом участке цепи выражается
произведением силы тока на напряжение между концами участка.
Нередко говорят о мощности электрического тока, потребляемой из сети, желая
этим выразить мысль, что при помощи электрического тока («за счет тока»)
совершается работа моторов, нагреваются плитки и т. д. В соответствии с этим на
приборах нередко обозначается их мощность, т. е. мощность тока, необходимая для
нормального действия этих приборов. Так, например, 220-вольтовая электроплитка
мощности 500 Вт есть плитка, для нормальной работы которой требуется ток около
2,3 А при напряжении 220 В (так как 2,3 А•220 В »500 Вт).
Если в формуле (58.1) ток выражен в амперах, а напряжение в вольтах, то
мощность получится в джоулях в секунду (Дж/с), т. е. в ваттах (Вт) (см. том I).
На практике употребляют также более крупную единицу мощности киловатт: 1
кВт=1000 Вт. Таким образом, один ватт есть мощность, выделяемая током один
ампер в проводнике, между концами которого поддерживается напряжение один
вольт. В электротехнике применяется единица работы, называемая киловатт-часом
(кВт•ч): один киловатт-час равен работе, совершаемой током мощности один
киловатт в течение одного часа. Нетрудно сосчитать, что 1 кВт•ч=3600000 Дж. В
киловатт-часах обычно выражают энергию, на которую электростанции подают счета
потребителям электроэнергии. Конечно, такой единицей работы можно пользоваться
не только в электротехнике, но и для оценки работы любой машины, например
пароходного или автомобильного двигателя.
11.
Определение показаний приборов (амперметр и
вольтметр) при последовательном и параллельном соединении проводников.
12.
Режимы работы цепи (согласования, холостого хода и
т. д.)
·
В режиме холостого хода источник питания отсоединен от нагрузки и работает ’’
вхолостую”. Сопротивление внешнего участка цепи , ток равен 0.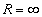
·
В режиме короткого замыкания источник питания замкнут накоротко. Режим является
аварийным. Ток короткого замыкания Iк.з. во много раз превышает значение
номинального тока.
·
Номинальным режимом называют такой режим, на который рассчитаны источник питания
и приемники электроэнергии заводом изготовителем. Процесс преобразования
электроэнергии в другие виды идет без постороннего нагрева, т.е. в допустимых
пределах по паспорту (Uн; Iн ; Pн и т.д.)
В этом режиме соблюдаются наилучшие условия работы: экономичность,
долговечность и т.д.
· Под согласованным
режимом понимают такой режим, когда источник или приемник работают с
максимально возможной мощностью. На практике этот режим применяется в
радиотехнических установках и схемах, где низкий коэффициент .полезного
действия.
13.
Сила тока короткого замыкания.
Режим короткого замыкания (рис. 21). Коротким замыканием
(к. з.) называют такой режим работы источника, когда его зажимы замкнуты
проводником, сопротивление которого можно считать равным нулю. Практически к.
з. возникает при соединении друг с другом проводов, связывающих источник с
приемником, так как эти провода имеют обычно незначительное сопротивление и его
можно принять равным нулю. К. з. может происходить в результате неправильных
действий персонала, обслуживающего электротехнические установки (рис. 22, а),
или при повреждении изоляции проводов (рис. 22,б, в); в последнем случае эти
провода могут соединяться через землю, имеющую весьма малое сопротивление, или
через окружающие металлические детали (корпуса электрических машин и аппаратов,
элементы кузова локомотива и пр.).
При коротком замыкании ток
Iк.з = E
/ R0 (15)
Ввиду того что внутреннее сопротивление источника Ro обычно очень мало,
проходящий через него ток возрастает до весьма больших значений. Напряжение же
в месте к. з. становится равным нулю (точка К на рис. 20), т. е. электрическая
энергия на участок электрической цепи, расположенный за местом к. з., поступать
не будет.
Если точки a и b замкнуть проводником, сопротивление
которого мало по сравнению с внутренним сопротивлением источника
(R << r), тогда в цепи потечет ток короткого замыкания
Сила
тока короткого замыкания – максимальная сила тока, которую можно получить от
данного источника с электродвижущей силой e
и внутренним сопротивлением r.
14.
Проводимость электрической цепи.
Всякий проводник можно характеризовать не только его сопротивлением, но и
так называемой проводимостью — способностью проводить электрический ток.
Проводимость есть величина, обратная сопротивлению. Единица проводимости
называется сименсом (См). 1 См равен 1/1 Ом. Проводимость обозначают буквой G
(g). Следовательно,
G = 1 / R (4)
Удельное электрическое сопротивление и проводимость. Атомы разных веществ
оказывают прохождению электрического тока неодинаковое сопротивление.