Эконометрика. Корреляционный анализ
Задача 1
По данным основных показателей производства с/х
предприятий:
а. Построить график зависимости между
двумя признаками, определив какой из них будет результативным, а какой
факторным;
б. Установить тип зависимости и МНК,
определить параметры уравнений регрессии (линейного степенного, показательного
и т. п.);
в. Оценить тесноту связи;
г. Оценить качество и адекватность
уравнений регрессии;
д. Оценить статическую зависимость.
Зависимость изучить по следующим парам признаков
(не менее 5 предприятий):
число работников предприятия и валовый доход.
регрессия уравнение корреляция
детерминация
Дано:
|
№ п/п
|
Число работников, сот. чел
|
Валовый доход, млн. руб
|
|
1
|
12,8
|
9,1
|
|
2
|
4,3
|
9,1
|
|
3
|
4,2
|
5,2
|
|
4
|
4,8
|
2,7
|
|
5
|
7,8
|
1,0
|
|
6
|
9,0
|
7,6
|
|
7
|
3,5
|
2,9
|
|
8
|
6,2
|
7,9
|
|
9
|
8,1
|
3,5
|
|
10
|
1,7
|
0,6
|
|
11
|
5,7
|
8,6
|
|
12
|
11,3
|
18,8
|
|
13
|
3,0
|
1,7
|
|
14
|
4,0
|
1,6
|
|
15
|
4,2
|
9,3
|
|
16
|
4,6
|
2,8
|
|
17
|
2,4
|
0,2
|
|
18
|
7,4
|
3,1
|
|
19
|
3,9
|
2,8
|
|
20
|
4,4
|
2,0
|
Решение.
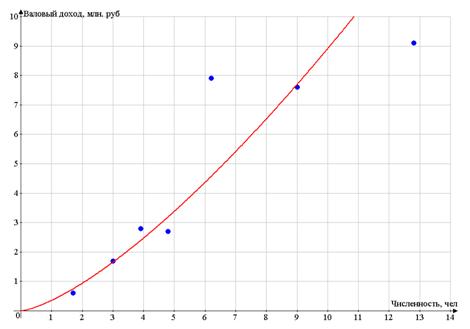
Предварительный анализ:
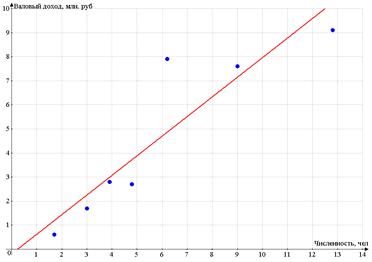
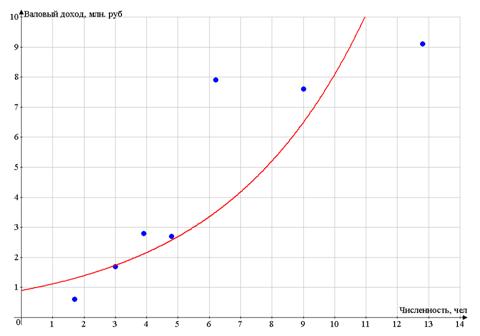
Построим поле корреляции - по оси абсцисс
откладываем значения фактора Х - числа работников, по оси ординат - валовый
доход.
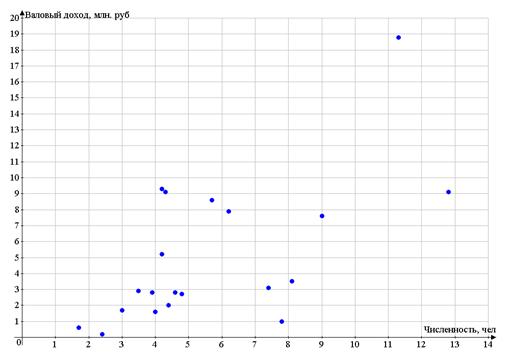
Разброс точек очень большой
Поэтому для рассмотрения возьмем предприятия №№
1, 4, 6, 8, 10, 13, 19.
|
№ п/п
|
Число работников, сот. чел
|
Валовый доход, млн. руб
|
|
1
|
1
|
12,8
|
9,1
|
|
2
|
4
|
4,8
|
2,7
|
|
3
|
6
|
9,0
|
7,6
|
|
4
|
8
|
6,2
|
7,9
|
|
5
|
10
|
1,7
|
0,6
|
|
6
|
13
|
3,0
|
1,7
|
|
7
|
19
|
3,9
|
2,8
|
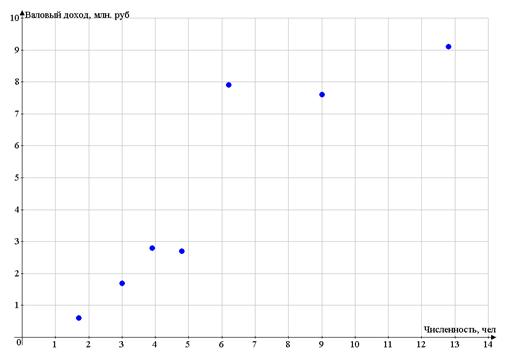
. Построение регрессионных моделей
Построение уравнения регрессии сводится к оценке
его параметров. Классический подход - применение метода наименьших квадратов
(МНК). При этом сумма квадратов отклонений фактических значений результативного
признака у от теоретических значений 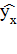 должна
быть минимальной, т. е
должна
быть минимальной, т. е
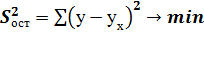 .
.
А. Линейная модель
Линейная регрессия сводится к нахождению
уравнения вида
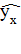 = a + b ⋅
x или
y = a + b ⋅
x + ε
.
= a + b ⋅
x или
y = a + b ⋅
x + ε
.
Уравнение вида  х
= a + b ⋅
x позволяет по заданным значениям фактора x находить теоретические значения
результативного признака, подставляя в него фактические значения фактора x .
х
= a + b ⋅
x позволяет по заданным значениям фактора x находить теоретические значения
результативного признака, подставляя в него фактические значения фактора x .
Построение линейной регрессии сводится к оценке
ее параметров - a и b. Классический подход к оцениванию параметров линейной
регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить
такие оценки параметров a и b, при которых сумма квадратов отклонений
фактических значений результативного признака y от теоретических ɵyx
минимальна:
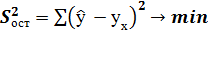 .
.
Для оценки параметров необходимо вычислить суммы
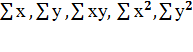 .
.
Составим таблицу:
|
Вспомогательные расчеты для
линейной регрессионной модели
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п
|
Х
|
У
|
Х^2
|
Y^2
|
XY
|
У*
|
(У-У*)
|
(У-У*)^2
|
A
|
|
|
1
|
12,8
|
9,1
|
163,84
|
82,81
|
116,48
|
10,2446
|
-1,1446
|
1,31013
|
12,5781
|
|
|
2
|
4,8
|
2,7
|
23,04
|
7,29
|
12,96
|
3,71975
|
-1,0198
|
1,03989
|
37,7686
|
|
|
3
|
9
|
7,6
|
81
|
57,76
|
68,4
|
7,1453
|
0,4547
|
0,20675
|
5,98288
|
|
|
4
|
6,2
|
7,9
|
38,44
|
62,41
|
48,98
|
4,8616
|
3,0384
|
9,23186
|
38,4607
|
|
|
5
|
1,7
|
0,6
|
2,89
|
0,36
|
1,02
|
1,19137
|
-0,5914
|
0,34972
|
98,5618
|
|
|
6
|
3
|
1,7
|
9
|
2,89
|
5,1
|
2,25166
|
-0,5517
|
0,30433
|
32,4506
|
|
|
7
|
3,9
|
2,8
|
15,21
|
7,84
|
10,92
|
2,98571
|
-0,1857
|
0,03449
|
6,63236
|
|
|
Итого
|
41,4
|
32,4
|
333,42
|
221,36
|
263,86
|
32,4
|
9,4E-15
|
12,477
|
232,435
|
|
|
Среднее
|
5,91429
|
4,62857
|
47,6314
|
31,6229
|
37,6943
|
|
|
1,782
|
38,7392
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение
линейной регрессии
|
|
|
|
|
|
|
σх =
|
3,55706
|
|
σy =
|
3,19362
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b=
|
0,81561
|
|
a=
|
-0,1952
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у = -0,1952 + 0,81561х
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные формулы:
σх
= 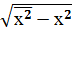 =
=
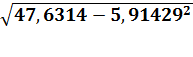 =
3,55706
=
3,55706
σу
= 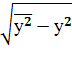 =
=
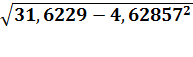 =
3,19362
=
3,19362
b = 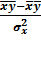 =
=
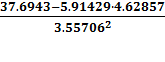 =
0.8156
=
0.8156
a = 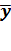 -
b
-
b = 4.62857 -
0.8156*5.91429 = - 0.1952
= 4.62857 -
0.8156*5.91429 = - 0.1952
у = -0,1952 + 0,81561х
Значение коэффициента регрессии b
показывает, что увеличение числа работников (х) на 100 человек приводит к росту
валовой продукции (у) в среднем 0,81561 млн. руб.
Для характеристики изменчивости результативного
признака часто используют относительную скорость изменения, называемой темпом
изменения Т (логарифмической производной) или безразмерный показатель -
эластичность или среднюю эластичность, которая характеризует изменчивость
результативного признака в % при вариации на 1% от среднего уровня:
Т = 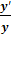 =
(lny)’; Э
=
=
(lny)’; Э
= 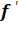 ’
’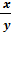 ;
;
 =
=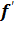 (
(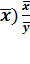
Для линейной модели:
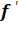 =
(a + bx)’
Þ Э =
=
(a + bx)’
Þ Э = 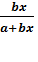 Þ
Þ
 =
b
=
b 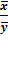
В нашем случае:
Э = 
 =
= 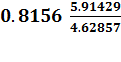 =
1,042%
=
1,042%
Таким образом, при увеличении числа работников
на 1% от среднего уровня валовая продукция увеличится на 1,042%.
Контроль в программе Advenced
Grapher 8.0
Формула: Y(x)
= -0.1951671 + 0.815607x
Стандартное отклонение: 1,442057;
R2
= 0.8252358
Б. Степенная модель
Перед построением степенной модели y
= axb произведем
линеаризацию путем логарифмирования обеих частей уравнения:
lg y = lg a + b*lg x = C + bX
где У
= lg y X = lg x C = lg a
|
Вспомогательные расчеты для
степенной регрессионной модели
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п
|
Х
|
У
|
Х^2
|
Y^2
|
XY
|
У*
|
(У-У*)
|
(У-У*)^2
|
A
|
|
1
|
1,10721
|
0,95904
|
1,22591
|
0,91976
|
1,06186
|
1,1001
|
-0,141063042
|
0,01989878
|
14,7088
|
|
2
|
0,68124
|
0,43136
|
0,46409
|
0,18607
|
0,29386
|
0,50482
|
-0,073453831
|
0,00539547
|
17,0283
|
|
3
|
0,95424
|
0,88081
|
0,91058
|
0,77583
|
0,84051
|
0,88633
|
-0,00552042
|
3,0475E-05
|
0,62674
|
|
4
|
0,79239
|
0,89763
|
0,62788
|
0,80573
|
0,71127
|
0,66015
|
0,237477904
|
0,05639575
|
26,4562
|
|
5
|
0,23045
|
-0,2218
|
0,05311
|
0,04922
|
-0,0511
|
-0,1252
|
-0,096688807
|
0,00934873
|
43,5832
|
|
6
|
0,47712
|
0,23045
|
0,22764
|
0,05311
|
0,10995
|
0,21956
|
0,010886863
|
0,00011852
|
4,7242
|
|
7
|
0,59106
|
0,44716
|
0,34936
|
0,19995
|
0,2643
|
0,3788
|
0,068361332
|
0,00467327
|
15,288
|
|
Итого
|
4,83372
|
3,6246
|
3,85858
|
2,98968
|
3,23063
|
3,6246
|
4,996E-16
|
0,095860998
|
122,415
|
|
Среднее
|
0,69053
|
0,55123
|
0,49828
|
0,46152
|
0,5178
|
7,13715E-17
|
|
17,4879
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение степенной регрессии
|
|
|
|
|
|
σx=
|
0,27275
|
|
σy=
|
0,47975
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b=
|
1,39749
|
|
C =
|
-0,4472
|
|
|
|
|
|
|
Лианеризованное уравнение
|
|
|
|
|
|
Y = -0,4472 + 1,39749X
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выполняем потенцирование линеаризованного
уравнения и получаем искомую степенную модель:
у = 10-0,4472 * х1,3975 =
0,3571х1,3975
эластичность:
Э = (а
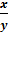 =
=
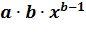
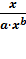 =
b = 1,39749 %
=
b = 1,39749 % 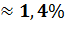
Эластичность степенной модели постоянна и
совпадает с коэффициентом регрессии b.В
нашем случае увеличение числа работников на 1% приводит к увеличению валовой
продукции на 1,4%.
В. Показательная модель.
Построение уравнения показательной кривой у = a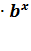 предшествует
процедурв линеаризации путем логарифмирования обеих частей уравнения
предшествует
процедурв линеаризации путем логарифмирования обеих частей уравнения
lg y = lg a + x*lg b = C + Bx
где Y = lg y B
= lg b C = lg a
Составляем таблицу в Excel:
|
Вспомогательные вычисления для
показательной регрессионной модели
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п
|
х
|
У
|
x^2
|
Y^2
|
xY
|
У*
|
(У-У*)
|
(У-У*)^2
|
A
|
|
1
|
12,8
|
0,95904
|
163,84
|
0,91976
|
12,2757
|
1,17552
|
-0,216482034
|
0,046864471
|
22,5728
|
|
2
|
4,8
|
0,43136
|
23,04
|
0,18607
|
2,07055
|
0,41136
|
0,019999664
|
0,000399987
|
4,63638
|
|
3
|
9
|
0,88081
|
81
|
0,77583
|
7,92732
|
0,81255
|
0,068265846
|
0,004660226
|
7,75032
|
|
4
|
6,2
|
0,89763
|
38,44
|
0,80573
|
5,56529
|
0,54509
|
0,352535109
|
0,124281003
|
39,2741
|
|
5
|
1,7
|
-0,2218
|
2,89
|
0,04922
|
-0,3771
|
0,11525
|
-0,337101111
|
0,113637159
|
151,951
|
|
6
|
3
|
0,23045
|
9
|
0,05311
|
0,69135
|
0,23943
|
-0,00897933
|
8,06284E-05
|
3,89645
|
|
7
|
3,9
|
0,44716
|
15,21
|
0,19995
|
1,74392
|
0,3254
|
0,121761856
|
0,014825949
|
27,2302
|
|
Итого
|
41,4
|
3,6246
|
333,42
|
2,98968
|
29,897
|
3,6246
|
6,93889E-16
|
0,30475
|
257,311
|
|
Среднее
|
5,91429
|
0,5178
|
47,6314
|
0,4271
|
4,271
|
0,5178
|
9,91271E-17
|
|
36,7587
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение показательной регрессии
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σx =
|
3,557057
|
|
σy =
|
0,479752
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В =
|
0,09552
|
|
A =
|
-0,04713
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y = -0,04713 + 0,09552*x
|
|
|
|
|
Произведем потенцирование полученного уравнения
у = 10-0,04713 100,09552х
= 0,897*1,246х
Эластичность:
Э = (а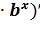
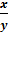 =
=
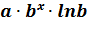
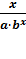 =
x
=
x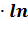 b
Þ
b
Þ
Þ 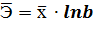 =
=
 =
1.3 %.
=
1.3 %.
Г. Гиперболическая модель.
Уравнение равносторонней гиперболы: у = а + b*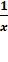 преобразуем заменой z =
преобразуем заменой z = 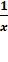 к
виду: у = а + b*z
к
виду: у = а + b*z
Составляем таблицу в
Excel:
|
Вспомогательные расчеты для
гиперболичкой регрессионной модели
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п
|
z
|
y
|
z^2
|
y^2
|
zy
|
y*
|
(y
-
y*)
|
(
y -
y*)^2
|
A
|
|
1
|
0,07813
|
9,1
|
0,0061
|
82,81
|
0,71094
|
7,4739
|
1,626104738
|
2,64421662
|
17,8693
|
|
2
|
0,20833
|
2,7
|
0,0434
|
7,29
|
0,5625
|
5,29451
|
-2,594505902
|
6,731460877
|
96,0928
|
|
3
|
0,11111
|
7,6
|
0,01235
|
57,76
|
0,84444
|
6,92178
|
0,678216709
|
0,459977905
|
8,9239
|
|
4
|
0,16129
|
7,9
|
0,02601
|
62,41
|
1,27419
|
6,0819
|
1,818101813
|
3,305494202
|
23,0139
|
|
5
|
0,58824
|
0,6
|
0,34602
|
0,36
|
0,35294
|
-1,0642
|
1,664183052
|
2,76950523
|
277,364
|
|
6
|
0,33333
|
1,7
|
0,11111
|
2,89
|
0,56667
|
3,20229
|
-1,502292117
|
2,256881606
|
88,3701
|
|
7
|
0,25641
|
2,8
|
0,06575
|
7,84
|
0,71795
|
4,48981
|
-1,689808293
|
2,855452066
|
60,3503
|
|
Итого:
|
1,73684
|
32,4
|
0,61074
|
221,36
|
5,02963
|
32,4
|
1,08802E-14
|
21,023
|
571,984
|
|
Среднее:
|
0,24812
|
4,62857
|
0,08725
|
31,6229
|
0,71852
|
4,62857
|
1,55431E-15
|
|
81,712
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение гиперболической регрессии
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σz =
|
0,16027
|
|
σy =
|
3,19362
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
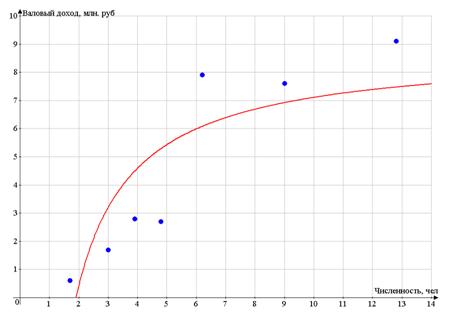
b =
|
-16,738
|
|
a =
|
8,78153
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 8,7815 - 16,7377(z)
|
|
|
|
|
Получаем гиперболическую модель:
у = 8,7815 - 16,7377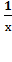
Оценим эластичность:
Э = 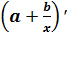
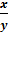 =
=
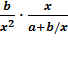 =
=
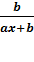 =
=
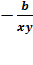 Þ
Þ
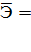
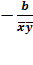
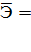
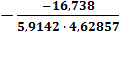 =
0.61 %
=
0.61 %
. Оценка тесноты связи, качества и
точности модели
Уравнение регрессии всегда дополняется
показателем тесноты связи. При использовании линейной регрессии в качестве
такого показателя выступает линейный коэффициент корреляции rxy,
который можно рассчитать по следующим формулам:
rxy, =  =
=
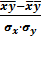 Þ
rxy, = b
Þ
rxy, = b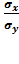
Линейный коэффициент корреляции находится в
пределах: [-1; 1] . Чем ближе абсолютное значение rxy к единице, тем
сильнее линейная связь между факторами (при rxy = ±1 имеем строгую
функциональную зависимость). Но следует иметь в виду, что близость абсолютной
величины линейного коэффициента корреляции к нулю еще не означает отсутствия
связи между признаками. При другой (нелинейной) спецификации модели связь между
признаками может оказаться достаточно тесной.
При нелинейных зависимостях лучше использовать
другой показатель - индекс корреляции 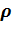 ,
тесно связанный с коэффициентом детерминации R2:
,
тесно связанный с коэффициентом детерминации R2:
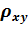 =
= 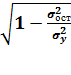
где 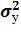 =
=
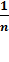
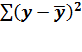 -
общая дисперсия результативного признака у;
-
общая дисперсия результативного признака у;
 =
= 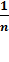
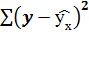 -
остаточная дисперсия
-
остаточная дисперсия
Величина данного показателя находится в
пределах: 0 ≤ ρxy
≤1.
Чем ближе значение индекса корреляции к единице,
тем теснее связь рассматриваемых признаков, тем более надежно уравнение
регрессии.
Квадрат индекса корреляции носит название
индекса детерминации и характеризует долю дисперсии результативного признака y
, объясняемую регрессией, в общей дисперсии результативного признака:
 ,
,
О качестве модели можно судить по относительным
ошибкам (ошибкам аппроксимации). Нежелательно, чтобы относительные ошибки
превышали 8 - 10% от уровня наблюдаемых у.
А. Линейная модель
rxy = b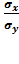 = 0,81561
= 0,81561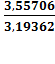 = 0,908
= 0,908
так как rxy  0,7
и положителен, то связь прямая и очень сильная.
0,7
и положителен, то связь прямая и очень сильная.
Определим коэффициент детерминации:
R2
= 1 - 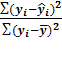 =
rxy2 = 0.8245
=
rxy2 = 0.8245
Изменение валового выпуска с/х продукции на
90,8% объясняется вариацией числа работников. Доля неучтенных факторов
составляет 100 - 82,45 = 17,55%.
Контроль в программе Advenced
Grapher 8.0
Формула: Y(x)
= -0.1951671 + 0.815607x
Расчетная в задании: Y(x)
= -0.1952 + 0.815617x
Стандартное отклонение: 1,442057;
R2
= 0.8252358
Б. Степенная модель
Индекс корреляции и коэффициент детерминации:
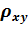 =
= 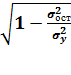 =
=
 =
=
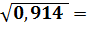 0.956
0.956
R2
= 0,914
В случае степенной модели вариация валового
выпуска на 95.6 % объясняется вариацией числа работников. Доля неучтенных
факторов составляет 8.6 %.
Коэффициент детерминации степенной модели выше
коэффициента детерминации линейной модели, но различия незначительны - менее 10
%. (6,2 %). Значение индекса близко к 1, что свидетельствует об очень сильной
взаимосвязи исследуемых факторов.
Контроль в программе Advenced
Grapher 8.0
Формула: Y(x)
= 0,3571002*х1,3974895
Расчетная в задании: Y(x)
= 0,3571*х1,3975
Стандартное отклонение: 1,9881345;
R2
= 0.9138602
В. Показательная модель
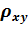 =
= 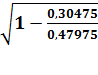 =
=
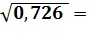 0,852
0,852
R2
= 0,726
Связь в этой модели удовлетворительная
Контроль в программе Advenced
Grapher 8.0
Формула: Y(x)
= 0,8971571*2,450054х
Расчетная в задании: Y(x)
= 0,897*2,46х
Стандартное отклонение: 3,0569256;
R2
= 0.7261552
Г. Гиперболическая модель
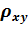 =
= 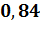
R2
= 0,7056
Связь в этой модели удовлетворительная.
Контроль в программе Advenced
Grapher 8.0
Формула: Y(x)
= 8,7815289 - 16,7377103/х
Расчетная в задании: Y(x)
= 8,7815 - 16,7377/х
Стандартное отклонение: 1,8718524
R2
= 0,7055368
Вывод: Расчеты произведены правильно, о чем
свидетельствуют данные стандартной расчетной Программы
Расчет относительных ошибок произведён в
предыдущих расчетах.
. Оценка статистической значимости
регрессионных уравнений
Статистическую значимость уравнений регрессии
оцениваем при помощи критерия Фишера (F
- тест).
Пусть основная гипотеза Н0 состоит в
предположении, что R2
= 0? А альтернативная Н1 - R2
 0.
Основная гипотеза Н0 принимается в том случае, если расчетная F-статистика
меньше критического значения:
0.
Основная гипотеза Н0 принимается в том случае, если расчетная F-статистика
меньше критического значения:
Fфакт =
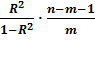
 Fкрит
(α,
df1
= m; df2
= n - m
- 1)
Fкрит
(α,
df1
= m; df2
= n - m
- 1)
в противном случае принимается гипотеза Н1
где df
- число степеней свободы;
m - число факторов в
модели;
n - число
наблюдений.
Для линейной модели:
Fфакт =
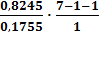 =
23,49
=
23,49
Критическое значение критерия Фишера при уровне
значимости 0,05; m = 1; n
= 7 равна 5,59. Так как Fфакт
 Fкрит,
то при доверии 95% принимается гипотеза Н1 о неслучайной природе выявленной
зависимости и статистической значимости показателей тесноты связи.
Fкрит,
то при доверии 95% принимается гипотеза Н1 о неслучайной природе выявленной
зависимости и статистической значимости показателей тесноты связи.
Для остальных моделей:
Степенная модель: Fфакт
=
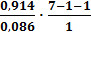 =
53,14
=
53,14
Показательная модель: Fфакт
=
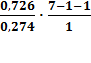 =
13,25
=
13,25
Гиперболическая модель: Fфакт
=
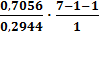 =
11,98
=
11,98
Таким образом, все модели выдержали тест на
значимость, т. к. во всех случаях Fфакт
 Fкрит.
Улучшение достоверности уменьшает критическую область: при уровне достоверности
α
= 0,01
критическое значение увеличивается до 12,25, и тогда в этом случае
гиперболическая модель отпадает.
Fкрит.
Улучшение достоверности уменьшает критическую область: при уровне достоверности
α
= 0,01
критическое значение увеличивается до 12,25, и тогда в этом случае
гиперболическая модель отпадает.
Сравним регрессионные модели по всем показателям
и выделим лучшую
|
Сравнительный анализ характеристик
регрессионных моделей
|
|
Модель
|
Линейная
|
Степенная
|
Показательная
|
Гиперболическая
|
|
rxy/
|
0.908
|
0.956
|
0.852
|
0.840
|
|
R2/r2
|
0.8245
|
0.914
|
0.726
|
|
Э
|
1.042%
|
1.4%
|
1.3%
|
0.61%
|
|
А
|
38.74%
|
17.49%
|
36.76%
|
81.712%
|
|
F
|
23.49
|
53.14
|
13.25
|
11.98
|
Показатели тесноты связи указывают, что очень
сильная связь исследуемых признаков: числа работников х и валовой продукции у у
степенной и линейной модели (лучшая степенная); у показательной и
гиперболической моделей связь удовлетворительно тесная
Наибольший коэффициент детерминации у степенной
модели - 0,914, отличие от линейной меньше 10%. Значительно отстают
показательная и гиперболическая модели.
Степенная модель оказалась и более эластичной -
1,4%.
Наилучшим образом экспериментальные и
теоретические значения результативного признака согласуются для степенной
модели : А = 17,49%. Наихудшее согласование у гиперболической модели.
F-тест на значимость
выдержали все модели при уровне значимости 0,05
Таким образом, для степенной модели получены
наилучшие показатели тесноты связи.
Графики моделей приведены в предыдущих расчетах.
Программа Advenced
Grapher 8/ 0 показывает
ещё следующие возможные регрессионные модели:
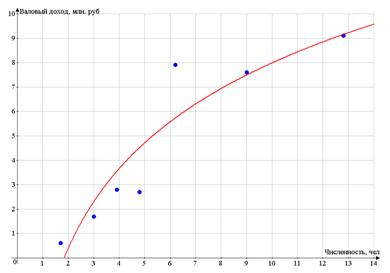
Логарифмическая модель:
Y(x)
= 4.7189419*ln(x)
-2.8745813
Стандартное отклонение 1,2853802
R2 = 0.8611484
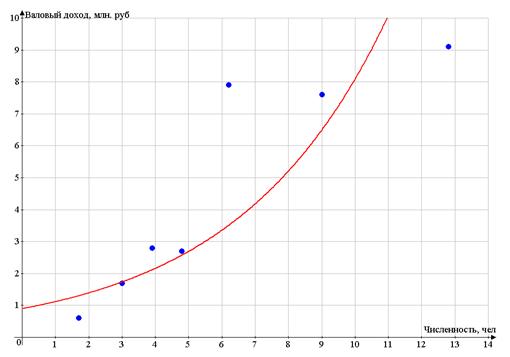
Экспотенциальная модель:
У(х) = 0,8971571*е0,22х
Стандартное отклонение: 3,0569228
R2 = 0.7261548
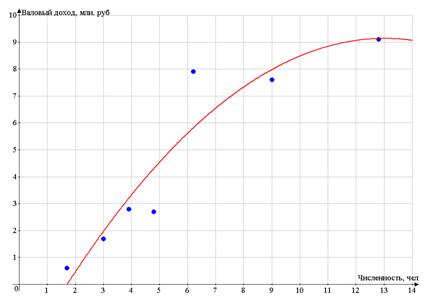
Полиноминальна модель
У(х) = -0,0714504х2 + 1,8598х -
2,9675345
Стандартное отклонение: 1,1326346
R2 = 0.8921867
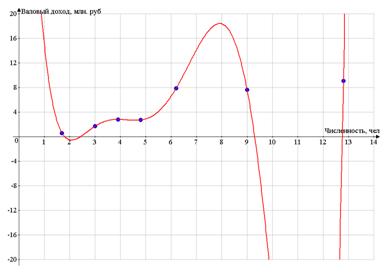
Лучшая
Y(x)
= 0,0080221х6 - 0,2899243х5 + 4,0186219х4 -
27,2974512х3 + 95,8786377х2 - 163,8950124х + 106,6035793
R2 = 0.9861976
Стандартное отклонение: 0,040621
4. Составление прогноза
Прогноз валовой продукции выполняем по лучшей
модели - степенной.
Вначале рассчитаем прогнозной значение числа
работников на уровне 90% от среднего значения:
хр = 0,9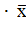 = 0,9
= 0,9 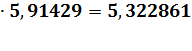
Точечный прогноз:
найдем значение ур подстановкой в
уравнение регрессии:
ур = 0,3571*5,3228611,3975 =
3,695
для построения доверительного интервала вычислим
предварительно среднюю стандартную ошибку прогноза mp
и предельную ошибку 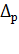 .
.
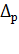 = tтабл
= tтабл
 mp
mp
mp
= σост
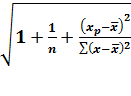
где σост
= 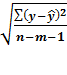
для степенной модели остаточная сумма: 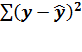 =
0,09586 в логарифмической форме, в действительной: 1,247, тогда
=
0,09586 в логарифмической форме, в действительной: 1,247, тогда
σост
= 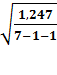 =
0,4993 = 0,5
=
0,4993 = 0,5
вычислим квадратичную сумму отклонений фактора х
от среднего значения:
 = n
= n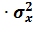 = 7
= 7  3.55706
= 24.89942
3.55706
= 24.89942
Стандартная ошибка прогноза:
mp = 0,5 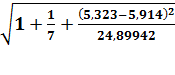 =
0,538
=
0,538
при уровне значимости 0,05 и степени свободы df
= 7 - 1 - 1 = 5 определим критическое значение критерия Стьюдента tтабл
=
2,57, следовательно, предельная ошибка
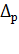 = tтабл
= tтабл
 mp
=
2,57*0,538 = 1,382
mp
=
2,57*0,538 = 1,382
Таким образом, можно определить нижнюю и верхнюю
границы доверительного интервала:
ymin = yp - 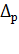 =
3.695 - 1.382 = 2.313max = yp +
=
3.695 - 1.382 = 2.313max = yp + 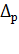 =
3.695 + 1.382 = 5.077
=
3.695 + 1.382 = 5.077
выполненный прогноз достаточно надежен (95%), но
точность невысока, так как диапазон верхней и нижней границы доверительного
интервала составляет 5,077/2,313 = 2,2 раза.
Задача 2
По данным основных показателей производства с/х
предприятий:
а. Построить матрицу коэффициентов
корреляции;
б. Вычислить стандартизированные
коэффициенты, ранжировать факторы по силе их влияния;
в. Построить линейное уравнение
множественной регрессии в нормальном масштабе;
г. оценить тесноту связи факторов с
результативным признаком;
д. оценить качество и адекватность модели;
е. оценить статистическую значимость
уравнения в целом и целесообразность включения в модель каждого из факторов.
Число работников на 100 га пашни (х1), затраты
на производство продукции на 100 га пашни (х2) и валовая продукция в
сопоставимых ценах на 100 га пашни (у).
Дано:
|
№ п/п
|
Площадь пашни, га
|
Число работников, сот. чел
|
Затраты на производство продукции,
млн. руб.
|
Валовый доход, млн. руб
|
|
1
|
110
|
12,8
|
27,5
|
9,1
|
|
2
|
69
|
4,3
|
13,5
|
9,1
|
|
3
|
44
|
4,2
|
20,0
|
5,2
|
|
4
|
75
|
4,8
|
15,8
|
2,7
|
|
5
|
75
|
7,8
|
20,4
|
1,0
|
|
6
|
85
|
9,0
|
29,1
|
7,6
|
|
7
|
50
|
3,5
|
7,5
|
2,9
|
|
8
|
63
|
6,2
|
20,8
|
7,9
|
|
9
|
67
|
8,1
|
17,3
|
3,5
|
|
10
|
21
|
1,7
|
2,5
|
0,6
|
|
11
|
82
|
5,7
|
16,5
|
8,6
|
|
12
|
102
|
11,3
|
34,6
|
18,8
|
|
13
|
49
|
3,0
|
9,1
|
1,7
|
|
14
|
55
|
4,0
|
12,7
|
1,6
|
|
15
|
55
|
4,2
|
15,7
|
9,3
|
|
16
|
73
|
4,6
|
13,9
|
2,8
|
|
17
|
23
|
2,4
|
4,0
|
0,2
|
|
18
|
83
|
7,4
|
32,7
|
3,1
|
|
19
|
37
|
3,9
|
9,1
|
2,8
|
|
20
|
60
|
4,4
|
14,5
|
2,0
|
Решение.
Преобразуем таблицу в показателях на 100 га
пашни
|
№№
|
Число работников, сот. чел
|
Затраты на производство продукции,
млн. руб.
|
Валовый доход, млн. руб
|
|
Х1
|
Х2
|
У
|
|
1
|
11,64
|
25,0
|
8,273
|
|
2
|
6,23
|
19,565
|
13,188
|
|
3
|
9,55
|
45,455
|
11,818
|
|
4
|
6,4
|
21,067
|
3,6
|
|
5
|
10,4
|
27,2
|
1,333
|
|
6
|
10,59
|
34,235
|
8,941
|
|
7
|
7,0
|
15,00
|
5,8
|
|
8
|
9,84
|
33,016
|
12,54
|
|
9
|
12,09
|
25,821
|
5,224
|
|
10
|
8,10
|
11,905
|
2,857
|
|
11
|
6,95
|
20,122
|
10,488
|
|
12
|
11,08
|
33,922
|
18,431
|
|
13
|
6,12
|
18,571
|
3,469
|
|
14
|
7,27
|
23,1
|
2,91
|
|
15
|
7,64
|
28,545
|
16,91
|
|
16
|
6,30
|
19,041
|
3,836
|
|
17
|
10,43
|
17,391
|
0,87
|
|
18
|
8,92
|
39,40
|
3,735
|
|
19
|
10,54
|
24,6
|
7,568
|
|
20
|
7,33
|
24,167
|
3,333
|
. вычисляем средние значения факторов Хi
и У, несмещенные среднеквадратические отклонения и коэффициенты корреляции,
используя стандартные программы Excel:
среднее значение выборочных данных - СРЗНАЧ();
среднеквадратическое отклонение - СТАНДОТКЛОН().
|
Характеристика положения и
разброса факторов
|
|
|
|
|
|
|
Х1
|
Х2
|
У
|
|
СРЗНАЧ
|
8,721
|
25,3562
|
7,2562
|
|
СТАНДОТКЛОН
|
2,02527
|
8,42908
|
5,15017
|
|
Коэффициенты межфакторной и парной
корреляции
|
|
|
Х1
|
Х2
|
У
|
|
|
Х1
|
1,00000
|
|
|
|
|
Х2
|
0,46155
|
1,00000
|
|
|
|
У
|
0,13817
|
0,44012
|
1,00000
|
|
|
|
|
|
|
|
|
|
Судя по коэффициентам корреляции умеренное
влияние на объем валовой продукции оказывает производство продукции на 100 га
пашни rxy
 0.4
и довольно слабое - количество человек, занятых в производстве:
0.4
и довольно слабое - количество человек, занятых в производстве:
rxy
 0.4.
0.4.
Матрица коэффициентов корреляции будет включать
коэффициенты корреляции У с Х1 и Х2 и коэффициенты
межфакторной корреляции
R = 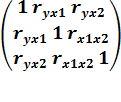 =
=

detR = 1(1-0.461552) -
0.13817(0.13817 - 0.46155*0.44012) + 0.44012(0.13817*0.46155 - 0.44012) =
0.78697 - (-0.00898) + (-0.16564) =
= 0.63031
2. Проверяем наличие мультиколлинеарности
средипеременных. Вычисляем определитель матрицы межфакторных коэффициентов
корреляции:
det2R = 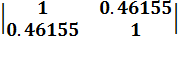 =
1 - 0.461552 = 0.78697
=
1 - 0.461552 = 0.78697
Определитель ближе к 1, чем к нулю, что говорит
о возможном отсутствии мультиколлениарности
Проверим основную гипотезу Н0 о независимости
переменных detR = 1/
Гипотеза принимается в случае 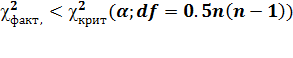 .
.
В противном случае следует принять
альтернативную гипотезу Н1 о наличии мультиколлениарности detR
= 0
Фактическое значение критерия:
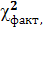 = [n
- 1 -
= [n
- 1 -  (2m
+ 5)lgDetR = 20 - 1 -
(2m
+ 5)lgDetR = 20 - 1 -  (2*2
+ 5)lg0.78697 =
19.844
(2*2
+ 5)lg0.78697 =
19.844
меньше критического значения 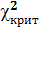 =
43,8 при уровне значимости 0,05 и числе степеней свободы df
= 0.5*20*14 = 140, То подтверждается гипотеза Н0 о независимости переменных.
=
43,8 при уровне значимости 0,05 и числе степеней свободы df
= 0.5*20*14 = 140, То подтверждается гипотеза Н0 о независимости переменных.
Совокупное влияние факторов на результат
характеризуется коэффициентами множественной детерминации и корреляции. При
линейной зависимости коэффициент множественной корреляции можно определить,
зная матрицу парных коэффициентов корреляции и определителя.
Ryx1x2 = 
Тогда множественный коэффициент корреляции:
Ryx1x2
=  =
0.446
=
0.446  0,5.
0,5.
Следовательно, тесноту связи исследуемых
факторов (численности и затрат на производство на 100 га пашни) с объемом
валовой продукции можно оценить как среднюю.
3. Составим уравнения множественной
регрессии
Сначала найдем стандартизированные коэффициенты
регрессии из системы уравнений:



Уравнение регрессии в стандартизированном
масштабе:
ty
= -0.08256tx1
+ 0.47825tx2
+ 
так как 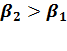 по
модулю, то по силе влияния на объем валовой продукции больше влияют затраты на
производство.
по
модулю, то по силе влияния на объем валовой продукции больше влияют затраты на
производство.
Используя формулы перехода, находим коэффициенты
регрессии и свободный член линейного уравнения:
b1 = b1
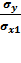 Þ
b1 = -0.08256
Þ
b1 = -0.08256  = - 0.212
= b2
= - 0.212
= b2
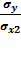 Þ
b1 = 0.47823
Þ
b1 = 0.47823 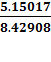 =0.292
=0.292
a = 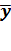 -
-
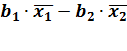 Þ
a = 7.2562 - (-0.21)
Þ
a = 7.2562 - (-0.21) 8.721 - 0.292
8.721 - 0.292  25.3562
= 1.6836
25.3562
= 1.6836
Уравнение регрессии в нормальном масштабе:
у = 1,6836 - 0,21х1 + 0,292х2
+ 
увеличение валового объема продукции достигается
путем увеличения численности работающих или снижением издержек на производство.
Снижение затрат на производство на 1 руб/га
увеличивает валовый объем на 0,292 процентных пункта и увеличение работающих на
100 чел приводит к увеличению валового объема на 0,21 процентный пункт.
. Проверим значимость уравнения в целом
при помощи критерия Фишера
Коэффициент детерминации R2
= 0,199. Тогда согласно критерию Фишера:
Fфакт
= 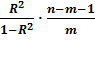 =
=
 =
2.125 не превышает
=
2.125 не превышает
Fкрит
= (α - 0,05; df1
= 2; df2
= 17) = 3.59
Это говорит об отсутствии статистической
значимости коэффициента детерминации и линейного уравнения множественности
регрессии в целом.
Проверим также значимость включенных в уравнение
переменных
Вычислим приращение коэффициента детерминации за
счет каждого фактора Х.
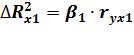 = 0.08256*0.13817
= 0.0114
= 0.08256*0.13817
= 0.0114
 = 0.47823*0.44012
= 0.21
= 0.47823*0.44012
= 0.21
Основная гипотеза принимается при условии:
Fфакт
= 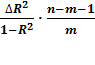
 Fкрит
= (α - 0,05; df1
= 1; df2
= 17)
Fкрит
= (α - 0,05; df1
= 1; df2
= 17)
Fфакт х1
= 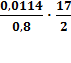 =
0,121
=
0,121  Fкрит
= (α - 0,05; df1
= 1; df2
= 17) = 4,45
Fкрит
= (α - 0,05; df1
= 1; df2
= 17) = 4,45
Fфакт х2
= 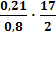 =
2,231
=
2,231  Fкрит
= (α - 0,05; df1
= 1; df2
= 17) = 4,45
Fкрит
= (α - 0,05; df1
= 1; df2
= 17) = 4,45
Во обоих случаях основная гипотеза Н0
принимается, следовательно, для построения модели объема валовой продукции оба
фактора не значимы!
5. Проведем оценку качества модели
Для этого вычислим теоретические значения объема
валовой продукции для каждого набора факторов, абсолютные и относительные
ошибки
|
Абсолютные и относительные ошибки
|
|
множественной регрессивной модели
|
Утеор
|
Е=У-Утеор
|
А,%
|
Е^2
|
|
1
|
6,5392
|
1,7338
|
20,9573
|
3,00606
|
|
2
|
6,08828
|
7,09972
|
53,8347
|
50,406
|
|
3
|
12,951
|
-1,133
|
9,58673
|
1,2836
|
|
4
|
6,49116
|
-2,8912
|
80,3101
|
8,35883
|
|
5
|
7,442
|
-6,109
|
458,29
|
37,3199
|
|
6
|
9,45632
|
-0,5153
|
5,76356
|
0,26555
|
|
7
|
4,5936
|
1,2064
|
20,8
|
1,4554
|
|
8
|
9,25787
|
3,28213
|
26,1733
|
10,7724
|
|
9
|
6,68443
|
-1,4604
|
27,9562
|
2,13286
|
|
10
|
3,45886
|
-0,6019
|
21,0662
|
0,36224
|
|
11
|
6,09972
|
4,38828
|
41,8409
|
19,257
|
|
12
|
9,26202
|
9,16898
|
49,7476
|
84,0701
|
|
13
|
5,82113
|
-2,3521
|
67,8043
|
5,53252
|
|
14
|
6,9021
|
-3,9921
|
137,186
|
15,9369
|
|
15
|
5,63917
|
11,2708
|
66,6519
|
127,032
|
|
16
|
5,92057
|
-2,0846
|
54,3423
|
4,34544
|
|
17
|
4,57147
|
-3,7015
|
425,457
|
13,7009
|
|
18
|
11,3152
|
-7,5802
|
202,95
|
57,4594
|
|
19
|
6,6534
|
0,9146
|
12,0851
|
0,83649
|
|
20
|
7,20106
|
-3,8681
|
116,054
|
14,9619
|
|
Итого
|
142,349
|
2,77545
|
1898,86
|
458,495
|
|
Среднее
|
7,49203
|
0,14608
|
99,9398
|
|
Средняя ошибка аппроксимации оказалась за
рамками допустимых значений, вследствие чего качество построенной модели плохо
Задача 3
1. Применив необходимое и достаточное
условие идентификации определить идентифицировано ли каждое уравнение модели;
. Определить метод оценки параметров
модели;
. На основе приведенной формы модели
определить все возможные структурные коэффициенты.
Дано:
Структурная форма модели:
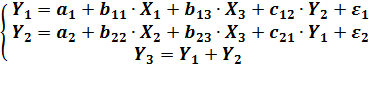
Приведенная форма модели:

Решение:
. Заданная модель имеет три эндогенные (У1,
У2, У3) и три экзогенные переменные (Х1, Х2,
Х3).
Проверим каждое уравнение системы на необходимое
и достаточное условие идентификации.
Необходимое условие заключается в выполнении
счётного правила:
D + 1 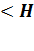 -
уравнение неиндентифицировано;
-
уравнение неиндентифицировано;
D + 1 = Н -
уравнение точно идентифицировано;
D + 1 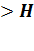 -
уравнение сверхидентифицировано
-
уравнение сверхидентифицировано
Где Н - число эндогенных переменных в уравнении;
D - число
отсутствующих экзогенных переменных в уравнении, но присутствующих в системе.
Проверяем это правило для всех исследуемых
уравнений:
|
Первое уравнение
|
Второе уравнение
|
Третье уравнение
|
|
Присутствуют Y1
Y2
|
Отсутствует Х2
|
Присутствуют Y1
Y2
|
Отсутствует Х1
|
Присутствуют Y1
Y2 Y3
|
Отсутствует Х1
X2 X3
|
|
Н = 2
|
D
= 1
|
Н = 2
|
D
= 1
|
Н = 3
|
D
= 3
|
|
D
+ 1 = Н
|
D
+ 1 = Н
|
D
+ 1  Н Н
|
|
Уравнение точно идентифицировано
|
Уравнение точно идентифицировано
|
Уравнение сверхидентифицировано
|
Достаточное условие идентификации заключается в
том, что определитель матрицы, составленной из коэффициентов при переменных,
отсутствующих в исследуемом уравнении, не равен 0, и ранг этой матрицы должен
быть не менее числа эндогенных переменных в системе без единицы.
Построим матрицу коэффициентов системы
|
Уравнение
|
Х1
|
Х2
|
Х3
|
Y1
|
Y2
|
Y3
|
|
Первое
|
b11
|
0
|
b13
|
-1
|
c12
|
0
|
|
Второе
|
0
|
b22
|
b23
|
c21
|
-1
|
0
|
|
Третье
|
0
|
0
|
0
|
1
|
1
|
-1
|
Так как в первом уравнении отсутствуют две
переменные Х2 и Y3,
из коэффициентов при них во втором и третьем уравнениях получается квадратная
матрица второго порядка:
|
Уравнение
|
Х2
|
Y3
|
|
Второе
|
b22
|
0
|
|
Третье
|
0
|
-1
|
Определитель данной матрицы не равен нулю:
DetA = -1 b22
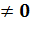 Þ
rangA = 2, что совпадает
с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2. Достаточное
условие для первого уравнения выполняется и оно точно идентифицировано.
Þ
rangA = 2, что совпадает
с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2. Достаточное
условие для первого уравнения выполняется и оно точно идентифицировано.
Во втором уравнении отсутствуют две переменные Х1
и Y3,
из коэффициентов при них во втором и третьем уравнениях получается квадратная
матрица второго порядка:
|
Уравнение
|
Х1
|
Y3
|
|
Первое
|
b11
|
0
|
|
Третье
|
0
|
-1
|
Определитель данной матрицы не равен нулю:
DetВ = -1 b11
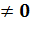 Þ
rangВ = 2, что
совпадает с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2.
Достаточное условие для второго уравнения выполняется и оно точно
идентифицировано.
Þ
rangВ = 2, что
совпадает с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2.
Достаточное условие для второго уравнения выполняется и оно точно
идентифицировано.
В третьем уравнении отсутствует три переменных Х1
, Х2 и Х3
из коэффициентов при них во втором и третьем
уравнениях получается прямоугольная матрица :
|
Уравнение
|
Х1
|
Х2
|
Х3
|
|
Первое
|
b11
|
0
|
b13
|
|
Второе
|
0
|
b22
|
b23
|
Из элементов этой матрицы можно составить
определители второго порядка, отличные от нуля:
DetС
= b11b22 
DetС
= b11b23 
DetС = - b13b22
 Þ
rangС = 2, что
совпадает с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2.
Достаточное условие выполняется
Þ
rangС = 2, что
совпадает с числом эндогенных переменных в системе без 1, т. е. 3 - 1 = 2.
Достаточное условие выполняется
Следовательно, первые два уравнения точно
идентифицированы, третье - сверхидентифицируема, таким образом, вся система
сверхидентифицируема.
5. Определение структурных коэффициентов
Так как первые два уравнения точно
идентифицированы, находим соответствующие структурные коэффициенты путем
следующих преобразований:
Для определения структурных коэффициентов
первого уравнения за основу возьмем первое приведенное уравнение, в котором
необходимо избавиться от Х2 и ввести переменную Y2.
Поэтому выражаем Х2 из второго приведенного уравнения и подставляем
его в первое:
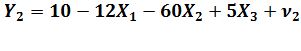 Þ
Þ
Х2 = 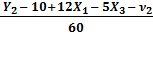 Þ
Þ

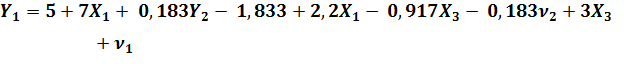
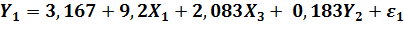
Таким образом, а1 = 3,167; b11
= 9,2; b13
= 2,083; c12
= 0,183
Для определения структурных коэффициентов
второго уравнения за основы берем второе приведенное уравнение, где необходимо
избавиться от Х1 и ввести переменную Y1.
Поэтому выражаем Х1 из первого приведенного уравнения и подставляем
его во второе:
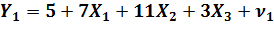 Þ
Þ
Х1 = 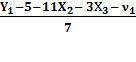 Þ
Þ
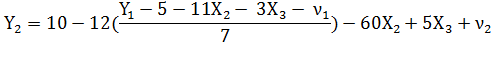
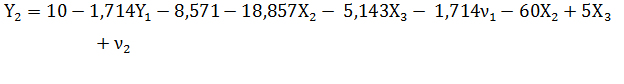
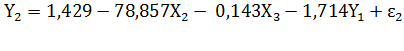
Таким образом, а2 = 1,429; b22
=  78,857;
b23
=
78,857;
b23
=  0,143;
c21
=
0,143;
c21
= 1,714
1,714
В силу того, что третье уравнение сверхиндентифицируемо
его структурные коэффициенты не подлежат точному определению. Для их расчета
можно применить двухшаговый метод наименьших квадратов: на основе первого
приведенного уравнения вычисляют теоретические значения  1
и используя или наблюдаемые значения Х2, вычисляют параметры
третьего структурного уравнения, применяя МНК.
1
и используя или наблюдаемые значения Х2, вычисляют параметры
третьего структурного уравнения, применяя МНК.
Задача 71
По условным поквартальным данным розничного
товарооборота областей Х за три года (в % к уровню 1-го квартала):
а. Построить график временного ряда;
б. Построить аддитивную или
мультипликативную модель временного ряда;
в. Оценить качество модели через
показатели средней абсолютной ошибки, среднего относительного отклонения и
коэффициента детерминации.
|
Исходные данные
|
|
Поквартальный розничный
товарооборот, %
|
|
Номер квартала
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
100
|
93,5
|
95,6
|
102,1
|
107,8
|
96,3
|
95,7
|
98,2
|
105,1
|
99,3
|
98,9
|
101,9
|
Решение:
. Построение временного ряда
По оси абсцисс откладываем кварталы, по оси
ординат - размер товарооборота

Очевидно, что имеется тенденция к снижению
розничного товарооборота:
О чем говорит «красная» аппроксимация.
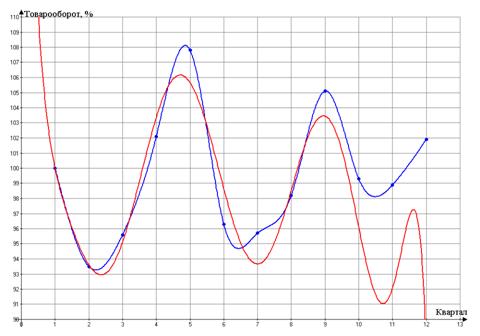
Поскольку амплитуда колебаний изменяется от
квартала к кварталу, возможно, лучшее соответствие покажет мультипликативная
модель.
. Построение аддитивной и
мультипликативной моделей
Построим аддитивную и мультипликативную модели
динамического ряда из трех компонент: тренда; квартальной; случайной.
yадд
= Т
+ S + E
yмульт
= Т
 S
S
 E
E
Начнем с выделения квартальной компоненты. Для
этого произведем сглаживание временного ряда посредством усреднения уровней
временного ряда по 4 соседним кварталам, каждый раз продвигаясь вперед на 1 шаг
- вычисляем скользящую среднюю:
CCk = 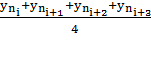
k = 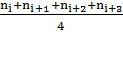
где 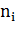 -
номер квартала
-
номер квартала
Для первых 4 кварталов:
k = 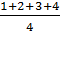 =
2,5
=
2,5
CCk
= 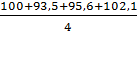 =
97,8
=
97,8
Затем оцениваем квартальные (сезонные)
компоненты
Аддитивные: Sадд
=
у - ЦCC
Мультипликативные: Sмульт
= у/ЦСС
Дальнейшие расчеты произведем в Excel:
|
Выравнивание исходного ряда и
|
|
оценка сквартальных компонент
|
|
№
|
У
|
СС
|
ЦСС
|
Sa=y-ЦСС
|
Sм=y/ЦСС
|
|
1
|
100
|
|
|
|
|
|
2
|
93,5
|
|
|
|
|
|
3
|
95,6
|
97,8
|
97,8
|
-2,2
|
0,97751
|
|
4
|
102,1
|
97,8
|
97,8
|
4,3
|
1,04397
|
|
5
|
107,8
|
99,75
|
98,775
|
9,025
|
1,09137
|
|
6
|
96,3
|
100,45
|
100,1
|
-3,8
|
0,96204
|
|
7
|
95,7
|
100,475
|
100,463
|
-4,7625
|
0,95259
|
|
8
|
98,2
|
99,5
|
99,9875
|
-1,7875
|
0,98212
|
|
9
|
105,1
|
98,825
|
99,1625
|
1,05988
|
|
10
|
99,3
|
99,575
|
99,2
|
0,1
|
1,00101
|
|
11
|
98,9
|
100,375
|
|
|
|
|
12
|
101,9
|
|
|
|
|
|
Итого
|
1194,4
|
|
|
6,8125
|
8,07048
|
|
Средняя
|
99,5333
|
|
|
|
|
Сезонная составляющая изменяется от квартала к
кварталу, поэтому вычисляем усредненные величины за период наблюдения. Для
этого просуммируем S отдельно за
каждый квартал и находим их средние значения. Кроме того, в моделях с
квартальной компонентой обычно полагают, что сезонные воздействия за год должны
нивелировать друг друга. В случае построения аддитивной модели сумма
квартальных компонент должна быть нулевой. Так как на самом деле сумма
отличается от нуля необходимо произвести коррекцию:
Кадд = 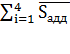
 0
Þ
kадд =
Кадд /4 Þ Sадд
=
0
Þ
kадд =
Кадд /4 Þ Sадд
=
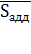 -
kадд
-
kадд
Разделим 12 кварталов на 3 года
Расчет сезонной аддитивной модели
|
1
|
2
|
3
|
4
|
Итого
|
|
1 год
|
|
|
-2,2
|
4,3
|
|
|
2 год
|
9,025
|
-3,8
|
-4,7625
|
-1,7875
|
|
|
3 год
|
5,9375
|
0,1
|
|
|
|
|
Итого
|
14,9625
|
-3,7
|
-6,9625
|
2,5125
|
|
|
Среднее
|
4,9875
|
-1,2333
|
-2,3208
|
0,8375
|
2,27083
|
|
S
|
4,41979
|
-1,801
|
-2,8885
|
0,26979
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поправка
|
0,56771
|
|
|
|
|
Здесь корректирующая поправка kадд
=2,27083/4
=0,56771
В мультипликативной модели сумма квартальных
компонент должна быть равна числу периодов кварталов
Кадд = 
 4
Þ
kадд =
4/Кадд Þ Sмульт
=
4
Þ
kадд =
4/Кадд Þ Sмульт
=
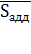 *
kадд
*
kадд
Расчет сезонной мультипликативной модели
|
1
|
2
|
3
|
4
|
Итого
|
|
1 год
|
|
|
0,97751
|
1,04397
|
|
|
2 год
|
1,09137
|
0,96204
|
0,95259
|
0,98212
|
|
|
3 год
|
1,05988
|
1,00101
|
|
|
|
|
Итого
|
2,15125
|
1,96305
|
1,9301
|
2,02609
|
|
|
Среднее
|
0,71708
|
0,65435
|
0,64337
|
0,67536
|
2,69016
|
|
S
|
1,06623
|
0,97295
|
0,95662
|
1,0042
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поправка
|
1,4869
|
|
|
|
|
Корректирующий множитель: kадд
=
4/2,69016 = 1,4869.
За исследуемый промежуток времени максимальный
объем товарооборота приходится на 5-ый квартал и составляет 107,8 %.
3. Нахождение тренда
Сформируем динамические ряды, в которых
исключаем сезонную компоненту из наблюдений для аддитивной модели (y
- S) и для
мультипликативной модели (y/S)
и найдем для них уравнения линейного тренда Т = a
+ bt, где в качестве независимой
переменной выступает фактор времени t
- текущий номер квартала. Параметры тренда определяются МНК или при помощи
встроенных функций в Excel:
КОРРЕЛ() для определения коэффициента корреляции; ОТРЕЗОК() - свободного члена
в линейном уравнении тренда; НАКЛОН() - коэффициента регрессии.
|
Расчет линейного тренда
|
|
№ кв
|
у
|
Аддитивная модель
|
Мультипликативная модель
|
|
|
Sадд
|
у-Sадд
|
Тадд
|
Sмульт
|
у/S мульт
|
Тмульт
|
|
1
|
100
|
4,41979
|
95,580208
|
97,1946
|
1,06623
|
93,7884
|
96,8709
|
|
2
|
93,5
|
-1,801
|
95,301042
|
97,6198
|
0,97295
|
96,0993
|
97,3625
|
|
3
|
95,6
|
-2,8885
|
98,488542
|
98,0451
|
0,95662
|
99,9351
|
97,8541
|
|
4
|
102,1
|
0,26979
|
101,83021
|
98,4703
|
1,0042
|
101,673
|
98,3457
|
|
5
|
107,8
|
4,41979
|
103,38021
|
98,8955
|
1,06623
|
101,104
|
98,8374
|
|
6
|
96,3
|
-1,801
|
98,101042
|
99,3207
|
0,97295
|
98,9771
|
99,329
|
|
7
|
95,7
|
-2,8885
|
98,588542
|
99,7459
|
0,95662
|
100,04
|
99,8206
|
|
8
|
98,2
|
0,26979
|
97,930208
|
100,171
|
1,0042
|
97,7896
|
100,312
|
|
9
|
105,1
|
4,41979
|
100,68021
|
100,596
|
1,06623
|
98,5716
|
100,804
|
|
10
|
99,3
|
-1,801
|
101,10104
|
101,022
|
0,97295
|
102,061
|
101,295
|
|
11
|
98,9
|
-2,8885
|
101,78854
|
101,447
|
0,95662
|
103,385
|
101,787
|
|
12
|
101,9
|
0,26979
|
101,63021
|
101,872
|
1,0042
|
101,474
|
102,279
|
|
КОРРЕЛ
|
|
0,5932121
|
|
|
0,65119
|
|
|
ОТРЕЗОК
|
|
96,769413
|
|
|
96,3793
|
|
|
НАКЛОН
|
|
0,4252185
|
|
|
0,49161
|
|
Таким образом, получаем следующие линейные
тренды:
Тадд = 96,7694 + 0,4252 tмульт
= 96,3793 + 0,4916 t
4. Для оценки качества и сравнения двух
моделей вычисляем теоретические значения уровней ряда (T
+ S) и (T*S),
абсолютные ошибки еадд = у - ( T
+ S), eмульт
=
у/(T*S),
ошибки аппроксимации А и средние значения.
|
Расчет абсолютных и относительных
ошибок
|
|
№ кв
|
аддитивная модель
|
мультипликативная модель
|
|
T+S
|
/e/
|
e^2
|
A
|
T*S
|
/e/
|
e^2
|
A
|
|
1
|
101,614
|
1,61442
|
2,60636
|
1,61442
|
103,287
|
0,96818
|
0,93737
|
0,96818
|
|
2
|
95,8188
|
2,31881
|
5,37687
|
2,48001
|
94,7291
|
0,98703
|
0,97422
|
1,05564
|
|
3
|
95,1565
|
0,44347
|
0,19667
|
0,46388
|
93,6093
|
1,02127
|
1,04298
|
1,06827
|
|
4
|
98,7401
|
3,35992
|
11,2891
|
3,29081
|
98,7585
|
1,03384
|
1,06882
|
1,01257
|
|
5
|
103,315
|
4,4847
|
20,1126
|
4,16021
|
105,383
|
1,02293
|
1,04639
|
0,94892
|
|
6
|
97,5197
|
1,21968
|
1,48763
|
1,26654
|
96,6423
|
0,99646
|
0,99293
|
1,03474
|
|
7
|
96,8574
|
1,1574
|
1,33958
|
1,20941
|
95,4905
|
1,00219
|
1,00439
|
1,04723
|
|
8
|
100,441
|
2,24095
|
5,02187
|
2,28203
|
100,733
|
0,97485
|
0,95034
|
0,99272
|
|
9
|
105,016
|
0,08383
|
0,00703
|
0,07976
|
107,48
|
0,97786
|
0,9562
|
0,93041
|
|
10
|
99,2206
|
0,07944
|
0,00631
|
0,08
|
98,5556
|
1,00755
|
1,01516
|
1,01466
|
|
11
|
98,5583
|
0,34172
|
0,11678
|
0,34553
|
97,3716
|
1,0157
|
1,03164
|
1,02699
|
|
12
|
102,142
|
0,24183
|
0,05848
|
0,23732
|
102,708
|
0,99213
|
0,98433
|
0,97364
|
|
Итого
|
|
17,5862
|
47,6192
|
17,5099
|
|
12
|
12,0048
|
12,074
|
|
Среднее
|
|
1,59874
|
|
1,59181
|
|
1,09091
|
|
Soct/Sобщ
|
|
|
0,15397
|
|
|
|
0,08337
|
|
|
R^2
|
|
|
0,84603
|
|
|
|
0,91663
|
|
По результатам вычислений очевидно, что лучшей
является мультипликативная модель с меньшими ошибками и большим коэффициентом
детерминации.